Phase transfer catalysts between polar and non-polar media: a molecular dynamics simulation of tetrabutylammonium iodide at the formamide/hexane interface

Abstract

A molecular dynamics simulation of tetrabutylammonium iodide (TBAI) in the free liquid surface of formamide (FA) and in the interface of formamide and hexane (HX) was performed. TBAI was treated as 18 sites in a flexible model, five sites were employed for formamide and six for hexane. The simulation lasted 425 ps for each system at 300 K. Dynamic and orientational properties of both systems are discussed. The thickness of the polar/non-polar interface amounts to 10–14 Å. Furthermore, the anion moves over large distances in the polar phase whereas the cation remains in the interface. Penetration into the non-polar liquid is not observed for either ionic species. Only a minor influence of the salt on the orientation of formamide, which is preferential at the surface compared with the bulk, is observed and a minor effect on the length distribution of the hexane as a measure of the coiled or elongated arrangement is found.

---

1 Introduction

In synthetic organic chemistry, transfer reactions between organic and inorganic phases often have to be catalysed. The basic concepts in this field of phase transfer catalysis (PTC) have been described by Makosza and Serafinowa,¹ Starks² and Brändström.³ Different catalysts differ in their efficiency, i.e., the ionic transfer rate; an overview was given by Dehmlow and Dehmlow.⁴ One class of reagents regarded as most effective is the tetraalkylonium salts, and extensive studies have been carried out of different properties such as activity coefficients,⁵ osmotic coefficients,⁶ solution behaviour,⁷ surface tension⁸ and Raman⁹ and NMR spectra.¹⁰

The fact that the anions are hydrophilic and the cations are hydrophobic owing to their CH₂/CH₃ groups in polar solvents was described in terms of electric double layers, a concept based on the work of Helmholtz,¹¹ Gouy,^12,13 Chapman¹⁴ and Stern.¹⁵ It gave rise to the question in which phase the catalytic process itself would take place. Some studies^2,16 suggested the cation as phase transferring whereas this was attributed to the anion in others.^17,18

In PTC, two substances each in one separate phase (polar⇌non-polar) react with each other in the presence of a catalytic reagent. The place of interest is therefore the phase boundary between the polar and non-polar solvent with an embedded salt.

Experimental methods sensitive for the interphase region were therefore applied for clarification. Electron spectroscopy fulfils this demand because of the low mean free path of the electrons of up to only a few nanometres. This technique was adapted for liquid surfaces in 1973 by Siegbahn and Siegbahn [X-ray photoelectron spectroscopy (XPS), electron spectroscopy for chemical analysis (ESCA)].¹⁹ A first investigation of phase transfer catalysts was performed by Ballard et al. using ultraviolet photoelectron spectroscopy (UPS),²⁰ and subsequently more detailed studies were carried out by Siegbahn and co-workers.^21–25 Another electron spectroscopic technique was presented by Keller et al. in 1986,²⁶viz., metastable induced electron spectroscopy (MIES), which is highly surface sensitive owing to the repulsive interaction potential, meaning that excited helium atoms (having thermal kinetic energies and an electronic energy of 19.8 eV in the triplet state) cannot penetrate into the liquid. The spectra therefore yield information on the outermost surface layers. The PTC reagent tetrabutylammonium iodide has been investigated using MIES.^27,28 A summary of results on all phase transfer catalysts explored with MIES so far was recently given by Oderbrodhage.²⁹

This high surface sensitivity of electron spectroscopy means in this case that an interface between two solvents cannot be accessed because the polar liquid is covered by the second liquid with a macroscopic thickness. All studies applying electron spectroscopy therefore have to be carried out at a liquid/vacuum interface which serves as a model system for the real situation.

Owing to this experimental restriction, the aim of the present study was to use molecular dynamics computer simulation to study the behaviour of one phase transfer catalyst between two different solvents. This was performed in two main steps. In the first, the surface of formamide (HCONH₂) (FA) enriched with tetrabutylammonium iodide [(C₄H₉)₄NI] (TBAI) was simulated. Subsequently hexane (C₆H₁₄) (HX) molecules were adsorbed from the gas phase. This configuration was kept together by two compressing walls below the formamide and above the hexane for equilibration. The second step was performed by removing the restricting walls, simulating a free slab of this two-phase system. Different properties of all three conditions were then compared.

In Section 2, details of the simulation and potential parameters are outlined, Section 3 deals with results on different orientational and dynamic properties of the two systems and these are discussed in Section 4.

2 The model system and simulation parameters

2.1 Simulation parameters

The interaction potentials used consist of two parts, intermo lecular and intramolecular. The parameters for the respective molecules listed in Tables 1–4 were adapted from the GROMOS force field.³⁰ The interaction within one molecule is constituted by bending, stretching and dihedral contributions. Furthermore, Lennard-Jones interaction between different atomic sites can explicitly be rejected and a specific Coulomb term can be taken into account:

Table 1 Parameters of formamide moleculea

Atoms: 5
Atom	na	Mass/u	Charge (e)	√ C12/(eV Å^12)^1/2	√ C6/(eV Å^6)^1/2
C	1	13	0.50	425.38	7.752
O	2	16	−0.50	128.41	4.951
N	3	14	−0.85	202.42	5.897
H2	4	1	0.425	0.00	0.0
H3	5	1	0.425	0.00	0.0

---

Stretching: 4
na 1	na 2	b0/Å	kb/eV Å^−2
1	2	1.229	52.07
1	3	1.335	43.39
3	4	0.960	38.83
3	5	0.960	38.83

---

Bending: 4
na 1	na 2	na 3	Θ0 (°)	kΘ/eV°^−1
2	1	3	122.90	5.207
1	3	4	119.80	3.037
1	3	5	119.80	3.037
4	3	5	120.40	3.471

---

Dihedrals: 2
na 1	na 2	na 3	na 4	a0	a1	a2	a3	a4	a5
a na=number of atoms.
2	1	3	5	0.4339	0	−0.4339	0	0	0
2	1	3	4	0.4339	0	−0.4339	0	0	0

---

Table 2 Parameters of tetrabutylamoniumiodide molecule^a

Atoms: 18
Atom	na	Mass/u	Charge (e)	√ C12/(eV Å^12)^1/2	√ C6/(eV Å^6)^1/2
N^+	1	14	−0.56	202.43	5.897
CH2	2	14	0.39	507.35	8.520
CH2	3	14	0	507.35	8.520
CH2	4	14	0	507.35	8.520
CH3	5	15	0	618.08	10.380
o	o	o	o	o	o
I^−	18	127	−1	4795	30.970

---

Stretching: 22
na 1	na 2	b0/Å	kb/eV Å^−2	na 1	na 2	b0/Å	kb/eV Å^−2
a Parameters are listed for only one of the four alkyl branches. na=number of atoms.
1	2	1.51	70	3	4	1.52	34.703
2	3	1.52	34.703	4	5	1.54	34.703

---

Table 3 Parameters of tetrabutylamonium iodide molecule (second part)^a

Bending: 12, parameters apply for all bending interactions
na 1	na 2	na 3	Θ0 (°)	kΘ/eV°^−1
1	2	3	109.47	2.601

---

Dihedrals: 8, parameters apply for all dihedral interactions
na 1	na 2	na 3	na 4	a0	a1	a2	a3	a4	a5
1	2	3	4	0.09617	−0.125986	−0.135982	0.031712	0.271965	0.3264265

---

Excluded Lennard-Jones J: 12
na 1	na 2	na 1	na 2	na 1	na 2
2	7	2	11	2	15
6	3	6	11	6	15
10	3	10	7	10	15
14	3	14	7	14	11

---

Included Coulomb: 6
na 1	na 2	na 1	na 2	na 1	na 2
a na=number of atoms.
18	1	18	2	18	6
18	10	18	14

---

Table 4 Parameters of hexane molecule^a

Atoms: 6
Atom	na	mass/u	charge (e)	√ C12/(eV Å^12)^1/2	√C6/(eV Å^6)^1/2
CH3	1	15	0	618.08	10.380
CH2	2	14	0	507.35	8.520

---

Stretching: 5, parameters apply for all stretching interactions
na 1	na 2	b0/Å	kb/eV Å^−2
1	2	1.54	34.703

---

Bending: 4, parameters apply for all bending interactions
na 1	na 2	na 3	Θ0 (°)	kΘ/eV °^−1
1	2	3	109.47	2.601

---

Dihedrals: 3, parameters apply for all dihedral interactions
na 1	na 2	na 3	na 4	a0	a1	a2	a3	a4	a5
1	2	3	4	0.09617	−0.125986	−0.135982	0.031712	0.271965	0.326426

---

Excluded Lennard-Jones: 2
na 1	na 2
a na=number of atoms.
1	5
2	6

---

Table 5 Diffusion constants (Ų ps⁻¹)

bx	by	bz	isx	isy	isz	osx	osy	osz
FA—
System 1	0.1345	0.1378	0.1284	0.1496	0.1621	0.1318	0.1840	0.2523	0.1604
System 2	0.3413	0.3074	0.3273	0.3208	0.2986	0.2901	0.5461	0.5541	0.3912
HX—
System 2	0.3549	0.3632	0.2973	0.3633	0.3186	0.2681	0.6604	0.5658	0.6033
TBAI—
System 1	0.0728	0.1188	0.0544
System 2	0.1401	0.1354	0.1142
N(TBAI)—
System 1	0.1485	0.1685	0.0702
System 2	0.1366	0.1132	0.0893
I(TBAI)—
System 1	0.0785	0.0870	0.0450
System 2	0.2020	0.1704	0.1090

---

Scheme 1

Formamide, shown in Fig. 1, is represented by a five-site model. H1 is condensed into the carbon atom and not treated explicitly. For the TBAI molecule (Fig. 2) CH₃ and CH₂ g roups of the alkyl chains are also taken as one site each. Between the I⁻ and the remaining cation, no preferential distance is given. It can move freely, only coupled by Coulomb forces. This is important in order to investigate the behaviour of both ionic species seperately. In the case of hexane (Fig. 3) the same applies as for the butyl tetrahedron: CH₃ and CH₂ groups are represented as one site.

Fig. 1 Formamide, the polar solvent simulated.

Fig. 2 Tetrabutylammonium iodide (TBAI), the PTC catalyst studied as reference system with MIES.

Fig. 3 The hexane molecule simulated as a non-polar phase.

The support planes used to keep the system in a planar geometry during the equilibration are mirror planes with Lennard-Jones centers at the (x, y, −z)-position of the respective simulated site. Simulation of a free liquid surface was realized with periodic boundary conditions in x and y (the surface plane) with a size of (25.8 Å)². The walls in z perpend icular to the surface have a distance of 1000 Å. Since this geometry is in principle periodic in z, an Ewald summation was not carried out because the number of k-vectors to be calculated would have been high. Instead, a shiftet force algorithm was used with a cut-off distance of 9.5 Å for van der Waals interaction and 11.5 Å for the Coulomb part, respectively. A 0.5 fs time step and neighbour list updated every tenth step were used. The final runs were all performed with a fixed temperature of 300 K.

2.2 Setting up the ensembles

In system 1, the slab of formamide contains 256 molecules. Four TBAI molecules were adsorbed from the gas phase via a start velocity in the −z direction towards the formamide/vacuum interface. This two-component system was then equilibrated for 200 ps. Subsequently, three runs of 142 ps each were performed to evaluate the data presented in the next section. They reveal information of a free surface of FA (named FA/vacuum interface) and FA with embedded salt (named FA–TBAI/vacuum interface).

The three-component system of FA, TBAI and HX was built up from system 1 by adding 256 hexanes as a grid of 8×8×4 above the FA+TBAI surface. Below the formamide slab, i.e. the FA/vacuum interface without salt, a support plane was installed in order to keep the lower boundary fixed. A second support plane above the hexane was lowered with a velocity of 0.7 Å ps⁻¹ condensing the gas-phase hexane until both planes had a distance of 96 Å. With fixed support planes an equilibration of 177 ps was performed before the system was compressed further to a thickness (better: distance of the support planes) of 77 Å. As for system 1, three runs of 142 ps duration each were used for further equilibration.

In order to simulate a free liquid bilayer with enclosed salt in system 2, the support planes were set to a distance of 109 Å and equilibrated for further 282 ps. Subsequently the planes were removed totally and in a test run of 35 ps the stability of the system was found to be satisfactory. No evaporation or broadening was observed. In three runs of 142 ps each different results presented in the next section were obtained for three different interfaces: formamide/vacuum (lower surface), th e FA–TBAI/hexane interface with embedded salt (inner surface) and the hexane/vacuum interface (upper suface).

In addition to the interfaces mentioned above, we also looked at the behaviour of the liquid bulk phases of FA and HX not influenced by either the interface with vacuum or by embedded TBAI.

3 Results

3.1 System 1: formamide+tetrabutylammonium iodide

Fig. 4 shows the depth profile of the solution of TBAI in formamide. Since we are especially interested in the salt behaviour, only the interface region is enlarged in the plot. The line labeled FA represents the formamide contribution. TBAI denotes the sum over all 18 sites of the salt, N⁺ the nitrogen contribution representing the central atom of the cation and I⁻ the anion depth distribution. The signals for TBAI, N⁺ and I⁻ are enlarged in the y-direction for clarity.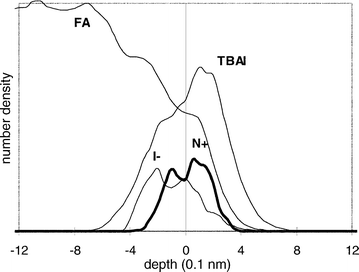

Fig. 4 Particle number density for the FA–TBAI/vacuum interface.

The density profile of the complete salt which is dominated by the hydrocarbon chains (16 of 18 sites) reflects the hydrophobicity of the cation: the butyl tetrahedron has a tendency to be positioned in the outermost surface layer. N⁺ and I⁻ show slightly different behaviour. As the central atom of the cation, the nitrogen more or less resembles the number density profile of the entire molecule. In contrast, the centre of the anion distribution is shifted away from the surface towards the bulk phase of formamide.

The mobility of the different species was the next value to be analysed. As a measure for the translational dynamics the mean square displacement in all three directions was used, defined by

Fig. 5 shows the mean square displacement for the solvent formamide. For t→∞ the slope equals the diffusion constant. The three different lines represent the motion in the three Cartesian directions. The resulting diffusion values are listed in Table 5. The rows b_x, b_y, b_z represent bulk values in the x-, y- and z-directions, is_xyz denotes the inner surface and os_xyz denotes the outer surface values. Diffusion constants are given for FA, HX, TBAI and for the central cation atom and the anion separately. System 1 is the case without hexane and system 2 is the free liquid slab with polar and non-polar phases.

Fig. 5 Mean square displacement.

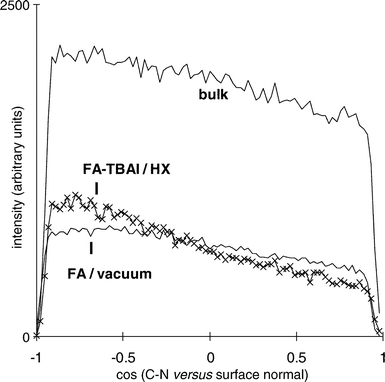
The orientation of the formamide molecule depending on its location (bulk or surface) was the next feature to be evaluated. As representive of the C–N bond, the FA backbone, was taken. Fig. 6 shows its orientation with respect to the surface normal, the z-axis. The values for the interfaces are normalized to each other for better comparison. For the bulk region an equal angular distribution is found. The molecules which are affected neither by the liquid/vacuum interface nor by the presence of the salt in the other surface are randomly oriented. Formamide in the interfacial regions deviates from the equal distribution and reveals a preferential orientation. A cosine of −1 on the left on the abscissa denotes a C–N bond perpendicular to the surface with nitrogen pointing towards the liquid and the C-atom exposed to vacuum and vice versa for a cosine of 1 on the right. In both interfaces the formamide shows a tendency to point the HCO group out of the liquid wherea s the NH₂ group is closer to the liquid. In a simulation of pure formamide³¹ the same behaviour could be seen. This tendency is found both for the outer salt free surface and for the so-called inner surface enriched with salt. The effect is more pronounced in the FA–TBAI/vacuum interface. Both distributions also differ for molecules lying more or less parallel in the surface plane (cosine≈0). Their amount in the FA–TBAI/vacuum interface is lower compared with the FA/vacuum interface.

Fig. 6 Orientation of the C–N bond of formamide with respect to the surface normal (z-axis). Values for the interfaces are normalized to each other.

3.2 System 2: formamide+tetrabutylammonium iodide+hexane

The free liquid slab without confinements exhibits a depth profile as shown in Fig. 7. The interfacial region with co-existence of FA and HX extends over ∽14 Å. The TBAI and central cation atom distribution are located at the same position, whereas the anion behaviour shows drastic changes compared with the other systems investigated: I⁻ is traced over distances of more than 20 Å and shows a clear tendency to move from the interface towards the bulk region of the polar solvent.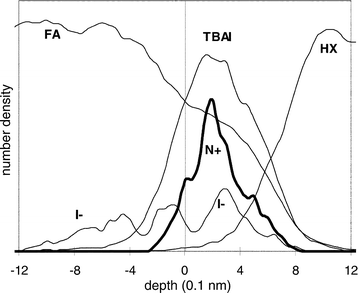

Fig. 7 Particle number density for the FA–TBAI/hexane interface.

The presence of the anion has an influence on the molecular orientation (Fig. 8). In both inner and outer surfaces the formamide HCO group protrudes from the liquid. Again this effect is stronger in the salt enriched interface. In contrast to system 1, a preferential orientation can also be found for bulk formamide.

Fig. 8 Orientation of the C–N bond of formamide with respect to the surface normal (z-axis). Values for the interfaces are normalized to each other.

The relaxed situation in the free liquid slab is reflected by the length distribution of the hexane as shown in Fig. 9. The favoured configuration is elongated hexane molecules. Only the interface with FA contains a larger amount of coiled hexane. The number of trans configurations within one hexane molecule shown in Fig. 10 also indicates the highest percentage of stretched HX in the surface exposed to vacuum.

Fig. 9 Length distribution of hexane.

Fig. 10 Number of trans configurations in the hexane molecules.

4 Discussion

This study was aimed at elucidating the behaviour of tetrabutylammonium ions and the respective anion located at the interface of a polar (formamide) and a non-polar (hexane) liquid. For system 1 with FA+TBAI, one finding is that the molecular mobility of the formamide in the free surface region is between 25 and 83% higher than in the bulk phase for the three Cartesian coordinates. Within the salt enriched surface FA moves with only 64–82% of the value for the salt free region. For the salt it can be stated that the mean square displacement is roughly 20% of the formamide value. The comparatively large TBAI molecule is slow compared to the solvent. This might be due to the H-bonded network which is known to exist for this solvent.

The situation is changed by the presence of the alkane in the second system investigated: the mean square displacement of formamide is enhanced by a factor between 1.8 and 2.9. This is interpreted as being due to a disturbance of the H-bonded formamide network by the alkane.

The depth profiles demonstrate several facets. The overlap of organic and inorganic phases that can be interpreted as the interface thickness amounts to about 10–14 Å. A molecular dynamic study of ion transfer over a water/1,2-dichloroethane interface reported by Benjamin³² provides values of ∽10 Å. The second feature is a different centre of the cationic and anionic distribution. This finding is in line with models treating platinum catalysts in terms of electric double layers.

Neither ionic species protrudes into the non-polar phase. This is in accordance with Benjamin's result³² that the ion transport across the interface of two immiscible liquids is an activated rather than a simple diffusive process. The present simulation cannot clarify whether diffusion never occurs owing to the limited time and volume taken into account in the calculations. However, the probability is clearly low compared with ion movement within the non-polar medium.

In a molecular dynamics study of tetramethylammonium chloride in aqueous solutions,³³ the authors found only minor influences of salt molecules on the structure of the solvent. In the present work it is shown that the preferential orientation of formamide is slightly pronounced by TBAI molecules which strengthen the ordering of the formamide surface. In the FA–TBAI/HX interface one finds a higher percentage of co iled hexane molecules than in the bulk phase, their amount being even lower in the XH/vacuum interface.

References

1. M. Makosza and B. Serafinowa, Rocz. Chem., 1965, 39, 1223.
2. C. M. Starks, J. Am. Chem. Soc., 1971, 93, 195.
3. A. Brändström, Preparative Ion Pair Extraction, an Introduction to Theory and Practice, Apotekorsocieteten, Hässle Läkemedel, Stockholm, 1974..
4. E. V. Dehmlow and S. S. Dehmlow, Phase Transfer Catalysis, Verlag Chemie, Weinheim, 3rd edn., 1993..
5. H. S. Frank, J. Phys. Chem., 1963, 67, 1554.
6. S. Lindenbaum and G. E. Boyd, J. Phys. Chem., 1964, 68(4), 911.
7. R. M. Diamond, J. Phys. Chem., 1963, 67(4), 2513.
8. K. Tamaki, Bull. Chem. Soc. Jpn., 1974, 47, 2764.
9. S. Koda, J. Goto, T. Chikusa and H. Nomura, J. Phys. Chem., 1989, 93, 4959.
10. M. Krell, M. C. R. Symons and J. Barthel, J. Chem. Soc., Faraday Trans. 1, 1987, 83, 3419.
11. H. Helmholtz, Wied. Ann. Phys., 1879, 7, 337.
12. G. Gouy, J. Phys., 1910, 9, 457.
13. G. Gouy, Ann. Phys., 1917, 7, 129.
14. D. L. Chapman, Philos. Mag., 1913, 25, 475.
15. O. Stern, Z. Electrochem., 1924, 30, 508.
16. C. M. Starks and R. M. Owens, J. Am. Chem. Soc., 1973, 95, 3613.
17. A. Brändström, Adv. Phys. Org. Chem., 1977, 15, 267.
18. D. Landini, A. Maia and F. Montanari, J. Chem. Soc., Chem. Commun., 1977, 112.
19. H. Siegbahn and K. Siegbahn, J. Electron Spectrosc. Relat. Phenom., 1973, 2, 319.
20. R. E. Ballard, J. Jones and E. Sutherland, Chem. Phys. Lett., 1984, 112(4), 310.
21. S. Holmberg, R. Moberg, Z. Cai Yuan and H. Siegbahn, J. Electron Spectrosc. Relat. Phenom., 1986, 41, 337.
22. S. Holmberg, Z. Cai Yuan, R. Moberg and H. Siegbahn, J. Electron Spectrosc. Relat. Phenom., 1988, 47, 27.
23. R. Moberg, F. Bökman, O. Bohman and H. O. G. Siegbahn, J. Am. Chem. Soc., 1991, 113, 3663.
24. F. Bökman, O. Bohman and H. O. G. Siegbahn, J. Phys. Chem., 1992, 96, 2278.
25. F. Bökman, O. Bohman and H. O. G. Siegbahn, Acta Chem. Scand., 1992, 46, 403.
26. W. Keller, H. Morgner and W. A. Müller, Mol. Phys., 1986, 57, 623.
27. H. Morgner, J. Oberbrodhage, K. Richter and K. Roth, J. Phys.: Condens. Matter, 1991, 3, 5639.
28. H. Morgner and J. Oberbrodhage, J. Phys.: Condens. Matter, 1995, 7, 7427.
29. J. Oberbrodhage, J. Electron Spectrosc. Relat. Phenom., 1998, 95, 171.
30. W. F. van Gunsteren and H. J. Berendson, GROMOS Library Manual, Biomos, Groningen, 1987..
31. J. Oberbrodhage, H. Morgner, O. Tapia and H. Siegbahn, Int. J. Quantum Chem., 1997, 63, 1123.
32. I. Benjamin, Science, 1993, 261, 1558.
33. E. Hawlicka and T. Dlugoborski, Chem. Phys. Lett., 1997, 268, 325.

---