Effect of matrix and substituent on the electronic structure of trapped benzene radical cations

Abstract

The structure and dynamics of the radical cations produced from benzene, monodeuterated benzene and toluene in various low-temperature matrices were characterized by EPR and ENDOR spectroscopy. It was found that the nature of the matrix had a dramatic effect on the EPR spectra of benzene cation. Rigid structures corresponding to the ²B_1g and ²B_2g states are revealed in solid argon and halocarbon (CFCl₃) matrices, respectively, whereas only dynamically averaged patterns are observed in other hosts used (krypton, xenon, sulfur hexafluoride). Deuterium monosubstitution has no appreciable effect on the cation structure observed in argon and halocarbon matrices, which implies matrix control of the preferred electronic state. In contrast, the toluene radical cation exhibits only a ²B_2g-like structure both in argon and in CFCl₃ matrices, that is, the internal structural effect strongly predominates over environment effects in this case. The results are discussed in qualitative terms taking into consideration the matrix and substituent effects on the charge distribution in benzene cation.

---

Introduction

Benzene radical cation, one of the simplest highly symmetrical molecular ions, is a fundamentally important species from spectroscopic and chemical points of view. Spectroscopic studies of benzene cation and its analogues provide unique information on the static and dynamic structural distortions and related matrix effects for symmetrical systems in condensed media. The basic Jahn–Teller distortion resulting from vibronic coupling removes orbital degeneracy of the ²E_1g state to yield two states with a lower symmetry. The characteristic vibronic level structure has been studied in detail for a number of symmetrically substituted halobenzene radical cations using optical absorption spectroscopy and laser-induced fluorescence (see, e.g., refs. 1–6). Recently, direct manifestation of the Jahn–Teller coupling for unsubstituted benzene cation was obtained in gas-phase experiments using high resolution zero kinetic energy (ZEKE) threshold photoionization spectroscopy.⁷ The latter study made it possible finally to draw conclusions about the shape of isolated C₆H₆^+• and its fluctionality (i.e., dynamics) yielding an apparent D_6h symmetry.

An obvious consequence of the static Jahn–Teller effect in the radical cation of benzene is loss of magnetic equivalence of the six protons in the distorted structures. The two Jahn–Teller states of D_2h symmetry denoted ²B_1g (acute minimum) and ²B_2g (obtuse minimum) are characterized by essentially different spin density distribution (Scheme 1) [in some work publications^7,8 these states are alternatively denoted ²B_2g (acute minimum, corresponding to ²B_1g in our notation) and ²B_3g (obtuse minimum, corresponding to ²B_2g in our notation)].

Scheme 1

In the case of b_2g SOMO, which is often described as ‘symmetrical orbital ’ (Ψ_s) regarding the symmetry with respect to the vertical C(1)–C(4) plane, the major spin density is located at C(1) and C(4). On the other hand, for b_1g SOMO (‘antisymmetric orbital ’, Ψ_A), the spin density is equally distributed between four carbon atoms at the 2, 3, 5 and 6 positions (although substituted benzene cations generally have lower molecular symmetry, using the terms ‘symmetrical ’ and ‘antisymmetric’ SOMO makes it possible to extend this consideration to benzene derivatives, if we assume that the SOMO is mainly confined to the aromatic ring π-system). As a result, the proton hyperfine coupling parameters are characteristic of the two states, and they should be readily distinguishable by magnetic resonance techniques, i.e., EPR and ENDOR.

EPR evidence for stabilization of the ²B_2g state of benzene radical cation in a halocarbon (CFCl₃) matrix at 4.2–77 K was first reported by Iwasaki et al. in 1983.⁹ The results of their studies clearly demonstrated major coupling with two protons at C(I) and C(4), while the other set of four protons revealed comparatively small hyperfine coupling, which is completely consistent with the Ψ_s nature of SOMO. Although the static distortion for C₆H₆^+• was unambiguously established,⁹ it is difficult to determine the role of matrix-assisted effect in stabilization of the specific state. Meanwhile, a number of EPR studies of benzene cation generated in the cavity-type matrices, such as silica gel, molecular sieves and zeolites, revealed only a dynamically averaged structure with six equivalent protons [α(6H)=0.43 mT] at temperatures down to 3.5 K.^10–14 The averaging results from rapid (on the EPR time-scale) rotation or pseudo-rotation of the cation about the sixfold symmetry axis.¹¹ This implies that stabilization of a rigid distorted structure of C₆H₆^+• in a CFCl₃ matrix at relatively high temperatures (up to 77 K) is due to matrix interaction. It is worth noting that theoretical calculations^8,14–17 gave contradictory results and predicted, in general, small difference in the energy of the isolated Jahn–Teller states (²B_1g and ²B_2g). Most important, direct experimental data obtained by ZEKE technique⁷ show a reverse energy ordering of the states under consideration (²B_1g below ²B_2g) and a very small barrier for pseudo-rotation (8 cm⁻¹, that is, only a few per cent of the zero-point energy of the Jahn–Teller active ν₆ bending mode). Thus, it seems highly probable that the matrix interactions may affect crucially not only the dynamic behavior of the cation, but also the relative stability of the two states in solid media. Furthermore, the EPR spectrum of the monodeuterated benzene cation (C₆H₅D^+•) generated on a silica gel gave an indication of possible stabilization of the rigid state characterized by the Ψ_A SOMO at the lowest attainable temperature (3.5 K).¹²

As the situation in the condensed phase was far from clear, we recently undertook a reinvestigation of the structure and dynamics of benzene radical cation in low-temperature matrices. The Linköping group obtained the ENDOR spectra of C₆H₆^+• in a CFCl₃ matrix. Taking the advantage of high resolution provided by this technique made it possible to determine accurate parameters of the hyperfine coupling tensor for all the protons.¹⁸ In general, the results are in complete accord with the conclusions of Iwasaki et al.⁹ concerning the Ψ_s character of SOMO that implies a ²B_2g ground state of the cation. In the most recent study by the Linköping group,¹⁹ a combination of EPR, ENDOR and ESEEM spectroscopy was applied to characterize the electronic structure and dynamics of C₆H₅D^+• and C₆D₆^+• in a CFCl₃ matrix; these studies also suggested Ψ_s-type SOMO for deuterium substituted benzene cation. The Moscow group first generated benzene radical cation in a solid argon matrix using the classical matrix isolation procedure.²⁰ In contrast with halocarbon matrix experiments, the predominating quintet EPR signal obtained in argon provides evidence for the Ψ_A nature of SOMO, which means a ²B_1g ground state. In this paper we present further analysis and a comparison of matrix effects on the structure of C₆H₆^+•, C₆H₅D^+• and C₆H₅CH₃^+• on the basis of EPR data. [When this paper was being prepared for publication, we became aware of a paper by Toriyama and Okazaki²¹ reporting evidence for stabilization of the ²B_2g distorted state of benzene radical cation in irradiated phenyl-substituted MCM-41 mesoporous silicates even at 77 K. Although the authors suggested that this result reflects intrinsic distortion of the cation (which seems to be in conflict with ZEKE and argon matrix studies), their findings on the role of the matrix in stabilization of the distorted state are in general agreement with our conclusions.]

Experimental

Reagent grade benzene and fluorotrichloromethane (CFCl₃) and high-purity argon, krypton and xenon (all >99.99%) were used as received. Sulfur hexafluoride (99.98%) was obtained from Halogen (Russia), and monodeuterated benzene C₆H₅D (>98%) was supplied by Aldrich.

The apparatus for EPR matrix isolation studies at the Karpov Institute has been described in detail previously.^22–24 An original laboratory-made cryostat with a vacuum resonator cavity was used. The rare gases containing typically 0.1 mol% of benzene were additionally doped with small amounts (0.2 mol%) of electron scavengers (CFCl₃ or CFCl₂CF₂Cl). The samples were prepared by slow controlled deposition of the gaseous mixtures on the tip of a cooled sapphire rod at a specially adjusted temperature (18–20 K for argon, 30–32 K for krypton, 45–50 K for xenon and sulfur hexafluoride). It should be noted that the rod used had a cylindrical shape with a truncated conical tip.²³ The deposited samples were visualized as small ‘bulbs’. In this case, the effect of partial orientation, which could have a certain significance for the spot-like samples obtained on a flat rod, appears to be negligible. After the deposition, the samples were irradiated with fast electrons (1.2 MeV) using an EG-2.5 Van de Graaff type accelerator to the total absorbed dose of ca. 20 kGy at 15–16 K. The EPR spectra were measured at 8–100 K using an X-band (9.4 GHz) spectrometer manufactured by SPIN (St. Petersburg, Russia).

The experimental procedure and setup used in Linköping have been described elsewhere.^14,19

Results

1. Matrix effects on the EPR spectra of C₆H₆^+•

Examples of the EPR spectra of benzene radical cations generated by irradiation of benzene in halocarbon, solid rare gas and cavity-type matrices and measured at temperatures below 20 K are shown in Fig. 1. The EPR spectrum of C₆H₆^+• in a CFCl₃ matrix taken at 15 K [Fig. 1(a)] exhibits an anisotropic triplet pattern, which is characteristic of the static yielding the Ψ_s SOMO.^19,18 On the other hand, the anisotropic quintet spectrum pattern observed in an argon matrix [Fig. 1(b)] can be attributed to stabilization of an alternative distorted structure characterized by the Ψ_A SOMO (a detailed discussion and simulation were presented previously).²⁰ In this case, it is worth noting that the spectrum observed immediately after irradiation at 16 K appears to result from a mixture of the two structures, but the quintet spectrum becomes predominant after annealing the sample at 30–34 K.²⁰ Note that this energy ordering of the two states is in general accord with that observed for benzene radical cation in the gas phase.⁷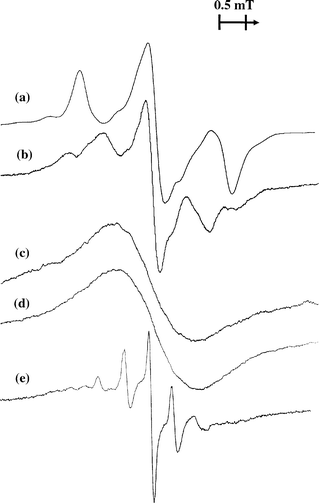

Fig. 1 EPR spectra of benzene radical cations measured at low temperatures in various solid media: (a) CFCl₃, 15 K; (b) argon, 16 K (the sample was annealed at 34 K for 5 min after electron irradiation at 16 K); (c) krypton, 10 K; (d) SF₆ , 12 K; and (e) H-ZSM-5 zeolite, 4 K. The cations were produced by X-radiation or fast electron irradiation.

The EPR spectra of C₆H₆^+• in all other matrices tested gave no conclusive evidence for static distortion of the cation. Indeed, the spectrum measured in an SF₆ matrix at 12 K shows a broadened signal (ΔH=1.5 mT) without defined structure [Fig. 1(d)]. Most probably, this spectrum is due to incomplete dynamic averaging (‘slow pseudo-rotation’). In the case of an SF₆ matrix, the spectrum exhibits only some reversible narrowing (to 1.2 mT) on increasing the measurement temperature up to 80 K. Further warming of the sample to 90–95 K results in reversible transformations of the spectrum, showing the appearance of some structure with a line separation of ca. 0.45 mT, which indicates a dynamically averaged structure. However, in the latter case, the signal from C₆H₆^+• is obscured by the presence of spurious lines arising from matrix radicals, which become narrow and intense in this temperature region.

A similar spectrum is observed in the case of the krypton matrix [Fig. 1(c)]. Again, the signal is as a virtually structureless singlet (ΔH=1.55 mT). Only slight reversible changes in the signal shape (narrowing) were observed upon variations in the measurement temperature between 10 and 50 K. As mentioned perviously,²⁰ the spectrum of C₆H₆^+• obtained in a xenon matrix at 16–70 K also exhibits a broadened singlet-like signal.

It is understood that the assignment of the broad structureless signals recorded in krypton, SF₆ and xenon matrices might seem rather speculative. Nevertheless, the observed linewidth of the signal envelope is just in line with that expected for C₆H₆^+•; a poorly resolved signal with a similar envelope was observed previously for C₆H₆^+• in a CFCl₂CF₂Cl matrix at intermediate temperature (77 K).⁹ Also, it is worth noting that the involvement of neutral radicals (i.e., phenyl or cyclohexadienyl) can be definitely excluded, because the signals from these species should have a larger total spread and could be easily detected if present in the spectrum. Furthermore, the hyperfine structure with a splitting of ca. 0.45 mT observed in the case of the SF₆ matrix at higher temperatures is actually characteristic of monomeric benzene radical cations (the dimeric cations, which also could be trapped, show half that splitting value, i.e., ca. 0.22 mT).

The case of ‘rapid pseudo-rotation’ resulting in complete dynamic averaging is illustrated well by the spectrum of C₆H₆^+• obtained in an H-ZSM-5 zeolite host at low temperatures [Fig. 1(e)]. A well resolved pattern of somewhat anisotropic narrow lines with a separation of 0.45 mT is characteristic of six equivalent protons (as is obvious, the outermost components of the expected septet are poorly detected because of their low intensity predicted by the binomial rule). Qualitatively similar spectra were observed previously for C₆H₆^+• in various cavity-type matrices in a wide temperature range.^10–14

Table 1 summarizes the available characteristics of C₆H₆^+• in various matrices. The isotropic proton hyperfine coupling constants are given, where possible, in order to illustrate the effective spin density distribution in different cases. It is worth noting that the rigid states are characterized by anisotropic proton hyperfine coupling tensors typical of α-protons, so the values given in Table 1 were derived from the analysis discussed previously.^9,18,20

Table 1 Data on hyperfine coupling parameters and structure of benzene radical cation in various solid matrices

Matrix	Temperature/ K	Isotropic hyperfine coupling constant/mT	Assignment of electronic state	Ref.
a See ref. 16 for detailed assignment of the proton hyperfine coupling tensors.b See ref. 17 for proton hyperfine coupling tensor.
CFCl3	4–77	0.90 (2H); 0.19 (4H)^a	^2B2g	9, 18
100	0.43 (6H)	Dynamically
averaged
Argon	8–39	0.64 (4H)^b	^2B1g	20
Krypton	10	Unresolved structure	Dynamic (?)	This work
Xenon	16	Unresolved structure	Dynamic (?)	20
SF6	12	Unresolved structure	Dynamic (?)	This work
93	0.45 (6H)	Dynamically
averaged
SiO2	77	0.43 (6H)	Dynamically	10–12
averaged
HY	3.5–203	0.43 (6H)	Dynamically	11, 12
averaged
H-ZSM-5,	4.2–180	0.45 (6H)	Dynamically	14, this
Na-ZSM-5	averaged	work

---

2. EPR of C₆H₅D^+• and C₆H₅CH₃^+• in an argon matrix

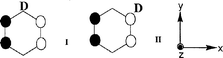
As described in a separate paper,¹⁹ both EPR and ENDOR data are consistent with favorable stabilization of the Ψ_S rigid distorted state of C₆H₅D^+• in a CFCl₃ matrix, which is similar to the ²B_2g state observed for C₆H₆^+•. Furthermore, the ratio of the two forms corresponding to D atoms occupying ‘low spin density’ and ‘ high spin density’ positions is very close to the statistically expected value (2:1).

Fig. 2(a) shows the EPR spectra of C₆H₅D irradiated in an argon matrix in the presence of an electron scavenger. The total spread of the spectra is close to that observed for C₆H₅D^+• in a CFCl₃ matrix,¹⁹ but the signal shape exhibits a marked difference. Whereas the EPR spectrum of the radical cation in CFCl₃ is clearly a superposition of doublet and triplet signals,¹⁹ the pattern observed in argon shows a poorly resolved structure, which seems to result from a larger number of superimposing components filling the spectral space. As discussed previously, the ground state of the C₆H₆^+• radical cation trapped in an argon matrix appears to be a ²B_1g state characterized by Ψ_A SOMO. If it is also true for C₆H₅D^+•, one should consider two possible forms of this species (I and II) with D occupying low and high spin density positions, respectively (Scheme 2).

Scheme 2

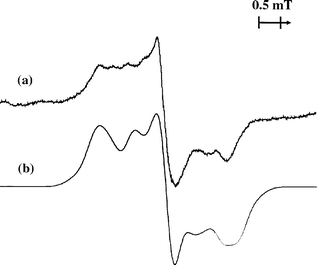Fig. 2 (a) EPR spectrum of the deposited mixture argon–C₆H₅D–CFCl₃ (1000:1:2) irradiated with fast electrons and measured at 16 K; (b) simulated spectrum for the 1:1 mixture of the forms I and II C₆H₅D^+• cations (Ψ_A SOMO). The simulation was carried out using an axially symmetrical g-tensor (g₁=g₂=2.0029; g₃=2.0023⁹) and the hyperfine coupling tensors given in Table 2.

The statistically expected abundance ratio of I to II is 1:2. Since deuterium hyperfine coupling is small enough, the EPR spectra of the two forms could be roughly described as quintet (form I, similar to C₆H₆^+•) and quartet (form II, one proton is ‘lost’).

Using the hyperfine coupling tensor parameters determined for C₆H₆^+•20 and taking into account the scaling factor of 6.51 for D nucleus (Table 2), we carried out a series of simulations, varying the ratio of I to II. Fig. 2(b) shows the simulated spectrum obtained for a ratio of 1:1, which appears to reproduce satisfactorily the envelope of the experimental spectrum. Although the component ratio could not be determined accurately from the simulation because of a number of uncertainties and oversimplifications, we may note that the abundance of the component with D in a low spin density position appears to be higher than its statistical weight.

Table 2 Hyperfine tensor parameters (in mT) and direction cosines used in EPR and ENDOR simulations for different forms of C₆H₅D^+•

				Direction cosines
Form	H/D position	Ai/mT	X	Y	Z
I	H(2, 3, 5, 6)	A1=−0.93	±0.5	0.8667	0
A2=−0.3	0.8667	±0.5	0
A2=−0.69	0	0	1
II	H(3, 5, 6)	A1=−0.93	±0.5	0.8667	0
A2=−0.3	−0.8667	±0.5	0
A3=−0.69	0	0	1
D(2)	A1=−0.143	±0.5	0.8667	0
A2=−0.046	−0.8667	±0.5	0
A3=−0.106	0	0	1

---

It is difficult to determine whether there is an admixture of the other electronic state (Ψ_S SOMO) from the spectrum of C₆H₅D^+• in an argon matrix. However, it should be noted that the spectrum shows only slight reversible changes upon warming the sample up to 35 K. Thus, in contrast to the case of C₆H₆^+•, we have no evidence for interconversion between two distorted structures as a result of trapping site relaxation.

The results obtained show that for both matrices substitution of one hydrogen atom for deuterium in benzene radical cation has little effect on the preferred electronic structure, which is controlled essentially by the nature of the matrix. It is of interest to follow the relationship between the effects of matrix and substituent for a stronger perturbation, which may result from alkyl substitution in the benzene ring. The simplest example of this kind is toluene radical cation. In the case of halocarbon matrices, the latter species exhibits a well defined spectrum resulting from the state characterized by Ψ_S SOMO.^25,26 To our knowledge, the EPR spectrum of toluene radical cation has still not been characterized in solid rare gas matrices. Fig. 3(a) shows the EPR spectrum of toluene irradiated in an argon matrix in the presence of an electron scavenger. The spectrum is very similar to those obtained previously for toluene cation in halocarbon hosts.^25–27 It is fairly well reproduced by simulation using the hyperfine coupling constants a(3H)=1.9 mT and a(1H)=1.3 mT [Fig. 3(b)]. The splitting is clearly due to methyl protons and the proton in a para-position, respectively. Hence, the ground state of C₆H₅CH₃^+• is characterized by the Ψ_S SOMO, independent of the matrix used.

Fig. 3 (a) EPR spectrum of the deposited mixture argon–toluene–CFCl₃ irradiated with fast electrons at 16 K; (b) simulated spectrum of toluene radical cation (see text for the hyperfine coupling constants).

Discussion

These EPR studies of benzene radical cations trapped in various solid hosts demonstrate remarkable matrix effects on the structure and dynamics of these species. The first step in understanding the observed peculiarities seems to be to sort out the different types of stabilization of the radical cations depending on the matrix structure and dominant interactions.

First, we may consider the ‘ cavity-type matrices’, where the radical cations are stabilized owing to isolation in pores or channels with rigid walls. Synthetic and natural zeolites represent the most important class of such hosts. The size and shape of cavities are strictly determined by the host matrix structure. If a guest molecule can be accommodated in the cavity, subsequent ionization will produce a loosely bound isolated radical cation. In this case, interaction with the matrix is assumed to be weak, and the dynamics of compact cations may be rapid enough even at very low temperatures. Actually, it is this situation that probably occurs for benzene radical cations in H-ZSM-5 zeolite. In principle, an electro static interaction with the cavity ‘walls’ may play a certain role in some zeolites, resulting in slowing of the dynamics and the appearance of a broad component, which has been detected in the EPR spectra of benzene cation in HY at the lowest temperatures.¹¹

The stabilization of benzene radical cation in low-temperature atomic and molecular matrices appears to be due to another kind of trapping process. In this case, a guest molecule can be treated as a ‘defect ’ replacing one or several atoms (molecules) in the host lattice. Certainly, such a substitution is accompanied by some deformation of the surrounding lattice, so the actual volume of disturbed matrix per guest molecule is fairly large. The configuration of traps may vary essentially depending on the size and shape of the guest molecule, and there is no longer simple direct matching between host and guest molecular geometry. Radical cations produced by ionization of the trapped molecules bear positive charge that induces electronic polarization of the surrounding matrix atoms or molecules. This electrostatic interaction appears to be the predominant factor determining the relative stability of different trap configurations, so the positive charge distribution in the radical cation is of crucial importance. Ionization of trapped molecules at low temperatures may produce a number of unrelaxed trap configurations, whereas subsequent annealing allows some reorganization to yield the most stable (equilibrium) trap configuration that means irreversible changes. The dynamics of the radical cations in low-temperature matrices observed by reversible changes in the EPR spectra are determined by the trap size and matrix ‘softness’ (both of these concepts are rather intuitive).

Among the low-temperature matrices, solid rare gases seem to represent a relatively simple case, because they consist of only one sort of atoms, which can be treated, in a first approximation, as rigid spheres. Nevertheless, even in this case the actual trap configuration is unknown. A correct dynamic simulation procedure should include large clusters (at least two coordination spheres). However, we can make some judgments from merely qualitative considerations. Since the diameter of argon atoms is the smallest (0.38 nm) one may expect that defects (traps) will be relatively compact. Benzene radical cations trapped in an argon matrix exhibit a rigid distorted structure, and there is no evidence for dynamic averaging in the temperature range 8–39 K.²⁰ As electrostatic interaction with the matrix is of primary significance, we should consider the positive charge distribution in the two possible structures of C₆H₆^+•. The limiting cases for both states can be illustrated by the ‘ resonance structures’. In the case of Ψ_S SOMO (²B_2g state), a relatively higher positive charge can be found at the C(1) and C(4) atoms (Scheme 3).

Scheme 3

Similarly, for a Ψ_A SOMO (²B_1g state), one can imagine a set of four resonance structures, which describe higher positive charge density at C(2, 3, 5, 6) (Scheme 4). Although the formulas shown are nothing more than conventional images, strongly exaggerated (the actual difference in charge distribution is not so large), they are appropriate for the demonstration of general trends and illustration of the concept of spin and charge separation, which is useful for further interpretation of matrix and substituent effects.

Scheme 4

In the case of argon, the matrix atoms are comparatively small, spherically symmetrical and ‘electronically rigid’ (low polarizability). This implies delocalized interaction and, in general, a more favorable trap configuration can be achieved for the ²B_1g state with positive charge distributed over four carbon atoms (and the adjacent four hydrogen atoms), which allows electrostatic interaction with a larger number of surrounding matrix atoms. This simple qualitative idea of more efficient ‘solvation’ of the state with a more symmetrical charge distribution may explain our experimental findings. Indeed, the spectrum taken immediately after irradiation at 16 K probably represents a mixture of the two states, whereas trapping site relaxation upon annealing leads to favorable stabilization of the ²B_1g state.²⁰

One may expect similar behaviour for benzene radical cations in krypton and xenon matrices. However, the corresponding EPR spectra show broadened patterns, which can be interpreted as a result of a dynamic process analogous to ‘hindered pseudo-rotation’ (see above). This means that the dynamics of the radical cation are not completely frozen at temperatures down to 10–12 K. The reason for this observation is not fully clear. We may suggest tentatively that the difference is because of a larger size of the defect traps for heavier rare gases due to the larger diameter of matrix atoms (0.40 and 0.44 nm for Kr and Xe, respectively) and easier deformation of a matrix lattice.

To a certain extent, a sulfur hexafluoride matrix is analogous to solid rare gases. The molecules of SF₆ are highly symmetrical (octahedral, that is, close to spherical) and exhibit a high ionization potential (close to that of argon). Furthermore, the outer fluorine atoms surrounding guest cations are of low polarizability. An essential feature of this matrix results from the fact that the diameter of matrix molecules is relatively large (in comparison with rare gas atoms). Hence replacement of only one SF₆ molecule creates a sufficiently large substitutional trap, which can accommodate compact guest molecules and ions. In this view, it is not surprising that the pseudo-rotation of benzene radical cations in sulfur hexafluoride is not completely frozen even at 12 K. We should note that cyclopropane radical cations exhibit pseudo-rotation with τ⁻¹≈10⁸ s⁻¹ in solid sulfur hexafluoride at this temperature, as evidenced by simulation of the EPR spectra.²⁸ At elevated temperatures the frequency of molecular motion becomes higher. Nevertheless, in the case of C₆H₆^+•, complete dynamic averaging yielding a septet EPR spectrum occurs only above 90 K. A sharp increase in the molecular motion frequency in an SF₆ matrix around 90–95 K is demonstrated by the reversible appearance of relatively narrow and intense lines from matrix radicals due to averaging of the anisotropic part of the ¹⁹F coupling (at lower temperatures these lines are extremely broadened and very weak because of a large anisotropic coupling constant). These changes in the EPR spectra apparently result from matrix softening near the polymorphic phase transition point (95 K).

A CFCl₃ matrix (and also other Freons) appears to represent an essentially different case. The matrix molecules possess lower symmetry; furthermore, the chlorine atoms have comparatively higher polarizability. For this reason, localized interaction with a positive ion (complex formation) becomes highly probable. Indeed, the reversible formation of well defined 1:1 complexes between solute radical cations and CFCl₃ molecules was directly evidenced by hyperfine coupling with chlorine and fluorine nuclei observed in a number of cases.^29–31 The cation–matrix interaction was also proved by an ESEEM experiment.³² It seems reasonable that the localized electrostatic interaction (weaker or stronger) commonly occurs for the radical cations trapped in a CFCl₃ matrix, although the spin density delocalization to matrix nuclei for π-type radical cations may be negligible. If this is the case for benzene, we may expect favorable stabilization of the state with more localized positive charge, i.e., the ²B_2g state (as illustrated by limiting structures 1 and 2). Most probably, the interaction is relatively weak; however, it is sufficient to determine well defined energy separation of the Jahn–Teller states at low temperatures, so we do not observe any admixture of the ²B_1g state. In these terms, the change in the EPR spectrum observed in CFCl₃ at 90 K may be interpreted as reversible complex dissociation.⁹

In general, it is not uncommon that changing the matrix may result in inversion of the energy ordering of different electronic states for trapped radical cations. The most prominent example is probably trans-decalin cation, which has been extensively characterized in various media.^33,34 Furthermore, a strong matrix effect on the basic Jahn–Teller distortion has been demonstrated for tetramethylallene radical cation.³⁵ Nevertheless, our findings for benzene radical cation appear to be of major interest because of the simplicity, high symmetry and seeming rigidity of this species. Further, it is interesting to follow the relationship between matrix effects and internal disturbance of the π-electronic system of the cation induced by substitution in the aromatic ring.

The substitution of an H for a D atom may be considered as a first step. We should draw attention to two main results obtained in our study of monodeuterated benzene radical cation. First, comparison of the data obtained for C₆H₆^+• and C₆H₅D^+• shows that the nature of the matrix plays a predominating role in the determination of the electronic structure of the radical cation. Indeed, in a CFCl₃ matrix both C₆H₆^+• and C₆H₅D^+• exhibit a structure characterized by the Ψ_S SOMO, whereas in the case of an argon matrix both species reveal a structure described by the Ψ_A SOMO. This means that deuterium monosubstitution does not affect the nature of the ground state, which is controlled by matrix interactions. Second, there is no strong preference (selection) for the position occupied by the D atom in respect of SOMO. In the case of Ψ_S SOMO, the relative deuterium populations in low and high spin density sites are nearly statistical. In the case of Ψ_A SOMO, there appears to be some excess deuterium population in the low spin density state; however, the preference is rather weak (especially if we take into account uncertainty in the determination of the relative contributions from the two forms). Meanwhile, it has been reported³⁶ that CH₂D₂^+• radical cation showed remarkable selection: D atoms occupied low spin density positions, whereas H atoms were found in high spin density sites. This effect appears to result from the difference in C–H (C–D) bond parameters for low and high spin density sites for a methane cation. In particular, one may expect that the force constants (and the corresponding stretching frequencies) for C–H(D) bonds in low spin density sites are higher than those for high spin density sites, and this leads to lower energy of the state, where the former positions are occupied by D atoms (i.e., deuterium substitution in these positions results in larger stabilization of methane radical cation). The absence of a distinct preference in the case of benzene cation means that the energy difference between the forms with D occupying high and low spin density sites is very small for both electronic states. Hence both our observations reveal that deuterium monosubstitution in benzene cation brings about only negligible perturbation, which cannot change the trend determined by cation–matrix interactions.

In contrast, the substitution of a hydrogen atom for a methyl group has a pronounced effect on the electronic structure of benzene cation, which can be easily understood on the basis of simple qualitative considerations. Electron donation from a methyl group leads to favorable stabilization of the state with Ψ_S SOMO because of efficient positive charge delocalization to the substituent. In this case, one can see a clear manifestation of partial separation of positive charge and spin density²⁶ illustrated by ‘ resonance’ structures 1 and 2. The methyl group is predominantly associated with a cationic site, whereas the para-position becomes a predominant radical site, which is revealed by the large hyperfine coupling constant with proton in the para-position. The situation bears some resemblance to the case of the formation of a localized cation–matrix complex; however, the effect of ‘internal’ stabilization of the positive charge due to the substituent is certainly much stronger. This stabilization completely predominates over relatively weak matrix interactions, so there are no matrix effects for toluene radical cation. Such a result is in line with experimental and calculation data showing that the positions of methyl substituents strongly determine the nature of SOMO for the radical cations of xylene isomers,²⁵ and also for trimethyl- and tetramethylbenzene derivatives,³⁷ independent of the matrix used.

Conclusion

Benzene radical cation in solid matrices demonstrates an outstanding example of matrix-assisted distortions controlled by relatively weak interactions. The basic Jahn–Teller effect acts only as a driving force, whereas stabilization of the distorted states is due to matrix effects. The isolated Jahn–Teller states are nearly degenerate in energy, so even slight matrix perturbations crucially affect the relative population of these states at low temperatures. Hence it would be of interest to examine the structure and dynamics of benzene cation in an ‘ ideal’ rigid non-disturbing medium. From a general spectroscopic point of view, solid neon is considered to be the closest case to such a ‘ gas-phase-like’ rigid matrix because of its extremely low polarizability. Currently we are attempting to solve the experimental problems to obtain unequivocal spectra of benzene cation in a neon matrix.

In this work, we restricted our task to the qualitative interpretation and generalization of various matrix and substituent effects on the structure and dynamics of benzene radical cations, and there is scope for a more rigorous treatment and quantum-mechanical and dynamic calculations. Finally, we should note that the remarkable ‘flexibility ’ and matrix sensitivity of benzene radical cation make it a very interesting test system for structural and dynamic studies in solid matrices.

Acknowledgements

This work was supported by joint INTAS–RFBR grant No. 95-0008 and by the Swedish National Science Research Council (NFR). The Moscow group acknowledges the technical assistance of N. A. Shmakova, V. K. Ivanchenko and N. S. Nekhoroshev.

References

1. C. Cossart-Magos, D. Cossart and S. Leach, J. Chem. Phys., 1978, 69, 4313.
2. V. E. Bondybey, T. A. Miller and J. H. English, J. Chem. Phys., 1979, 71, 1088.
3. V. E. Bondybey, T. A. Miller and J. H. English, Phys. Rev. Lett., 1980, 44, 1344.
4. T. J. Sears, T. A. Miller and V. E. Bondybey, J. Chem. Phys., 1980, 72, 6070.
5. V. E. Bondybey, T. J. Sears, T. A. Miller, C. Vaughn, J. H. English and R. H. Shiley, Chem. Phys., 1981, 61, 9.
6. T. J. Sears, T. A. Miller and V. E. Bondybey, J. Chem. Phys., 1981, 74, 3240.
7. R. Linder, K. Muller-Dethlefs, E. Wedum, K. Haber and E. R. Grant, Science, 1996, 271, 1698.
8. K. Raghavachari, R. C. Haddon, T. A. Miller and V. E. Bondybey, J. Chem. Phys., 1983, 79, 1387.
9. M. Iwasaki, K. Toriyama and K. Nunome, J. Chem. Soc., Chem. Commun., 1983, 202.
10. O. Edlund, P.-O. Kinell, A. Lund and A. Shimizu, J. Chem. Phys., 1967, 46, 3679.
11. T. Komatsu and A. Lund, J. Phys. Chem., 1972, 76, 1727.
12. R. Erickson, M. Lindgren, A. Lund and L. Sjöqvist, Colloids Surf. A, 1993, 72, 207.
13. A. Volodin, V. Bolshov and G. Panov, J. Phys. Chem., 1994, 98, 7548.
14. E. A. Piocos, D. W. Werst, A. D. Trifunac and L. A. Eriksson, J. Phys. Chem., 1996, 100, 8408.
15. M.-B. Huang and S. Lunell, J. Chem. Phys., 1990, 92, 6081.
16. H. Kato, K. Hirao and M. Sano, J. Mol. Struct., 1983, 104, 489.
17. K. Takeshita, J. Chem. Phys., 1994, 101, 2192.
18. R. Kadam, R. Erickson, T. Komaguchi, M. Shiotani and A. Lund, Chem. Phys. Lett., 1998, 290, 371.
19. R. M. Kadam, Y. Itagaki, N. P. Benetis, A. Lund, R. Erickson, M. Huber and W. Hilczer, Phys. Chem. Chem. Phys., 1999, 1, 4967.
20. V. I. Feldman, A. Yu. Orlov and F. F. Sukhov, Chem. Phys. Lett., 1999, 300, 713.
21. K. Toriyama and M. Okazaki, Phys. Chem. Chem. Phys., 1999, 1, 2607.
22. V. I. Feldman, Acta Chem. Scand., 1997, 51, 181.
23. V. I. Feldman, F. F. Sukhov, N. S. Nekhoroshev, V. K. Ivanchenko and N. A. Shmakova, Khim. Vys. Energ., 1998, 32, 18.
24. F. F. Sukhov, Dissertation, Dr. Sci. (Chemistry), Karpov Institute of Physical Chemistry, Moscow, 1988..
25. M. Tabata and A. Lund, Z. Naturforsch., A: Phys. Phys. Chem. Kosmophys., 1983, 38, 428.
26. D. N. Ramakrishna Rao, H. Chandra and M. C. R. Symons, J. Chem. Soc., Perkin Trans. 2, 1984, 1201.
27. A. A. Zezin, V. I. Feldman and F. F. Sukhov, Khim. Vys. Energ., 1995, 29, 172.
28. M. Iwasaki, K. Toriyama and K. Nunome, Faraday Discuss. Chem. Soc., 1984, 78, 19.
29. D. Becker, K. Plante and M. D. Sevilla, J. Phys. Chem., 1983, 87, 1648.
30. M. C. R. Symons, Chem. Soc. Rev., 1984, 13, 393.
31. M. C. R. Symons, B. W. Wren, H. Muto, K. Toriyama and M. Iwasaki, Chem. Phys. Lett., 1986, 127, 424.
32. J. Westerling and A. Lund, Chem. Phys., 1990, 140, 421.
33. V. I. Melekhov, O. A. Anisimov, L. Sjöqvist and A. Lund, Chem. Phys. Lett., 1990, 174, 95.
34. M. V. Barnabas and A. D. Trifunac, Chem. Phys. Lett., 1991, 187, 565.
35. X.-Z. Qin and A. D. Trifunac, J. Phys. Chem., 1991, 95, 6466.
36. L. B. Knight, Jr., G. M. King, J. T. Petty, M. Matsushita, T. Momose and T. Shida, J. Chem. Phys., 1995, 103, 3377.
37. D. N. Ramakrishna Rao and M. C. R. Symons, J. Chem. Soc., Perkin Trans. 2, 1985, 991.

---

Footnote

† Correspondence should be sent to the Karpov Institute address.

---