Impact of solvent granularity and layering on tracer hydrodynamics in confinement
Abstract
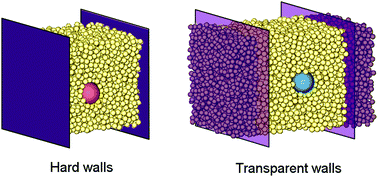
Classic hydrodynamic arguments establish that when a spherical tracer particle is suspended between parallel walls, tracer–wall coupling mediated by the solvent will cause the tracer to exhibit position-dependent diffusivity. We investigate how the diffusivity profiles of confined tracers are impacted by the diameter size-ratio of the tracer to solvent: starting from the classic limit of infinite size-ratio (i.e., continuum solvent), we consider size-ratios of four or less to examine how hydrodynamic predictions are disrupted for systems where the tracer and solvent are of similar scale. We use computer simulations and techniques based on the Fokker–Planck formalism to calculate the diffusivity profiles of hard-sphere tracer particles in hard-sphere solvents, focusing on the dynamics perpendicular to the walls. Given wall separations of several tracer diameters, we first consider confinement between hard walls, where anisotropic structuring at the solvent lengthscale generates inhomogeneity in the tracer free-energy landscape and undermines hydrodynamic predictions locally. We then introduce confining planes that we term transparent walls, which restrict tracer and solvent center-accessibilities while completely eliminating static anisotropy, and reveal position-dependent signatures in tracer diffusivity solely attributable to confinement. With or without suppressing static heterogeneity, we find that tracer diffusivity increasingly deviates on a local basis from hydrodynamic predictions at smaller size-ratios. However, hydrodynamic theory still approximately captures spatially-averaged dynamics across the pores even for very small tracer–solvent size-ratios over a wide range of solvent densities and wall separations.

 Please wait while we load your content...
Please wait while we load your content...