Structural transitions and hysteresis in clump- and stripe-forming systems under dynamic compression

Abstract

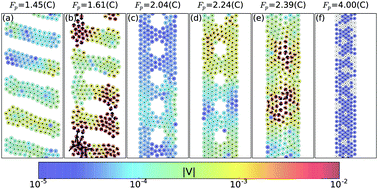
Using numerical simulations, we study the dynamical evolution of particles interacting via competing long-range repulsion and short-range attraction in two dimensions. The particles are compressed using a time-dependent quasi-one dimensional trough potential that controls the local density, causing the system to undergo a series of structural phase transitions from a low density clump lattice to stripes, voids, and a high density uniform state. The compression proceeds via slow elastic motion that is interrupted with avalanche-like bursts of activity as the system collapses to progressively higher densities via plastic rearrangements. The plastic events vary in magnitude from small rearrangements of particles, including the formation of quadrupole-like defects, to large-scale vorticity and structural phase transitions. In the dense uniform phase, the system compresses through row reduction transitions mediated by a disorder-order process. We characterize the rearrangement events by measuring changes in the potential energy, the fraction of sixfold coordinated particles, the local density, and the velocity distribution. At high confinements, we find power law scaling of the velocity distribution during row reduction transitions. We observe hysteresis under a reversal of the compression when relatively few plastic rearrangements occur. The decompressing system exhibits distinct phase morphologies, and the phase transitions occur at lower compression forces as the system expands compared to when it is compressed.