Infrared photodissociation spectroscopy of (Al2O3)2–5FeO+: influence of Fe-substitution on small alumina clusters†
Sreekanta
Debnath‡
 ab,
Marcel
Jorewitz
a,
Knut R.
Asmis
ab,
Marcel
Jorewitz
a,
Knut R.
Asmis
 *a,
Fabian
Müller‡
*a,
Fabian
Müller‡
 abc,
Julius B.
Stückrath§
abc,
Julius B.
Stückrath§
 c,
Florian A.
Bischoff
c,
Florian A.
Bischoff
 c and
Joachim
Sauer
c and
Joachim
Sauer
 *c
*c
aWilhelm-Ostwald-Institut für Physikalische und Theoretische Chemie, Universität Leipzig, Linnéstrasse 2, 04103 Leipzig, Germany. E-mail: knut.asmis@uni-leipzig.de
bFritz-Haber-Institut der Max-Plank-Gesellschaft, Faradayweg 4-6, 14195 Berlin, Germany
cInstitut für Chemie, Humboldt-Universität zu Berlin, Unter den Linden 6, 10099 Berlin, Germany. E-mail: js@chemie.hu-berlin.de
First published on 15th August 2022
Abstract
The infrared photodissociation spectra of He-tagged (Al2O3)nFeO+ (n = 2–5), are reported in the Al–O and Fe–O stretching and bending spectral region (430–1200 cm−1) and assigned based on calculated harmonic IR spectra from density functional theory (DFT). The substitution of Fe for an Al center occurs preferentially at 3-fold oxygen coordination sites located at the cluster rim and with the Fe atom in the +III oxidation state. The accompanying elongation of metal oxygen bonds leaves the Al–O network structure nearly unperturbed (isomorphous substitution). Contrary to the Al2FeO4+ (n = 1), valence isomerism is not observed, which is attributed to a smaller M:O ratio (M = Al, Fe) and consequently decreasing electron affinities with increasing cluster size.
Introduction
Research on aluminium oxide has attracted considerable attention because of its versatile use, for example as photocatalyst, catalyst support,1 coating,2 or abrasive material, and in nanosensors.3 The desired characteristics of alumina for the different applications are based on its micro- and macroscopic structure as well as its electronic properties. It is, however, well known that alumina is rarely free of impurities, such as Fe3+, Cr3+, or Ti4+ ions, replacing Al3+ centers.4 With up to 9 wt%, iron is the most common foreign ion in Al2O3. Those impurities change the microscopic structure of the oxide and its macroscopic properties e.g. optical behavior, magnetism and catalytic activity.5–12Detailed experimental information about the change in local lattice structure due to incorporated Fe ions in solid Al2O3 is scarce. While changes of the electronic structure can be probed via UV/Vis adsorption,6,11,12 Mössbauer13,14 or electron paramagnetic resonance (EPR)15 spectroscopy, modern X-ray methods such as extended X-ray absorption fine structure (EXAFS) and X-ray absorption near edge structure (XANES) are necessary to determine coordination environments and bond distances of the metal centers. Kou and co-workers,16 as well as Tai and co-workers,17 report an average Fe–O bond distance of 198–202 pm for Fe-doped γ-Al2O3 and a coordination number (CN) of 4.9 for iron, indicating a mixture of tetrahedral and octahedral coordination. Grunwaldt and co-workers18 find a much larger value for the mean bond distance (219 pm) but almost the same CN (4.7). For the system Fe/α-Al2O3 Gaudry and co-workers19 give an average Fe–O bond distance of 198 pm and assume octahedral oxygen coordination. All authors emphasize the fact that two different oxygen coordination shells around iron exist (distorted coordination), resulting in shorter (∼192 pm) and longer (>205 pm) Fe–O bonds.
It is experimentally well known that the introduced Fe3+(d5) ions are in a high-spin (S = 5/2) state.15 Solid state calculations showed that the iron impurity is most stable in the layers close to, or at the surface.20,21 Substituting an Al3+ with an Fe3+ ion in the topmost layer of the γ-Al2O3 (110) surface results in an energy gain of about 50 kJ mol−1.20
While for samples of doped bulk alumina the distribution of Fe impurities cannot be controlled and local structure information for the impurity is difficult to obtain, gas-phase studies on isolated metal oxide clusters of well-defined compositions provide the possibility to study the impurity site in isolation. In particular, the combination of cryogenic ion trap vibrational spectroscopy22,23 with density functional theory (DFT) is a reliable tool for the determination of the structure and the electronic properties of isolated polynuclear metal oxide clusters.23–26
In the present study, we investigate how an Fe impurity influences the structure and magnetic properties of Al oxide clusters. While mass-selective experiments are difficult for neutral clusters, they can be readily performed on cluster ions. Therefore, we have previously used the (Al2O3)nAlO+ series of cluster cations as model systems for alumina.27 These clusters still feature a closed-shell electronic structure and exclusively trivalent aluminium and divalent oxygen ions27 – just as bulk alumina. With increasing n, also the clusters’ composition approaches the one of Al2O3. Hence, it is expected that the clusters (Al2O3)nAlO+ represent suitable model systems for the local structure of alumina in general and the distorted surface layers of Al2O3 in particular.
Here, we adopt the (Al2O3)nFeO+ series as model systems for Fe-doped Al2O3. Substitution of one of the Al3+ ions with an Fe3+ ion converts the (Al2O3)nAlO+ series to a model for Fe/Al2O3. Note that the nomenclature (Al2O3)nFeO+ does not imply that an FeO+ unit is added to Al2O3, but rather that an Al3+ has been replaced with Fe3+ in the closed-shell systems (Al2O3)nAlO+.
Our goal is to identify the preferred substitution site and coordination environment of the Fe atom in the clusters of increasing size (n = 2–5) and hence decreasing iron-to-aluminium ratio. Furthermore, we are interested in the local electronic structure of the dopant, including its spin and oxidation state. A previous study on the first member of the series (n = 1),28 (Al2O3)FeO+ ≡ Al2FeO4+, revealed the formation of an unexpected structure different from that of Al3O4+ as a consequence of valence isomerism: In an intramolecular redox reaction, iron is reduced to +II, accompanied by the formation of a terminal oxygen radical. Consequently, the question arises if such a change of oxidation state also occurs in the larger clusters.
Experimental methods
The infrared photodissociation (IRPD) experiments were carried out on a 10 K ion-trap tandem mass spectrometer29 using the widely tuneable, intense IR radiation from the Fritz-Haber-Institute Free Electron Laser (FHI FEL).30 In brief, (Al2O3)nFeO+ ions (n = 2–5) are produced in a pulsed laser vaporization source by focusing a frequency-doubled Nd:YAG laser (50 Hz, 10–15 mJ) onto a rotating Fe/Al (30/70 wt%) metal rod (Plasmaterials). The resulting plasma is quenched with a gas pulse of 0.5% O2 seeded in He. Cluster ions are formed during expansion through a clustering channel downstream from the rod and pass through a skimmer.The beam of ions is then collimated and thermalized close to room temperature in a He-gas filled radio frequency (RF) ion guide, mass-selected using a quadrupole mass filter, and focused into a cryogenically cooled RF ring-electrode ion-trap. The trap is continuously filled with He-buffer gas and held at a temperature of 12 K. Many collisions of the trapped ions with the buffer gas provide gentle cooling of the internal degrees of freedom close to the ambient temperature. At sufficiently low ion-trap temperatures, ion-He complexes are formed via three-body collisions.31
All ions are extracted from the ion trap and focused both temporally and spatially into the center of the extraction region of an orthogonally-mounted reflectron time-of-flight (TOF) tandem mass spectrometer. Here, the ions are irradiated with an attenuated, counter-propagating IR laser pulse produced by the FHI FEL (430–1200 cm−1, 5Hz), with a bandwidth of ∼0.5% full width at half maximum (FWHM) and a pulse energy of 0.7–2.5 mJ. Parent, as well as photofragment ion yields, are monitored simultaneously as a function of the irradiation wavelength. IRPD scans are recorded by averaging over 100 TOF mass spectra per wavelength step (3 cm−1). Typically, at least three scans are summed to obtain the final IRPD spectrum. The photodissociation cross-section σIRPD is determined as described previously.32,33
Computational methods
All calculations were performed with the Turbomole program package V7.5.1.34–36 A global energy minimization for the clusters of the compositions (Al2O3)nFeO+ (n = 2–5) was carried out employing a genetic algorithm (GA).37,38 The GA stopped when the energy of the most stable isomer as well as the averaged energy of all unique structures per generation did not change anymore. Thereby, 1200 structures were created for (Al2O3)2FeO+ and 1700 for each of the (Al2O3)3–5FeO+ systems.In the GA optimizations, the BP8639,40 exchange-correlation density functional was used together with a split valence basis set (def2-SVP41) for the sake of computational efficiency. The total electronic spin of all investigated systems in this step was fixed at S = 5/2, i.e. the high-spin state of the Fe atom. Thus, the spin unrestricted Kohn–Sham (UKS) formalism was required to handle the open-shell electronic structure. The resolution of the identity (RI) approximation was used to accelerate the Coulomb fitting in the global structure search of the largest cluster (n = 5).
The most stable unique isomers of each composition were re-optimized employing the TPSSh,42 the PBE043 and the B3LYP44–46 exchange-correlation functionals in conjunction with the def2-TZVP triple-zeta basis set.47 Vibrational frequencies were calculated within the double-harmonic approximation. The resulting stick spectra were convolved with Gaussian functions of 15 cm−1 full width at half maximum (FWHM) to account for the width of the experimentally observed bands.
All vibrational frequencies were scaled to account for anharmonic effects and the systematic error of the used density functional concerning the force constants. The scaling factor of 1.0175 was obtained by maximizing the cosine similarity score (vide infra) of the simulated TPSSh spectrum for Al2FeO4+ (n = 1) and the respective IRPD result. This factor is slightly different from the one used in the previous study (1.0132)28 since a different basis set was used.
The influence of the He-tagging atoms was investigated recently for the cluster Al2FeO4+ (n = 1) and found to be negligible.28 It is, therefore, not further considered in this work.
As an objective measure for the agreement of experimental and theoretical spectra, the cosine similarity score S is used. S expresses the similarity between the two spectra. It is based on the two vectors A and B, which hold the intensity values of the experimental and predicted spectrum at the same grid of irradiation energies, respectively. The score is calculated using eqn (1), i.e. by the normalized dot product of A and B.28
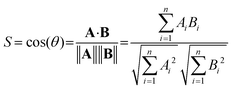 | (1) |
The score can vary from zero to unity, and S values closer to unity indicate greater similarity.
Results and discussion
In Fig. 1, the IRPD spectra of He-tagged (Al2O3)nFeO+ with n = 2–5 are compared with those previously reported for the He-tagged all-Al analogs (Al2O3)nAlO+ in the spectral region from 430 to 1200 cm−1 (see Table S2, ESI† for experimental band positions).27 The spectrum of Al2FeO4+ (n = 1) has been published recently by Müller et al.28 Based on our previous studies for monometallic Al- and Fe-oxide clusters, we group the observed IR absorptions into three characteristic spectral regions: (i) 1200–900 cm−1, (ii) 900–600 cm−1 and (iii) 600–430 cm−1.48–52 These regions cover (i) Al–O stretching modes involving the shortest (≤173 pm) Al–O bonds, (ii) Fe–O stretching modes together with medium-length (174–178 pm) Al–O bond stretches and (iii) ring breathing modes as well as stretching and bending modes involving the longest (>180 pm) Al–O bonds.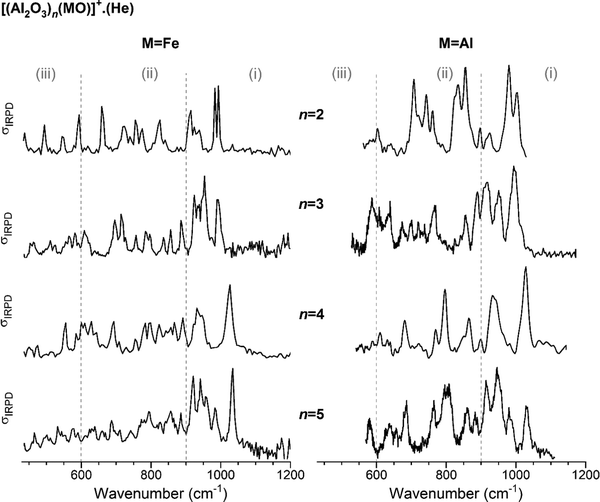 | ||
| Fig. 1 Experimental IRPD spectra of He-tagged (Al2O3)n(MO)+ with n = 2–5. Spectra for M = Fe (present study, singly He-tagged clusters) are shown on the left-hand side and those for M = Al (from ref. 27, multiple He-tagging) on the right-hand side panel. See Table S2, ESI† for band positions and assignments. Three characteristic spectral regions are indicated by the dashed lines: (i) 1200–900, (ii) 900–600, and (iii) <600 cm−1. | ||
For each n, the spectra with (left) and without (right) Fe-substitution exhibit similar features, in particular in the region (i), but there are also noticeable differences in the number of peaks, their positions and intensities predominantly in regions (ii) and (iii). The degree of agreement between corresponding spectra increases with increasing n. This observation is supported by the cosine similarity score analysis, which yields S values of 0.49, 0.68, 0.85 and 0.86 for n = 2–5, respectively. As can be expected, a decreasing relative Fe content with increasing cluster size leads to decreasing distortion of the alumina framework and hence more similar IRPD spectra.
The most intense absorption bands of the (Al2O3)nFeO+ clusters are seen in the region (i), and the highest-energy transition is found in the spectrum of the largest cluster, n = 5, at 1034 cm−1. Spectra of the all-Al species also show the most intense absorption in the region (i). Regions (ii) and (iii) are rich with IR signatures and the spectral congestion naturally increases with increasing cluster size for both types of clusters.
Fig. 2 gives an overview of isomers for the cluster compositions (Al2O3)nFeO+ resulting from global energy minimization using a genetic algorithm and DFT together with some isomers that were previously obtained for the pure aluminium oxide cations (Al2O3)nAlO+.27 All isomers are labelled with the notation nxk, where n is the number of formal (Al2O3) units present in the cluster, x = a, b, c indicates different framework motifs sorted by increasing relative energy, and k is an index to discriminate different Fe-substitution positions within a motif. To address pure Al-oxide systems, the right subscript “Al” is added. Note, the present labeling is different from that used in our original (Al2O3)1–4AlO+ study.27
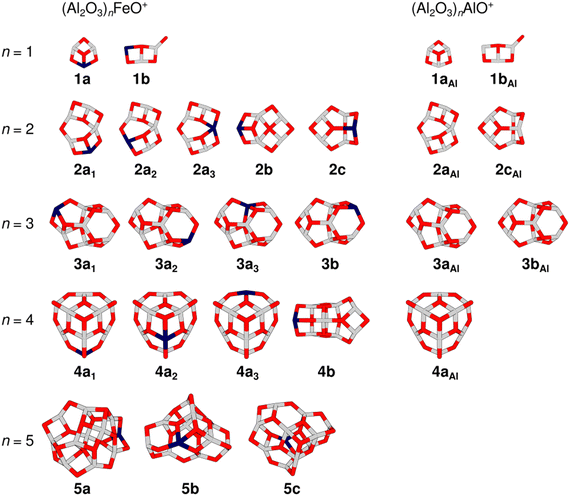 | ||
| Fig. 2 Overview of TPSSh/def2-TZVP low-energy isomers of (Al2O3)nFeO+ (left-hand side) and (Al2O3)nAlO+ (right-hand side). Isomer labels are given below each structure (gray: aluminium, dark blue: iron, red: oxygen). Table S1 in the ESI† lists the relative energies of the isomers. | ||
Calculated harmonic IR spectra of the different isomers for each cluster size were compared with their corresponding experimental spectrum to identify the best matching one. Fig. 3 shows the finally assigned structures and their IR spectra; see Fig. S1–S5 in the ESI† for the spectra of all remaining isomers.
The global minimum-energy isomer predicted for Al4FeO7+ (n = 2) is a sheet-like structure (2a1) with a four-fold coordinated Al atom and a bridging two-fold coordinated O atom. The Fe atom is three-fold coordinated. Fig. S2, ESI† depicts other calculated low-energy isomers and compares their calculated IR spectra with the experimental one. The isomers 2a2 and 2a3 share their structural motif with 2a1 but the Fe atom is located at different metal sites. Both are higher in energy, 52 and 95 kJ mol−1, respectively (Table S1, ESI†). In 2a3 the Fe atom takes the four-fold coordinated position.
Isomer 2a1 (C1, no symmetry) represents the lowest energy structure and its spectrum results in the highest similarity score (Fig. S2, ESI†). However, no straightforward explanation for the splitting of the observed peak at 993 cm−1 can be given. A possible origin might be a Fermi resonance between the intense fundamental predicted at 999 cm−1, which mainly results from the motion of bridging two-fold coordinated O atoms (Al–μ2O–Al), and a combination band consisting of framework modes.
The highest-energy experimental peak (993 cm−1) involves stretching of the shortest Al–O bonds (169–173 pm). Al–O stretching bands of four- and three-fold coordinated Al atoms (μ4Al/μ3Al) are assigned to the experimental peaks at 825 cm−1 (calc. 830 cm−1) and 593 cm−1 (calc. 598 cm−1), respectively. Fe–O stretching modes exclusively appear in the region (ii); the corresponding bond lengths are 177–208 pm. The Fe–O motions are all coupled with the stretching of Al–O bonds of medium length (173–178 pm). Almost decoupled Fe–μ2O–Al stretching modes are assigned to the transitions predicted at 664 and 632 cm−1 (experiment 659 and 619 cm−1).
The IRPD spectrum of the all-Al analog Al5O7+ (Fig. 1) contains contributions of two energetically close-lying isomers, 2aAl and 2cAl (ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3),27 also shown in Fig. 2. While 2aAl is similar in structure to the sheet-like 2a1, the analog of the cage-like structure 2cAl is 2c, which is 31 kJ mol−1 less stable than 2a1 and is not observed at our experimental conditions. Indeed, a considerable difference in the experimental spectra of Al4FeO7+ and Al5O7+ (Fig. 1) can be seen mostly in the regions (i) and (ii), confirming these structural differences.
3),27 also shown in Fig. 2. While 2aAl is similar in structure to the sheet-like 2a1, the analog of the cage-like structure 2cAl is 2c, which is 31 kJ mol−1 less stable than 2a1 and is not observed at our experimental conditions. Indeed, a considerable difference in the experimental spectra of Al4FeO7+ and Al5O7+ (Fig. 1) can be seen mostly in the regions (i) and (ii), confirming these structural differences.
Proceeding to Al6FeO10+, i.e. n = 3, the cage-like non-symmetric (C1) structure 3a1 (Fig. 3) is the most stable isomer and the origin of the measured IRPD spectrum. It consists of six- and four-membered rings, similar to the analogous 3aAl structure of Al7O10+. The Fe atom is again three-fold coordinated with bond lengths between 178 and 206 pm.
The similarity of the IRPD spectra of Al6FeO10+ and Al7O10+ (cf.Fig. 1) supports the assumption of their identical structural motifs. While the spectrum of the pure alumina cluster was assigned to a 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of 3aAl and 3bAl, most of the peaks observed for Al6FeO10+ can be assigned to a single isomer. This is the lowest energy isomer 3a1 and its simulated IR spectrum also yields the highest cosine similarity score S = 0.84 (Fig. S3, ESI†). Unlike the IRPD spectra of all the other cluster sizes, the highest-energy peak for n = 3 is not the most intense one. This peak (992 cm−1) is assigned to the stretching mode involving the shortest (170–173 pm) μ3Al–O bonds from the outer rim of the cluster (calc.: 996 cm−1). The most intense experimental band at 953 cm−1 results from the combination of stretching motions of μ4Al–O units (calc.: 956 cm−1). The μ4Al–O bonds are shorter (174–175 pm) than those in 2a1 and the corresponding IRPD band is blue-shifted compared to the spectrum of the n = 2 cluster and appears in the region (i). Region (ii) is rich with IR signatures from multiple Al–O and Fe–O stretching modes. Fe-μ2O stretching motions are observed at 714 cm−1 (calc.: 715 cm−1).
1 mixture of 3aAl and 3bAl, most of the peaks observed for Al6FeO10+ can be assigned to a single isomer. This is the lowest energy isomer 3a1 and its simulated IR spectrum also yields the highest cosine similarity score S = 0.84 (Fig. S3, ESI†). Unlike the IRPD spectra of all the other cluster sizes, the highest-energy peak for n = 3 is not the most intense one. This peak (992 cm−1) is assigned to the stretching mode involving the shortest (170–173 pm) μ3Al–O bonds from the outer rim of the cluster (calc.: 996 cm−1). The most intense experimental band at 953 cm−1 results from the combination of stretching motions of μ4Al–O units (calc.: 956 cm−1). The μ4Al–O bonds are shorter (174–175 pm) than those in 2a1 and the corresponding IRPD band is blue-shifted compared to the spectrum of the n = 2 cluster and appears in the region (i). Region (ii) is rich with IR signatures from multiple Al–O and Fe–O stretching modes. Fe-μ2O stretching motions are observed at 714 cm−1 (calc.: 715 cm−1).
The global minimum-energy structure for Al8FeO13+ is the conical structure 4a1 (Fig. 3). Compared to its all-Al analog, its symmetry is reduced from C3v to Cs upon substitution of a three-fold coordinated Al with an Fe atom in the outer rim of 4aAl. The structure consists of a tip that is similar to the structure of Al3O4+,27 which is linked to a 12-membered Al5FeO6 ring by three bridging μ2O atoms. Iron substitution at the other two unique metal positions leads to the isomers 4a2 and 4a3, which are 13 kJ mol−1 and 20 kJ mol−1 less favorable, respectively. While 4a1 and 4a3 feature three-fold coordinated Fe centers, the transition metal is bound to four O atoms in 4a2. The simulated spectra of the three isomers 4a1–3 yield very similar S values (Fig. S4, ESI†). However, all used DFT methods agree that 4a1 is the most stable structure (Table S1, ESI†) and, hence, it is assigned to Al8FeO13+.
Similar to the smaller clusters, the shortest Al–O bonds (169–172 pm) are found in the 12-membered ring forming the outer rim. The associated Al–μ2O stretching bands are observed with the broad absorption at the highest energy (1026 cm−1) having the highest intensity. The simulated spectrum reveals two very close-lying features at 1031 and 1033 cm−1, which could contribute to the larger width of the experimental peak. All three Fe–O bonds have almost identical lengths (183 pm) and result in stretching bands, which can be found in region (iii).
In comparison to the spectrum of Al8FeO13+, the Al9O13+ spectrum shows fewer features, in line with its higher symmetry (Csvs. C3v). However, the features in the region (i) remain similar due to the identical outer ring structure of these isomers. The influence of the Fe atom on the IRPD spectrum and hence on the isomer-specific features manifests in the region 550–900 cm−1 due to slight changes in the framework introduced by the longer Fe–O bonds.
For the largest cluster, Al10FeO16+, the assignment of the IRPD spectrum to a specific isomer is difficult. The most stable structure at the TPSSh level is 5a. Isomers 5b and 5c are, however, only 10 and 16 kJ mol−1 less favorable (Table S1, ESI†), i.e. within the uncertainty range of the applied functionals. The relative stabilities of the three isomers change when B3LYP and PBE0 instead of TPSSh are used (Table S1, ESI†). Both methods favor 5b, suggesting that the energetic ordering predicted by TPSSh might not be reliable in this particular case. Hence, it can be assumed that 5b is more stable and therefore more abundant in the experiment.
All three isomers have irregular cage structures (Fig. 2) consisting of six- and four-membered rings. In 5a and 5c, the Fe atom is three-fold coordinated, whereas it is four-fold coordinated in 5b. Compared to the IRPD spectrum, 5a reaches the lowest similarity score. In contrast, 5b and 5c result in much better, almost identical spectral agreements (Fig. S5, ESI†). However, neither the spectrum of 5b nor of 5c alone reproduces all observed IRPD bands, indicating substantial contribution from at least one other low-energy isomer. The characteristic feature at 983 cm−1, for example, could be explained by a contribution of 5a. Still, taking into account, that none of the used density functionals predicts 5c to be the most stable isomer, and that there is high spectral similarity for 5b (S = 0.79), the latter is assumed the primarily present isomer of Al10FeO16+.
The most intense band in the IRPD spectrum of Al10FeO16+ at 1034 cm−1 is not only the highest-energy absorption of this cluster but also among the series of mixed and all-Al oxide systems reported in this paper (Fig. 1). It is, just as the other features in region (i), associated with the stretching motions of the shortest bridging μ2O–Al bonds (167–174 pm). At this cluster size, it becomes difficult to identify the IR-signature of the Fe center, because the corresponding stretching modes are strongly coupled with other vibrational modes of the system. The Fe–O bond lengths range from 179 to 202 pm.
Based on the assignments made, the structural influence of Fe-doping on small alumina clusters can be discussed. Table 1 lists the average Al–O bond lengths for (Al2O3)nAlO+ and (Al2O3)nFeO+ as well as all particular Fe–O bond lengths of the assigned isomers. Moreover, the (average) coordination numbers (CN) of the Al and Fe sites are given. Aluminium tends to form shorter bonds with oxygen than iron. The average length is about 176 pm, for both the pure and the substituted clusters. The only exception seems to be Al6MO10+ (n = 3, M = Al, Fe), where an averaged value of 180 pm arises. Indeed, there are some much longer Al–O bonds (193–208 pm and 188–200 pm for the undoped and doped cluster, respectively, cf. Fig. S6, ESI†) in the corresponding isomer, which increase the average value and the standard deviation. Most of them are associated with the central, four-fold coordinated O atom. Its higher coordination number might be the reason for the weaker interaction with the surrounding Al atoms and, therefore, for the longer bond distances. This assumption is supported by the longer mean Al–O bonds in solid state α-Al2O3 (Table 1: >186 pm), where oxygen is also four-fold coordinated.
| M:O | Bond distances [pm] | CN | EAverte | ||||
|---|---|---|---|---|---|---|---|
| Al–Oab | Al–Oac | Fe–O | Ald | Fe | |||
| a Average Al–O bond distances with uncertainty of one standard deviation. b Reference values for all-Al clusters, (Al2O3)nAlO+. c Fe-doped cluster, (Al2O3)nFeO+. d Averaged over all Al atoms in the respective Fe-doped cluster. e Vertical electron affinity of Fe-doped clusters. f Electron affinity for 1a. g Taken from ref. 19. h Taken from ref. 16. i Taken from ref. 18. j Taken from ref. 17. | |||||||
| 1b | 0.750 | 176 ± 8 | 175 ± 7 | 183, 194 | 3.0 | 2.0 | 7.31f |
| 2a1 | 0.714 | 176 ± 7 | 176 ± 6 | 177, 181, 208 | 3.3 | 3.0 | 6.65 |
| 3a1 | 0.700 | 180 ± 12 | 180 ± 11 | 178, 179, 205 | 3.7 | 3.0 | 6.34 |
| 4a1 | 0.692 | 175 ± 6 | 175 ± 6 | 183, 183, 183 | 3.4 | 3.0 | 5.68 |
| 5b | 0.688 | 180 ± 10 | 178 ± 7 | 179, 191, 200, 202 | 3.6 | 4.0 | 6.00 |
| Fe/α-Al2O3g | 0.667 | 186, 197 | 190, 205 | ||||
| Fe/γ-Al2O3h | 0.667 | 191, 205 | 4.9 | ||||
| Fe/γ-Al2O3i | 0.667 | 192, 245 | 4.7 | ||||
| Fe/γ-Al2O3j | 0.667 | 194, 209 | 6.0 | ||||
The iron oxygen bonds have a length of at least 177 pm and can be as long as 208 pm. In most clusters, there are one or two shorter (<184 pm) and one longer (>194 pm) Fe–O bonds. This agrees well with the experimental observation of shorter and longer Fe–O bonds in solid Fe-doped Al2O3 (Table 1). However, the absolute values slightly deviate: both the Al–O and the Fe–O bonds in the crystal lattice are longer than those of the gas phase clusters. As mentioned above, this is a consequence of the higher CNs of both metal and oxygen atoms in the solid state and the resulting weaker atom-to-atom interactions.
With decreasing metal-to-oxygen ratio (M![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) O), the (mean) CN of Al, as well as Fe, increases, reaching a value of (or close to) four for Al10FeO16+. In corundum or hematite each metal site has octahedral oxygen coordination. Hence, larger clusters with M:O approaching 2:3 will also tend towards a CN of six. It is also interesting to see that in Fe/γ-Al2O3 the Fe atoms are surrounded by two oxygen coordination shells, responsible for the longer and shorter Fe–O bonds.16,18 Each of those shells results in a (partial) CN of about 2.4 for iron, which is in turn comparable to the valency of the Fe in the small clusters (3.0).
O), the (mean) CN of Al, as well as Fe, increases, reaching a value of (or close to) four for Al10FeO16+. In corundum or hematite each metal site has octahedral oxygen coordination. Hence, larger clusters with M:O approaching 2:3 will also tend towards a CN of six. It is also interesting to see that in Fe/γ-Al2O3 the Fe atoms are surrounded by two oxygen coordination shells, responsible for the longer and shorter Fe–O bonds.16,18 Each of those shells results in a (partial) CN of about 2.4 for iron, which is in turn comparable to the valency of the Fe in the small clusters (3.0).
Analysis of the structures of (Al2O3)nFeO+ (n = 1–5) reveals that Al prefers trigonal planar or tetrahedral O atom coordination while Fe seems more flexible and adapts also to two-fold coordinated environments.28 These observations are in line with the results for Fe-doped nanocrystals or nanoparticles,12 in which dopant Fe atoms preferably replace Al atoms of the Al2O3 network mostly in the surface layer21 without inducing major distortions or even structural changes.53 While structural deviations from the corresponding all-Al clusters are evident for the clusters with larger Fe![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Al ratios (n = 1–3), starting from Al8MO13+ the cluster framework is virtually identical for M = Fe and Al, proving the suitability of iron as a dopant for Al2O3.
Al ratios (n = 1–3), starting from Al8MO13+ the cluster framework is virtually identical for M = Fe and Al, proving the suitability of iron as a dopant for Al2O3.
Regarding spin multiplicity and oxidation state of the iron centers, it turns out that a Fe(III) high-spin d5 configuration (sextet, S = 5/2) is always the most stable situation. The presence of a high-spin Fe(III)-center in (Al2O3)2–5FeO+ is in agreement with observations for solid Fe/Al2O3, where EPR and Mössbauer spectroscopy suggests Fe(III) high-spin sites.15
Table S1 (ESI†) lists the relative stabilities of different spin isomers calculated with several density functionals (TPSSh, B3LYP, PBE0), showing that the preference for high-spin Fe(III) is independent of the choice of functional. At the TPSSh level, the quartets (S = 3/2) and doublets (S = 1/2) are 18–65 kJ mol−1 and 75–119 kJ mol−1 less stable than the sextets, respectively. The orbital analysis (see 〈S2〉 values, Table S1, and spin density plots, Fig. S7, ESI†) reveals that the quartet states feature three unpaired electrons in the d states (〈S2〉 close to 3.75). In the doublets, however, there are also three unpaired electrons, two with spin up, and one with spin down, resulting in 〈S2〉 values close to 1.75 instead of 0.75 for only a single unpaired electron. It can be concluded that a strong multireference character of the transition metal sites in the larger clusters (n = 2–5) is absent for the sextets and quartets, so that DFT is a suitable method to describe them. The doublets, however, should be handled with more sophisticated wavefunction-based methods.
Contrary to Al2FeO4+ (n = 1), the clusters with n = 2–5 are not subject to an intramolecular redox reaction. Hence, terminal oxygen radicals are absent. A possible reason for this can be the M:O ratio, which, for n = 2–5, is smaller than 0.75 (value for magnetite), tending towards 0.667 (value for hematite) with increasing cluster size. In an infinitely large cluster the latter ratio is approached and all metal sites would formally be in oxidation state +III. For the magnetite value (0.75), however, there needs to be a mixture of sites with +III and +II. Smaller M:O values intrinsically require higher formal oxidation states of the metal sites.
The decomposition of the isomerization energy from the isomer with Fe3+ (d5)/O2− to the one with Fe2+ (d6)/O˙− into electron affinities (EA) and the isomerization energy between the neutral species was helpful in the case of Al2FeO4+.28 In this decomposition, the electron affinity of the Fe(III)-containing isomer is the driving force for the valence isomerism since both the Fe(II)–O bond cleavage and the re-ionization (O radical formation) consume energy. Table 1 contains the calculated EA values for the clusters with n = 1–5. They are much smaller (<6.7 eV) for (Al2O3)2–5FeO+ than for Al2FeO4+ (7.3 eV). As described above, the smaller M:O ratio of the larger clusters favors, i.e. stabilizes the higher +III oxidation state of the Fe site and prevents the oxygen radical formation.
Conclusions
In agreement with the results for Fe-doped Al2O3 nanoparticles12 and solid corundum, the substitution of a single Al atom with an Fe atom has little influence on the structure of the larger clusters of the homolog series (Al2O3)nFeO+ (n = 1–5). Only the first two members (n = 1, 2) significantly change their structure, as can be concordantly seen from the experiment (spectra) and theory (structure prediction). A slightly different bonding environment is observed between Fe and O, compared to the Al–O bonds. The former bonds are longer and high-spin Fe(III) is found in three-fold coordination, while Al sites with four-fold coordination increase the cluster's stability. The Fe atom preferentially occupies lower-coordination sites at the rim of the clusters. With increasing cluster size (n > 1) the M:O ratio approaches the ideal value of hematite (0.667), leading to decreasing electron affinities and, as a consequence, the absence of Fe3+/O2− ↔ Fe2+/O˙− valence isomerism that is present in Al2FeO4+ (n = 1).This study reveals an intimate relationship between structural and electronic properties of the investigated (Al2O3)nFeO+ gas phase clusters and both solid and nanoparticle-like Fe-doped Al2O3. This observation confirms their use as model systems54 for further studies, e.g. reactivity studies with H2, H2O, CO, and CO2, the educts and byproducts of the Fischer–Tropsch process, which uses calcinated Fe/Al2O3 as a catalyst. Furthermore, together with Fe atoms, strong local magnetic moments (d5 high-spin) are introduced in the alumina clusters enabling a possible application in spin-based quantum devices. An investigation of alumina models with two Fe-substituted metal sites and their resulting spin couplings could elucidate the suitability of such systems.
Author contributions
S. D. planned and performed the experimental work, including evaluation of the data using the cosine similarity score. M. J. assisted during the beam-time measurements. F. M. did the electronic structure calculations, assisted by J. B. S. for the systems n = 3 and n = 5. S. D. and F. M. wrote the manuscript and prepared the figures. F. B. supervised F. M. J. S. and K. R. A. designed the study, coordinated the project, supervised the research, contributed to the data interpretation and revised the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has been funded by the German Research Foundation (DFG) within the Collaborative Research Centre 1109 “Metal Oxide − Water Systems” and within project 430942176 “Mixed Metal Oxide Clusters: Model Systems for Catalytically Active Materials” (Asmis/Sauer). It has also been supported by the “Fonds der Chemischen Industrie”.References
- M. Trueba and S. P. Trasatti, Eur. J. Inorg. Chem., 2005, 3393–3403 CrossRef CAS.
- G. V. Franks and Y. Gan, J. Am. Ceram. Soc., 2007, 90, 3373–3388 CrossRef CAS.
- J. Álvarez, C. Serrano, D. Hill and J. Martínez-Pastor, Opt. Lett., 2013, 38, 1058–1060 CrossRef PubMed.
- A. W. Deer, R. A. Howie and J. Zussman, An Introduction to the Rock-Forming Minerals, The Mineralogical Society, London, 3rd edn, 2013 Search PubMed.
- N. Kristianpoller, A. Rehavi, A. Shmilevich, D. Weiss and R. Chen, Nucl. Instrum. Methods Phys. Res., 1998, 141, 343–346 CrossRef CAS.
- T. Monteiro, C. Boemare, M. J. Soares, E. Alves, C. Marques, C. McHargue, L. C. Ononye and L. F. Allard, Nucl. Instrum. Methods Phys. Res., 2002, 191, 638–643 CrossRef CAS.
- E. Gaudry, D. Cabaret, P. Sainctavit, C. Brouder, F. Mauri, J. Goulon and A. Rogalev, J. Phys.: Condens. Matter, 2005, 17, 5467–5480 CrossRef CAS.
- V. B. Mikhailik, P. C. F. Di Stefano, S. Henry, H. Kraus, A. Lynch, V. Tsybulskyi and M. A. Verdier, J. Appl. Phys., 2011, 109, 053116 CrossRef.
- G. Rani and P. D. Sahare, Adv. Powder Technol., 2014, 25, 767–772 CrossRef CAS.
- J. A. Loiland, M. J. Wulfers, N. S. Marinkovic and R. F. Lobo, Catal. Sci. Technol., 2016, 6, 5267–5279 RSC.
- Z. K. Heiba, M. B. Mohamed, A. M. Wahba and N. G. Imam, J. Electron. Mater., 2018, 47, 711–720 CrossRef CAS.
- M. Farahmandjou, A. Khodadadi and M. Yaghoubi, J. Supercond. Nov. Magn., 2020, 33, 3425–3432 CrossRef CAS.
- H.-J. Wan, B.-S. Wu, C.-H. Zhang, H.-W. Xiang, Y.-W. Li, B.-F. Xu and F. Yi, Catal. Commun., 2007, 8, 1538–1545 CrossRef CAS.
- V. G. d Resende, A. Cordier, E. D. Grave, C. Laurent, S. G. Eeckhout, G. Giuli, A. Peigney, G. M. d Costa and R. E. Vandenberghe, J. Phys. Chem. C, 2008, 112, 16256–16263 CrossRef.
- A. Priem, P. J. M. van Bentum, W. R. Hagen and E. J. Reijerse, Appl. Magn. Reson., 2001, 21, 535–548 CrossRef CAS.
- Y. Kou, H.-l Wang, J.-z Niu and W.-j Ji, J. Phys. Chem., 1996, 100, 2330–2333 CrossRef CAS.
- A. Tomita, T. Miki, T. Tango, T. Murakami, H. Nakagawa and Y. Tai, Chem. Phys. Chem., 2015, 16, 2015–2020 CrossRef CAS PubMed.
- A. Boubnov, H. Lichtenberg, S. Mangold and J. D. Grunwaldt, J. Phys. Conf. Ser., 2013, 430, 012054 CrossRef CAS.
- E. Gaudry, A. Kiratisin, P. Sainctavit, C. Brouder, F. Mauri, A. Ramos, A. Rogalev and J. Goulon, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 094108 CrossRef.
- G. Feng, C.-F. Huo, Y.-W. Li, J. Wang and H. Jiao, Chem. Phys. Lett., 2011, 510, 224–227 CrossRef CAS.
- M. Jiang, B. Nie, Z. Yang, M. Ni and Z. Chen, J. Nucl. Mater., 2020, 533, 152102 CrossRef CAS.
- K. R. Asmis, M. Brümmer, C. Kaposta, G. Santambrogio, G. von Helden, G. Meijer, K. Rademann and L. Wöste, Phys. Chem. Chem. Phys., 2002, 4, 1101–1104 RSC.
- K. R. Asmis, Phys. Chem. Chem. Phys., 2012, 14, 9270–9281 RSC.
- K. R. Asmis and J. Sauer, Mass Spectrom. Rev., 2007, 26, 542–562 CrossRef CAS PubMed.
- K. R. Asmis and J. Sauer, Mass Spectrom. Rev., 2008, 27, 205 CrossRef.
- H. Schwarz and K. R. Asmis, Chem. – Eur. J., 2019, 25, 2112–2126 CrossRef CAS PubMed.
- G. Santambrogio, E. Janssens, S. Li, T. Siebert, G. Meijer, K. R. Asmis, J. Döbler, M. Sierka and J. Sauer, J. Am. Chem. Soc., 2008, 130, 15143–15149 CrossRef CAS PubMed.
- F. Müller, J. B. Stückrath, F. A. Bischoff, L. Gagliardi, J. Sauer, S. Debnath, M. Jorewitz and K. R. Asmis, J. Am. Chem. Soc., 2020, 142, 18050–18059 CrossRef PubMed.
- D. J. Goebbert, G. Meijer and K. R. Asmis, AIP Conf. Proc., 2009, 1104, 22–29 CrossRef CAS.
- W. Schöllkopf, S. Gewinner, H. Junkes, A. Paarmann, G. von Helden, H. P. Bluem and A. M. M. Todd, The new IR and THz FEL facility at the Fritz Haber Institute in Berlin, SPIE, 2015 Search PubMed.
- M. Brümmer, C. Kaposta, G. Santambrogio and K. R. Asmis, J. Chem. Phys., 2003, 119, 12700–12703 CrossRef.
- N. Heine and K. R. Asmis, Int. Rev. Phys. Chem., 2015, 34, 1–34 Search PubMed.
- N. Heine and K. R. Asmis, Int. Rev. Phys. Chem., 2016, 35, 507 Search PubMed.
- R. Ahlrichs, M. K. Armbruster, R. A. Bachorz, H. Bahmann, A. Baldes, M. Bär, H.-P. Baron, R. Bauernschmitt,F. A. Bischoff and S. Böckeret al., TURBOMOLE (7.5.1), TURBOMOLE GmbH, 2021, https://www.turbomole.org.
- O. Treutler and R. Ahlrichs, J. Chem. Phys., 1995, 102, 346–354 CrossRef CAS.
- K. Eichkorn, F. Weigend, O. Treutler and R. Ahlrichs, Theor. Chem. Acc., 1997, 97, 119–124 Search PubMed.
- M. Sierka, J. Döbler, J. Sauer, G. Santambrogio, M. Brümmer, L. Wöste, E. Janssens, G. Meijer and K. R. Asmis, Angew. Chem., Int. Ed., 2007, 46, 3372–3375 CrossRef CAS PubMed.
- D. M. Deaven and K. M. Ho, Phys. Rev. Lett., 1995, 75, 288–291 CrossRef CAS PubMed.
- J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824 CrossRef PubMed.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS PubMed.
- A. Schäfer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571–2577 CrossRef.
- V. N. Staroverov, G. E. Scuseria, J. Tao and J. P. Perdew, J. Chem. Phys., 2003, 119, 12129–12137 CrossRef CAS.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- P. Gruene, J. T. Lyon, G. Meijer, P. Lievens and A. Fielicke, Ideas in Chemistry and Molecular Sciences, 2010, pp. 183–206 DOI:10.1002/9783527630530.ch7.
- X. Song, M. R. Fagiani, S. Gewinner, W. Schöllkopf, K. R. Asmis, F. A. Bischoff, F. Berger and J. Sauer, J. Chem. Phys., 2016, 144, 244305 CrossRef PubMed.
- X. Song, M. R. Fagiani, S. Gewinner, W. Schöllkopf, K. R. Asmis, F. A. Bischoff, F. Berger and J. Sauer, Chem. Phys. Chem., 2017, 18, 868–872 CrossRef CAS PubMed.
- M. R. Fagiani, X. Song, S. Debnath, S. Gewinner, W. Schöllkopf, K. R. Asmis, F. A. Bischoff, F. Müller and J. Sauer, J. Phys. Chem. Lett., 2017, 8, 1272–1277 CrossRef CAS PubMed.
- T. M. Maier, A. D. Boese, J. Sauer, T. Wende, M. Fagiani and K. R. Asmis, J. Chem. Phys., 2014, 140, 204315 CrossRef PubMed.
- A. Khodadadi, M. Farahmandjou, M. Yaghoubi and A. R. Amani, Int. J. Appl. Ceram. Technol., 2019, 16, 718–726 CrossRef CAS.
- J. Sauer and H.-J. Freund, Catal. Lett., 2015, 145, 109–125 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: The PDF file contains the calculated IR spectra of several low-energy isomers for (Al2O3)1–5FeO+ in comparison with their respective IRPD spectrum (Fig. S1–S5), a Table with relative energies of all studied isomers (M = Fe, Al) obtained with different density functionals (Table S1), a table listing the experimentally observed IR bands for (Al2O3)2–5FeO+ (Table S2), and a figure showing relevant bond distances of the assigned isomers (Fig. S6). The ZIP compressed folder contains XYZ coordinate files for all calculated isomers. Each of these files also comprises the total electronic and zero point vibrational energy of the respective molecule. See DOI: https://doi.org/10.1039/d2cp02938c |
| ‡ These authors contributed equally to this work. |
| § Present address: Mulliken Center for Theoretical Chemistry, Clausius-Institute for Physical and Theoretical Chemistry, University of Bonn, Beringstr. 4, 53115 Bonn, Germany. |
| This journal is © the Owner Societies 2022 |