Computational insight into effective decomposition of NOX gas pollutants using N-vacancies in graphitic carbon nitride†
Yuewen
Yang
 a,
Yanling
Zhao
*a and
Ruiqin
Zhang
a,
Yanling
Zhao
*a and
Ruiqin
Zhang
 *ab
*ab
aDepartment of Physics, City University of Hong Kong, Hong Kong SAR 999077, China. E-mail: aprqz@cityu.edu.hk; apzyl@cityu.edu.hk
bShenzhen JL Computational Science and Applied Research Institute, Shenzhen 518131, China
First published on 24th November 2023
Abstract
Nitrogen oxide (NOX) gas pollutants pose severe threats to human health, the ozone layer, and the global climate, and thus finding suitable materials and methods to efficiently remove NOX has been of great interest for years. By studying the related photocatalysis and surface reactions, we herein propose to use the graphitic carbon nitride (g-CN) film with N-vacancies (g-CNNV) to decompose NOX. Based on density functional theory (DFT) and time-dependent DFT calculations, we revealed the decomposition mechanism of NO/NO2 gas on g-CNNV. We found that the N–O bond cleavage of NOX is usually accompanied by the N occupying the N-vacancy and oxygen formation, and subsequent light excitation promotes the oxygen desorption from the g-CN surface through photochemical processes of intersystem crossing and conical intersection. We demonstrated that the g-CNNV film under illumination can effectively decompose NOX into harmless oxygen. Therefore, coating the g-CNNV film on the outer walls of buildings or chimneys may be a promising green and economical strategy for NOX removal, given that the sunlight and surface defects can synergistically affect the electronic states of adsorbates and facilitate their favorable transformation by gas–solid interaction. This work offers a deep understanding of the fundamental process of surface photocatalytic reactions.
Introduction
Nitrogen oxides (NOX, including about 95% NO and 5% NO2),1 as the unavoidable primary pollutants in exhaust gas, are harmful to the human respiratory tract, ozone layer, and atmospheric composition.2 Owing to the positive standard Gibbs free energies of formation (ΔfGO) of 0.90 eV for NO and 0.53 eV for NO2 at room temperature and one standard atmospheric pressure,3 their reverse processes (i.e. NOX decomposition into non-toxic N2 and O2) are supposed to be thermodynamically favorable. However, the chemical reaction of NOX → N2 + O2 is very hard to directly achieve experimentally, which may be due to the extremely high barrier that makes it kinetically hard to occur.4 Great efforts have been made for over 40 years to efficiently remove NOX pollutants,5–8 through selective catalytic reduction (SCR), selective non-catalytic reduction (SNCR), wet scrubbing, electron beam, adsorption method, electrochemical method, non-thermal plasma method (Table S1†), etc. As an SCR method, the NOX decomposition on the material surface by photocatalytic assistance may be a green and economical strategy since cheap and efficient materials are expected to be screened from extensive and diverse candidates, such as noble metals,5 metal oxides,6 and carbon-based materials.7–10Owing to the advantages of low price, stability, and non-toxicity, carbon-based catalysts have attracted great attention in the field of NOX removal. To suppress the NOX emission from charcoal combustion, the solid char bound with nitrogen (char(N)) is often used as a NO-reducing agent.7 Many efforts in experiments and calculations have been made to study the possible reaction pathways between NO and char(N).11–15 It was computationally demonstrated that the heteroatom N distributed on the edge of the char(N) is usually the active site to chemically anchor the NO and reduce the energy barrier of NO reduction to N2.14 Since the graphitic carbon nitride (g-CN) material contains N, it was also adopted to study the NOX removal.4,16–21 However, direct NO decomposition into N2 and O2 on pure g-CN was not observed until the temperature was raised to 450 °C with a low conversion efficiency of 0.6% and 550 °C with a conversion efficiency of 8.9%.16 Higher temperatures of over 700 °C are expected to effectively decompose NO, but such temperatures are not suitable for the stable existence of g-CN. Computationally, the NOX is demonstrated to be merely physisorbed on pristine g-CN and a large activation energy (3.62 eV) is required for NO decomposition into N and O radicals on g-CN.17 Therefore, the catalytic ability of pristine g-CN is not ideal for NOX removal. The difference in the catalytic abilities between char(N) and pristine g-CN is attributed to their different N amounts. The few N heteroatoms in char(N) play the role of active sites in regulating the electron polarization and energy levels of frontier molecular orbitals, while the large amount of N in pristine g-CN makes the electron distribution so even that it is almost inert to NOX.
To enhance the catalytic activity of g-CN for NOX removal, experimental studies have attempted to dope Zn,4 Bi,18 the IIA group of elements (like Mg, Ca, Sr, and Ba),19 or N defects20 into the pristine g-CN. In these works, the NOX removal efficiencies have been substantially increased to ∼30–69%, especially for Zn- and Ba-doped g-CN with efficiencies as high as 69.4% and 62%. While the synthesis procedures of doping heteroatoms into g-CN are complicated, the g-CN with N vacancies (g-CNNV) can be easily synthesized by controlling the annealing temperature and condensation time.21–23 The N defects were identified as catalytic sites by the in situ diffuse reflectance infrared Fourier transform spectroscopy (DRIFTS) technique, which demonstrated the photocatalytic activity of g-CNNV with a NO removal efficiency of 43.6%, much higher than the 29.9% of pristine g-CN.20 For practical applications, it is very cost-effective to develop such metal-free and easy-to-synthesize g-CNNV films to be placed outdoors to remove NOX pollutant gases in the ambient environment.
By far, there is still a lack of direct experimental evidence that NO is indeed decomposed into products of N2 and O2,16 which indicates that the mechanism of NOX decomposition has not been sufficiently studied. Computational studies based on density functional theory (DFT) can be an ideal approach to provide a molecular-level understanding and demonstrate the chemical reaction mechanism according to experimental observation. For example, Cantatore et al. have used DFT to propose a novel strategy for the catalytic reduction of NO via oligomerization on B-doped graphene, where the energy landscapes showed the channels of NO decomposition into N2, N2O, NO2, and O2via N2O2− and N3O3− intermediates.24 Few computational studies of the NOX decomposition mechanism using g-CN as a catalyst are available, which triggers us to perform a DFT study on the gas–solid interaction between NOX and g-CNNV.
In this work, we computationally demonstrate whether the carbonaceous material of g-CNNV can effectively remove NOx gas pollutants. The NOX decomposition mechanism on g-CNNV will be elucidated by carrying out a series of DFT and time-dependent DFT (TD-DFT) calculations. The role of g-CNNV in the NOX decomposition will be revealed by showing the energy profiles for the chemical reactions of NOX with g-CNNV in the ground and excited states. This work would be of great significance for understanding the strong attractions of N vacancies of g-CN film to NOX molecules and their fundamental process of photo-assisted decompositions.
Computational methods and models
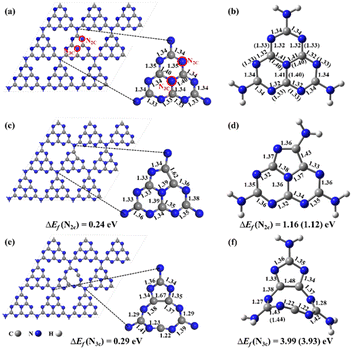
The previous experimental studies proved that g-CN was composed of numerous heptazines (also named tri-s-triazines) with a layered structure using X-ray diffraction patterns and X-ray photoelectron spectroscopy.22,23 Accordingly, a buckled and single-layered g-CN surface in a supercell of 3 × 3 × 1 (Fig. 1a) was constructed for anchoring the NOX species.25 To well study the chemical reactions and photochemical properties of NOX decomposition on the substrate, a cluster model was used, and the structure was cut out from the pristine g-CN and saturated by H atoms, named heptazine (stoichiometry: C6N10H6) (Fig. 1b). The N vacancy (NV) can be a missing two-coordinated N atom (N2C), named g-CNNV (N2C) (Fig. 1c) and heptazineNV (N2C) (Fig. 1d), and also be a missing three-coordinated N atom (N3C), named g-CNNV (N3C) (Fig. 1e) and heptazineNV (N3C) (Fig. 1f).The simulations of periodic systems in this work were implemented using the Vienna Ab initio Simulation Package (VASP).26,27 The vacuum layers were set as 15 Å to avoid the slab–image interaction. The Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional based on the generalized gradient approximation (GGA) is adopted with Grimme's D3 correction to well consider the van der Waals (vdW) interaction between the slab and adsorbents.28,29 For the plane-wave basis set, the electron–ion interaction is described by the projector augmented wave (PAW) method with a cutoff energy of 450 eV.30,31 The Monkhorst–Pack grids for k-space were set as 5 × 5 × 1. The forces for reaching equilibria of geometry optimizations were set as less than 0.01 eV Å−1 and the energy convergence criterion was 1.0 × 10−6 eV per atom. The electron population for adsorbents attached to the surface was analyzed using the Bader charge code.32 To investigate the thermal stability of NV in g-CNNV film, ab initio molecular dynamics (AIMD) simulation was performed in the NVT ensemble at temperatures of T = 500 K and 700 K for 10 ps with a time step of 2 fs.
All the cluster calculations were conducted on the Gaussian 09 program package.33 The ωB97XD exchange–correlation functional was employed for geometry optimizations and frequency calculations with the basis set of 6-31G(d,p) or aug-cc-pVDZ. The ωB97XD functional has been frequently employed in many previous g-CN studies.34–38 Local minima are confirmed without imaginary frequencies and transition states (TS) are confirmed with only one imaginary frequency, followed by the intrinsic reaction coordinate (IRC) calculations to verify that the TS is connected with the desired reactant and product. The charge transfer was analyzed by the natural population analysis (NPA) method.39 TD-ωB97XD/6-31G(d,p) and TD-ωB97XD/aug-cc-pVDZ calculations were performed to study the photochemical properties involved in the NOX decomposition in excited states. The spatial distributions of photogenerated holes and electrons were analyzed using the Multiwfn Code.40
The geometries optimized from supercells and clusters (Fig. 1a–f) are almost the same except for the heavier deformation of heptazineNV (N3C) than g-CNNV (N3C) due to the nine-membered ring which is strongly buckled in the cluster model. For N2C vacancy, the stable five-membered ring can be formed in both heptazineNV (N2C) and g-CNNV (N2C). The bond lengths of the heptazine backbone (Fig. 1b, d, and 1f) calculated with two basis sets of 6-31G(d,p) and aug-cc-pVDZ are very close, which indicates that the cluster structures predicted at the medium level of ωB97XD/6-31G(d,p) are comparable to the high level of ωB97XD/aug-cc-pVDZ.
To compare the thermal stability of the NV between N2C and N3C, the formation energy (ΔEf) is calculated as:
| ΔEf = Eg-CNNV/heptazineNV + μN − Eg-CN/heptazine, |
The adsorption energy (ΔEads) for NOX on the substrate is calculated as:
| ΔEads = Etot(complex) − Etot(NOX) − Etot(substrate), |
To consider the effects of temperature and entropy on the energy profiles of NOx decomposition on the substrate, Gibbs free energy is calculated as ΔG = ΔE + ΔZPE − TΔS.44,45 ΔG stands for the Gibbs free energy difference, ΔE is the difference of the internal energy between the products and the reactants, and ΔZPE is the change in the zero-point energy and ΔS is the change in the entropy.
Results and discussion
Active N2C vacancy for NO/NO2 chemisorption
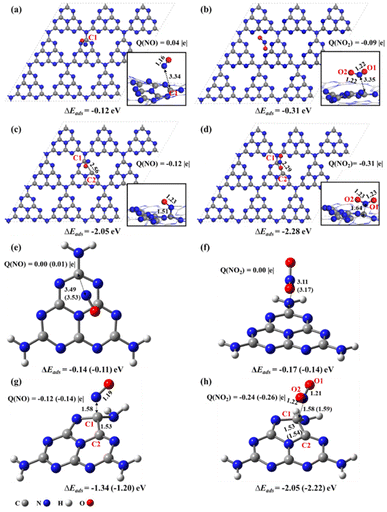
For pristine g-CN in the supercell (Fig. 2a and b), there only exists the physisorption with NO/NO2, as demonstrated by the long-range distance of 3.43/3.35 Å, small adsorption energies of −0.12/−0.31 eV, and slight charge transfer of less than 0.10 |e| between NO/NO2 and g-CN, in agreement with a previous study.17 These data well explain the low catalytic activity of pristine g-CN in the experimental work.16 By contrast, when there exists an N2C vacancy in the substrate, chemical bonding between NO/NO2 and g-CNNV (Fig. 2c and d) can be formed, as supported by the shorter distance of 1.51/1.64 Å between the N of NO/NO2 and the substrate C1 atom near the N2C, stronger adsorption energies of −2.05/−2.28 eV, and significant electron transfer of −0.12/−0.31 |e| from g-CNNV to NO/NO2. This indicates that the N2C vacancy is indeed an active site in the g-CNNV film for attracting NOX species, consistent with the previous experimental detection by situ-DRIFTS.20The calculated band gap of pristine g-CN is predicted to be 2.82 eV (Fig. S1a†), close to the experimental value of 2.74 eV.23 When the N2C vacancy is formed, the valence bands and conduction bands of g-CNNV (N2C) both move to lower energy levels and the band gap decreases to 2.52 eV (Fig. S1b†). This indicates that the g-CNNV with N2C vacancy is more favourable for the visible-light absorption than pristine g-CN to help convert NOX pollutants into harmless species.
With the cluster models, the NO/NO2 attachments on the perfect heptazine (Fig. 2e and f) and heptazineNV containing N2C (Fig. 2g and h) are also physisorption and chemisorption between NO/NO2 and heptazine/heptazineNV, as confirmed by the N–C1 distances and the charge transfer between the NO/NO2 and substrates. Consistent with the results based on supercell models, the NO/NO2 molecule acts as an electron acceptor when reaching the N2C vacancy. The C1–C2 bond of heptazineNV is slightly elongated to 1.53/1.53 Å by ωB97XD/6-31G(d,p) and 1.53/1.54 Å by ωB97XD/aug-cc-pVDZ due to the chemical bonding with NO/NO2. Similar results of cluster systems, compared to those of supercells, indicate that the cluster models instead of periodic ones can describe the NOX decomposition reactions on g-CNNV film.
The above results indicate that the g-CNNV/heptazineNV containing N2C vacancy is sensitive to the effective capture of NOX pollutant gas through gas–solid interaction. The NOX always has the N atom preferentially pointing towards the substrate, i.e. the N-oriented configuration is energetically lower than the O-oriented one for chemical bonding. This is fundamentally attributed to the favorable orbital matching between the N of NOX and the substrate. The frontier unoccupied molecular orbitals (MO) of NO/NO2 (Fig. S2a and b†) show that due to the significant orbital distribution on N, which is more than that on O, N is the more active site to form covalent bonds with the substrate. In addition, the frontier occupied MO of heptazineNV (Fig. S2c†) shows that the orbital is localized on the C1–C2 bond near the N2C vacancy (i.e. α-state HOMO), but basically uniformly distributes on the C3N3-rings of heptazine (Fig. S2d†), reflecting that the pristine g-CN is inert while the g-CNNV containing N2C vacancy is active to adsorbents.
NO decomposition catalyzed by the N2C vacancy
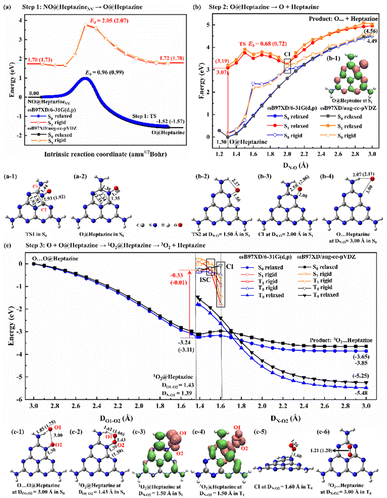
The NO decomposition catalyzed by N2C vacancy undergoes three steps, starting from the NO@heptazineNV configuration (Fig. 2g). Step 1 (Fig. 3a) is the N-intercalation into heptazineNV to leave the O chemically attached to heptazine (i.e. O@heptazine) in the ground state (S0). Step 2 (Fig. 3b) is the O-detachment from heptazine in the first singlet excited state (S1) under illumination. And step 3 (Fig. 3c) is the combination of the detached O with the remaining O@heptazine to eventually form triplet O2 (3O2) by photo assistance. The following discussion focusing on the DFT-calculated energy profiles will demonstrate that the overall reaction NO + heptazineNV → 3O2 + heptazine is feasible.For step 1, when the N of NO is chemically bound with the C1 atom of heptazineNV, the C1–C2 bond will be stretched until broken, and meanwhile, the C2 atom will attract the N atom of NO to form a new bond, so that the N (of NO) can be inserted into the middle of C1 and C2 to form a new conjugated bond of C1![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–C2 and heptazineNV becomes a perfect heptazine. In the TS1 structure (Fig. 3a-1), the distance of C1–C2 (DC1–C2) is enlarged to 1.93/1.92 Å and that of C2–N (DC2–N) is shortened to 1.93/1.92 Å, until the O of NO bonds with the perfect heptazine cluster, i.e. O@heptazine (Fig. 3a-2) with 2.34/2.35 Å for DC1–C2 and 1.35 Å for DC2–N by ωB97XD/6-31G(d,p) or ωB97XD/aug-cc-pVDZ. More details on the geometry transformation of N-intercalation into heptazineNV can be clearly supported by the distance evolutions of DC1–C2, DC1–N, DC2–N, and DN–O extracted from the IRC calculations (Fig. S3a and b†), which present the C1–C2 bond cleavage, C1
N–C2 and heptazineNV becomes a perfect heptazine. In the TS1 structure (Fig. 3a-1), the distance of C1–C2 (DC1–C2) is enlarged to 1.93/1.92 Å and that of C2–N (DC2–N) is shortened to 1.93/1.92 Å, until the O of NO bonds with the perfect heptazine cluster, i.e. O@heptazine (Fig. 3a-2) with 2.34/2.35 Å for DC1–C2 and 1.35 Å for DC2–N by ωB97XD/6-31G(d,p) or ωB97XD/aug-cc-pVDZ. More details on the geometry transformation of N-intercalation into heptazineNV can be clearly supported by the distance evolutions of DC1–C2, DC1–N, DC2–N, and DN–O extracted from the IRC calculations (Fig. S3a and b†), which present the C1–C2 bond cleavage, C1![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–C2 bond formation, and eventually O (of NO) chemisorbed on heptazine.
N–C2 bond formation, and eventually O (of NO) chemisorbed on heptazine.
The energy barrier (Eb) and the reaction energy for step 1 in S0 are estimated to be 0.96/0.99 eV and −1.52/−1.57 eV by ωB97XD/6-31G(d,p) or ωB97XD/aug-cc-pVDZ. The small energy barrier and exothermic reaction energy indicate that the N-intercalation of NO into heptazineNV easily proceeds in S0. To demonstrate that step 1 occurs preferentially in S0, we also calculated the potential energy surfaces (PES) in S1 for comparison, by taking representative points from the IRC curve in S0 and performing TD-DFT single-point energy calculations in S1. The almost parallel S0- and S1-PES indicate the impossibility of conical intersection (CI) from S1 decay to S0 states. The higher energy barrier (2.05/2.07 eV) and endothermic reaction heat (0.02/0.05 eV) in S1 predicted by TD-ωB97XD/6-31G(d,p) or TD-ωB97XD/aug-cc-pVDZ confirm that step 1 prefers S0 to S1 to occur. Therefore, the N2C vacancy contained in g-CNNV can effectively trap the N atom of NO at room temperature without illumination.
For step 2, the desorption of the O atom from heptazine must be accomplished with light assistance to overcome the endothermic energy generated by the O–N bond cleavage. In S0, the DN–O elongation based on O@heptazine corresponds to an energy profile of a nearly linear lifting until a high plateau; the spontaneous O-detachment from heptazine is thus not going to happen at room temperature. To avoid climbing the uphill slope of PES in S0, illumination can be used to change the chemical reaction route. The calculated UV-vis spectra (Fig. S3c and d†) of O@heptazine show that the most significant absorption peaks appear at ∼205 nm with a vertical excitation energy of ∼6 eV, belonging to the near UV region of sunlight. As the high excited-state always quickly decays to the S1 according to Kasha's rule,46 the photo-induced hole and electron distributions of O@heptazine in S1 are presented (Fig. 3b-1). It is found that both the O and N of NO carry positively charged holes upon UV-light irradiation, demonstrating the existence of Coulomb repulsion between them, which is favorable for the O-detachment from heptazine in S1.
The S1-PES by a relaxed scanning of TD-DFT shows that the N–O bond breaking of O@heptazine undergoes a very low energy barrier of ∼0.7 eV that is easy to overcome. The TS2 structure in S1 (Fig. 3b-2) appears at DN–O = 1.50 Å, which shows the breaking of the N–O bond and the formation of the N–H⋯O hydrogen bond. With the O atom moving away from heptazine, the PES in S1 and S0 states (i.e. the curves with filled symbols) approach each other, indicating a high possibility of CI. This conjecture is further supported by the S0-PES (with hollow symbols) through the rigid scanning using the relaxed S1-geometries, which is much closer to the S1-PES. The approximate CI point (Fig. 3b-3) is probably located at DN–O = 2.00 Å, where the N–O bond is basically broken while the N–H⋯O hydrogen bond still exists. After the decay from S1 to S0 states, the O-desorption process corresponds to a slow uphill slope of S0-PES, which is mainly dominated by the continuous vanishing of the O–N bond. It is noted that the N–H⋯O hydrogen bond is forming, with the length changing from 2.58/2.86 Å in CI at DN–O = 2.00 Å (Fig. 3b-3) to 2.07/2.11 Å in product O⋯heptazine at DN–O = 3.00 Å (Fig. 3b-4). This is reasonable because the surface edge is usually active for binding with external species. In step 2, the photochemical process plays an important role in helping the O-desorption from the surface to avoid walking along the long and steep uphill of PES in S0 and reach the final platform as close as possible.
In step 3 (Fig. 3c), if the O escapes from binding with the N of heptazine to form a free O atom, it will probably combine with other remaining O@heptazine to form a noncovalent interaction configuration, O⋯O@heptazine (Fig. 3c-1), and finally release oxygen gas under illumination. Step 3 is actually the reaction between the O@heptazine produced in step 1 and the free O atom produced in step 2. Starting from the O⋯O@heptazine configuration (Fig. 3c-1), where O1 forms a hydrogen bond with the H at the edge of heptazine while O2 covalently binds with heptazine, accompanied with the O1 and O2 distance (DO1–O2) of 3.00 Å, the S0-PES shows a smooth decrease with DO1–O2 in the range of 3.00–1.43 Å. The significant energy decrease of 3.24/3.11 eV through a relaxed scanning of ωB97XD/6-31G(d,p) or ωB97XD/aug-cc-pVDZ is mainly due to the formation of the singlet O2 (1O2) on heptazine, i.e.1O2@heptazine (Fig. 3c-2).
However, the triplet O2 (3O2) is the final stable state in the atmosphere, thus the multiplicity conversion of oxygen gas from singlet to triplet is supposed to be achieved by photo-assistance.47 Starting from 1O2@heptazine, we first performed the relaxed PES scanning in both S0 and T0 states by manually fixing the DN–O2 in the range of 1.40–3.00 Å. The turning point of PES trends in S0 and T0 appears at DN–O2 = 1.70 Å, after which the 3O2 is more stable on heptazine than 1O2, consistent with a natural phenomenon. The diverse intersystem crossing (ISC) should occur before DN–O2 = 1.70 Å. We thus compared the energies in S1 or T1 states at DN–O2 = 1.40, 1.50, and 1.60 Å by relaxed or rigid scanning (Table S2†). Based on 1O2@heptazine, the calculated UV-Vis spectra (Fig. S3e and f†) show that 1O2@heptazine at DN–O2 = 1.40 Å can absorb near-UV light sensitively and then quickly decay to the S1 state. Because the S1 energy is lower than T1 at DN–O2 = 1.40 Å while it is reversed at DN–O2 = 1.50 Å, the system is supposed to converse the spin state from the S1 to T1 states through the ISC during DN–O2 = 1.40–1.50 Å.47 Distinct from the S1-state photoinduced carrier distribution at DN–O2 = 1.50 Å (Fig. 3c-3), when the system reaches the T1 state, a significant coulombic repulsion occurs between O2 and heptazine in the T1-state (Fig. 3c-4). This demonstrates that the ISC from S1 to T1 states will greatly promote the release of the 3O2 from heptazine. The energy order reversal between T1 and T0 states at DN–O2 = 1.50 and 1.60 Å shows that the CI point (Fig. 3c-5) is probably located at DN–O2 = 1.50–1.60 Å, after which the system will decay back to the ground state. Notably, unlike the rising outline of the S0-PES for O leaving heptazine (Fig. 3b), the T0-PES (Fig. 3c) shows a descending trend when 3O2 is getting away from heptazine. We attribute this difference to the formation of the strong chemical bond in 3O2, which has a more significant effect on the T0-PES than the N–O bond cleavage. For example, the bond order (BO) in 3O2 when DN–O2 = 1.60 Å is calculated to be 1.64 by ωB97XD/6-31G(d,p), while it increased to 1.85 when DN–O2 = 3.00 Å. Overall, the surface photocatalysis in step 3 plays an important role in driving the system to undergo the electronic-state transitions of S0 → S17/S12 → S1 → T1 → T0, so that the 3O2 molecule eventually detaches from heptazine smoothly (Fig. 3c-6).
NO2 decomposition catalyzed by the N2C vacancy
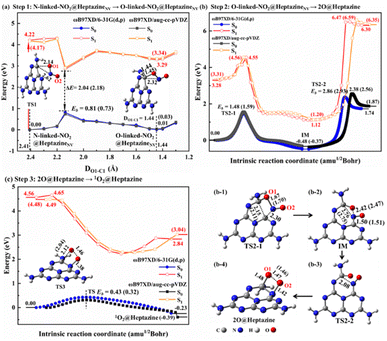
Although NO2 is a minor NOX pollutant gas, it is more toxic than NO and can react with water to form harmful HNO3, HNO2, and NO, and thus it is also very necessary to study its removal. In this work, we theoretically propose that the NO2 decomposition process catalyzed by N2C vacancy would go through four steps, i.e. step 1: thermal isomerization (Fig. 4a), step 2: N-intercalation (Fig. 4b), step 3: 1O2 formation (Fig. 4c), and step 4: photo-assisted 3O2 release.To facilitate the N-intercalation into heptazineNV, NO2@heptazineNV (Fig. 2h) needs first to form a favorable stereo-structure, which can be achieved by thermal isomerization from N-linked to O-linked-NO2@heptazineNV configurations (Fig. 4a). The isomerization process corresponds to a low energy barrier (Eb) of 0.81/0.73 eV for TS1 and a small energy increase of 0.01/0.03 eV for O-linked-NO2@heptazineNV, as predicted by ωB97XD/6-31G(d,p) or ωB97XD/aug-cc-pVDZ in S0. This indicates that the ambient NO2 gas can be flexibly chemisorbed on heptazineNVvia N-linkage or O-linkage under slight temperature fluctuations. Besides, the chemisorption isomerization prefers to occur in S0, as the PES in S1 is far from that in S0 with a large energy difference of over 2 eV between their closest points.
For step 2, the N-intercalation of NO2 into heptazineNV is accompanied by the N2C vacancy filled with N of NO2 and two O of NO2 chemisorbed on heptazine, i.e. 2O@heptazine. The energy profiles by IRC calculations (Fig. 4b) show that this process will undergo two TSs with the energy barriers of 1.48/1.59 eV for TS2-1 and 2.86/2.93 eV for TS2-2, and two local minima with the energy decrease of −0.48/−0.37 eV for the intermediate (IM) and energy increase of 2.22/2.24 eV for 2O@heptazine, as predicted by ωB97XD/6-31G(d,p) or ωB97XD/aug-cc-pVDZ in S0. This indicates that the chemical reaction from O-linked-NO2@heptazineNV to IM is easier and faster than that from IM to 2O@heptazine. In TS2-1, when the O1 of the NO2 molecule is bound to the C1 atom of heptazineNV, the C1–C2 and O1–N bonds are significantly enlarged to 2.15/2.11 and 1.67/1.70 Å, and simultaneously the N–C2 bond is formed. The O1–N distance of 2.42/2.47 Å in IM indicates that the NO2 molecule is totally decomposed. In TS2-2, after the N is bound with C2, the N is trying to reach the C1 atom to form the conjugated C1![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–C2 bond. However, the steric effect from structural deformation and Coulomb repulsion from negatively charged O1 strongly hinder the N atom from approaching C1, thus resulting in a higher barrier and a larger endothermic reaction energy. Hence, from O-linked-NO2@heptazineNV to 2O@heptazine, the N atom binding with the C1 atom is a rate-determining reaction. The other distance evolutions of DC1–C2, DC1–N, DC2–N, and DO1–N extracted from IRC calculations (Fig. S4a–d†) clearly support the breaking of the C1–C2 bond, formation of the C1
N–C2 bond. However, the steric effect from structural deformation and Coulomb repulsion from negatively charged O1 strongly hinder the N atom from approaching C1, thus resulting in a higher barrier and a larger endothermic reaction energy. Hence, from O-linked-NO2@heptazineNV to 2O@heptazine, the N atom binding with the C1 atom is a rate-determining reaction. The other distance evolutions of DC1–C2, DC1–N, DC2–N, and DO1–N extracted from IRC calculations (Fig. S4a–d†) clearly support the breaking of the C1–C2 bond, formation of the C1![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–C2 bond, and chemical bonding of O1 and O2 with the C1 and C2 atoms of heptazine. In addition, to demonstrate that step 2 prefers to occur in S0, the IRC curves in S1 are calculated by extracting representative points from IRC curves in S0. The almost parallel curves between the S1 and S0 states show the absence of CI points; therefore, it is not necessary to use sunlight to force the N-intercalation of NO2 into heptazineNV.
N–C2 bond, and chemical bonding of O1 and O2 with the C1 and C2 atoms of heptazine. In addition, to demonstrate that step 2 prefers to occur in S0, the IRC curves in S1 are calculated by extracting representative points from IRC curves in S0. The almost parallel curves between the S1 and S0 states show the absence of CI points; therefore, it is not necessary to use sunlight to force the N-intercalation of NO2 into heptazineNV.
For step 3, the reaction from 2O@heptazine to 1O2@heptazine is also favorable to proceed in S0 owing to the non-crossed PES between the S0 and S1 states (Fig. 4c). In TS3, the O1 atom leaves the C1 atom for combining with the O2 atom to form a 1O2 molecule, which will link with heptazine through the N–O2 bond, named 1O2@heptazine. The energy barrier for TS3 is predicted to be 0.43 or 0.32 eV by ωB97XD/6-31G(d,p) or ωB97XD/aug-cc-pVDZ, which is easy to overcome at room temperature. The distance evolutions of DC1–O1, DN–O2, and DO1–O2 extracted from IRC calculations (Fig. S4e and f†) clearly support the breaking of the C1–O1 bond and the stable attachment of the 1O2 to heptazine by the N–O2 bond.
For the last step 4, the oxygen gas should also be converted from singlet to triplet through photo-assisted ISC for a final release from heptazine. This step is exactly the same as the second half of step 3 during NO decomposition, referring to the PES as a function of DN–O2 (Fig. 3c). Thus, the results and discussion about step 4 of NO2 decomposition are omitted.
NO/NO2 decomposition catalyzed by the N2C vacancy at T = 300 K and P = 1.00 atm
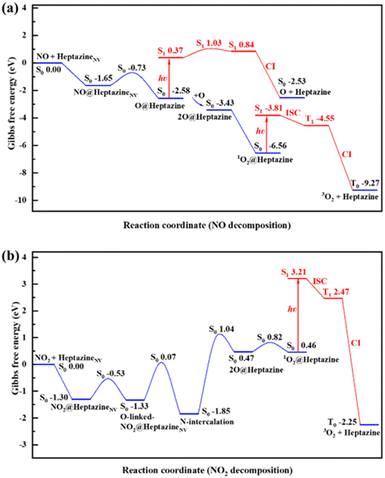
The aforementioned energy profiles merely reflect the change of potential energies in the NO/NO2 decomposition process.To consider the effects of temperature and entropy increase on the NO/NO2 decomposition on heptazineNV, the Gibbs free energy barrier (Gb) and the change (ΔG) of each step were additionally calculated at room temperature, T = 300 K (Fig. 5), and a higher temperature, T = 500 K, with ambient pressure P = 1.00 atm (Fig. S5†).48 Notably, because of the ignorable difference in calculated results of energy profiles between ωB97XD/6-31G(d,p) and ωB97XD/aug-cc-pVDZ, we hereafter only calculated the Gibbs free energies at the level of ωB97XD/6-31G(d,p).
In summary, the NO/NO2 decomposition mechanism on heptazineNV is as follows:
For NO decomposition at 300 K (Fig. 5a), from reactants of NO and heptazineNV to NO@heptazineNV, and then to O@heptazine, the exothermic free energies (ΔG = −1.65 and −0.93 eV) and mild barrier (Gb = 0.92 eV) indicate that NO can be easily captured by the N2C vacancy of heptazineNV. Compared with the favorable N-intercalation of NO into heptazineNV, the subsequent O-desorption from heptazine (i.e. O@heptazine → O + heptazine) becomes unfavorable to occur in the S0 state, which is an endothermic reaction. The free energy difference between O@heptazine and products of O and heptazine in S0 is calculated to be ΔG = 0.05 eV. But under illumination, the O@heptazine will be first photoexcited (ΔG = 2.95 eV), then go through a free energy barrier (Gb = 0.66 eV) in S1, and finally decay back to the products of O and heptazine in S0 through a CI point. And the ΔG decreased to −2.16 eV through photo assistance.
It becomes favorable for the reaction to spontaneously occur in the ambient atmosphere, since light irradiation can alleviate the difficulty of O-desorption. Hence, the room temperature environment exposed to sunlight might promote the release of O from heptazine.
Once O becomes free from heptazine, it will combine with the remaining O@heptazine to form 1O2 on heptazine with a free energy decrease (ΔG = −0.85 eV), which is a spontaneous reaction at room temperature. Although the subsequent process from 1O2@heptazine to 3O2 release from heptazine is also spontaneous (ΔG = −2.71 eV), the different electron spin means that it must undergo photoexcitation (ΔG = 2.75 eV), ISC from S1 to T1 (ΔG = −0.74 eV), and decay from T1 to T0 through CI (ΔG = −4.72 eV) to be successful. The photoexcitation can be continuously provided by sunlight, which can thus ensure the smooth release of 3O2 from heptazine. Overall, the rate-determining step for NO decomposition on heptazineNV is the N-intercalation of NO into heptazineNV with a mild energy barrier.
For NO2 decomposition (Fig. 5b), the process from reactants of NO2 and heptazineNV to the N-intercalation phase is spontaneous with the negative ΔG = −1.30, −0.03, −0.52 eV and mild barriers of Gb = 0.77, 1.40 eV. However, the later process towards 2O@heptazine is relatively difficult to occur due to the large barrier of Gb = 2.89 eV and endothermic free energy of ΔG = 2.32 eV. The following processes from 2O@heptazine to 1O2@heptazine (small barrier of Gb = 0.35 eV) and from 1O2@heptazine to 3O2@heptazine (the same as that in NO decomposition) can occur smoothly.
At a higher temperature of T = 500 K (Fig. S5 and Table S3†), the adsorption free energy of NO/NO2 on heptazineNV becomes less exothermic, i.e. from −1.65 to −1.30 eV for NO and from −1.30 to −0.88 eV for NO2, which may be attributed to the higher temperature accelerating molecular vibrations while increasing the detachment possibility of gas species on the solid substrate. In particular, the free energy barriers for NO2 decomposition on heptazineNV at T = 500 K are all lifted relative to those at T = 300 K, which indicates that the increase in temperature cannot facilitate the NO2 decomposition by g-CNNV film. Meanwhile, the temperature effect on the Gibbs free energy changes and barriers for NO decomposition reactions is much less than that for NO2 decomposition. The room-temperature environment where the g-CNNV film is applied may be as favorable as higher temperatures for NO removal.
Notably, once the N vacancy of g-CNNV is occupied by the N of NOX, the g-CNNV film will turn into pristine g-CN and lose the activity for the decomposition of NOX gas pollutants. Therefore, the g-CNNV film in practical applications needs to be refreshed regularly through post-annealing treatment to recover the surface reactivity and photocatalytic activity for NOx removal. Note that, by post-annealing the pristine g-CN film at 400 °C with constant N2 flow, some N atoms can be removed from the tri-s-triazine network to form the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds.22
C bonds.22
In addition, it is demonstrated that the N2C vacancy in g-CNNV film can be well maintained even at higher temperatures. By performing AIMD simulations at T = 500 K and 700 K, the total energies of g-CNNV (N2C) keep fluctuating toward stable values (Fig. S6a and b†) and meanwhile there are no significant conformational changes in g-CNNV (N2C) during the 10 ps simulations.
Last, it is known that CO or SO2 in pollutants may poison the catalyst surface and reduce the activity.41 Therefore, we also tested the adsorptions of common pollutants CO and SO2 on the surface of g-CNNV (N2C). It is found that the CO and SO2 molecules are just weakly adsorbed on the g-CNNV (N2C) surface with much smaller adsorption energies of −0.12 eV (Fig. S6c†) and −0.28 eV (Fig. S6d†) than those of NO (−2.05 eV, Fig. 2c) and NO2 (−2.28 eV, Fig. 2d). The charge transfer between CO/SO2 and the surface is almost negligible (less than 0.01e). It is thus demonstrated that the g-CNNV catalyst is excellent for resisting CO and SO2 poisoning.
Conclusions
To reduce the emission of NOX gas pollutants in human production and life, here we propose a green strategy for NOX removal utilizing the g-CN film containing N vacancies (g-CNNV). Our computational results show that the g-CNNV surface can act as a photocatalyst and reactant to synergistically promote the NO/NO2 decomposition into triplet 3O2, while the N of NO/NO2 occupies the N vacancy. The NO/NO2 decomposition on g-CNNV film undergoes multiple steps including chemisorption, N intercalation, singlet 1O2 formation, and triplet 3O2 release. Among them, the N-intercalation of NO into g-CNNV during NO decomposition and chemisorption of two O atoms on g-CN during NO2 decomposition are their respective rate-determining steps. N vacancies play a key role in trapping NOX on the surface and subsequently forming favorable configurations for NOX decomposition. The illumination can help overcome the high barrier in the ground state, achieve intersystem conversion for O2 molecules from singlet to triplet states, and decay from the excited to ground states through the CI point. The influence of temperature in the process of NO decomposition by g-CNNV film is smaller than that of NO2. This work offers a deep understanding of the reaction mechanism of surface photocatalysis for NOX removal and also a promising strategy for solving practical problems in which coating a well-polymerized g-CN film with adjustable N vacancies (i.e. C-rich g-CN) on the outer walls of buildings or chimneys may be effective for NOX removal under sunlight irradiation.Author contributions
Y. W. Yang: methodology, data curation, and writing – original draft. Y. L. Zhao: methodology, writing – review & editing. R. Q. Zhang: funding, computational resources, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge the financial support from the Environment and Conservation Fund of Hong Kong (43/2021) and Shenzhen Natural Science Foundation (JCYJ20190813164801693). This work was carried out using the computational facilities, CityU Burgundy, managed and provided by the Computing Services Centre at the City University of Hong Kong (https://www.cityu.edu.hk/).References
- Z. Que, X. Ai and S. Wu, Int. J. Miner., Metall. Mater., 2021, 28, 1453–1461 CrossRef CAS
.
- M. V. Twigg, Appl. Catal., B, 2007, 70, 2–15 CrossRef CAS
.
- NIST-JANAF Thermochemical Tables, https://janaf.nist.gov/ Search PubMed.
- J. Zhu, Y. Wei, W. Chen, Z. Zhao and A. Thomas, Chem. Commun., 2010, 46, 6965–6967 RSC
.
- B.-s. Tu, W. Sun, Y.-j. Xue, W. Q. Zaman, L.-m. Cao and J. Yang, ACS Sustainable Chem. Eng., 2017, 5, 5200–5207 CrossRef CAS
.
- C. M. Kalamaras, G. G. Olympiou, V. I. Pârvulescu and B. Cojocaru, Appl. Catal., B, 2017, 206, 308–318 CrossRef CAS
.
- F. Guo, M. J. Jensen, L. L. Baxter and W. C. Hecker, Energy Fuels, 2014, 28, 4762–4768 CrossRef CAS
.
- J. Yang, S. Yuan, S. Wang, M. Yang, B. Shen, Q. Zhang, Z. Zhang, F. Wang, L. Xu and Z. Wang, Energy Fuels, 2020, 34, 8726–8731 CrossRef CAS
.
- K. Feng, Y. Hu and T. Cao, Fuel, 2022, 316, 123148 CrossRef CAS
.
- J. Yang, L. Chen, S. Yuan, M. Yang, Y. Huang, J. Su, Z. Zhang, Z. Wang, L. Xu and B. Shen, J. Phys. Chem. C, 2021, 125, 24381–24395 CrossRef CAS
.
- Y.-F. Chen, S. Su, Y.-W. Song, T. Liu, Z.-H. Wang, T. Shu, M.-X. Qing, Y. Wang, S. Hu and Z.-X. Zhang,
et al.
, Combust. Flame, 2022, 237, 111823 CrossRef CAS
.
- H. Zhang, X. Jiang and J. Liu, Combust. Flame, 2020, 220, 107–118 CrossRef CAS
.
- H. Zhang, J. Liu, J. Shen and X. Jiang, Energy, 2015, 82, 312–321 CrossRef CAS
.
- J. Yang, L. Chen, J. Su, Y. Huang, M. Zhang, M. Gao, M. Yang, S. Yuan, X. Wang and B. Shen, Fuel, 2022, 321, 124065 CrossRef CAS
.
- M. Dong, H. Wang, L. Xu, Y. Zou, B. Shen, X. Wang and J. Yang, J. Phys. Chem. A, 2022, 126, 6148–6159 CrossRef CAS PubMed
.
- M. Vennewald, A. Iemhoff, D. Ditz and R. Palkovits, Catal. Sci. Technol., 2022, 12, 1741–1745 RSC
.
- Y. Ren, Q. Han, Y. Zhao, H. Wen and Z. Jiang, J. Hazard. Mater., 2021, 404, 124153 CrossRef CAS PubMed
.
- G. Jiang, X. Li, M. Lan, T. Shen, X. Lv, F. Dong and S. Zhang, Appl. Catal., B, 2017, 205, 532–540 CrossRef CAS
.
- M. Zhou, G. Dong, J. Ma, F. Dong, C. Wang and J. Sun, Appl. Catal., B, 2020, 273, 119007 CrossRef CAS
.
- J. Cao, J. Zhang, X. Dong, H. Fu, X. Zhang, X. Lv, Y. Li and G. Jiang, Appl. Catal., B, 2019, 249, 266–274 CrossRef CAS
.
- P. Niu, L. C. Yin, Y. Q. Yang, G. Liu and H. M. Chen, Adv. Mater., 2014, 26, 8046–8052 CrossRef CAS PubMed
.
- J. Bian, L. Xi, J. Li, Z. Xiong, C. Huang, K. M. Lange, J. Tang, M. Shalom and R. Q. Zhang, Chem. J., 2017, 12, 1005–1012 CAS
.
- P. Niu, G. Liu and H.-M. Cheng, J. Phys. Chem. C, 2012, 116, 11013–11018 CrossRef CAS
.
- V. Cantatore and I. Panas, J. Chem. Phys., 2016, 144, 151102 CrossRef PubMed
.
- Y. Yang, C. Yin, K. Li, H. Tang, Y. Wang and Z. Wu, J. Electrochem. Soc., 2019, 166, F755–F759 CrossRef CAS
.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS
.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed
.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed
.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed
.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS
.
- W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens.Matter, 2009, 21, 084204 CrossRef CAS PubMed
.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci and G. A. Petersson, et al., Gaussian 09, Gaussian, Inc., Wallingford, CT, 2013 Search PubMed
.
- J. Ehrmaier, X. Huang, E. J. Rabe, K. L. Corp, C. W. Schlenker, A. L. Sobolewski and W. Domcke, J. Phys. Chem. A, 2020, 124, 3698–3710 CrossRef CAS PubMed
.
- J. Ehrmaier, T. N. V. Karsili, A. L. Sobolewski and W. Domcke, J. Phys. Chem. A, 2017, 121, 4754–4764 CrossRef CAS PubMed
.
- X. Huang and W. Domcke, J. Phys. Chem. A, 2021, 125, 9917–9931 CrossRef CAS PubMed
.
- N. Ullah, S. Chen, Y. Zhao and R. Zhang, J. Phys. Chem. Lett., 2019, 10, 4310–4316 CrossRef CAS PubMed
.
- N. Ullah, S. Chen and R. Zhang, Phys. Chem. Chem. Phys., 2021, 23, 23090–23095 RSC
.
- A. E. Reed, R. B. Weinstock and F. Weinhold, J. Chem. Phys., 1985, 83, 735–746 CrossRef CAS
.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed
.
- Y. Yang, K. Li, Y. Meng, Y. Wang and Z. Wu, New J. Chem., 2018, 42, 6873–6879 RSC
.
- Y. Meng, X. Qu, K. Li, Y. Yang, Y. Wang and Z. Wu, J. Phys. Chem. C, 2019, 123, 5176–5187 CrossRef CAS
.
- N. Wang, Y. Yang, Y. Wang, K. Li and Z. Wu, Results in Surfaces and Interfaces, 2022, 7, 100055 CrossRef
.
- Y. Meng, K. Li, Y. Yang, Y. Wang and Z. Wu, J. Electrochem. Soc., 2018, 165, F145–F151 CrossRef CAS
.
- T. Lu and Q. Chen, Comput. Theor. Chem., 2021, 1200, 113249 CrossRef CAS
.
- M. Kasha, Discuss. Faraday Soc., 1950, 9, 14–19 RSC
.
- M. Kasha, Acta Phys. Pol., A, 1999, 95, 15–36 CrossRef CAS
.
- S. Liu, L. Cheng, K. Li, Y. Wang, Y. Yang and Z. Wu, J. Mol. Graphics Modell., 2018, 80, 293–298 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ta05872g |
| This journal is © The Royal Society of Chemistry 2024 |