Open Access Article
Open Access ArticlePt single crystal surfaces in electrochemistry and electrocatalysis
Juan M.
Feliu
 * and
Enrique
Herrero
* and
Enrique
Herrero

Instituto de Electroquímica, Universidad de Alicante, Apdo. 99, E-03080 Alicante, Spain. E-mail: juan.feliu@ua.es
First published on 20th November 2023
Abstract
In this review, recent advances in the use of platinum single-crystal surfaces in electrochemistry are addressed. The starting point is the voltammetric characterization in a supporting electrolyte because the profile can be used as a fingerprint of the surface, allowing the surface quality and solution cleanliness to be established. The signals appearing in these voltammograms have been assigned to the adsorption of H, OH, and the anions in the supporting electrolyte. Then, the distinctive behavior of the Pt(111) electrode regarding the adsorption of species and the electrocatalysis in comparison with the other single-crystal surfaces is discussed. For the H/OH adsorption, the (111) ordered domain is the only one in which both processes appear in different potential windows. For the remaining ordered domains, steps, and kinks, both processes overlap, giving rise to signals that correspond to the competitive adsorption/desorption of OH and H. This fact implies that OH may be adsorbed on the surface at potentials as low as 0.15 V, which is a paradigm shift in the up-to-now prevailing understanding of the electrochemical behavior of platinum electrodes and has important implications for the elucidation of the mechanism of electrocatalytic reactions. The effects of this new knowledge on the proposed reaction mechanisms for the oxidation of CO and small organic molecules and the reduction of oxygen and hydrogen peroxide are discussed in detail. Since the elucidation of the reaction mechanisms requires in many cases the use of computational modeling, the conditions that the models should fulfill to reach valid conclusions are discussed. Relevant examples, which highlight the importance of the local structure of the interphase in the electrochemical behavior are given.
Broader contextThe use of single-crystal electrodes not only allows the surface structure dependence of electrochemical reactions to be demonstrated and analyzed but is also of vital importance in elucidating reaction mechanisms. For that, a combination of experimental and theoretical results is used. Thus, the results obtained from them have important and practical applications. However, the experiments should be carried out properly and the analysis of the results should take into account all the relevant species and parameters of the interphase. In this review, the most relevant aspects of the electrochemical and electrocatalytic behavior of platinum single-crystal electrodes are dealt with, emphasizing the adsorbed species and properties of the interphase that affect the electrocatalytic behavior. |
Introduction
Electrochemical reactions take place at the electrode|electrolyte interphase. During these reactions, a specific interaction between the electrode and some of the species involved in the reaction is frequently detected. In these cases, an important dependence of the reaction rate on the surface composition and structure of the electrode is found. Since the alteration of the composition of the electrode is easily implemented, this dependence was the first one to be studied, and good correlations between the activity and the properties of the materials have been found.1,2 On the other hand, a clear understanding of the surface structure effects on electrochemistry and electrocatalysis required the use of model electrode surfaces with a controlled structure. For that, single-crystal electrodes have become essential tools to study the surface structure dependence of the electrochemical reactions. Moreover, for reactions in which several electrons are exchanged, multiple reaction pathways are common. Under these circumstances, not only the reaction rate but also the relative rate of the different pathways will change depending on the surface structure, creating a complex scenario. Thus, the simplification of the surface structure brought about by using single-crystal electrodes has allowed for untangling the reaction mechanisms and the understanding of how surface structure affects electrochemical reactivity.Among single-crystal electrodes, platinum has been the most studied metal because it has the best electrocatalytic properties of all pure metals. For this reason, the properties of new materials are usually compared to those of platinum. Additionally, it is known that electrocatalytic reactions are structure sensitive, and thus the reference behavior is that of single crystal electrodes. The correct use of platinum single-crystal surfaces in electrochemistry required the development of the flame annealing technique by Clavier.3 From that point, the knowledge of how the surface structure of the electrode affects electrocatalysis has advanced significantly, and detailed reaction mechanisms have been proposed by using them. Moreover, the experimental results have been complemented by computational modeling, since single-crystal surfaces can be implemented in density functional theory (DFT) calculations. In this respect, experiments should be carried out properly so that the observed differences are a real consequence of the different surface structures. Likewise, all the possible species at the interphase and the different adsorption properties of the single-crystal surfaces should be considered when analyzing the results. Also in the modeling, all the species relevant to the reaction should be included. In this review, all these factors will be analyzed, so that a correct interpretation of the results can be made.
Voltammetric characterization of platinum single crystal electrodes
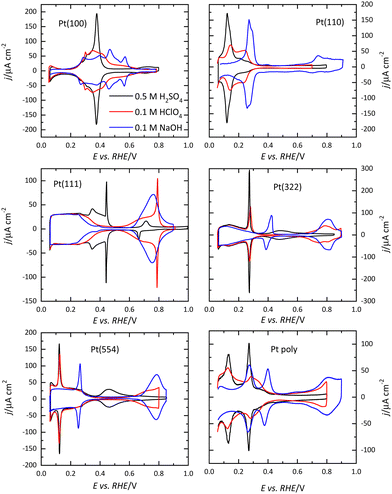
Voltammetric profiles of the platinum single-crystal electrodes have been used as fingerprints for their characterization since they are strongly dependent on the surface structure. Thus, distinctive signals can be associated with the presence of (111), (100), and (110) terraces or steps, as has been extensively described.4,5 These electrochemical signals are not only important because they allow for the characterization of the surface quality and cleanliness, but also because they correspond to surface processes that take place at different potentials. These processes have to be taken into account if the reactivity of these surfaces for different electrocatalytic reactions is to be analyzed and rationalized. Fig. 1 shows the voltammetric profiles of representative platinum single-crystal surfaces in perchloric acid, sulfuric acid, and sodium hydroxide solutions. In all cases, these signals correspond to the adsorption of hydrogen, or the anion present in the electrolytic solution. For sulfuric acid solutions, the adsorbed anion is sulfate, whereas in perchloric acid or sodium hydroxide solutions adsorbed OH gives rise to part of the signals. It should be highlighted that the interaction of perchlorate anions with the surface is non-specific (that is, it is purely coulombic), and thus, hydroxyl anions are the species specifically interacting with the surface.It should be stressed that these voltammetric profiles are stable upon cycling between 0.06 V and 0.8–0.9 V (all electrode potentials are potentials are referred to the RHE scale unless otherwise stated). The presence of impurities in the solution leads to the diminution of the characteristic signals upon cycling.6 This is especially evident for the sharp peaks observed for the Pt(111) or Pt(100) electrodes in the different media. Fig. 2 shows the voltammetric profiles of a Pt(111) electrode in perchloric and sulfuric acid solutions with different amounts of uncontrolled impurities. As can be observed, those impurities adsorb on the surface, blocking progressively the surface and preventing the hydrogen and anion adsorption. Since the presence of these impurities can alter the electrochemical behavior of the electrodes, it is strongly recommended to stop the experiment and clean the cell again.
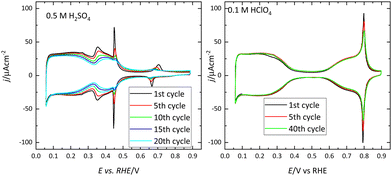 | ||
| Fig. 2 Evolution upon cycling of the voltammetric profiles of a Pt(111) electrode in 0.5 M H2SO4 and 0.1 M HClO4 with different levels of impurities. Scan rate: 50 mV s−1. | ||
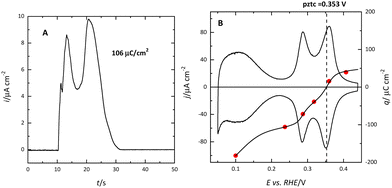
As Fig. 1 shows, the voltammetric profiles of the different platinum surfaces are very sensitive to the surface structure. However, the electrochemical signals do not contain any chemical specificity. Thus, the identification of the process responsible for the signals requires the use of other techniques. The first technique that allowed for the identification of the species is the charge displacement method.7–9 In this method, a neutral probe, N, which adsorbs strongly on the surface, replaces the adsorbed species generating a transient current during its adsorption process. Thus, if hydrogen is adsorbed on the surface, the measured current will be positive, because it corresponds to an oxidative process:
| Pt–H + N → Pt–N + H+ + e− | (1) |
| Pt–A + N → Pt–N + An− + ne− | (2) |
For Pt(100), the charge curve in HClO4 or NaOH solutions changes its sign at ca 0.4 V, in the middle of the voltammetric signals. This fact implies that H and OH adsorption processes overlap. Thus, at 0.1 V the surface is covered by a monolayer of adsorbed hydrogen, whereas at 0.6 V, an OH layer covers the electrode.14 In sulfuric acid solutions, the voltammetric profile shows an intense peak at 0.36 V which is related to the competitive adsorption between sulfate and hydrogen. A similar situation is observed for the Pt(110) electrode, where the characteristic peaks contain contributions both from adsorbed OH and H. For this electrode, the voltammetric profile is very sensitive to the annealing conditions due to the presence of surface reconstructions.15,16 Thus, when the electrode is cooled down in reductive conditions, the (1 × 2) reconstruction is obtained and the profile has two main peaks. On the other hand, electrodes cooled down in the presence of CO present a voltammogram with multiple peaks, characteristic of the (1 × 1) structure (Fig. 4).
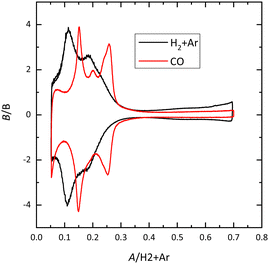 | ||
| Fig. 4 Voltammetric profile for the Pt(110) electrode in 0.1 M HClO4 cooled down in different atmospheres. Scan rate: 50 mV s−1. | ||
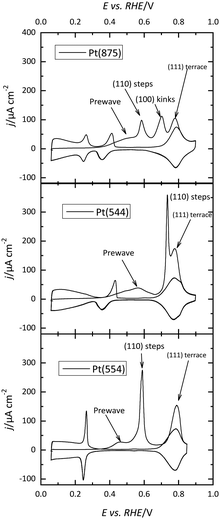
The presence of steps on the different terraces also gives rise to distinctive signals. Steps with (110) or (100) symmetry on the (111) terraces result in the appearance of peaks at potentials below 0.45 V, as shown in Fig. 1. The peak potential of these step signals depends on the pH and the cation present in the solutions.17,18 Thus, for surfaces with (111) terraces and (110) steps a new peak at 0.125 V in perchloric or sulfuric acid solutions and at 0.28 V in NaOH appears on the voltammetric profile. The charge under this peak is proportional to the step density.19,20 On the other hand, the characteristic peaks for (100) steps on (111) terraces appear at ca. 0.26, 0.32, and 0.45 V for the perchloric acid, sulfuric acid, and NaOH solutions, respectively. In any case, the process giving rise to the peaks is the replacement of adsorbed hydrogen, which is present on the step sites at low potentials, by adsorbed OH in perchloric acid solutions, as recent Raman spectroscopy results have demonstrated.21 The presence of steps on the (100) terraces also modifies the voltammetric profile. Although the peaks are less defined than those on the (111) terraces, peaks at low potentials for the steps appear for all the electrolytes.22
The voltammetric profile of a polycrystalline electrode is the result of the contribution of the different sites on the surface, as has been thoroughly described.23,24 Thus, the peak at 0.125 V in sulfuric or perchloric acid media and that at 0.28 V in NaOH contains the contributions of the (110) symmetry sites, as observed for the Pt(110) and the stepped surfaces containing (110) symmetry steps (Fig. 1). The short-order domains with (100) symmetry give rise to the peaks at 0.28, 0.32, and 0.44 V in sulfuric acid, perchloric acid, and NaOH, respectively, which is the same potential for the signal of the (100) steps on the (111) terraces. On the other hand, long-range (100) ordered domains contribute with signals above the peak for the (100) short-order domains. The contribution of the (111) ordered domains can only be observed in sulfuric acid media because the adsorption of sulfate gives rise to a wave around 0.5 V. For the other two electrolyte solutions, the flat voltammetric profile obtained in all the electrolyte solutions between 0.06 and 0.35 V, makes impossible its analysis only using the voltammetry.
The uniqueness of the Pt(111) behavior
The adsorption of H and OH
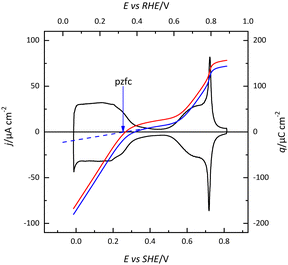
The (111) surface of the fcc metals is the one in which the surface atoms have the highest coordination number, 9. The surface atoms on the (100) plane have a coordination number of 8, and this number is lower for the atoms on the (110) plane or in the steps. This implies that the surface energy of the (111) surface is the lowest. Since electrocatalysis is based on the interaction of reactant species or intermediates with the surface, the different surface energy results in different electrocatalytic behavior. A clear example of the effect of the surface energy is observed in the adsorption of H and OH. As mentioned before, the Pt(111) electrode is the only one in which the contributions from these species appear in separate regions. This fact implies that between 0.4 and 0.6 V in perchloric acid and NaOH solutions, no species are specifically adsorbed on the electrode surface. Thus, the total charge at these potentials corresponds to the free charge because the contributions to the charge from the adsorbed species can be neglected. Since the values of the charge in this region are small, a precise determination of the free charge requires that the values of the charge calculated using the CO displacement technique are properly assessed. For that, the displaced charge has to be corrected by the residual free charge remaining on the electrode after CO adsorption, as has been extensively reported.25,26 Using this correction, the curves for the total charge can be calculated (Fig. 5). The extrapolation of the linear region in the curve where no species are specifically adsorbed allows for the calculation of the potential of zero free charge. It should be stressed that two potentials of zero charge can be determined for platinum electrodes, the potential of zero total charge (pztc) and the potential of zero free charge (pzfc).11 The pztc is experimentally measurable from the total charge curves and corresponds to the potential value at which the total charge curve crosses the zero value. On the other hand, the pzfc can be only determined using non-thermodynamical approaches. As mentioned before, the assumption here is that the observed behavior in the region where no species are specifically adsorbed can be extrapolated outside this region.26This strategy has made it possible to calculate the potential of pzfc for the Pt(111) surface in different pH values.27 It has been shown that the pzfc is pH-independent in the SHE scale, which is located at 0.228 V. As will be shown later, this value is very important because it corresponds to the potential at which the field across the interphase is null. As Frumkin demonstrated, the electric field can affect significantly the electrocatalytic activity of the electrode.28 Thus, depending on the solution pH, the reaction can take place at potentials in which the surface charge is positive or negative, affecting the interaction of the different reactants and intermediates with the surface. Additionally, the pzfc is related to other physical properties, such as the work function.29 In fact, there is a linear correlation between the work function and the pzfc for the different surfaces. Using the work function difference between the Pt(111) surface and the two other basal planes (Pt(100) and Pt(110)),30 the pzfc of these latter surfaces is expected to be at potentials close to 0 V vs. SHE. For this reason, in acidic solutions, anions are immediately adsorbed as soon as hydrogen is desorbed from the surface, because the free charge is positive and there is a strong coulombic interaction between the surface and the anions, in addition to the possible chemical interaction that favors the specific adsorption. This competitive adsorption between hydrogen and anions results in sharp peaks,31 such as those observed in sulfuric acid solutions, shown in Fig. 1.
The estimated value of the pzfc for the Pt(111) electrode has been later confirmed by the other independent measurements. The first one is the determination of the potential of maximum entropy (pme) of the formation of the interphase using the laser-induced temperature jump.32,33 This method allows the calculation of the entropy change in the formation of the interphase. At the potential of maximum entropy, it is assumed that there is no net orientation of the water molecules on the surface. Since the electric field generated by the presence of a surface charge induces the preferential orientation of the water, the pme should be very close to the pzfc charge.34 It should be recalled that for metals that do not give rise to adsorption processes, such as gold, the pzc corresponds to the value of the pzfc on Pt. Other molecular probes, such as N2O8,35,36 or peroxodisulfate37–39 reduction have confirmed the validity of these values. At high electrolyte concentrations (in the absence of specific adsorption), a capacity maximum is observed at the pzfc.40 The predicted minimum by the Gouy–Chapman theory is only observed at very low electrolyte concentrations at pH values around 4.41–43 This deviation from the Gouy–Chapman model has been attributed to the strong interaction of water molecules and ions with the Pt(111) surface so that the distribution of ions does not follow a purely electrostatic mean-field Poisson–Boltzmann distribution.43
Another important characteristic of the free charge curves on platinum is the modification of the surface free charge that takes place upon OH adsorption. Theoretical free charge curves for Pt(111) electrodes in acidic solutions show a non-monotonic behavior.44,45 At the onset of OH adsorption in acidic solutions, the charge is positive, whereas the completion of the adlayer leads to a rapid diminution in the free charge, which becomes negative. This behavior has been explained due to the presence of partially charged adsorbed species and the appearance of chemisorption-induced surface dipoles, which affect the water structure.46
Oxidation of small organic molecules.
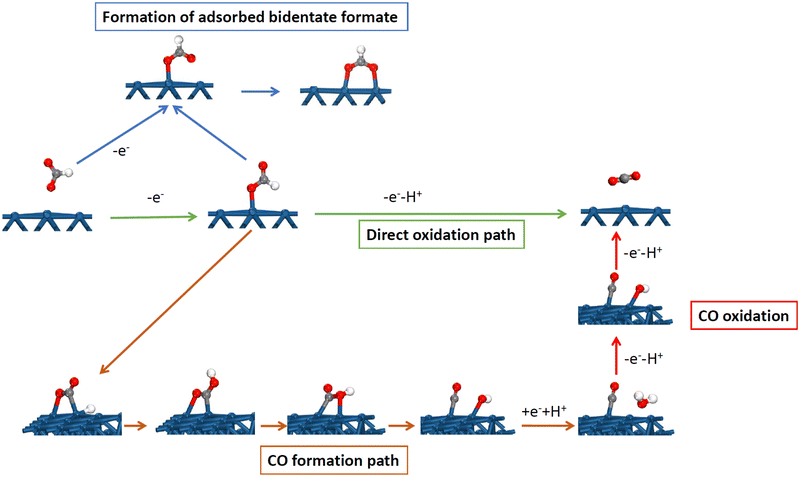
The distinct behavior of the Pt(111) electrode is not only observed for the H and OH adsorption but also for many other reactions and processes. One of the clearest cases is observed for the formic acid oxidation reaction. On platinum, the reaction takes place according to a dual path mechanism, one going through an active intermediate leading directly to CO2, while, in the second path, adsorbed CO is formed as an intermediate.47,48 A detailed mechanism is shown in Fig. 6, including the main intermediates. Adsorbed CO is considered a poison intermediate because it blocks the surface and its oxidation only takes place at high potentials. This general behavior has an important exception with the Pt(111) electrode. Although initial experiments showed the formation of adsorbed CO during the reaction,49,50 it was later demonstrated that this reaction occurred on the defects of the Pt(111) surface.51,52 For this reason, small amounts of bismuth, which are preferentially adsorbed on the defects of the surface, completely inhibit the CO formation route.49 These results were later confirmed by the studies with stepped surfaces,51 where the decoration by a foreign atom of the step leads to the complete inhibition of the CO formation route.Theoretical studies have shown the reason for the absence of CO formation for Pt(111).53,54 CO and formic acid have the same oxidation state so the reaction from formic acid to yield CO is a pure chemical dehydration reaction in which no electrons are transferred. However, on the platinum surface, the reaction proceeds through several steps (Fig. 6). The first one is the formation of monodentate adsorbed formate, which is also intermediate in the route through the active intermediate. This is an oxidative step in which one electron is exchanged. In the second step, the hydrogen bonded to the carbon atom is relocated to the non-bonded oxygen atom through the interaction with the surface to form adsorbed COOH. This step requires a favorable interaction of the hydrogen atom with the surface. After that, the OH group of the adsorbed COOH bonds to the platinum surface, leading to the cleavage of the C–OH bond with the formation of adsorbed OH and CO. Finally, OH is desorbed to OH− in a reductive step transferring one electron. The consequence of this mechanism is that the CO formation path requires favorable interaction with adsorbed OH and H to proceed, which agrees with the experimental observations.52,55,56 On Pt(110) and Pt(100), the CO formation reaction takes place at the potentials close to the pztc, where small coverages of OH and H are present on the surface.52,55,56 The same happens for the step sites, where the maximum rate for the formation of adsorbed CO occurs at the peak potential for the step signal. However, for the Pt(111) electrode, both processes take place in separated potential regions, and thus, the CO formation reaction is highly inhibited because there is no region in which adsorbed OH and H are present simultaneously on the surface. Additionally, the activation energy for the transformation of the monodentate adsorbed formate to adsorbed COOH on the Pt(111) electrode has a calculated activation energy much higher than that calculated for the Pt(100) or stepped electrodes.53 Clearly, in this case, the different activity between the basal planes for the formation of adsorbed CO is related to the different anion (OH) adsorption on them.
The different activity in 0.1 M HClO4 between Pt(111) and Pt(100) for the direct route through the active intermediate can be also considered a consequence of the different anion adsorption. Monodentate adsorbed formate is proposed to be the active intermediate, which is in equilibrium with the most stable form, the bidentate adsorbed formate. Since the adsorbed behavior of formate should be very similar to that of acetate, its adsorption on the Pt(100) electrode takes place in a fast process as soon as hydrogen is desorbed.22 For this reason, there is a fast exchange of formate anions between the interfacial region and the surface, which favors the formation and oxidation of monodentate adsorbed formate. On the other hand, this process extends over a larger potential window on the Pt(111) electrode57 and occurs at a lower rate, and thus, the currents are smaller. Microkinetic modeling has been able to reproduce the experimental behavior, providing valuable insights on the double layer effects on the reactivity.58
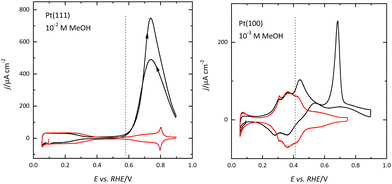
The differences in the OH adsorption between surfaces also give rise to the differences in the methanol oxidation reaction. Recent results have shown that the initial step in the reaction, the formation of an adsorbed methoxy species, requires the presence of adsorbed OH.59,60 On the Pt(111) electrode, adsorbed OH is observed for E > 0.55 V, and this potential is the onset of methanol oxidation (Fig. 7). The dehydrogenation of the adsorbed methoxy will lead to the formation of adsorbed CO, which is readily oxidized at those potentials. For this reason, there is no accumulation of CO on the surface during the oxidation process.59 On the other hand, since adsorbed OH is present on the surface for E < 0.35 V on the Pt(100) surface, CO formation can be detected from these potentials (Fig. 7). However, since the effective oxidation of adsorbed CO only takes place at E > 0.6 V, there is a fast accumulation of adsorbed CO on the surface reaching high CO coverages.59,61,62 The formation of a compact CO layer hinders its oxidation because adsorbed OH is required for this process, and thus the small currents that can be measured for the methanol oxidation reaction at 0.5 V, decay rapidly due to the formation of adsorbed CO. Once CO is readily oxidized on the surface, currents are larger than those measured for the Pt(111) surface.
The Pt(111) electrode has also a very distinctive behavior for the ethanol oxidation reaction. The mechanism has two main routes, one giving rise to the formation of acetic acid as the final product with the exchange of four electrons and one producing two CO2 molecules after the cleavage of the C–C bond and the exchange of twelve electrons. Pt(111) shows the highest activity for the formation of acetic acid both in acidic and alkaline solutions.63–65 However, in acidic solutions, the specific adsorption of acetic acid as acetate, which takes place at E > 0.4 V, inhibits the reaction.64,66 On alkaline solutions, since the surface charge is negative at the potentials at which the reaction takes place, acetate is not adsorbed. On the other hand, IR experiments show that the formation of CO2 on this electrode is negligible.63 In fact, electrochemical and IR experiments confirm that the steps on the (111) terraces catalyze the cleavage of the C–C bond and that the (111) terraces are inactive for that.67,68 DFT results show that the activation energy for the cleavage of the C–C bond on the terrace sites is significantly higher than that calculated for the step sites.69 Additionally, the explanation for the high activity for the formation of acetic acid is that the commensurate water structure that can be formed on the (111) terrace facilitates the transfer of the OH group required for the oxidation of ethanol to acetic acid.65
In the mechanism for the oxidation of these small organic molecules, CO always appears as an intermediate. For this reason, its oxidation has been thoroughly studied. It has been found that on Pt(111), adsorbed CO forms several structures depending on the coverage and the presence of CO in the solution. The different structures have been characterized by STM, and correspondence with the FTIR spectra has been established.70 For Pt(100), ordered structures have also been observed by STM.71 Regarding its oxidation mechanism, it is generally accepted that it takes place according to a Langmuir–Hinshelwood mechanism, in which adsorbed OH reacts with adsorbed CO.72 Recent results using shell-isolated nanoparticle-enhanced Raman spectroscopy (SHINERS) have pointed out the presence of adsorbed OH and COOH species during the oxidation process on Pt(111) and Pt(100) electrodes, confirming the existence of a Langmuir–Hinshelwood mechanism.73 However, the existence of a route through an Eleay–Rideal mechanism cannot be discarded, especially for the initial stages of the oxidation of saturated adlayers.74
The kinetics in the oxidation of the CO adlayer have been studied in different electrolytes and single-crystal electrodes. In acidic media, a single oxidation (stripping) peak is obtained for all the single-crystal electrodes. To determine the reaction kinetics, chronoamperometric transients have been measured and simulated. It has been found that the transients and voltammetric peaks are accurately described using a mean-field Langmuir–Hinslewood mechanism.74–77 For this mechanism to take place, it has to be assumed that, during the oxidation process, CO is very mobile on the surface, so it can be considered to be randomly distributed on the surface.78 The analysis of the dependence of the rate constant with the surface structure reveals that steps and defects are key elements in the oxidation process.76,79,80 Thus, the kinetic rate constants for the stepped surfaces containing (111) terraces increase with the step density, and a perfect (111) surface should have a negligible rate constant.76 However, the opposite behavior is obtained for stepped surfaces with (100) terraces, whereas for long terraces, the rates diminish with the step density.81 Partial oxidation experiments of CO layers have also shown that the sites that are first freed are those corresponding to the terrace, whereas those on top of the step remain covered by CO until the final stages of the oxidation reaction.82 In fact, those sites are the ones with the highest adsorption energy for CO.
The situation is completely different in alkaline media. For stepped surfaces with (111) terraces, different peaks are observed, depending on the step symmetry (Fig. 8).83–86 Characteristic peaks are associated with the presence of steps with different symmetry and terraces, in addition to pre-peaks. These pre-peaks, which can be also observed in acidic media, are more frequent in alkaline solutions.86 When analyzing the kinetics of the oxidation process, transients also do not follow the mean-field mechanism and seem to be better described by a nucleation and growth mechanism,85,87 which would imply that the CO molecules are immobile. Partial stripping experiments indicate a sequential stripping of CO from the surface.85,86 The oxidation in the pre-peak region only involves a relaxation of the CO adlayer, since hydrogen adsorption is still fully blocked. Then, CO is oxidized on the lower part of the steps, giving rise to the characteristic voltammetric peak at low potentials characteristics of the presence of steps. Afterward, CO is stripped from terrace sites and finally from the top part of the step in a single voltammetric peak. Oxidation kinetics show a clear dependence on the CO adsorption potential,86 indicating that the conditions in which the CO adlayer is formed have a significant impact on the oxidation kinetics. In fact, for Langmuir–Hinshelwood mechanisms, the initial stages of the oxidation depend on the presence of defects in the CO adlayer, since on those defects OH adsorption may take place.88 Thus, depending on the CO adlayer formation conditions, the number of defects on the adlayer may change altering oxidation kinetics. As mentioned before, the different experimental behavior between acidic and alkaline media has been explained through a change in the mobility of CO depending on the absolute electrode potential.86 However, the issue is still under discussion and more experimental and theoretical results are required to fully understand the origin of these differences.
 | ||
| Fig. 8 CO stripping profiles for different stepped and kinked surfaces in 0.1 M NaOH. The arrows indicate the origin of the different peaks. Scan rate: 50 mV s−1. | ||
The oxygen and hydrogen peroxide reduction reaction
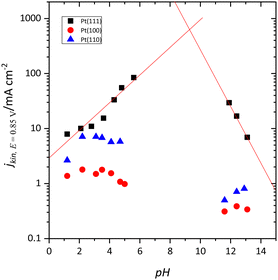
At first sight, the qualitative behavior of the Pt(111) electrode for the oxygen reduction reaction (ORR) follows the same principles as the other single-crystal electrodes. For the low-index planes in perchloric acid solutions, the order is Pt(110) > Pt(111) > Pt(100),89–91 although DFT calculations indicate that the most active plane should be the Pt(111) surface.92 However, when the reaction is studied as a function of the solution pH in the absence of specific adsorption, it was found that the activity trend for the Pt(111) electrode is different from the other two basal planes.93 Thus, the activity of the Pt(100) and Pt(110) surfaces diminishes as the pH increases (Fig. 9). On the other hand, for the Pt(111) surface, the electrocatalytic activity increases from pH 1 to 6 and diminishes from 11 to 13.94 Although it is not possible to study the mid-pH region due to the absence of convenient a buffer solution for these pH values in which the anions do not interact specifically with the Pt surface, the extrapolation of the observed trend at low and high pH values indicates that the activity of the Pt(111) electrode should be maximum at pH ca. 8–9 (Fig. 9). For these pH values, the pzfc is close to the onset of the reaction, which suggests that a neutral charge on the electrode surface activates the reaction for this surface. The different activity trends vs. pH observed for the other two electrodes have to be associated with the adsorbed OH layer. It should be highlighted that adsorbed OH is an intermediate of the ORR. Theoretical studies indicate that the reduction of OH is the rate-determining step in the ORR mechanism on Pt.95 For the Pt(110) and Pt(100) planes, OH desorption takes place at potentials much more negative than the onset for the ORR, and thus its coverage remains constant in the whole activation region.On the other hand, the onset of the ORR on the Pt(111) surface coincides with the onset of OH desorption. As mentioned before, the completion of the OH layer leads to significant changes in the free charge of the electrode, which becomes more negative.44,45 Thus, for the Pt(100) and Pt(110) electrodes, the charge at the onset of the ORR is always negative since the desorption of OH takes place at low potentials, and, as pH increases, it becomes even more negative. For the Pt(111) surface, since the onset of the reaction coincides with that of the OH desorption, the free charge is positive in acidic solutions and becomes more negative as the pH increases, activating the reaction for the pH in which the free charge is almost zero.
The relevant role of adsorbed OH in the ORR has been recently highlighted in the studies carried out in D2O, which confirms that the reduction of OH is the limiting step on Pt. An inverted isotopic effect has been found by the substitution of H for D.96 Thus, the activity in D2O is higher than that recorded in H2O. This effect has been explained as a consequence of the weaker OD adsorption as compared to that of OH, as the shift to higher potential values of OD adsorption indicates.
The surface charge not only affects the ORR onset but also the different routes in the complex mechanism. This effect has been clearly shown in the hydrogen peroxide reduction reaction (HPRR). Hydrogen peroxide is an intermediate in some of the paths of the ORR mechanism and the comparison between the behavior of the ORR and HPRR can shed light on the mechanisms of both reactions. On Pt(111) in solutions with pH = 1, HPRR is inhibited at E < 0.3 V vs. RHE.97–100 This effect is also observed for the ORR in this region because the reaction yields H2O2 instead of water. Initially, it was proposed that this inhibition was caused by the adsorption of hydrogen which occurs at E < 0.35 V. However, experiments at different pH showed that the inhibition occurs at constant charge and not constant hydrogen coverage, highlighting that the free charge is responsible for the inhibition. In fact, for the Au(100) electrode in alkaline solutions, the transition between the four electrons and two electrons mechanism also takes place at constant free charge.101
Modeling the behavior of the platinum single-crystal electrodes
The studies of the electrochemical interphase are complex, especially due to the presence of the solvent, generally water, and the ions of the supporting electrolyte. Thus, the reactivity not only depends on the interactions between the reactants and intermediates with the surface, but also on the cross interactions between solvent, surface, reactants, and solution ions. Also, there is an additional set of variables that affects the reactivity which is the electrode potential/free charge. For a given solution composition, there is a univocal relationship between the electrode potential and the free charge, so setting the value of the electrode potential fixes the value of the free charge and vice versa. In general, adsorption processes are better described when the free charge is used as the independent variable.102The experimental complexity of the electrochemical interphase, with the presence of water, prevents the use of the electron spectroscopy techniques used to study heterogeneous catalysis. To fill the gaps in the experimental research, DFT and molecular dynamics have proven to be very useful tools. Although the computational power is increasing every day, the full inclusion of all the elements in the electrochemical interphase in the model is still not feasible. Thus, DFT models should include all relevant parameters affecting reactivity, while ensuring reasonable duration for calculations, so that the essential elements that shape the reactivity are captured. For that, single-crystal surfaces are the typical choice because they can be easily modeled with reasonably low computational costs using periodic models, and thus experimental results with single-crystal electrodes can be understood with the help of theoretical calculations.
The first element to be considered is the state of the surface. Until recently, when the reactivity of Pt single-crystal electrodes was modeled, it was always assumed that no species were adsorbed on the surface. However, this is not true. As described before, on the platinum surface under aqueous electrochemical conditions, H, OH, or both species are adsorbed on the surface. The only exception is the Pt(111) between 0.4 and 0.55 V, in which no species but water are adsorbed. Thus, the DFT models to study electrocatalytic reactions should include the adsorbed species present on the interphase at the potentials at which they take place because they alter the reactivity. The DFT calculations that included the presence of adsorbed OH in the model have served to rationalize the observed experimental reactivity and to explain the different behavior of methanol in electrochemical and UHV environments.59 In electrochemical environments, the cleavage of the C–H bond is the rate-determining step, whereas in UHV the first step in the oxidation process, the formation of the adsorbed methoxy species is the slowest step.62,103 The explanation for this different behavior lies in the presence of adsorbed OH in electrochemical environments, which catalyze the formation of adsorbed methoxy. Similar effects on the formation of adsorbed ethoxy have been observed for ethanol oxidation.65 In this case, adsorbed OH not only facilitates this step but also the oxidation of the adsorbed species to acetic acid.
A second important element that has to be included in the models is the water environment.104 Water molecules interact with polar species and can modify the reactivity. The simplest way to include water effects is through implicit water models, which in some cases, can be enough to capture the essential effects. In other cases, where the presence of hydrogen bonds of the different species may have an impact on the reaction energetics, additional water molecules can be added. In fact, recent results in the modeling of the double layer and its impact on electrocatalysis reveal that the local hydrogen-bond network in the water has important effects on the structure and properties of the double layer, shaping the electrocatalytic process.105 In order to improve implicit solvation models, which computationally are less demanding, parameterized implicit solvation models have been proposed that can reproduce experimental results and those obtained with explicit water models.106 Another important conclusion obtained from models trying to reproduce experimental results is that the electrostatic interactions are much stronger than those expected by the mean-field Poisson–Boltzmann equation,38 as observed from the experimental results of the effect of the concentration in the capacity minimum around the pzfc for the Pt(111) electrode.43
The final important element is the free charge/electrode potential. As mentioned before, both parameters are interrelated. It should be highlighted that during an electrochemical reaction, charge flows through the circuit, thus total charge at the interphase changes. However, the free charge at the electrode remains constant. The simulation of systems in which the total charge changes requires the use of Grand Canonical DFT (GC-DFT).107,108 Due to the complexity of this GC-DFT, in many cases, only the initial and final states of a given step are calculated using DFT, and the activation energies are supposed to be proportional to the difference between the initial and final states of the reaction step.95 This strategy has been successfully applied to the ORR and the calculations have provided significant insights into the reaction. This is because the proposed intermediates: adsorbed OOH, O, and OH, are very small species all bonded to the surface by an O atom. The similar chemical nature of these species allows for a correlation between the energy of the different steps and the activation energy. In more complex reactions, with different atoms bonded to the surface and possible geometries, the activation energies are no longer proportional to the difference between the initial and final energy of the species in the step, as happens for the formic acid oxidation reaction.
The potential dependence of the different steps is normally calculated using the so-called computational hydrogen electrode.109 Although the method allows for the determination of the rate-determining step, as has been the case for the ORR, it is not able to predict the differences in behavior between acidic and alkaline solutions. The changes in reactivity between acidic and alkaline environments are due to two main factors: the first one is the water structure and the second one is the free charge. Normally, in DFT simulations, the surface charge of the electrode is zero, so the reaction conditions are close to those obtained at the pzfc. As mentioned before, the surface charge in alkaline solutions is clearly negative, and this can significantly affect the energetics of the different species involved. This effect has been shown for instance for adsorbed hydrogen on Pt(111), where the nature of the adsorbed species is different depending on the surface charge.110 Thus, the different reactivity observed between acidic and alkaline solutions can be only understood if the free charge of the electrode is included in the model.
Due to the computational complexity of the electrochemical interface examples with a complete model are rare. Recently, there have been numerous efforts to obtain a detailed picture of the interphase in contact with the Pt(111) electrode to reproduce experimental results and to obtain valuable insights into the reactivity of platinum electrodes using GC-DFT calculations including explicit water layers and ab initio molecular dynamics (AIMD).111–115 Those results highlight the importance of the local hydrogen-bond network in the structure and properties of the double layer, which affects the electrocatalysis.105 GC-DFT111 and AIMD116 have been able to reproduce the capacity maximum around the pzfc, and the existence of an ion distribution that does not follow the mean-field Poisson–Boltzmann distribution.43
Author contributions
J. M. F. Conceptualization, formal analysis, resources, writing – review & editing. E. H. Conceptualization, formal analysis, resources, writing – first draft, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has been financially supported by the Ministerio de Ciencia e Innovación (Project PID2022-137350NB-I00), and Generalitat Valenciana (Project PROMETEO/2020/063).Notes and references
- S. Trasatti, Surf. Sci., 1995, 335, 1–9 CrossRef CAS.
- S. Trasatti, Electrochim. Acta, 1991, 36, 1659–1667 CrossRef CAS.
- J. Clavilier, R. Faure, G. Guinet and R. Durand, J. Electroanal. Chem., 1980, 107, 205–209 CrossRef CAS.
- V. Climent and E. Herrero, Electrochemical behavior of single crystal electrodes on model processes, 2020 Search PubMed.
- J. M. Feliu, E. Herrero and V. V. Climent, in Catalysis in Electrochemistry: From Fundamentals to Strategies for Fuel Cell Development, ed. E. Santos and W. Schmickler, John Wiley & Sons, Inc., Hoboken, 2011, pp. 127–163 Search PubMed.
- N. Fröhlich, J. Fernández-Vidal, F. V. Mascaró, A. J. Shih, M. Luo and M. T. M. Koper, Electrochim. Acta, 2023, 466, 143035 CrossRef.
- J. Clavilier, R. Albalat, R. Gomez, J. M. Orts, J. M. Feliu and A. Aldaz, J. Electroanal. Chem., 1992, 330, 489–497 CrossRef CAS.
- V. Climent, G. A. Attard and J. M. Feliu, J. Electroanal. Chem., 2002, 532, 67–74 CrossRef CAS.
- E. Herrero, J. M. M. Feliu, A. Wieckowski and J. Clavilier, Surf. Sci., 1995, 325, 131–138 CrossRef CAS.
- J. Clavilier, R. Albalat, R. Gómez, J. M. Orts and J. M. Feliu, J. Electroanal. Chem., 1993, 360, 325–335 CrossRef CAS.
- A. N. Frumkin and O. A. Petrii, Electrochim. Acta, 1975, 20, 347–359 CrossRef CAS.
- A. M. Funtikov, U. Stimming and R. Vogel, J. Electroanal. Chem., 1997, 428, 147–153 CrossRef CAS.
- A. M. Funtikov, U. Linke, U. Stimming and R. Vogel, Surf. Sci., 1995, 324, L343–L348 CrossRef CAS.
- V. Climent, R. Gómez, J. M. Orts and J. M. Feliu, J. Phys. Chem. B, 2006, 110, 11344–11351 CrossRef CAS PubMed.
- G. A. Attard and A. Brew, J. Electroanal. Chem., 2015, 747, 123–129 CrossRef CAS.
- G. A. Attard, K. Hunter, E. Wright, J. Sharman, R. Martínez-Hincapié and J. M. Feliu, J. Electroanal. Chem., 2017, 793, 137–146 CrossRef CAS.
- I. T. McCrum and M. J. Janik, J. Phys. Chem. C, 2016, 120, 457–471 CrossRef CAS.
- X. Chen, I. T. McCrum, K. A. Schwarz, M. J. Janik and M. T. M. Koper, Angew. Chem., Int. Ed., 2017, 56, 15025–15029 CrossRef CAS PubMed.
- A. Rodes, K. Elachi, M. A. Zamakhchari and J. Clavilier, J. Electroanal. Chem., 1990, 284, 245–253 CrossRef CAS.
- A. Rodes, K. Elachi, M. A. Zamakhchari and J. Clavilier, in Fundamental Aspects of Heterogeneous Catalysis Studied by Particle Beams, ed. H. H. Brongersma and R. A. Vansanten, 1991, vol. 265, pp. 75–82 Search PubMed.
- R. Rizo, J. Fernández-Vidal, L. J. Hardwick, G. A. Attard, F. J. Vidal-Iglesias, V. Climent, E. Herrero and J. M. Feliu, Nat. Commun, 2022, 13, 2550 CrossRef CAS PubMed.
- K. Domke, E. Herrero, A. Rodes and J. M. Feliu, J. Electroanal. Chem., 2003, 552, 115–128 CrossRef CAS.
- J. Solla-Gullón, P. Rodríguez, E. Herrero, A. Aldaz and J. M. Feliu, Phys. Chem. Chem. Phys., 2008, 10, 1359–1373 RSC.
- F. J. Vidal-Iglesias, R. M. Arán-Ais, J. Solla-Gullón, E. Herrero and J. M. Feliu, ACS Catal., 2012, 2, 901–910 CrossRef CAS.
- M. J. Weaver, Langmuir, 1998, 14, 3932–3936 CrossRef CAS.
- R. Gómez, V. Climent, J. M. Feliu and M. J. Weaver, J. Phys. Chem. B, 2000, 104, 597–605 CrossRef.
- R. Rizo, E. Sitta, E. Herrero, V. Climent and J. M. J. M. Feliu, Electrochim. Acta, 2015, 162, 138–145 CrossRef CAS.
- A. Frumkin, Z. fur Phys. Chem., 1933, 164A, 121–133 CrossRef.
- S. Trasatti, Electrochim. Acta, 1990, 35, 269–271 CrossRef CAS.
- S. Trasatti, J. Electroanal. Chem., 1971, 33, 351–378 CrossRef CAS.
- N. Garcia-Araez, J. J. Lukkien, M. T. M. Koper and J. M. Feliu, J. Electroanal. Chem., 2006, 588, 1–14 CrossRef CAS.
- V. Climent, B. A. Coles and R. G. Compton, J. Phys. Chem. B, 2002, 106, 5258–5265 CrossRef CAS.
- V. Climent, B. A. Coles and R. G. Compton, J. Phys. Chem. B, 2002, 106, 5988–5996 CrossRef CAS.
- V. Climent, B. A. Coles and R. G. Compton, J. Phys. Chem. B, 2001, 105, 10669–10673 CrossRef CAS.
- G. A. Attard, O. Hazzazi, P. B. Wells, V. Climent, E. Herrero and J. M. Feliu, J. Electroanal. Chem., 2004, 568, 329–342 CrossRef CAS.
- G. A. Attard and A. Ahmadi, J. Electroanal. Chem., 1995, 389, 175–190 CrossRef.
- R. Martínez-Hincapié, V. Climent and J. M. Feliu, Electrochem. Commun., 2018, 88, 43–46 CrossRef.
- L. Zhang and J. Huang, J. Phys. Chem. C, 2020, 2020, 16951–16960 CrossRef.
- R. Martínez-Hincapié, V. Climent and J. M. Feliu, J. Electroanal. Chem., 2019, 847, 113226 CrossRef.
- N. Garcia-Araez, V. Climent, E. Herrero, J. M. M. Feliu and J. Lipkowski, Electrochim. Acta, 2006, 51, 3787–3793 CrossRef CAS.
- K. Doblhoff-Dier and M. T. M. Koper, Curr. Opin. Electrochem., 2023, 39, 101258 CrossRef CAS.
- K. Ojha, K. Doblhoff-Dier and M. T. M. Koper, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2116016119 CrossRef CAS PubMed.
- K. Ojha, N. Arulmozhi, D. Aranzales and M. T. M. Koper, Angew. Chem., Int. Ed., 2020, 59, 711–715 CrossRef CAS PubMed.
- J. Huang, T. Zhou, J. Zhang and M. Eikerling, J. Chem. Phys., 2018, 148, 044704 CrossRef PubMed.
- J. Huang, A. Malek, J. Zhang and M. H. Eikerling, J. Phys. Chem. C, 2016, 120, 13587–13595 CrossRef CAS.
- J. Huang, Curr. Opin. Electrochem., 2022, 33, 100938 CrossRef CAS.
- A. Capon and R. Parsons, J. Electroanal. Chem., 1973, 45, 205–231 CrossRef CAS.
- A. Capon and R. Parsons, J. Electroanal. Chem., 1973, 44, 239–254 CrossRef CAS.
- E. Herrero, A. Fernández-Vega, J. M. Feliu and A. Aldaz, J. Electroanal. Chem., 1993, 350, 73–88 CrossRef CAS.
- S. G. Sun and J. Clavilier, J. Electroanal. Chem., 1987, 236, 95–112 CrossRef CAS.
- M. D. Maciá, E. Herrero and J. M. Feliu, Electrochim. Acta, 2002, 47, 3653–3661 CrossRef.
- V. Grozovski, V. Climent, E. Herrero and J. M. Feliu, Phys. Chem. Chem. Phys., 2010, 12, 8822 RSC.
- A. Ferre-Vilaplana, J. V. V. Perales-Rondón, C. Buso-Rogero, J. M. M. Feliu and E. Herrero, J. Mater. Chem. A, 2017, 5, 21773–21784 RSC.
- E. Herrero and J. M. Feliu, Curr. Opin. Electrochem., 2018, 9, 145–150 CrossRef CAS.
- V. Grozovski, V. Climent, E. Herrero and J. M. Feliu, ChemPhysChem, 2009, 10, 1922–1926 CrossRef CAS PubMed.
- V. Grozovski, J. Solla-Gullón, V. Climent, E. Herrero and J. M. Feliu, J. Phys. Chem. C, 2010, 114, 13802–13812 CrossRef CAS.
- V. Grozovski, F. J. Vidal-Iglesias, E. Herrero and J. M. Feliu, ChemPhysChem, 2011, 12, 1641–1644 CrossRef CAS PubMed.
- X. Zhu, J. Huang and M. Eikerling, JACS Au, 2023, 3, 1052–1064 CrossRef CAS PubMed.
- D. S. Mekazni, R. M. Arán-Ais, A. Ferre-Vilaplana and E. Herrero, ACS Catal., 2022, 12, 1965–1970 CrossRef CAS.
- M. A. Kamyabi, R. Martínez-Hincapié, J. M. Feliu and E. Herrero, Surfaces, 2019, 2, 177–192 CrossRef CAS.
- V. Grozovski, V. Climent, E. Herrero and J. M. Feliu, J. Electroanal. Chem., 2011, 662, 43–51 CrossRef CAS.
- E. Herrero, K. Franaszczuk and A. Wieckowski, J. Phys. Chem., 1994, 98, 5074–5083 CrossRef CAS.
- C. Busó-Rogero, E. Herrero and J. M. Feliu, ChemPhysChem, 2014, 15, 2019–2028 CrossRef PubMed.
- F. Colmati, G. Tremiliosi-Filho, E. R. Gonzalez, A. Berná, E. Herrero and J. M. Feliu, Faraday Discuss, 2008, 140, 379–397 RSC ; discussion 417-37.
- R. Rizo, A. Ferre-Vilaplana, E. Herrero and J. M. Feliu, ACS Sustainable Chem. Eng., 2022, 11, 4960–4968 CrossRef.
- M. J. Prieto and G. Tremiliosi-Filho, Electrochem. Commun., 2011, 13, 527–529 CrossRef CAS.
- J. Souza-Garcia, E. Herrero and J. M. Feliu, ChemPhysChem, 2010, 11, 1391–1394 CrossRef CAS PubMed.
- F. Colmati, G. Tremiliosi-Filho, E. R. Gonzalez, A. Berná, E. Herrero, J. M. Feliu, G. Tremiliosi, E. R. Gonzalez, A. Berna, E. Herrero and J. M. Feliu, Phys. Chem. Chem. Phys., 2009, 11, 9114–9123 RSC.
- A. Ferre-Vilaplana, C. Buso-Rogero, J. M. Feliu and E. Herrero, J. Phys. Chem. C, 2016, 120, 11590–11597 CrossRef CAS.
- M. W. Severson, C. Stuhlmann, I. Villegas and M. J. Weaver, J. Chem. Phys., 1995, 103, 9832–9843 CrossRef CAS.
- M. Wakisaka, T. Ohkanda, T. Yoneyama, H. Uchida and M. Watanabe, Chem. Commun., 2005, 2710–2712 RSC.
- B. Love and J. Lipkowski, ACS Symp. Ser., 1988, 378, 484–496 CrossRef CAS.
- M. Su, J. C. Dong, J. B. Le, Y. Zhao, W. M. Yang, Z. L. Yang, G. Attard, G. K. Liu, J. Cheng, Y. M. Wei, Z. Q. Tian and J. F. Li, Angew. Chem., Int. Ed., 2020, 59, 23554–23558 CrossRef CAS PubMed.
- M. Bergelin, E. Herrero, J. M. M. Feliu and M. Wasberg, J. Electroanal. Chem., 1999, 467, 74–84 CrossRef CAS.
- N. P. Lebedeva, M. T. M. Koper, J. M. Feliu and R. A. van Santen, J. Electroanal. Chem., 2002, 524, 242–251 CrossRef.
- N. P. Lebedeva, M. T. M. Koper, J. M. Feliu and R. A. van Santen, J. Phys. Chem. B, 2002, 106, 12938–12947 CrossRef CAS.
- S. C. S. Lai, N. P. Lebedeva, T. H. M. Housmans and M. T. M. Koper, Top. Catal., 2007, 46, 320–333 CrossRef CAS.
- A. V. Petukhov, W. Akemann, K. A. Friedrich and U. Stimming, Surf. Sci., 1998, 402, 182–186 CrossRef.
- N. P. Lebedeva, M. T. M. Koper, E. Herrero, J. M. Feliu and R. A. Van Santen, J. Electroanal. Chem., 2000, 487, 37–44 CrossRef CAS.
- N. P. Lebedeva, A. Rodes, J. M. Feliu, M. T. M. Koper and R. A. van Santen, J. Phys. Chem. B, 2002, 106, 9863–9872 CrossRef CAS.
- F. J. Vidal-Iglesias, J. Solla-Gullón, J. M. Campiña, E. Herrero, A. Aldaz and J. M. Feliu, Electrochim. Acta, 2009, 54, 4459–4466 CrossRef CAS.
- M. J. S. Farias, A. A. Tanaka, G. Tremiliosi and J. M. Feliu, Electrochem. Commun., 2011, 13, 338–341 CrossRef CAS.
- G. Garcia and M. T. M. Koper, Phys. Chem. Chem. Phys., 2008, 10, 3802–3811 RSC.
- G. Garcia and M. T. M. Koper, J. Am. Chem. Soc., 2009, 131, 5384–5385 CrossRef CAS PubMed.
- M. J. S. Farias, C. Busó-Rogero, A. A. Tanaka, E. Herrero and J. M. Feliu, Langmuir, 2020, 36, 704–714 CrossRef CAS PubMed.
- M. J. S. Farias, C. Busó-Rogero, R. Gisbert, E. Herrero and J. M. Feliu, J. Phys. Chem. C, 2014, 118, 1925–1934 CrossRef CAS.
- G. Garcia and M. T. M. Koper, Phys. Chem. Chem. Phys., 2009, 11, 11437–11446 RSC.
- C. A. C. A. Angelucci, E. Herrero and J. M. J. M. Feliu, J. Phys. Chem. C, 2010, 114, 14154–14163 CrossRef CAS.
- M. D. Maciá, J. M. Campiña, E. Herrero and J. M. Feliu, J. Electroanal. Chem., 2004, 564, 141–150 CrossRef.
- A. Kuzume, E. Herrero and J. M. Feliu, J. Electroanal. Chem., 2007, 599, 333–343 CrossRef CAS.
- N. M. Marković, R. R. Adžić, B. D. Cahan and E. B. Yeager, J. Electroanal. Chem., 1994, 377, 249–259 CrossRef.
- J. Greeley, J. Rossmeisl, A. Hellman and J. K. Nørskov, Z. fur Phys. Chem., 2007, 221, 1209–1220 CrossRef CAS.
- R. Rizo, E. Herrero and J. M. J. M. Feliu, Phys. Chem. Chem. Phys., 2013, 15, 15416–15425 RSC.
- V. Briega-Martos, E. Herrero and J. M. J. M. Feliu, Electrochim. Acta, 2017, 241, 497–509 CrossRef CAS.
- A. Kulkarni, S. Siahrostami, A. Patel and J. K. Nørskov, Chem. Rev., 2018, 118, 2302–2312 CrossRef CAS PubMed.
- Y. Yang, R. G. Agarwal, P. Hutchison, R. Rizo, A. V. Soudackov, X. Lu, E. Herrero, J. M. Feliu, S. Hammes-Schiffer, J. M. Mayer and H. D. Abruña, Nat. Chem., 2022, 1–7 Search PubMed.
- V. Briega-Martos, E. Herrero and J. M. Feliu, Chin. J. Catal., 2020, 41, 732–738 CrossRef CAS.
- V. Briega-Martos, E. Herrero and J. M. J. M. Feliu, Electrochim. Acta, 2020, 334, 135452 CrossRef CAS.
- V. Briega-Martos, G. A. B. Mello, R. M. Arán-Ais, V. Climent, E. Herrero and J. M. Feliu, J. Electrochem. Soc., 2018, 165, J3045–J3051 CrossRef CAS.
- J. Huang, V. Climent, A. Groß and J. M. Feliu, Chin. J. Catal., 2022, 43, 2837–2849 CrossRef CAS.
- A. Prieto, J. Hernández, E. Herrero and J. M. Feliu, J. Solid State Electrochem., 2003, 7, 599–606 CrossRef CAS.
- E. Herrero, J. Mostany, J. M. Feliu and J. Lipkowski, J. Electroanal. Chem., 2002, 534, 79–89 CrossRef CAS.
- K. Franaszczuk, E. Herrero, P. Zelenay, A. Wieckowski, J. Wang and R. I. I. Masel, J. Phys. Chem., 1992, 96, 8509–8516 CrossRef CAS.
- S. N. Steinmann and C. Michel, ACS Catal., 2022, 12, 6294–6301 CrossRef CAS.
- P. Li, Y. Jiao, J. Huang and S. Chen, JACS Au, 2023, 3, 2640–2659 CrossRef CAS PubMed.
- G. Bramley, M. T. Nguyen, V. A. Glezakou, R. Rousseau and C. K. Skylaris, J. Chem. Theory Comput., 2020, 16, 2703–2715 CrossRef CAS PubMed.
- A. Bhandari, C. Peng, J. Dziedzic, L. Anton, J. R. Owen, D. Kramer and C. K. Skylaris, J. Chem. Phys., 2021, 155, 24114 CrossRef CAS PubMed.
- R. Sundararaman, W. A. Goddard and T. A. Arias, J. Chem. Phys., 2017, 146, 114104 CrossRef PubMed.
- J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jónsson, J. Phys. Chem. B, 2004, 108, 17886–17892 CrossRef.
- V. Briega-Martos, A. Ferrer-Vilaplana, E. Herrero and J. M. Feliu, Electrochim. Acta, 2020, 354, 136620 CrossRef CAS.
- J. J. Hinsch, A. Bouzid, J. C. Barker, J. J. White, F. Mortier, H. Zhao and Y. Wang, J. Phys. Chem. C, 2023, 127, 19857–19866 CrossRef CAS.
- A. Groß and S. Sakong, Chem. Rev., 2022, 122, 10746–10776 CrossRef PubMed.
- J. Huang, Curr. Opin. Electrochem., 2022, 33, 100938 CrossRef CAS.
- J. B. Le and J. Cheng, Curr. Opin. Electrochem., 2020, 19, 129–136 CrossRef CAS.
- J. Huang, Y. Zhang, M. Li, A. Groß and S. Sakong, J. Phys. Chem. Lett., 2023, 14, 2354–2363 CrossRef CAS PubMed.
- J. B. Le, Q. Y. Fan, J. Q. Li and J. Cheng, Sci. Adv., 2020, 6, eabb1219 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2024 |