Open Access Article
Open Access ArticleSolvent-mediated isotope effects strongly influence the early stages of calcium carbonate formation: exploring D2O vs. H2O in a combined computational and experimental approach†
Michael
King‡
 a,
Jonathan T.
Avaro‡
ab,
Christine
Peter
a,
Karin
Hauser
a,
Jonathan T.
Avaro‡
ab,
Christine
Peter
a,
Karin
Hauser
 a and
Denis
Gebauer
a and
Denis
Gebauer
 *c
*c
aDepartment of Chemistry, University of Konstanz, Universitätsstr. 10, 78457 Konstanz, Germany
bEmpa, Lerchenfeldstrasse 5, 9014 St. Gallen, Switzerland
cInstitute of Inorganic Chemistry, Leibniz University of Hannover, Callinstr. 9, 30167 Hannover, Germany. E-mail: gebauer@acc.uni-hannover.de
First published on 8th December 2021
Abstract
In experimental studies, heavy water (D2O) is employed, e.g., so as to shift the spectroscopic solvent background, but any potential effects of this solvent exchange on reaction pathways are often neglected. While the important role of light water (H2O) during the early stages of calcium carbonate formation has been realized, studies into the actual effects of aqueous solvent exchanges are scarce. Here, we present a combined computational and experimental approach to start to fill this gap. We extended a suitable force field for molecular dynamics (MD) simulations. Experimentally, we utilised advanced titration assays and time-resolved attenuated total reflection Fourier transform infrared (ATR-FTIR) spectroscopy. We find distinct effects in various mixtures of the two aqueous solvents, and in pure H2O or D2O. Disagreements between the computational results and experimental data regarding the stabilities of ion associates might be due to the unexplored role of HDO, or an unprobed complex phase behaviour of the solvent mixtures in the simulations. Altogether, however, our data suggest that calcium carbonate formation might proceed “more classically” in D2O. Also, there are indications for the formation of new structures in amorphous and crystalline calcium carbonates. There is huge potential towards further improving the understanding of mineralization mechanisms by studying solvent-mediated isotope effects, also beyond calcium carbonate. Last, it must be appreciated that H2O and D2O have significant, distinct effects on mineralization mechanisms, and that care has to be taken when experimental data from D2O studies are used, e.g., for the development of H2O-based computer models.
Introduction
Deuteration of compounds is often employed to investigate reaction mechanisms based on the so-called kinetic isotope effect,1 where doubling of the masses due to the change from hydrogen (H) to deuterium (D) reduces the vibrational frequency of the involved bonds.2,3 This effect also allows shifting the vibrational modes of the aqueous solvent background in IR spectroscopic studies to explore, e.g., protein dynamics.4–7 In proton nuclear magnetic resonance spectroscopy, for instance, replacing H2O by D2O allows one to get rid of unwanted solvent resonance.8 However, when changing the solvent from light to heavy water, also thermodynamic effects have to be considered.9 Not only quantum nuclear effects but also electronic effects come into play and affect a variety of properties.10 The O–D bond is shorter than the O–H bond, i.e., 0.985(5) Å vs. 0.990(5) Å,11,12 rendering the average number of hydrogen bonds within the bulk of D2O slightly higher.13 Also, the peaks in the radial distribution function are more pronounced in the case of D2O.14 Thus, D2O is more ordered than H2O.14–17 This, in turn, causes different macroscopic and microscopic properties of these aqueous solvents. For example, the compressibility and polarizability of D2O are higher than those of H2O.18 Some further selected differences can be found in Table 1, and more details in ref. 9, 19 and 20.| H2O | D2O | |
|---|---|---|
| a The measurements for H2O were done at 1 atm, for D2O at 1 bar. | ||
| Melting point (101.325 kPa) [°C]19 | 0.00 | 3.82 |
| Boiling point (101.325 kPa) [°C]19 | 100.00 | 101.42 |
| C p,m [J K−1 mol−1]24 | 75.23 | 84.67 |
| C V,m [J K−1 mol−1]24 | 74.44 | 84.42 |
| Density (25 °C)a [g cm−3]19 | 0.997048 | 1.1044 |
| Temperature of maximum density [°C]19 | 4.0 | 11.2 |
| Compressibility [10−10 Pa−1]18 | 4.599 | 4.763 |
| Diffusion coefficient [10−5 cm2 s−1]25 | 2.272 | 2.109 |
| Polarizability of vapor near 100 °C [cm3 mol−1]9 | 58.5 | 61.7 |
The different properties of D2O also have consequences for solutes in heavy water. The neutral pH value of water increases from 7.0 to ∼7.4 when changing from H2O to D2O.21,22 Also, the pKa value of acids shifts by an increment in the range of 0.5–0.7 in D2O with respect to the value in H2O, e.g., for the second deprotonation step of carbonic acid pKDa − pKHa = 0.60,23 or 0.741.21 Even deuteration of aliphatic C-atoms near a carboxyl group (i.e., of C-alpha or C-beta atoms) affects the pKa value of the corresponding acids.26
The higher solubility of hydrocarbons and noble gases in D2O2,27,28 can be attributed to its higher compressibility (Table 1),29 reflecting the ability to form nano-cavities more easily than light water. This also leads to a higher hydrophobicity of D2O, even overcoming the opposing effect of stronger hydrogen bonds than in light water.30 This effect, however, depends on solute size, shape and charge and can switch from attractive to repulsive.29 The differences between light and heavy water can furthermore affect the stability of proteins, i.e., the melting temperatures of some proteins in heavy water increase relative to H2O.31 However, other proteins are less stable in D2O than in light water.32,33 Also, the phase behaviour of solutes is different in D2O. For instance, the critical micelle concentration is typically lower in D2O than in H2O.2,34,35 Also, ion solubilities, as well as solvation strengths differ,36–39e.g., the heat of transfer for CaCl2 between the waters is ΔHt(H2O − D2O) = −5.0 kJ mol−1.40
However, little is known about the effects of changing the aqueous solvent from light water to D2O on mineralization. Lee et al.41 explored thermodynamic effects of deuterium on the aqueous synthesis of inorganic materials, revealing new structural and magnetic properties of the obtained manganese and iron materials in D2O. Lundager Madsen reported no significant effect of magnetic fields on calcium carbonate precipitation when using D2O, in contrast to the observed effect in light water.42 Raudino et al.43 found that smaller crystals formed in D2O compared to H2O solutions in the case of alkaline earth carbonates. Furthermore, the conversion of calcite into aragonite in D2O seemed to be less favourable at high temperatures. Recently, Morris et al.44 studied the kinetics of amorphous calcium carbonate (ACC) precipitation in H2O and D2O, reporting very similar rates for the two aqueous solvents, suggesting that neither ion dehydration nor deprotonation of bicarbonate ions represented significant energetic barriers to the formation of ACC.
Considering the various effects of a solvent exchange from light to heavy water described above begs the question: which influences on the early stages of precipitation of calcium carbonate can be expected, in principle? In the following, we contemplate these possibilities within the frameworks of different existing nucleation theories.
Potential effects of D2O vs. H2O according to classical nucleation theory (CNT)
According to CNT, as schematically illustrated in Fig. 1 (top), the nucleation rate J can be expressed as:46| J = L·exp(−EA/kT)·exp(−Δgc/kT) | (1) |
| σ = kT·ln(IAP/Ksp) | (2) |
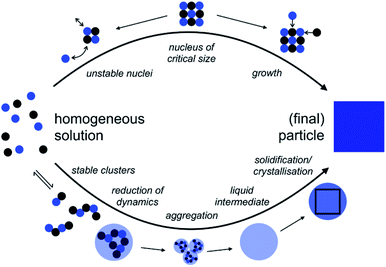 | ||
| Fig. 1 Comparison of the pathways from homogeneous solution to crystals according to the notions of classical nucleation theory (CNT, top) and the pre-nucleation cluster (PNC) pathway (bottom). For explanation see the text; adopted from ref. 45. | ||
The above considerations allow us to qualitatively analyze potential effects of the solvent change on classical nucleation behaviour. A change to heavy water is rather unlikely to affect the pre-factor, L, as this parameter is mainly associated with mineral bulk properties and nucleus shape. Regarding the kinetic barrier, in the case of calcium carbonate, computer simulations indeed suggested that no significant activation energies, e.g., due to de-hydration of the ions, exist,47 a notion that recent experiments seem to corroborate.44 This then leaves the thermodynamic barrier, and it is indeed conceivable that the change of the aqueous solvent alters the surface free energy and/or the solubility constant, Ksp. As the latter enters the quantitative expressions in a logarithm (eqn (2)) that then enters the rate expression in the denominator of an exponent (eqn (1)), any potential effects of the solvent change on the interfacial free energy are expected to dominate, as this parameter is cubed and then enters the exponent for calculating the nucleation rate J.
The surface tension of D2O is slightly less than that of H2O,48 which is attributed to the somehow larger molecular volume and, thus, a somewhat larger separation of the dipoles in heavy water, reducing the mutual attraction between the dipoles within the bulk of the solvent. In the absence of data on interfacial tensions between calcium carbonate and heavy water, it can thus be speculated that the solvent change to heavy water would also somewhat reduce the interfacial free energies of the different polymorphs and forms, potentially by increments that are similar in magnitude. Since the interfacial free energy is cubed for the calculation of Δgc at a given supersaturation, and then enters the exponent for estimating the nucleation rate, corresponding effects could become large even for small changes in interfacial free energy, but would promote rather than inhibit “classical nucleation” of calcium carbonate in D2O, with respect to the scenario in H2O.
Potential effects of D2O vs. H2O according to the pre-nucleation cluster (PNC) pathway
The so-called PNC pathway (Fig. 1, bottom) provides an alternative perspective on the mechanisms underlying the early stages of mineralization.45,49,50 Here, thermodynamically stable solute clusters (i.e., standard free energy of formation, ΔG0 < 0) form initially, independent of supersaturation. Their structural form is called a ‘dynamically-ordered liquid-like oxyanion polymer’ (DOLLOP).47 A change towards higher coordination numbers than in the initially chain-like DOLLOPs in larger PNCs was suggested to significantly reduce the PNC dynamics and thereby lead to phase separation.49,51 Indeed, the PNC size distribution depends on the actual IAP in solution, and a recently introduced quantitative framework allows predicting the specific IAPs, at which PNCs can and must transform into dense liquid calcium carbonate (nano)droplets, that is, of the corresponding liquid–liquid binodal and spinodal limits, respectively.52 Input parameters of the experimentally verified model are, essentially, the ion association constant, Kcluster, and the solubilities of the different polymorphs, Ksp,polym., accounting for the experimentally observed phenomenon of amorphous polymorphism in ACCs53–55 in the binodal limit, given by the corresponding IAPbinodal:52IAPbinodal = Apolym.·Ksp,polym.·ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kcluster Kcluster | (3) |
| IAPspinodal = 1/(Kcluster)2 | (4) |
Water plays an important role in the non-classical nucleation of calcium carbonate.54,61,62 For instance, the entropic contribution to the overall free energy change due to the release of hydration waters from ion hydration shells during ion association drives the formation of PNCs,63 and it is thus conceivable that the change from H2O to D2O might affect the ion association constant. For instance, since D2O is more ordered than H2O (cf. above), the entropic gain upon releasing hydration waters to a more ordered environment during ion association might be somewhat reduced in heavy water, which would render PNCs in D2O less stable than in H2O. Since the solubilities of the different polymorphs and forms might be affected too, within the framework of the quantitative PNC model,52 this would then shift the binodal and spinodal limits, eqn (3) and (4). With it, the critical point and the whole liquid–liquid coexistence region would be shifted, potentially giving rise even to the formation of distinct, potentially new proto-structures in ACC. In turn, new crystal polymorphs might become accessible. A changed locus of the miscibility gap would in any case alter the kinetics of liquid–liquid demixing from specific levels of supersaturation, opening up reaction channels for alternative pathways. For instance, in D2O, calcium carbonate might behave more ‘classically’. In our opinion, virtually anything is possible.
However, very little is known about the effects of changing the solvent from light to heavy water on calcium carbonate mineralization. Since strong effects are possible, which promise to shed new light on the nucleation mechanisms both from a kinetic and thermodynamic perspective, we studied the early stages of calcium carbonate formation in light and heavy water, and mixtures of light and heavy water, computationally and experimentally.
Results and discussion
Computer simulations of PNCs in light vs. heavy water
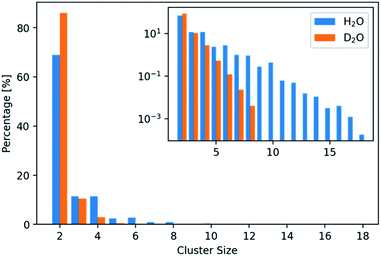
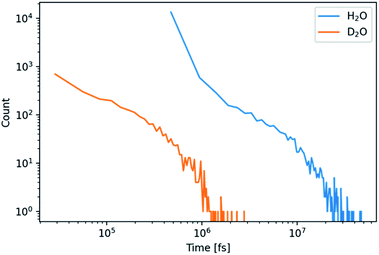
The development of a flexible heavy water model and its properties are described in the Experimental section on the computational methods (ESI, Experimental section and Fig. S1, S2, Tables S1 and S2†). In brief, the parameterization by scaling the charges of the flexible water model SPC/fw led to a good D2O model (SPC/HW/fw) that correctly represents the structure of heavy water and that can be combined with the CaCO3 model of Raiteri et al.64The formation of PNCs in D2O and H2O was simulated utilizing a cubic simulation box with a side length of 55 Å, containing 10 Ca2+- and 10 CO32−-ions. The resulting concentration was 0.1 M with respect to Ca2+-ions. 20 replicas with randomized ion positions were simulated per solvent. During the course of these simulations, clusters emerged and disappeared. These clusters were further analysed to search for differences in structure and kinetics between light and heavy water.
In addition, only half so many clusters containing more than two ions, were found in D2O with respect to H2O. We thus visualized the internal structure of ion aggregates by creating 2D histograms of angle–distance combinations within the clusters. Here, we looked at all ion pairs within a cut-off distance of 4.0 Å. Then we measured the distance and angle of a third ion within 8.0 Å and binned the values in histograms. The resulting histograms (Fig. S3 and S4†) show that the overall features stay the same. However, the features, especially at large angles, are less pronounced in D2O. This agrees with the observation of shorter and more compact clusters in D2O and indicates that the structure of the clusters differs between the two aqueous solvents.
 | ||
| Fig. 4 Potential of mean force for the distance between calcium and carbonate ions in H2O and D2O as indicated. | ||
The difference in mass between the two aqueous solvents is often considered to be the only difference, while changes of internal structure and polarizability are often neglected. So as to investigate the over-simplified assumption further, an H2O model with masses of D2O was simulated. The corresponding 2D histogram of the radius of gyration vs. cluster size (Fig. S6†) reveals no structural changes between the clusters in H2O and in H2O with increased masses, that is, in “pseudo-D2O”. Also, the distribution of cluster sizes persists after the mass change (Fig. S7†). Only the lifetime of these clusters in “pseudo-D2O” decreases (Fig. S8†). Thus, these simulations of “pseudo-D2O” reveal that the above-described change in behaviour arises from the change of the charge distribution within the solvent rather than from the mass difference of the two aqueous solvents.
Titration assays of calcium carbonate formation
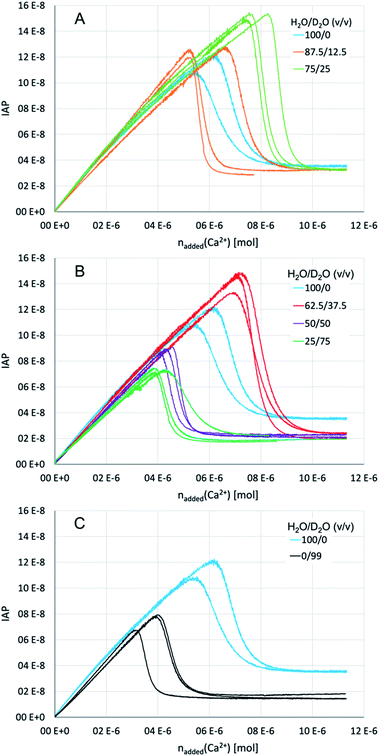
So as to elucidate the effects of a solvent change from light to heavy water experimentally, we performed titration experiments in different mixtures of the two aqueous solvents, as well as in pure H2O and 99% D2O. In brief, dilute calcium solution was added into dilute carbonate buffers, while the pH was maintained at a constant value by automatic counter-titration with dilute sodium hydroxide solution. The specific H2O/D2O ratio (v/v) in these solutions was the same, and adjusted to 100/0, 87.5/12.5, 75/25, 62.5/37.5, 50/50, 25/75 and 0/99 in separate repetitions. The pH of the respective mixtures was thereby adjusted to a value that corresponds to the same carbonate/bicarbonate ratio in the buffer in pure H2O at pH 9.00 (for details see ESI,† Experimental section). This is the equivalent pH of these aqueous mixtures enabling direct comparison of the titration profiles.Initially, the calcium carbonate ion activity product (IAP) increases linearly until it drops to a plateau during the course of the titration (Fig. 5). Due to the very slow titration, the linear parts of the curves represent equilibrated (meta)stable states.65 The slope of the pre-nucleation part (i.e., before the steep drop of the IAP) thus correlates with the equilibrium constant for ion association yielding PNCs, whereas a flatter slope points towards a larger equilibrium constant, i.e., more stable ion associates. On the other hand, the post-nucleation plateau value (i.e., after the steep drop of the IAP) represents the solubility of the initially precipitated phase. Note that the most soluble phase determines these solubility measurements, that is, ripening towards more stable (less soluble) forms is only visible in the titration profiles once the more soluble one has completely dissolved. In pure water, the IAP of ∼3.5 × 10−8 corresponds to the solubility of proto-calcite amorphous calcium carbonate (pc-ACC).53,65 At the same time, this IAP corresponds to the liquid–liquid binodal limit, IAPbinodal = ∼3.5 × 10−8, as demonstrated by THz spectroscopy,66 which can be quantitatively predicted based on eqn (3).52 Indeed, the IAP development upon exceeding the binodal limit represents liquid–liquid coexistence, and strong evidence suggests that the initially formed solid pc-ACC is formed via dehydration of the dense liquid precursors.52 In this sense, the delay between exceeding the binodal limit and the steep drop in IAP is associated with the kinetics of dehydration of phase-separated dense liquid rather than nucleation kinetics per se. In any case, it is obvious that the change from light to heavy water influences (i) the pre-nucleation slope, (ii) the point of nucleation, and (iii) the solubility of the initially precipitated phase. In the following, we discuss these observations individually.
On the other hand, there seem to be no distinct effects of the low heavy water contents on the ion association thermodynamics. However, with increasing heavy water contents (H2O/D2O ratios of 50/50 and 25/75, Fig. 5B), the pre-nucleation slope becomes noticeably flatter, with a minimum at 75% D2O. In terms of standard free energy of ion pair formation, the ion associates are by ca. 2 kJ mol−1 more stable in a mixture of H2O/D2O of 25/75 than in pure light water. However, the trend appears to be reversed in 99% heavy water (Fig. 5C), where the pre-nucleation slope is essentially parallel to the one observed in pure light water, even though the IAP development in 99% heavy water is curved downwards in the very early stage of the experiment (i.e., before the IAP values are reached that are established in the post-nucleation plateau), as opposed to pure light water. In this sense, the experimental data on ion association seems to contradict our results from computer simulations; if anything, ion associates are somewhat more stable in the presence of heavy water.
ATR-FTIR kinetic investigations
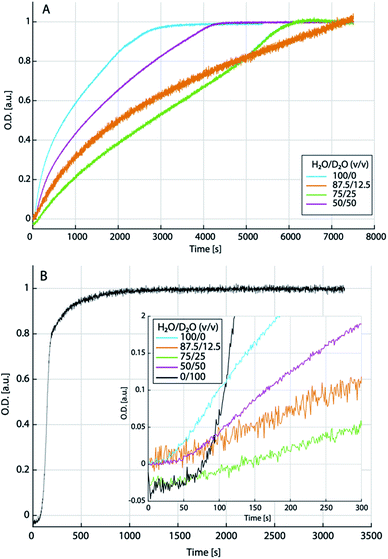
The titration experiments suggest that at relatively low levels of supersaturation (i.e., close to the binodal limit), low amounts of heavy water may inhibit the dehydration kinetics of liquid–liquid separated states towards the formation of solid ACCs, while even higher amounts of heavy water may, in turn, accelerate precipitation and crystallisation in this region of the phase diagram—if the liquid–liquid miscibility gap still exists in D2O containing solutions. In order to explore the precipitation kinetics from the putative spinodal regime of the phase diagram, i.e., at high levels of initial supersaturation, we implemented stopped-flow mixing experiments monitored over time by ATR-FTIR (see the ESI for experimental details†). Calcium chloride (0.2 M) and sodium carbonate (0.2 M) solutions were prepared in different H2O/D2O mixtures (100/0; 87.5/12.5; 75/25; 50/50 and 0/100) and corresponding normalised time transients after mixing were extracted at 869 cm−1, corresponding to the minimum of the second derivative of the ν2 carbonate vibrational band. These concentrations—at least for the pure H2O sample—lead to liquid–liquid demixing from the spinodal regime of the aqueous calcium carbonate phase diagram.52 However, as per the theory (eqn (4)), the altered ion association thermodynamics would shift the spinodal regime to lower IAPs for intermediate heavy water contents, due to the somewhat higher ion association constant.Indeed, the time transients (Fig. 6A) strongly differ for the different aqueous mixtures. In pure light water, we observe a steep initial increase, which gradually flattens, kinks, and then develops into a plateau. In an H2O/D2O mixture of 87.5/12.5, the initial increase is significantly flatter, and the transient does not seem to even come close to reaching a final plateau as observed in pure light water, within the observation time (note that due to the normalization to the plateau value, which is not reached in the experiment with 12.5% heavy water, the initial kinetics is probably the slowest in this mixture). However, a plateau is again reached in the 75/25 mixture within the observation time. In the 50/50 mixture, the kinetics are then again closest to the situation in pure water. Also qualitatively, the kinetics of calcium carbonate precipitation in the 50/50 mixture is similar to the pure light water system, while at low heavy water content (75/25), the transient exhibits rather distinct features. In almost pure heavy water (99.9%; Fig. 6B), on the other hand, the transient looks again completely distinct. Initially, there is a rather flat linear increase for ca. 50–70 s (inset of Fig. 6B) before the transient directly develops into a plateau value with the steepest increase and thus, fastest kinetics observed in all solvent mixtures. In the other solvent mixtures (see inset of Fig. 6B), but not pure light water, we find a similarly flat initial slope, however, the very steep increase as in 99.9% heavy water does not occur.
Only in the 50/50 mixture, there is a notable upwards kink after ca. 50 s, which then gradually levels off after ca. 150 s. In pure light water, a less steep increase than in heavy water occurs after ca. 25 s and we interpret this as the time required for a sufficient amount of calcium carbonate to sediment on the ATR crystal, rather than an induction time. Indeed, a similar “deadtime” is observed in all other transients. However, the extended, flat, initial linear regime in presence of heavy water could be interpreted as the presence of an induction time, which would then provide evidence that we did not probe the spinodal regime in presence of pure heavy water. Unfortunately, due to heavily convoluted carbonate and aqueous solvent bands, the single spectra (data not shown) cannot be evaluated towards an assignment of different calcium carbonate forms to the different kinetic stages in any solvent mixture, at this time.
Simulations of residence times of water molecules and water exchange
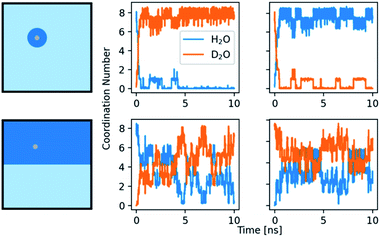
Our kinetic analyses provide evidence for distinct effects of the solvent mixtures in the binodal as well as putative spinodal regimes. In order to explore these observations further, computationally, we studied the residence time of water in the first solvation shell of the ions. The average time that a water molecule stays within the solvation shell was calculated utilizing a self-developed method by bookkeeping the ions and via a time correlation function (see ESI,† Experimental section, for details). The water exchange for calcium ions in heavy water is around two times slower than in light water (Table S4†). The errors observed for both methods show that the residence times of water vary substantially with a maximum value of 1.8 ns for calcium ions in light and 4.8 ns in heavy water, while the average times are on the order of experimentally determined values. Notably, previous calculations of the water residence time for calcium ions in light water with MD simulations yielded a large range of values, depending on the used force field,67 or more precisely, on the size of ions and the water models. An influence of the box size was also found, with a smaller box leading to shorter residence times.68 The difference between water and heavy water may occur due to the changes in mass and charge between the models. However, the change in charge from SPC to TIP3P is around +1.7%, while the change from SPC/fw to SPC/fw/HW is around +2.7%. In the case of SPC vs. TIP3P (GROMOS96 vs. GROMOS87), the residence time decreases by 10%. In the case of water to heavy water, it increases by over 100%. The increase in residence time for D2O seems to depend on the change in mass and maybe slightly stronger ion–water interactions.Moreover, in kinetic measurements, the mixing behaviour of the two aqueous solvents might play additional roles, i.e., the dynamics of light water/heavy water exchange of the ions and potential memory effects. Mixtures of H2O and D2O were simulated while the issue of the formation or presence of HDO molecules was not covered. Negative controls of pure H2O/D2O mixtures without ions showed a rapid mixing of both previously separated phases without any form of aggregation present. The interactions of the ions with the mixed solvents were tested with two setups. On one hand, an ion was simulated in one of the solvents. Then, the ion and a sphere of water, consisting of the first and second solvation shell (Ca2+: 5.4 Å; CO32−: 6.2 Å), was cut out and placed in a box of the other solvent. On the other hand, the box was split into two equal compartments and the ion placed in either one of them. After an equilibration with position restrains, the coordination number of light and heavy water in the first shell was monitored, as shown in Fig. 7. At first glance, the behaviours of the systems seem similar, independent of the placement in H2O or D2O. Yet, there are minor differences between the two solvents. In the first setup, with a calcium ion in a sphere of H2O placed in D2O, the H2O is completely dissolved in D2O and the ion is exclusively surrounded by D2O molecules during the second half of the simulation, from 5 ns after mixing onwards. When a sphere of D2O is placed in H2O, we observe a similar effect. However, at least one D2O molecule detaches and reattaches repeatedly during the whole course of the simulation. In the case of the second setup, with an equal amount of both solvents present, there are on average 1.7 more D2O molecules present around the ion than H2O molecules.
The fluctuation of H2O and D2O around the ion is smaller in the case where the ion is placed directly in D2O. Both setups show that the calcium ion is more attracted to D2O and is thus more influenced by it in mixtures. The second observation indicates that D2O could form a stable solvation shell upon time, maybe with stable, chelating motifs in it. The light water exchange with this solvation shell appears to be slower. The formation of a more stable solvation shell after some induction time is a known problem in MD simulation of magnesium ions, especially in conjunction with RNA.69–72 The better solubility of some ions and small molecules in D2O is also known, assumed to be caused by its different compressibility and hydrophobicity.29
Discussion
We observed various, distinct effects of the aqueous solvents, D2O vs. H2O, on the early stages of calcium carbonate formation, both computationally and experimentally. In MD simulations of ion association in D2O, to which end we developed a suitable force field that is also presented herein, the number of calcium carbonate clusters (PNCs) was reduced by a factor of two when compared to the situation in light water. Furthermore, the clusters in D2O were smaller and more compact than the ones found in H2O, and also shorter lived. This could indicate that nucleation processes in D2O might be “more classical” as the role of PNCs would be reduced, and the cluster distribution shifted more towards single ions or ion pairs—as reflected by a ca. 6 times smaller ion association constant in D2O than in H2O. Simulations of a “pseudo-D2O”, i.e., where only the mass of light water was altered, showed that rather than mass differences, the distinct charge distribution within the aqueous solvents is the key to the different behaviours. The residence time of water molecules on calcium ions is increased by a factor of 2.2–2.5 in D2O, and there seems to be a somewhat higher attraction of calcium ions to D2O molecules, indicating that the ion interactions are probably influenced already at low D2O concentrations in H2O solution. Furthermore, indications were found that the behaviour of the solvent mixtures was determined by its initial condition—i.e., whether a calcium ion was dissolved in D2O or H2O prior to mixing. All of the computationally observed differences between the behaviours of calcium carbonate in D2O and H2O are eventually due to changes in water properties, ion–water interactions and cluster formation, which could even lead to different calcium carbonate structures and formation pathways.Indeed, experimentally, we observed distinct effects of the solvent exchange as well, however, the influence on ion association has the opposite trend when compared to the computer simulations (i.e., ion associates become somewhat more stable in the presence of heavy water in experiments), and the effect is only on the order of thermal energy in terms of standard free energies. Also, with increasing D2O contents, there is no clear trend, and the behaviour somehow reverses again when approaching pure heavy water, in the binodal regime of calcium carbonate formation. This could indicate that in purest heavy water (note that for cost reasons, we employed 99% heavy water in the titration assays, but did use 99.9% heavy water in the ATR-IR-based kinetic analyses), there might actually be a (slight) decrease in stability of ion associates also in experiments. At low heavy water contents in the binodal regime of calcium carbonate formation, dehydration processes of dense liquids towards the formation of solid ACC seem to be weakly inhibited, which is in line with the computer simulations and the residence times of the water molecules on the ions. It is difficult to find information on the kinetics of the exchange of H and D between D2O and H2O in the literature. Mammoli et al.73 assessed the lifetime of proton exchange to be on the order of ∼1 ms in pure water. If this holds true also for the D nucleus, at least for the order of magnitude, corresponding exchanges should be no issue at all with regards to our ATR-FTIR kinetic analysis (where timescales of seconds are discussed). Also, the exchange of H/D should be slow enough so that the computational analysis of the lifetimes of water around calcium-ions are not affected, because the interconversion should be slower than ion–water exchange.
The complex dependence of the calcium carbonate formation pathway on different light/heavy water mixtures is also reflected in kinetic measurements of calcium carbonate formation from high initial levels of supersaturation. While in pure light water, we probed the spinodal regime towards calcium carbonate liquid–liquid demixing, in the presence of heavy water, we observed initial rather flat slopes that might point towards the presence of an induction time for calcium carbonate formation at the same initial IAPs. This suggests that in the presence of heavy water, we might still have probed the kinetics of precipitation of calcium carbonate in the binodal regime. At this point, it remains unclear whether the locus of the liquid–liquid miscibility gap was altered in unpredictable ways, if it even still exists, or whether indeed, calcium carbonate nucleation proceeded “more classically”. The latter might explain the observation of Lundager Madsen42 that there was no effect of magnetic fields on calcium carbonate formation in heavy water (as opposed to light water), since Coey’s theory74 on the effects of magnetic fields on scaling relies on the role of PNCs. The found influence of the solvent and solvent mixture on the point of nucleation of the initial solid is interesting in this regard, and low amounts of heavy water in H2O seem to inhibit the dehydration processes towards formation of solid ACC. The reverse observed behaviour at higher heavy water contents (i.e., promoting nucleation) might indeed reflect that a distinct pathway is populated under these conditions. Thus, above ca. 40% D2O, vaterite may form directly rather than via liquid–liquid separation and solid ACC. After all, this could occur even if liquid–liquid separation still happens in these solvent mixtures, i.e., when the kinetics of dehydration of “non-classical” intermediates is reduced and the classical rate of direct nucleation is increased (potentially, due to lower interfacial free energies of crystals in heavy water, cf. the introductory section). This could be the case to an extent that the classical pathway becomes significantly more populated than the “non-classical” one via PNCs, once heavy water contents are high enough, i.e., above ca. 40% heavy water. However, the kinetics of ACC formation might, on the other hand, be accelerated in these mixtures, so they are not observable in our experiments, and unfortunately, we were not able to isolate the intermediate states due to solubility issues of sodium carbonates in these aqueous solvent mixtures. Notably, it cannot be excluded that new, distinct forms of ACC or even crystalline calcium carbonate become accessible—for which there are at least some indications (Fig. S9†).
When comparing the results from experiment and computations, it has to be kept in mind that the latter did not account for HDO molecules, which might actually be an important species for explaining the experimentally observed behaviour, especially at low heavy water contents. Note that in these mixtures, no significant fractions of D2O are expected to be present, but they would rather be mixtures of mostly H2O and HDO. The changed trends observed in the titration assays may then correlate with the onset of the presence of significant D2O contents within H2O/HDO mixtures. Also, the unclear trends upon changing the compositions of the mixtures in a systematic fashion indicate that there might be a complex, underlying phase behaviour of the water systems, which seems to be rather complicated already in pure light water alone,75 and which might in turn distinctly affect the calcium carbonate formation pathway.
Conclusions
In our opinion, further studies of the differences in the behaviours of aqueous calcium carbonate systems in D2O and H2O, and mixtures thereof, open up unprecedented possibilities for obtaining a better understanding of nucleation and crystallisation mechanisms in the future, and we believe that also the behaviour of other mineral systems in such different aqueous systems should be explored. However, our study provides a warning towards usage of different experimental data, too. Many experiments use D2O as substitute for H2O, for example, so as to get rid of unwanted spectral backgrounds, or for other reasons (also see the introduction section). However, in terms of mineralisation, our data unambiguously demonstrates that the pathway can be considerably altered, depending on the specific solvent (mixture). Notably, experimental data from heavy water systems are sometimes used for the creation of H2O-based (!) models in computer simulations, where the original solvent may not even be mentioned in citations, and mechanisms are then erroneously treated to arise from light water properties. Thus, considering the distinct differences between the waters might even reconcile previous, seemingly contradicting results.Author contributions
Conceptualization: DG, KH, CP; data curation: JTA, MK, CP; formal analysis: JTA, MK, DG; funding acquisition: CP, KH, DG; investigation: JTA, MK; methodology: JTA, MK, CP, KH, DG; project administration: CP, KH, DG; resources: CP, KH, DG; software: JTA, MK, CP; supervision: CP, KH, DG; validation: JTA, MK; visualization: JTA, MK, DG; writing – original draft: MK, DG; writing – review & editing: JTA, MK, CP, KH, DG.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We gratefully acknowledge funding by the German Research Foundation (DFG) through SFB1214 (projects A02 and A04). The authors acknowledge support by the state of Baden-Württemberg through bwHPC and the German Research Foundation (DFG) through grant INST 35/1134-1 FUGG.Notes and references
- J. J. Katz, Am. Sci., 1960, 48, 544–580 CAS.
- G. C. Kresheck, H. Schneider and H. A. Scheraga, J. Phys. Chem., 1965, 69, 3132–3144 CrossRef CAS.
- S. Scheiner and M. Čuma, J. Am. Chem. Soc., 1996, 118, 1511–1521 CrossRef CAS.
- G. Zuber, S. J. Prestrelski and K. Benedek, Anal. Biochem., 1992, 207, 150–156 CrossRef CAS PubMed.
- K. Hauser, C. Krejtschi, R. Huang, L. Wu and T. A. Keiderling, J. Am. Chem. Soc., 2008, 130, 2984–2992 CrossRef CAS PubMed.
- M. Jawurek, J. Dröden, B. Peter, C. Glaubitz and K. Hauser, Chem. Phys., 2018, 512, 53–61 CrossRef CAS.
- A. Krüger, A. Bürkle, K. Hauser and A. Mangerich, Nat. Commun., 2020, 11, 2174 CrossRef PubMed.
- H. H. Mantsch, H. Saitô and I. C. P. Smith, Prog. Nucl. Magn. Reson. Spectrosc., 1977, 11, 211–272 CrossRef.
- G. Némethy and H. A. Scheraga, J. Chem. Phys., 1964, 41, 680–689 CrossRef.
- T. Clark, J. Heske and T. D. Kühne, ChemPhysChem, 2019, 20, 2461–2465 CrossRef CAS PubMed.
- A. Zeidler, P. S. Salmon, H. E. Fischer, J. C. Neuefeind, J. M. Simonson and T. E. Markland, J. Phys.: Condens. Matter, 2012, 24, 284126 CrossRef PubMed.
- R. L. Cook, F. C. D. Lucia and P. Helminger, J. Mol. Spectrosc., 1974, 53, 62–76 CrossRef CAS.
- A. K. Soper and C. J. Benmore, Phys. Rev. Lett., 2008, 101, 353 CrossRef PubMed.
- J. H. Root, P. A. Egelstaff and A. Hime, Chem. Phys., 1986, 109, 437–453 CrossRef CAS.
- B. Tomberli, C. J. Benmore, P. A. Egelstaff, J. Neuefeind and V. Honkimäki, J. Phys.: Condens. Matter, 2000, 12, 2597–2612 CrossRef CAS.
- R. T. Hart, C. J. Benmore, J. Neuefeind, S. Kohara, B. Tomberli and P. A. Egelstaff, Phys. Rev. Lett., 2005, 94, 047801 CrossRef CAS PubMed.
- R. A. Kuharski and P. J. Rossky, J. Chem. Phys., 1985, 82, 5164–5177 CrossRef CAS.
- M. N. Rodnikova, J. Mol. Liq., 2007, 136, 211–213 CrossRef CAS.
- CRC Handbook of Chemistry and Physics, ed. D. R. Lide, 89th edn, Taylor & Francis Ltd, 2019 Search PubMed.
- M. Chaplin, https://water.lsbu.ac.uk/water/, accessed July 2, 2020.
- R. A. Robinson, M. Paabo and R. G. Bates, J. Res. Natl. Bur. Stand., Sect. A, 1969, 73A, 299 CrossRef CAS PubMed.
- M. Ceriotti, W. Fang, P. G. Kusalik, R. H. McKenzie, A. Michaelides, M. A. Morales and T. E. Markland, Chem. Rev., 2016, 116, 7529–7550 CrossRef CAS PubMed.
- J. Curry and Z. Z. Hugus, J. Am. Chem. Soc., 1944, 66, 653–655 CrossRef CAS.
- M. Nakamura, K. Tamura and S. Murakami, Thermochim. Acta, 1995, 253, 127–136 CrossRef CAS.
- D. Eisenberg and W. Kauzmann, The Structure and Properties of Water, Oxford University Press, 2005 Search PubMed.
- A. Streitwieser and H. S. Klein, J. Am. Chem. Soc., 1963, 85, 2759–2763 CrossRef CAS.
- M. M. Lopez and G. I. Makhatadze, Biophys. Chem., 1998, 74, 117–125 CrossRef CAS PubMed.
- E. Wilhelm, R. Battino and R. J. Wilcock, Chem. Rev., 1977, 77, 219–262 CrossRef CAS.
- G. Hummer, S. Garde, A. E. García and L. R. Pratt, Chem. Phys., 2000, 258, 349–370 CrossRef CAS.
- G. Graziano, J. Chem. Phys., 2004, 121, 1878–1882 CrossRef CAS PubMed.
- B. Kuhlman and D. P. Raleigh, Protein Sci., 1998, 7, 2405–2412 CrossRef CAS PubMed.
- G. I. Makhatadze, G. M. Clore and A. M. Gronenborn, Nat. Struct. Biol., 1995, 2, 852–855 CrossRef CAS PubMed.
- R. Guzzi, L. Sportelli, C. L. Rosa, D. Milardi and D. Grasso, J. Phys. Chem. B, 1998, 102, 1021–1028 CrossRef CAS.
- G. C. Kresheck, J. Am. Chem. Soc., 1998, 120, 10964–10969 CrossRef CAS.
- Y. R. E. Silva and J. R. Grigera, RSC Adv., 2015, 5, 70005–70009 RSC.
- H. S. Taylor, E. R. Caley and H. Eyring, J. Am. Chem. Soc., 1933, 55, 4334–4335 CrossRef CAS.
- E. C. Noonan, J. Am. Chem. Soc., 1948, 70, 2915–2918 CrossRef CAS PubMed.
- A. A. Sunier and J. Baumbach, J. Chem. Eng. Data, 1976, 21, 335–336 CrossRef CAS.
- M. Jelińska-Kazimierczuk and J. Szydłowski, J. Solution Chem., 1996, 25, 1175–1184 CrossRef.
- J. Greyson and H. Snell, J. Phys. Chem., 1969, 73, 3208–3214 CrossRef CAS.
- J. Lee, N. D. Chasteen, G. Zhao, G. C. Papaefthymiou and S. M. Gorun, J. Am. Chem. Soc., 2002, 124, 3042–3049 CrossRef CAS PubMed.
- H. E. Lundager Madsen, J. Cryst. Growth, 2004, 267, 251–255 CrossRef CAS.
- M. Raudino, F. Sarri, D. Tatini, M. Ambrosi, G. D. Aloisi, B. W. Ninham, L. Dei and P. Lo Nostro, J. Solution Chem., 2020, 49, 289–305 CrossRef CAS.
- P. D. Morris, I. J. McPherson, G. N. Meloni and P. R. Unwin, Phys. Chem. Chem. Phys., 2020, 22, 22107–22115 RSC.
- D. Gebauer, Minerals, 2018, 8, 179 CrossRef.
- J. J. De Yoreo and P. G. Vekilov, Rev. Mineral. Geochem., 2003, 54, 57–93 CrossRef CAS.
- R. Demichelis, P. Raiteri, J. D. Gale, D. Quigley and D. Gebauer, Nat. Commun., 2011, 2, 590 CrossRef PubMed.
- G. Jones and W. A. Ray, J. Chem. Phys., 1937, 5, 505–508 CrossRef CAS.
- D. Gebauer, M. Kellermeier, J. D. Gale, L. Bergström and H. Cölfen, Chem. Soc. Rev., 2014, 43, 2348–2371 RSC.
- D. Gebauer and S. E. Wolf, J. Am. Chem. Soc., 2019, 141, 4490–4504 CrossRef CAS PubMed.
- A. F. Wallace, L. O. Hedges, A. Fernandez-Martinez, P. Raiteri, J. D. Gale, G. A. Waychunas, S. Whitelam, J. F. Banfield and J. J. De Yoreo, Science, 2013, 341, 885–889 CrossRef CAS PubMed.
- J. T. Avaro, S. L. P. Wolf, K. Hauser and D. Gebauer, Angew. Chem., Int. Ed., 2020, 59, 6155–6159 CrossRef CAS PubMed.
- D. Gebauer, P. N. Gunawidjaja, J. Y. P. Ko, Z. Bacsik, B. Aziz, L. J. Liu, Y. F. Hu, L. Bergström, C.-W. Tai, T.-K. Sham, M. Edén and N. Hedin, Angew. Chem., Int. Ed., 2010, 49, 8889–8891 CrossRef CAS PubMed.
- M. Farhadi Khouzani, D. M. Chevrier, P. Zhang, N. Hedin and D. Gebauer, Angew. Chem., Int. Ed., 2016, 55, 8117–8120 CrossRef CAS PubMed.
- J. H. E. Cartwright, A. G. Checa, J. D. Gale, D. Gebauer and C. I. Sainz-Díaz, Angew. Chem., Int. Ed., 2012, 51, 11960–11970 CrossRef CAS PubMed.
- L. Brečević and A. E. Nielsen, J. Cryst. Growth, 1989, 98, 504–510 CrossRef.
- D. J. Kelly, N. Clark, M. Zhou, D. Gebauer, R. V. Gorbachev and S. J. Haigh, Adv. Mater., 2021, 33, 2100668 CrossRef CAS PubMed.
- P. J. M. Smeets, A. R. Finney, W. J. E. M. Habraken, F. Nudelman, H. Friedrich, J. Laven, J. J. De Yoreo, P. M. Rodger and N. A. J. M. Sommerdijk, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, E7882–E7890 CrossRef CAS PubMed.
- J. Ihli, W. C. Wong, E. H. Noel, Y.-Y. Kim, A. N. Kulak, H. K. Christenson, M. J. Duer and F. C. Meldrum, Nat. Commun., 2014, 5, 3169 CrossRef PubMed.
- E. Ruiz-Agudo, C. V. Putnis and A. Putnis, Chem. Geol., 2014, 383, 132–146 CrossRef CAS.
- P. Raiteri and J. D. Gale, J. Am. Chem. Soc., 2010, 132, 17623–17634 CrossRef CAS PubMed.
- H. Du and E. Amstad, Angew. Chem., Int. Ed., 2020, 59, 1798–1816 CrossRef CAS PubMed.
- M. Kellermeier, P. Raiteri, J. K. Berg, A. Kempter, J. D. Gale and D. Gebauer, ChemPhysChem, 2016, 17, 3535–3541 CrossRef CAS PubMed.
- P. Raiteri, R. Demichelis and J. D. Gale, J. Phys. Chem. C, 2015, 119, 24447–24458 CrossRef CAS.
- D. Gebauer, A. Völkel and H. Cölfen, Science, 2008, 322, 1819–1822 CrossRef CAS PubMed.
- F. Sebastiani, S. L. Wolf, B. Born, T. Q. Luong, H. Cölfen, D. Gebauer and M. Havenith, Angew. Chem., Int. Ed., 2016, 56, 490–495 CrossRef PubMed.
- D. Di Tommaso and N. H. de Leeuw, J. Phys. Chem. B, 2008, 112, 6965–6975 CrossRef CAS PubMed.
- J. Anwar and P. K. Boateng, J. Am. Chem. Soc., 1998, 120, 9600–9604 CrossRef CAS.
- N. M. Fischer, M. D. Polêto, J. Steuer and D. van der Spoel, Nucleic Acids Res., 2018, 46, 4872–4882 CrossRef CAS PubMed.
- O. Allnér, L. Nilsson and A. Villa, J. Chem. Theory Comput., 2012, 8, 1493–1502 CrossRef PubMed.
- J. P. Larentzos and L. J. Criscenti, J. Phys. Chem. B, 2008, 112, 14243–14250 CrossRef CAS PubMed.
- N. Schwierz, J. Chem. Phys., 2020, 152, 224106 CrossRef CAS PubMed.
- D. Mammoli, N. Salvi, J. Milani, R. Buratto, A. Bornet, A. A. Sehgal, E. Canet, P. Pelupessy, D. Carnevale, S. Jannin and G. Bodenhausen, Phys. Chem. Chem. Phys., 2015, 17, 26819–26827 RSC.
- J. M. D. Coey, Philos. Mag., 2012, 92, 1–9 CrossRef.
- O. Mishima, Proc. Jpn. Acad., Ser. B, 2010, 86, 165–175 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1fd00078k |
| ‡ These authors contributed equally and retain the right to list their names first in their respective CVs. |
| This journal is © The Royal Society of Chemistry 2022 |