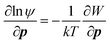Open Access Article
Open Access ArticleSpiers Memorial Lecture: Assembly-based pathways of crystallization
James J.
De Yoreo
 *ab,
Elias
Nakouzi
*ab,
Elias
Nakouzi
 a,
Biao
Jin
a,
Biao
Jin
 a,
Jaehun
Chun
a,
Jaehun
Chun
 ac and
Christopher J.
Mundy
ac and
Christopher J.
Mundy
 ad
ad
aPhysical Sciences Division, Pacific Northwest National Laboratory, Richland, WA 99352, USA. E-mail: james.deyoreo@pnnl.gov
bDepartment of Materials Science and Engineering, University of Washington, Seattle, Washington 98195, USA
cBenjamin Levich Institute, CUNY City College of New York, New York, 10031, USA
dDepartment of Chemical Engineering, University of Washington, Seattle, Washington 98195, USA
First published on 24th March 2022
Abstract
Solution crystallization of materials ranging from simple salts to complex supramolecular assemblies has long been viewed through the lens of classical nucleation and growth theories in which monomeric building blocks assemble into ordered structures through inherent thermal fluctuations that overcome a free energy barrier and continue to grow by the addition of such units to atomic steps. However, recent observations have revealed a rich set of hierarchical pathways during both nucleation and growth involving species of a higher order than monomers. While many studies have investigated and deduced the mechanisms underlying hierarchical nucleation pathways, much less research has been directed towards the development of a mechanistic picture of growth by the assembly of more complex units. Here, we review recent investigations into crystal growth by particle attachment, with an emphasis on oriented attachment. We discuss the relationship between interfacial structure, interparticle forces, and attachment dynamics, discuss the consequences of size dependent phase stability, and examine the impact of the ligand-functionalization of primary particles.
1. Introduction
The mechanisms by which crystalline structures form from solutions often diverge from the classical picture during both nucleation and growth. In that picture, nuclei of the final structure form through monomer-by-monomer addition to unstable clusters that overcome a free energy barrier via inherent thermal fluctuations,1–4 then continue to grow by monomer addition, generally at atomic step edges.5–7 However, research over the past two decades has revealed poorly understood, diverse crystallization pathways involving non-classical, hierarchical processes.9–14 That is, formation occurs via the assembly of “higher-order” species,9,11 including multi-ion complexes,17,18 oligomeric units,19–23 dense liquid phase (DLP) droplets,24–31 or amorphous17,32–41 or ordered42–62 particles (Fig. 1A). Reflecting the distinction between the addition of monomeric units and these higher order species, these hierarchical styles of nucleation and growth have been termed “crystallization by particle attachment” (CPA). The impact of CPA on the material’s structure and properties is extensive because such pathways often create intermediate states which are not otherwise accessible and final crystals that exhibit complex, hierarchical morphologies that lead to novel properties.36,63–65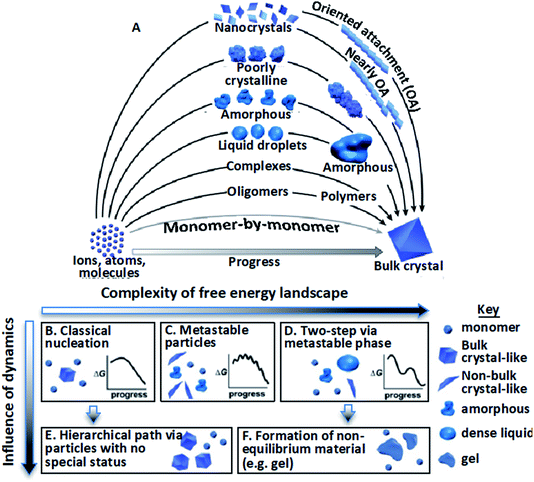 | ||
| Fig. 1 Stable bulk crystals often form from species of a higher order than monomers.11 (A) Pathways can be thermodynamic (B–D) or kinetic (E and F); (B) classical monomer-by-monomer addition; (C) metastable microscopic precursors; (D) metastable bulk precursors; (E) cluster/particle assembly; (F) kinetically trapped metastable or unstable products. In the previous project period, we focused primarily on complexes, oligomers, and nanocrystals. In the next, we will address the circled pathways in (A) corresponding to (D), (E), and (F). From ref. 11. Reprinted with permission from AAAS. | ||
Deviations from the classical crystallization pathway (Fig. 1B) can be expected for two reasons.11 First, complexities in the free energy landscape create metastable structures offering lower-barrier pathways to the final state (Fig. 1C and D). These can either be bulk phases on a phase diagram that are more stable than the solution but less stable than the final solid (Fig. 1C), or configurations that represent local minima that are less stable than the solution itself (Fig. 1D)—and thus can only exist transiently and microscopically—but that provide an environment in which the stable configuration appears more readily than in the bulk. The anatase and brookite phases of TiO2 are examples of the first type; they form more rapidly than the stable rutile phase because the lower surface energies of the metastable phases render the penalty associated with creating the new solid–solution interface of the nuclei smaller than that for rutile.70 Examples of the second case include proteins that form unstable protein-rich liquid droplets within which the first crystals nucleate because of the higher concentration.27–29
The second reason deviations arise stems from dynamical effects of two kinds (Fig. 1E and F):11 (1) high driving forces generate many pre- and post-critical particles that interact and assemble to form highly branched structures or coarsen to compact single crystals (Fig. 1E), and (2) low atomic mobility leaves the system stuck with particles of a metastable bulk phase, particles of an unstable (but locally metastable) microscopic phase, or in a globally unstable state (Fig. 1F), such as a gel. Though this conceptual framework of CPA is clear, the challenge we face in designing or interpreting crystallization processes is that predicting which pathway a system follows and why is generally beyond current understanding.
As Fig. 1A indicates, CPA encompasses hierarchical processes that occur during both the nucleation and growth phase. That is, the assembly of higher order species can occur prior to the establishment of a stable nucleus when the free energy is still increasing with cluster size, or it can occur in the post-nucleation stage, where it essentially constitutes colloidal aggregation. Numerous investigations have addressed the mechanisms through which hierarchical nucleation pathways arise. Here, we focus on the post-nucleation stage, with an emphasis on growth by oriented attachment (OA), a process first reported by Penn and Banfield in 1998 (ref. 53 and 71) in which nanocrystals aggregate into larger single crystals by attaching on identical facets with either crystallographic coalignment or, alternatively, between the two initial—or “primary”—particles.
OA leads to remarkable morphological outcomes, including the formation of tetrapods, chains and sheets, highly branched nanowires, and self-similar 3D mesocrystals. One study showed that OA coupled with strain relaxation is even responsible for the growth of commonly observed five-fold twin structures of noble metal nanoparticles.72 OA and, more generally, the particle-mediated growth of single crystals, has now been widely observed in semiconductors,73–76 metals,58,77 silicates,37,78 oxides,9,43,44,50,52–54,59,62,79,80 fluorides,81 carbonates,50 organic compounds,82 peptides,83 and proteins.84
Many styles of OA have been observed since the first report, extending the concept beyond attachment with crystallographic coalignment to include (1) attachment with some degree of misalignment, followed by relaxation through atomistic processes into a coaligned state,85 (2) attachment of metastable particles of a nanoscopic phase onto crystals of the bulk phase, followed by transformation to the bulk phase with the creation of a coherent interface,43 and (3) a special class of #2 in which the nanoscopic phase is amorphous.50 In all cases, the progression of OA reflects an interplay of the solution structure, forces, and motion (Fig. 2), in which crystal surfaces impose structure on the near-surface solution, leading to a set of interparticle forces, including hydration barriers, and van der Waals (vdW) and electrostatic forces. These interactions and forces are further modified by surface-bound ligands, which are a common feature of nanoparticle systems introduced during colloidal synthesis to stabilize the particles at the nanoscopic size. Moreover, these ligand functionalized interfaces create chemical gradients that can impact the formation of new primary particles and their subsequent attachment. In what follows, we discuss the relationship between interfacial structure, interparticle forces and particle dynamics, discuss the consequences of size dependent phase stability, and examine the impact of the ligand-functionalization of primary particles.
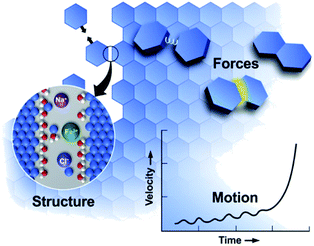 | ||
| Fig. 2 OA is a mesoscale response to forces defined by the molecular details of the interfacial region.11 These details create forces that drive particle motion. As particles move, the structure and forces evolve, transitioning from a regime of long-range to short-range interactions, leading to alignment and attachment. From ref. 11. Reprinted with permission from AAAS. | ||
2. Structure, forces, and motion
While the development of a quantitative framework for predicting particle interactions and assembly has its roots in colloidal physics and continuum-based Derjaguin–Landau–Verwey–Overbeek (DLVO) theory, nanocrystals present additional complexities: the face-specificity of dielectric properties, the presence of structured nanoscale interfaces, and the consequent solvent responses that should be of a comparable length scale. In essence, crystal structure is imprinted upon solvent structure, creating forces between particles whose consequent motion alters the intervening solvent structure, changes the forces, further drives motion, and eventually leads to attachment. Thus, the energetics are distinct from those of conventional colloidal phenomena and lead to the non-trivial coupling of scales, giving rise to hydrodynamic phenomena, such as strong coupling between translational and angular velocities. As such, theoretical progress at the nanoscale requires treatment of hydrodynamics consistent with the molecular level length scale of solvent-response and the concomitant fluctuations.2.1 Interfacial structure
As two approaching nanocrystals reach a separation of a few nanometers, the molecular details of the crystal–solution interface become increasingly important. Indeed, ions and water molecules at the interface behave differently from those in the bulk solution due to interactions with surface chemical groups, patterning against the crystal lattice, and—crucially in the context of CPA—confinement between the two approaching surfaces (Fig. 3A). Accordingly, resolving the interfacial structure and dynamics at the molecular scale will be necessary towards building a predictive understanding of CPA. To date, such a rigorous theoretical framework does not exist. While electrical double layer theories predict ion concentrations as a function of distance from a charged surface, these formulations do not resolve the spatial distribution of solvent molecules86 (despite studies involving a modified Poisson–Boltzmann formulation – see Section 2.2 for more details) beyond continuum approximations. Similarly, empirical models of ion adsorption and speciation remain largely informed at the bulk scale by experimental data and chemical intuition rather than robust local theoretical predictions.87 These models thus fail to capture an important and ubiquitous feature of nanoparticles in solution, namely a molecular based description of the double layers in the vicinity of the solid–solution interface.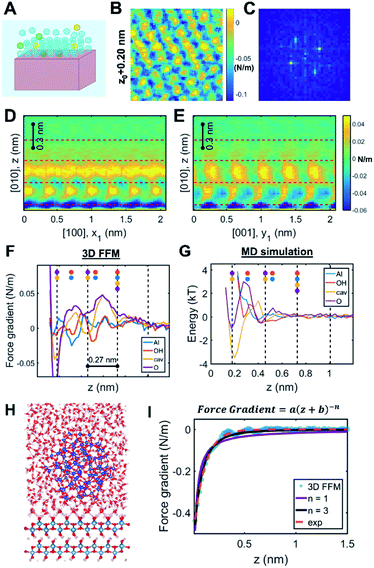 | ||
| Fig. 3 Solution structure at crystal–solution interfaces. (A) Scheme representing ion and water distribution; (B) lateral slice from the boehmite (010)–water 3D FFM measurement16 and (C) corresponding Fourier transform showing that the solution structure is templated by the underlying crystal lattice; (D and E) vertical slices of 3D FFM data along different crystallographic directions; (F) site-specific 3D FFM force gradient and (G) MD water potential of mean force profiles; (H) snapshot of a full-scale simulation of the boehmite–water–silica system; (I) fitting long-range interaction that is ascribed to hydrodynamic force due to confinement. Reprinted with permission from ref. 16. Copyright 2021 American Chemical Society. | ||
The “molecular layering of water at surfaces” was first reported by Israelachvili and Pashley, who used a surface force apparatus to measure short-range oscillatory forces between two mica surfaces immersed in aqueous solution.88 Since then, a range of experimental and simulation techniques have been employed to investigate the interfacial solution structure. Most notably, studies using X-ray reflectivity and diffraction have resolved a multitude of mineral–aqueous interfaces by measuring electron density profiles as a function of distance from the surface and fitting the data to candidate solution structure profiles.89–93 Spectroscopic methods, such as sum frequency generation spectroscopy, provide information on the water orientation at the interface, demonstrating the more limited degrees of freedom of surface-bound water molecules compared to those in the bulk.94,95 More recently, an emerging technique known as 3D fast force mapping (3D FFM) has enabled the visualization of solution structure by measuring the forces experienced by a nanosized probe as it navigates the interfacial region.96–103 These experimental methods are typically coupled to molecular dynamics (MD) simulations, which have evolved significantly in recent years to incorporate advanced force fields, reactivity parameters, and more accurate descriptions of surface chemistry.104–109 While each of these techniques is beset by technical limitations and interpretation challenges, they collectively provide complementary insights that have vastly improved our understanding of crystal–solution interfaces.
One recent case study investigated the boehmite (010)–water interface, which is the preferred crystallographic plane for boehmite oriented attachment in alkaline solution conditions.16 Using 3D FFM, the authors determined that the solution phase close to the surface showed the orthorhombic symmetry that is characteristic of boehmite, hence confirming that the underlying crystal lattice templates the distribution of interfacial water molecules (Fig. 3B and C). These patterns dissipate beyond one nanometer from the surface (Fig. 3D and E). Moreover, four laterally structured hydration layers were resolved with oscillatory features in the order of 0.27 nm, consistent with the size of a water molecule. The data showed distinct responses in the measured force gradients that were ascribed to water density distributions above each crystallographic lattice site (Fig. 3F). Comparison to MD simulations confirmed that the highest water densities occur at the sites adjacent to the boehmite hydroxyl groups, thus facilitating hydrogen bonding (Fig. 3G).
Beyond delineating the solution structure, these results provide important insights that are directly relevant to CPA.16 For example, the 3D FFM data showed additional hydration layers compared to the MD simulation of the free boehmite–water interface (Fig. 3F and G). After creating a suite of simulations with increasing degrees of complexity, the authors were able to reproduce the experimental results by applying a full-scale simulation of the boehmite–water–silica system (Fig. 3H). The conclusion was that confinement between the two surfaces, namely the silica probe and the boehmite substrate, causes an enhanced structuring of the intervening solution, which cannot be probed by “non-intrusive” tools such as X-ray reflectivity and sum frequency generation spectroscopy. Indeed, earlier studies have demonstrated extensive “water packing” in simple Monte Carlo simulations of rigid spheres confined between two infinite planes at close separations, even without incorporating the rigorous molecular and crystallographic details. Accordingly, the interface between two nanosized particles undergoing CPA is expected to follow a non-trivial behavior limited by two extreme cases: the intrinsic ordering of water molecules at a free-standing crystal surface and the extensive ordering due to close proximity between two finite-sized planes.
Another key observation pertains to a qualitative connection between the interfacial structure and other emergent interfacial properties.16 Specifically, the study hypothesized that the interfacial solution structure can cause unusual transport properties due to confinement, leading to “conservative” hydrodynamic forces within ∼1 nm separation between the probe and the surface (Fig. 3I). Interestingly, this result is, in fact, consistent with previous experimental studies that reported chemistry-dependent transport properties at confined liquids, such as the viscoelasticity of water110–113 as well as a reported unusual dielectric property of confined water (∼2 instead of the well-known bulk value, ∼80).114 Considering that these fundamental material/transport properties directly influence particle forces and dynamics, one can convincingly argue that the interfacial structure plays a determining role in the pathways and outcomes of CPA.
Perhaps the most elusive mystery is related to the dynamic nature of the crystal–solution interface, beyond simply an equilibrium distribution of water and ions. During a CPA event, the final “jump-to-contact” between the two nanoparticles predicates that the surface-bound water, ions, and ligands be released from the surface, or otherwise become included in the permanent crystal structure. The corresponding timescales and kinetic barriers for these processes remain difficult to resolve, and are perhaps best interrogated by molecular simulations that can provide valuable information on the desorption/exchange rates for the various interfacial species, as well as changes in the surface chemistry. On this note, recent simulations on anatase in vacuum and humid environments showed that the presence of adsorbed water in fact facilitates oriented attachment by delaying the particle collision and, thus, preventing random aggregation.115
2.2 Forces between crystalline particles
The propensity of nanoparticles to undergo CPA is dictated by a complex interplay between various short- and long-range forces, including electrostatics, dispersion, and hydration forces. These forces depend on fundamental material properties, such as the dielectric permittivity and dipole moments, as well as the physicochemical properties of the crystal surfaces (e.g., the presence of foreign molecules, such as ligands, and surface roughness). Competing with dynamic contributions, such as hydrodynamic forces (described in Section 2.3), the interplay is pivotal to the local/transient responses of particles and the resultant assemblies/microstructures.Long-range forces are mainly described by continuum models, such as the DLVO theory, which typically involve two components: the electrostatic interaction force and the dispersive van der Waals force (Fig. 4A). According to the DLVO theory, the electrostatic interaction force is described by the Poisson–Boltzmann (PB) model, which considers the electrostatic potential of the particle surface and the equilibrium distribution of mobile ions around the particle and relates the local average charge densities to the corresponding electrical fields and potentials. Key approximations implemented in the continuum PB model116 are: (i) describing the electrolyte solution as a continuous dielectric medium characterized by an average density of electrolytes, effectively averaging out the degrees of freedom of solvent molecules and mobile ions, (ii) considering an equilibrium distribution for mobile ions, implying that the gradient of the electrochemical potential needs to be vanished, and (iii) neglecting considerations of ion size and interactions. As such, the electrostatic interaction force between two surfaces is described as an osmotic pressure difference associated with the inhomogeneous distributions of ions.
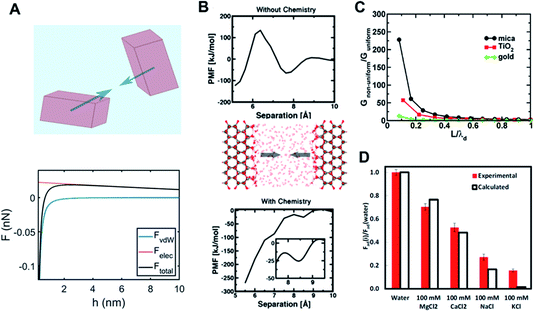 | ||
Fig. 4 Long- and short-range forces between crystalline particles. (A) Typical force–separation curves from DLVO theory along with a schematic of crystalline particles; (B) surface chemistry-dependent hydration forces between ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surfaces from repulsive (without hydroxylation) to attractive nature (with hydroxylation);15. (C) An increase in van der Waals interactions due to the interfacial structure as a function of the particle separation normalized with respect to the thickness of the interfacial layer (i.e., L/λd) over different mineral surfaces;68. (D) Normalized adhesion forces (with respect to an adhesion force for pure water) over different ions as to ion specificity and valence.69 (A and B) Reprinted with permission from ref. 15. Copyright 2018 American Chemical Society. (C) Reprinted with permission from ref. 68. Copyright 2015 American Chemical Society. (D) Reprinted with permission from ref. 69, copyright (2017) National Academy of Sciences. 0) surfaces from repulsive (without hydroxylation) to attractive nature (with hydroxylation);15. (C) An increase in van der Waals interactions due to the interfacial structure as a function of the particle separation normalized with respect to the thickness of the interfacial layer (i.e., L/λd) over different mineral surfaces;68. (D) Normalized adhesion forces (with respect to an adhesion force for pure water) over different ions as to ion specificity and valence.69 (A and B) Reprinted with permission from ref. 15. Copyright 2018 American Chemical Society. (C) Reprinted with permission from ref. 68. Copyright 2015 American Chemical Society. (D) Reprinted with permission from ref. 69, copyright (2017) National Academy of Sciences. | ||
The second component of DLVO, namely the van der Waals force, is described by Lifshitz theory, which assumes that each particle (macroscopic entity) can be fully represented by its corresponding dielectric spectra (i.e., as a function of frequency up to X-ray), inherently including many-body characteristics.117,118 Here, the interaction between fluctuating electromagnetic fields of the interacting particles in the presence of “screening” due to an intervening medium results in the van der Waals force. It is important to note that the van der Waals force is dominated by dielectric spectra differences between interacting bodies in the UV range, whereas frequency differences between bodies in the IR range insignificantly contribute to the overall force. This continuum-based approach for long-range forces has been successfully implemented for characterizing the stability and aggregation of colloids in various industrial and geological settings.
Nevertheless, by ignoring molecular details, the predictive capability of DLVO theory is significantly limited. As discussed in the previous section, “molecular granularity” becomes critical at smaller particle separations where the intervening solution cannot be treated as bulk. For example, one manifestation of the interfacial structure is the emergence of a short-range hydration force at about O(1) nm separation due to a competition between surface hydration and ion hydration.119–121 Note that ions differ appreciably in their relative preference for water–ion interactions over water–surface interactions (kosmotropic or structure-making vs. chaotropic or structure-breaking ions122). Therefore, the hydration force is intrinsically expected to show ion specificity (e.g., Hoffmeister series), in addition to its dependence on the ion concentration and valence; this nature has been confirmed using surface force apparatus (SFA) and atomic force microscopy (AFM) measurements.103,120,121,123,124 Interestingly, a recent study based on quantum density functional theory (qDFT)-based potential of mean forces calculations by Shen et al.15 clearly demonstrated that a hydration force becomes qualitatively different, depending on details of the surface chemistry of the ZnO (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface (i.e., hydroxylation) – see Fig. 4B.
0) surface (i.e., hydroxylation) – see Fig. 4B.
At sufficiently high ion concentrations, the competition between ion-surface and ion–ion interactions becomes more relevant. The average separation between ions scales as nb−1/3 (nb is the number density of the ion at bulk), whereas the length scale for the electrostatic interaction between ions against thermal energy is the Bjerrum length, λB (=q2/εkT), where q is the ionic charge, ε is the dielectric permittivity, k is the Boltzmann constant, and T is the temperature. Therefore, when λB ≫ nb−1/3, a strong ion correlation is expected, suggesting that ion–ion interactions must be considered. To this end, the incorporation of the molecular level detail of specific ion effects and loss of electrostatic screening due to the presence of an interface have been employed into modified PB (mPB) theory. This modification affords a more predictive tool for specific ion-surface segregation that gives rise to novel electrostatic phenomena.125,126 These theories incorporate ion concentration, size, and valence consistent with the aforementioned simple scaling argument.
While these descriptions for both long-range and short-range forces are generally reasonable, some unique features are specifically associated with CPA. First, the distinction between short-range and long-range forces becomes blurred for particles whose size is comparable to the length scale where molecular granularity becomes important. This implies that the molecular level description needs to be implemented into the continuum-based approach, leading to coupling between the forces coming from different scales. One example is a modified Lifshitz theory by Chun et al.,68 which implemented the inhomogeneity of dielectric properties near mineral–fluid interfaces into the conventional Lifshitz theory. The main conclusion was that the coupling of the solution response at different scales results in a much stronger van der Waals force, as demonstrated in Fig. 4C. Similarly, in the study of Li et al.,69 it was revealed that the adhesion forces between two mica surfaces is strongly dependent on ion concentration and specificity, which is attributed to molecular scale phenomena such as ion hydration (see Fig. 4D).
Perhaps one of the key results in the context of CPA is the observation of orientation-dependent adhesion forces between crystalline surfaces, ascribed to the anisotropy in dielectric permittivity127 and surface chemistry, giving rise to torque. Considering the orientation-dependent interaction potential (W), a torque balance between the interaction potential (∂W/∂p) and Brownian (kT) contributions can be described by an orientational probability distribution function (ψ), combined with:
We also note that unique material properties, such as a strong dipole moment or the existence of ligands on the nanocrystal surfaces, contribute additional forces. The former exhibited an attractive dipole–dipole force/torque at large separation that is responsible for ZnO oriented attachment (see Section 2.3),8 whereas the latter triggered a repulsive “steric” hindrance force, analogous to that due to adsorbed polymers, preventing particle attachment131,132 (see Section 4 for details).
2.3 Particle dynamics
Beyond simply characterizing the short-range and long-range forces, the coupling of these forces to particle dynamics is pivotal for obtaining a mechanistic understanding of CPA, a fact that has been largely underestimated or ignored (Fig. 5A). Such coupling can be represented via hydrodynamic mobility, which originates from a linear relationship between a translational/rotational velocity and force/torque.133,134 The hydrodynamic mobility reflects the effects of the particle shape and dimensions, as well as the solution viscosity. This component also includes a separation dependence where it would be applied for “relative” velocities and “relative” force/torque between a pair of particles.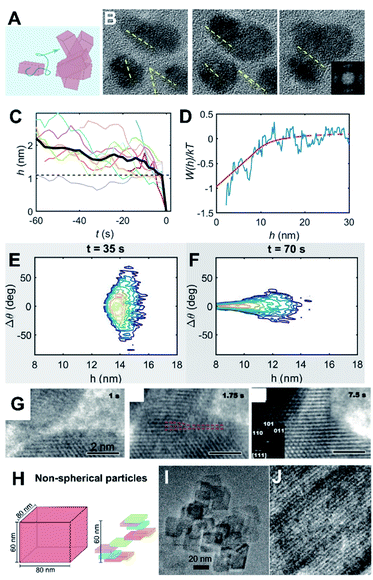 | ||
| Fig. 5 Coupling particle energetics to the dynamics of CPA. (A) Scheme representing particle diffusion and collisions; (B) oriented attachment of ZnO nanocrystals;8 (C) Evolution of particle separation during multiple attachment events; (D) interaction potential of ZnO attachment extracted from the ensemble assembly dynamics; (E and F) Langevin dynamics simulation starting from randomly aligned, far particles show convergence towards perfect alignment at long-range; (G) oriented attachment of iron oxyhydroxide;66 (H) Scheme of non-spherical particle shapes with different diffusion properties and (I and J) examples of oriented attachment outcomes.67 (A–E) Reproduced from ref. 8 with permission from Springer Nature. Copyright 2020. (G) From ref. 66. Reprinted with permission from AAAS. (H) Reprinted with permission from ref. 67. Copyright 2013 American Chemical Society. | ||
Assuming that particle inertia is negligible due to the size of nanocrystals, the linear relationship between a translational velocity (U) and force (F) for the translational motion can be described as U = MtF, where Mt is a hydrodynamic translational mobility tensor. An analogous relation exists for a rotational velocity (Ω) and torque (T), Ω = MrT, where Mr is a hydrodynamic rotational mobility tensor.135 The hydrodynamic mobility becomes critical when two particles are close each other, within a lubrication regime (typically about one tenth of the particle size), where a large hydrodynamic pressure builds up at an intervening space between particles due to their relative motion. Typically, this nature exerts an additional “repulsive” force of a purely dynamic origin. Note that such a hydrodynamic “lubrication” force is expected to be largest for a relative approaching motion along a line between centers of particles, which incidentally is the same direction as the forces described in Section 2.2 (radially symmetric for electrostatic, dispersion, and hydration for spherical particles). Consequently, the resultant translational motions by such forces can be attenuated in the presence of hydrodynamic mobility, leading to a decisive factor for the collision of two approaching particles. A similar nature is expected for the resultant rotational motion by applied torques.
One interesting point is that the hydrodynamic mobility for rotational motion is typically much higher than that for translational motion, especially at close separations. In the case of two interacting spheres, the hydrodynamic mobility remains invariant with respect to separation for rotational motion, in comparison to a decreasing linear dependence on separation for translational motion.135 The observation by Liu et al.8 illustrated that this rotational motion can be conducive for oriented attachment, forcing the nanocrystals to co-align, while a significant hydrodynamic attenuation for the approaching translational motion of the nanocrystals prevents the collision. For spherical nanocrystals, one can understand such coupling between forces/torques and translational/rotational motions based on Jeffrey and Onishi’s135 full mathematical descriptions and corresponding formulations for Mt and Mr. Recent in situ LP-TEM studies for Ag and Au nanoparticles by Lee et al.131,132 implemented hydrodynamic resistivity to rigorously understand the kinetics of the growth of particle clusters and the transient behavior of particles/clusters,132 leading to the superlattice formation based on the coupling between energetics and dynamics.
Recently, Liu et al. presented a case study that connected the energetics and dynamics of ZnO oriented attachment (Fig. 5B and C).8 Specifically, in situ TEM observations documented multiple attachment events and were used to calculate the interaction potential between ZnO crystals (Fig. 5D). The authors determined that dipole–dipole interactions, active at particle separations of >5 nm, are responsible for long-range alignment and subsequent aggregation with no appreciable barrier. This result was validated by Langevin dynamics simulations that coupled particle translational/rotational diffusivities to the experimentally measured potential (Fig. 5E and F). The main conclusion was that strongly polar nanocrystals are conducive for OA due to dipole–dipole forces/torques inducing their coalignment before the point where strong attractive potentials drive the final jump to contact. This result contrasts with an earlier study on dipole-free iron oxyhydroxide nanocrystals, wherein alignment was attributed to short-range interactions. In the latter case, the two approaching crystals linger at a separation of a couple nanometers, sample multiple relative orientations, and jump to contact once a crystallographic alignment has been achieved (Fig. 5G).66
An additional yet important point for particle dynamics comes from the shape of nanocrystals (Fig. 5H–J). Even without considering the crystallography-dependent forces described in Section 2.2, anisotropic particles exhibit cross-coupling between force/torque and translation/rotational velocities that is typically negligible for spherical particles. That is, translational motions can be induced by torques and vice versa. Furthermore, for nanocrystals, the characteristic time scales for translational and rotational motions, obtained from the respective diffusivities, are likely to be comparable,67 indicating appreciable coupling between rotational and translational diffusive motions. Considering the tensorial nature of the hydrodynamic mobilities (i.e., directionality), this suggests that the assembly kinetics of nanocrystals are heavily influenced by the orientation-dependent forces and hydrodynamic mobilities. A recent study67 convincingly demonstrated that such orientational dependence in both particle forces and dynamics is responsible for the qualitative nature of the assembly from a diffusion-limited to a reaction-limited case by a combination of dynamic light scattering and scaling analysis based on irregular-shaped boehmite nanocrystals.
Despite the importance of particle dynamics, hydrodynamic mobilities for non-spherical particles are relatively unknown, while those of certain representative cases, such as cylinders and ellipsoids133 and limited cases for sharp-edged particles (e.g., the face–face configuration between two cubic particles136) are known. The effect of particle shape on hydrodynamic mobility can be significant in magnitude, in comparison to a spherical case; a recent study based on the boundary element method, along with an integral representation of the Stokes flow via a hydrodynamic Green’s function (called the Oseen tensor), showed that the translational hydrodynamic mobility between two cubic particles in parallel configuration is much smaller than that between two spherical particles at the lubrication regime (i.e., O(ε3) vs. O(ε) scale, where ε is a normalized separation between two particles). It is worth noting that all descriptions above are based on continuum hydrodynamics where the infinitesimal volume of fluid is much larger than a molecular scale. Considering the unusual transport properties at confinement associated with interfacial structures from molecular nature, mentioned in Section 2.1, the fundamental concept for hydrodynamic mobility would need to be revisited and possibly reformulated, requiring further theoretical studies. This would be especially important because the last stage of particle assembly, the physical collision of nanocrystals, occurs at the lubrication regime due to the size of nanocrystals.
3. Nanoscopic phase primary particles
As noted in the Introduction, an important complexity of OA is that many systems start from primary particles of a phase that is stable only at the nanoscale,70,137,138 but produce final crystals of the stable bulk phase. Some of the systems in which this pathway has been studied in detail include iron oxides, for which ferrihydrite (FeOOH; Fh) precedes goethite,139 hematite (Fe2O3; Hm)80 or magnetite43 and akageneite precedes Hm,140 titanium oxide, for which anatase precedes rutile,48 and calcium sulfate, for which bassanite precedes gypsum.57 Here again, the style of OA varies and includes the oriented assembly of bassanite (CaSO4·0.5H2O) rods that then convert to gypsum (CaSO4·2H2O), the misoriented assembly of akageneite (β-FeOOH) rods followed by coarsening to Hm, the growth of branched TiO2via the lattice-matched attachment of anatase onto rutile, followed by transformation (Fig. 6), and a coupled dissolution–reprecipitation reaction in which Fh is replaced by nucleating Hm particles, which undergo OA as the new particles form (Fig. 7). | ||
| Fig. 6 Ex situ TEM data showing (A) a branched rutile nanowire, (B) the crystallographic relationship between the branches and trunk, and (C) attachment of the (103) faces of anatase nanoparticles onto the (101) faces of rutile nanowires, followed by transformation to rutile.48 Reprinted with permission from ref. 48. Copyright 2013 American Chemical Society. | ||
 | ||
| Fig. 7 (A–C) Ex situ TEM data showing (A) rhombohedral Hm formed during dissolution–reprecipitation from Fh in oxalate free solution; (B) Hm (H) spindles forming in a Fh (F) suspension containing sodium oxalate; (D–F) in situ TEM data showing the near-surface nucleation and attachment of Hm nanoparticles (D and E) during the initial period of Hm particle formation and (F) over an extended time period to show the development of Hm spindles.80 Reproduced from ref. 80 with permission from Springer Nature. Copyright 2021. | ||
While the appearance of precursor phases can occur for both kinetic and thermodynamic reasons, the latter is expected to be pervasive throughout systems with multiple polymorphs or closely related phases on the phase diagram. The underlying thermodynamic driver lies in the impact of surface energy α on the free energy of formation ΔG(R) of a particle with radius R. Sohnel et al.141 showed that there is a rough inverse scaling between the equilibrium solubility Ce of a phase and α. Thus, less soluble phases are more stable, but have higher surface free energy, implying that the crystal is more poorly matched energetically to the surrounding solution. As the particle radius R is reduced, the proportion of growth units that lie within the bulk of the particle relative to the surface decreases, with the ratio ∝ R. Consequently, as shown for a wide range of materials, at a sufficiently small particle size, the free energy per growth unit, which is the sum of the surface and bulk contributions, becomes smaller for metastable phase than for the bulk phase.137,138 In other words, the relative stabilities are reversed. Compounding this phenomenon is the impact of the inverse relationship between Ce and α on the relative probabilities of nucleating particles of the two phases. This effect is most easily seen by considering nucleation within the framework of classical nucleation theory (CNT). Within CNT, the rate of nucleation Jn scales with the exponential of the free energy barrier ΔG*, which in turn scales with the cube of the interfacial free energy α. That is, Jn ∝ e−ΔG*/kT and ΔG* ∝ α3, where k is Boltzmann’s constant and T is the temperature.3,4 Thus, as a particle first begins to nucleate and R is below the value at which the free energies of formation for the two phases cross over, the metastable bulk phase is both the most stable phase and faces a lower barrier to nucleation. Consequently, the first particles to appear are of the bulk metastable phase rather than the stable phase.
3.1 Nanoscopic phase as a particle source
The growth of branched rutile nanowires from anatase primary particles (Fig. 6A) presents a particularly interesting example of OA via a nanoscopic phase.48 After the anatase particles form, the solution remains supersaturated with respect to rutile, because it is the more stable bulk phase with the lower solubility. Thus, rutile wires, once they begin to form, can grow by classical ion-by-ion processes. However, the anatase (103) face is a near-perfect match for the rutile (101) face. Consequently, concomitant with the ion-by-ion growth of the wires, anatase particles attach to the rutile nanowires with perfect lattice matching and, after doing so, undergo a pseudomorphic transformation to rutile. Depending on which (103) face attaches to the rutile trunk (Fig. 6B), wires either extend in length or form branches meeting the trunk on (101) twin planes (Fig. 6C). This process occurs repeatedly to produce multiple generations of branches, all under crystallographic control.While the direct involvement of nanoscopic phase primary particles would seem to be a requirement for such phases to influence CPA, the growth of Hm mesocrystals starting from a Fh precursor illustrates a strikingly different process. When ferric nitrate and sodium hydroxide are mixed, a suspension of Fh rapidly forms. Eventually, this precursor phase dissolves as Hm nucleates and grows into well faceted rhombohedral Hm through classical growth processes (Fig. 7A). However, when sodium oxalate (Ox) is added to the initial Fh suspension, Hm forms a nanoporous spindle-shaped single crystal elongated along [001] and having a nearly constant aspect ratio, regardless of the absolute size or time after formation begins (Fig. 7B).80 The spindles are hierarchically organized across two length scales. At the shortest length scale, they consist of ∼5 nm crystallographically coaligned particles (Fig. 7C). These then form a second order structure consisting of chains of the Hm particles (Fig. 7C).
The first Hm particles always form either by the direct transformation of Fh to Hm or by the heterogeneous nucleation of Hm on Fh. However, as soon as a Hm particle forms, new particles begin to nucleate within a couple of nm of the first particle (Fig. 7D–F). Immediately after they nucleate, the daughter Hm particles attach to the parent particle next to which nucleation occurred (Fig. 7D–F). Repeated occurrences of these events lead to the formation of the self-similar Hm mesocrystals, which are elongated along the [001] direction because the rate of nucleation near the Hm (001) face of the particles exceeds that along other directions.
In this process of Hm mesocrystal formation, the Fh plays a number of key roles. First, it serves as a source of solute for the growing Hm particles. Second, it provides a buffer that fixes the Fe3+ concentration at the solubility limit of Fh. Due to the moderate difference in solubility between the two phases and the high Hm surface energy, the barrier to Hm nucleation is large (∼80 kT) and, thus, nucleation in the bulk solution is rare, consistent with the observation that the nucleation of new Hm particles in the solution far from a Hm particle is never observed in our experiments. Finally, the Fh provides a favourable environment for the sporadic nucleation of Hm, either through direct transformation or heterogeneous nucleation. Why Ox then enables rapid nucleation to occur in the vicinity of these initially formed Hm particles, limits the Hm particle size, and drives the subsequent attachment events to create the mesocrystals is discussed below.
4. Control by ligands and interfaces
4.1 Ligands as a source of bias
CPA is always accompanied by relaxation processes, leading to an evolution in the final particle morphology. For example, rapid particle attachment and slow relaxation processes lead to the formation of dendric structures, while slow particle attachment and rapid relaxation may drive spherical particle formation (Fig. 8A and B). To balance particle attachment and relaxation rates, various ligands can be introduced to tune the ligand–ligand and ligand–particle interaction strengths, as well as the particle–particle interactions.142–144 Taking Au nanocrystals as an example, the involvement of organic small molecules, such as CTAB, citrate, or ionic liquids, can drive the attachment of Au particles along the [111] direction and drive two-dimensional particle assembly.145–150 Sequence-defined biomolecules have also been shown to be effective ligands in nanocrystal synthesis and bring the added benefit of tunability, as illustrated by the regulation of Au nanoparticle shapes by peptoids (Fig. 8B–H).151,152 To develop a controllable and predictable synthesis strategy, an in-depth understanding of ligand control over particle attachment and relaxation is required.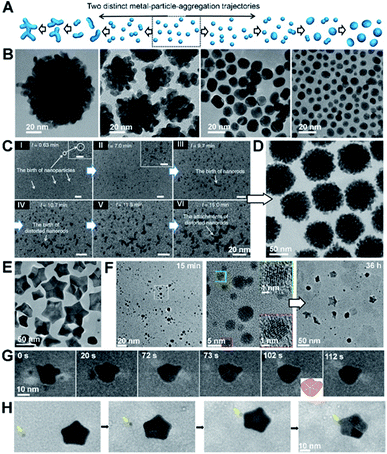 | ||
| Fig. 8 The regulation roles of peptoids in Au nanocrystal formation. (A) Schemes showing two distinct, well-known metal particle aggregation trajectories. (B) TEM images of Au nanoparticle morphologies induced by different peptoid sequences at pH 5.5. The morphology evolves from coral-shaped to spherical particles as peptoids move from high to low binding affinities. (C) Time dependent LP-TEM images showing the birth of Au nanoparticles (I, II), nanorods (III), distorted nanorods (IV), and clusters of distorted nanorods (V, VI) during the early stages of coral-shaped particle formation. (D) TEM image showing typical monodispersed spherical coral-shaped nanoparticles.151 (E) Representative TEM image showing five-fold twinned Au nanostars. (F) Time-dependent ex situ TEM images revealed some intermediate nanostructures during the Pep-1 induced formation of Au nanostars: Au nanoparticles with single crystalline characteristics formed at 15 min and Au stars emerged at 36 h. (G and H) Time dependent TEM images showing the formation and growth of one five-fold twinned nanocrystal through particle attachment (G) and the further growth of the regular five-fold twinned nanocrystal into a concave Au star by the attachment of small nanocrystals (marked by yellow arrow) on the corners (H).152 (A–D) Reproduced from ref. 151 with permission from Springer Nature. Copyright 2018. (E–H) Reproduced from ref. 152 with permission from Wiley-VCH GmbH. Copyright 2022. | ||
One approach using sequence-defined peptoids is to tune the design by systematically varying the hydrophobicity, number of carboxylate and amino groups, and side-chain positions to control the nanoparticle–ligand interactions. When used for Au nanoparticle synthesis, this approach enabled the controlled and predictable synthesis of spherical to coral-shaped nanoparticles (Fig. 8A and B).151 In all cases, the process starts with the random attachment of initially formed Au nanoparticles, resulting in the formation of distorted nanorods. These nanorods then randomly attach to one another to form clusters that are intermediates of the coral-shaped particles (Fig. 8C and D).
During the particle attachment process, the strength of the binding free energy of the peptoid onto the Au particle is directly correlated with the degree to which the interfacial free energy is lowered and, therefore, how low the driving force is for relaxation back to spherical particles. Moreover, the strong peptoid–Au binding affinity reduces the mobility of surface atoms, thus further slowing the kinetics of relaxation. Depending on how strong these effects are, the outcome can be coral-shaped particle formation or relaxation towards spherical particles. These results also highlight the important role of the peptoids in stabilizing small Au nanoparticles (i.e., inhibiting their direct growth) and enhancing CPA. Moreover, this work also showed that the interaction strengths between the Au surface and the peptoids are tuneable through the choice of sequence, which provides facile control over the Au nanocrystal morphology.
Inspired by the ability to control Au–peptoid interaction strengths, a different set of peptoid-based ligands was discovered that produce star-shaped Au nanoparticles (Fig. 8E),152 which consist of concave five-fold twinned particles with arms pointing along the [100] directions and bound by (111) side facets. Time dependent ex situ TEM investigations and direct observations of LP-TEM revealed a stepwise formation mechanism for the nanostars (Fig. 8F–H). The initial formation of small spherical single crystals (∼5 nm) was followed by their attachment and relaxation to form spherical five-fold twinned particles. Further attachment and relaxation events, in which attachment occurred preferentially near the ends of the growing arms, led to the well-developed five-fold twinned stars. Experimental analysis and simulation of peptoid–Au binding confirmed that the formation of the Au star is caused by a strong energetic preference of peptoid binding to Au(111) over Au(100) facets. Variations in growth parameters and peptoid design showed that the outcome is strongly affected by the ratio of peptoid to Au and the absolute and relative strengths of peptoid binding to the Au faces. These factors work together to define a balance between the rate and location of particle attachment events, the kinetics of relaxation towards equilibrium, and (111) facet stabilization.
4.2 Interface-driven nucleation and assembly
Interface-driven nucleation due to local chemical gradients has been observed in a number of systems through a combination of in situ and ex situ characterization.80,153,154 Those studies showed that, when ligands associate with a particle surface, they can bias nucleation to occur in the interfacial region, where attractive interactions then drive particle attachment. For example, pH-sensitive chemical gradients can drive near-surface nucleation and particle attachment of Au nanoparticles in the presence of citric anions.153 Using in situ AFM and LP-TEM to follow transient structural changes during the nucleation and growth of Au nanoparticles, the formation of small particles through secondary nucleation (Fig. 9A, marked with blue arrows) on or near the surface of existing particles with a typical distance of ∼1–2 nm (Fig. 9B) was documented. The new particles formed in the interfacial region, then attached to the existing particles, after which the aggregate either relaxed back towards a faceted morphology (Fig. 9A) or continued to expand outward through new aggregation events (Fig. 9C). The attachment of secondary particles to pre-existing particles proceeded through either a jump-to-contact at sufficiently small separation or the formation of a neck (Fig. 9C).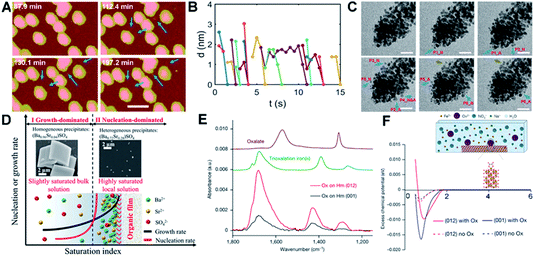 | ||
| Fig. 9 Interface-driven nucleation and assembly process. (A) In situ AFM observation of the particle mediated growth of Au seed crystals; blue arrows highlight newly formed particles. Scale bar is 100 nm; (B) the change in separation with time of the newly nucleated particles from the nearest primary particle; (C) Time dependent LP-TEM images showing the attachment of newly formed secondary particles. Time interval is ∼1 second between images. Secondary particles attaching to primary particles via diffusive jumps (particles 1, 2, 4–6, blue arrows) and via growing a neck (particle 3, brown arrows) were both evident. The suffixes _N and _A refer to particle nucleation and attachment, respectively. The scale bars are 20 nm.153 (D) Schematic showing cation enrichment at organic–water interfaces. Under slightly supersaturated bulk solutions (Ba50Sr50, bulk SI = 1.53), barite precipitates in bulk solution (SEM image, left inset) and grows quickly to micrometer-sized crystals, while a nucleation-dominated precipitation process at a highly supersaturated solution can be achieved near organic–water interfaces due to significant cation enrichment. The STEM image (right inset) shows nanometer-sized, Sr-rich heterogeneous precipitates [(Ba0.72Sr0.28)SO4] formed at organic films from Ba50Sr50 solution (local SI = 8.10).154 (E) Attenuated total reflection–Fourier transform infrared spectra of Ox adsorbed on Hm (001) versus Hm (012). Comparison of the spectra of adsorbed Ox to these reference spectra indicates that Ox is predominantly bound to Hm through direct surface Fe(III) coordination in a bidentate mononuclear fashion; (F) average potential of mean force (PMF) of Fe ions versus distance away from the surface, with (solid lines) and without (dashed lines) Ox. The inset is a schematic of the solution speciation and simulation set-up.80 (A–C) Reproduced from ref. 153 with permission from RSC. Copyright 2018. D Reprinted with permission from ref. 154, Copyright (2019) National Academy of Sciences. (E–F) Reproduced from ref. 80 with permission from Springer Nature. Copyright 2021. | ||
Both interfacial nucleation and neck formation imply a difference in the thermodynamic properties in the interfacial region. The molecular origin of this thermodynamic driving force lies in an interface-induced chemical potential gradient for citrate and [AuCl3(OH)]− anions that promotes the nucleation of secondary particles either through an increase in the local supersaturation or a decrease in the interfacial free energy in the interfacial region. Furthermore, the gradient in the chemical potential drives [AuCl3(OH)]− anions into the interparticle gap, which compensates for the energy cost of dehydration and attachment and/or promotes neck formation by promoting the adsorption and accumulation of citric ions on the Au surface.
Interface-driven nucleation has also been demonstrated in the precipitation process of barite at surfaces functionalized with organic monolayers, even in solutions undersaturated with respect to barite.154 In supersaturated solutions, this phenomenon leads to Sr incorporation levels not possible during barite formation in bulk solution. This mechanism has been hypothesized to provide an explanation for the wide occurrence of Sr-rich marine barites in seawater, which is globally undersaturated in barite. Investigations into the specific organic–mineral interaction at work during this process showed that the organic film induces significant cation enrichment near the film, implying, once again, that a change in interfacial chemistry associated with ion enrichment alters the thermodynamic properties of the interfacial region.
One of the most important findings of this study is that analysis of the phase diagram for the Sr-barite system implies that the formation of nanometer-sized, Sr-rich particles formed at the organic film (right inset in Fig. 9D) requires an increase in the local supersaturation to a saturation index (SI) of 8.10, when the SI in the bulk, where Sr-poor barite crystals form, is only 1.53 (left inset in Fig. 9D). Given that the chemical potential must be constant throughout the system and the increase in ion concentration near the film is a consequence of ion distribution to keep the chemical potential constant, these findings imply a decrease in the solubility of barite itself near the interface. As in the case of the Au-citrate system, these findings demonstrate that organic adsorbates can alter the local thermodynamic properties by concentrating ions, which affects the balance between nucleation and growth rates, causing the formation of crystals under conditions in which they do not form in the bulk or with sizes and compositions distinct from those that form in the bulk.
The understanding of interface-driven nucleation rate and growth rate differences suggests new approaches to achieving control over particle size and morphology during material synthesis. As discussed above (Fig. 7),80 the interface-driven nucleation and assembly of Hm through the dissolution of Fh in the presence of Ox can lead to the synthesis of self-similar Hm mesocrystals (Fig. 7C). The appearance of spheroidal Hm particles only ∼5 nm in size in the Fh aggregates or near Hm seeds, rather than far from any Fh or pre-existing Hm seeds, and the absence of large, faceted Hm crystals, shows that Ox plays an important role in stabilizing Hm nanoparticles and inhibiting their direct growth through classical monomer attachment. The in situ LP-TEM experiments demonstrate that new ‘daughter’ Hm particles repeatedly nucleate adjacent to—but not on—the Ox-covered seed surfaces, exhibiting an intervening edge-to-edge gap of ∼2 nm. Following formation, the daughter particles quickly attach to the seed surface (Fig. 7D–F), thereby forming the mesocrystals.
Measurement of the Ox binding degree to the Hm faces confirms the existence of Ox at the Hm particle surface due to strong binding affinity (Fig. 9E). The surface-bound Ox drives Fe3+ accumulation approximately 1 nm from the surface by creating a layer of negatively charged sites and stabilizing the interfacial diffuse layer of solvated Fe3+ (Fig. 9F). In addition, the interfacial gradients at the Ox-covered surfaces create an attractive interparticle potential that assists in driving particle attachment. Whether the new Hm particles are coaligned upon nucleation, or align prior to, during or following attachment is unclear from the experiments and remains an open question for further exploration.
5. Conclusions
Developing a quantitative framework for CPA that correctly captures the underlying physics by linking atomistic details to ensemble outcomes is crucial both for interpreting mineralization processes in geochemical and biological systems and advancing material synthesis. As discussed in this review, that framework must, first and foremost, be rooted in an ability to define the relationship between interfacial structure, interparticle forces and the dynamics of aggregation. However, the impact of interfacial chemistry, especially in the presence of surface bound ligands, introduces a complicating factor that alters the thermodynamic properties of the solution and/or the crystal in ways that are currently unclear. Moreover, the dependence of phase stability on particle size and the interplay of free energetics and kinetics in determining nucleation rates brings about a convolution of phase evolution and aggregative growth that further complicates predictions, enriching the plethora of potential outcomes. Associated with the relationship between structure, forces and motion, the impact of ligands and interfaces on both structure and thermodynamic properties near the interface, and the evolution of phases with particle size must be considered. The challenges these considerations define can be encapsulated by three major knowledge gaps: (1) how do the complexities of a particle system, including (a) interfacial solution structure and the resulting unique interfacial solution properties, (b) anisotropies in particle shape, and (c) solvent dielectric properties, affect the forces that drive CPA? (2) How do surface-bound organic ligands and solution electrolytes affect interfacial solution structure and the resultant dielectric and transport properties and interparticle forces to enhance or hinder OA? (3) How do the solution structure, size dependent solubilities and free energies of formation determine the progression of phases and probabilities of nucleation, particularly in the interfacial region? Future progress in developing a quantitative framework to describe CPA will depend on our ability to fill these gaps.Author contributions
All authors contributed to the writing of this review.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the US Department of Energy (DOE), Office of Basic Energy Sciences, Division of Materials Science and Engineering, Synthesis and Processing Science Program at Pacific Northwest National Laboratory (PNNL). PNNL is a Multiprogram National Laboratory operated for the DOE by Battelle under contract no. DE-AC05–76RL01830.Notes and references
-
J. W. Gibbs, The Collected Works of J. Willard Gibbs, Yale Univ. Press, New Haven, 1948 Search PubMed
.
-
J. W. Gibbs and A. W. Smith, in Transactions of the Connecticut Academy of Arts and Sciences, Volume III, Chapter V. and Chapter IX., Tuttle, Morehouse & Taylor, New Haven, New Haven, 1874, ch. V. & IX., pp. 108–248, 343–524 Search PubMed
.
-
D. Kashchiev, Nucleation: Basic Theory with Applications, Butterworth Heinemann, Oxford; Boston, 2000 Search PubMed
.
- D. Kashchiev, J. Chem. Phys., 2003, 118, 1837–1851 CrossRef CAS
.
- W. K. Burton, N. Cabrera and F. C. Frank, Nature, 1949, 163, 398–399 CrossRef CAS
.
- W. K. Burton, N. Cabrera and F. C. Frank, Philos. Trans. R. Soc., A, 1951, 243, 299–358 CrossRef
.
-
A. A. Chernov and E. I. Givargizov, Modern Crystallography III: Crystal Growth, Springer, Berlin, 1984 Search PubMed
.
- L. L. Liu, E. Nakouzi, M. L. Sushko, G. K. Schenter, C. J. Mundy, J. Chun and J. J. De Yoreo, Nat. Commun., 2020, 11, 1045 CrossRef CAS PubMed
.
-
H. Cölfen, in Handbook of Biomineralization: Biological Aspects and Structure Formation, ed. E. Bauerlein, Weinheim, Germany, 2008, pp. 39–64 Search PubMed
.
-
H. Cölfen and M. Antonietti, Mesocrystals and Nonclassical Crystallization, Wiley, Chichester, England; Hoboken, NJ, 2008 Search PubMed
.
- J. J. De Yoreo, P. U. P. A. Gilbert, N. A. J. M. Sommerdijk, R. L. Penn, S. Whitelam, D. Joester, H. Z. Zhang, J. D. Rimer, A. Navrotsky, J. F. Banfield, A. F. Wallace, F. M. Michel, F. C. Meldrum, H. Cölfen and P. M. Dove, Science, 2015, 349, aaa6760 CrossRef PubMed
.
- M. A. Duran-Olivencia, P. Yatsyshin, S. Kalliadasis and J. F. Lutsko, New J. Phys., 2018, 20, 083019 CrossRef
.
- D. Erdemir, A. Y. Lee and A. S. Myerson, Acc. Chem. Res., 2009, 42, 621–629 CrossRef CAS PubMed
.
- R. P. Sear, Int. Mater. Rev., 2012, 57, 328–356 CrossRef CAS
.
- Z. Z. Shen, J. Chun, K. M. Rosso and C. J. Mundy, J. Phys. Chem. C, 2018, 122, 12259–12266 CrossRef CAS
.
- E. Nakouzi, A. G. Stack, S. Kerisit, B. A. Legg, C. J. Mundy, G. K. Schenter, J. Chun and J. J. De Yoreo, J. Phys. Chem. C, 2021, 125, 1282–1291 CrossRef CAS
.
- W. J. E. M. Habraken, J. H. Tao, L. J. Brylka, H. Friedrich, L. Bertinetti, A. S. Schenk, A. Verch, V. Dmitrovic, P. H. H. Bomans, P. M. Frederik, J. Laven, P. van der Schoot, B. Aichmayer, G. de With, J. J. DeYoreo and N. Sommerdijk, Nat. Commun., 2013, 4, 1507 CrossRef PubMed
.
- A. Dey, P. H. H. Bomans, F. A. Mueller, J. Will, P. M. Frederik, G. de With and N. A. J. M. Sommerdijk, Nat. Mater., 2010, 9, 1010–1014 CrossRef CAS PubMed
.
- R. Demichelis, P. Raiteri, J. D. Gale, D. Quigley and D. Gebauer, Nat. Commun., 2011, 2, 590 CrossRef PubMed
.
- D. Gebauer and H. Cölfen, Nano Today, 2011, 6, 564–584 CrossRef CAS
.
- D. Gebauer, M. Kellermeier, J. D. Gale, L. Bergstrom and H. Cölfen, Chem. Soc. Rev., 2014, 43, 2348–2371 RSC
.
- D. Gebauer, A. Volkel and H. Cölfen, Science, 2008, 322, 1819–1822 CrossRef CAS PubMed
.
- X. Ma, S. Zhang, F. Jiao, C. J. Newcomb, Y. L. Zhang, A. Prakash, Z. H. Liao, M. D. Baer, C. J. Mundy, J. Pfaendtner, A. Noy, C. L. Chen and J. J. De Yoreo, Nat. Mater., 2017, 16, 767–774 CrossRef CAS PubMed
.
- S. Chung, S. H. Shin, C. R. Bertozzi and J. J. De Yoreo, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 16536–16541 CrossRef CAS PubMed
.
- L. B. Gower and D. J. Odom, J. Cryst. Growth, 2000, 210, 719–734 CrossRef CAS
.
- P. J. M. Smeets, A. R. Finney, W. J. E. M. Habraken, F. Nudelman, H. Friedrich, J. Laven, J. J. De Yoreo, P. M. Rodger and N. A. J. M. Sommerdijk, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, E7882–E7890 CrossRef CAS PubMed
.
- P. G. Vekilov, J. Cryst. Growth, 2005, 275, 65–76 CrossRef CAS
.
- P. G. Vekilov, Nanoscale, 2010, 2, 2346–2357 RSC
.
- O. Galkin, K. Chen, R. L. Nagel, R. E. Hirsch and P. G. Vekilov, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 8479–8483 CrossRef CAS PubMed
.
- A. F. Wallace, L. O. Hedges, A. Fernandez-Martinez, P. Raiteri, J. D. Gale, G. A. Waychunas, S. Whitelam, J. F. Banfield and J. J. De Yoreo, Science, 2013, 341, 885–889 CrossRef CAS PubMed
.
- X. L. Wang, I. M. Chou, W. X. Hu and R. C. Burruss, Geochim. Cosmochim. Acta, 2013, 103, 1–10 CrossRef CAS
.
- L. Addadi, S. Raz and S. Weiner, Adv. Mater., 2003, 15, 959–970 CrossRef CAS
.
- E. Beniash, J. Aizenberg, L. Addadi and S. Weiner, Proc. R. Soc. London, Ser. B, 1997, 264, 461–465 CAS
.
- E. Beniash, R. A. Metzler, R. S. K. Lam and P. U. P. A. Gilbert, J. Struct. Biol., 2009, 166, 133–143 CrossRef CAS PubMed
.
- K. C. Cao, J. Biskupek, C. T. Stoppiello, R. L. McSweeney, T. W. Chamberlain, Z. Liu, K. Suenaga, S. T. Skowron, E. Besley, A. N. Khlobystov and U. Kaiser, Nat. Chem., 2020, 12, 921–928 CrossRef CAS PubMed
.
- M. E. Davis, Nature, 2002, 417, 813–821 CrossRef CAS PubMed
.
- T. M. Davis, T. O. Drews, H. Ramanan, C. He, J. S. Dong, H. Schnablegger, M. A. Katsoulakis, E. Kokkoli, A. V. McCormick, R. L. Penn and M. Tsapatsis, Nat. Mater., 2006, 5, 400–408 CrossRef CAS PubMed
.
- A. Navrotsky, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 12096–12101 CrossRef CAS PubMed
.
- M. H. Nielsen, S. Aloni and J. J. De Yoreo, Science, 2014, 345, 1158–1162 CrossRef CAS PubMed
.
- Y. Politi, T. Arad, E. Klein, S. Weiner and L. Addadi, Science, 2004, 306, 1161–1164 CrossRef CAS PubMed
.
- P. J. M. Smeets, K. R. Cho, R. G. E. Kempen, N. A. J. M. Sommerdijk and J. J. De Yoreo, Nat. Mater., 2015, 14, 394–399 CrossRef CAS PubMed
.
- J. F. Banfield, S. A. Welch, H. Z. Zhang, T. T. Ebert and R. L. Penn, Science, 2000, 289, 751–754 CrossRef CAS PubMed
.
- J. Baumgartner, A. Dey, P. H. H. Bomans, C. Le Coadou, P. Fratzl, N. Sommerdijk and D. Faivre, Nat. Mater., 2013, 12, 310–314 CrossRef CAS PubMed
.
- N. D. Burrows, C. R. H. Hale and R. L. Penn, Cryst. Growth Des., 2013, 13, 3396–3403 CrossRef CAS
.
- H. Cölfen and M. Antonietti, Angew. Chem., Int. Ed., 2005, 44, 5576–5591 CrossRef PubMed
.
- V. K. Ivanov, P. P. Fedorov, A. Y. Baranchikov and V. V. Osiko, Russ. Chem. Rev., 2014, 83, 1204–1222 CrossRef CAS
.
- S. Kumar, Z. Wang, R. L. Penn and M. Tsapatsis, J. Am. Chem. Soc., 2008, 130, 17284–17286 CrossRef CAS PubMed
.
- D. S. Li, F. Soberanis, J. Fu, W. T. Hou, J. Z. Wu and D. Kisailus, Cryst. Growth Des., 2013, 13, 422–428 CrossRef CAS
.
- H. G. Liao, L. K. Cui, S. Whitelam and H. M. Zheng, Science, 2012, 336, 1011–1014 CrossRef CAS PubMed
.
- M. H. Nielsen, D. S. Li, H. Z. Zhang, S. Aloni, T. Y. J. Han, C. Frandsen, J. Seto, J. F. Banfield, H. Cölfen and J. J. De Yoreo, Microsc. Microanal., 2014, 20, 425–436 CrossRef CAS PubMed
.
- J. Park, H. M. Zheng, W. C. Lee, P. L. Geissler, E. Rabani and A. P. Alivisatos, ACS Nano, 2012, 6, 2078–2085 CrossRef CAS PubMed
.
- R. L. Penn, J. Phys. Chem. B, 2004, 108, 12707–12712 CrossRef CAS
.
- R. L. Penn and J. F. Banfield, Science, 1998, 281, 969–971 CrossRef CAS PubMed
.
- M. Raju, A. C. T. van Duin and K. A. Fichthorn, Nano Lett., 2014, 14, 1836–1842 CrossRef CAS PubMed
.
- L. Y. Ruan, H. Ramezani-Dakhel, C. Lee, Y. J. Li, X. F. Duan, H. Heinz and Y. Huang, ACS Nano, 2014, 8, 6934–6944 CrossRef CAS PubMed
.
- R. Q. Song and H. Cölfen, Adv. Mater., 2010, 22, 1301–1330 CrossRef CAS PubMed
.
- A. E. S. Van Driessche, L. G. Benning, J. D. Rodriguez-Blanco, M. Ossorio, P. Bots and J. M. Garcia-Ruiz, Science, 2012, 336, 69–72 CrossRef CAS PubMed
.
- J. M. Yuk, J. Park, P. Ercius, K. Kim, D. J. Hellebusch, M. F. Crommie, J. Y. Lee, A. Zettl and A. P. Alivisatos, Science, 2012, 336, 61–64 CrossRef CAS PubMed
.
- V. M. Yuwono, N. D. Burrows, J. A. Soltis and R. L. Penn, J. Am. Chem. Soc., 2010, 132, 2163–2165 CrossRef CAS PubMed
.
- H. Z. Zhang and J. F. Banfield, Chem. Mater., 2002, 14, 4145–4154 CrossRef CAS
.
- H. Z. Zhang and J. F. Banfield, J. Phys. Chem. Lett., 2012, 3, 2882–2886 CrossRef CAS
.
- H. Z. Zhang, J. J. De Yoreo and J. F. Banfield, ACS Nano, 2014, 8, 6526–6530 CrossRef CAS PubMed
.
- M. J. Bierman and S. Jin, Energy Environ. Sci., 2009, 2, 1050–1059 RSC
.
- R. R. Nair, H. A. Wu, P. N. Jayaram, I. V. Grigorieva and A. K. Geim, Science, 2012, 335, 442–444 CrossRef CAS PubMed
.
- D. B. Suyatin, J. Sun, A. Fuhrer, D. Wallin, L. E. Froberg, L. S. Karlsson, I. Maximov, L. R. Wallenberg, L. Samuelson and H. Q. Xu, Nano Lett., 2008, 8, 1100–1104 CrossRef CAS PubMed
.
- D. Li, M. H. Nielsen, J. R. I. Lee, C. Frandsen, J. F. Banfield and J. J. De Yoreo, Science, 2012, 336, 1014–1018 CrossRef CAS PubMed
.
- E. Nakouzi, J. A. Soltis, B. A. Legg, G. K. Schenter, X. Zhang, T. R. Graham, K. M. Rosso, L. M. Anovitz, J. J. De Yoreo and J. Chun, ACS Nano, 2018, 12, 10114–10122 CrossRef CAS PubMed
.
- J. Chun, C. J. Mundy and G. K. Schenter, J. Phys. Chem. B, 2015, 119, 5873–5881 CrossRef CAS PubMed
.
- D. S. Li, J. Chun, D. D. Xiao, W. J. Zhou, H. C. Cai, L. Zhang, K. M. Rosso, C. J. Mundy, G. K. Schenter and J. J. De Yoreo, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 7537–7542 CrossRef CAS PubMed
.
- A. Navrotsky, ChemPhysChem, 2011, 12, 2207–2215 CrossRef CAS PubMed
.
- R. L. Penn and J. F. Banfield, Am. Mineral., 1998, 83, 1077–1082 CrossRef CAS
.
- M. Song, G. Zhou, N. Lu, J. Lee, E. Nakouzi, H. Wang and D. Li, Science, 2020, 367, 40–45 CrossRef CAS PubMed
.
- M. P. Boneschanscher, W. H. Evers, J. J. Geuchies, T. Altantzis, B. Goris, F. T. Rabouw, S. A. P. van Rossum, H. S. J. van der Zant, L. D. A. Siebbeles, G. Van Tendeloo, I. Swart, J. Hilhorst, A. V. Petukhov, S. Bals and D. Vanmaekelbergh, Science, 2014, 344, 1377–1380 CrossRef CAS PubMed
.
- K. S. Cho, D. V. Talapin, W. Gaschler and C. B. Murray, J. Am. Chem. Soc., 2005, 127, 7140–7147 CrossRef CAS PubMed
.
- M. Kuno, Phys. Chem. Chem. Phys., 2008, 10, 620–639 RSC
.
- Z. G. Li, J. H. Sui, X. L. Li and W. Cai, Langmuir, 2011, 27, 2258–2264 CrossRef CAS PubMed
.
- H. G. Liao and H. M. Zheng, J. Am. Chem. Soc., 2013, 135, 5038–5043 CrossRef CAS PubMed
.
- A. I. Lupulescu and J. D. Rimer, Science, 2014, 344, 729–732 CrossRef CAS PubMed
.
- D. Li, F. Soberanis, J. Fu, W. Hou, J. Wu and D. Kisailus, Cryst. Growth Des., 2013, 13, 422–428 CrossRef CAS
.
- G. Zhu, M. L. Sushko, J. S. Loring, B. A. Legg, M. Song, J. A. Soltis, X. Huang, K. M. Rosso and J. J. De Yoreo, Nature, 2021, 590, 416–422 CrossRef CAS PubMed
.
- A. B. Bard, X. Z. Zhou, X. J. Xia, G. M. Zhu, M. B. Lim, S. M. Kim, M. C. Johnson, J. M. Kollman, M. A. Marcus, S. R. Spurgeon, D. E. Perea, A. Devaraj, J. Chun, J. J. De Yoreo and P. J. Pauzauskie, Chem. Mater., 2020, 32, 2753–2763 CrossRef CAS
.
- S. L. Burkett and M. E. Davis, J. Phys. Chem., 1994, 98, 4647–4653 CrossRef CAS
.
- J. J. Chen, E. B. Zhu, J. Liu, S. Zhang, Z. Y. Lin, X. F. Duan, H. Heinz, Y. Huang and J. J. De Yoreo, Science, 2018, 362, 1135–1139 CrossRef CAS PubMed
.
- A. E. S. Van Driessche, N. Van Gerven, P. H. H. Bomans, R. R. M. Joosten, H. Friedrich, D. Gil-Carton, N. A. J. M. Sommerdijk and M. Sleutel, Nature, 2018, 556, 89–94 CrossRef CAS PubMed
.
- D. S. Li, M. H. Nielsen, J. R. I. Lee, C. Frandsen, J. F. Banfield and J. J. De Yoreo, Science, 2012, 336, 1014–1018 CrossRef CAS PubMed
.
- O. M. Magnussen and A. Gross, J. Am. Chem. Soc., 2019, 141, 4777–4790 CrossRef CAS PubMed
.
-
W. Stumm, Chemistry of the Solid-Water Interface: Processes at the Mineral-Water and Particle-Water Interface in Natural Systems, Wiley-Interscience, New York, NY, 1992 Search PubMed
.
- J. N. Israelachvili and R. M. Pashley, Nature, 1983, 306, 249–250 CrossRef CAS
.
- L. Cheng, P. Fenter, K. L. Nagy, M. L. Schlegel and N. C. Sturchio, Phys. Rev. Lett., 2001, 87, 156103 CrossRef CAS PubMed
.
- S. J. T. Brugman, E. R. Townsend, M. M. H. Smets, P. Accordini and E. Vlieg, Langmuir, 2018, 34, 3821–3826 CrossRef CAS PubMed
.
- S. Pintea, W. de Poel, A. E. F. de Jong, R. Felici and E. Vlieg, Langmuir, 2018, 34, 4241–4248 CrossRef CAS PubMed
.
- P. Fenter and N. C. Sturchio, Prog. Surf. Sci., 2004, 77, 171–258 CrossRef CAS
.
- P. Fenter, C. Park, K. L. Nagy and N. C. Sturchio, Thin Solid Films, 2007, 515, 5654–5659 CrossRef CAS
.
- A. Tuladhar, S. M. Piontek and E. Borguet, J. Phys. Chem. C, 2017, 121, 5168–5177 CrossRef CAS
.
- S. Dewan, M. S. Yeganeh and E. Borguet, J. Phys. Chem. Lett., 2013, 4, 1977–1982 CrossRef CAS PubMed
.
- E. T. Herruzo, H. Asakawa, T. Fukuma and R. Garcia, Nanoscale, 2013, 5, 2678–2685 RSC
.
- T. Fukuma and R. Garcia, ACS Nano, 2018, 12, 11785–11797 CrossRef CAS PubMed
.
- H. Songen, B. Reischl, K. Miyata, R. Bechstein, P. Raiteri, A. L. Rohl, J. D. Gale, T. Fukuma and A. Kuhnle, Phys. Rev. Lett., 2018, 120, 116101 CrossRef PubMed
.
- K. Miyazawa, J. Tracey, B. Reischl, P. Spijker, A. S. Foster, A. L. Rohl and T. Fukuma, Nanoscale, 2020, 12, 12856–12868 RSC
.
- H. Songen, R. Bechstein and A. Kuhnle, J. Phys.: Condens. Matter, 2017, 29, 274001 CrossRef PubMed
.
- H. Songen, C. Marutschke, P. Spijker, E. Holmgren, I. Hermes, R. Bechstein, S. Klassen, J. Tracey, A. S. Foster and A. Kuhnle, Langmuir, 2017, 33, 125–129 CrossRef PubMed
.
- A. F. Payam, D. Martin-Jimenez and R. Garcia, Nanotechnology, 2015, 26, 185706 CrossRef PubMed
.
- D. Martin-Jimenez and R. Garcia, J. Phys. Chem. Lett., 2017, 8, 5707–5711 CrossRef CAS PubMed
.
- S. Kerisit, C. Liu and E. S. Ilton, Geochim. Cosmochim. Acta, 2008, 72, 1481–1497 CrossRef CAS
.
- S. Kerisit, M. Okumura, K. Rosso and M. Machida, Clays Clay Miner., 2016, 64, 389–400 CrossRef CAS
.
- Z. Shen, E. S. Ilton, M. P. Prange and S. N. Kerisit, J. Phys. Chem. C, 2017, 121, 13692–13700 CrossRef CAS
.
- S. N. Kerisit and J. J. De Yoreo, J. Phys. Chem. C, 2020, 124, 5480–5488 CrossRef CAS
.
- I. C. Bourg, S. S. Lee, P. Fenter and C. Tournassat, J. Phys. Chem. C, 2017, 121, 9402–9412 CrossRef CAS
.
- J. A. R. Willemsen, S. C. B. Myneni and I. C. Bourg, J. Phys. Chem. C, 2019, 123, 13624–13636 CrossRef CAS
.
- T. D. Li, H. C. Chiu, D. Ortiz-Young and E. Riedo, Rev. Sci. Instrum., 2014, 85 Search PubMed
.
- E. Riedo, Phys. Rev. Lett., 2008, 100, 106102 CrossRef PubMed
.
- Y. Zhu and S. Granick, Phys. Rev. Lett., 2001, 87, 096104 CrossRef CAS PubMed
.
- T.-D. Li, J. Gao, R. Szoszkiewicz, U. Landman and E. Riedo, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75 Search PubMed
.
- L. Fumagalli, A. Esfandiar, R. Fabregas, S. Hu, P. Ares, A. Janardanan, Q. Yang, B. Radha, T. Taniguchi and K. Watanabe, Science, 2018, 360, 1339–1342 CrossRef CAS PubMed
.
- M. Raju, A. C. van Duin and K. A. Fichthorn, Nano Lett., 2014, 14, 1836–1842 CrossRef CAS PubMed
.
- P. Grochowski and J. Trylska, Biopolymers, 2008, 89, 93–113 CrossRef CAS PubMed
.
-
L. Landau, Electrodynamics of Continuous Media, Landau and Lifshitz Course of Theoretical Physics, Elsevier Butterworth-Heinemann, Burlington, MA, 1984, vol. 8 Search PubMed
.
-
V. Parsegian, Van der Waals Forces, A Handbook for Biologists, Chemists, Engineers, and Physicists, Cambridge University Press, Cambridge, 2005 Search PubMed
.
- V. Parsegian and T. Zemb, Curr. Opin. Colloid Interface Sci., 2011, 16, 618–624 CrossRef CAS
.
- R. M. Pashley, J. Colloid Interface Sci., 1981, 80, 153–162 CrossRef CAS
.
- R. M. Pashley, J. Colloid Interface Sci., 1984, 102, 23–35 CrossRef CAS
.
- Y. Marcus, Chem. Rev., 2009, 109, 1346–1370 CrossRef CAS PubMed
.
- R. Pashley, J. Colloid Interface Sci., 1981, 83, 531–546 CrossRef CAS
.
- T. Baimpos, B. R. Shrestha, S. Raman and M. Valtiner, Langmuir, 2014, 30, 4322–4332 CrossRef CAS PubMed
.
- T. Colla, L. Nunes Lopes and A. P. Dos Santos, J. Chem. Phys., 2017, 147, 014104 CrossRef PubMed
.
- A. P. dos Santos and Y. Levin, J. Chem. Phys., 2015, 142, 194104 CrossRef PubMed
.
- V. M. Agranovich and V. L. Ginzburg, Phys.-Usp., 1962, 5, 323 CrossRef
.
- J. Chun, J.-L. Li, R. Car, I. A. Aksay and D. A. Saville, J. Phys. Chem. B, 2006, 110, 16624–16632 CrossRef CAS PubMed
.
- D. Saville, J. Chun, J.-L. Li, H. Schniepp, R. Car and I. A. Aksay, Phys. Rev. Lett., 2006, 96, 018301 CrossRef CAS PubMed
.
- X. Zhang, Y. He, M. L. Sushko, J. Liu, L. Luo, J. J. De Yoreo, S. X. Mao, C. Wang and K. M. Rosso, Science, 2017, 356, 434–437 CrossRef CAS PubMed
.
- J. Lee, E. Nakouzi, M. Song, B. Wang, J. Chun and D. S. Li, ACS Nano, 2018, 12, 12778–12787 CrossRef CAS PubMed
.
- J. Lee, E. Nakouzi, D. Xiao, Z. G. Wu, M. Song, C. Ophus, J. Chun and D. S. Li, Small, 2019, 15 Search PubMed
.
-
S. Kim and S. J. Karrila, Microhydrodynamics: Principles and Selected Applications, Courier Corporation, 2013 Search PubMed
.
-
W. B. Russel, W. Russel, D. A. Saville and W. R. Schowalter, Colloidal Dispersions, Cambridge university press, 1991 Search PubMed
.
- D. Jeffrey and Y. Onishi, J. Fluid Mech., 1984, 139, 261–290 CrossRef
.
- D. Xiao, Z. Wu, M. Song, J. Chun, G. K. Schenter and D. Li, Langmuir, 2018, 34, 1466–1472 CrossRef CAS PubMed
.
- A. A. Gribb and J. F. Banfield, Am. Mineral., 1997, 82, 717–728 CAS
.
- M. R. Ranade, A. Navrotsky, H. Z. Zhang, J. F. Banfield, S. H. Elder, A. Zaban, P. H. Borse, S. K. Kulkarni, G. S. Doran and H. J. Whitfield, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 6476–6481 CrossRef CAS PubMed
.
- V. M. Yuwono, N. D. Burrows, J. A. Soltis and R. L. Penn, J. Am. Chem. Soc., 2010, 132, 2163–2165 CrossRef CAS PubMed
.
- C. Frandsen, B. A. Legg, L. R. Comolli, H. Z. Zhang, B. Gilbert, E. Johnson and J. F. Banfield, CrystEngComm, 2014, 16, 1451–1458 RSC
.
- O. Söhnel, J. Cryst. Growth, 1982, 57, 101–108 CrossRef
.
- E. Zhu, S. Wang, X. Yan, M. Sobani, L. Ruan, C. Wang, Y. Liu, X. Duan, H. Heinz and Y. Huang, J. Am. Chem. Soc., 2019, 141, 1498–1505 CrossRef CAS PubMed
.
- J. Cassidy, D. Harankahage, J. Ojile, D. Porotnikov, L. Walker, M. Montemurri, B. S. L. Narvaez, D. Khon, M. D. E. Forbes and M. Zamkov, Chem. Mater., 2022, 34, 2484–2494 CrossRef CAS
.
- R. Li, A. Smolyakova, G. Maayan and J. D. Rimer, Chem. Mater., 2017, 29, 9536–9546 CrossRef CAS
.
- W. Qin, A. Agarwal, M. K. Choudhary, J. C. Palmer and J. D. Rimer, Chem. Mater., 2019, 31, 3228–3238 CrossRef CAS
.
- N. A. Merrill, F. Yan, H. Jin, P. Mu, C. L. Chen and M. R. Knecht, Nanoscale, 2018, 10, 12445–12452 RSC
.
- M. Monahan, B. Cai, T. Jian, S. Zhang, G. Zhu, C. L. Chen, J. J. De Yoreo and B. M. Cossairt, Nanoscale, 2021, 13, 1273–1282 RSC
.
- L. Liu, D. Song, B. Jin, M. A. Sinnwell, J. Liu, J. J. De Yoreo and M. L. Sushko, J. Phys. Chem. C, 2020, 124, 24215–24222 CrossRef CAS
.
- C. Zhu, S. Liang, E. Song, Y. Zhou, W. Wang, F. Shan, Y. Shi, C. Hao, K. Yin and T. Zhang, Nat. Commun., 2018, 9, 1 CrossRef CAS PubMed
.
- U. Anand, J. Lu, D. Loh, Z. Aabdin and U. Mirsaidov, Nano Lett., 2016, 16, 786–790 CrossRef CAS PubMed
.
- F. Yan, L. Liu, T. R. Walsh, Y. Gong, P. Z. El-Khoury, Y. Zhang, Z. Zhu, J. J. De Yoreo, M. H. Engelhard, X. Zhang and C. L. Chen, Nat. Commun., 2018, 9, 2327 CrossRef PubMed
.
- B. Jin, F. Yan, X. Qi, B. Cai, J. Tao, X. Fu, S. Tan, P. Zhang, J. Pfaendtner, N. Y. Naser, F. Baneyx, X. Zhang, J. J. DeYoreo and C. L. Chen, Angew. Chem., Int. Ed., 2022, 134, e202201980 Search PubMed
.
- Y. Cheng, J. Tao, G. Zhu, J. A. Soltis, B. A. Legg, E. Nakouzi, J. J. De Yoreo, M. L. Sushko and J. Liu, Nanoscale, 2018, 10, 11907–11912 RSC
.
- N. Deng, A. G. Stack, J. Weber, B. Cao, J. J. De Yoreo and Y. Hu, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 13221–13226 CrossRef CAS PubMed
.
| This journal is © The Royal Society of Chemistry 2022 |