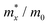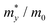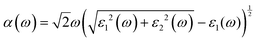C3N2: the missing part of highly stable porous graphitic carbon nitride semiconductors†
Xinyong
Cai
 a,
Jiao
Chen
a,
Hongyan
Wang
a,
Jiao
Chen
a,
Hongyan
Wang
 *a,
Yuxiang
Ni
*a,
Yuxiang
Ni
 a,
Yuanzheng
Chen
a,
Yuanzheng
Chen
 *ab and
R. Bruce
King
*c
*ab and
R. Bruce
King
*c
aSchool of Physical Science and Technology, Key Laboratory of Advanced Technology of Materials, Ministry of Education of China, Southwest Jiaotong University, Chengdu 610031, China. E-mail: hongyanw@swjtu.edu.cn; cyz@swjtu.edu.cn
bBeijing Computational Science Research Center, Haidian District, Beijing 100193, China
cDepartment of Chemistry and Center for Computational Chemistry, University of Georgia, Athens, Georgia 30602, USA. E-mail: rbking@uga.edu
First published on 7th March 2023
Abstract
Two-dimensional (2D) porous graphitic carbon nitrides (PGCNs) with semiconducting features have attracted wide attention because of built-in pores with various active sites, large surface area, and high physicochemical stability. However, only a few PGCNs have been synthesized, covering a 1.23–3.18 eV band gap. We systematically investigate two new 2D PGCN monolayers, T-C3N2 and H-C3N2, including possible pathways for their experimental synthesis. Based on first-principles calculations, the mechanical, electronic, and optical properties of T-C3N2 and H-C3N2 have been systematically investigated. These two architectural frameworks exhibit contrasting mechanical characteristics owing to their structural differences. Both T-C3N2 and H-C3N2 monolayers are predicted to be intrinsic semiconductors. Exceptionally, the stacking bilayers of T-C3N2 can transform into a rare 2D nodal-line semimetal structure. The narrow bandgap (0.35 eV) of the T-C3N2 monolayer and its extraordinary transformation in the bilayer electronic structure fill the vacancy of PGCNs as electronic devices in the middle/long wave infrared region. C3N2 structures possess ultrahigh anisotropic carrier mobilities (×104 cm2 V−1 s−1) and exceptional absorption coefficients (×105 cm−1) in the near-infrared and visible light regions, suggesting its possible optoelectronic applications. The findings expand the scope of 2D PGCNs and offer guides for their experimental realization.
New conceptsTwo-dimensional (2D) porous graphitic carbon nitrides (PGCNs) with semiconducting features have attracted wide attention since g-C3N4 was synthesized. However, only a few PGCNs have been synthesized. Herein, we systematically investigate two 2D PGCNs, namely, H-C3N2 and hitherto unreported T-C3N2. According to the synthetic methods of reported PGCNs, such as C2N-h2D (Nat. Commun., 2015, 6, 6486–6492), the realization of H-C3N2 is quite feasible in the experiment. More notably, first-principles calculations show T-C3N2 has much lower cohesive energy than H-C3N2, which leads to the higher stability of the former. It also implies a possibility of experimental realization of T-C3N2. Both T-C3N2 and H-C3N2 monolayers are predicted to be intrinsic semiconductors with 0.35 eV and 1.97 eV bandgap, respectively. The proposal for T-C3N2 not only enriches PGCN semiconductors but also introduces a clear direction for the experimental realization of more highly stable PGCNs. Another novel feature is that the stacking bilayers of T-C3N2 can transform into a rare 2D nodal-line semimetal, which expands its optoelectronic application. Besides, two C3N2 structures possess ultrahigh anisotropic carrier mobilities (×104 cm2 V−1 s−1) and exceptional absorption coefficients (×105 cm−1) in the near-infrared and visible light regions, further suggesting its possible optoelectronic applications. |
1. Introduction
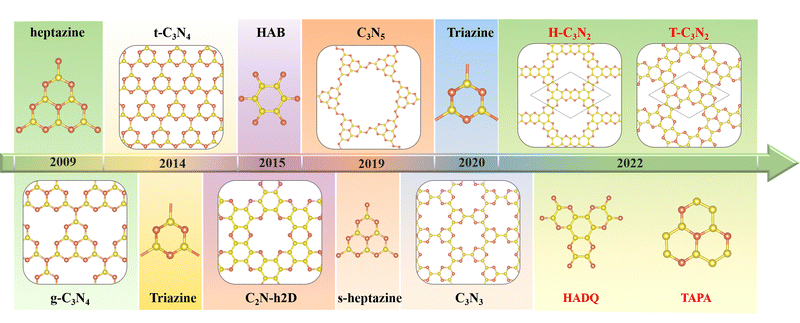
The first synthesized two-dimensional (2D) porous graphitic carbon nitride (PGCN) was g-C3N4, reported in 2009, with a band gap of about 2.70 eV.1 This carbon nitride allotope, with a layered structure analogous to graphite, was found to be more stable than the other four carbon nitride allotropes of the same stoichiometry, namely a-C3N4, b-C3N4, cubic C3N4, and pseudocubic C3N4, all of which exhibit three-dimensional structures of various types. The discovery of graphitic g-C3N4 has triggered considerable research interest owing to its high physicochemical stability, various active sites, built-in pore distribution, and large surface area.2 However, its relatively poor conductivity has limited its electronic and electrochemical applications. Nevertheless, its unique optical properties, suitable conduction band minimum, and valence band maximum make g-C3N4 useful as a photocatalyst for hydrogen evolution by water splitting and for the degradation of some pollutants at room temperature.1,3The successful synthesis of g-C3N4 by the thermal polycondensation of the nitrogen-rich symmetrical hexaminoheptazaphenalene (commonly abbreviated as “heptazine”) with ammonia elimination led to the experimental and theoretical investigation of other PGCNs. Theoretically, the assembly of suitably chosen nitrogen-rich organic monomers through covalent bond formation is feasible. Thus several PGCNs have been successfully synthesized in recent years by polycondensation reactions between suitably chosen oligomers (Scheme 1). For example, C3N5, with a band gap of 1.76 eV, was obtained in 2018 by combining an azo unit (linker) with the hexagonal heptazine motif in the form of hexaminoheptazaphenalene (node).4 In 2019, C3N5 was synthesized as a low bandgap semiconductor for photocatalytic, photovoltaic, and adsorbent applications.5 Apart from g-C3N4 and C3N5, the three most representative PGCNs, namely the highly symmetrical t-C3N4,6 C2N-h2D,7 and C3N3,8 were synthesized and studied experimentally owing to their moderate band gaps (2.40 eV, 2.47 eV and 3.18 eV, respectively) and architectural features similar to g-C3N4. The pyridinic nitrogen atoms surrounding the PGCNs pores provide sites for the absorption of metal ions through coordination. Consequently, the PGCNs can be used as electrode materials for metal-ion batteries.9 Double-layered C2N-450 in lithium-ion (Li-ion) battery was found experimentally to display high reversible capacities of 933.2 (383.3) and 40.1 (179.5) mA h g−1 at 0.1 and 10 C. Furthermore, its monolayer is predicted to exhibit the maximum theoretical capacities of 2939 mA h g−1 among PGCNs.10–12
 | ||
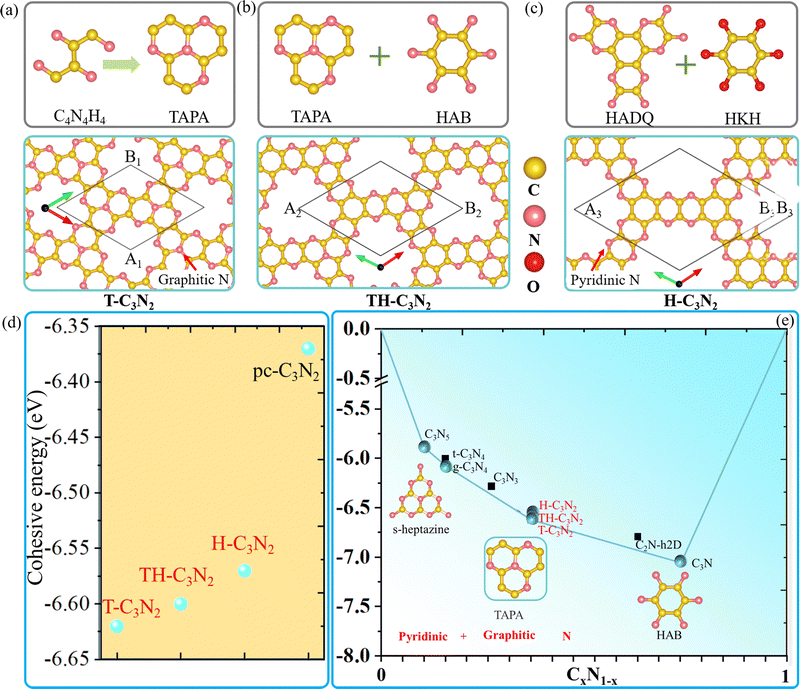
| Scheme 1 The main synthetic progress of reported PGCN, C3N2, and their synthetic precursors. Yellow and magenta balls correspond to carbon and nitrogen atoms, respectively. | ||
Limited efficient synthetic methods and the instability of the PGCNs prevent them from being more widely synthesized and studied experimentally, despite the publication of many theoretical predictions.12–22 The main bottleneck is the lack of suitable organic molecule building blocks. Theoretically, the possibility of experimental synthesis of a given structure is determined by its thermodynamic stability.23 Recently, our group proposed that the coexistence of graphitic and pyridinic nitrogen atoms in PGCNs could lead to more stable structures thermodynamically.12 The crucial role of the coexistence of graphitic and pyridinic N in determining the stability of PGCNs has been theoretically confirmed by Searles et al.11 with subsequent experimental proof by the synthesis of C3N5 and g-C3N4. Analogous to the synthesis of covalent organic frameworks (COF),24,25 the key to the successful synthesis of PGCNs is the availability of suitable organic building blocks meeting the above requirement.
In connection with the synthesis of PGCNs, we propose two feasible nitrogen-containing building blocks, namely 2,3,6,7,10,11-hexamine dipyrazino quinoxaline (HADQ) and 1,4,7,9b-tetraazaphenalene (TAPA). These building blocks can be used to synthesize three novel C3N2 allotropes with hexagonal pores, namely, T-C3N2, TH-C3N2, and H-C3N2. First principle calculations confirm that T-C3N2 with the highest graphitic nitrogen concentration exhibits the highest stability. The mechanical, electronic, and transport properties of C3N2 allotrope monolayers with and without graphitic nitrogen are explored and compared in this paper. The band gaps, carrier mobilities, and optical properties are discussed in order to illustrate their promising applications in nanoelectronic and photovoltaic devices.
2. Computational details
All simulations, including structural search and property calculations, were performed by the density functional theory (DFT) method implemented in the Vienna ab initio simulation package (VASP).26 The electron–ion interaction was considered in the projected augmented wave (PAW)27 method, and the exchange–correlation term was treated using Perdew–Burke–Ernzerhof (PBE)28 parametrization involved in the generalized gradient approximation (GGA).29 The kinetic energy cutoff was set to 700 eV with optimized structures of 20 Å vacuum region between the adjacent images in the z-direction to avoid the interaction between neighboring layers. Meanwhile, the total energy and atomic force converged on each atom when they were less than 10−6 eV and 1 meV Å−1, respectively. The Brillouin zone was sampled with a resolution of 0.03 × 2π Å−1. These studies were followed by using the Heyd–Scuseria–Ernzerh of hybrid functional (HSE06)30 to obtain more accurate band gaps of T-C3N2 monolayers in electronic calculations. van der Waals's interaction was considered using the semiempirical DFT-D2 approach31 in the bilayer structures of PGCNs. Phonon dispersion calculations were carried out in the supercell with at least 96 atoms for T-C3N2, as used in the Phonopy code.32 Molecular dynamics (MD) simulations in the NVT ensemble were used to estimate the thermal stability of T-C3N2. Evaluation of the energetic stabilities of monolayers and the bilayers with different stackings was based on calculations of the cohesive energies (Ec) of the carbon nitride monolayers and the binding energies (Eb) of the bilayers H-C3N2 and T-C3N2 using the equations: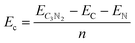 | (1) |
 | (2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N = 3
N = 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.
2.
3. Results and discussion
3.1. Design and feasibility for experimental realization of C3N2 monolayers
Similar to t-C3N46 and g-C3N4,1 H-C3N2 and T-C3N2 allotropes could be also synthesized by different organic unit molecules (details in the Design scheme). As shown in Scheme 1, the s-heptazine, triazine, and hexaaminobenzene (HAB) trihydrochloride are the basic building blocks of the synthesized CN compounds (i.e., C3N5, g-C3N4, t-C3N4, C3N3, C2N-h2D, and C3N).1,5,6,8,34,35 HAB reacts with the other hexaketocyclohexane (HKH) octahydrate organic molecule to produce C2N-h2D,35 where the carbonyl group reacts with amino leaving N atoms.35 Thus, we propose that α-C3N212 (also labeled H-C3N2) monolayer could be synthesized through a possible synthesis scheme between HADQ36 and HKH (Fig. 1c and Fig. S2 in the ESI†). HADQ was just synthesized for the first time in 2021 and used to prepare 2D metal–organic framework (MOF) Co3(HADQ)2,36 similar to 2D MOF Co3(HAB)237 based on the HAB and transition metal Cobalt. The similar structural feature between HADQ and HAB opens the possibility for the experimental realization of H-C3N2. In addition to HADQ, another one containing-N organic unit 1,4,7,9b-tetraazaphenalene (TAPA)38,39 is proposed to construct a new allotrope C3N2 monolayer (labeled T-C3N2). According to the synthetic process of tricycloquinazoline, which was used to prepare covalent quinazoline networks (CQNs), T-C3N2 allotrope could be synthesized40,41 (Fig. 1a and Fig. S3, ESI†). Apart from H-C3N2 and T-C3N2, the combination of TAPA and HAB also forms another allotrope labeled TH-C3N2 (Fig. 1b and Fig. S4, ESI†).From the experimental perspective, the synthesis reaction between HADQ and HKH to form H-C3N2 is quite feasible because the dehydration reaction between amino and carbonyl usually occurs in the synthesis of COFs, such as aza-COF-2,42–45 FA-PON,42,46,47 TQBQ-COF,48 and F-COF.49 Solvents and catalysts are sometimes different, but primary monomers are unchanged. According to the synthesis of C2N-h2D,10,35 aza-COF-2,42,43 and FA-PON46,47,50(Fig. S2, ESI†) and their same edge functional group (i.e. amino), we propose that using the main organic reactants (i.e. HADQ and HKH) and N-methyl-2-pyrrolidone (NMP) in the presence of a few drops of sulfuric acid (H2SO4) as catalysts could produce preliminary materials via a bottom-up wet-chemical reaction, where the reaction mixture needs to be heated 175–185 °C under argon or N2 atmosphere. Similarly, in the synthesis of mCQN and CQN-1, Zinc chloride (ZnCl2) was always used as the solvent and catalyst and reacted with 2-aminobenzonitrile (ABN) and 2,5-diamino-1,4-benzenedicarbonitrile (DBDN) for the condensation of aromatic ortho-aminonitriles to produce tricycloquinazoline linkages (Fig. S3a and b, ESI†).41 For T-C3N2, thus, we predict mixing 1,2-diamino-1,2-dicyanoethylene (DDE) and anhydrous ZnCl2 under 300–400 °C could yield preliminary materials. Furthermore, by comparing the cohesive energy of three C3N2 monolayers with the result of PSO (ESI†), T-C3N2 has the lowest cohesive energy and its synthesis is thermodynamically reliable.23 Therefore, T-C3N2 and H-C3N2 are the focus of our research.
The lattice parameters of T-C3N2 monolayer are A1 = B1 = 8.36 Å, which is smaller than those of H-C3N2 (A3 = B3 = 12.29 Å).12 Both T-C3N2 and H-C3N2 monolayers have regular periodic hexagon holes, the diameter of which is 5.53 Å for the former and 9.72 Å for the latter. According to the atomic chemical environment and symmetry, the nitrogen atoms have different arrangements in H-C3N2 and T-C3N2, exhibiting a hexagonal lattice and a kagome lattice, respectively. The pores of H-C3N2 are surrounded by pyridinic nitrogen atoms bonded to two carbon atoms (Fig. 1c). In comparison, the pore of T-C3N2 is surrounded by six fringed pyridinic nitrogen atoms and six graphitic nitrogen bonded with three carbon atoms within TAPA to form the kagome lattice (Fig. 1a). The space groups P6/m of C6h symmetry and P6/mmm of D6h symmetry are found for T-C3N2 and H-C3N2, respectively. T-C3N2 can be seen as the combination of C3N34 with graphitic nitrogen, as well as C2N-h2D35 with pyridinic-nitrogen and the same hexagon-hole (Fig. S5, ESI†). The optimized C–C and C–N bond lengths of the C3N2 allotropes and related carbon nitrides are compared in Table 1.
| Space group | Lattice parameter (Å) | Average bond lengths | ||
|---|---|---|---|---|
| C–C (Å) | C–N (Å) | |||
| T-C3N2 | P2/m | 8.63 | 1.45/1.40 | 1.31/1.42 |
| HT-C3N2 |
P![[6 with combining macron]](https://www.rsc.org/images/entities/i_char_0036_0304.gif)
|
10.39 | 1.47/1.43 | 1.34/1.34 |
| H-C3N2 | P6/mmm | 12.29 | 1.48/1.45 | 1.32/1.35 |
| C2N-h2D | P6/mmm | 8.33 | 1.47/1.43 | 1.34 |
| C3N | P6/mmm | 4.86 | 1.40 | 1.40 |
Fig. 1d shows that H-C3N2, TH-C3N2, and T-C3N2 have increasingly larger cohesive energies than pc-C3N2,16 suggesting that the coexistence of graphitic and pyridinic nitrogen leads to more stable structures.51 The cohesion energy of the three C3N2 monolayers increases sequentially with decreasing graphitic nitrogen concentration. Higher concentrations of graphitic nitrogen further stabilize the structures in PGCNs compared to pyridinic nitrogen. It explains why the most stable CN monolayer experimentally is hole-free C3N in which all nitrogen atoms are graphitic.
Considering the cohesive energy of the T-C3N2 monolayer and the synthesized carbon nitrides, C3N5, g-C3N4, and T-C3N2 monolayers are on the cyan global stability line, suggesting that the coexistence of graphitic and pyridinic nitrogen are identified to be much more stable PGCNs. However, the metastable structures t-C3N4, C2N-h2D, and C3N3, which were constructed with only pyridinic N, are not on the stability lines in the convex hull (Fig. 1e).23 It signifies that metastable C2N-h2D (C3N3) monolayer could decompose into C3N2. The C2N-h2D (C3N3) monolayer has been synthesized, which further strengthens the synthesis feasibility of C3N2 monolayers.52 The graphitic nitrogen concentration in the stable structures increases from 0.1 in C3N5 to 1 in C3N (Fig. S6, ESI†), suggesting that a likely growing trend of graphitic nitrogen concentration exists in highly stable PGCNs.
The electron localization function (ELF) in Fig. S7a (ESI†) clearly shows that the bonds between graphitic carbon atoms and graphitic(pyridinic) nitrogen atoms are strongly covalent for T-C3N2. The nonbonding lone electron pairs of the pyridinic nitrogen atoms surround the hexagon-holes uniformly, suggesting strong chemisorption capacity. No imaginary frequency is observed in the phonon spectra of the T-C3N2 monolayer. The phonon mode also exhibits good stability for T-C3N2 (Fig. S7b, ESI†). The highest phonon mode (47.99 THz) of T-C3N2 is larger than those of H-C3N2 (47.57 THz),12 C2N-h2D (46.98 THz),53 and g-C3N4 (45 THz)54 monolayers and only less than that of C3N (49.16 THz).55 First-principles molecular dynamical simulations are used to survey the thermal stabilities in a 3 × 2 supercell of T-C3N2 at the selected temperatures of 500 K, 750 K, and 1000 K (Fig. S7c and d, ESI†). The original framework at 750 K is retained even up to 1000 K indicating that the T-C3N2 monolayer maintains stability under high temperatures.
3.2. Mechanical performance of C3N2 monolayers
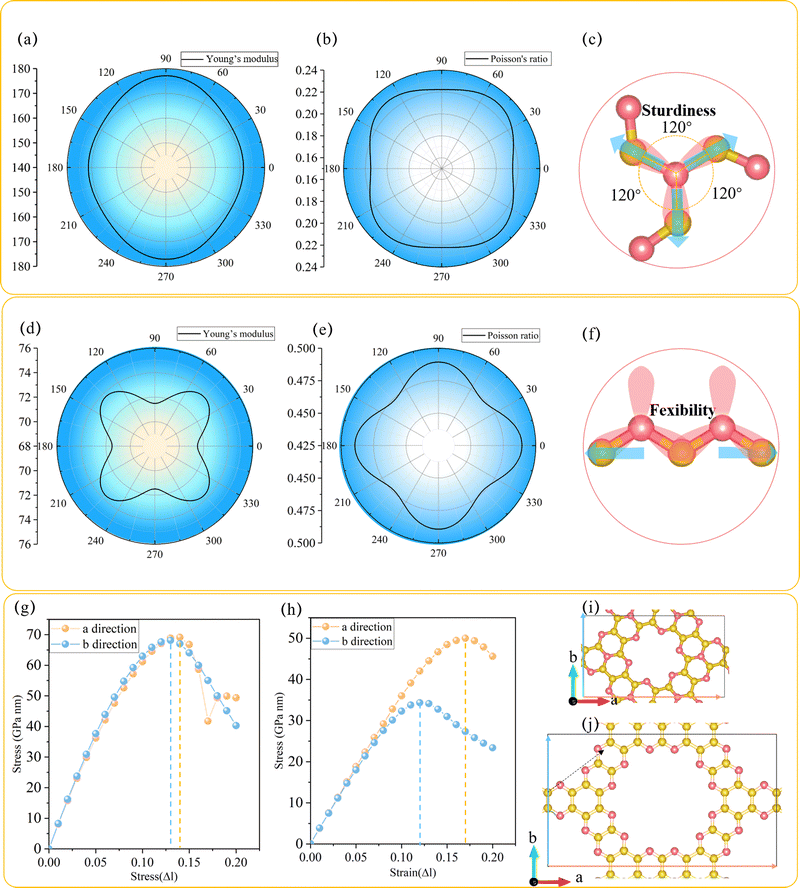
In order to explore the mechanical performance of C3N2 monolayers, the linear elastic constants were calculated for the most stable such monolayer, namely T-C3N2. The 2D linear elastic constants were found to be C11 = 180 N m−1, C22 = 180 N m−1, C12 = 40 N m−1 and C44 = 70 N m−1, all of which are larger than those in H-C3N2.12 These satisfy the Born–Huang criteria for a rectangular cell, namely C11C22 − C122 > 0 and C44 > 0.15 Thus T-C3N2 is also mechanically stable. The orientation-dependent Young's modulus Y and Poisson's ratio ν of T-C3N2 and H-C3N2 monolayers are plotted in Fig. 2a and b and Fig. 2d and e, respectively, according to the expressions of eqn (S1) and (S2) (ESI†). Compared to the maximum Y of H-C3N2, T-C3N2 shows greater robustness. The robustness difference between T-C3N2 and H-C3N2 mainly results from the graphitic nitrogen within the TAPA unit and the pyridinic nitrogen of HADQ. The sp2-hybridization with three σ bonds between the graphitic nitrogen atoms and the three adjacent carbon atoms separated by 120° solidifies the structure in three directions owing to its strong electronegativity (Fig. 2c). The pyridinic nitrogen atoms are bonded to only two adjacent carbon atoms, including two σ bonds and one π bond, to form the swing hinge (Fig. 2f). The maximum Y of T-C3N2 is 177 N m−1, close to g-C3N4 (172 N m−1),15 larger than C3N5 (38 N m−1),15 C2N-h2D (159 N m−1),56 and smaller than C3N (341 N m−1).57The stress variation to the uniaxial tensile strains is calculated and plotted in Fig. 2g–j. The ideal tensile strengths of T-C3N2 are 69.12 and 68.13 GPa nm, corresponding to the critical strains of 14% and 13% upon uniaxial strain along the a and b directions, respectively. The critical strains of T-C3N2 are similar to those of C2N-h2D,58 larger than those of C3N5 (12%) and g-C3N4 (11%).15 The ideal tensile strengths of T-C3N2 are greater than those of H-C3N2, whereas the critical strains along two directions are smaller than the latter, indicating that H-C3N2 has better flexibility. Although the maximum critical strain (17%) of H-C3N2 can withstand only 3% larger than that of T-C3N2, it can be significant from a macroscopic point of view. The flexibility of H-C3N2 is derived from the flexible hinges formed by the pyridinic nitrogen atoms bonded to two C atoms in the zigzag (a) direction, where the direction of the uniaxial strain force is parallel to the open and close direction of the hinge. In the armchair (b) direction of H-C3N2, the uniaxial strain force is not parallel to the hinge but to the C–C bond, thereby inhibiting the flexibility in the corresponding direction. The flexibility of H-C3N2 leads to a Poisson's ratio of H-C3N2 (C12/C11 = 0.49)12 larger than those of the T-C3N2 (0.22) and C2N-h2D (0.28)58 monolayers. The high sturdiness of T-C3N2 and the flexibility of H-C3N2 provide more candidates for PGCNs used as nanomechanical, microelectronic, and optoelectronic materials.
3.3. The electronic structures of C3N2 monolayers and bilayer
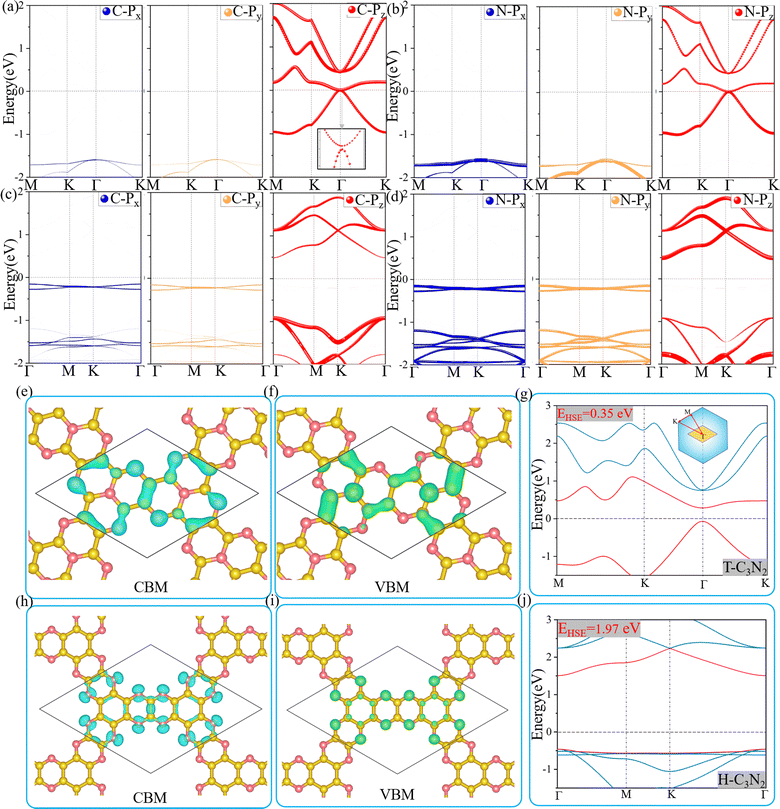
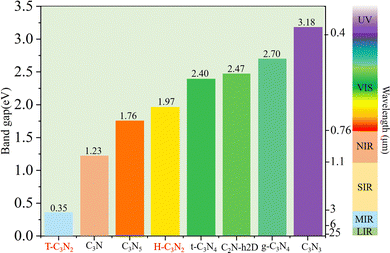
Optoelectronic detectors' detection range depends on the band gap of a semiconductor. The electronic structures of H-C3N2 and T-C3N2, along with the high symmetry path (Γ–M–K–Γ), are shown in Fig. 3. In the PBE level, according to the orbital-projected band structures and partial charge densities in Fig. 3a and b, e and f, the valence band maximum (VBM) of T-C3N2 has contributions mainly from pz orbitals of C and pyridinic N atoms. In contrast, the conduction band minimum (CBM) of T-C3N2 mainly consists of pz orbitals of C and graphitic N atoms. The H-C3N2 can be seen as a new structure by adding an ethanedinitrile (C2N2) unit to each side of the built-in hexagonal hole in the C2N-h2D monolayer. Adding ethanedinitrile brings valence bands closer to the Fermi energy level in the electronic structure, creating a lower band gap (Fig. S8a and e, ESI†). This bandgap change is caused by C-px+y (N-px+y) coupling of the ethanedinitrile (C2N2) unit with C-px+y (N-px+y) of the other C (N) atoms, which make up the VBM of H-C3N2 (Fig. 3c and d, i and Fig. S8b and c, f and g, ESI†). The CBM of H-C3N2 is composed of the C-pz and N-pz orbitals similar to the C2N-h2D monolayer (Fig. 3c and d, h and Fig. S8d and h, ESI†).Accurate band gaps of T-C3N2 and H-C3N2 were calculated using the HSE06 method. The resulting band gaps for H-C3N2 and T-C3N2 of 1.97 eV and 0.35 eV were approximately twice those obtained by the PBE method. The band gap of more than 1.23 eV for H-C3N2 meets the primary requirement of catalytically entirely splitting water. The CBM of H-C3N2 was found to be lower than the reduction potential of hydrogen and higher than the oxidation potential of O2/H2O, and its VBM is lower than the oxidation potential of O2/H2O (Fig. S9, ESI†). The band edges of CBM and VBM only support the oxidation potential of O2/H2O. The band gap of 0.35 eV for T-C3N2 conforms to the gap in the mid-infrared region of the series of carbon nitride semiconductors as photoelectronic detectors, where band gaps of C3N, C3N5, t-C3N4, C2N-h2D, g-C3N4, and C3N3 monolayers are 1.23 eV,59 1.76 eV,5 2.40 eV,6 2.47 eV,6 2.70 eV,1 and 3.18 eV,60 respectively (Fig. 4).
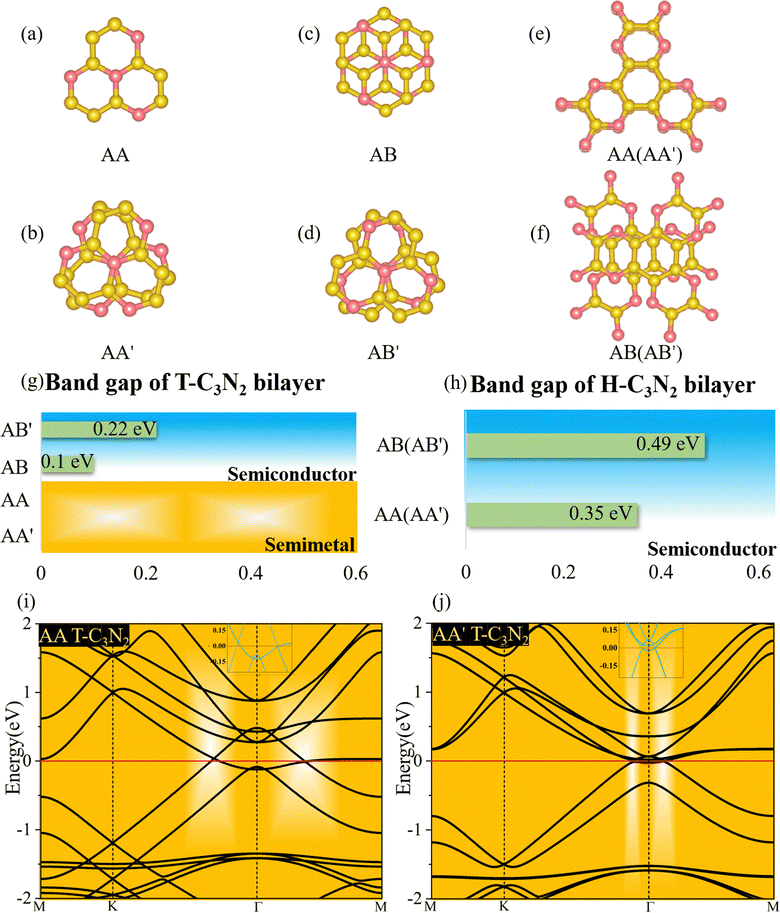
Two-dimensional carbon nitrides are always synthesized in their stacking forms,5,35 such as t-C3N4 in the form of triplets6 and C3N in the inversion symmetric AA′ and AB′ stacking form.59 The four different stacking configurations AA, AB, AA′, and AB′ for H-C3N2 and T-C3N2 are present in Fig. 5a–f. AB is the most favorable configuration with the lowest energy among different malposed bilayers in Fig. S5 (ESI†). For bilayer T-C3N2, the AB′, AA′, and AA stacking configurations are all higher in energy than the AB stacking bilayer configuration successively 0.02 eV, 0.55 eV, and 0.71 eV in the unit cell, respectively. Owing to almost equal lattice constants, the AA′ stacking bilayer has the smallest interlayer spacing of 2.71 Å as compared with interlayer spacings of 3.07 Å, 3.08 Å, and 3.40 Å for the AB′, AB, and AA stacking bilayers, respectively (Fig. S10, ESI†). Both AB and AB′ stacking bilayers have larger band gaps (100 meV and 220 meV) than that (11 meV) of the T-C3N2 monolayer. The electronic structure transforms from direct to indirect semiconduction (Fig. 5g). For bilayer H-C3N2, its AA (AB) stacking bilayer is the same as the AA′ (AB′), and the former is higher in energy than the latter by 0.87 eV in the unit cell. Lattice constants of AA (AA′) and AB (AB′) stacking bilayers are almost equal to that of the H-C3N2 monolayer, while the interlayer spacings are distinctly different (3.62 Å and 2.99 Å) as presented in Fig. S10 (ESI†). Band gaps of both AA (AA′) and AB (AB′) stacking bilayers decrease compared with the H-C3N2 monolayer by PBE method, as well as they are 0.35 eV and 0.49 eV (Fig. 5h), respectively, retaining the direct band gap feature at the Γ symmetry point. While the interlayer spacings of AA (AA′) stacking bilayers are smaller than AB (AB′), the smaller band gap of the former relative to the latter indicates the stronger interlayer interaction of AA (AA′) stacking bilayers. Beyond all expectations, both AA and AA′ stacking bilayers of T-C3N2 are nodal-line semimetals under van der Waals's interaction, forming a closed ring centered at the Γ point. To be more explicit, we calculate band structures of AA and AA′ stacking bilayers of T-C3N2 with a large number of k points(30 × 30 × 1) by the PBE method (Fig. 5i and j). As seen in Fig. 5i and j, the AA stacking bilayer has a bigger closed ring than the AA′ stacking bilayer. This is attributed to the weaker van der Waals's interaction with the larger interlayer spacing according to the differential charge density of the AA stacking bilayer (Fig. S11a, ESI†), with weak charge transfer between layers. However, the smaller interlayer spacing of the AA′ stacking bilayer leads to charge accumulation between graphitic N atoms within the TAPA molecules of the upper layer and the lower layer leading to covalent bonds (Fig. S11b, ESI†) similar to those in bilayer g-C3N4.61 Because of the linear band dispersion near the node-line loop, the conductivity in T-C3N2 bilayer (AA and AA′) is expected to be relatively high, implying that it can be a promising candidate for transparent conductors in touch screens and solar cells.62
3.4 Carrier mobilities and optical properties of T-C3N2 and H-C3N2 monolayers
The carrier mobilities of semiconductor materials determine the performance of electronic devices. In this connection the carrier mobilities of C3N2 monolayers were evaluated based on deformation potential theory,63 using the formula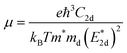 containing the three variables C2d, m*, md, and E2d, which are the elastic constants, the effective mass, the average effective mass (
containing the three variables C2d, m*, md, and E2d, which are the elastic constants, the effective mass, the average effective mass (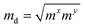 ) and the deformation potential constant, respectively. The other constants e, kB, ℏ, and T respectively stand for electron charge, Boltzmann constant, Planck constant, and room temperature (300 K). According to the formula, the carrier mobility is most affected by the deformation potential constant and the effective mass. In terms of orientation, the effective mass is essentially isotropic in the x and y directions, similar to the elastic constant (Fig. S12a and b, ESI†). This is particularly evident for H-C3N2 and can also be seen from the band dispersion near the VBM and CBM at the high symmetry point Γ (Fig. S12d, ESI†). In detail, T-C3N2 has smaller effective masses than H-C3N2 (Fig. S12c, ESI†), down to 0.11 m0 in the x-direction of the hole. This low effective mass leads to ultrahigh mobility (27.76 × 103 and 23.20 × 103 cm2 V−1 s−1) in the x-direction, despite its larger deformation potential constant. The large deformation potential constant relative to the electron indicates the VBM is sensitive to the strain (Fig. S12e, ESI†). The VBM is mainly determined by the pyridinic nitrogen atoms, implying the strain force has a greater influence on the pyridinic nitrogen atoms. For the CBM, the main contribution is from the graphitic nitrogen atoms, and the stronger bond makes the CBM less affected by the strain force, leading to a smaller deformation potential constant compared with the hole (Fig. S12d, ESI†). The H-C3N2 monolayer only has pyridinic nitrogen atoms, and thus the strain results in similar deformation potential constants with structural isotropy. The small deformation potential constant of H-C3N2 in combination with the relatively small effective mass of its CBM also leads to ultrahigh electron mobility (25.39 × 103 cm2 V−1 s−1 and 22.67 × 103 cm2 V−1 s−1 in Table 2), while the large effective mass results in low hole mobility (0.16 × 103 and 0.15 × 103 cm2 V−1 s−1 in Table 2), leading to pronounced electron-hole anisotropic mobility. The carrier mobilities of T-C3N2 and H-C3N2 are comparable to C3N monolayer/AB bilayer (Table 2), as well as larger than those of the AB′ bilayer (6.22 × 103 cm2 V−1 s−1) and the AA′ bilayer (1.20 ×103 cm2 V−1 s−1) of C3N,59 C2N-h2D,7 and black phosphorus (6.00 × 103 cm2 V−1 s−1).64
) and the deformation potential constant, respectively. The other constants e, kB, ℏ, and T respectively stand for electron charge, Boltzmann constant, Planck constant, and room temperature (300 K). According to the formula, the carrier mobility is most affected by the deformation potential constant and the effective mass. In terms of orientation, the effective mass is essentially isotropic in the x and y directions, similar to the elastic constant (Fig. S12a and b, ESI†). This is particularly evident for H-C3N2 and can also be seen from the band dispersion near the VBM and CBM at the high symmetry point Γ (Fig. S12d, ESI†). In detail, T-C3N2 has smaller effective masses than H-C3N2 (Fig. S12c, ESI†), down to 0.11 m0 in the x-direction of the hole. This low effective mass leads to ultrahigh mobility (27.76 × 103 and 23.20 × 103 cm2 V−1 s−1) in the x-direction, despite its larger deformation potential constant. The large deformation potential constant relative to the electron indicates the VBM is sensitive to the strain (Fig. S12e, ESI†). The VBM is mainly determined by the pyridinic nitrogen atoms, implying the strain force has a greater influence on the pyridinic nitrogen atoms. For the CBM, the main contribution is from the graphitic nitrogen atoms, and the stronger bond makes the CBM less affected by the strain force, leading to a smaller deformation potential constant compared with the hole (Fig. S12d, ESI†). The H-C3N2 monolayer only has pyridinic nitrogen atoms, and thus the strain results in similar deformation potential constants with structural isotropy. The small deformation potential constant of H-C3N2 in combination with the relatively small effective mass of its CBM also leads to ultrahigh electron mobility (25.39 × 103 cm2 V−1 s−1 and 22.67 × 103 cm2 V−1 s−1 in Table 2), while the large effective mass results in low hole mobility (0.16 × 103 and 0.15 × 103 cm2 V−1 s−1 in Table 2), leading to pronounced electron-hole anisotropic mobility. The carrier mobilities of T-C3N2 and H-C3N2 are comparable to C3N monolayer/AB bilayer (Table 2), as well as larger than those of the AB′ bilayer (6.22 × 103 cm2 V−1 s−1) and the AA′ bilayer (1.20 ×103 cm2 V−1 s−1) of C3N,59 C2N-h2D,7 and black phosphorus (6.00 × 103 cm2 V−1 s−1).64
| 2D | C 2D x (N m−1) | C 2D y (N m−1) | E x 2d (eV) | E y 2d (eV) | μ x × 103 (cm2 V−1 s−1) | μ y × 103 (cm2 V−1 s−1) | Exp. | |||
|---|---|---|---|---|---|---|---|---|---|---|
| T-C3N2 | e | 0.37 | 0.48 | 180 | 180 | 1.76 | 1.86 | 7.94 | 5.48 | |
| h | 0.11 | 0.13 | 180 | 180 | 3.24 | 3.26 | 27.76 | 23.20 | ||
| H-C3N2 | e | 0.27 | 0.27 | 94 | 94 | 1.04 | 1.10 | 25.39 | 22.67 | |
| h | 2.90 | 3.00 | 94 | 94 | 1.20 | 1.22 | 0.16 | 0.15 | ||
| C3N59,65 | e | 0.76 | 0.45 | 371.2 | 371.2 | 6.34 | 6.47 | 0.226 | 0.62 | 0.136 |
| h | 0.12 | 0.85 | 371.1 | 371.1 | 5.82 | 9.47 | 10.8 | 0.08 | 1.108 | |
| C3N(AB)65 | e | 0.75 | 0.43 | 742.6 | 742.6 | 6.21 | 6.38 | 0.48 | 1.39 | |
| h | 0.11 | 0.83 | 742.3 | 742.3 | 5.25 | 10.05 | 31.5 | 0.15 | ||
Besides carrier mobility, the absorption coefficient is also crucial for optoelectronic devices. The absorption properties of C3N2 monolayers are calculated based on the dielectric function ε(ω) = ε1(ω) + iε2(ω), where ω is the frequency. The absorption coefficient α(ω) was calculated from
where α and β refer to the x and y directions, and Ω is the volume of the unit cell. The indices c and v refer to the conduction and valence band states, respectively. μck are the corresponds to an eigenstate with wave vector k. T-C3N2, a direct semiconductor with a narrow band gap of 0.35 eV, has the highest 2.25 × 105 cm−1 absorption coefficient in the visible-light region, almost equal to H-C3N2 (Fig. 6a). The absorption coefficients of the synthesized C3N5, g-C3N4, and C2N-h2D were also computed at the HSE06 level (Fig. 6b). The absorption coefficient of T-C3N2 is smaller than that of C2N-h2D in the visible-light region but significantly larger than that C3N5 and g-C3N4. More importantly, T-C3N2 is a good candidate for an infrared photodetector. In addition, T-C3N2 has the potential to be superior to other PCGNs for near-infrared solar harvesting/utilizing techniques because of absorption coefficients of up to 2.25 × 105 cm−1.
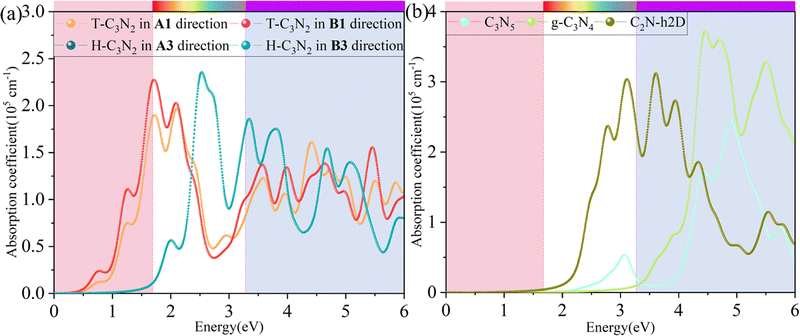 | ||
| Fig. 6 Calculated in-plane absorption coefficients of (a) T-C3N2 and H-C3N2 monolayers in comparison with synthesized (b) C3N5, g-C3N4, and C2N-h2D at the HSE06 level. | ||
4. Conclusion
In summary, we have designed low-energy structures (i.e., the T-C3N2 and TH-C3N2) in combination with the PSO algorithm approach, proposed theoretically their logical synthesis paths related to the experimental realization of other carbon nitride monolayers (C2N-h2D, C3N5, g-C3N4, C3N, and so on), and systematically investigated T-C3N2 and H-C3N2 monolayers based on ab initio calculations. Based on the convex hull of T-C3N2, C3N5, and g-C3N4, we proposed that highly stable PGCNs tend to consist of graphitic and pyridinic nitrogen atoms with higher graphitic nitrogen concentration with an increasing x/y ratio in CxNy. The calculations also confirmed that the T-C3N2 monolayer is thermodynamically most favorable among the three C3N2 monolayers. Mechanically, the presence of graphitic nitrogen atoms symmetrically bonded to three C atoms leads to considerable rigidity of T-C3N2, while hinges formed by pyridinic nitrogen atoms bonded to only two carbon atoms make H-C3N2 more flexible. Moreover, T-C3N2 and H-C3N2 are direct semiconductors with band gaps of 0.35 eV and 1.97 eV, respectively. Furthermore, their bilayers exhibit a different band gap reduction than the corresponding monolayer. Especially for T-C3N2, the AA and AA′ stacking bilayers lead to a transition from a semiconductor to a semimetal. Both T-C3N2 and H-C3N2 have high carrier mobilities, anisotropic character, and excellent visible-light absorption. In addition, T-C3N2 exhibits a strong absorption coefficient in the near-infrared region. These appealing properties suggest that the T-C3N2 and H-C3N2 monolayers are promising candidates for use in electronic and photovoltaic devices.Author contributions
X. C. conceived the idea, performed the DFT calculations, and wrote the original draft, J. C., Y. N. analyzed the data, H. W., Y. C., R. B. K. reviewed and edited the paper.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
This work was supported by the Sichuan Science and Technology program (2022ZYD0024; 2021YFG0228) and the China Postdoctoral Science Foundation (2021M690325).References
- X. Wang, K. Maeda, A. Thomas, K. Takanabe, G. Xin, J. M. Carlsson, K. Domen and M. Antonietti, Nat. Mater., 2009, 8, 76–80 CrossRef CAS PubMed.
- K. S. Lakhi, D. H. Park, K. Al-Bahily, W. Cha, B. Viswanathan, J. H. Choy and A. Vinu, Chem. Soc. Rev., 2017, 46, 72–101 RSC.
- S. Yang, Y. Gong, J. Zhang, L. Zhan, L. Ma, Z. Fang, R. Vajtai, X. Wang and P. M. Ajayan, Adv. Mater., 2013, 25, 2452–2456 CrossRef CAS PubMed.
- L. Huang, Z. Liu, W. Chen, D. Cao and A. Zheng, J. Mater. Chem. A, 2018, 6, 7168–7174 RSC.
- P. Kumar, E. Vahidzadeh, U. K. Thakur, P. Kar, K. M. Alam, A. Goswami, N. Mahdi, K. Cui, G. M. Bernard, V. K. Michaelis and K. Shankar, J. Am. Chem. Soc., 2019, 141, 5415–5436 CrossRef CAS PubMed.
- G. Algara-Siller, N. Severin, S. Y. Chong, T. Bjorkman, R. G. Palgrave, A. Laybourn, M. Antonietti, Y. Z. Khimyak, A. V. Krasheninnikov, J. P. Rabe, U. Kaiser, A. I. Cooper, A. Thomas and M. J. Bojdys, Angew. Chem., Int. Ed., 2014, 53, 7450–7455 CrossRef CAS PubMed.
- Q. M. Bing, W. Liu, W. C. Yi and J. Y. Liu, J. Power Sources, 2019, 413, 399–407 CrossRef CAS.
- J. Feng and M. Li, Adv. Funct. Mater., 2020, 30, 2001502–2001509 CrossRef CAS.
- D. Adekoya, S. Qian, X. Gu, W. Wen, D. Li, J. Ma and S. J. N.-M. L. Zhang, Nano-Micro Lett., 2021, 13, 1–44 CrossRef CAS PubMed.
- J. Xu, J. Mahmood, Y. Dou, S. Dou, F. Li, L. Dai and J. B. Baek, Adv. Mater., 2017, 29, 1702007–1702014 CrossRef PubMed.
- D. Wu, B. Yang, H. Chen and E. Ruckenstein, Energy Storage Mater., 2019, 16, 574–580 CrossRef.
- X. Cai, W. Yi, J. Chen, L. Lu, B. Sun, Y. Ni, S. A. T. Redfern, H. Wang, Z. Chen and Y. Chen, J. Mater. Chem. A, 2022, 10, 6551–6559 RSC.
- L. Tan, C. Nie, Z. Ao, H. Sun, T. An and S. Wang, J. Mater. Chem. A, 2021, 9, 17–33 RSC.
- C. Kou, Y. Tian, L. Gao, M. Lu, M. Zhang, H. Liu, D. Zhang, X. Cui and W. Yang, Nanotechnology, 2020, 31, 495707–495713 CrossRef CAS PubMed.
- B. Mortazavi, F. Shojaei, M. Shahrokhi, M. Azizi, T. Rabczuk, A. V. Shapeev and X. Zhuang, Carbon, 2020, 167, 40–50 CrossRef CAS.
- L. Tsetseris, 2D Mater., 2016, 3, 021006–021011 CrossRef.
- H. Chen, S. Zhang, W. Jiang, C. Zhang, H. Guo, Z. Liu, Z. Wang, F. Liu and X. Niu, J. Mater. Chem. A, 2018, 6, 11252–11259 RSC.
- S. Yao, X. Zhang, A. Chen, Z. Zhang, M. Jiao and Z. Zhou, J. Mater. Chem. A, 2019, 7, 19290–19296 RSC.
- B. Mortazavi, M. Shahrokhi, A. V. Shapeev, T. Rabczuk and X. Zhuang, J. Mater. Chem. C, 2019, 7, 10908–10917 RSC.
- Q. Wei, Y. Yang, A. Gavrilov and X. Peng, Phys. Chem. Chem. Phys., 2021, 23, 4353–4364 RSC.
- J. M. Cao, Z. Q. Huang, G. Macam, Y. F. Gao, N. V. R. Nulakani, X. Ge, X. Ye, F. C. A. Chuang and L. Huang, Appl. Phys. Lett., 2021, 118, 133104 CrossRef.
- Y. Wu, Y. Chen, C. Ma, Z. Lu, H. Zhang, B. Mortazavi, B. Hou, K. Xu, H. Mei, T. Rabczuk, H. Zhu, Z. Fang, R. Zhang and C. M. Soukoulis, Phys. Rev. Mater., 2020, 4, 064001 CrossRef CAS.
- O. I. Malyi, K. V. Sopiha and C. Persson, ACS Appl. Mater. Interfaces, 2019, 11, 24876–24884 CrossRef CAS PubMed.
- K. Geng, T. He, R. Liu, S. Dalapati, K. T. Tan, Z. Li, S. Tao, Y. Gong, Q. Jiang and D. Jiang, Chem. Rev., 2020, 16, 8814–8933 CrossRef PubMed.
- D. Jiang, X. Chen, K. Geng, R. Liu, K. T. Tan, Y. Gong, Z. Li, S. Tao and Q. Jiang, Angew. Chem., Int. Ed., 2019, 59, 5050–5091 Search PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- P. E. Blochl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- J. Paier, R. Hirschl, M. Marsman and G. Kresse, J. Chem. Phys., 2005, 122, 234102–234114 CrossRef PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2006, 124, 219906 CrossRef.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5 CrossRef CAS.
- Q. C. Tong, J. Lv, P. Y. Gao and Y. C. Wang, Chin. Phys. B, 2019, 28, 106105 CrossRef CAS.
- J. Mahmood, E. K. Lee, M. Jung, D. Shin, H. J. Choi, J. M. Seo, S. M. Jung, D. Kim, F. Li, M. S. Lah, N. Park, H. J. Shin, J. H. Oh and J. B. Baek, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 7414–7419 CrossRef CAS PubMed.
- J. Mahmood, E. K. Lee, M. Jung, D. Shin, I. Y. Jeon, S. M. Jung, H. J. Choi, J. M. Seo, S. Y. Bae, S. D. Sohn, N. Park, J. H. Oh, H. J. Shin and J. B. Baek, Nat. Commun., 2015, 6, 6486–6492 CrossRef CAS PubMed.
- R. Iqbal, S. Ali, G. Yasin, S. Ibraheem, M. Tabish, M. Hamza, H. Chen, H. Xu, J. Zeng and W. Zhao, Chem. Eng. J., 2022, 430, 132642 CrossRef CAS.
- J. Park, M. Lee, D. Feng, Z. Huang, A. C. Hinckley, A. Yakovenko, X. Zou, Y. Cui and Z. Bao, J. Am. Chem. Soc., 2018, 140, 10315–10323 CrossRef CAS PubMed.
- J. L. V. Winkle, J. D. McClure and P. H. Williams, J. Org. Chem., 1966, 31, 3300–3306 CrossRef.
- W. Leupin, D. Magde, G. Persy and J. Wirz, J. Am. Chem. Soc., 1986, 108, 17–22 CrossRef CAS.
- I. I. Ponomarev and S. V. Vinogradova, Bull. Acad. Sci. USSR, Div. Chem. Sci., 1990, 39, 2229 CrossRef.
- O. Buyukcakir, R. Yuksel, Y. Jiang, S. H. Lee, W. K. Seong, X. Chen and R. S. Ruoff, Angew. Chem., Int. Ed., 2019, 58, 872–876 CrossRef CAS PubMed.
- Z. Meng, A. Aykanat and K. A. Mirica, Chem. Mater., 2018, 31, 819–825 CrossRef.
- Z.-Q. Lin, J. Xie, B.-W. Zhang, J.-W. Li, J. Weng, R.-B. Song, X. Huang, H. Zhang, H. Li, Y. Liu, Z. J. Xu, W. Huang and Q. Zhang, Nano Energy, 2017, 41, 117–127 CrossRef CAS.
- C. Ma, X. Li, J. Zhang, Y. Liu and J. J. Urban, ACS Appl. Mater. Interfaces, 2020, 12, 16922–16929 CrossRef CAS PubMed.
- X. Li, H. Wang, H. Chen, Q. Zheng, Q. Zhang, H. Mao, Y. Liu, S. Cai, B. Sun, C. Dun, M. P. Gordon, H. Zheng, J. A. Reimer, J. J. Urban, J. Ciston, T. Tan, E. M. Chan, J. Zhang and Y. Liu, Chem, 2020, 6, 933–944 CAS.
- I. Ahmad, F. Li, C. Kim, J.-M. Seo, G. Kim, J. Mahmood, H. Y. Jeong and J.-B. Baek, Nano Energy, 2019, 56, 581–587 CrossRef CAS.
- L. Meng, S. Ren, C. Ma, Y. Yu, Y. Lou, D. Zhang and Z. Shi, Chem. Commun., 2019, 55, 9491–9494 RSC.
- R. Shi, L. Liu, Y. Lu, C. Wang, Y. Li, L. Li, Z. Yan and J. Chen, Nat. Commun., 2020, 11, 178 CrossRef CAS PubMed.
- J. Mahmood, I. Ahmad, M. Jung, J.-M. Seo, S.-Y. Yu, H.-J. Noh, Y. H. Kim, H.-J. Shin and J.-B. Baek, Commun. Chem., 2020, 3, 31 CrossRef CAS PubMed.
- C. Shu, L. Fang, M. Yang, L. Zhong, X. Chen and D. Yu, Angew. Chem., Int. Ed., 2022, 61, e202114182 CAS.
- S. Bu, N. Yao, M. A. Hunter, D. J. Searles and Q. Yuan, npj Comput. Mater., 2020, 6, 128 CrossRef CAS.
- T. Yu, S. Zhang, F. Li, Z. Zhao, L. Liu, H. Xu and G. Yang, J. Mater. Chem. A, 2017, 5, 18698–18706 RSC.
- H. Sahin, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 085421 CrossRef.
- H. S. Li, H. Q. Hu, C. L. Bai, C. J. Bao, C. L. Liu, Q. L. Wang, F. Guo, Z. B. Feng, H. W. Yu, M. Chen and K. G. Qu, Catalysts, 2020, 10, 836 CrossRef CAS.
- A. Taheri, C. Da Silva and C. H. Amon, J. Appl. Phys., 2020, 127, 184304 CrossRef.
- L. Zhu, Q. Xue, X. Li, T. Wu, Y. Jin and W. Xing, J. Mater. Chem. A, 2015, 3, 21351–21356 RSC.
- B. Mortazavi, Carbon, 2017, 118, 25–34 CrossRef CAS.
- S. Guan, Y. C. Cheng, C. Liu, J. F. Han, Y. H. Lu, S. A. Yang and Y. G. Yao, Appl. Phys. Lett., 2015, 107, 231904 CrossRef.
- W. Wei, S. Yang, G. Wang, T. Zhang, W. Pan, Z. Cai, Y. Yang, L. Zheng, P. He, L. Wang, A. Baktash, Q. Zhang, L. Liu, Y. Wang, G. Ding, Z. Kang, B. I. Yakobson, D. J. Searles and Q. Yuan, Nat. Electron., 2021, 4, 486–494 CrossRef CAS.
- K. Srinivasu, B. Modak and S. K. Ghosh, J. Phys. Chem. C, 2014, 118, 26479–26484 CrossRef CAS.
- F. Wu, Y. Liu, G. Yu, D. Shen, Y. Wang and E. Kan, J. Phys. Chem. Lett., 2012, 3, 3330–3334 CrossRef CAS.
- F. Bonaccorso, Z. Sun, T. Hasan and A. C. Ferrari, Nat. Photonics, 2010, 4, 611–622 CrossRef CAS.
- J. Bardeen and W. Shockley, Phys. Rev., 1950, 80, 72–80 CrossRef CAS.
- L. Li, F. Yang, G. J. Ye, Z. Zhang, Z. Zhu, W. Lou, X. Zhou, L. Li, K. Watanabe, T. Taniguchi, K. Chang, Y. Wang, X. H. Chen and Y. Zhang, Nat. Nanotechnol., 2016, 11, 593–597 CrossRef CAS PubMed.
- X. Wang, Q. Li, H. Wang, Y. Gao, J. Hou and J. Shao, Phys. B, 2018, 537, 314–319 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Design scheme of T-C3N2, H-C3N2, and TH-C3N2; the computational details; atomic configurations for C3N, C2N-h2D, and T-C3N2; the graphitic N concentration in CNs; ELF, phonon spectrum and MD simulations of the T-C3N2 monolayer; electronic structures and the DOS of C2N-h2D and H-C3N2 monolayers; the band structure of H-C3N2 relative to the vacuum level; the different stacking bilayers of H-C3N2 and T-C3N2; the differential charge density of AA and AA′ stacking bilayers T-C3N2; carrier effective masses, in-plane stiffness, and the deformation potential constant. See DOI: https://doi.org/10.1039/d2nh00440b |
| This journal is © The Royal Society of Chemistry 2023 |