Thermodynamics of nano- and macrocrystalline anatase using cell voltage measurements†
Received
2nd June 2009
, Accepted 1st October 2009
First published on
9th November 2009
Abstract
In view of increasing scientific and technological interest in nanomaterials, it is important to examine whether or, more exactly, to what extent the thermodynamic parameters change with size. Electrochemical e.m.f. measurements which provide a direct and elegant access to these thermodynamic data have been used in this study to investigate the excess contributions of anatase due to nano-size. The e.m.f. measurements are carried out (250–450 °C) on different particle sizes (1.2 μm–5 nm) using the cell: Au, O2, Na2Ti6O13, TiO2 (anatase) |Na-β′′ alumina |TiO2 (rutile), Na2Ti6O13, O2, Au. The e.m.f. observed is closely related to the difference of the Gibbs energies of formation (ΔfG°) of the titania crystals on both sides. Such cell voltage measurements with various sizes of anatase (1200, 100, 15, and 5 nm) as working electrodes enable us to calculate the excess enthalpy and entropy due to surface contributions and to provide refined data for the macroscopic anatase. No electrochemical Ostwald ripening or chemical Ostwald ripening was observed in the case of anatase nanoparticles up to 500 °C.
1. Introduction
Nano-size effects currently receive considerable attention both in experimental as well as in theoretical respect not only due to their fundamental significance but also in view of potential applications. A variety of size effects on transport phenomena is primarily discussed in the context of electronic materials. The most striking example is the quantum confinement in nano-electronics.1,2 Anologous to nano-electronics, another emerging area of interest is nano-ionics within which a number of true size effects as well as trivial size effects have been discussed in literature in the context of transport,3–7 energy conversion and storage.7–10 Another often cited example is the change of thermodynamic stability, for example, the suppression of the melting point in the case of nano-sized Au particles by several hundreds of degrees,1 which is due to the excess surface free energy of small particles according to:| | μnanoMX = μ∞MX + (2![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) / /![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) )VM )VM | (1) |
where ![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) is the average surface tension,
is the average surface tension, ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) is the average radius and VM is the molar volume.
is the average radius and VM is the molar volume.
Very few experiments have been carried out to indeed measure the excess surface contribution in the case of nanoparticles. Among them, the excess surface enthalpy measured using calorimetry experiments on nanoparticles of alumina and titania by the group of Navrotsky are worth mentioning.11,12 Electrochemical e.m.f. measurements are known to provide accurate measurements of the reaction enthalpy but also, if temperature dependent measurements are performed, of reaction entropy.13–16 The present article aims at the measurement of surface energies and entropies of nano-sized anatase using a specially designed electrochemical e.m.f. cell.
The electrochemical e.m.f. cell used in the present study over the temperature range 250–450 °C, comprises the working and reference electrodes separated by a solid sodium electrolyte, Na-β′′ alumina. In both electrodes, the sodium potentials are fixed as shown later in eqn (2) and (3), differing only in the thermodynamic effects of different morphologies and/or size. The respective half cells have been successfully used by Holzinger et al.16 as reference cells for a potentiometric CO2 sensor. The cell reactions involved here proved to be highly reversible and stationary. In the present investigation, while the reference electrode of the cell is made of a composite of Na2Ti6O13 (2 μm), rutile (2 μm) and gold powder (400 nm), the working electrode is comprised of Na2Ti6O13, anatase particles of various sizes (1.2 μm, 100 nm, 15 nm and 5 nm) and gold powder. The working and reference electrodes are prepared by mixing gold power with respective electrode materials using a mortar and pestle for about an hour and cold pressing the product using a uni-axial hydrostatic press. We also performed experiments with rutile particles of 25 nm to display the excess potential developed in this electrochemical e.m.f. cell due to size reduction.
The electrochemical e.m.f. cell used in the present study over the temperature range 250–450 °C is presented below. Different cells are made using various working electrodes with anatase of 1.2 μm, 100 nm, 15 nm, and 5 nm.
The advantage of the present electrochemical cell is that the e.m.f. which is measured directly provides the difference of the Gibbs energies of formation (ΔfGo) of the titania particles on both sides.
In more details, the electrode reactions are:
| | | 6TiO2 (anatase) + 2Na+ + 2e−(I) + (1/2)O2 ⇆ Na2Ti6O13 (I) | (2) |
| | | Na2Ti6O13(II) ⇆ 2Na+ + 2e−(II) + (1/2)O2 + 6TiO2 (rutile) | (3) |
Since the oxygen pressure as well as titania phases (see reaction 4a) are the same for both
electrodes (I, II), the overall
cell reaction can be written as
| | TiO2(anatase, ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) ) ⇆ TiO2(rutile, ) ⇆ TiO2(rutile, ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) = ∞) = ∞) | (4a) |
or electrochemically more precisely as
| | 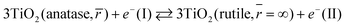 | (4b) |
The electrochemical equilibrium condition yields
| |  | (5) |
where

and

refer to the electrochemical potential of electrons at the leads in contact with the working and
reference electrodes, respectively, while
F and
E refer to Faraday constant and the reversible
cell voltage.
With μorutile = μorutile(∞)
| |  | (6) |
Eqn (5) can also be written as
| | 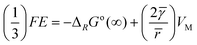 | (7) |
where Δ
RGo(∞) is the Gibbs energy of converting macroscopic anatase into macroscopic
rutile.
VM,
![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif)
,
![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif)
all refer to anatase,
VM, the molar volume, being 20.5 × 10
−6 m
3 mol
−1. A more detailed discussion of the e.m.f. in nanocrystalline systems is given in
ref. 15 and 17.
In the present experiment, anatase particles of 1.2 μm, 100 nm, 15 nm, and 5 nm have been used. From eqn (7), the excess surface contributions and hence the mean surface tension ![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) for the anatase particle is determined and from its temperature dependence, ΔHs and ΔSs have been estimated.
for the anatase particle is determined and from its temperature dependence, ΔHs and ΔSs have been estimated.
3. Results and discussion
First of all, it was tested that the symmetrical cells with macroscopic rutile on both sides showed zero voltage in the entire temperature window (E = 0 was fulfilled up to an accuracy of 0.01 mV after a waiting period of typically 1 h). Fig. 1a and 1b show typical excess e.m.f. obtained for the nano-sized rutile of 25 nm versus time at different temperatures. It is seen clearly that the stable excess e.m.f. (with a variation of ±0.05 mV over a period of 2 h) is a consequence of the thermodynamically stable open circuit voltage (OCV) expected for a binary system such as titania in contrast to the example of single component silver nanoparticles, that unavoidably grow with time due to electrochemical Ostwald ripening hence characterized by unstable e.m.f. values.15 In binary or multinary compounds only one ion needs to be reversibly exchanged for the establishment of a reproducible e.m.f. The low mobility of the other(s) guarantees morphological stability (confirmed by the scanning electron microscopic images recorded after the cell reaction). Cell measurements of this type allow us not only to measure interfacial tensions of TiO2, but also to quantitatively address the individual stabilities of different modifications as a function of size. Stability issues concerning rutile and anatase have been a matter of intensive debate in the literature, in particular in view of size effects.11,18,19
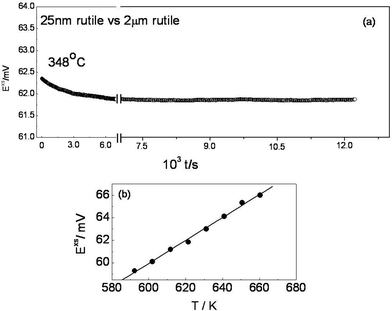 |
| | Fig. 1 (a) Typical results of e.m.f. measurements for TiO2 binary system at 348 °C. After a short transient occurring on a T-change, the excess e.m.f. Exs is found to be very stable (here ∼61.75 mV). The graph 1b shows the temperature dependence of the e.m.f. for 25 nm vs. 2 μm rutile in the reversible T-range. | |
As seen from eqn (7), the excess Gibbs free enthalpy due to finite size, ΔGxs, and thus the experimentally accessible excess potential, Exs, can be expressed as a function of the effective particle radius, ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) ,
,
| |  | (10) |
Though the evaluation is straightforward, the interpretation deserves some remarks. One difficulty lies in the averaging. As we address a multiphase arrangement, the surface tensions are not tensions of pure surfaces, rather tensions of contacted surfaces. In addition, these interfaces are typically out of equilibrium. Furthermore, it is most likely that owing to the chemical potential gradients inside the grains, the highest weight in the averaging procedure has to be put on the
electrode/electrolyte interfaces.
15 We also assume that in the size range considered,

. Furthermore, it is well-known in the thermodynamic literature that the strain dependence of surface tension effects can contribute to or even dominate what was called
![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif)
in the above.
Let us start our discussion with the electrochemical cells constructed with macro-grained rutile on the reference end and macro-grained anatase on the working electrode end, directly reflecting relative thermodynamic stabilities. The e.m.f. values obtained for the cell using 1.2 μm anatase as working electrode against 2 μm rutile as the reference electrode on either side directly verify that rutile is more stable compared to anatase in the measured T-range. In literature there are various reports referring to the stability of anatase versus rutile. Table 1 gives representative literature results of the Gibbs energy of formation (Δ(ΔfGo)) of rutile and anatase. Our stabilization value is obviously the smallest, but perhaps the most reliable as it stems from a direct comparison. This electrochemical e.m.f. study on macro-crystalline anatase (1.2 μm) versus bulk rutile (2 μm) presents a direct evidence for the stability of rutile against anatase (see Fig. 2), with the difference in their Gibbs energy of formation being 1.75 ± 0.035 kJ mol−1 (390 °C). Recently, first-principle calculations of phase stability of titania predicted that anatase is more stable than rutile at 0 K and ambient pressure.20 Interestingly, our results, when extrapolated to T = 0 K, i.e., ΔfHo = −9.448 × 105 J mol−1 and −9.438 × 105 J mol−1 for anatase and rutile, respectively, at 0 K, indicate the same, i.e. that anatase is more stable than rutile. Note that this extrapolation requires that the behaviour is strictly linear down to T = 0 K, if this assumption is fulfilled, the cross-over for the stability reversal occurs at −13 °C (260 K), that is, below this temperature the anatase phase becomes more stable than the rutile one. Because of the very small difference in the slopes in Fig. 2, these numerical data are very uncertain.
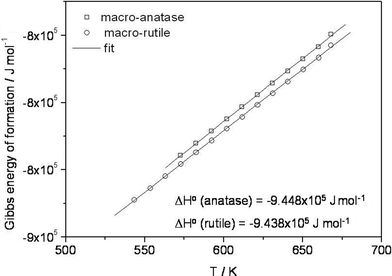 |
| | Fig. 2 Comparison of the Gibbs energy of formation for bulk anatase obtained from this electrochemical e.m.f. study with the values for bulk rutile phase from the literature.21 | |
Table 1 Differences in the Gibbs energy of formation (Δ(ΔfGo)) between rutile and anatase at 390 °C
| (Δ(ΔfGo)) in kJ mol−1 at 390 °C |
References |
| 6.15 |
JANAF tables21 |
| 11.52 |
Barin & Knacke tables22 |
| 1.75 ± 0.035 |
Present study using e.m.f. cells |
Similar e.m.f. cells have been constructed with anatase whose sizes varied from 100 nm, 15 nm, to 5 nm. Fig. 3 refers to the e.m.f. generated in the case of 15 nm anatase against 2 μm rutile bulk. The arrow at high temperature refers to the transition of anatase to the rutile phase, indicating the sensitivity of the e.m.f. technique to such a transition in contrast to other techniques such as differential scanning calorimetry, or X-ray diffraction (results are not shown here). The low temperature arrow in Fig. 3 gives the lower limit of the reversible T-range.16
 |
| | Fig. 3 E.m.f. of the cell with anatase of 15 nm size. High-temperature arrow refers to the phase transformation of the anatase to the rutile phase resulting in lower e.m.f. values due to the rutile to anatase phase transformation, indicating the sensitivity of the measurement. The low T arrow indicates the lower T limit, that is set by loss of reversibility of the reaction due to poor conductivity of the Na-β′′ alumina electrolyte. This temperature range also corresponds to the results of Holzinger et al.16 | |
Examination of the size of titania particles before and after the e.m.f. measurements using FESEM revealed that the particles down to 5 nm in the case of anatase did not show any significant growth. No electrochemical Ostwald ripening or chemical Ostwald ripening was observed in the case of anatase nanoparticles. This indicates that at least one component of TiO2, either oxygen or more probably titanium is sufficiently sluggish (in terms of partial conductivity).
Fig. 4a presents the Gibbs energy of formation for macro-crystalline anatase (1.2 μm) as well as for nanocrystalline anatase of 100, 15, and 5 nm. For a quantitative analysis of this excess contribution, the excess Gibbs energy of formation is plotted against the inverse of grain size as shown in Fig. 4b. It is worth noting that for very large anatase size, the plot in Fig. 4b (excess Gibbs energy of formation versus inverse of radius of anatase nanoparticles) converges to zero excess Gibbs energy in agreement with the fact that there is no surface contribution. This provides further confidence in our evaluation of the data obtained from the present measurements using electrochemical cells. According to eqn (7), the slopes of these curves in Fig. 4b at various temperatures yield the average surface tensions. Fig. 4c presents the plot of the effective surface tension so-obtained versus temperature, the analysis of which provides the surface enthalpy  as well as surface entropy
as well as surface entropy  contribution (if adsorption effects can be neglected, γ can be conceived as a surface free energy that can be split into an enthalpy and an entropy term). Table 2 summarizes the results obtained in the present study. The surface enthalpy
contribution (if adsorption effects can be neglected, γ can be conceived as a surface free energy that can be split into an enthalpy and an entropy term). Table 2 summarizes the results obtained in the present study. The surface enthalpy  obtained in the present study, 1.1 J m−2, is found to be higher compared with 0.4 J m−2 reported by Ranada et al.,11 based on the molten calorimetry technique, while comparable with the values of 1.32 J m−2 at 298 K obtained by Zhang and Banfield19 as well as from the density functional theory calculations in the range 0.53–1.09 J m−2 for the 110, 001, 103 and 110 faces of anatase.23 The discrepancy in the values observed for the excess surface enthalpy in these experiments, mainly between the electrochemical e.m.f. measurements reported here and the molten calorimetry experiment reported by Ranade et al., is not surprising even if the error bars are neglected, and strain effects ignored. This is due to the presence of different crystallographic surfaces, and more importantly of the TiO2/electrolyte contact as far as γ is concerned [ref. 15].
obtained in the present study, 1.1 J m−2, is found to be higher compared with 0.4 J m−2 reported by Ranada et al.,11 based on the molten calorimetry technique, while comparable with the values of 1.32 J m−2 at 298 K obtained by Zhang and Banfield19 as well as from the density functional theory calculations in the range 0.53–1.09 J m−2 for the 110, 001, 103 and 110 faces of anatase.23 The discrepancy in the values observed for the excess surface enthalpy in these experiments, mainly between the electrochemical e.m.f. measurements reported here and the molten calorimetry experiment reported by Ranade et al., is not surprising even if the error bars are neglected, and strain effects ignored. This is due to the presence of different crystallographic surfaces, and more importantly of the TiO2/electrolyte contact as far as γ is concerned [ref. 15].
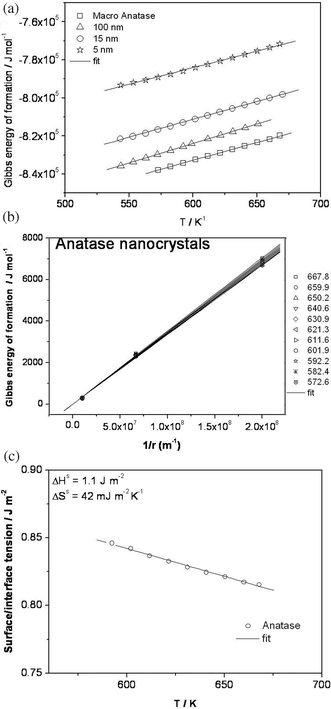 |
| | Fig. 4 (a) Gibbs energy of formation of nanocrystalline anatase of 100 nm, 15 nm and 5 nm as compared to bulk anatase. (b) Plot of excess Gibbs energy of formation versus inverse of radius of the anatase nanoparticles. The numbers within the plot refer to different measurement temperatures expressed in Kelvin. It is seen that at large particle size the excess Gibbs energy drops to zero confirming the validity of this experiment. (c) Plot of surface/interface tension versus temperature for the anatase nano-particles. | |
Table 2 Thermodynamic properties estimated from the electrochemical e.m.f. measurements on anatase phase
| Thermodynamic properties |
Anatase phase |
| ΔfHo |
−9.448 × 105 J mol−1 |
| ΔfSo |
187 J K−1 mol−1 |

|
1.1 J m−2 |

|
0.042 J m−2 K−1 |
4. Conclusions
The present paper provides enthalpies and entropies of anatase as a function of size derived from electrochemical measurements. The effective surface enthalpy is found to be 1.1 J m−2 K−1 while the effective surface entropy is 0.042 J m−2. It has to be kept in mind that these values are averaged over the actually present interfaces including contact interface with the electrolyte and can also include strain contributions. We also give very reliable enthalpies and entropies for macrocrystalline anatase and macrocrystalline rutile. The enthalpy differences between rutile and anatase are a little smaller than reported before. If reaction enthalpies and entropies can be considered as constant down to T = 0, anatase which is less stable at normal and elevated temperatures, is found to become more stable than rutile at extremely low temperatures, a result that was predicted recently by ab initio modeling.11
Acknowledgements
The authors thank M. Ahrens, W. Sitte, H. Li, and R. Merkle for useful discussions.
References
- Ph. Buffat and J.-P. Borel, Phys. Rev., 1976, A 13, 2287.
-
(a) F. Rosei, J. Phys.: Condens. Matter, 2004, 16, S1373 CrossRef CAS;
(b) E. L. Brus, J. Chem. Phys., 1984, 80, 4403 CrossRef CAS;
(c) Y. Wang and H. Herron, J. Phys. Chem., 1991, 95, 525 CrossRef CAS.
-
(a) J. Maier, Solid State Ionics, 1987, 23, 59 CrossRef CAS;
(b) J. Maier, Z. Phys. Chem., 2003, 217, 415 CrossRef CAS;
(c) N. Sata, K. Eberman, K. Eberl and J. Maier, Nature, 2000, 408, 946 CrossRef CAS;
(d) S. Kim and J. Maier, J. Electrochem. Soc., 2002, 149, J73 CrossRef CAS;
(e) P. Balaya, J. Jamnik, J. Fleig and J. Maier, Appl. Phys. Lett., 2006, 88, 62109 CrossRef;
(f) X. X. Guo, I. Matei, J. Jamnik, J.-S. Lee and J. Maier, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 125429 CrossRef.
- H. L. Tuller, Solid State Ionics, 2000, 131, 143 CrossRef CAS.
- J. Schoonman, Solid State Ionics, 2000, 135, 5 CrossRef CAS.
- A. Tschöpe, Solid State Ionics, 2001, 139, 267 CrossRef CAS.
- J. Maier, Nat. Mater., 2005, 4, 805 CrossRef.
- P. Poizot, S. Laruelle, S. Grugeon, L. Dupont and J.-M. Tarascon, Nature, 2000, 407, 496 CrossRef CAS.
- P. Balaya, H. Li, L. Kienle and J. Maier, Adv. Funct. Mater., 2003, 13, 621 CrossRef CAS.
- Yu. Zhukovskii, P. Balaya, E. Kotomin and J. Maier, Phys. Rev. Lett., 2006, 96, 058302 CrossRef.
- M. R. Ranade, A. Navrotsky, H. Z. Zhang, J. F. Banfield, S. H. Elder, A. Zaban, P. H. Borse, S. K. Kulkarni, G. S. Doran and H. J. Whitfield, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 6476 CrossRef CAS.
- J. M. McHale, A. Auroux, A. J. Perrota and A. Novrotsky, Science, 1997, 277, 788 CrossRef CAS.
- P. Knauth, G. Schwitzgebel, A. Tschöpe and S. Villain, J. Solid State Chem., 1998, 140, 295 CrossRef CAS.
- K. T. Jacob, K. P. Jayadevan, R. M. Mallya and Y. Waseda, Adv. Mater., 2000, 12, 440 CrossRef CAS.
- A. Schroeder, J. Fleig, H. Drings, R. Wuerschum, J. Maier and W. Sitte, Solid State Ionics, 2004, 173, 95 CrossRef CAS.
- M. Holzinger, J. Maier and W. Sitte, Solid State Ionics, 1996, 86–88, 1055 CrossRef CAS.
- O. Delmer and J. Maier, Phys. Chem. Chem. Phys., 2009, 11, 6424 RSC.
- A. A. Gribb and J. F. Banfield, Am. Mineral., 1997, 82, 717 CAS.
- H. Zhang and J. F. Banfield, J. Mater. Chem., 1998, 8, 2073 RSC.
- J. Muscat, V. Swamy and N. M. Harrison, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 224112 CrossRef.
- JANAF Thermodynamic Tables (1985) J. Phys. Chem. Ref. Data 14, Supplement 1, 1680–1684.
-
I. Barin and O. Knacke, Thermochemical Properties of Inorganic Substances, Springer-Verlag, Berlin, 1973 Search PubMed.
- M. Lazzeri, A. Vittadini and A. Selloni, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 119901 CrossRef.
Footnotes |
| † Dedicated to Prof. Martin Jansen on the occasion of his 65th birthday. |
| ‡ Current address: Department of Mechanical Engineering and Engineering Science Programme, National University of Singapore, Singapore–117576. |
|
| This journal is © the Owner Societies 2010 |
Click here to see how this site uses Cookies. View our privacy policy here. ![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) /
/![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) )VM
)VM![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) is the average surface tension,
is the average surface tension, ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) is the average radius and VM is the molar volume.
is the average radius and VM is the molar volume.
![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) ) ⇆ TiO2(rutile,
) ⇆ TiO2(rutile, ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) = ∞)
= ∞)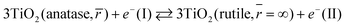

 and
and  refer to the electrochemical potential of electrons at the leads in contact with the working and reference electrodes, respectively, while F and E refer to Faraday constant and the reversible cell voltage.
refer to the electrochemical potential of electrons at the leads in contact with the working and reference electrodes, respectively, while F and E refer to Faraday constant and the reversible cell voltage.

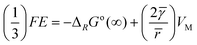
![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) ,
, ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) all refer to anatase, VM, the molar volume, being 20.5 × 10−6 m3 mol−1. A more detailed discussion of the e.m.f. in nanocrystalline systems is given in ref. 15 and 17.
all refer to anatase, VM, the molar volume, being 20.5 × 10−6 m3 mol−1. A more detailed discussion of the e.m.f. in nanocrystalline systems is given in ref. 15 and 17.
![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) for the anatase particle is determined and from its temperature dependence, ΔHs and ΔSs have been estimated.
for the anatase particle is determined and from its temperature dependence, ΔHs and ΔSs have been estimated.
![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) ,
,
 . Furthermore, it is well-known in the thermodynamic literature that the strain dependence of surface tension effects can contribute to or even dominate what was called
. Furthermore, it is well-known in the thermodynamic literature that the strain dependence of surface tension effects can contribute to or even dominate what was called ![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) in the above.
in the above.


 as well as surface entropy
as well as surface entropy  contribution (if adsorption effects can be neglected, γ can be conceived as a surface free energy that can be split into an enthalpy and an entropy term). Table 2 summarizes the results obtained in the present study. The surface enthalpy
contribution (if adsorption effects can be neglected, γ can be conceived as a surface free energy that can be split into an enthalpy and an entropy term). Table 2 summarizes the results obtained in the present study. The surface enthalpy  obtained in the present study, 1.1 J m−2, is found to be higher compared with 0.4 J m−2 reported by Ranada et al.,11 based on the molten calorimetry technique, while comparable with the values of 1.32 J m−2 at 298 K obtained by Zhang and Banfield19 as well as from the density functional theory calculations in the range 0.53–1.09 J m−2 for the 110, 001, 103 and 110 faces of anatase.23 The discrepancy in the values observed for the excess surface enthalpy in these experiments, mainly between the electrochemical e.m.f. measurements reported here and the molten calorimetry experiment reported by Ranade et al., is not surprising even if the error bars are neglected, and strain effects ignored. This is due to the presence of different crystallographic surfaces, and more importantly of the TiO2/electrolyte contact as far as γ is concerned [ref. 15].
obtained in the present study, 1.1 J m−2, is found to be higher compared with 0.4 J m−2 reported by Ranada et al.,11 based on the molten calorimetry technique, while comparable with the values of 1.32 J m−2 at 298 K obtained by Zhang and Banfield19 as well as from the density functional theory calculations in the range 0.53–1.09 J m−2 for the 110, 001, 103 and 110 faces of anatase.23 The discrepancy in the values observed for the excess surface enthalpy in these experiments, mainly between the electrochemical e.m.f. measurements reported here and the molten calorimetry experiment reported by Ranade et al., is not surprising even if the error bars are neglected, and strain effects ignored. This is due to the presence of different crystallographic surfaces, and more importantly of the TiO2/electrolyte contact as far as γ is concerned [ref. 15].



