Polarizable continuum model associated with the self-consistent-reaction field for molecular adsorbates at the interface
Jing-Bo
Wang
,
Jian-Yi
Ma
and
Xiang-Yuan
Li
*
College of Chemical Engineering, Sichuan University, 610065, Chengdu, P. R. China. E-mail: xyli@scu.edu.cn
First published on 7th November 2009
Abstract
In this work, a new procedure has been developed in order to realize the self-consistent-reaction field computation for interfacial molecules. Based on the extension of the dielectric polarizable continuum model, the quantum-continuum calculations for interfacial molecules have been carried out. This work presents an investigation into how the molecular structure influences the adsorbate–solvent interaction and consequently alters the orientation angle at the air/water interface. Taking both electrostatic and non-electrostatic energies into account, we investigate the orientation behavior of three interfacial molecules, 2,6-dimethyl-4-hydroxy-benzonitrile, 3,5-dimethyl-4-hydroxy-benzonitrile and p-cyanophenol, at the air/water interface. The results show that the hydrophilic hydroxyl groups in 2,6-dimethyl-4-hydroxy-benzonitrile and in p-cyanophenol point from the air to the water side, but the hydroxyl group in 3,5-dimethyl-4-hydroxy-benzonitrile takes the opposite direction. Our detailed analysis reveals that the opposite orientation of 3,5-dimethyl-4-hydroxy-benzonitrile results mainly from the cavitation energy. The different orientations of the hydrophilic hydroxyl group indicate the competition of electrostatic and cavitation energies. The theoretical prediction gives a satisfied explanation of the most recent sum frequency generation measurement for these molecules at the interface.
1. Introduction
A detailed knowledge of the interface properties, such as electric permittivity, interfacial viscosity, orientational angle and its distribution, plays an essential role in the understanding of various chemical processes occurring at the interface.1,2 Intrinsic to the interface layer is the broken centrosymmerty which determines the orientational structure and rotational dynamics.3–6 As a consequence, second harmonic generation (SHG) and sum frequency generation vibrational spectroscopy (SFG-VS) can be employed to investigate the interfacial phenomena, because they are dipole forbidden in centrosymmetric media and can produce a dipolar second order signal that is specific to the interface.7,8Among the various surface properties, molecular orientation has gained widespread interest to researchers. A few years ago, Eisenthal and co-workers9 determined the absolute orientation of the molecule through phase measurement of nonlinear susceptibility. Shen et al.10 separately measured the orientations of submoieties of a complicated molecule and therefore deduced the conformation and orientation of the molecule. Later on, Wang presented the null angle method11 which is capable of accurate determination of both the orientation angle and its distribution. Recently, rotation matrix formulation12 and heterodyne-detected electronic SFG13 were developed to obtain the absolute orientation of the interfacial molecule. On the other hand, many theoretical studies were carried out to gain some instructional results. In this aspect, there have been a number of molecular dynamics simulations for the structure and rotation of the interfacial molecules.4–6,14,15 Some authors used the polarizable continuum model (PCM) to study phase transfer energies16 and molecular orientation.17,18 Relying on the ability of the integral equation formalism (IEF) that describes the reaction field of any complex medium with a known Green’s function, diffuse interfaces with position dependent dielectric constants19 were introduced based upon physical intuition. Those studies demonstrate the applicability of PCM to the interfacial systems.
In a recent paper, Wang and co-workers studied 2,6-dimethyl-4-hydroxy-benzonitrile (26DHB) and 3,5-dimethyl-4-hydroxy-benzonitrile (35DHB) at the air/water interface by SFG-VS.20 From spectral measurements, they concluded that these two molecules adopt different orientations. The hydroxyl group in 26DHB points down toward the water phase, while the same group in 35DHB points up toward the air side. The tilt angles for both 26DHB and 35DHB at the air/water interface are around 25–45° from the interface normal. The appearance of opposite directions of hydroxyl groups arouses our interest and encourages us to find a proper answer for this phenomenon.
In a previous work,17 we developed an approach to the investigation on the orientation of an interfacial system, based on the dielectric polarizable continuum model (DPCM).21 However, the procedure in that paper was implemented without considering the mutual polarization between the interfacial molecule and the media. As an approximation, in that paper we isolated the calculation of the charge distribution of the interfacial molecule in homogeneous medium and then simply integrate the interaction energy between the solute charges and the polarization charges. In this paper, we have developed a few of the subroutines in Gamess22 in order for the treatment by a self-consistent-reaction field (SCRF) which takes mutual polarization into account.
Three interfacial molecular systems, 26DHB, 35DHB and p-cyanophenol (PCP) have been taken in the test calculations. The analysis of solvation energy shows that the methyl groups not only affect the electrostatic interaction energy but also change the cavitation energy. Then the different orientations of 26DHB and 35DHB from experimental measurement can find theoretical interpretation.
The rest of the paper is organized as follows: in the next section we present briefly the theoretical method for the solvation energy at the interface, by making some extension of DPCM to the interfacial system for electrostatic energy. Section 3 describes the parameter choice and mentions the computational details. In Section 4, we discuss the orientation behavior of the test molecules at the air/water interface. A brief summary is given in Section 5.
2. Continuum model for an interfacial system
The basic formulation of DPCM21 is based on a quantum mechanical (QM) description of the solute molecule, whereas the surrounding solvent is taken into account implicitly via a solute–solvent interaction potential characterized by the dielectric constant. The interaction potential is computed in terms of a set of point charges on the tesserae of the molecular cavity. The well-known generating polyhedra (GEPOL)23 procedure can be used to generate a realistic cavity upon the molecular structure. Here we only give the key formulations and show our extension to the interfacial system. Because several experimental and theoretical studies suggested that the weakly associating interfaces are molecularly sharp,15,24–26 we suppose that the interface can be described as a flat and ideal plane.Differing from the case of homogeneous medium, in the interface case we need to divide the cavity created by the solute immersed in two different solvents into two different cavity parts, ∑01 and ∑02, corresponding to a sharp change in the dielectric constant, from ε0 = 1 inside the cavity to ε1 or ε2 outside the cavity.16 Here ε1 and ε2 stand for the dielectric constants of two different solvents. In order to account for the interface effect for molecular energy, we have to introduce another surface, ∑12, which separates portions of the space occupied by the two different solvents. Based on the extension of DPCM, we can obtain a set of point charges placed on this phase separation surface. The surface is partitioned with a square tessellation. Taking into account the intersection of some cavity tesserae and surface tesserae, we have developed an algorism to create these tesserae elaborately. The fine tessellation in an intersection portion guarantees the accuracy of the interface effect. Our fine tessellation is based on the GEPOL23 procedure.
In PCM program implementation, the solute charge distribution is separated into nuclear and electronic contributions and then the polarization charge is also divided into two counterparts. For simplification, we confine ourselves to the case of the electronic part. The detailed implementation of nuclear contributions can be found in ref. 27. Its extension to the interfacial system is similar to the electronic part. By combining boundary conditions, the linear equations for polarization charges induced by the electronic charge can be given in the following matrix form
| DA−1qe = −Een | (1) |
 | (2) |
 | (3) |
 | (4) |
 | (5) |
The energy of the interfacial system consists of electrostatic and non-electrostatic ones, i.e.,
| G = Gel + ΔGcav + ΔGdis-rep | (6) |
 | (7) |
 exposed to solvent 1.
exposed to solvent 1.  has a similar meaning but to solvent 2.
has a similar meaning but to solvent 2.  and
and 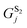 are the parameterized cavitation energies for a sphere in solvents 1 and 2, respectively. Unlike the usual PCM approach, special attention should be paid to the quantity Aplane which is the area corresponding to the cutting section of the interface by the occupation of the molecular cavity. In eqn (7), γS1/S2 denotes the interface tension and can be estimated as
are the parameterized cavitation energies for a sphere in solvents 1 and 2, respectively. Unlike the usual PCM approach, special attention should be paid to the quantity Aplane which is the area corresponding to the cutting section of the interface by the occupation of the molecular cavity. In eqn (7), γS1/S2 denotes the interface tension and can be estimated as| γS1/S2 = |γS1 − γS2| | (8) |
The energies of dispersion and repulsion are expressed as the sums of energy integrals proposed by Claverie30,31
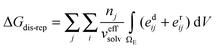 | (9) |
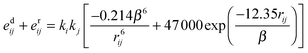 | (10) |
On the basis of the procedure illustrated above, we have developed some subroutines and linked them into Gamess22 to calculate the energy terms in eqn (6) for interfacial systems. It is important to note that the various terms in eqn (6) depend on a different definition of the cavity surface.32 In this work, the cavitation energy is computed by using a van der Waals surface formed by spheres centered on atoms with Bondi radii.33 ΔGdis-rep is calculated with the solvent accessible surface, i.e. a van der Waals surface augmented by the radius of the atom type of the solvent.
For computation of the electrostatic energy, the cavity can factually be constructed in different ways, such as the united atom for Hartree–Fock (UAHF),32 united atom Kohn–Sham topological model (UAKS), atomic radii of the universal force field (UFF)34 and scaled atomic van der Waals radii (α = 1.2) cavity. The benchmark test35,36 shows that the UAKS cavity performs sometimes better for the solvation energy and thermodynamic property, but UAHF and UFF cavities were often adopted in practice and the calculated solvation energies for the neutral molecules are found close to those by UAKS.35 From our experience, it is difficult to find a method that performs well in all cases in the cavity construction. Considering that the scaled atomic van der Waals radii cavity is available in Gamess codes, we take this method for our purpose. The cavity constructed in this way is close to UFF method in Gaussian.
3. Computational details
The structures of the three interfacial molecules, 26DHB, 35DHB and PCP, are depicted in Scheme 1. The number indicates the coordinate of the atom along the principal axis with respect to the mass center of the molecule. It is convenient to define a Cartesian reference frame, with the interface plane lying on the XY plane and the Z axis pointing towards the air phase. As shown in Fig. 1, we define the depth z to measure the depth of the molecular mass center into the water phase and the orientational angle θ to show the orientation of the principal axis of the molecule with respect to the surface normal n. The direction of the principal axis is set from the hydroxyl group to the cyano group, whereas the surface normal is defined from the water phase to the air. | ||
| Scheme 1 | ||
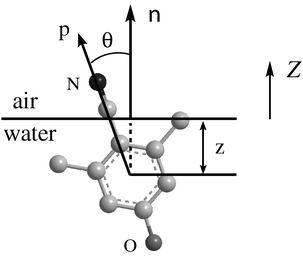 | ||
| Fig. 1 Schematic depiction of the molecule at the interface. θ stands for the orientational angle of the principal axis with respect to the surface normal (Z axis) and z is the depth of the mass center into the water phase. | ||
Calculations have been performed at the HF level using the 6-31+G* basis set. Molecular geometries are optimized in vacuum and kept fixed in all subsequent calculations. This assumption is reasonable because several authors found that the geometry optimized in solution is nearly identical to the one in the gas phase.37,38 The parameters necessary to calculate the energy for ΔGel, ΔGcav and ΔGdis-rep are the standard values contained in Gamess program.22 The static dielectric constants are 78.39 and 1.000536 for water and air, respectively. The surface tension of water is 72.14 dyn cm−1 at a temperature of 25 °C.39
The surface construction for an interfacial system in this work needs to be stated. For the partition of the plane interface, we take a square region into account and divide it into smaller square grids (1 Å wide). A test calculation shows that the electrostatic energy is not very sensitive to the grid size; therefore a finer tessellation seems unnecessary. In order to guarantee the convergence of the electrostatic energy calculation, we have inspected the dependency of the electrostatic energy on the cut-off radius for the interface plane. Fig. 2 shows the numerical results of the interfacial molecules with a horizontal pattern (z = 0, θ = 90). The unit degree for the angle is omitted throughout this paper. It is found that the electrostatic energy keeps almost unchanged when the cut-off radius goes beyond 30 Å.
 | ||
| Fig. 2 Dependence of the electrostatic solvation energy on the cut-off radius at the air/water interface. Open square: 26DHB; open circle: 35DHB; open triangle: PCP. c = 0 indicates the neglect of the interface contribution. | ||
The parameters that define the fine partition of the volume ΩE can be determined as follows: placing the solute molecule in a homogeneous medium, and then calculating ΔGdis-rep based on the volume and surface integrations. In this way, we compare the results and adjust the parameters and then finally choose a cubic length of 42 Å and the grid size of 0.125 Å.
4. Results and discussion
The common chemical sense about molecular properties suggests that the hydrophilic molecular group will point toward the water phase in order to form the hydrogen bond. Such an arrangement will give rise to an increasing in the electrostatic interaction between the solute and the polar solvent. For example, the SHG phase measurements revealed that the hydroxyl group of phenol points into the bulk water.9 The absolute phase measurements applied to p-nitrophenol and p-bromophenol at the air/water interface revealed that all of these phenols have their hydroxyl pointing toward the bulk water. This indicates that the molecular orientation is dominated by the hydroxyl group rather than the molecular dipole moment, because the permanent dipole moments of p-nitrophenol and p-bromophenol take the opposite direction to phenol.40 Other experimental studies such as p-nitrophenol (PNP) and 2,6-dimethyl-p-nitrophenol (dmPNP) at the water/cyclohexane interface41 and m-cyanophenol (MCP) and PCP at the air/water interface42 revealed the same phenomena too. In addition, these experimental observations elucidated that subtle variations in the molecular structure can lead to considerably different local environments experienced by the molecule at the interface. To our knowledge, 35DHB molecule is the only molecule that has its hydroxyl pointing away from the water phase. It is the aim of the present work to work out an explanation for the unusual behavior, by investigating the dependence of the solvation energy on the molecular structure and orientation.For given values of z and θ, we can calculate the solvation energy by performing a single point calculation by the procedure developed in this work. By changing the depth and the orientation angle, the solvation energy profile of ΔG(z,θ) for 26DHB, 35DHB and PCP can be scanned, as shown in Fig. 3. For 26DHB, there is an obvious low-lying domain in the energy surface in the range of z = 0–3 and θ = 0–40, but for 35DHB the low-lying domain exists in the range of z = −0.5–2 and θ = 160–180. Similar to 26DHB, the low-lying domain for PCP system is located in the range of z = 1–3 and θ = 0–30. The global minima of ΔG(z,θ) have been found at z = 1 and θ = 0 for 26DHB and PCP but z = 0.5 and θ = 180 for 35DHB. The opposite orientations related to the hydroxyl group will be discussed in detail in the following sections.
 | ||
| Fig. 3 Energy surface of ΔG(z,θ) for (a) 26DHB, (b) 35DHB and (c) PCP. The variables are within the range of z = −5–5 and θ = 0–180. The step length for the energy surface scanning is 0.5 Å for z and 10° for θ. | ||
The average orientation angle can be calculated from the energy surface with the following formulation42–44
 | (11) |
Now we survey the factors that lead to the opposite orientation and show the effect of the aromatic substitution of methyl. Fig. 4 depicts the θ-dependency of the electrostatic solvation energy ΔGel at z = 0 for 26DHB and 35DHB. It is obvious that this quantity of 26DHB is lower than 35DHB in the range of θ < 90, but the situation turns over in the case of θ > 90. The energy surfaces exhibit the same tendency in the range of z = −2.5–5 but it becomes non-apparent when a cyano group starts entering the water. The methyl groups impose on the electrostatic solvation in two ways. Firstly, the cavity surface is larger in the presence of a methyl group and thus the electrostatic interaction decreases. On the other hand, the methyl group induces a different solvation environment and directly affects the electronic density of the molecule. The dipole moments for 26DHB, 35DHB and PCP located at z = 0 and θ = 0 are 5.54, 6.52 and 2.39 Debye, respectively. There are increments of a dipole moment in the presence of methyl groups. Different dipole moments reflect the influence of the methyl group on electronic density. The presence of methyl groups in the mentioned systems gives rise to decreasing of the electrostatic interaction. In the case of θ < 90, the lower parts of 26DHB and 35DHB are immersed in water (see Fig. 1). The extra methyl groups in 35DHB weaken the electrostatic interaction as compared to 26DHB in which the methyl groups are at the opposite side of the hydroxyl group. In the case of θ > 90, the upper part, i.e., the cyano group terminal of 26DHB and 35DHB enters the water phase. The methyl groups in 26DHB yield the same impact and hence the electrostatic solvation energy of 26DHB becomes higher than 35DHB. So we conclude that the variations in the molecule structure can alter the local solvation environments significantly.
 | ||
| Fig. 4 Electrostatic solvation energy against the orientation angle at z = 0. Open square: 26DHB; open circle: 35DHB. | ||
Further information can be extracted from Fig. 4. Let us take 35DHB as an example. The open circle curve shows that the system will be more stable at θ > 90. This indicates that 35DHB tends to point its hydroxyl group to the air phase. This trend has been found in the range of z = −5–1. In order to see what roles the other terms in eqn (6) play, Fig. 5 has been given to show the θ-dependence of the solvation energy at z = 1 and at z = 0.5 for 26DHB and 35DHB, respectively. The depth is selected according to the global minimum for those two molecules. Comparing the square curve (pure electrostatic) and the triangle one (electrostatic plus dispersion-repulsion) in Fig. 5, we can draw a conclusion that the dispersion–repulsion energy is insensitive toward the orientation angle for 26DHB, but the θ-dependence of the dispersion–repulsion is obvious for 35DHB. Further, we take the cavitation energy into account, as shown by the open circle curves in Fig. 5a, the total solvation energy goes up before θ = 80 and then becomes flat. We recall that the methyl groups of 26DHB immerse in water at θ = 180, so the cavity occupied by the methyl groups causes an increase in the cavation energy, and hence the systems become less stable at θ = 180. Unlike 26DHB, the situation becomes converse for 35DHB. The cavitation energy at θ = 0 is found ca 3 kcal mol−1 larger than that at θ = 180. The total solvation energy, as shown by the open circle curve in Fig. 5b, takes its minimum at θ = 180. Therefore, we conclude that the cavitation energy plays an important role in the molecular orientation at the interface.
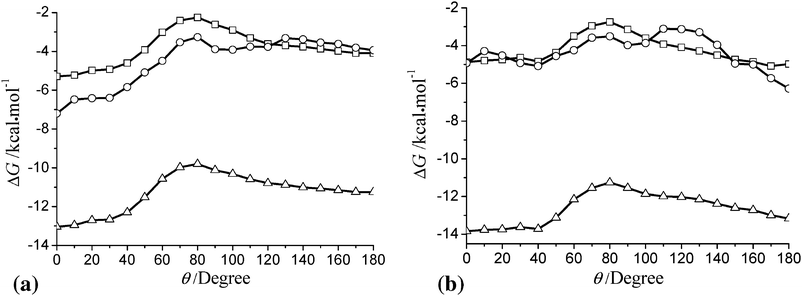 | ||
| Fig. 5 The θ-dependence of the solvation energy (a) for 26DHB at z = 1 and (b) for 35DHB at z = 0.5. Open squares: electrostatic; open triangles: electrostatic plus dispersion-repulsion; open circles: total solvation energy. | ||
With eqn (11), the average orientation angle of PCP at the air/water interface is 75 degree, while 26DHB and 35DHB take the angles 40 for the former and 130 for the latter. Such orientation angles imply that the methyl groups tend to go out of the water phase, in favor of the gain of lower cavitation energy. It can be understood that the presence of two methyl groups leads to a more upright orientation. This trend is consistent with the experimental results for PNP and dmPNP at the water/cyclohexane interface.41 The more upright orientations for 26DHB and 35DHB can reduce the cavitation energy of interfacial systems.
We turn to examining the influence of the depth on the solvation energy. The decomposition of ΔG(z,θ) can provide more detailed information on the molecular behavior at the interface. A similar study has been reported in ref. 16. As shown in Fig. 6, we have presented the energy components for 35DHB at the air/water interface. It can be seen that the electrostatic energy has a gentle variation when the cyano group and the phenyl ring cross through the interface (from z = 4 to z = −2), while a slightly steep variation occurs when the hydroxyl group crosses the interface as well (z = ∼−3). Moreover, the cavitation energy changes considerably during the transition of the methyl group from the air side to the water phase. This is straightforward if we notice that the entrance of the methyl group from air to water needs surface work to create a cavity. In addition, the dispersion energy curve keeps going down until z = −8.
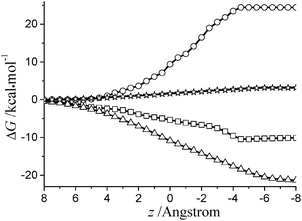 | ||
| Fig. 6 Energy profiles for the components of the solvation energy at θ = 180 for 35DHB. Open square: electrostatic; open circle: cavitation; open triangle: dispersion; open asterisk: repulsion. | ||
Because of the different behavior of the various components, we can see that the total solvation energy has a minimum and maximum (see open circle curve in Fig. 7). At the energy minimum (z = 0.5), the cyano group of 35DHB is fully immersed in water and the carbon atom of the hydrophobic benzene ring reaches the interface and becomes partially dehydrated. In particular, from Fig. 7, it turns out that the minimum value is obtained as a compensation between the electrostatic and non-electrostatic energies whereas the maximum is almost completely due to the non-electrostatic contributions. We have found that 26DHB and PCP molecules have curved shapes similar to 35DHB, except that the electrostatic energy has a steeper variation when the hydroxyl group of 26DHB and PCP crosses the interface.
 | ||
| Fig. 7 Drawing of the total solvation energy against the depth of the molecule at θ = 180. Open square: electrostatic part; open triangle: the non-electrostatic contributions of ΔGcav plus ΔGdis-rep; open circle: total solvation energy. | ||
5. Conclusions
In the present study we extend the DPCM to the interfacial system and realize the ab initio calculation of the electrostatic solvation energy. The computations of cavitation and dispersion-repulsion energies are described in detail. Fine tessellation is realized for the treatment of the intersection portion between cavity tesserae and interface teeserae. The accurate computation of the solvation energy provides us with a tool for the study of the behavior of interfacial molecules.In application, we have investigated the relation between a molecule structure and its orientation at the interface. The methyl groups in 26DHB and 35DHB apply a considerable impact on the solvation energy. It is easy to understand that the methyl groups affect the cavitation energy owing to the change of the cavity surface. Besides, they apply influence on the electrostatic solvation energy by changing the solvation environment, although nonpolar. Therefore, molecular orientation depends on the molecular structure. This work presents the reasons why the molecular axes of 26DHB and 35DHB take different directions at the air/water interface. In our case, 26DHB and 35DHB have the same structure except for the position of the methyl groups. So, the electrostatic solvation energies for the two cases are approximately the same, and both systems will take the energy minimum at almost the same orientation, if only the electrostatic energy is taken into account. However, when we consider the surface work caused by immersing the methyl groups from air to water, the situation is quite different. The cavitation energy in some cases can drive the interfacial molecule to the opposite direction. The average orientation angles have been predicted according to eqn (11). We obtain an average orientation angle of about 40 for 26DHB, 130 for 35DHB and 75 for PCP. Compared with the orientation distributions from experiments, i.e., 25–45 for 26DHB, 135–155 for 35DHB and 65–85 for PCP, the theoretical results are in reasonable agreement with the experimental measurements.
Another parameter that we consider is the depth of the interfacial molecule to the water phase. From the 2-D drawing of the solvation energies, we have found that the energy minimum appears at z = 1 Å for both 26DHB and PCP, while at z = 0.5 Å for 35DHB. This indicates that all three molecules tend to be centered at the interface, regardless of the different directions of the molecular principal axes.
The theoretical computation in this work gives a reasonable explanation for the opposite orientations of the molecules which have similar chemical structures. Our efforts reveal that the cavitation energy will be dominant in the molecular orientation, provided that the influence from the electrostatic part and the dispersion-repulsion is not significant. The present study shows that, from a theoretical viewpoint, a proper chemical modification on the phenyl ring is probably valid for the change of the molecular orientation at the interface.
Acknowledgements
We thank Dr Hong-Fei Wang for the helpful discussions. This work is supported by the National Natural Science Foundation of China (Nos. 20533070, 20873087).References
- K. B. Eisenthal, Chem. Rev., 2006, 106, 1462–1477 CrossRef CAS.
- I. Benjamin, Chem. Rev., 2006, 106, 1212–1233 CrossRef CAS.
- D. Zimdars, J. I. Dadap, K. B. Eisenthal and T. F. Heinz, J. Phys. Chem. B, 1999, 103, 3425–3433 CrossRef CAS.
- M. L. Johnson, C. Rodriguez and I. Benjamin, J. Phys. Chem. A, 2009, 113, 2086–2091 CrossRef CAS.
- S. Paul and A. Chandra, J. Chem. Theory Comput., 2005, 1, 1221–1231 CrossRef CAS.
- C. D. Wick, I. W. Kuo, C. J. Mundy and L. X. Dang, J. Chem. Theory Comput., 2007, 3, 2002–2010 CrossRef CAS.
- T. F. Heinz, H. W. K. Tom and Y. R. Shen, Phys. Rev. A: At., Mol., Opt. Phys., 1983, 28, 1883–1885 CrossRef CAS.
- J. H. Hunt, P. Guyot-Sionnest and Y. R. Shen, Chem. Phys. Lett., 1987, 133, 189–192 CrossRef CAS.
- K. Kemnitz, K. Bhattacharyya, J. M. Hicks, G. R. Pinto and K. B. Eisenthal, Chem. Phys. Lett., 1986, 131, 285–290 CrossRef CAS.
- X. Zhuang, P. B. Miranda, D. Kim and Y. R. Shen, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 12632–12640 CrossRef CAS.
- Y. Rao, Y. S. Tao and H. F. Wang, J. Chem. Phys., 2003, 119, 5226–5236 CrossRef CAS.
- Y. Rao, M. Comstock and K. B. Eisenthal, J. Phys. Chem. B, 2006, 110, 1727–1732 CrossRef CAS.
- S. Yamaguchi and T. Tahara, J. Chem. Phys., 2008, 129, 101102 CrossRef.
- D. Michael and I. Benjamin, J. Phys. Chem. B, 1998, 102, 5145–5151 CrossRef CAS.
- I. Benjamin, J. Chem. Phys., 1992, 97, 1432–1445 CrossRef.
- L. Frediani, C. S. Pomelli and J. Tomasi, Phys. Chem. Chem. Phys., 2000, 2, 4876–4883 RSC.
- J. Y. Ma, J. B. Wang, X. Y. Li, Y. Huang, Q. Zhu and K. X. Fu, J. Comput. Chem., 2008, 29, 198–210 CrossRef CAS.
- K. X. Fu, Y. Huang and X. Y. Li, J. Phys. Chem. B, 2006, 110, 10088–10094 CrossRef CAS.
- L. Frediani, R. Cammi, S. Corni and J. Tomasi, J. Chem. Phys., 2004, 120, 3893–3907 CrossRef CAS.
- F. Wang, Z. Huang, Z. F. Cui and H. F. Wang, Chin. J. Chem. Phys., 2009, 22, 197–203 CrossRef CAS.
- S. Miertus, E. Scrocco and J. Tomasi, Chem. Phys., 1981, 55, 117–129 CrossRef CAS.
- M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. J. Su, T. L. Windus, M. Dupuis and J. A. Montgomery, J. Comput. Chem., 1993, 14, 1347–1363 CrossRef CAS.
- J. L. Pascual-Ahuir, E. Silla and I. Tunon, J. Comput. Chem., 1994, 15, 1127–1138 CAS.
- A. Pohorille and I. Benjamin, J. Chem. Phys., 1991, 94, 5599–5605 CrossRef CAS.
- P. Linse, J. Chem. Phys., 1987, 86, 4177–4187 CrossRef CAS.
- W. H. Steel, Y. Y. Lau, C. L. Beildeck and R. A. Walker, J. Phys. Chem. B, 2004, 108, 13370–13378 CrossRef CAS.
- R. Cammi and J. Tomasi, J. Comput. Chem., 1995, 16, 1449–1458 CrossRef CAS.
- J. Langlet, P. Claverie, J. Caillet and A. Pullman, J. Phys. Chem., 1988, 92, 1617–1631 CrossRef CAS.
- R. A. Pierotti, Chem. Rev., 1976, 76, 717–726 CrossRef CAS.
- M. J. Huron and P. Claverie, J. Phys. Chem., 1972, 76, 2123–2133 CrossRef CAS.
- M. J. Huron and P. Claverie, J. Phys. Chem., 1974, 78, 1862–1867 CrossRef CAS.
- V. Barone, M. Cossi and J. Tomasi, J. Chem. Phys., 1997, 107, 3210–3221 CrossRef CAS.
- A. Bondi, J. Phys. Chem., 1964, 68, 441–451 CrossRef CAS.
- A. K. Rappe, C. J. Casewit, K. S. Colwell, W. A. Goddard III and W. M. Skiff, J. Am. Chem. Soc., 1992, 114, 10024–10035 CrossRef CAS.
- Y. Takano and K. N. Houk, J. Chem. Theory Comput., 2005, 1, 70–77 CrossRef.
- A. Dinescu and A. E. Clark, J. Phys. Chem. A, 2008, 112, 11198–11206 CrossRef CAS.
- C. G. Zhan and D. A. Dixon, J. Phys. Chem. B, 2003, 107, 4403–4417 CrossRef CAS.
- J. B. Foresman, T. A. Keith, K. B. Wiberg, J. Snoonian and M. J. Frisch, J. Phys. Chem., 1996, 100, 16098–16014 CrossRef CAS.
- J. A. Dean, Lange’s Handbook of Chemistry, McGraw-Hill Book Company, New York and London, 1999 Search PubMed.
- K. B. Eisenthal, Chem. Rev., 1996, 96, 1343–1360 CrossRef CAS.
- W. H. Steel and R. A. Walker, J. Am. Chem. Soc., 2003, 125, 1132–1133 CrossRef.
- M. C. Kido Soule, D. K. Hore, D. M. Jaramillo-Fellin and G. L. Richmond, J. Phys. Chem. B, 2006, 110, 16575–16583 CrossRef.
- X. Zhuang, D. Wilk, L. Marrucci and Y. R. Shen, Phys. Rev. Lett., 1995, 75, 2144–2147 CrossRef CAS.
- I. Benjamin, J. Phys. Chem. A, 1998, 102, 9500–9506 CrossRef CAS.
| This journal is © the Owner Societies 2010 |
