Valence electron energy-loss spectroscopy of silicon negative electrodes for lithium batteries†
Julien Danetab, Thierry Brousseb, Karsten Rasima, Dominique Guyomarda and Philippe Moreau*a
aInstitut des Matériaux Jean Rouxel (IMN), Université de Nantes, CNRS, 2 rue de la Houssinière, BP32229, 44322 Nantes Cedex 3, France. E-mail: Philippe.Moreau@cnrs-imn.fr
bLaboratoire de Génie des Matériaux et Procédés Associés (LGMPA-EA2664)-Polytech Nantes, Université de Nantes, rue Christian Pauc-BP50609, 44306 Nantes Cedex 3, France
First published on 9th November 2009
Abstract
All compounds present in the lithium–silicon binary phase diagram were synthesized and analyzed by electron energy-loss spectroscopy. In order to limit beam damage, and to develop a fast and local method of characterizing silicon negative electrodes, the valence energy-loss spectrum region was investigated, in particular the very intense plasmon peak in these alloys. Experimental spectra are in strong agreement with theoretical ones obtained from density functional theory. These results constitute a database for LixSi alloys’ plasmon energies. The method is applied to the study of the first discharge of a silicon electrode, thus identifying a Li2.9±0.3Si phase in equilibrium with Si on the voltage plateau. A nucleation process of this phase in the pristine Si is revealed, as well as a possible over-lithiation beyond the end of discharge Li15Si4 crystalline phase.
1. Introduction
Lithium batteries will soon be a major source of energy storage for applications such as electric transportation, power tools and load leveling of intermittent renewable energies. While current Li-ion battery technology uses graphitized carbon as the negative electrode,1 in order to increase practical energy density, much effort is being devoted to develop new positive and negative electrodes.2–5 Silicon-based systems are very promising as negative electrodes,6–11 with a maximum theoretical capacity ten times that of graphite and safer behavior against reactions with solvent or electrolytes.12 The practical use of silicon is, however, hindered by a massive 280% volume change during the charge–discharge process. Such a drastic change leads to loss of electric connections in the electrode, a phenomenon enhanced by pulverization of particles, especially in the case of crystals compared to amorphous alloys.13Reduced fading during cycling can be obtained by the use of silicon nanowires,14 or thin films.15 Better behavior can also be achieved by carefully tailoring, with carbon nanotubes and nanofibers, the conductive network in the composite electrode,16 or by maintaining a two phase structure during cycling.17 Whatever the preferred solution, the performance of the electrode is governed by phenomena taking place at a nanometre scale.
For instance, a 5 nm passivation layer can prevent electronic transport in the composite electrode but can also favor ionic migration of species from the electrolyte into the active material.18 Rapid spatial variations in composition can produce detrimental fractures in the structure but also favor kinetic reorganization for higher power performances.19 Optimisation of future electrodes thus implies a better understanding of the electrochemical process, and local determination of electrode composition is of major assistance in that research.
Many studies rely on X-ray diffraction (XRD) to analyze sample composition during cycling. Due to its intrinsic coherence length, XRD is not the most suitable choice, especially since a large loss of crystallinity occurs while cycling.17 Electron diffraction could be of some help to gain information at the nanoscale.7,14,20 The high electron beam sensitivity of Li-containing samples, particularly for accelerating voltages above 100 kV, could, however, induce an amorphization even before any pattern is acquired. Instead, an extremely fast analysis technique is required.
Electron energy-loss spectroscopy (EELS) in a transmission electron microscope (TEM) has been shown to be a powerful tool for nanoscale characterisation, in particular for lithium batteries.21–23 Most studies focus on core loss edges (Si L2,3 edge, Li K edge or transition metal L2,3 edge in positive electrodes),20 which often demand very thin samples and acquisition times over a few seconds. In the case of LixSi electrodes, these two requirements are extremely difficult to fulfill. For this reason, with an intensity 10–100 times larger than that of Li or Si core loss edges, valence electron energy-loss spectroscopy (VEELS)24 is particularly well suited for LixSi alloy characterization. For metallic alloys, this region of the EELS spectrum (energy-losses below 50 eV) is rather simple and essentially consists of a single large and well defined peak called the plasmon peak. In Al–Li alloys, a direct linear relationship is found between the plasmon energy and the lithium content.25,26 A precise lithium quantification can thus be obtained from the position of the plasmon peak.
In this work, after section 2, we determine the applicability of this method to LixSi alloys and demonstrate its superiority to core loss analysis. This experimental study is confirmed by first principles calculations. The aim of this new method is to obtain a better understanding of the electrochemical process at work in real silicon electrodes. In section 4, precise analysis of the first discharge of a crystalline silicon based electrode is performed, proving the feasibility of the method and revealing a nucleation process in the course of silicon crystal alloying.
2. Experiments and calculation methods
LixSi alloys were prepared in an argon glove box, by introducing silicon powder (Alfa Aesar, 99.999%, 1–5 μm) and lithium ribbons (Aldrich, 99.9%) in a stainless steel tube (inner diameter 9 mm, external diameter 12 mm, length 7 cm). The total mass of each sample was approximately 0.5 g. The tube was closed in the glove box by forcing the tube extremity into a stainless steel lid. The lid was then welded outside the glove box. All samples were heated at 550 °C for 100 h, under a steady flow of Varigon® (95% Ar, 5% H2) in order to limit tube oxidation. Tubes were opened inside the glove box, LixSi alloys were then crushed in an agate mortar and introduced into a capillary glass (∅: 0.3 μm). X-Ray diffraction patterns were recorded on an INEL diffractometer over a 1 h acquisition time. Sealed capillaries were proven to be air tight for at least this period of time.For the electrochemical study, composite electrodes were prepared by mixing 80 wt% crystalline silicon (1–5 μm, Alfa Aesar), 12 wt% carbon black (super P, Erachem) and 8 wt% carboxymethylcellulose (DS = 0.7, Mw = 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, Aldrich). This electrode composition is very close to that used in the reference study performed by Li and Dahn,9 and was proven to lead to good cycling properties.16 Mixing was performed in a silicon nitride vial with three silicon nitride balls (diameter = 9.5 mm). After adding water, the ball milling was done for an hour at 500 rpm. The slurry was then cast onto a copper disk and dried under vacuum for an hour at 55 °C. The Swagelok cells were prepared with lithium as the negative electrode and LiPF6 dissolved in an ethylene and diethylene carbonate (volume ratio 1
000, Aldrich). This electrode composition is very close to that used in the reference study performed by Li and Dahn,9 and was proven to lead to good cycling properties.16 Mixing was performed in a silicon nitride vial with three silicon nitride balls (diameter = 9.5 mm). After adding water, the ball milling was done for an hour at 500 rpm. The slurry was then cast onto a copper disk and dried under vacuum for an hour at 55 °C. The Swagelok cells were prepared with lithium as the negative electrode and LiPF6 dissolved in an ethylene and diethylene carbonate (volume ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) solution as electrolyte. The galvanostatic mode was used with a C/100 cycling rate (i.e. discharge within 100 h), based on a 3579 mAh g−1 theoretical capacity.
1) solution as electrolyte. The galvanostatic mode was used with a C/100 cycling rate (i.e. discharge within 100 h), based on a 3579 mAh g−1 theoretical capacity.
Electron energy-loss spectra (EELS) were obtained with a Gatan 666 spectrometer, modified to include a CCD camera instead of a photodiode array.27 The spectrometer was attached to a Hitachi HF2000 TEM. Samples were deposited onto a holey carbon copper grid in the glove box. A vacuum transfer sample holder (Gatan 626) was used to transfer grids into the TEM without any air contact. In order to limit electron beam damage, the TEM was operated at 100 kV and a 50 nm probe size was used. Convergence and collection angles were 1.4 mrad and 4.55 mrad, respectively. With a 0.08 eV/pixel dispersion, the energy resolution was approximately 0.8 eV. Total acquisition times were 10 ms for VEELS spectra, and 10 s for Li and Si edges. All spectra were corrected for the gain and dark counts of the CCD camera. Deconvolution by the zero loss peak, Fourier ratio (high losses) and Fourier Log (low losses) deconvolutions were performed with the PEELS program.28
First principles calculations of EELS spectra were performed with WIEN2k,29 a full potential density functional code. Augmented plane wave plus local orbitals (APW + LO) basis sets were used for the self consistent field calculations. Calculations were all carried out within the general gradient approximation (GGA) using Perdew, Burke, and Ernzerhof’s exchange and correlation potential.30 Atomic coordinates were taken from ICSD cards (#652258 for Si; #87408 for Li7Si3; #660135 for Li13Si4; #159397 for Li15Si4; #41691 for Li12Si7, #44907 for Li22Si5; #44367 for Li).31 The plane wave basis set was defined by RMT×Kmax = 7.0. Shifted k-point meshes with 8–35 irreducible k-points for the self consistent field calculations were used depending on the size of the Brillouin zone. For calculation of dielectric functions [ε(E)],32 the Optic program was used with 72–1050 irreducible k-points. In the case of the Li7Si3 structure, considering all sites fully occupied in the ICSD card #87408, the expected composition is Li7.5Si3. Due to partial occupancies of the Li 6c and Li 3b sites (occ = 0.95 and 0.80, respectively), the composition of this phase is given as Li7Si3. Partial occupancy cannot be treated explicitly in WIEN2k. Since, in the case of the plasmon energy calculations, the number of valence electrons is the main criteria, we chose to remove 0.5 electrons per formula unit from the structure. These 0.5 electrons were then added as a background charge, in the same manner as for a calculation with a core hole. Another calculation including the 0.5 electrons leads to a plasmon energy 0.15 eV higher than the calculation presented in Table 1 (without the 0.5 extra electrons). This shift is within the experimental and calculation errors. Dielectric functions (including intra-band transitions) were calculated in the optical approximation (q = 0) up to 70 eV. In case of anisotropic structures, mean values of the energy-loss functions were considered.
| Compound (LixSi) | x from core losses | n/Å−3 | Ep/eV Drude | Ep/eV WIEN2k | Ep/eV Exp. |
|---|---|---|---|---|---|
| Si (x = 0) | 0 | 0.200 | 16.6 | 17.0 | 16.83 (0.05) |
| Li12Si7 (x = 1.7) | 1.5 | 0.131 | 13.5 | 14.1 | 14.21 (0.03) |
| Li7Si3 (x = 2.3) | 2.5 | 0.123 | 13.0 | 13.6 | 13.82 (0.04) |
| Li13Si4 (x = 3.3) | 3.1 | 0.108 | 12.2 | 13.1 | 12.83 (0.02) |
| Li22Si5 (x = 4.4) | 4.2 | 0.102 | 11.9 | 12.9 | 12.74 (0.03) |
| Li | — | 0.0463 | 8.0 | 7.4 | 7.5 (0.1) |
In order to check on the influence of the possible amorphous state of the alloys, we performed the same WIEN2k calculations (to obtain the dielectric functions) using a simulated amorphous structure. This structure was generated using a DFT molecular dynamics scheme as implemented in the VASP DFT-package,33 with atomic potentials of the PAW-PBE type.30 The starting configuration was a supercell of the Pbam Li13Si4 orthorhombic structure containing 104 Li and 32 Si atoms, respectively. This composition was chosen since it is close to that obtained later in section 4 for the amorphous alloy. The cell was kept at a simulation temperature of 1500 °C for roughly 9 ps (4500 time steps of 2 fs), which proved sufficient for a substantial displacement of both Si and Li atoms of several Ångströms (root-mean square displacement after 9 ps: Si-9.4 Å, Li-13.6 Å). The initial crystallographic relations were completely neutralized. The so-obtained configuration was subsequently “quenched” to 600 °C for 9 ps and finally relaxed back to a local structural minimum via a conjugated gradient routine. Our protocol is thus different from that recently used by Chevrier and Dahn,34 but leads to very similar results. In order to facilitate the comparison with the crystalline structure, 90° angles were preserved during the relaxation leading to very minor changes compared to the full cell optimization.
3. Results and discussion on reference alloys
All compositions of alloys appearing in the Li–Si phase diagram35 were prepared, namely: Li12Si7 (x = 1.71 in LixSi), Li7Si3 (x = 2.33), Li13Si4 (x = 3.25) and Li22Si5 (x = 4.4). For all samples, X-ray diffraction patterns correspond well with PDF files (#89-0005 for Li7Si3; #41-1308 for Li12Si7; #89-0009 for Li13Si4 and #73-2049 for Li22Si5),36 without detectable impurities. The patterns are presented in Fig. 1. Prior to EELS analysis in the TEM, the local crystalline nature of samples was checked by electron diffraction. Due to the rapid beam damage, oriented diffraction patterns were usually extremely difficult to obtain. As an example, the diffraction pattern for Li22Si5 is presented in Fig. 2 along with a typical TEM image.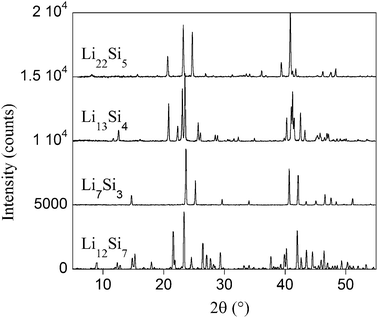 | ||
| Fig. 1 X-Ray diffraction patterns recorded in sealed capillaries for all alloys corresponding to PDF files #41-1308 for Li12Si7; #89-0005 for Li7Si3; #89-0009 for Li13Si4 and #73-2049 for Li22Si5. | ||
![TEM image of a typical Li22Si5 crystal with the corresponding diffraction pattern ([101] zone axis). The white circle at the arrow extremity represents the 50 nm probe size used for EELS analyses. Labels 1 to 4 in the diffraction pattern correspond to (020), (1̄11), (111̄) and (131̄) indexations, respectively.](/image/article/2010/CP/b915245h/b915245h-f2.gif) | ||
Fig. 2 TEM image of a typical Li22Si5 crystal with the corresponding diffraction pattern ([101] zone axis). The white circle at the arrow extremity represents the 50 nm probe size used for EELS analyses. Labels 1 to 4 in the diffraction pattern correspond to (020), (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 11), (11 11), (11![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) and (13 ) and (13![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) indexations, respectively. ) indexations, respectively. | ||
Experimental VEELS spectra are presented in Fig. 3a for the alloys, as well as for Si and Li. The Li spectrum was obtained from ref. 37. All spectra were normalized using the energy loss function (ELF) sum rule:26
 | (1) |
 | ||
| Fig. 3 Experimental (a) and calculated (b) plasmon spectra for Li (line with black diamonds), Li22Si5 (thick line), Li13Si4 (line with open circles), Li7Si3 (dashed line), Li12Si7 (thin line) and Si (line with squares). Inset: fit (line) of the Li7Si3 experimental spectrum (dots) using the Drude model (see text). | ||
Successive VEELS spectra recorded on the same area show a continuous upward shift of the plasmon peak energy, the shift being consistent with a rapid selective elimination of lithium in LixSi alloys under the electron beam. This demonstrates this imperative necessity to use VEELS rather than core loss EELS to limit the influence of beam damage.
According to Drude’s theory, in EELS experiments, collective excitation of electrons in a material can produce a very intense peak called the plasmon peak. To a first approximation, the position of this peak is linked to the number of electrons per unit volume and its full width at half maximum (FWHM) to the degree of freedom of these electrons.26 In the case of LixSi alloys, valence electrons are involved in the creation of such a peak. Other peaks can also be observed, essentially on the low energy side of the main plasmon peak (around 5 eV for example). This intensity is due to interband transitions, which are not included in Drude’s simple theory. The inset in Fig. 3, however, shows that Drude’s model is well suited to the description of the plasmon region over a very large energy range (5–25 eV) in the alloys. Along with other parameters, this fit provides the resonance energy for plasma oscillation, Ep, also called the volume plasmon energy. In order to limit the influence of low energy peaks, plasmon energies were in fact fitted using the Drude model26 over the top 30% of the plasmon peak intensity. The results are given in Table 1. The fitting procedure is fast, robust and precise, leading to an error less than 0.05 eV for each individual spectrum. In each sample, the statistical treatment of the results (using conventional Student statistics) for multiple analysis points leads to an accuracy better than 0.1 eV in all cases.
Multiple points were analyzed for t/λ ranging from 0.4 to 2.5 (t is the thickness of the analyzed area and λ, the mean free path for valence-electron excitation). For very thin samples, surface plasmons can be created. By modifying the low energy side shape of the volume plasmon peak, Ep could become slightly dependant on the thickness of the sample. Such an effect was not observed in our measurements.
Drude’s theory provides a way for calculating the expected volume plasmon energy:26
 | (2) |
In the evaluation of n, 1 electron for each lithium atom and 4 electrons for each silicon atom were considered. Both calculated values (n and Ep) are presented in Table 1. The calculated values for Ep reproduce the experimental trend well.
This Drude calculation, however, represents only a crude approximation and does not provide information on the normalized intensity or the overall shape of the spectra. In order to be certain of our reference volume plasmon peak positions, first-principles Ep energies using WIEN2k are also presented in Table 1. These values were obtained by fitting the calculated plasmon peaks (Fig. 3b) with a Drude model in the same way as the experimental spectra, showing an even better fit with experimental Ep values, with a maximum 0.3 eV discrepancy. In order to obtain such an extremely good agreement, both in absolute intensity and plasmon peak positions, the calculated full width at half maximum (FWHM) must be adjusted to that of the experiment. For alloys, FWHMs were chosen between 4.7 and 5.8 eV. The broadening included in interband transitions (KRAM program) was found to be in fact close to 0.8 eV in most compounds. In the case of Li, a 0.8 eV broadening was introduced for intraband transitions, since the main contribution to the intensity originates from intraband transitions. These broadenings combine both the effects of the experimental energy resolution (around 0.7 eV) and the effects of q dependency of the dielectric function. The remaining discrepancies may be due to other approximations made in calculations: excitonic or local field effects are not included. Anisotropy and surface effects are also neglected.26
The compositions of reference alloys were also checked using the standard method based on Li K and Si L edges. A typical spectrum with the fitted background used to extract edge counts is presented in Fig. 4. Backgrounds were impossible to fit with some confidence using the usual E−r function, as already mentioned by Hofer for Si L2,3 edges.38 The fits are extremely difficult due to the presence of the plasmon peaks (first, second…), whose intensities depend on the thickness of each sample. A large number of parameters must then be considered and are extremely dependent on the quality of the spectra. In our case, the best results were obtained by fitting multiple Lorentzian functions approximately centered on the successive plasmon peaks. The ratio of intensities introduced were given by Poisson statistics.26
 | ||
| Fig. 4 Li and Si edges extraction from a Li7Si3 raw spectrum (line with dots). Fitted backgrounds (dashed lines) and resulting edges (thick lines). | ||
Since hydrogenic cross sections produce better results for light elements,38 they were chosen for the analysis of spectra in DigitalMicrograph.39 The resulting compositions are given in Table 1. The estimated accuracy is around 10% based on the combined imprecision of the theoretical cross sections and the background fitting.
Even if, in theory, core loss EELS determination of composition is a very competitive technique, experience shows that for real silicon electrodes, such experiments were unsuccessful. The combination of thickness requirements (small enough) and acquisition time constraints prevented the obtainment of reliable results.
It is thus essential to demonstrate that composition determination based instead on the plasmon technique can be applied on real electrodes and can give useful information on the electrochemical process. This is the aim of the next section.
4. Application to the first discharge of a crystalline silicon electrode
Li and Dahn studied the first discharge of a crystalline silicon electrode using mainly XRD and electrochemical data.9 Their main conclusions are: (i) for x < 3.5, a two-phase domain between crystalline Si and an amorphous Li3.5±0.2Si phase exists; (ii) for x > 3.5, a crystalline Li15Si4 (x = 3.75) is gradually formed. For Limthongkul et al.,7 the composition of the amorphous phase is given as x = 2.2 (rather than 3.5). For the first time at a local scale, the study of plasmon energies during the first discharge should be able to resolve this discrepancy.In a two-phase domain, two phases with constant properties coexist, the proportions of which vary along the voltage plateau. The amount of the second phase (the lithiated phase in our case) increases at the expense of the first (silicon).
In order to put this electrochemical process to the test, various compositions along the first discharge (Fig. 5) were analyzed. Compositions are calculated assuming that a full discharge leads to a Li15Si4 compound (3579 mAh g−1 specific capacity). Their plasmon energies are presented in Table 2 and the corresponding characteristic spectra are presented in Fig. 6.
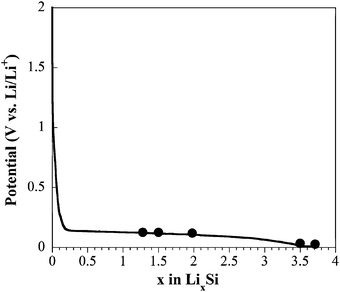 | ||
| Fig. 5 Typical first discharge curve with spots indicating samples investigated by plasmon energy analysis. Galvanostatic mode at C/100 rate with LiPF6 in EC/DC as electrolyte. | ||
| State of discharge | Ep/eV |
|---|---|
| x = 1.3 | 13.25 (0.04) |
| x = 1.5 | 13.26 (0.04) |
| x = 2.0 | 13.3 (0.1) |
| End of discharge | 12.67 (0.08) |
| End of discharge then E = 10 mV | 12.36 (0.05) |
 | ||
| Fig. 6 Ex situ experimental spectra for a Si electrode during first discharge. x = 1.5 (dashed line), end of discharge (line with dots), end of discharge with a constant potential at 10 mV (thin line). Spectrum presenting a contribution of un-reacted silicon (line with white disks) compared to a simulation using effective medium theory (thick line). | ||
For compositions with x < 3.0, a single 13.25 (0.05) eV plasmon energy is consistently obtained (Table 2). This value corresponds to dozens of spectra obtained on different crystals at a very local scale (50 nm probe). For samples clearly in the two-phase domain, this is at first surprising since two plasmon peaks are expected: one for silicon and one for the lithiated phase. These findings can in fact be quite well understood if one remembers that lithium insertion proceeds by the surface of the micron-sized silicon particles. Given that the EELS technique typically probes samples with thicknesses in the order of 100 to 200 nm (for the VEELS region), solely the lithiated phase is expected to be observed. Since a stable plasmon energy is measured for the lithiated phase, these results are in fact in perfect agreement with a two-phase process during the first discharge.
The composition of this alloy can be obtained from the previous reference alloys study. A 13.25 eV energy corresponds to x = 2.9 ± 0.3. The rather large uncertainty in this value is not due to the determination of the plasmon energy (0.05 eV error). The variation of the plasmon energy in reference alloys is in fact not perfectly linear (Table 1), and only a mean value can be estimated. The Li2.9Si composition falls more or less between the compositions found by Li and Dahn9 (x = 3.5), and Limthongkul et al. (x = 2.2).7
The calculated plasmon energy obtained for the simulated amorphous alloy is 13.2 eV. This value is extremely close to that calculated for the same composition (Li13Si4) crystalline phase (13.1 eV, Table 1). The state (amorphous or crystalline) of the alloy thus has a minor effect on the plasmon energy and the method remains quite general independently of this parameter. Fine structures at the lithium K edge are, however, noticeably more pronounced in the crystalline case than in the amorphous one. With an energy resolution better than 0.5 eV (not available with our microscope), a local study of the electrode crystallinity could thus be envisaged.
Other plasmon energies were sometimes observed on some particular areas in the same samples. An example is shown in Fig. 6 (line with empty circles). They are most often associated with a higher energy peak close to the silicon plasmon energy. In order to interpret these results, one can consider that the interface between crystalline Si and Li2.9Si is not sharp. The beam can then probe an area where some nucleation of the Li2.9Si phase occurs in the initial Si crystal. In this tens-of-nanometres area (the typical probe size), the plasmon energy should then be given by the effective medium theory.40 This theory was already applied to explain experimental plasmon energies following the formation of Al nano-particles in an AlF3 matrix.41 The effective dielectric function is given by:
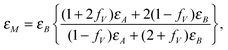 | (3) |
We note that core loss determination of local compositions in this case would be extremely inaccurate. A mixture of Si and Li2.9Si phases could not be differentiated from a single LixSi phase (with thus x < 2.9). Li K edge and Si L2,3 edges are indeed essentially independent on the considered phase. This, along with the extreme beam sensitivity of the alloys, suggests that compositions based on core loss measurements should be revisited.20
At the end of the discharge, a crystalline Li15Si4 phase is expected.9Ep calculated for this phase (x = 3.75) using the WIEN2k program is 13.0 eV. This calculated value is consistent with those presented in Table 1 for x = 3.3 (Ep = 13.1 eV) and x = 4.4 (Ep = 12.9 eV). The experimental value is thus expected to be close to 12.8 eV (between 12.83 eV and 12.74 eV). At the end of the discharge, the measured experimental value is in fact 12.67 (0.08) eV. This value, slightly lower than expected, is still in good agreement with the formation of a Li15Si4 phase at the end of the discharge.
Another electrode was first discharged like the previous one, but was then maintained at 10 mV until the current dropped below 7 mA g−1 (corresponding to a C/500 rate). Ep values between 12.2 and 12.4 eV were found (see Table 2 and the spectrum in Fig. 6). Even if these values are close to the value found for Li15Si4, they are significantly lower. This result suggests that even more lithium can be inserted in Si and that Li15Si4 is not the extreme limit composition at the end of the discharge. Li15Si4 could thus accommodate slightly more lithium than the nominal composition, like other LixSi alloys do.42 Recent findings by Key et al. suggest that Li15Si4 is not a line phase.43 Following an under potential deposition process, some nucleation of Li in the Li15Si4 phase could also exist. The slight downward shift observed in the plasmon energy could then be explained using the effective medium theory. However, we rule out electrochemical plating of grains (with a 10 nm Li layer for example), since such a large layer would lead to a peak clearly appearing around 7.5 eV (plasmon peak for Li), which was not observed. These results should motivate more experiments on the subject.
5. Conclusion
The VEELS method in a TEM has been utilized to construct a database for LixSi plasmon energies. As a result, the composition of any such alloy may be determined with a spatial resolution close to 10 nm. The VEELS method could certainly be developed further to reach even better spatial resolutions. Experimental results were confirmed by theoretical calculations based on density functional theory. The numerous advantages of this method over conventional techniques such as diffraction and core-loss EELS were illustrated by studying a standard crystalline silicon electrode, the composition of which was obtained during the first discharge.The advantages of the plasmon-based method over the core loss analysis are numerous:
(i) acquisition times for VEELS spectra are at least a factor 100 faster than those of core losses. This is essential in the case of highly beam-sensitive materials such as LixSi alloys,
(ii) processing of the spectra is straightforward, independent of the expertise of the analyst,
(iii) in composite electrodes, when alloys are covered by polymers or carbon, the extraction of edge counts in core loss spectra becomes extremely difficult. Such is not the case of the plasmon region, where plasmon peaks always stand out from the sometimes complex shape of the VEELS spectrum,
(iv) without any difficulty using VEELS spectra, multiple points were analyzed for t/λ ranging from 0.4 to 2.5. In the context of composite electrodes, where it is hard to find proper analysis areas (oxidation, contamination or electrolyte decomposition surface layers), this is also a very useful benefit of the VEELS method over the core loss method.
Even if further experiments are necessary to realise the full extent of the utility of the effective medium theory used in this paper, it has also been shown that the study of the nucleation of new phases along the electrochemical process is possible. Comparison could be made with recent results published on lithiation of amorphous silicon.34
The usefulness of the method should be especially obvious in the subsequent charge and discharge cycles. For instance, the composition of the alloy obtained during the first charge is not precisely known (z≈ 2 in Li and Dahn’s paper9). The method could also be generalized to other alloys with Sn, Sb, Ge or Al.10 All these elements indeed present a well-defined plasmon peak,44 which should allow a fast determination of local compositions.
In a recent review by Tarascon’s group and co-workers,10 it was concluded that the future of Li-based alloys for negative electrodes may well depend “on advances in analytical instrumentation as it is becoming critical to study nano-scale effects”. We are confident that the examination of plasmon peak positions in a TEM will be part of these new developments, thus improving our understanding of the complex alloying process.
References
- J. M. Tarascon and M. Armand, Nature, 2001, 414, 359–367 CrossRef CAS
.
- M. M. Thackeray, S.-H. Kang, C. S. Johnson, J. T. Vaughey, R. Benedek and S. A. Hackney, J. Mater. Chem., 2007, 17, 3112–3125 RSC
.
- F. Gillot, M.-P. Bichat, F. Favier, M. Morcrette, M.-L. Doublet and L. Monconduit, Electrochim. Acta, 2004, 49, 2325–2332 CrossRef CAS
.
- P. Poizot, S. Laruelle, S. Grugeon, L. Dupont and J. M. Tarascon, Nature, 2000, 407, 496–499 CrossRef CAS
.
- F. Robert, P. E. Lippens, J. Olivier-Fourcade, J.-C. Jumas and M. Morcrette, J. Power Sources, 2005, 146, 492–495 CrossRef CAS
.
- H. Li, X. Huang, L. Chen, Z. Wu and Y. Liang, Electrochem. Solid-State Lett., 1999, 2, 547–549 CrossRef CAS
.
- P. Limthongkul, Y.-I. Jang, N. J. Dudney and Y.-M. Chiang, J. Power Sources, 2003, 119–121, 604–609 CrossRef CAS
.
- T. D. Hatchard and J. R. Dahn, J. Electrochem. Soc., 2004, 151, A838–A842 CrossRef CAS
.
- J. Li and J. R. Dahn, J. Electrochem. Soc., 2007, 154, A156–A161 CrossRef CAS
.
- D. Larcher, S. Beattie, M. Morcrette, K. Edstrom, J.-C. Jumas and J.-M. Tarascon, J. Mater. Chem., 2007, 17, 3759–3772 RSC
.
- M. Alias, O. Crosnier, I. Sandu, G. Jestin, A. Papadimopoulos, F. Le Cras, D. M. Schleich and T. Brousse, J. Power Sources, 2007, 174, 900–904 CrossRef CAS
.
- Y. Wang and J. Dahn, Electrochem. Solid-State Lett., 2006, 9, A340–A343 CrossRef CAS
.
- L. Y. Beaulieu, K. C. Hewitt, R. L. Turner, A. Bonakdarpour, A. A. Abdo, L. Christensen, K. W. Eberman, L. J. Krause and J. R. Dahn, J. Electrochem. Soc., 2003, 150, A149–A156 CrossRef CAS
.
- C. K. Chan, H. Peng, G. Liu, K. McIlwrath, X. F. Zhang, R. A. Huggins and Y. Cui, Nat. Nanotechnol., 2008, 3, 31 CrossRef CAS
.
- T. Takamura, S. Ohara, M. Uehara, J. Suzuki and K. Sekine, J. Power Sources, 2004, 129, 96–100 CrossRef CAS
.
- B. Lestriez, S. Desaever, J. Danet, P. Moreau, D. Plee and D. Guyomard, Electrochem. Solid-State Lett., 2009, 12, A76–A80 CrossRef CAS
.
- M. N. Obrovac and L. J. Krause, J. Electrochem. Soc., 2007, 154, A103–A108 CrossRef CAS
.
- B. Kang and G. Ceder, Nature, 2009, 458, 190–193 CrossRef CAS
.
- C. Delmas, M. Maccario, L. Croguennec, F. Le Cras and F. Weill, Nat. Mater., 2008, 7, 665–671 CrossRef CAS
.
- G. W. Zhou, H. Li, H. P. Sun, D. P. Yu, Y. Q. Wang, X. J. Huang, L. Q. Chen and Z. Zhang, Appl. Phys. Lett., 1999, 75, 2447–2449 CrossRef CAS
.
- V. Mauchamp, P. Moreau, L. Monconduit, M.-L. Doublet, F. Boucher and G. Ouvrard, J. Phys. Chem. C, 2007, 111, 3996–4002 CrossRef CAS
.
- L. Laffont, C. Delacourt, P. Gibot, M. Y. Wu, P. Kooyman, C. Masquelier and J. M. Tarascon, Chem. Mater., 2006, 18, 5520–5529 CrossRef CAS
.
- I. Sandu, P. Moreau, D. Guyomard, T. Brousse and L. Roue, Solid State Ionics, 2007, 178, 1297–1303 CrossRef CAS
.
- V. J. Keast, J. Electron Spectrosc. Relat. Phenom., 2005, 143, 97 CrossRef CAS
.
- D. B. Williams and J. W. Edington, J. Microsc., 1976, 108, 113–145 CAS
.
- R. F. Egerton, Electron Energy-Loss Spectroscopy in the Electron Microscope, Plenum Press, New York, 1996 Search PubMed
.
- A. Gloter, A. Douiri, M. Tencé and C. Colliex, Ultramicroscopy, 2003, 96, 385–400 CrossRef CAS
.
- P. Fallon and C. A. Walsh, PEELS programme, University of Cambridge, England, 1996 Search PubMed
.
- P. Blaha, K. Schwarz, G. K. H. Madsen, D. Kvaniscka and J. Luitz, WIEN2k, An Augmented Plane Wave + Local Orbitals Program for Calculating Crystal Properties, ed. K. Schwarz, Techn. Universität Wien, Austria, 2001 Search PubMed
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS
.
- NIST/FIZ, Inorganic Crystal Structure Database, NIST/FIZ, Version 1.4.5 edn, 2008.
- C. Ambrosch-Draxl, J. A. Majewski, P. Vogl and G. Leising, Phys. Rev. B: Condens. Matter, 1995, 51, 9668–9676 CrossRef
.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS
.
- V. L. Chevrier and J. R. Dahn, J. Electrochem. Soc., 2009, 156, A454–A458 CrossRef CAS
.
- C. van der Marel, G. J. B. Vinke and W. van der Lugt, Solid State Commun., 1985, 54, 917–919 CrossRef CAS
.
- PDFMaintEx library., Version: 9.0.133. edn, July 2008.
- V. Mauchamp, P. Moreau, G. Ouvrard and F. Boucher, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 045117–045119 CrossRef
.
- F. Hofer, Microsc., Microanal., Microstruct., 1991, 2, 215–230 CrossRef CAS
.
- DigitaMicrograph, DigitaMicrograph, Gatan Inc., Pleasanton, USA, 3.9.3 edn, 2003.
- J. C. Maxwell-Garnett, Philos. Trans. R. Soc. London, Ser. A, 1904, 203, 385 CrossRef
.
- C. A. Walsh, Philos. Mag., 1989, 59, 227 Search PubMed
.
- C. J. Wen and R. A. Huggins, J. Solid State Chem., 1981, 37, 271–278 CrossRef CAS
.
- B. Key, R. Bhattacharyya, M. Morcrette, V. Seznéc, J.-M. Tarascon and C. P. Grey, J. Am. Chem. Soc., 2009, 131, 9239 CrossRef CAS
.
- C. C. Ahn, Transmission Electron Energy Loss Spectrometry in Materials Science and the EELS atlas, Wiley-VCH, 2004 Search PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available: Core losses for LixSi reference alloys, and comparison between experimental and theoretical spectra. See DOI: 10.1039/b915245h |
| This journal is © the Owner Societies 2010 |
