VaporFit: an open-source software for accurate atmospheric correction of FTIR spectra

Abstract

This paper introduces VaporFit, an open-source software for automated atmospheric interference correction in Fourier-transform infrared (FTIR) spectroscopy, based on a refined correction algorithm. It significantly improves the accuracy and reproducibility of chemical and biological FTIR analysis by effectively removing variable contributions from water vapor and carbon dioxide that often obscure spectral features. Unlike traditional methods relying on subtraction of a single reference spectrum, which struggle with atmospheric variability, VaporFit employs a multispectral least-squares approach to automatically optimize subtraction coefficients based on multiple atmospheric measurements recorded throughout the experiment. The software provides a user-friendly graphical interface (GUI) and built-in tools, including objective smoothness metrics and a principal component analysis (PCA) module, to facilitate parameter selection and intuitively evaluate correction quality. Furthermore, we offer practical recommendations for data acquisition strategies tailored for effective atmospheric correction. VaporFit, the user guide, and sample data sets are freely available at https://zenodo.org/records/15411176 and https://github.com/piobruzdpg/VaporFit/releases/tag/v1.0.

---

1 Introduction

FTIR spectroscopy is a simple yet highly informative method for obtaining structural information about compounds, including biomacromolecules. It also enables real-time observation of structural changes occurring during chemical reactions or phase transitions. Intermolecular interactions in solutions are a particularly valuable subject for investigation using FTIR spectroscopy. However, their study necessitates high-quality spectra characterized by high spectral resolution and minimal noise. This is crucial because the difference signals reflecting these subtle interactions are typically of very low intensity, making them susceptible to masking by noise. While essential for such demanding applications, obtaining high-quality, noise-free spectra is a general challenge in FTIR, largely due to spectral features from the atmosphere inside the spectrometer or sample chamber. Residual atmospheric noise can obscure spectral features, affecting data interpretation. Thus, achieving precise noise removal is vital for improving accuracy, sensitivity, and reproducibility in FTIR spectroscopy.^1–4

This interference mainly stems from water vapor (H₂O, D₂O, or HDO when heavy water is used) and carbon dioxide (CO₂), as well as, in some cases, other volatile compounds in the samples used in the laboratory. Each component absorbs light independently, and their proportions depend on factors beyond the experimenters control, such as ambient humidity, the number of people in the room, frequency of opening the sample compartment, purity of purging gases, solvent content, and even the stability of the infrared source. To minimize it, instruments are typically purged with dry gas (nitrogen or dried air). However, this method may be imperfect since purging gas may contain impurities. Pressure fluctuations–caused by frequent chamber openings or gas regulator malfunctions–can also introduce inconsistencies in internal atmosphere properties.

In this article, we introduce VaporFit, a free, open-source software based on a new version of the atmosphere correction algorithm. The new, streamlined version of the algorithm has been stripped of elements that proved unnecessary (e.g., considering the baseline at the stage of optimizing correction parameters). The philosophy of the Python script has been changed, and the entire core of the algorithm has been enclosed in a single class, which significantly facilitates its potential use in users' own projects and possible modification. We also elucidate why the algorithm works at all and what factors influence the limitations of its applicability. The most important functionality from the perspective of an average user is the graphical user interface (GUI), which significantly facilitates correction for people less advanced in programming. The GUI currently includes tools facilitating more rational selection of smoothing parameters and a PCA (Principal Component Analysis) module allowing for visual assessment of correction quality.

2 Materials and methods

Three exemplary spectral series are available in the VaporFit repositories: (1) a series of aqueous solutions of betaine (N,N,N-trimethylglycine) in water in the range from 4.0 to 10.0 mol kg⁻¹, (2) a series of D₂O solutions in H₂O in the range of mole fractions from 0.0 to 1.0, (3) a series in which a 20 μL drop of a urea solution with an initial concentration of 1.0 mol kg⁻¹ was allowed to dry freely for 20 minutes on an ATR crystal.

2.1 Chemicals and solutions

Sources of reagents: (1) betaine, anhydrous, 98% (Alfa Aesar); (2) D₂O, NMR grade (VWR Chemicals); (3) urea, 99.8% (VWR Chemicals); (4) hen egg white lysozyme, crystalline (Sigma-Aldrich). All reagents were used as is. All solutions were prepared by weight using an XS205 Dual-Range analytical balance from Mettler Toledo (Switzerland). Demineralized water, used for preparing the solutions, showed conductivity of 0.06 μS cm⁻¹. The water source was a demineralization station from HydroLab (Poland).

2.2 FTIR spectrometer

All spectra used to illustrate the operation of the algorithm and the VaporFit program were recorded using a Bruker Invenio-R FTIR spectrometer (Germany), equipped with a single-reflection diamond ATR accessory or a thermostatted transmission cuvette with a 56 μm spacer and CaF₂ windows. The system was purged with dry nitrogen generated by a NiGen LCMS 40-1 generator from Claind (Italy). Measurement parameters (number of scans and resolution) were varied to demonstrate the effectiveness of the software. These parameters are provided under each figure, and the information is also available in the project repositories.

2.3 Algorithm description

The atmospheric spectrum subtraction algorithm (see Fig. 1), initially proposed in our previous paper⁵ and refined in this study, is based on an iterative least-squares minimization. The residual function minimized in this algorithm, r_ν, is defined as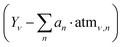:where: Y_ν – measured sample spectrum before correction, – the spectrum after applying the current atmospheric correction coefficients, atm_ν,n – n-th recorded atmospheric spectrum, a_n – subtraction coefficient for the n-th vapor spectrum, optimized using the least-squares method, Ȳ_ν – estimated spectrum after ideal atmospheric correction, obtained by smoothing the difference . This smoothed spectrum serves as the target for the optimization in each iteration.

Fig. 1 Scheme of the iterative correction of spectra affected by atmospheric contribution. All symbols are consistent with eqn (1).

Unlike classical subtraction, which relies on a single reference spectrum, this algorithm dynamically combines multiple vapor spectra with optimized coefficients a_n. The core idea is an iterative process: starting with initial coefficients (set to 0.1 in the current version of the VaporFit code), the algorithm calculates a currently corrected spectrum. This spectrum is then smoothed to provide an estimation (Ȳ_ν) of what the ideal, atmospheric-free spectrum should look like. The difference between the currently corrected spectrum and this smoothed estimation forms the residual (r_ν). The least-squares method then adjusts the coefficients a_n to minimize this residual, effectively driving the currently corrected spectrum closer to its smoothed version, thereby removing sharp atmospheric features while preserving the broad sample bands (see an example in Fig. 2). The corrected spectrum is then the result of applying the final, optimized coefficients a_n. The corrected spectrum Ȳ_ν is approximated using Savitzky–Golay (SG) smoothing.⁶ The SG method requires two key parameters:

Fig. 2 The effect of correction using the VaporFit software on a series of ATR-FTIR spectra of betaine aqueous solutions (with varying betaine concentrations between 4 and 10 mol kg⁻¹) is presented. Subtraction coefficients for two atmospheric spectra (middle panel; one measured at the beginning of the series—blue, and one at the end—orange) were optimized using the following Savitzky–Golay parameters: polynomial order 3, window size 11. This sample dataset is available as part of the VaporFit distribution. Resolution 2 cm⁻¹, 128 scans per spectrum.

• Polynomial order – the degree of the polynomial used for local approximation,

• Window size – the number of adjacent points used for fitting.

Proper selection of these parameters may be crucial for the algorithms effectiveness (see Fig. 3).

Fig. 3 Influence of Savitzky–Golay smoothing parameters on spectral smoothing in the OH/COO⁻ band region of the 10th spectrum of the betaine test set (the same as in Fig. 2).

3 Discussion

3.1 Key changes and updates

This manuscript builds upon our previous work⁵ by introducing several key advancements that enhance both the theoretical understanding and the practical application of the atmospheric correction algorithm:

• Streamlining of the algorithm code by removing unnecessary elements and functionalities.

• Introduction of a GUI and additional tools for optimizing SG parameters and evaluating result quality.

• Code improvement for better understanding of results and enabling its use in custom projects (see Section 3.1.1).

• Precise identification of the rationale behind the algorithm's effectiveness and its limitations (see Sections 3.2.3 and 3.4.1).

• Demonstration of its effectiveness also in the case of correction of other types of FTIR spectral interference, such as the CO₂ band (see Section 3.2.3).

• Comparison to other popular methods for this type of correction (see Section 3.3).

• Based on our current experience, we propose unified recommendations for conducting measurements and using the algorithm (see section 3.4).

3.1.1 Code improvement, graphical user interface, and new functions. The core algorithm has been optimized by eliminating unnecessary computation steps and simplifying parameter dependencies. These refinements not only reduce the computational load but also facilitate more intuitive interpretation of the correction outputs. One of the key modifications in the algorithm is the removal of baseline correction during atmospheric spectrum fitting. The original algorithm included a quadratic baseline term alongside atmospheric spectra.⁵ However, including the baseline did not provide any benefits, and its parameters were always close to zero, regardless of the quality of the corrected spectral series. Our analysis showed that baseline fluctuations were inherently removed with atmospheric spectra, making the explicit baseline function redundant. Removing entire sections related to baseline fitting facilitated understanding of the code and interpretation of the generated results, especially the resulting correction parameters.

To improve accessibility, we have translated the original command-line script into an open-source desktop application featuring a user-friendly graphical interface. The new software, VaporFit, includes support for batch processing, visual inspection of input/output spectra, and export of correction parameters, significantly lowering the barrier to adoption by non-expert users.

The previous version of the algorithm required the user to specify SG parameters, but the quality of correction using them could only be visually assessed by the user after the calculations were completed. VaporFit introduces several tools to facilitate the selection of these parameters. The program now performs parallel corrections in the background for several defined window sizes around the one selected in the GUI and allows visualizing quantitative indicators. Their visualization allows for a more rational assessment of which combination of smoothing parameters yields the smoothest series of spectra. For series typically measured in our laboratory, default parameters (polynomial order 3, window size 11) are usually optimal. However, it should be noted that these parameters may differ for spectra with significantly larger or smaller band full width at half maximum (FWHM) or different spectral resolution compared to those presented in this work.

To enhance the selection process for Savitzky–Golay smoothing parameters, VaporFit provides objective smoothness metrics. These include:

• Spectral Smoothness Index (SSI, eqn (2), where y_i are the spectral values at points i, and N is the number of data points):

• Second derivative variance (SDV).

• Standard deviation of residual signal (SD, where residual is the result of the subtraction between the corrected spectrum and its smoothed version).

In general, lower values for these metrics indicate smoother signals, thus aiding in optimal parameter choice. However, interpretation depends on specific signal characteristics, requiring users to develop their own assessment strategies.

Principal component analysis (PCA) is another tool that VaporFit uses to visually check how well atmospheric correction works across a whole series of spectra. We recommend selecting SG parameters based on a visual comparison of the pre- and post-correction principal components (PCs) of spectral series. If atmospheric interference is present, it appears as contamination in principal components before correction (see Fig. 4). After successful correction, these bands should ideally disappear. In addition to principal component shapes, the PCA module provides explained variance values, estimating the minimum number of components required before and after correction. However, atmospheric spectra rarely appear as pure components, as their contributions often correlate with sample spectrum changes. Thus, variance trends should be interpreted cautiously, and a reduction in variance does not always indicate complete atmospheric component removal.

Fig. 4 The first two principal components (PCs) of the betaine test set shown in Fig. 2 were obtained both before and after correction. Subtraction coefficients were determined using the following SG parameters: polynomial order 3, window size 11. The contribution of atmospheric spectra is mainly visible between 1800 and 1500 cm⁻¹ before correction and disappears after correction.

Users can also inspect correction coefficients determined for each atmospheric spectrum, aiding experiment monitoring and further analysis of changes in atmospheric composition during experiments (see Fig. 5).

Fig. 5 Optimized subtraction coefficients for two atmospheric spectra, which were used to correct the spectra in Fig. 2. Colors correspond to the middle panel of Fig. 2. The initial atmospheric spectrum was measured at the beginning of the experiment, and the final one was measured at the end. Clearly, the contribution of the initial atmospheric spectrum diminishes over time, while the second one increases. The change is gradual, but that is not always the case.

3.2 Implementation and reuse

To facilitate the integration of our method into other workflows, we provide the full Python implementation of the core fitting procedure in the form of a class, AtmFitParams. This class in its current form encapsulates all steps necessary to subtract atmospheric spectra (e.g., H₂O and CO₂) from an experimental spectrum. The class handles parameter initialization, residual calculation, least-squares fitting, and spectrum correction, and can be easily incorporated into other programs or workflows by instantiating it with the wavenumber axis and the relevant spectral data (measured spectrum/spectra and atmospheric spectra). The AtmFitParams class provides a minimal, functional implementation suitable for integration into other codebases. The full program, VaporFit, facilitates data input and initialization, performs consistency checks, offers visualization capabilities, and includes safeguards against repeated execution and common user errors (a full description of this class is included in the manual available in the VaporFit repositories).

3.2.1 Constructor arguments. The class is initialized with the following arguments:

• Wavenb – 1D array of wavenumbers.

• Spectrum – 1D or 2D array of the measured spectrum or spectra.

• atm_spectra – 2D array of atmospheric reference spectra (e.g., water vapor, CO₂).

• sg_poly, sg_points (optional) – Savitzky–Golay smoothing parameters (polynomial order and window size).

3.2.2 Main methods. The class defines the following public methods:

• fit( ) – performs non-linear least-squares fitting of atmospheric spectra to the measured spectrum and returns the best-fit scaling coefficients.

• atm_subtract( ) – applies the fitted parameters to subtract atmospheric contributions and returns the corrected spectrum.

An internal method residuals (params) is used during the optimization procedure to compute the smoothed residual signal that is minimized in the fitting process. Although it is publicly accessible, it is intended for internal use only and not meant to be called directly by the user.

VaporFit source code or its fragments can be customized for specific research needs. It is available under the GNU GPL v3.0 license, which includes an additional citation requirement. VaporFit in its current version uses the following Python packages: NumPy,⁷ SciPy,⁸ Matplotlib.⁹

3.2.3 Why it works?. The key to the algorithm's success lies in the difference in the spectral characteristics (specifically band widths) between the sample and atmospheric spectra, and how smoothing exploits this difference. The main principle is the significant difference in the width of the bands of the spectrum being corrected and the spectrum (or spectra) being subtracted. Smoothing, and thus appropriately selected SG coefficients, should strongly affect narrow bands, almost clipping their sharp peaks, while having a marginal effect on the shape of broad bands being corrected. If the correction parameters are ideal, i.e., coefficients that effectively subtract narrow noise bands from broad ones have been successfully selected, then the smoothing step has almost no effect on the corrected spectrum and removes only inherent instrumental noise. After ideal correction, the difference (residual, r_ν in eqn (1)) between the cleaned and smoothed (Ȳ_ν) spectrum should yield a difference of almost zero. If the correction were incomplete, the spectrum after correction would still contain residual atmospheric bands, irregularities, dips, or other types of differential bands, different from the natural noise of a given method or instrument. Smoothing the remnants of such narrow bands on the surface of broad bands would result in a wavy surface of the resulting spectrum. This would create a smoothed spectrum, but the difference between the spectrum before and after smoothing would already be different from zero and noticeable.

The requirement for a difference in the smoothability of the corrected and correcting signals has a very important consequence. Such correction would not be possible if the FWHM of the bands of both types of signals or spectra were similar, as both would be similarly affected or not affected at all by the smoothing step. In that case, the difference before and after smoothing (residual) would always be either zero or completely random. On the other hand, even if the spectrum contamination is very large, almost ideal correction is still possible if the FWHM of the bands of both signals are significantly different. An example is the heavily contaminated series of betaine solution spectra in Fig. 2, where the bending OH and carbonyl bands and other skeletal bands of betaine have much larger FWHM than the gaseous water bands, and still the correction is very good.

For these reasons, it is possible to use the algorithm to remove other types of interference. Initially developed for FTIR spectrum correction in the amide I band of proteins, VaporFit has also proven effective for other spectral regions, including the CO₂ asymmetric stretching band (∼2400 cm⁻¹). This capability enables efficient CO₂ interference removal, which can obscure key vibrational bands of CN groups, sulfur-based groups, or, as in Fig. 6, D₂O stretching bands.

Fig. 6 ATR-FTIR spectra of H₂O/D₂O mixtures (x_H2O = 0–1) in the OD stretching region. Subtraction coefficients for three CO₂ spectra (one measured at the beginning of the series–blue, one in the middle–orange, and one at the end–green) were optimized using the following Savitzky–Golay parameters: polynomial order 3, window size 11. This sample dataset is available as part of the VaporFit distribution. Resolution 4 cm⁻¹, 128 scans per spectrum.

3.3 Comparison with other correction methods

If a single spectrum is measured, for example, only for band identification, the problem of atmospheric influence is marginal, as automatic software algorithms (e.g., in OPUS or OMNIC) handle correction quite well. However, atmospheric interference becomes critical when analyzing subtle spectral changes or resolving complex band structures like amide I and I bands in proteins (1700–1600 cm⁻¹). These bands, used to determine protein secondary structure, are particularly sensitive to noise, as their narrow range and typical resolutions of 4–1 cm⁻¹ limit the available data points.

At first glance, manual atmospheric correction may seem simple: recording an empty chamber spectrum and subtracting it from sample spectra using a scaling factor. However, two major challenges arise. First, for large spectral series, manually adjusting the subtraction coefficient is tedious and time-consuming, requiring trial and error. Second, atmospheric conditions fluctuate, altering spectral shape and intensities. As shown in Fig. 7(a), the composition of the atmosphere inside the instrument or sample chamber can change due to sample evaporation. In this case, the sample contained large amounts of D₂O. The atmospheric spectra for temperatures of 40.0 °C and 50.0 °C in this figure contain bands of gaseous heavy and ordinary water, as well as likely semi-heavy water. This type of measurement is common in protein structure studies, so this type of atmospheric variability should be taken into account. In such a case, it would be practically impossible to correctly subtract all contributions using a single atmospheric spectrum.

Fig. 7 Correction of transmission FTIR spectra of hen egg white lysozyme in D₂O (50 mg mL⁻¹) in the temperature range 30–50 °C. (a) Atmospheric spectra recorded at temperatures 30.0 °C, 40.0 °C and 50.0 °C; they clearly show the emerging bands of gaseous D₂O. (b) Spectra of the tested sample in the range of amide I′–II′′ bands before atmospheric background correction. (c) Spectra of the sample after applying atmospheric correction for the corresponding temperatures. Resolution 2 cm⁻¹, 128 scans per spectrum.

It should also be emphasized that the ro-vibrational bands of gaseous phases are very narrow and react strongly to any environmental changes (e.g., temperature, humidity) and clearly distort the spectral image in the regions of approximately 3600 cm⁻¹ and 1600 cm⁻¹, even if the atmosphere itself does not change its chemical composition. This variability can be illustrated by the example of atmospheric spectra from Fig. 2. Both spectra were measured with a time difference of approximately 1 hour. We calculated the differences between both spectra in the ranges of the OH and CO₂ bands, and the results are presented in Fig. 8. Although the instrument was purged with dry nitrogen, and from the user's perspective, the conditions during the measurement did not change, an hour's difference in the measurement of these two atmospheric spectra made direct subtraction of one from the other ineffective. Instead of improving spectral quality, subtraction can introduce sharp differential bands, adding noise rather than eliminating it. Thus, a single atmospheric spectrum is rarely effective unless background, atmospheric, and sample spectra are recorded in quick succession.

Fig. 8 Differences between two atmospheric spectra from the betaine spectra test set. Subtraction coefficients were chosen such that the average absorbance value of all points was close to zero. (a) Difference in the amide I band range (as in Fig. 2), (b) difference in the CO₂ band range. Although both spectra were measured approximately 1 hour apart, complete subtraction of the spectra is not possible.

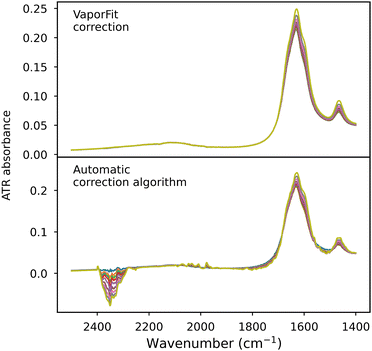
VaporFit also performs better compared to automatic atmospheric correction methods available in spectrometer software, which are typically based on a database of atmospheric spectra provided for a range of different measurement parameters for a given series of instruments. They work well, but only if the time difference between the background spectrum and the actual spectrum is small (i.e., when the amount of water vapor has not changed significantly) or when the conditions inside and outside the instrument remain practically unchanged, which is rather rare. These types of methods are excellent for routine, fast, and undemanding measurements, but they can introduce artifacts that become problematic for very precise measurements, for example, in studies of interactions in solutions or determining protein secondary structure. This is clearly visible in Fig. 9, although it should be noted that the series was measured approximately 30 minutes after the dry nitrogen source was initialized, so this effect is more pronounced than in most situations. However, the distorted CO₂ bands, distortions around 2000 cm⁻¹, and a number of small bands in the water vapor range overlapping with the solution bands are clearly impossible to correct effectively with standard methods. Our team's experience shows that artifacts introduced in spectra that require high quality, even if barely visible, can affect subsequent analysis steps. An example of this is protein spectra in the amide I band range, whose deconvolution depends on the effectiveness of the correction. Small irregularities and artefacts present on the band surface can determine the position, or even the existence, of small component bands. For this reason, automatic correction is never used in our laboratory for this type of measurement.

Fig. 9 Comparison of the quality of correction results for a series of urea solution spectra (20 μL, 1.0 mol kg⁻¹) drying freely for 20 minutes on an ATR crystal (concentration, apart from the initial one, is not strictly defined, and the experiment simulates experiments where reaction or process kinetics are studied). The upper series shows spectra corrected in the VaporFit program using two atmospheric spectra, measured before and after the actual series; the lower series shows spectra corrected using the automatic correction method available in the OPUS program. The clear artifacts in the lower series are impossible to remove by any correction method. This sample dataset is available as part of the VaporFit distribution. Resolution 4 cm⁻¹, 64 scans per spectrum.

A greater problem arises when measuring series for which temperature change is crucial. In such cases, the variability of atmospheric spectra and their composition absolutely cannot be ignored. Subtracting a single atmospheric spectrum throughout the entire series makes no sense, and the only solution when using the manual single spectrum subtraction method is most often to measure the background spectrum before and an atmospheric spectrum after each sample spectrum. It should be emphasized that even when purging the instrument with dry nitrogen or another gas, the stability of the atmosphere during continuous heating of the cuvette or the measurement accessory stage is very poor, and the spectrum measured even in such a configuration will have clear atmospheric bands, similar to Fig. 8. The procedure proposed in this publication, i.e., measuring one starting background spectrum and several (min. two) atmospheric spectra covering the entire temperature variability (see Section 3.4 and Fig. 10), provides much better results at a much lower cost of work and time. An example is the series of transmission spectra of lysozyme solutions in D₂O in the temperature range, presented in Fig. 7, for which it was possible to measure and correct the protein spectra in the range of the amide I′, amide II, and amide II′′ bands. The background spectrum for the series was measured once at 30.0 °C. Each of the atmospheric spectra simultaneously compensated for any background fluctuations related to temperature changes and atmosphere composition.

Fig. 10 Proposed scheme for recording a series of FTIR spectra. Blue (BKG) represents the background spectrum, green (S) denotes the proper spectra, and red (A) represents the atmospheric spectra. Measure the first atmospheric spectrum at the beginning (before the proper spectra or after the 1st to 3rd spectrum) and also as the last spectrum of the series. Additional atmospheric spectra can be measured multiple times during the session.

In the context of striving for the most accurate atmospheric correction, it is also worth mentioning the concept of measurements with increased spectral resolution (oversampling), as suggested by Goormaghtigh et al.⁴ This approach, which involves recording spectra with a resolution higher than nominally required for broad sample bands, aims to better characterize narrow, sharp gaseous bands, which facilitates their differentiation from the sample signal. Although this strategy is valuable, it is associated with experimental challenges, such as extended measurement time and potentially greater sensitivity to dynamic changes in atmosphere composition during acquisition – a problem that we illustrated with the example of the difficulty in compensating for two atmospheric spectra measured at a time interval (Fig. 8). We believe that the multispectral algorithm implemented in VaporFit, through its ability to adaptively select combinations of reference atmospheric spectra, could be a valuable complement to data collected by the oversampling method. This would allow for more effective handling of atmosphere variability even with high-resolution measurements, while minimizing the difficulties associated with manual correction of single, very “sharp” reference spectra.

3.4 Best practices and suggestions

The following recommendations are based on our laboratory experience and may not be universally applicable. Each VaporFit user may develop their own data acquisition and correction strategies. Also, we may have described the problems with SG parameter selection too cautiously; in real-world applications, the choice is not as critical as it might seem. In most cases, their default values in the VaporFit main panel are acceptable, and the margin of error is quite wide.

• We advise recording the background spectrum once at the beginning of the experiment for serial measurements (as in Fig. 10). Although seemingly counterintuitive, this approach often increases consistency within a spectral series. However, because atmospheric absorption can make the raw recorded spectra look noisy, obscuring important bands and hindering real-time quality assessment, this approach can make measurements stressful. To mitigate this, humidity reduction techniques should be used.

• We recommend recording at least two atmospheric spectra—one near the beginning and one at the end of an experiment involving spectra series (see Fig. 11 for a comparison of the results of correction with a single atmospheric spectrum and with two different ones). In most cases, their linear combination effectively corrects all spectra measured between them. It is, of course, possible to correct with just one atmospheric spectrum, although a single spectrum may not exhibit variations due to temperature, pressure, and humidity fluctuations in the laboratory.

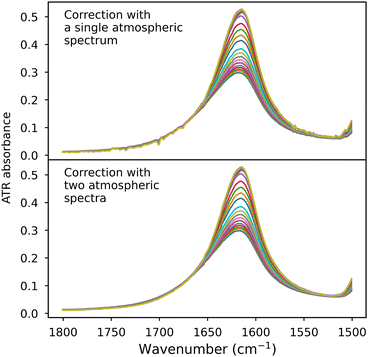Fig. 11 Comparison of correction quality using a single atmospheric spectrum versus two atmospheric spectra. The dataset is the same as in Fig. 2.

• VaporFit performs best when correcting with a small number of atmospheric spectra (2–5), making experimental planning easier. Using too many atmospheric spectra may lead to overfitting, introducing baseline fluctuations and unnecessary noise instead of improving correction accuracy. We suspect that the reason for this is the limitations of the least-squares method used for optimizing correction parameters.

• Correction is most effective when the FWHM of sample bands is significantly larger than that of atmospheric bands. In other words, the more distinct the sample spectrum is from atmospheric interference, the easier the correction process.

• A key requirement for the method to work correctly is that the spectrum must be smoothable, as Ȳ_ν in eqn (1) should reflect the real spectrum devoid of atmospheric components. This means bands should be relatively broad or recorded at sufficiently high resolution. Standard resolution of 2–4 cm⁻¹ for protein and aqueous solution spectra should be sufficient.

• Proposed default SG parameters in VaporFit (3/11, i.e., polynomial of degree 3 and 11 smoothing points) work very well for the measurements mentioned in this publication.

• SG parameters, used for Ȳ_ν estimation, influence correction accuracy. If the parameters are set too tightly or too loosely, the algorithm might converge at an unsatisfactory stage. This could result in theoretical spectra that aren’t smooth enough or are too smooth, which could then cause atmospheric spectra to be subtracted with random coefficients. Excessively high values lead to an unrealistically estimated spectrum Ȳ_ν, increasing noise in the final corrected spectra (see Fig. 3). We recommend setting the lowest practical polynomial order (typically 3 for 4 cm⁻¹ to 2 cm⁻¹ FTIR spectra). For fingerprint FTIR spectra, the best SG window size is usually between 5 and 21 points, depending on the FWHM and spectral resolution of the main bands. This parameter primarily determines the smoothing effect. For correction with a single atmosphere spectrum, the algorithm is relatively insensitive to SG parameter selection.

• Atmospheric correction should be performed before ATR correction. The atmospheric spectrum is primarily related to gases in the optical path inside the instrument, not the atmosphere above the crystal, and therefore does not depend on the optical properties of the crystal or the sample. ATR correction can treat atmospheric bands as sample bands, thus incorrectly assigning them variability specific to the sample's refractive index. Correcting such a spectrum may later be impossible or very difficult.

• The method may be less effective for spectra with strong oscillations, irregularities, or high local variability, though typical FTIR measurements rarely pose such issues. Naturally, the atmospheric spectrum, which is going to be subtracted, is not subject to this restriction.

3.4.1 Problems and perspectives. The program is based on optimizing subtraction parameters using the least-squares method. This is one of the simpler and more straightforward optimization approaches, but the introduction of a non-intuitive spectrum smoothing step that has proven to yield significantly better results than the manual subtraction method of a single spectrum based on visual inspection and provides qualitatively superior results to automatic atmosphere correction methods available in software like OPUS or OMNIC.

A limitation resulting from the optimization method used is the relatively small number of atmospheric spectra that can be subtracted simultaneously. We estimate that 5 spectra are reasonable, although much depends on the measurement conditions and this number may vary upwards or downwards. Although in the vast majority of cases, two spectra covering the variability of conditions throughout the experiment (according to our proposed measurement scheme) are sufficient for satisfactory correction, the ideal solution would be the possibility of building one's own database of atmospheric spectra characteristic of a given laboratory and spectrometer, which would eliminate the need for measuring atmospheric spectra at all. Such a database would be created based on many atmospheric spectra measured over time (month or a year), considering factors such as air humidity, measurement parameters, and possibly others. Here, we see the potential for method development, which could be based on the use of more advanced optimization algorithms or machine learning methods that would handle fitting several hundred or several thousand spectra more effectively. The current streamlined version of the algorithm should be much easier to use for this type of modification. In our opinion, building such a database would only make sense at a “local” level, i.e., within one measurement station, as the variability of conditions between laboratories and the variability in instrument quality is too large and would require even more work.

As indicated in Section 3.2.3 (“Why it works?”), the primary reason why the algorithm works is the difference in the smoothability of the corrected and atmospheric spectra. One of the steps of the algorithm is smoothing using the Savitzky–Golay method, which works very well for FTIR spectra of solutions, typical organic compounds, and biomolecules. However, there are phenomena (e.g., Fano resonance) or other types of spectroscopy in which signals are characterized by bands with asymmetric shapes and sharp peaks. In such situations, smoothing with the method implemented in the algorithm may be ineffective and lead to the formation of artifacts, as with suboptimal values of SG parameters (see Fig. 3). However, it would probably be possible to use other less destructive signal smoothing methods, such as denoising using wavelets. The current form of the algorithm extracted as a class should facilitate this type of modification.

We suspect that VaporFit, or the core algorithm itself, could become an invaluable tool in the data preparation stage for machine learning and related algorithms. It effectively removes unnecessary variability in spectra, resulting in cleaner input data that is better suited for advanced analytical techniques, including machine learning methods. Models based on, among other things, the analysis of environmental data collected by FTIR or the construction of such databases would thus become more reliable, as the variance element associated with this type of spectral contamination would be entirely absent during model training. This is crucial because the spectrum of water vapor or other gaseous interferences is very similar across different samples and could be misinterpreted by an ML algorithm as a characteristic feature for a given class of compounds, leading to errors in identification. Spectra cleaned with VaporFit are particularly useful for algorithms that identify functional groups directly from FTIR data, significantly enhancing the efficiency of spectral interpretation. Data prepared in this way are particularly applicable in environmental analyses, e.g., for identifying pollutants in complex samples.^10,11 Similarly to the previously described method proposed by Goormaghtigh,⁴ ML models would significantly benefit from the pre-processing step utilizing VaporFit, among other tools.

4. Conclusions

In this work, we presented VaporFit – open-source software for automated correction of atmospheric interference (mainly water vapor and CO₂) in FTIR spectra, based on the least-squares method and a multispectral correction approach. VaporFit is distinguished not only by its high effectiveness but also by its accessibility – thanks to simplified code, a graphical user interface, and built-in tools for optimizing smoothing parameters and evaluating correction quality (including PCA). A key element of the work is also the presentation of a recommended measurement procedure scheme, which enables effective experiment planning and recording of data suitable for subsequent correction. Crucially, the automated and human-independent nature of the correction ensures consistency and makes the processed data highly suitable for subsequent analysis using other methods, such as chemometrics or machine learning. Thanks to this, VaporFit is a comprehensive, flexible, and practical tool supporting high-quality FTIR analysis, especially in studies requiring high precision and repeatability, e.g., in chemistry and biophysics.

Author contributions

Przemysław Pastwa: data curation, investigation, validation, writing – review & editing. Piotr Bruździak: conceptualization, software, methodology, visualization, writing – original draft, writing – review & editing.

Data availability

The Python 3.11 source code, compiled versions for Windows and macOS (arm64), the user guide, and sample data for VaporFit are freely available. The version of the software used in this study is 1.0. An archived version of the software (v1.0) for long-term access and citation is available via the Zenodo repository record (https://zenodo.org/records/15411176).¹² The source code for version 1.0 is also available as a GitHub Release at https://github.com/piobruzdpg/VaporFit/releases/tag/v1.0. The main project repository can be found at https://github.com/piobruzdpg/VaporFit.

Conflicts of interest

There are no conflicts to declare.

References

1. W. Ahmed, E. L. Osborne, A. V. Veluthandath and G. Senthil Murugan, Anal. Chem., 2024, 96, 18052–18060.
2. M. J. Baker, J. Trevisan, P. Bassan, R. Bhargava, H. J. Butler, K. M. Dorling, P. R. Fielden, S. W. Fogarty, N. J. Fullwood, K. A. Heys, C. Hughes, P. Lasch, P. L. Martin-Hirsch, B. Obinaju, G. D. Sockalingum, J. Sulé-Suso, R. J. Strong, M. J. Walsh, B. R. Wood, P. Gardner and F. L. Martin, Nat. Protoc., 2014, 9, 1771–1791.
3. P. Lasch, Chemom. Intell. Lab. Syst., 2012, 117, 100–114.
4. E. Goormaghtigh, V. Raussens and J.-M. Ruysschaert, Biochim. Biophys. Acta, Rev. Biomembr., 1999, 1422, 105–185.
5. P. Bruździak, Spectrochim. Acta, Part A, 2019, 223, 1–4.
6. A. Savitzky and M. J. E. Golay, Anal. Chem., 1964, 36, 1627–1639.
7. C. R. Harris, K. J. Millman, S. J. van der Walt, R. Gommers, P. Virtanen, D. Cournapeau, E. Wieser, J. Taylor, S. Berg, N. J. Smith, R. Kern, M. Picus, S. Hoyer, M. H. van Kerkwijk, M. Brett, A. Haldane, J. F. del Río, M. Wiebe, P. Peterson, P. Gérard-Marchant, K. Sheppard, T. Reddy, W. Weckesser, H. Abbasi, C. Gohlke and T. E. Oliphant, Nature, 2020, 585, 357–362.
8. P. Virtanen, R. Gommers, T. E. Oliphant, M. Haberland, T. Reddy, D. Cournapeau, E. Burovski, P. Peterson, W. Weckesser, J. Bright, S. J. van der Walt, M. Brett, J. Wilson, K. J. Millman, N. Mayorov, A. R. J. Nelson, E. Jones, R. Kern, E. Larson, C. J. Carey, İ. Polat, Y. Feng, E. W. Moore, J. VanderPlas, D. Laxalde, J. Perktold, R. Cimrman, I. Henriksen, E. A. Quintero, C. R. Harris, A. M. Archibald, A. H. Ribeiro, F. Pedregosa, P. van Mulbregt and SciPy 1.0 Contributors, Nat. Methods, 2020, 17, 261–272.
9. J. D. Hunter, Comput. Sci. Eng., 2007, 9, 90–95.
10. A. A. Enders, N. M. North, C. M. Fensore, J. Velez-Alvarez and H. C. Allen, Anal. Chem., 2021, 93, 9711–9718.
11. S. Zhong, K. Zhang, M. Bagheri, J. G. Burken, A. Gu, B. Li, X. Ma, B. L. Marrone, Z. J. Ren, J. Schrier, W. Shi, H. Tan, T. Wang, X. Wang, B. M. Wong, X. Xiao, X. Yu, J.-J. Zhu and H. Zhang, Environ. Sci. Technol., 2021, 55, 12741–12754.
12. P. Pastwa and P. Bruździak, piobruzdpg/VaporFit: VaporFit v1.0, Zenodo repository, 2025, 10.5281/zenodo.15411175, Version 1.0; Source code and data archive.

---