Dynamical insights into denitrogenation of 1-pyrazoline: exploring pathways via transition states and a second-order saddle

Abstract

The mechanism of 1-pyrazoline denitrogenation has garnered significant attention due to its remarkable stereoselectivity. In this study, the thermal denitrogenation mechanism of 1-pyrazoline was investigated using ab initio classical trajectory simulations to elucidate post-transition state and post-second-order saddle dynamics. Trajectories initiated from the synchronous transition state region predominantly followed the minimum energy pathway, forming the trimethylene diradical intermediate, which subsequently yielded cyclopropane with a preference for single inversion of the configuration. Additionally, the post-second-order saddle dynamics revealed that most trajectories followed the minimum energy path, offering alternative pathways for cyclopropane formation with retention of the configuration. In contrast, trajectories initiated from asynchronous transition state regions mostly deviated from the minimum energy path, leading to longer-lived diazenyl diradicals while still favoring single inversion in the final products. Despite significant diradical lifetimes, trajectories from all six transition-state regions exhibited a preference for single inversion cyclopropane formation, suggesting that product selectivity is dictated by dynamical effects rather than the reaction pathway.

---

1 Introduction

Cyclopropanes are basic structural units found in many natural products and biologically active compounds that have important pharmaceutical applications. This makes them valuable in drug design and synthesis.^1–7 As a result, numerous methods have been devised to generate them in an optically pure state.^8–12 One of the methods widely used for the preparation of cyclopropane derivatives is the denitrogenation of 1-pyrazolines under thermal and photochemical conditions.^13–25 In this context, the mechanism of denitrogenation of 1-pyrazolines has been the subject of multiple studies in the gas phase,^{16–18,26,27} solution phase,^19,20 and solid state.^24,25 It is now acknowledged that both thermal and photochemical denitrogenation involve diazenyl and/or trimethylene diradical intermediates.^19,28–30 The photochemical denitrogenation of 1-pyrazoline has been reported to follow a stepwise mechanism involving a trimethylene-type diradical intermediate, which closes more rapidly than the C–C bond rotations to form stereospecific cyclopropanes with retention of the configuration.^{14,19,24,25,31}

In contrast, the thermal denitrogenation of 1-pyrazolines results in stereoselective products.^{16,18,20–23,26,32} Various mechanisms have been proposed from several experimental and theoretical studies to explain the product selectivity. Crawford and Mishra¹⁶ reported that thermal denitrogenation of cis- and trans-3,5-dimethyl-1-pyrazoline produced trans- and cis-1,2-dimethylcyclopropane, respectively, as the major product indicating inversion at one of the reacting carbon centers. They proposed a synchronous denitrogenation pathway leading to the trimethylene diradical intermediate followed by a conrotatory ring closure to explain the formation of the major single-inverted cyclopropane.

Subsequent studies, however, suggested complexities in the reaction mechanism. The stereochemically random ring closure observed during the thermolysis of cyclopropane^8,33–35 prompted Condit and Bergman²⁶ to investigate the thermal denitrogenation of exo- and endo-2-methyl-3,4-diazabicyclo[3.3.0]oct-3-enes. Their aim was to restrict the formation of a trimethylene diradical intermediate by attaching a short 3-carbon bridge to the C1 and C2 positions of 1-pyrazoline, thereby controlling the stereochemistry of the products. However, denitrogenation of both exo- and endo-2-methyl-3,4-diazabicyclo[3.3.0]oct-3-enes still resulted in a major single-inverted cyclopropane,²⁶ suggesting that denitrogenation in these molecules occurred through a sequential C–N cleavage mechanism.

Later, Bergman and coworkers¹⁸ studied the denitrogenation of cis- and trans-3-ethyl-5-methyl-1-pyrazoline and proposed that the reaction involved the non-linear extrusion of N₂ by pseudo-conrotation of C–C bonds. A theoretical study by Jean and Hiberty²⁷ at the 3 × 3 CI/STO-3G level, for the thermal decomposition of 1-pyrazoline revealed that stepwise denitrogenation pathways via trans and gauche diradicals were energetically more favorable compared to the synchronous and non-linear extrusion pathways.

To gain deeper insights into the mechanisms, we recently mapped the potential energy profile for all possible denitrogenation pathways of 1-pyrazoline using CASSCF and CASPT2 methods with different basis sets.³⁶ In contrast to Jean and Hiberty's study,²⁷ we found that the synchronous denitrogenation pathway is energetically more favorable than the asynchronous pathways. The main cause of this discrepancy is possibly due to differences in the methodological treatment, since Jean and Hiberty²⁷ used a relaxed geometry scan to evaluate the energy barriers. The partially optimized transition state structures reported by them could not be obtained by full optimization at the CASSCF(4,4) level.³⁶ The synchronous denitrogenation of 1-pyrazoline leads to a trimethylene diradical intermediate, which undergoes ring closure to form cyclopropane via conrotatory or disrotatory rotation of the terminal methylene group. The barrier for conrotatory and disrotatory closure of the trimethylene diradical intermediate to cyclopropane is ∼1 kcal mol⁻¹. Consequently, if denitrogenation occurs synchronously, a racemic mixture of cyclopropane is expected.^37–39 Therefore, the formation of a major single-inverted cyclopropane observed experimentally could not be solely explained by the energetics of the reaction.

To investigate dynamic effects in the stereoselective formation of single-inverted cyclopropane, we conducted an ab initio classical trajectory study at the CASSCF level of theory for 1-pyrazoline and its substituted isotopomer trans-3,5-di-¹⁵H-1-pyrazoline where an isotopic mass of 15 amu (to represent CH₃ group) was assigned to the H atoms.⁴⁰ The simulations revealed that out of 4000 trajectories integrated from the reactant region of 1-pyrazoline, 314 (7.85 ± 0.83%) were reactive. Denitrogenation occurred via both the synchronous and asynchronous paths, resulting in the major single-inverted cyclopropane consistent with the experimental findings. Additionally, the trajectories revealed a non-traditional second-order saddle (SOS) pathway (∼4%), which involved a planar second-order saddle point.

Although our study provided valuable insights into the overall reaction dynamics, statistically reliable data is still desirable to rationalize the nonstatistical product distribution and the pathways involved, particularly those related to the newly identified SOS pathway. In addition to improving trajectory statistics, the present study is focused on two key aspects: (i) the origin of the nonstatistical product distribution and (ii) the post-second-order saddle dynamics.

In an earlier study,⁴⁰ the origin of the nonstatistical product distribution observed in both experiments and simulations could not be conclusively determined. It is important to note that such distributions can arise due to incomplete intramolecular vibrational energy redistribution (IVR) before the system accesses the transition state regions, or due to dynamical effects associated with post-transition state (post-TS) dynamics, especially when intermediates are present along the reaction pathways. To address this, the current study investigates the post-TS dynamics of 1-pyrazoline denitrogenation from the synchronous and asynchronous transition state regions independently, in order to examine the dynamical effects influencing product selectivity. In addition, we examine the post-SOS dynamics by initiating trajectories from the SOS region. This approach is expected to improve statistical reliability and provide insights into the dynamics and product distribution associated with the SOS pathway.

2 Computational details

In our previous work,³⁶ we conducted a detailed study of the energetics underlying the thermal denitrogenation of 1-pyrazoline using the CASSCF and CASPT2 methods, employing various active spaces and the 6-31+G*, 6-311+G*, cc-pVDZ, aug-cc-pVDZ, and cc-pVTZ basis sets. We found that the CASSCF(4,4)/6-31+G* level of theory accurately describes the denitrogenation pathways when compared to benchmark CASPT2(12,12) energies. Therefore, the CASSCF(4,4)/6-31+G* level of theory was selected as the method of choice for the on-the-fly classical trajectory simulations performed in this study.

Ab initio classical trajectory simulations were performed by computing the forces on-the-fly at each step using the CASSCF(4,4)/6-31+G* level of theory.^41–45 The active space for the CASSCF(4,4) calculations involved the σ and σ* orbitals of both the C–N bonds. Initial coordinates and momenta for the trajectory simulations were selected using the microcanonical normal mode sampling procedure.⁴⁶

Batches of 300 trajectories were initiated independently from the synchronous and various asynchronous transition state regions, with an excess energy of (E_tot − E_a) kcal mol⁻¹, where E_tot is the energy available to the reactant 1-pyrazoline, and E_a corresponds to the classical energy barrier of the respective transition state. The total energy (E_tot) was calculated as follows: among the different pathways mapped for the denitrogenation of 1-pyrazoline,³⁶ the transition state TS4f corresponding to the asynchronous step-wise path, had the highest barrier of 52.84 kcal mol⁻¹ (Fig. S1–S4, ESI†). Assuming a Boltzmann distribution of energies at TS4f for the experimental temperature (510.45 K),¹⁶ the excess energy available to TS4f was calculated as E_excess = E_zpe + E_vib + E_rot + E_rc, where E_zpe, E_vib, and E_rot are the zero-point-energy, average vibrational energy, and average rotational energy of TS4f, respectively. The energy along the reaction coordinate, E_rc, was taken as RT. The total energy of the reactant was then calculated as E_tot = E_TS4f + E_excess, yielding a value of 119.10 kcal mol⁻¹.

Additionally, 300 trajectories were initiated from the SOS region, with an excess energy of (E_tot − E_SOS) kcal mol⁻¹ to investigate post-second-order saddle dynamics, where E_SOS = 44.12 kcal mol⁻¹ is the SOS energy. Initial coordinates and momenta for these trajectories were selected using the microcanonical normal mode sampling procedure described in our previous work.⁴⁷ All classical trajectory calculations were performed using a modified version of VENUS/NWChem^48,49 on an Intel(R) Xeon(R) CPU E5-2697A v4@2.60 GHz computer. The trajectories were integrated using the velocity-Verlet algorithm with a step size of 0.3 fs over a total simulation time of 1 ps.

3 Results and discussion

3.1 Denitrogenation pathways

We recently reported in detail the various denitrogenation pathways for 1-pyrazoline obtained using the CASSCF and CASPT2 methods.³⁶ Here, we discuss these pathways for completeness in the context of the present study. Fig. 1 provides a summary of the denitrogenation paths obtained for the thermal denitrogenation of 1-pyrazoline at the CASSCF(4,4)/6-31+G* level of theory. The thermal denitrogenation of 1-pyrazoline can happen via three different pathways.

Fig. 1 Summary of the possible denitrogenation paths, (a)–(c), obtained for the thermal denitrogenation of 1-pyrazoline at the CASSCF(4,4)/6-31+G* level of theory.

(a) Synchronous denitrogenation. The synchronous denitrogenation path involves the simultaneous breaking of both C–N bonds through the transition state TS1, leading to the formation of a trimethylene diradical intermediate, Int1. Int1 can then close to cyclopropane via con- or dis-rotation of the terminal methylene groups or can form alkene through proton migration. Conrotatory closure of the terminal methylene groups of Int1 results in single-inverted (SI) cyclopropane, while disrotatory closure leads to cyclopropane with double inversion (DI) or retention (Ret) of the configuration. A flipping motion of the central methylene (CH₂) group connects TS1 to the symmetric transition state TS1′via a second-order saddle point SOS, from which the dissociation of N₂ can occur directly (Fig. S1, ESI†).

(b) Asynchronous step-wise denitrogenation. This pathway involves the breaking of one of the C–N bonds to form the diazenyl diradical (DZ) intermediate, followed by the breaking of the other C–N bond. Since, the PES is symmetrical about the C–N bond cleavage, the asynchronous cleavage of either C1–N5 or C3–N4 bonds would result in similar structures. Here, we discuss the pathways where the C1–N5 bond is cleaved first. Two distinct paths for the asynchronous cleavage of the C1–N5 bond of 1-pyrazoline were identified, depending on the type of diazenyl diradical intermediate formed (Fig. S2 and S3, ESI†).³⁶

(i) Pathways via a planar-like diazenyl diradical intermediate. In this path, a planar diazenyl diradical intermediate Int3a is formed via the transition state TS3a through the anti-clockwise rotation of the C3–N4 bond. The terminal methylene group of the diazenyl diradical has a planar-like geometry (∠C3C2C1H6 ∼ −44°, ∠C3C2C1H10 ∼ 157°). From Int3a, free rotation of the N₂ group about the C3–N4 bond can occur, leading to the formation of Int3bviaTS3b, and subsequently returning to the reactant with further rotation through TS3c. Thus, Int3b can also be accessed by clockwise rotation of the C3–N4 bond viaTS3c. The dissociation of the second C–N bond (C3–N4) can occur from either Int3a or Int3b with simultaneous closure of the three-membered ring to form SI cyclopropane. Alternatively, breaking the second C–N bond may lead to the formation of Int1, which can subsequently close to cyclopropane with SI, DI, or Ret configurations.

(ii) Pathways via a perpendicular-like diazenyl diradical intermediate. Anti-clockwise rotation of the C3–N4 bond can also yield a diazenyl diradical that has a perpendicular-like geometry (∠C3C2C1H6 ∼ −72°, ∠C3C2C1H10 ∼ 90°) viaTS4a. Similar to the pathways involving the planar-like diazenyl diradical intermediate, rotation of the N₂ group about the C3–N4 bond generates the rotational isomers Int4b and Int4f. From these intermediates, SI cyclopropane can form directly, or cyclopropane with SI, DI, or Ret configurations can form viaInt1. While Int4b and Int4f are connected to each other by TS4f, Int4b can also return to the reactant viaTS4c.

(c) Asynchronous concerted denitrogenation. This pathway involves the asynchronous breaking of one of the C–N bonds, specifically the C1–N5 bond, via the transition state TS5. It leads to the formation of cyclopropane with an SI configuration (Fig. S4, ESI†).

From the potential energy profiles, the following observations can be made: (i) synchronous and asynchronous stepwise denitrogenation of 1-pyrazoline results in cyclopropane with SI, DI, and Ret configurations, and (ii) asynchronous concerted denitrogenation of 1-pyrazoline results in cyclopropane with an SI configuration. The asynchronous concerted path has an energy barrier (ΔE^‡ = 48.21 kcal mol⁻¹) approximately 8 kcal mol⁻¹ higher than the synchronous pathway and about 1–3 kcal mol⁻¹ higher than the stepwise asynchronous pathway. Energetically, the synchronous pathway is the most favorable, yielding cyclopropane with SI, DI, and Ret configurations. However, the experimental observation of a major SI cyclopropane indicates that dynamical effects play a crucial role in determining product selectivity. Below, we discuss the results of the ab initio classical trajectory simulations performed from different transition state regions to elucidate the dynamics and mechanisms of the denitrogenation reaction.

3.2 Trajectories initiated from the synchronous transition state (TS1) region

The transition state vector for the synchronous path transition state TS1 involves simultaneous stretching of both the C–N bonds. A total of 300 trajectories were initiated randomly from the TS1 region. The statistics of the products formed in these trajectories are given in Table 1. Out of 300 trajectories, 101 returned to the reactant, 198 led to cyclopropane (Cp), and one resulted in an alkene. From TS1, 163 of 198 trajectories form Cp, while the remaining 35 trajectories form the reactant first and subsequently recross the TS region to form Cp. Among these 35 recrossing trajectories, 21 dissociated via the synchronous denitrogenation pathway, while 14 followed the asynchronous pathway. Since the focus is on understanding the post-transition-state dynamics, the 35 recrossing trajectories were excluded from the product analysis. Consequently, the analysis was performed on the remaining 163 trajectories. Of these, 86 (52.7%) formed SI cyclopropane, 59 (36.2%) formed DI cyclopropane, and 18 (11.0%) formed cyclopropane with retention of the configuration.

Table 1 Number of trajectories forming reactants (R), propylene (Py), Int1, and Cp, and those exhibiting recrossing, for sets of 300 trajectories integrated from TS1, SOS, TS3a, TS3c, TS4a, TS4c, and TS5 regions^a

Region	R	Py	Int1	Recrossing	Cp
				R → Cp	SI	DI	Ret	Total
a The fraction of trajectories forming different products are also given as percentages. b The experimental data is for trans-3,5-dimethyl-1-pyrazoline.
TS1	101	1		35	86	59	18	163
					53%	36%	11%
SOS	63	1	1	18	54	60	103	217
					24.9%	27.6%	47.5%
TS3a	26			3	123	79	69	271
					45%	29%	25%
TS3c	20			8	137	76	59	272
					50%	28%	22%
TS4a	36		1	22	124	55	62	241
					51%	23%	26%
TS4c	7		1	4	147	103	38	288
					51%	36%	13%
TS5	10			2	189	53	46	288
					65.6%	18.4%	16%
Experiment^18^b					73%	16%	10%

---

To determine whether the denitrogenation process was synchronous or asynchronous, the changes in C3–N4 and C1–N5 bond distance over time were monitored for the 163 trajectories. Of these, 154 trajectories (Fig. 2(a)) dissociated via the synchronous denitrogenation pathway, while the remaining 9 trajectories (Fig. 2(b)) followed an asynchronous path despite starting from the synchronous transition-state region. A plot of the angle ∠C1–C2–C3–N4 versus the C3–N4 distance (Fig. 3) reveals that most trajectories followed the minimum energy path (MEP). All trajectories dissociating from TS1 formed the trimethylene diradical intermediate (Int1), which either closed to form Cp or formed an alkene without ring closure. Interestingly, six trajectories were found to dissociate from the SOS region.

Fig. 2 Plot of the C1–N5 and C3–N4 distances for all trajectories initiated from the TS1 region following (a) synchronous and (b) asynchronous denitrogenation pathways. The trajectories are projected onto a two-dimensional PES obtained from a relaxed scan of the C–N distances for 1-pyrazoline.

Fig. 3 Polar plot of ∠C1–C2–C3–N4 vs. C3–N4 distance for TS1, TS1′, IRC path (MEP), and the 163 trajectories that form Cp from TS1.

To investigate the observed experimental product selectivity, the atomic-level mechanisms from TS1 to Cp by the ring closure of Int1 were followed for the 154 synchronous trajectories. The stereochemistry of cyclopropane obtained is expected to be influenced by the lifetime of Int1 (i.e., how long the system remains in the diradical region) and the number of rotations of the terminal methylene groups before closure.

We calculated the lifetime of the diradical intermediate Int1 by tracking the electron densities of the σ_C–N and σ_C–N* orbitals during dissociation for all trajectories. An electron density greater than 0.45 on the σ_C–N* orbital was used as the criterion for a radical. The lifetime distribution of the trimethylene diradicals (Fig. S5(a), ESI†) exhibited an exponential decay, with an initial equilibration time of ∼100 fs. The average lifetime of the diradical was found to be 128 fs, comparable to the experimental lifetime value of 120 ± 20 fs observed for cyclopropane isomerization.⁵⁰

Since the barrier for the rotation of the terminal methylene groups in Int1 is ∼1 kcal mol⁻¹, these groups can rotate multiple times before closing to form Cp. The number of rotations of the terminal methylene groups corresponding to the C1 and C3 atoms was calculated by monitoring the dihedral angles ∠C3C2C1H6 and ∠C1C2C3H8 over time. These rotations were denoted as (n_C1,n_C3). The number of terminal methylene rotations and the average lifetimes of the trimethylene diradical intermediate, obtained from 154 trajectories, are shown in Fig. S5(b) and (c) (ESI†). As seen in Fig. S5(b) (ESI†), the majority of the trajectories exhibit (0, 0), (0, 1), (1, 0), or (1, 1) rotations in the terminal methylene groups. When compared to trajectories with (1, 0), (0, 1), or (1, 1) rotations, the average lifetime of trajectories with (0, 0) rotation is shorter (86 fs), indicating that shorter Int1 lifetimes favor the formation of Cp with retention of the configuration. The maximum inversion observed was (2, 7) in a trajectory that spent 359 fs in the Int1 region before forming Cp.

It is interesting to look at the nature of the HOMO and LUMO during the reaction. The HOMO and LUMO of the stationary points TS1, Int1, and Cp along the MEP of synchronous denitrogenation are shown in Fig. 4(a). At TS1, the HOMO and LUMO are σ_C–N bonding and σ_C–N* anti-bonding orbitals, respectively. These orbitals change to p-type orbitals on the C1 and C3 atoms in Int1 and subsequently to σ_C–C and σ_C–C* of the C1–C3 bond in Cp. Fig. 4(b)–(d) show the plots of the C1–C3 bond distance and the electron densities of the σ_C–N and σ_C–N* orbitals versus time. We can see that the initial electron densities in the σ_C–N (ρ₁) and σ_C–N* (ρ₂) orbitals are ∼1.6 and ∼0.4, respectively. During the course of the reaction, ρ₁ decreases and ρ₂ increases until the diradical is formed when ρ₁ and ρ₂ are ∼1.0. During the cyclopropane formation from the diradical, since the pπ and pπ* orbitals change their character to σ_C–C (ρ₁) and σ_C–C* (ρ₂) orbitals, ρ₁ and ρ₂ now become ∼2.0 and ∼0, respectively.

Fig. 4 (a) Orbital correlation diagram for the synchronous denitrogenation path from TS1 to Int1 and Cp. Plot of C1–C3 bond distance (top panel) and electron densities (ρ₁ and ρ₂, bottom panel) in the σ_C–N and σ_C–N* orbitals vs. time for trajectories initiated at the TS1 region for (b) Type 1 trajectories with a short diradical lifetime, (c) Type 2 trajectories with a longer diradical lifetime, and (d) trajectories showing Cp isomerization.

Detailed analysis of the C1–C3 bond distance and orbital electron densities revealed two trajectory types. In Type 1 trajectories (Fig. 4(b)), the dissociation of the C–N bonds and the C1–C3 bond closure occur simultaneously. The system traverses the diradical region and the products are formed within 100 fs. All of the Type 1 trajectories either undergo (0, 0), (0, 1), (1, 0), or (1, 1) inversions at the C1 and C3 carbon atoms. 43 (55.1%) of the 78 Type 1 trajectories close to form SI cyclopropane, 26 (33.3%) form DI cyclopropane, and 9 (11.5%) form Cp with retention of the configuration. In Type 2 trajectories (Fig. 4(c)), the system remains in the diradical region for a longer time before closing to Cp. These trajectories show multiple inversions at the C1 and C3 carbon centres. 37 (48.7%) out of 76 Type 2 trajectories close to form SI cyclopropane, 31 (40.8%) form Cp with double inversion, and 8 (10.5%) trajectories form Cp with the retention of the configuration.

It is clear that Type 1 trajectories with shorter Int1 lifetimes have a higher preference for the formation of SI cyclopropane than Type 2 trajectories. In contrast, prolonged residence of the system in the Int1 region, facilitates efficient IVR reducing the preference for the formation of SI Cp relative to DI Cp. Only ∼11% of trajectories close to Cp with the retention of the configuration. Additionally, 14 trajectories exhibited cyclopropane isomerization, involving ring opening and subsequent reclosure (Fig. 4(d)).

3.3 Post-second-order saddle dynamics

The dynamical simulations from the reactant (1-pyrazoline)⁴⁰ revealed that about 7% of the trajectories undergoing synchronous denitrogenation followed the SOS path. Therefore, it is of interest to explore the post-second-order saddle dynamics from the SOS region to understand the atomic-level mechanisms and their importance in product selectivity. To this end, we computed 300 trajectories initiated at the SOS region by assuming a microcanonical distribution of energies among all modes, with an excess energy of 74.98 kcal mol⁻¹ available at the SOS.

Out of 300 trajectories, 235 resulted in Cp, 1 trajectory yielded an alkene, 1 trajectory was trapped in the Int1 region for the integration time, and the remaining 63 trajectories returned to the reactant. From the SOS, 217 of the 235 trajectories formed Cp, while the remaining 18 formed the reactant first and subsequently recrossed the SOS region to form Cp. Of the 217 products formed, 54 (24.9%) resulted in the SI configuration, 60 (27.6%) gave the DI configuration, and 103 (47.5%) gave the Ret configuration. As observed in our previous study,⁴⁰ this clearly indicates that the SOS path provides an alternative mechanism for the formation of a major retention of the configuration product.

The mechanisms followed by the 235 reactive trajectories can be classified into the following four pathways (Fig. 5): (i) SOS → Cp (directly or viaInt1). 217 of the 235 trajectories move in the forward direction from the SOS region to form Cp directly, or form TMD, which then results in Cp. (ii) SOS → TS0 → R → TS1 → Cp. One trajectory passes the TS0 region and then forms Cpvia the TS1 region. (iii) SOS → TS0 → R → SOS → Cp. Two trajectories first form the reactant from SOS and then form Cp after recrossing the SOS region. (iv) SOS → R → TS1/TS1′ → Cp. 14 trajectories first form the reactant and then proceed viaTS1/TS1′ to form Cp. Interestingly, one trajectory follows the asynchronous path after forming the reactant from the SOS region.

Fig. 5 Plot of ϕ_S (°) and d_S (Å) for (a) 217 trajectories projected on the relaxed PES for the synchronous path for 1-pyrazoline. These trajectories move in the forward direction towards Cp/TMD from the SOS region, (b) one trajectory that first goes to TS0 from the SOS region, forms the reactant, and then passes through TS1 forming Cp, (c) two trajectories that first form the reactant from the SOS region and then form CpviaSOS, and (d) 14 trajectories that first form the reactant from the SOS region and then form CpviaTS1 or TS1′. ϕ_S = (ϕ₁ − ϕ₂)/2, where ϕ₁ and ϕ₂ are the dihedral angles ∠C1C2C3N4 and ∠C3C2C1N5, and d_S is the mean of the two C–N bond distances.

The diradical lifetime distribution and the number of inversions (n_C1, n_C3) at the C1 and C3 atoms for the 217 trajectories that directly form Cp from the SOS region are shown in Fig. S6 (ESI†). We can see that most of the trajectories (98/217) have (0, 0) inversions at the C1 and C3 carbon atoms, resulting in the formation of Cp with retention of the configuration and have an average diradical lifetime of 60 fs.

Along the dissociation path from the SOS, the changes in electron densities of the C–N σ and σ* orbitals were tracked for the 217 trajectories. In 150 of the 217 trajectories, C–N dissociation and C1–C3 bond closure occur simultaneously, and Cp is formed within 100 fs (Fig. S7(a), ESI†). The remaining 67 trajectories spend more time in the diradical region (Fig. S7(b), ESI†).

It is interesting to look at the stereochemistry of Cp formed from these trajectories. For the trajectories that spent less than 100 fs in the diradical region, 25/150 (17%) gave SI Cp, 30/150 (20%) gave DI Cp, and 95/150 (63%) resulted in Cp with retention of the configuration. For the 67 trajectories that spent more time in the diradical region, 29 (43%) gave SI Cp, 30 (45%) gave DI Cp, and only 8 (12%) gave Cp with retention of the configuration.

As seen above, the trajectories that spend less time in the diradical region have a higher preference for the formation of Cp with retention of the configuration. Trajectories that spend longer time in the diradical region produce a racemic mixture of SI and DI Cp, with only 12% of them resulting in Cp with retention of the configuration, which is similar to the results observed for trajectories initiated in the TS1 region. In 34 trajectories, the Cp formed from SOS undergoes ring isomerization (Fig. S7(c), ESI†).

3.4 Trajectories integrated from the asynchronous step-wise transition state regions

We computed sets of 300 trajectories, initiated from each of the four asynchronous stepwise path transition states (TS3a, TS3c, TS4a, TS4c), using a microcanonical sampling procedure. The transition states connect the reactant and diazenyl diradicals. The transition state vector associated with TS3a, TS3c, TS4a, and TS4c corresponds to simultaneous stretching of the C1–N5 bond and torsional motion about the C3–N4 bond (∠C2–C3–N4–N5 angle). Table 1 summarizes the outcomes of the trajectories integrated from the different asynchronous stepwise transition states.

As shown in Table 1, the trajectories follow four distinct paths: (i) formation of the reactant, R, (ii) remaining in the Int1 region throughout the integration time, (iii) initial formation of the reactant followed by recrossing the transition state region to form Cp, and (iv) formation of Cpvia different intermediates. Recrossing trajectories were excluded from the product analysis. The table shows that the majority of trajectories originating from the four transition states result in the formation of Cp, primarily with the SI configuration, followed by double inversion and retention of the configuration.

We further investigated the atomic-level mechanisms underlying the formation of Cp. In transitioning from the reactant to Cpvia the asynchronous stepwise transition states along the MEP, the N₂ group undergoes a clockwise/anticlockwise rotation about the C3–N4 bond concurrent with the dissociation of the C1–N5 bond. In the transition states, the C1–N5 bond is already broken and it is of interest here to understand the process of C3–N4 bond breaking from the transition states.

If trajectories follow the MEP, the C3–N4 bond can dissociate from Int3a/Int4a or Int3b/Int4b. However, due to the presence of excess kinetic energy, trajectories may deviate from the MEPs and follow dynamically driven pathways. To investigate the mechanism of C3–N4 bond dissociation, we tracked changes in the ∠C2–C3–N4–N5 dihedral angle as a function of the C3–N4 bond distance across all trajectories.

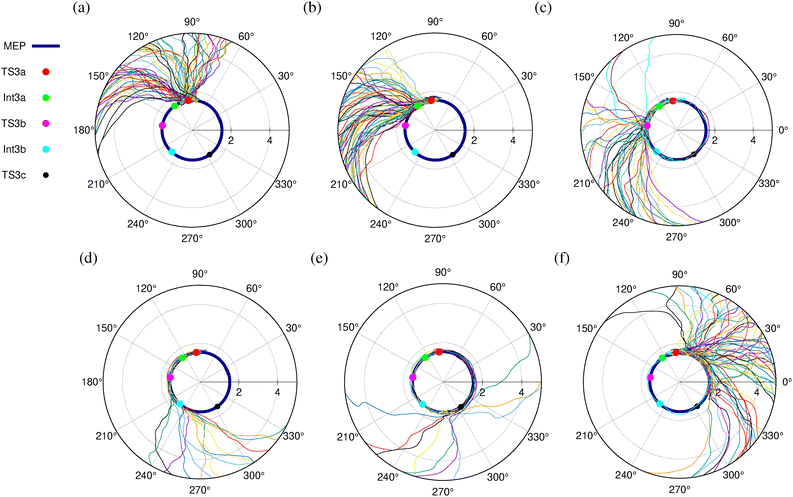
The polar plot of the dihedral angle ∠C2–C3–N4–N5 vs. C3–N4 bond distance for the MEP and 271 TS3a trajectories that form Cp is shown in Fig. 6. We can see that the trajectories follow various dynamical reaction pathways that deviate from the MEP, with the C3–N4 bond dissociating at varying ∠C2–C3–N4–N5 values. Based on the dissociation patterns, trajectories were classified into six categories. Fig. 6(a) shows 69 trajectories that dissociate directly from the TS3a region without passing through the DZ intermediates. Fig. 6(b) depicts 62 trajectories proceeding to the diradical intermediate Int3a from TS3a, where the C3–N4 bond subsequently dissociates. In 40 trajectories, the N₂ group rotates clockwise or anticlockwise about the C3–N4 bond, closely following the MEP, and the C3–N4 bond later dissociates via the TS3b region, as shown in Fig. 6(c). Similarly, the C3–N4 bond dissociates from the Int3b and TS3c regions in 14 and 10 trajectories, respectively, as shown in Fig. 6(d) and (e).

Fig. 6 Plot of ∠C2–C3–N4–N5 vs. C3–N4 for the minimum energy path, all the stationary points along the minimum energy path, and the 271 trajectories that form Cp from the transition state TS3a, following different dynamical pathways (a) to (f).

In 76 trajectories, the N₂ group rotates clockwise about the C3–N4 bond, accompanied by the dissociation of the C3–N4 avoiding the TS3c/Int3b region (Fig. 6(f)), taking a non-IRC route to form Cp. In one trajectory, the N₂ group completes a 360° rotation about the C3–N4 bond before its dissociation. Notably, the stationary points TS3a, TS3b, and TS3c are not directly connected to the diradical Int1 or the product Cp, making direct C3–N4 bond cleavage from these regions a dynamical pathway that avoids MEPs.

We performed a similar analysis for the trajectories initiated from the TS3c, TS4a, and TS4c regions and the corresponding ∠C2–C3–N4–N5 vs. C3–N4 bond distance plots are shown in Fig. S8–S10 (ESI†), respectively. Table 2 outlines the mechanisms of C3–N4 bond dissociation followed by the trajectories integrated from the four asynchronous step-wise transition states TS3a, TS3c, TS4a, and TS4c. We can see that only 76, 48, 69, and 45 trajectories integrated from TS3a, TS3c, TS4a, and TS4c, respectively, exhibit C3–N4 bond dissociation from the Int3a/Int4a or Int3b/Int4b regions of the PES following the MEP. For these 76, 48, 69, and 45 trajectories, a plot of ∠C1C2C3N4 bond angle vs. C3–N4 bond distance reveals that the C3–N4 bond dissociates either directly from Int3a and Int3b (Fig. 7(a) and (b), and Fig. S11–S13, ESI†) via the transition states TS3d and TS3f, respectively, or via an S_H2-like mechanism through the transition states TS3e/TS4d and TS3g/TS4e, respectively. In the S_H2-like mechanism, the axial N₂ group of the DZ radical changes to the equatorial position, followed by the C3–N4 bond dissociation to yield SI Cp (See Fig. S2, and S3, ESI†). A similar S_H2 mechanism was proposed to explain the substantial stereochemical inversion in housane formation in the photochemical denitrogenation of diazabicycloheptene.⁵¹

Table 2 The atomic level mechanisms of C3–N4 bond dissociation followed by trajectories integrated from TS3a, TS3c, TS4a, and TS4c regions

TSs	Int3a/Int4a	Int3b/Int4b	TS3a/TS4a	TS3b/TS4b	TS3c/TS4c	Non-IRC region
TS3a	62	14	69	40	10	76
TS3c	8	40	7	19	161	37
TS4a	54	15	121	26	5	20
TS4c	9	36	5	15	158	65

---

Fig. 7 Plots of ∠C1–C2–C3–N4 versus C3–N4 for the minimum energy path, all stationary points along the minimum energy path, and the TS3a trajectories that dissociate from the (a) Int3a and (b) Int3b. (c) Snapshots of a sample trajectory in which the C3–N4 bond dissociates in the TS3a region of the PES. (d) Snapshots of a trajectory in which the N₂ group rotates 273 around the C3–N4 bond before dissociating via the S_H2-like transition state TS3g.

Fig. 7 presents snapshots of two sample trajectories integrated from the TS3a region. In the first trajectory (Fig. 7(c)), the C3–N4 bond dissociates directly from the TS3a region, and Cp forms in approximately 225 fs. In the second trajectory (Fig. 7(d)), the N₂ group dissociates via the S_H2-like transition state TS3g. Here, the terminal methylene group (CH₂) completes a 360 rotation in about 145 fs, after which the N₂ group rotates about the C–N bond in tandem with the rotation of both CH₂ groups until ∼205 fs to form Int3b. The N₂ group of Int3b subsequently transitions from an axial to an equatorial position around 300 fs, after which the N₂ group dissociates, forming Cp.

Since asynchronous trajectories pass through both the DZ and TMD diradical regions, the amount of time the system spends in these regions influences the stereochemistry of the Cp formed. To investigate this, we calculated the total diradical lifetime and the individual lifetimes of the DZ and TMD diradicals by monitoring the electron densities of the HOMO and LUMO orbitals during the dissociation process. The C–N bond lengths were used to distinguish the lifetimes of the DZ and TMD diradicals. When both C–N distances exceed 4.5 Å, the diradical is designated as TMD. This threshold was selected because the longest C–N distance corresponding to the TSs along the asynchronous paths is approximately 4.5 Å.

Fig. S14–S17 (ESI†) present the plots of the C3–N4 bond distance versus time and the difference in electron density between the HOMO and LUMO orbitals during the dissociation process for the TS3a, TS3c, TS4a, and TS4c trajectories following different pathways, respectively. In most trajectories that dissociate directly from the transition state regions from which they are integrated, the dissociation of the C3–N4 bond and the closure of the C–C bond occur simultaneously, forming Cp within 200 fs. As the trajectories explore the DZ region of the PES, their lifetimes increase.

Fig. S18–S21 (ESI†) show the distribution of the total diradical lifetimes (DZ + TMD), the diazenyl diradical lifetimes, and the trimethylene diradical lifetimes for the TS3a, TS3c, TS4a, and TS4c trajectories, respectively. The total lifetime distributions exhibit a nearly exponential decay, with an initial equilibration time of approximately 150 fs, and the average total lifetimes were 206 fs, 192 fs, 199 fs, and 178 fs for the TS3a, TS3c, TS4a, and TS4c trajectories, respectively. Notably, the diazenyl diradicals are longer-lived compared to the TMD radicals and account for the majority of the diradical lifetimes.

Additionally, we calculated the number of inversions at the C1 and C3 stereocenters. Fig. S22 (ESI†) illustrates the number of inversions at the C1 and C3 stereocenters before forming Cp for the TS3a, TS3c, TS4a, and TS4c trajectories. The majority of these trajectories undergo (0, 0), (0, 1), (1, 0), and (1, 1) inversions at the stereocenters. For TS3a, TS3c, and TS4a trajectories, the major SI Cp product arises primarily from inversion at the C1 center, whereas for TS4c trajectories, the major SI Cp results largely from inversion at the C3 center.

3.5 Trajectories initiated from the asynchronous concerted transition state (TS5) region

The reaction coordinate vector for TS5 involves the stretching of the C1–N5 bond and the torsional motion of ∠C1–C2–C3–N4. At TS5, the C1–N5 bond length is 3.8 Å, and the ∠C1–C2–C3–N4 is −112.33°. A total of 300 trajectories were initiated from the TS5 region using microcanonical normal mode sampling of states with an energy of 70.89 kcal mol⁻¹. Of these, 10 trajectories lead to the reactant, while 290 resulted in Cp. Among the reactive trajectories, 288 proceeded directly from the TS region to form Cp, while the remaining 2 initially access the reactant region before recrossing the TS region to form Cp.

Out of the 288 trajectories, 189 (65.6%) yield SI Cp, 53 (18.4%) result in DI Cp, and 46 (16.0%) produce Cp with retention of the configuration. The preference for SI Cp formation observed in the TS5 trajectories aligns with the product stereochemistry experimentally reported for trans-3,5-dimethyl-1-pyrazoline.^16,18

To investigate the mechanism of Cp formation from the transition state region, we monitored ∠C1–C2–C3–N4 and ∠C2–C3–N4–N5 as functions of the C3–N4 bond distance during the trajectories. Fig. 8(a) and (b) illustrate the changes in ∠C2–C3–N4–N5 versus C3–N4 bond distance and ∠C1–C2–C3–N4 versus C3–N4 bond distance for the MEP, TS5, and the 288 trajectories that form Cp from TS5, respectively. Most trajectories dissociate directly from the TS5 region of the PES, forming Cp following the MEP. The rest of the trajectories follow various dynamical paths that deviate from the MEP associated with TS5. In these cases, the C3–N4 bond dissociates at different ∠C2–C3–N4–N5 and ∠C1–C2–C3–N4 angles follow the asynchronous, stepwise denitrogenation pathway (Fig. 8(a)), even though they were initiated from the TS5 region.

Fig. 8 Polar plots of (a) ∠C2–C3–N4–N5 versus C3–N4 bond distance and (b) ∠C1–C2–C3–N4 versus C3–N4 bond distance for TS5, MEP, and the 288 TS5 trajectories that form Cp.

To further explore the mechanism of Cp formation from TS5, we calculated the total diradical lifetime and the individual lifetimes of the DZ and TMD diradicals by monitoring the electron densities of the HOMO and LUMO orbitals during the dissociation process. Fig. S23 (ESI†) shows the correlation between the number of (n_C1, n_C3) rotations and the time spent in the DZ and TMD diradical regions. As illustrated in Fig. S23(a) (ESI†), the lifetime distribution exhibits an initial equilibration time followed by an exponential decay with an average lifetime of 138.32 fs. The majority of trajectories involve inversions at the C3 carbon center ((0,1) inversion), leading to the formation of SI Cp. Fig. S23(c) and (d) (ESI†) indicate that the system spends most of its time in the DZ diradical region of the PES, briefly passing through the TMD region prior to forming Cp.

Interestingly, the average diradical lifetime for trajectories showing (0,1) inversion is the shortest (56 + 9 = 65 fs). This contrasts with trajectories integrated from the synchronous and asynchronous stepwise transition state regions, where trajectories showing (0,0) inversion exhibited the shortest diradical lifetimes.

3.6 Product energy partitioning

We computed the energies of the product fragments from post-TS trajectories initiated from various transition states during the dissociation process. During the formation of the products Cp and N₂, the total kinetic energy available to the system is redistributed among the translational, rotational, and vibrational degrees of freedom of the products. Investigating the internal energies of the formed products is therefore of interest. The products were identified by monitoring the two C–N bonds during the course of the trajectory. The products were considered formed if the two C–N bond lengths reached 15 Å and the C(1)–C(3) bond was formed, resulting in ring closure. The internal energies of the N₂ and Cp groups were calculated as described elsewhere.⁵²

The average relative translational energies (Ē_trans), rotational energies of Cp (Ē_rot (Cp)), and rotational energies of N₂ (Ē_rot (N₂)) were determined for trajectories integrated from the synchronous transition state (TS1), the asynchronous transition states (TS3a, TS3c, TS4a, TS4c, TS5), and the SOS region. The results are shown in Fig. 9.

Fig. 9 Plots of average (a) relative translational energies (kcal mol⁻¹), (b) rotational energies of Cp, and (c) rotational energies of N₂ as a function of the mean C–N distance d_S (Å) for trajectories integrated from the TS1, SOS, TS3a, TS3c, TS4a, TS4c, and TS5 regions.

As depicted in Fig. 9(a), the Ē_trans between the Cp and N₂ fragments initially increases with d_S during the C–N bond-breaking process, eventually plateauing at ∼5 Å for all trajectories integrated from different transition state regions (TS1, TS3a, TS3c, TS4a, TS4c, TS5) and the SOS region. However, due to differences in the pathways followed by synchronous (TS1, SOS) and asynchronous (TS3a, TS3c, TS4a, TS4c, TS5) trajectories, variations in post-TS/SOS kinetic energy release are observed.

Trajectories from TS1 and SOS regions exhibit higher Ē_trans because they involve synchronous breaking of both C–N bonds and immediate formation of the C1–C3 bond. This is accompanied by lower Ē_rot for both N₂ and Cp, as shown in Fig. 9(b) and (c). Notably, Ē_trans is slightly higher for SOS trajectories compared to TS1 trajectories, as the former involves direct formation of Cp rather than the intermediate Int1 seen in the latter.

In contrast, trajectories from asynchronous transition states exhibit lower Ē_trans due to the involvement of TMD and DZ intermediates, which facilitate energy redistribution among the internal degrees of freedom. Among these, TS5 trajectories exhibit relatively higher Ē_trans because, in most cases, the C3–N4 bond dissociates directly from the transition state region, forming SI Cp in approximately 65 fs. This is consistent with the lower average rotational energy of the N₂ fragment observed in TS5 trajectories compared to those initiated from other asynchronous stepwise transition states (TS3a, TS3c, TS4a, TS4c).

For trajectories following asynchronous stepwise pathways, the N₂ group rotates around the C3–N4 bond to access different asynchronous intermediates before breaking the C3–N4 bond to form Cp. This results in higher Ē_rot for both Cp and N₂, as shown in Fig. 9(b) and (c).

4 Summary and conclusions

The post-transition state and post-second-order saddle dynamics of the thermal denitrogenation of 1-pyrazoline were investigated using ab initio classical trajectory simulations. Trajectories were initiated from different transition state regions corresponding to synchronous and asynchronous pathways, which involve simultaneous and sequential breaking of the two C–N bonds, respectively.

Trajectories initiated from the synchronous transition state (TS1) region predominantly followed the minimum energy pathway, leading to the formation of the trimethylene diradical (Int1). This intermediate subsequently formed cyclopropane (Cp) with a preference for single inversion of the configuration. In contrast, most of the trajectories integrated from the SOS region exhibited no inversion at the terminal C1 and C3 carbon centers of Int1, resulting in Cp with retention of the configuration.

For trajectories initiated from the asynchronous transition state regions, most did not follow the minimum energy pathway (MEP). Although these trajectories accessed both the diazenyl diradical and trimethylene diradical regions, the average lifetimes of the diazenyl diradical were longer than those of the trimethylene diradical. The majority of the trajectories initiated from the TS5 region followed the minimum energy path corresponding to a concerted N₂ extrusion via an S_H2 pathway and resulted in significant inversion at the C3 carbon bonded to the N₂ group in the transition state.

During the dissociation process, all trajectories passed through the diradical region, regardless of the pathway followed. The TS1 and SOS trajectories, which follow the synchronous path, exhibited shorter trimethylene diradical lifetimes, averaging 128 fs and 100 fs, respectively. In contrast, asynchronous trajectories initiated from the TS3a, TS3c, TS4a, and TS4c regions displayed longer diradical (DZ+TMD) lifetimes, with averages of 206 fs, 192 fs, 199 fs, and 178 fs, respectively. However, the trimethylene diradical in these asynchronous pathways remained short-lived, with average lifetimes of 55 fs, 55 fs, 46 fs, and 54 fs, respectively. Interestingly, the average diradical (DZ+TMD) lifetime for TS5 trajectories following the S_H2 pathway was the shortest (∼65 fs). The non-exponential distribution of diradical lifetimes observed in trajectories initiated from different transition-state regions possibly indicates incomplete intramolecular vibrational energy redistribution, leading to a nonstatistical product distribution.^53,54

In the simulations, the SI products ranged from 50% to 65.6% for 1-pyrazoline, depending on the pathway followed, compared to 73% observed in the experiments for trans-3,5-dimethyl-1-pyrazoline.¹⁶ When weighted by the expected incidence corresponding to the channels, the product distributions for the SI, DI, and retention products become 52.2%, 35.9%, and 11.8%, respectively. The discrepancies in the product distributions can be attributed to the effect of the methyl substituent, which is not considered in the present study.

In the literature, various intuitive synchronous pathways^16,18 as well as asynchronous pathways backed by CI calculations^26,27 have been proposed to account for the major SI Cp product observed experimentally in the thermal denitrogenation of 1-pyrazoline. Interestingly, our trajectory simulations reveal that the preference for SI Cp formation is independent of the reaction pathway. Both synchronous and asynchronous pathways yield similar stereochemical distributions of products, with trajectories from all six transition state regions showing a preference for SI Cp formation. Despite the significant lifetimes of diradical intermediates, the observed preference for SI Cp formation underscores the importance of dynamical effects in product formation and suggests the possibility of dynamical matching, as described by Carpenter.⁵⁵

Data availability

The data supporting this article are available from the corresponding author upon reasonable request.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank NISER Bhubaneswar for the computational facilities.

References

1. H.-U. Reissig and R. Zimmer, Chem. Rev., 2003, 103, 1151–1196.
2. C. A. Carson and M. A. Kerr, Chem. Soc. Rev., 2009, 38, 3051–3060.
3. P. Tang and Y. Qin, Synth., 2012, 44, 2969–2984.
4. D. Y.-K. Chen, R. H. Pouwer and J.-A. Richard, Chem. Soc. Rev., 2012, 41, 4631–4642.
5. R. D. Taylor, M. MacCoss and A. D. Lawson, J. Med. Chem., 2014, 57, 5845–5859.
6. T. T. Talele, J. Med. Chem., 2016, 59, 8712–8756.
7. J. Shearer, J. L. Castro, A. D. Lawson, M. MacCoss and R. D. Taylor, J. Med. Chem., 2022, 65, 8699–8712.
8. R. G. Bergman, J. Am. Chem. Soc., 1969, 91, 7405–7411.
9. R. Faust, Angew. Chem., Int. Ed., 2001, 40, 2251–2253.
10. H. Lebel, J.-F. Marcoux, C. Molinaro and A. B. Charette, Chem. Rev., 2003, 103, 977–1050.
11. C. Ebner and E. M. Carreira, Chem. Rev., 2017, 117, 11651–11679.
12. L. Dian and I. Marek, Chem. Rev., 2018, 118, 8415–8434.
13. D. E. Lewis, Angew. Chem., Int. Ed., 2013, 52, 11704–11712.
14. K. L. Rinehart Jr and T. V. Van Auken, J. Am. Chem. Soc., 1960, 82, 5251.
15. P. S. Engel, Chem. Rev., 1980, 80, 99–150.
16. R. J. Crawford and A. Mishra, J. Am. Chem. Soc., 1966, 88, 3963–3969.
17. H. Meier and K.-P. Zeller, Angew. Chem., Int. Ed. Engl., 1977, 16, 835–851.
18. T. C. Clarke, L. A. Wendling and R. G. Bergman, J. Am. Chem. Soc., 1977, 99, 2740–2750.
19. E. Muray, O. Illa, J. A. Castillo, Á. Álvarez-Larena, J. L. Bourdelande, V. Branchadell and R. M. Ortuño, J. Org. Chem., 2003, 68, 4906–4911.
20. M. Hamaguchi, M. Nakaishi, T. Nagai and H. Tamura, J. Org. Chem., 2003, 68, 9711–9722.
21. J. L. Garcia Ruano, S. A. Alonso de Diego, M. R. Martn, E. Torrente and A. M. Martin Castro, Org. Lett., 2004, 6, 4945–4948.
22. J. L. Garcia Ruano, M. T. Peromingo, M. R. Martn and A. Tito, Org. Lett., 2006, 8, 3295–3298.
23. D. Cruz Cruz, F. Yuste, M. R. Martin, A. Tito and J. L. Garcia Ruano, J. Org. Chem., 2009, 74, 3820–3826.
24. S. Shiraki, C. S. Vogelsberg and M. A. Garcia-Garibay, Photochem. Photobiol. Sci., 2012, 11, 1929–1937.
25. T. Y. Chang, D. M. Adrion, A. R. Meyer, S. A. Lopez and M. A. Garcia-Garibay, J. Org. Chem., 2022, 87, 2277–2288.
26. P. B. Condit and R. G. Bergman, J. Chem. Soc., Chem. Commun., 1971, 4b-6.
27. P. C. Hiberty and Y. Jean, J. Am. Chem. Soc., 1979, 101, 2538–2543.
28. P. Cadman, H. Meunier and A. Trotman-Dickenson, J. Am. Chem. Soc., 1969, 91, 7640–7644.
29. G. Loper and F. Dorer, J. Am. Chem. Soc., 1973, 95, 20–27.
30. P. Mahata, A. K. Rauta and B. Maiti, J. Chem. Phys., 2022, 157, 194302.
31. J. Jiménez, J. Bourdelande and R. M. Ortuño, Tetrahedron, 1997, 53, 3777–3786.
32. M. Hamaguchi, M. Nakaishi, T. Nagai, T. Nakamura and M. Abe, J. Am. Chem. Soc., 2007, 129, 12981–12988.
33. W. L. Carter and R. G. Bergman, J. Am. Chem. Soc., 1968, 90, 7344–7346.
34. R. G. Bergman and W. L. Carter, J. Am. Chem. Soc., 1969, 91, 7411–7425.
35. J. A. Berson and J. M. Balquist, J. Am. Chem. Soc., 1968, 90, 7343–7344.
36. R. Pradhan and U. Lourderaj, Phys. Chem. Chem. Phys., 2017, 19, 27468–27477.
37. C. Doubleday, K. Bolton and W. L. Hase, J. Am. Chem. Soc., 1997, 119, 5251–5252.
38. C. Doubleday, K. Bolton and W. L. Hase, J. Phys. Chem. A, 1998, 102, 3648–3658.
39. D. J. Mann and W. L. Hase, J. Am. Chem. Soc., 2002, 124, 3208–3209.
40. R. Pradhan and U. Lourderaj, Phys. Chem. Chem. Phys., 2019, 21, 12837–12842.
41. B. O. Roos, Adv. Chem. Phys., 1987, 399–445.
42. W. Hehre, L. Radom, P. v. R. Schleyer and J. A. Pople, Ab Initio Molecular Orbital Theory, J. Wiley and Sons, New York, 1986.
43. T. H. Dunning Jr, J. Chem. Phys., 1989, 90, 1007–1023.
44. R. A. Kendall, T. H. Dunning Jr and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806.
45. P. Ren, C. Wu and J. W. Ponder, J. Chem. Theory Comput., 2011, 7, 3143–3161.
46. W. L. Hase, Classical trajectory simulations: Initial conditions, Wiley Online Library, 2002, vol. 1, pp. 402–407.
47. K. Yadav, R. Pradhan and U. Lourderaj, Faraday Discuss., 2022, 238, 183–203.
48. U. Lourderaj, R. Sun, S. C. Kohale, G. L. Barnes, W. A. de Jong, T. L. Windus and W. L. Hase, Comput. Phys. Commun., 2014, 185, 1074–1080.
49. M. Valiev, E. Bylaska, N. Govind, K. Kowalski, T. Straatsma, H. V. Dam, D. Wang, J. Nieplocha, E. Apra, T. Windus and W. de Jong, Comput. Phys. Commun., 2010, 181, 1477–1489.
50. S. Pedersen, J. Herek and A. Zewail, Sci., 1994, 266, 1359–1364.
51. A. Sinicropi, C. S. Page, W. Adam and M. Olivucci, J. Am. Chem. Soc., 2003, 125, 10947–10959.
52. W. L. Hase, Encyclopedia of Computational Chemistry, 2002, vol. 1, pp. 399–402.
53. U. Lourderaj and W. L. Hase, J. Phys. Chem. A, 2009, 113, 2236–2253.
54. B. Jayee and W. L. Hase, Annu. Rev. Phys. Chem., 2020, 71, 289–313.
55. B. K. Carpenter, J. Am. Chem. Soc., 1985, 107, 5730–5732.

---

Footnote

† Electronic supplementary information (ESI) available: Potential energy profiles for synchronous and asynchronous pathways; plots of C–C bond distances and electron densities; plots of dihedral angles and C–N bond distances; plots of C–N bond distances vs. time; lifetime distribution plots for diradicals; matrix displaying number of inversions at carbon centers. See DOI: https://doi.org/10.1039/d5cp00798d

---