Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Synthesis and properties of anhydrous rare-earth phosphates, monazite and xenotime: a review
Saehwa Chong *a,
Brian J. Riley
*a,
Brian J. Riley *a,
Xiaonan Lu
*a,
Xiaonan Lu a,
Jincheng Du
a,
Jincheng Du b,
Thiruvillamalai Mahadevanb and
Vinay Hegdec
b,
Thiruvillamalai Mahadevanb and
Vinay Hegdec
aPacific Northwest National Laboratory, Richland, WA 99354, USA. E-mail: saehwa.chong@pnnl.gov; brian.riley@pnnl.gov; Tel: +1-509-375-2469 Tel: +1-509-372-4651
bUniversity of North Texas, Denton, TX 76203, USA
cCitrine Informatics, Redwood City, CA 94063, USA
First published on 13th June 2024
Abstract
The synthesis methods, crystal structures, and properties of anhydrous monazite and xenotime (REPO4) crystalline materials are summarized within this review. For both monazite and xenotime, currently available Inorganic Crystal Structure Database data were used to study the effects of incorporating different RE cations on the unit cell parameters, cell volumes, densities, and bond lengths. Domains of monazite-type and xenotime-type structures and other AXO4 compounds (A = RE; X = P, As, V) are discussed with respect to cation sizes. Reported chemical and radiation durabilities are summarized. Different synthesis conditions and chemicals used for single crystals and polycrystalline powders, as well as first-principles calculations of the structures and thermophysical properties of these minerals are also provided.
1 Introduction
Monazite and xenotime compounds are anhydrous rare-earth (RE) phosphates with the chemical formula REPO4 but with different crystal symmetries. The mineral name “monazite” is derived from “monazein” meaning “to be solitary” in Greek, and the mineral name “xenotime” is derived from the combined words of “xenos” and “time” meaning “foreign” and “honor” in Greek.1 Naturally occurring monazite and xenotime minerals are often found as accessory minerals along with allanite, sphene, fluorite, and apatite in granitic rocks, pegmatites, carbonatites, and gneisses.1,2 The monazite and xenotime minerals found in nature often contain mixed RE elements as well as thorium and/or uranium along with other oxides, and the deposits are found in various countries including Australia, Brazil, Canada, China, India, Italy, Madagascar, Sri Lanka, and the United States.1,3–5 For example, the compositions of natural monazites from seven different regions were 35–65 mass% of mixed REs, 24–30 mass% of P2O5, 0–16 mass% of UO2, 4–14 mass% of ThO2, and 2–7 mass% of other oxides, and among the mixed REs, La, Ce, and Nd were the major components.2,3,6 The natural xenotime mineral generally contains mixed heavy REs (i.e., RE = Gd → Lu + Y, Sc) and less actinides compared to monazite (i.e., RE = La → Dy). The compositions of natural xenotime from two regions were 62–65 mass% of mixed RE oxides, 29–36 mass% of P2O5, 0.1–1.6 mass% of UO2, 0.2–0.3 mass% of ThO2, and 0.1–1.3 mass% of other oxides, and among the mixed REs, Y, Gd, Dy, and Er were the major components.7,8 Rhabdophane minerals are hydrated RE-phosphates with the chemical formula of REPO4·xH2O and they are found as accessory minerals in granitic rocks. Rhabdophane minerals generally contains mixed REs with relatively high amounts of Ce and La elements, U and Th actinides, and one water molecule (7–8 mass%) per formula unit.9 Studies have shown that the rhabdophane structure can transform to the monoclinic monazite structure through heat treatments.10,11Both monazite and xenotime compounds have attractive physical and chemical properties over a wide range of applications including nuclear waste forms,12–20 light emitting materials (e.g., as scintillators for γ-ray or X-ray detection, as thermophosphors),1,21–25 and coating materials.26–28 For applications in nuclear waste forms, the REPO4 compounds have been studied extensively due to high chemical durabilities, resistance to radiation damage, a wide variety of natural analogs, and their potential to incorporate RE, U, and Th elements in the structures.12–15,17,29 The flexibility of the RE–O bond distances in REOx polyhedra, while maintaining the structure, enables the incorporation and substitution of different heavy radioactive cations. This possibility of monazite and xenotime to incorporate many different radionuclides into a single structure makes it an ideal waste form that eliminates the need to determine the radionuclide partition coefficients between phases and concerns for differences in mechanical properties and corrosion mechanisms.12 Both monazite and xenotime can be synthesized relatively easily (see Section 2 for details), and their chemical durabilities are much higher (up to a factor of 20 in leach rates for certain elements) than borosilicate glass waste forms.12 Natural monazite was shown to maintain high retention of fission products during erosion, which was attributed to its slow dissolution rate.13 In addition, both compounds have high thermal stabilities with melting temperatures above 2000 °C.12
Monazite compounds can be used as light emitting materials with interesting optical properties.21–23 Wang et al.21 investigated the luminescence behavior of Eu-doped LaPO4 nanorods and showed the emission spectrum dependency on polarization for electric and magnetic dipole transitions. With high quantum efficiency and a high degree of polarization, the Eu-doped LaPO4 nanorods can be used as high resolution probes in 3D flow-shear tomography.21 Hashimoto et al.22 observed that doping a small amount of Th and borate into monazite compounds containing mixed RE cations of La, Ce, and/or Tb improved the light emission intensity and stability of green light, and these phosphors used in fluorescent lamps can minimize the brightness loss at high temperatures. Jeon et al.23 doped La- and Ca-containing monazite compounds with Eu and/or Dy ions, and single-phase white-light emission was observed at near-ultraviolet excitation.
The LaPO4 monazite has also been explored as a coating material to minimize high-temperature oxidation.26–28 Morgan et al.27 showed that LaPO4 and alumina interfaces without impurities were stable and retained the ability to debond after heat treatment at 1600 °C in air but observed the formation of La-containing β-alumina-magnetoplumbite in the presence of alkali metal or divalent elements near the interface. Kuo and Kriven26 showed that three laminates composed of LaPO4 as one component and Al2O3, Y3Al5O12, or LaAl11O18 as the other component were thermally stable up to 1600 °C and could be used as high-temperature materials in an oxidizing environment. Boakye et al.28 showed that coating the SiC fibers with LaPO4 did not degrade fiber strength, and a heat treatment at 1200 °C for 1–20 h in argon resulted in the formation of La2Si2O7, while the monazite was stable with SiC when the same heat treatment was done in air.
In this review, synthesis methods, crystal structures, and properties of anhydrous REPO4 compounds are summarized. Studies on the chemical durability and radiation stability, as well as different models for phase stability of monazite and xenotime are also summarized.
2 Synthesis methods
Different methods, including flux-assisted, solid state, hydrothermal, aqueous, dehydration, and gel-based methods, have been used for the synthesis of monazite and xenotime compounds. Table 1 summarizes the synthesis conditions for REPO4 compounds.| RE | Form | Method | Precursors | Flux | Ratio | T (°C) | td (h) | Tc (°C) | rc (°C h−1) | Ref. |
|---|---|---|---|---|---|---|---|---|---|---|
| a The molar ratio of REPO4 to flux. The td is the dwell time, “Tc” represents the temperature that the mixture was slowly cooled to grow single crystals, and rc is the cooling rate. | ||||||||||
| La | S | Flux | La2O3, PbHPO4 | Pb2P2O7 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 24 24 |
1300 | 12 | 975 | 2 | 30 |
| La | S | Flux | La2O3, PbHPO4 | Pb2P2O7 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 17 17 |
1360 | 16 | 900 | 1 | 31 |
| La | S | Hydrothermal | LaCl3·7H2O, H3PO4 | — | — | 140 | 12 | — | — | 32 |
| La | S | Hydrothermal | La(NO3)3·6H2O, NaH2PO4 | — | — | 120–200 | — | — | — | 33 |
| La | P | Solid state | La2O3, NH4H2PO4 | — | — | 1350 | 2 | — | — | 34 |
| La | P | Solid state | La2O3, NH4H2PO4 | — | — | 1250 | 24 | — | — | 35 |
| La | P | Aqueous | La2O3, H3PO4 | — | — | 80–200 | 1–48 | — | — | 36 |
| La | P | Dehydration | LaPO4·xH2O | — | — | 500 | 1 | — | — | 10 |
| Ce | S | Flux | CeO2, PbHPO4 | Pb2P2O7 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 24 24 |
1300 | 12 | 975 | 1 | 30 |
| Ce | S | Hydrothermal | Ce(NO3)3·6H2O, H3PO4 | — | — | 140 | 12 | — | — | 32 |
| Ce | P | Solid state | CeO2, NH4H2PO4 | — | — | 1350 | 2 | — | — | 34 |
| Ce | P | Dehydration | CePO4·xH2O | — | — | 800 | 1 | — | — | 37 |
| Ce | P | Dehydration | CePO4·xH2O | — | — | 600 | 1 | — | — | 10 |
| Pr | S | Flux | Pr6O11, PbHPO4 | Pb2P2O7 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 24 24 |
1300 | 12 | 975 | 2 | 30 |
| Pr | P | Solid state | Pr2O3, NH4H2PO4 | — | — | 1250 | 24 | — | — | 35 |
| Pr | P | Solid state | Pr2O3, NH4H2PO4 | — | — | 1350 | 2 | — | — | 34 |
| Pr | P | Dehydration | PrPO4·xH2O | — | — | 700 | 1 | — | — | 10 |
| Nd | S | Flux | Nd2O3, KH2PO4 | K6P4O13 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 4 |
1000 | 24 | 840 | <0.2 | 38 |
| Nd | S | Flux | Nd2O3, Li2CO3, MoO3 | Li2Mo2O7 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 4 |
1020 | 720 | — | <0.2 | 39 |
| Nd | S | Flux | Nd2O3, PbHPO4 | Pb2P2O7 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 24 24 |
1300 | 12 | 975 | 2 | 30 |
| Nd | S | Flux | Nd2O3, PbHPO4 | Pb2P2O7 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 17 17 |
1360 | 16 | 900 | 1 | 40 |
| Nd | P | Solid state | Nd2O3, NH4H2PO4 | — | — | 1350 | 2 | — | — | 34 |
| Nd | P | Dehydration | NdPO4·xH2O | — | — | 700 | 1 | — | — | 10 |
| Sm | S | Flux | Sm2O3, PbHPO4 | Pb2P2O7 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 24 24 |
1300 | 12 | 975 | <4 | 30 |
| Sm | P | Solid state | Sm2O3, NH4H2PO4 | — | — | 1350 | 2 | — | — | 34 |
| Sm | P | Dehydration | SmPO4·xH2O | — | — | 700 | 1 | — | — | 10 |
| Eu | S | Flux | Eu2O3, PbHPO4 | Pb2P2O7 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 24 24 |
1300 | 12 | 975 | <4 | 30 |
| Eu | P | Solid state | Eu2O3, NH4H2PO4 | — | — | 1350 | 2 | — | — | 34 |
| Gd | S | Flux | Gd2O3, PbHPO4 | Pb2P2O7 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 24 24 |
1300 | 12 | 975 | <4 | 30 |
| Gd | P | Solid state | Gd2O3, NH4H2PO4 | — | — | 1350 | 2 | — | — | 34 |
| Gd | P | Dehydration | GdPO4·xH2O | — | — | 800 | 1 | — | — | 10 |
| Tb* | P | Aqueous | Tb(NO3)3·nH2O, H3PO4 | — | — | 950 | 8 | — | — | 41 |
| Dy* | P | Aqueous | Dy(NO3)3·nH2O, H3PO4 | — | — | 730 | 4 | — | — | 41 |
| Tb | S | Flux | Gd2O3, PbHPO4 | Pb2P2O7 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 24 24 |
1300 | 12 | 975 | <4 | 30 |
| Tb | P, S | Aqueous-flux | Tb(NO3)3·xH2O, NH4H2PO4 | Na2CO3-MoO3 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50a 50a |
1350 | 15 | 870 | 3 | 42 |
| Dy | P | Dehydration | DyPO4·xH2O | — | — | 1050 | 1 | — | — | 10 |
| Dy | P, S | Aqueous-flux | Dy(NO3)3·xH2O, NH4H2PO4 | NaHCO3-MoO3 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50a 50a |
1375 | 144–168 | 870 | 3 | 43 |
| Ho | P, S | Aqueous-flux | Ho(NO3)3·xH2O, NH4H2PO4 | Na2CO3-MoO3 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50a 50a |
1350 | 15 | 870 | 3 | 42 |
| Er | P, S | Aqueous-flux | Er(NO3)3·xH2O, NH4H2PO4 | NaHCO3-MoO3 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50a 50a |
1375 | 144–168 | 870 | 3 | 43 |
| Tm | P, S | Aqueous-flux | Tm(NO3)3·xH2O, NH4H2PO4 | Na2CO3-MoO3 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50a 50a |
1350 | 15 | 870 | 3 | 42 |
| Yb | S | Flux | Yb2O3, PbHPO4 | Pb2P2O7 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 24 24 |
1300 | 12 | 975 | 0.5 | 30 |
| Lu | P, S | Aqueous-flux | Lu(NO3)3·xH2O, NH4H2PO4 | Na2CO3-MoO3 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50a 50a |
1350 | 15 | 870 | 3 | 42 |
| Y | P, S | Aqueous-flux | Y(NO3)3·xH2O, NH4H2PO4 | NaHCO3-MoO3 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50a 50a |
1375 | 144–168 | 870 | 3 | 43 |
| Y | S | Flux | Y2O3, PbHPO4 | Pb2P2O7 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 24 24 |
1357 | Several days | 897 | 1 | 44 |
| Sc | S | Flux | Sc2O3, PbHPO4 | Pb2P2O7 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 24 24 |
1357 | Several days | 897 | 1 | 44 |
Feigelson30 synthesized single crystals of LaPO4, CePO4, PrPO4, NdPO4, SmPO4, EuPO4, and GdPO4 monazite compounds as well as TbPO4 and YbPO4 xenotime compounds using Pb2P2O7 flux. The mixture of RE oxides and lead hydrogen phosphate (PbHPO4) with the mass ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 24 was placed in the Pt crucible and heated to 1300 °C at 300 °C h−1 and dwelled for 12 h at 1300 °C, and PbHPO4 was converted to lead pyrophosphate (Pb2P2O7) on heating. The mixture was slowly cooled to 975 °C at <4 °C h−1 and then naturally cooled to room temperature as the authors believed that crystallization did not proceed below 975 °C. The single crystals of monazite compounds were separated from the flux using diluted HNO3 solution. The monazite crystals had platelike morphologies, and the crystal sizes of LaPO4, PrPO4, and NdPO4 were ∼6 mm × ∼3 mm × ∼0.5 mm (the crystal sizes of other monazites were not reported). Decreasing cooling rate increased the crystal sizes of xenotime compounds. For YbPO4, a plate crystal with dimensions of 45 mm × 25 mm × 0.25 mm was obtained when cooled at 0.5 °C h−1. The single crystal or polycrystalline compound of TbPO4 could be prepared using TbO2−x with PbHPO4 or H3PO4 respectively, and similar optical characteristics were observed from each compound. For the flux matrix, Pb2P2O7 was the main phase, but other phosphates including Pb5P4O15, Pb4P2O9, and/or Pb3P2O8 were found with loss of phosphorus after formation of REPO4.
24 was placed in the Pt crucible and heated to 1300 °C at 300 °C h−1 and dwelled for 12 h at 1300 °C, and PbHPO4 was converted to lead pyrophosphate (Pb2P2O7) on heating. The mixture was slowly cooled to 975 °C at <4 °C h−1 and then naturally cooled to room temperature as the authors believed that crystallization did not proceed below 975 °C. The single crystals of monazite compounds were separated from the flux using diluted HNO3 solution. The monazite crystals had platelike morphologies, and the crystal sizes of LaPO4, PrPO4, and NdPO4 were ∼6 mm × ∼3 mm × ∼0.5 mm (the crystal sizes of other monazites were not reported). Decreasing cooling rate increased the crystal sizes of xenotime compounds. For YbPO4, a plate crystal with dimensions of 45 mm × 25 mm × 0.25 mm was obtained when cooled at 0.5 °C h−1. The single crystal or polycrystalline compound of TbPO4 could be prepared using TbO2−x with PbHPO4 or H3PO4 respectively, and similar optical characteristics were observed from each compound. For the flux matrix, Pb2P2O7 was the main phase, but other phosphates including Pb5P4O15, Pb4P2O9, and/or Pb3P2O8 were found with loss of phosphorus after formation of REPO4.
Similar to Feigelson's flux method, Mullica et al.31,40,45 synthesized the single crystals of LaPO4, PrPO4, NdPO4, SmPO4, EuPO4, and GdPO4 using Pb2P2O7 as a flux. The mixture of RE oxides and PbHPO4 with the mass ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 17 was placed in a Pt crucible and heated to 1360 °C for 16 h. After heat treatment, the mixture was slowly cooled to 900 °C at 1 °C h−1 and then naturally cooled to room temperature.
17 was placed in a Pt crucible and heated to 1360 °C for 16 h. After heat treatment, the mixture was slowly cooled to 900 °C at 1 °C h−1 and then naturally cooled to room temperature.
Hirsch et al.35 used a solid-state method to prepare polycrystalline powders of LaPO4, PrPO4, and mixed La1−xPrxPO4 monazite compounds. The appropriate amounts of RE oxides and NH4H2PO4 (ADP) were homogenized, pressed into pellets, placed in alumina crucibles, and heated at 1250 °C for 24 h at ambient atmosphere, and the final products were pure monazites.35 Perrière et al.34 used a similar method to synthesize LaPO4, CePO4, PrPO4, NdPO4, SmPO4, EuPO4, and GdPO4. The mixture of RE oxides and ADP was heated at 1350 °C for 2 h in air twice to make pure monazite powders.34
Khalili et al.36 prepared LaPO4 monazite, Lu2O3 xenotime, and Yb2O3 xenotime using RE2O3 and H3PO4. Powder of RE2O3 (0.002 mol) was added to round bottomed flask containing 13.7 mL of 14.6 M H3PO4 and stirred with magnetic stir for 1–24 h. The solution was diluted by adding 100 mL of water and refluxed at 130 °C for 2 h. The precipitate was filtered and washed with DIW. The sample was dried overnight and then heated to 80 °C for 1 h, and half of sample was heated at 200 °C for up to 48 h for complete dehydration. Sample heated at 80 and 200 °C were compared. The synthesized LaPO4 monazite was a polycrystalline powder containing some rhabdophane, and the xenotime powders were pure LuPO4 and YbPO4 compounds.
Cao et al.32 synthesized LaPO4 and CePO4 nanorods using LaNO3, CeNO3, and H3PO4 precursors. Here, 1 M La(NO3)3 or 1 M Ce(NO3)3 and 0.7 M H3PO4 were added to a solution of cetrimonium bromide in cyclohexane and n-pentanol. Solutions were mixed for 30 min and transferred to autoclaves. The autoclaves were heated at 140 °C for 12 h and cooled to room temperature. The crystals were washed with ethanol and DIW several times and dried in vacuum at room temperature. The obtained LaPO4 and CePO4 nanorods had about 5 μm lengths and 20–60 nm diameters.
Li and Ma33 synthesized LaPO4:Eu crystals using La(NO3)3·6H2O and Eu(NO3)3·5H2O with a molar ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.05 dissolved in DIW, and addition 5 mL of 1 M NaH2PO4 aqueous solution was done while stirring. Here, HNO3 or NaOH were added to adjust to a specific pH. The solution was put into an autoclave and heated at different temperature (120–180 °C). The resulting product was centrifuged and washed with DIW and dried at 60 °C for 12 h.
0.05 dissolved in DIW, and addition 5 mL of 1 M NaH2PO4 aqueous solution was done while stirring. Here, HNO3 or NaOH were added to adjust to a specific pH. The solution was put into an autoclave and heated at different temperature (120–180 °C). The resulting product was centrifuged and washed with DIW and dried at 60 °C for 12 h.
Wang et al.39 synthesized a single crystal of NdPO4 using Li2Mo2O7 as a flux. The Li2CO3 and MoO3 powders were used to prepare the Li2Mo2O7 flux. The mixture of Nd2O3 and Li2Mo2O7 with the mass ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 was placed in the Pt crucible and heated to 1020 °C for 24 h. A seed crystal was immersed in the solution and rotated at 30 rpm, and the single crystal was grown in the mixture cooling at 0.05–0.2 °C h−1 for ∼30 d. The resulting single crystal had the size of several millimeters.
4 was placed in the Pt crucible and heated to 1020 °C for 24 h. A seed crystal was immersed in the solution and rotated at 30 rpm, and the single crystal was grown in the mixture cooling at 0.05–0.2 °C h−1 for ∼30 d. The resulting single crystal had the size of several millimeters.
Poitrasson et al.46 synthesized polycrystalline NdPO4 and GdPO4 compounds using a combined method of gelation and flux-assisted growth. The NdPO4 gel was prepared by dissolving Nd(NO3)3 and adding (NH4)2HPO4 solution. Precipitation of NdPO4 occurred while drying for several days, and the final NdPO4 product was obtained after briefly heating above 600 °C to remove NH3 and nitrates. The recovered NdPO4 powder was mixed with Li2MoO4 and MoO3 in the mass ratio of ∼2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, respectively, and placed in a Pt crucible. The crucible was heated at 800 °C for 24 h, and polycrystalline NdPO4 powder was recovered by dissolving the flux in boiling water. A similar method was used for GdPO4 synthesis.
1, respectively, and placed in a Pt crucible. The crucible was heated at 800 °C for 24 h, and polycrystalline NdPO4 powder was recovered by dissolving the flux in boiling water. A similar method was used for GdPO4 synthesis.
Different studies showed that monazite compounds can be easily synthesized by heat-treating rhabdophane. Jonasson and Vance10 showed that La-, Ce-, Pr-, Nd-, Sm-, and Gd-rhabdophane compounds converted to corresponding monazite compounds in 500–900 °C range after dehydration in 100–400 °C range. They observed that Dy rhabdophane compound converted to mixed phases of monazite and xenotime compounds at 950 °C and complete xenotime compound at 1050 °C.10 Adelstein et al.37 prepared CePO4 monazite by heating Ce rhabdophane at 800 °C for 1 h. However, a different study by Mesbah et al.47 showed that heating Nd, Eu, Gd, and Dy rhabdophane compounds at 200–500 °C converted them to NdPO4, EuPO4, GdPO4, and DyPO4 with tetragonal P3121 space group, which is different symmetry from monazite or xenotime.
Heuser et al.41 synthesized TbPO4 and DyPO4 with monazite structures using rhabdophane of TbPO4·nH2O and DyPO4·nH2O. The rhabdophane compounds were made using a similar precipitation method by Boakye et al.48 Solutions containing RE(NO3)3·nH2O and H3PO4 were mixed while controlling the RE![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P ratio and pH, and the precipitates were collected. The rhabdophane powders were heated at 200 °C for 2 h. Subsequently, Tb and Dy rhabdophane powders were heated at 950 °C for 8 h and 730 °C for 4 h, respectively, to convert to corresponding monazite compounds. The heating temperature and time were selected to avoid possible formation of xenotime structures.
P ratio and pH, and the precipitates were collected. The rhabdophane powders were heated at 200 °C for 2 h. Subsequently, Tb and Dy rhabdophane powders were heated at 950 °C for 8 h and 730 °C for 4 h, respectively, to convert to corresponding monazite compounds. The heating temperature and time were selected to avoid possible formation of xenotime structures.
3 Crystal structures
Monazite crystallizes in the monoclinic P21/n space group (REs are coordinated by nine oxygens), and xenotime crystallizes in the tetragonal I41/amd space group (REs are coordinated by eight oxygens) and is isostructural to zircon (ZrSiO4). Monazite compounds of lanthanides contain the lanthanide elements with larger ionic radii (ri) including La, Ce, Pr, Nd, Pm, Sm, Eu, Gd, Tb, and Dy whereas xenotime compounds contain the heavy lanthanide elements with smaller ri including Gd, Tb, Dy, Ho, Er, Tm, and Lu along with Sc and Y. The structural parameters of monazite and xenotime compounds at ambient conditions (293–300 K and 1 atm) reported in the Inorganic Crystal Structure Database (ICSD) are provided in Tables 2 and 3, respectively. It should be noted that, for the REPO4 compounds with RE elements, the mid-range of lanthanides (i.e., Gd, Tb, Dy) can crystallize in both monazite and xenotime structures. Formation of monazite or xenotime for Gd, Tb, and Dy elements can be controlled by synthesis conditions (see Section 2 for details). Fig. 1 shows the relationship of monazite and xenotime structures with respect to the crystal radii (rc) from Shannon.49 The unit cell parameters of the PmPO4 compound have been reported,50 but the overall structure data has not been reported in the ICSD. As for other RE elements, namely Y and Sc, YPO4 and ScPO4 (pretulite) have the xenotime structure. Both monazite and xenotime structures are commonly found in non-phosphate compounds including RE vanadates (REVO4) and RE arsenates (REAsO4).1 Details of the monazite and xenotime structures are discussed in the following sections.| RE | a (Å) | b (Å) | c (Å) | β (°) | V (Å3) | ρ (g cm−3) | RE–O (Å) | P–O (Å) | ICSD | Ref. |
|---|---|---|---|---|---|---|---|---|---|---|
| La | 6.7825 | 6.9896 | 6.6218 | 102.9602 | 305.92 | 5.08 | 2.5845 | 1.5493 | 46788 | 36 |
| La | 6.8313 | 7.0705 | 6.5034 | 103.27 | 305.73 | 5.08 | 2.5787 | 1.5384 | 79747 | 51 |
| La | 6.8413 | 7.078 | 6.5153 | 103.322 | 307 | 5.06 | 2.5855 | 1.6602 | 92155 | 52 |
| La | 6.825 | 7.057 | 6.482 | 103.21 | 303.94 | 5.11 | 2.5739 | 1.5350 | 201479 | 31 |
| La | 6.84133 | 7.07590 | 6.51233 | 103.28918 | 306.8 | 5.06 | 2.5729 | 1.5591 | 431743 | 35 |
| Ce | 6.77 | 7.04 | 6.46 | 104 | 298.74 | 5.23 | 2.6188 | 1.5421 | 22265 | 53 |
| Ce | 6.77 | 7.01 | 6.45 | 103.63 | 297.48 | 5.25 | 2.5467 | 1.5662 | 27860 | 54 |
| Ce | 6.79 | 7 | 6.46 | 104 | 297.92 | 5.24 | 2.5971 | 1.5154 | 33598 | 55 |
| Ce | 6.77 | 6.99 | 6.45 | 103.6 | 296.67 | 5.26 | 2.5360 | 1.6405 | 39135 | 56 |
| Ce | 6.77 | 6.99 | 6.45 | 103.63 | 296.63 | 5.26 | 2.5413 | 1.6024 | 43077 | 57 |
| Ce | 6.77 | 7.04 | 6.46 | 104 | 298.74 | 5.23 | 2.6084 | 1.6128 | 64850 | 53 |
| Ce | 6.7902 | 7.0203 | 6.4674 | 103.38 | 299.93 | 5.21 | 2.5586 | 1.5333 | 79746 | 51 |
| Ce | 6.788 | 7.0163 | 6.4650 | 103.43 | 299.49 | 5.21 | 2.5554 | 1.5375 | 79748 | 51 |
| Ce | 6.8072 | 7.00689 | 6.47476 | 103.781 | 299.94 | 5.21 | 2.5652 | 1.5318 | 133669 | 58 |
| Ce | 6.7551 | 6.9804 | 6.4687 | 103.707 | 296.33 | 5.27 | 2.5450 | 1.5316 | 133670 | 58 |
| Ce | 6.8004 | 7.0231 | 6.4717 | 103.46 | 300.6 | 5.19 | 2.5615 | 1.5397 | 182582 | 37 |
| Ce | 6.777 | 6.993 | 6.445 | 103.54 | 296.95 | 5.26 | 2.5506 | 1.5271 | 201029 | 59 |
| Ce | 6.78985 | 7.01813 | 6.46662 | 103.42415 | 299.72 | 5.21 | 2.5580 | 1.5330 | 243620 | 60 |
| Pr | 6.741 | 6.961 | 6.416 | 103.63 | 292.59 | 5.35 | 2.5323 | 1.5320 | 62161 | 40 |
| Pr | 6.7596 | 6.9812 | 6.4344 | 103.53 | 295.21 | 5.31 | 2.5395 | 1.5368 | 79749 | 51 |
| Pr | 6.77078 | 6.99017 | 6.44265 | 103.52914 | 296.46 | 5.28 | 2.5325 | 1.5631 | 431753 | 35 |
| Nd | 6.722 | 6.933 | 6.390 | 103.72 | 289.3 | 5.49 | 2.5192 | 1.5321 | 62162 | 40 |
| Nd | 6.732 | 6.930 | 6.383 | 103.61 | 289.42 | 5.49 | 2.5183 | 1.5369 | 62311 | 61 |
| Nd | 6.7352 | 6.9500 | 6.4049 | 103.68 | 291.31 | 5.45 | 2.5242 | 1.5371 | 79750 | 51 |
| Sm | 6.6818 | 6.8877 | 6.3653 | 103.86 | 284.42 | 5.73 | 2.4988 | 1.5370 | 79751 | 51 |
| Sm | 6.73167 | 6.94489 | 6.44964 | 103.899 | 292.7 | 5.57 | 2.5358 | 1.5305 | 133668 | 58 |
| Sm | 6.669 | 6.868 | 6.351 | 103.92 | 282.35 | 5.77 | 2.4932 | 1.5310 | 201839 | 45 |
| Eu | 6.6813 | 6.8618 | 6.3491 | 103.96 | 282.48 | 5.81 | 2.4902 | 1.5393 | 79752 | 51 |
| Eu | 6.639 | 6.823 | 6.318 | 104.00 | 277.69 | 5.91 | 2.4749 | 1.5299 | 201840 | 45 |
| Gd | 6.6435 | 6.8414 | 6.3281 | 103.976 | 279.1 | 6 | 2.4760 | 1.5383 | 79753 | 51 |
| Gd | 6.621 | 6.823 | 6.310 | 104.16 | 276.39 | 6.06 | 2.4693 | 1.5298 | 201841 | 45 |
| Gd | 6.652 | 6.847 | 6.336 | 103.99 | 280.02 | 5.98 | 2.4833 | 1.5373 | 230368 | 62 |
| Gd | 6.33571 | 6.84840 | 6.6516 | 104.023 | 280 | 5.98 | 2.4827 | 1.5325 | 252925 | 63 |
| Tb | 6.61993 | 6.81106 | 6.31653 | 104.1091 | 276.21 | 6.11 | 2.4571 | 1.5579 | 18864 | 41 |
| Dy | 6.59737 | 6.78650 | 6.30380 | 104.1887 | 273.63 | 6.25 | 2.4487 | 1.5536 | 18863 | 41 |
| RE | a (Å) | b (Å) | c (Å) | V (Å3) | ρ (g cm−3) | RE–O (Å) | P–O (Å) | ICSD | Ref. |
|---|---|---|---|---|---|---|---|---|---|
| Gd | 6.9670 | 6.9670 | 6.1112 | 296.63 | 5.64 | 2.3758 | 1.5541 | 118105 | 64 |
| Tb | 6.9414 | 6.9414 | 6.0704 | 292.49 | 5.77 | 2.3726 | 1.5302 | 29316 | 65 |
| Tb | 6.940 | 6.940 | 6.068 | 292.26 | 5.77 | 2.3822 | 1.5228 | 35704 | 66 |
| Tb | 6.9309 | 6.9309 | 6.0606 | 291.14 | 5.79 | 2.365 | 1.5359 | 79755 | 51 |
| Tb | 6.9391 | 6.9391 | 6.0694 | 292.25 | 5.77 | 2.3575 | 1.546 | 168751 | 67 |
| Dy | 6.91 | 6.91 | 6.04 | 288.4 | 5.93 | 2.3469 | 1.548 | 26440 | 68 |
| Dy | 6.907 | 6.907 | 6.046 | 288.43 | 5.93 | 2.3496 | 1.5491 | 35705 | 66 |
| Dy | 6.9052 | 6.9052 | 6.0384 | 287.92 | 5.94 | 2.3513 | 1.5372 | 79756 | 51 |
| Dy | 6.909 | 6.909 | 6.038 | 288.22 | 5.93 | 2.5927 | 1.3327 | 192553 | 69 |
| Ho | 6.882 | 6.882 | 6.025 | 285.36 | 6.05 | 2.3465 | 1.5326 | 35706 | 66 |
| Ho | 6.8773 | 6.8773 | 6.0176 | 284.62 | 6.07 | 2.3428 | 1.5319 | 79757 | 51 |
| Ho | 6.8842 | 6.8842 | 6.0255 | 285.56 | 6.05 | 2.34 | 1.5408 | 246677 | 70 |
| Ho | 6.8919 | 6.8919 | 6.0336 | 286.59 | 6.02 | 2.335 | 1.5525 | 257644 | 71 |
| Ho | 6.886 | 6.886 | 6.027 | 285.78 | 6.04 | 2.3499 | 1.5251 | 257646 | 71 |
| Er | 6.863 | 6.863 | 6.007 | 282.93 | 6.16 | 2.3289 | 1.542 | 15670 | 72 |
| Er | 6.860 | 6.860 | 6.003 | 282.5 | 6.17 | 2.3361 | 1.5313 | 36052 | 73 |
| Er | 6.8507 | 6.8507 | 5.9968 | 281.44 | 6.19 | 2.3303 | 1.5356 | 79758 | 51 |
| Tm | 6.839 | 6.839 | 5.986 | 279.98 | 6.26 | 2.3252 | 1.5326 | 36053 | 73 |
| Tm | 6.8293 | 6.8293 | 5.9798 | 278.89 | 6.29 | 2.3098 | 1.5544 | 79759 | 51 |
| Tm | 6.8219 | 6.8219 | 5.97988 | 278.29 | 6.3 | 2.3238 | 1.5195 | 257645 | 71 |
| Yb | 6.816 | 6.816 | 5.966 | 277.17 | 6.42 | 2.3095 | 1.5439 | 36054 | 73 |
| Yb | 6.8093 | 6.8093 | 5.9639 | 276.53 | 6.44 | 2.313 | 1.5319 | 79760 | 51 |
| Lu | 6.792 | 6.792 | 5.955 | 274.71 | 6.53 | 2.3045 | 1.5327 | 2505 | 74 |
| Lu | 6.7443 | 6.7443 | 6.0105 | 273.39 | 6.56 | 2.2974 | 1.5481 | 46792 | 36 |
| Lu | 6.7827 | 6.7827 | 5.9467 | 273.58 | 6.55 | 2.3002 | 1.5337 | 79761 | 51 |
| Lu | 6.7895 | 6.7895 | 5.9560 | 274.56 | 6.53 | 2.3093 | 1.5327 | 162336 | 75 |
| Lu | 6.792 | 6.792 | 5.954 | 274.67 | 6.53 | 2.2998 | 1.5386 | 201133 | 76 |
| Lu | 6.7967 | 6.7967 | 5.9593 | 275.29 | 6.51 | 2.3096 | 1.533 | 246684 | 70 |
| Y | 6.876 | 6.876 | 6.186 | 292.47 | 4.18 | 2.243 | 1.7179 | 24514 | 77 |
| Y | 6.878 | 6.878 | 6.036 | 285.54 | 4.28 | 2.387 | 1.5365 | 28554 | 78 |
| Y | 6.9 | 6.9 | 6.026 | 286.9 | 4.26 | 2.2494 | 1.6709 | 56113 | 79 |
| Y | 6.8947 | 6.8947 | 6.0276 | 286.53 | 4.26 | 2.345 | 1.54 | 79754 | 51 |
| Y | 6.885 | 6.885 | 6.022 | 285.46 | 4.28 | 2.3324 | 1.5503 | 117962 | 80 |
| Y | 6.90706 | 6.90706 | 6.0348 | 287.91 | 4.24 | 2.403 | 1.5302 | 133671 | 58 |
| Y | 6.8817 | 6.8817 | 6.0177 | 284.99 | 4.29 | 2.3365 | 1.5435 | 201131 | 76 |
| Sc | 6.578 | 6.578 | 5.796 | 250.79 | 3.71 | 2.2295 | 1.5606 | 16648 | 81 |
| Sc | 6.5787 | 6.5787 | 5.7963 | 250.86 | 3.7 | 2.2116 | 1.5336 | 74483 | 82 |
| Sc | 6.574 | 6.574 | 5.791 | 250.27 | 3.71 | 2.2067 | 1.5341 | 201132 | 76 |
| Sc | 6.578 | 6.578 | 5.796 | 250.79 | 3.7 | 2.2078 | 1.5367 | 257305 | 83 |
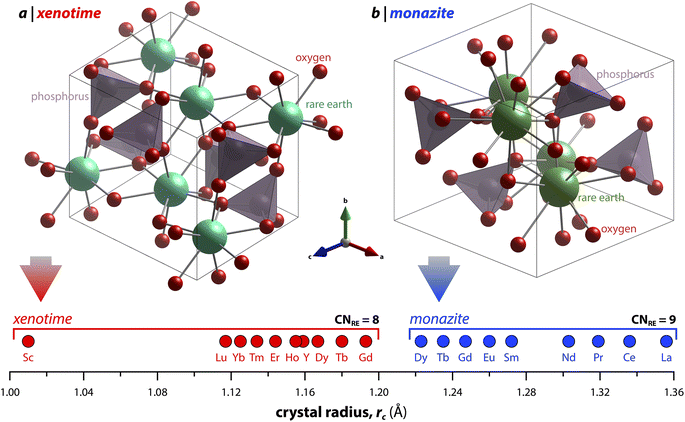 | ||
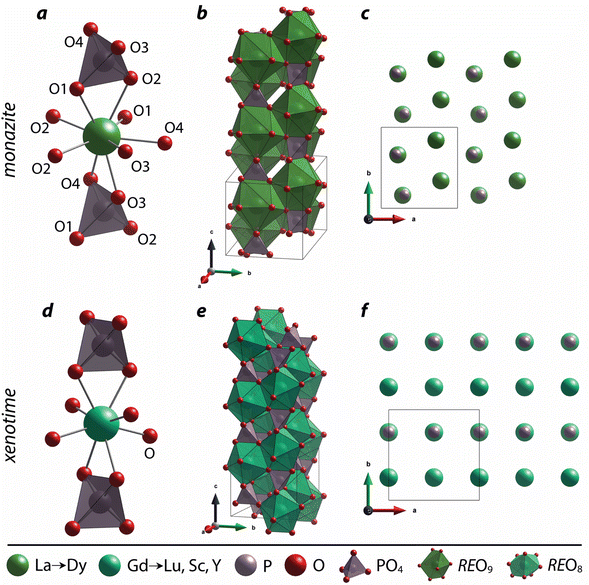
| Fig. 1 Illustration showing the relationship of (a) xenotime and (b) monazite structures of REPO4 to the RE crystal radii (rc) from Shannon.49 LuPO4 (ICSD 46792) and LaPO4 (ICSD 46788) were used to create the (a) xenotime and (b) monazite unit cell structures, respectively. | ||
The nine oxygen atoms coordinating the REs in monazite include five oxygen atoms forming a nearly equatorial pentagon whereas the other four oxygen atoms form a tetrahedron interpenetrating the pentagon (Fig. 2), and this coordination of REO9 was described as a pentagonal interpenetrating tetrahedral polyhedron (PITP).31,45 The interpenetrating tetrahedron of REO9 shares the edges with two adjacent PO4 tetrahedra (Fig. 2a), resulting in a chain-like structure along the c axis (Fig. 2b). Fig. 2c shows the atomic arrangement of RE and P atoms projected down [001].
Distortion of REO9 polyhedra and PO4 tetrahedra in the monazite structure was reported in the literature.1,59 The monazite structure has four oxygen atom positions (i.e., O1, O2, O3, and O4), and the O2 atom is shared by three RE cations and a P cation whereas O1, O3, and O4 atoms are shared by only two RE cations and a P cation. This bonding results in REO9 polyhedra with one longer RE–O2 distance compared to other eight RE–O distances. For example, the difference in RE–O bonding results in one longer ∼2.8 Å RE–O2 bond length compared to ∼2.5–2.6 Å of other eight RE–O bond lengths in CePO4.59 This RE-O coordination also affected the distortion of PO4 tetrahedra with different P–O bond lengths and O–P–O bond angles within a given PO4 tetrahedron.59 The distortion index84 value (D) can be used to show the average deviation of RE–O bond distances from their means within the REO9 polyhedra of monazite, and this is shown in eqn (1) where li is the distance from the central atom (i.e., RE) to the ith coordinating atom, and lav is the average bond length. The distortion indices of REO9 in monazite are in the range of 0.03–0.11 and were relatively higher than the distortion indices (0.01–0.06) of REO8 in the xenotime structures. The larger D value of REOx in monazite compared to xenotime was largely due to the one long RE–O2 bond. The distorted REO9 polyhedron in monazite has a set of nine different RE–O bond lengths, and this coordination is correlated to its capability to incorporate various cations and polyoxoanions in the structure.14 Generally, this type of irregular coordination of metal ions does not induce severe symmetry, charge, or size constraints on the incorporated cation.15,59
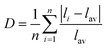 | (1) |
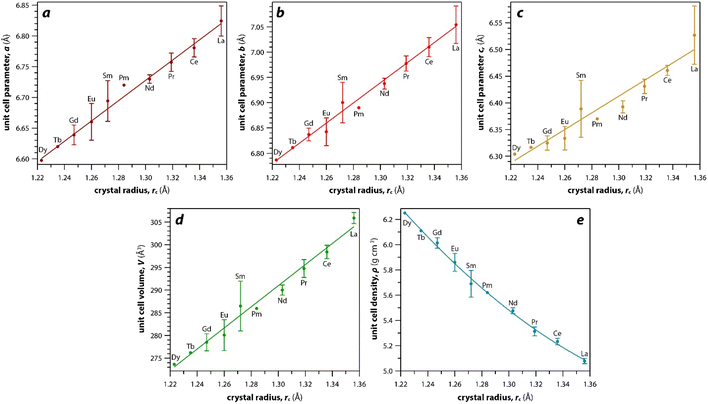
As mentioned earlier, the monazite structures incorporate light RE cations, including La → Dy. With larger RE cations (i.e., larger rc values)49 in the crystal structure, the unit cell parameters (i.e., a, b, c) and volumes (V) increase linearly whereas the densities (ρ) decrease nonlinearly (Fig. 3). Fig. 3 was drawn using the average values of a, b, c, V, and ρ of monazite compounds at atmospheric conditions reported in ICSD for each given RE. The crystal structure data of PmPO4 was not reported in the ICSD, and the unit cell parameter values from a study by Weigel et al.50 were used to fit the trendline.
The RE–O bond distances of monazite compounds were compared, and larger cations in REO9 polyhedra resulted in longer average RE–O bond distances (Fig. 4a). As discussed above, the RE cation in the monazite structure is coordinated by nine oxygen atoms, but presenting a single-digit coordination number might not be accurate in relatively distorted coordination polyhedra. The effective coordination numbers (CNeff)85–87 can be used to express more reasonable coordination numbers by accounting for all the surrounding atoms with a weighting scheme. The CNeff values of REO9 were calculated using eqn (2) and (3) where wi is the bond weight of the ith bond, lav is defined in eqn (4), li was defined above, and lmin is the shortest bond distance in the coordination polyhedron. These equations were formulated by combining the concepts of Pauling with effective coordination numbers and mean fictive ri values.87 The average CNeff value calculated for each RE element in monazites is plotted in Fig. 4b, and REO9 polyhedra with larger cations generally show higher CNeff values.
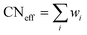 | (2) |
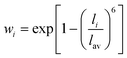 | (3) |
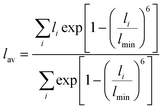 | (4) |
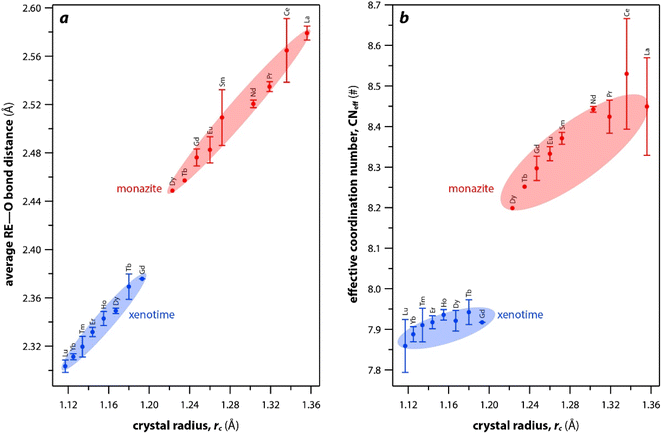 | ||
| Fig. 4 (a) Average RE–O bond distances and (b) effective coordination numbers of REOx polyhedral with respect to RE rc in monazite and xenotime structures. | ||
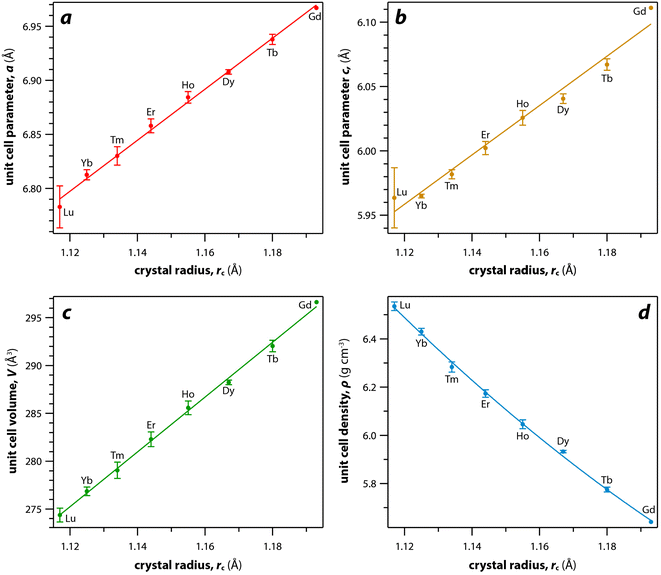
For the REO8 coordination in xenotime, each oxygen atom is shared by two RE atoms and one P atom. Similar to monazite, the REO8 polyhedra share the edges with two adjacent PO4 tetrahedra (Fig. 2d), forming a chain-like structure along the c axis (Fig. 2e). Fig. 2f shows the atomic arrangement of RE and P atoms projected down [001]. With smaller RE cations in the xenotime structures compared to monazite, the D values of REO8 polyhedra in xenotime structures are lower than those reported for monazite structures. The xenotime compounds have shorter RE–O distances (2.2–2.4 Å) compared to monazites (2.4–2.6 Å) (Fig. 4a). The P–O bond distances of tetrahedra in xenotime compounds are generally shorter than those in monazite, but the differences are not significant. Xenotime has only one atomic position for the oxygen atom whereas monazite has four oxygen atomic positions. For both monazite and xenotime compounds, RE–P distances are dependent on the RE size, and xenotime has one RE–P distance along the chain whereas the monazite has two different RE–P distances. The RE–P distances of xenotime crystals are generally longer than those of monazite, and RE–P distances between RE3+ and P5+ cations in xenotime are generally <3 Å. The CNeff values of xenotime compounds are smaller, in the range of 7.8–8.0, and smaller than monazite as expected (Fig. 4b). The unit cell parameters and volumes increase linearly with larger RE cations in the structures whereas the densities decrease nonlinearly (Fig. 5).
The RE3+ cations at RE sites in the monazite and xenotime structures can be substituted by mixed +3 cations, a combination of +2 and +4 cations, or a combination of +2, +3, and +4 cations. Table 4 shows the list of synthetic monazite and xenotime compounds with mixed RE and summarizes the compositional effects. For monazites with mixed RE cations, increasing the average size of mixed cations in the structures increases the unit cell parameters and volumes as expected.88–90 De Biasi et al.88 synthesized La1−xCexPO4 (x = 0–1) monazite compounds and showed that increasing La contents increased the unit cell parameters and cell volumes. Similarly, Terra et al.89 observed that increasing La contents in La1−xGdxPO4 (x = 0–1) monazites increased the unit cell parameters and cell volumes. Thust et al.91 observed that increasing Eu content in La1−xEuxPO4 (x = 0–1) monazite compounds increased the elastic stiffness coefficients, densities, heat capacities, and coefficients of thermal expansion (CTE). Arinicheva et al.92 observed that microhardness, fracture toughness, unit cell parameters, and cell volumes decreased linearly with increasing Eu content in La1−xEuxPO4 (x = 0–1) monazite compounds. Van Emden et al.90 synthesized Nd1−xYxPO4 (x = 0.05–0.3) monazite compounds using a solid state method at 1000 °C and showed that increasing Nd content increased the unit cell parameters and cell volumes. The same group also observed co-crystallization of both monazite and xenotime in Nd1−xYxPO4 compounds when synthesized at 1200 °C.90 Hay et al.93 synthesized the Gd1−xDyxPO4 (x = 0–1) xenotime compounds and observed that pressure and/or shear stress can cause phase transformation of xenotime to monazite. Strzelecki et al.94 investigated the thermodynamic properties of Er1−xYbxPO4 (x = 0–1) xenotime compounds and observed that increasing Er content increased the enthalpies of formation and decreased the Gibbs free energies. The unit cell parameters and cell volumes of Er1−xYbxPO4 (x = 0–1) increased with higher Er content as predicted by Vegard's law.94 Xiao et al.95 synthesized Eu3+-doped xenotime single crystals including TbPO4, HoPO4, ErPO4, YbPO4, LuPO4, and YPO4 with the Eu concentration of 200 ppm relative to the host RE cations. They observed that incorporation of Eu cations distorted the local structure around RE sites and affected the rotations of PO4 tetrahedra in the xenotime structures, and distortion levels were worse for xenotimes with large RE cations.95 Rafiuddin et al.96 synthesized solid solutions of La1−xYbxPO4, La1−xYxPO4, and Sm1−xHoxPO4 (x = 0–1) and observed that these compounds with large differences in RE sizes resulted in the presence of both monazite and xenotime phases in the final product, and the phase fractions were dependent on the corresponding RE contents.
| Composition | Struct. | Compositional effect | Ref. |
|---|---|---|---|
| La1−xCexPO4 (x = 0–1) | M | Increasing La content increased the unit cell lengths and volumes | 88 |
| La1−xGdxPO4 (x = 0–1) | M | Increasing La content increased the unit cell lengths and volumes | 89 |
| La1−xEuxPO4 (x = 0–1) | M | Increasing Eu content increased the elastic stiffness coefficients, density, heat capacity, and CTE | 91 |
| La1−xEuxPO4 (x = 0–1) | M | Increasing Eu content decreased the hardness, toughness, unit cell lengths, and cell volume | 92 |
| Nd1−xYxPO4 (x = 0.05–0.3) | M | Increasing Nd content increased the unit cell parameters and cell volumes | 90 |
| Gd1−xDyxPO4 (x = 0–1) | X | Increasing Gd content increased the maximum indentation loadings | 93 |
| Er1−xYbxPO4 (x = 0–1) | X | Increasing Er content increased the enthalpies of formation and unit cell parameters and decreased the Gibbs free energy values | 94 |
| REPO4 (RE = Tb, Ho, Er, Yb, Lu, Y) doped with Eu3+ | X | Incorporation of Eu cations distorted the local structure around RE sites and affected the rotations of PO4 tetrahedra, and the distortion level was worse for xenotimes with larger RE cations | 95 |
| La1−xYbxPO4, La1−xYxPO4, Sm1−xHoxPO4 (x = 0–1) | M, X | Both monazite and xenotime phases were present in the final product depending on the concentration of corresponding RE elements | 96 |
For the monazites with a mixed combination of +2 and +4 cations at RE sites, Pb, Cd, or alkaline earth metals (e.g., Mg, Ca, Sr, Ba) can be incorporated with actinide cations (e.g., Th, U, Np), respectively. The chemical formula is (Mx2+)(M(1–x)4+)PO4 and many examples have been documented, including Ca0.5Th0.5PO4,97 Mg0.5Th0.5PO4,98 Sr0.5Th0.5PO4,99 Pb0.5Th0.5PO4,99 Ca0.5U0.5PO4,100 Mg0.5U0.5PO4,98 Sr0.5U0.5PO4,98 Ca0.5Np0.5PO4,101 Ca0.5Np0.35Pu0.15PO4,102 and Ca0.5Th0.4U0.1PO4.103 For the monazites with mixed combinations of +2 cations (e.g., Ba, Ca, Cd, Mg, Pb, Sr), +3 cations (REs), and +4 cations (actinides) can occupy RE sites, and the site occupancies of cations with different oxidation states can vary at the RE sites (e.g., Ca1/3Nd1/3U1/3PO4, La0.808Ba0.096Th0.096PO4, Ca0.146Nd0.716Th0.151PO4).98,99,104 The monovalent cations (e.g., Li, Na, K, Rb, Cs) with +3 RE cations or Ce4+ can occupy the RE site of compounds that have similar structures to monazites [e.g., Na3La(PO4)2, LiCe2(PO4)3, K2Ce(PO4)2].105,106
AXO4 monazite-type structure stabilities can be dependent on various factors such as composition, temperature, pressure, and the irradiation conditions. Clavier et al.14 reviewed crystal chemistry of the AXO4 monazite-type compounds in terms of field of stability versus composition, with all the substitution possibilities on the cationic and anionic sites leading to the monazite structure.
Several models, which include structure-field maps (Fig. 6a)107,108 and classification diagrams (see Fig. 6b for a modified Bastide diagram),109–112 have been developed to correlate the stability of the monazite-type structure with geometric criteria. These representations provide opportunities to predict the structure of a compound. The challenge persists regarding the boundaries of the stability domain within this field. Numerous studies have investigated the stability domain of the monazite-type structure, aiming to develop predictive models that could anticipate whether a compound might take on the monazite structure. Carron et al.113 calculated that a value of 1.86 (ratio between the X–O bond length in the AXO4 compounds and the ri, denoted as X/ri) seems to specify the size limit of both the cation and the anion at the xenotime-monazite structural frontier. This ratio led to them113 proposing the potential for anionic isomorphous substitution among RE-phosphates, RE-silicates, RE-arsenates, and RE-vanadates. Macey114 further determined that monazite and zircon structures have X/ri < 1/1.56 and X/ri > 1/1.56, respectively.
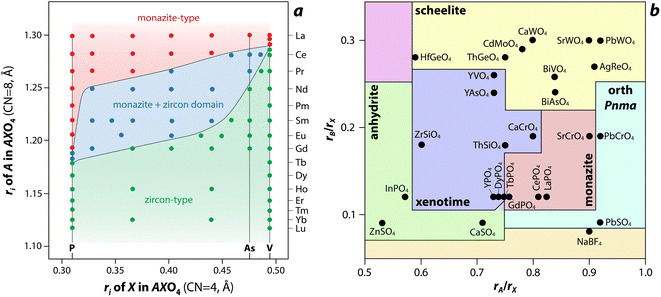 | ||
| Fig. 6 (a) Structure-field map of monazite and xenotime compounds based on the ionic radius (ri) of A (e.g., RE) and X (e.g., P) in AXO4 compounds.107 Reprinted with permission from Aldred.107 Copyright 1984 American Chemical Society. (b) Modified Bastide diagram for ABX4 compounds. Reprinted with permission from Hay et al.115 Copyright 2013 Elsevier. | ||
Podor and Cuney97 subsequently explored the stability range of the monazite structure, primarily concentrating on (M1–2x3+)(Mx2+)(Mx4+)PO4 compounds, where stability depends on three parameters (x, average ri, and the ratio of M elements). Nonetheless, discrepancies with experimental observations could still occur, particularly concerning miscibility gaps. Kolitsch and Holtstam116 devised a visual representation outlining the stability regions of both monazite and zircon-type structures, relying on existing data for REXO4 (X = P, As, V) compounds. While this diagram offers a broad view of the monazite structure stability field, it is insufficient to correctly describe the partial solid solutions between two REXO4 compounds, especially those involving a light RE element and a heavy RE element, and the presence of a miscibility gap.14
4 Properties
4.1 Mechanical and thermal properties
Monazite and xenotime compounds exhibit interesting mechanical and thermal properties across different compositions and structures. Table 5 summarizes the mechanical properties of monazite and xenotime including Young's modulus (E), bulk modulus (B), shear modulus (G), hardness (H), and flexural strength (FS). Fig. 7 shows the relationships between Young's, bulk, and shear moduli and RE rc of monazite and xenotime. As the RE rc values decrease, this results in increases for the Young's modulus, bulk modulus, and shear modulus, and this can be due to stronger interatomic bonding as the average RE–O distances are smaller for RE cations.117 Different modulus values from various studies are also affected by sample preparation and sintering conditions for the pellets.117,118| RE | Struct. | E (GPa) | B (GPa) | G (GPa) | H (GPa) | FS (Mpa) |
|---|---|---|---|---|---|---|
| La | M | 132,118 133,117 134,119 139.1*,120 144*,119 151 (ref. 34) | 99,119 117,117 107*,119 109.8*,120 134*121 | 51,117 53,119 54*,120 56*,119 58 (ref. 34) | 4.6,118 5 (ref. 122) | 109,34 100 (ref. 123) |
| Ce | M | 146.5*,120 150,117 162*119 | 118.6*,120 121,117 126*,119 137.2*121 | 56.6*,120 58,117 63*119 | — | 183 (ref. 123) |
| Pr | M | 150.1*,120 164 (ref. 34) | 113.5*,120 139.7*121 | 58.6*,120 64 (ref. 34) | — | 94 (ref. 34) |
| Nd | M | 154.1*,120 157,117 164,34 168*119 | 114.1*,120 127,117 135*,119 142.3*121 | 60.4*,120 61,117 63,34 65*119 | — | 122,34 97 (ref. 123) |
| Pm | M | 157.4*120 | 117.1*120 | 61.7*120 | — | — |
| Sm | M | 160,117 160.3*,120 172*119 | 116.2*,120 127,117 140*,119 146*121 | 62,117 63.1*,120 66*119 | — | 135 (ref. 123) |
| Eu | M | 162,117 163.1*,120 174*,119 202 (ref. 34) | 118.1*,120 127,117 143*,119 147.1*121 | 62,117 64.2*,120 67*,119 79 (ref. 34) | — | 99 (ref. 34) |
| Gd | M | 165.2*,120 172,117 180*,119 199 (ref. 93) | 121*,120 137,117 150*,119 149*121 | 64.9*,120 67,117 69*119 | 7.8,93 7.9 (ref. 124) | — |
| Tb | M | 164.5*120 | 123.3*120 | 64.4*120 | — | — |
| Dy | M | 165.4*120 | 127.6*120 | 64.4*120 | — | — |
| Tb | X | 48 (ref. 93) | 138.8*121 | — | 1.3,93 5.7 (ref. 124) | — |
| Dy | X | 127 (ref. 32) | 141.5*121 | — | 4.6,118 6.6 (ref. 124) | — |
| Ho | X | 166.2*71 | 138.9*,71 143.4*121 | 63.9*71 | — | — |
| Er | X | 178*125 | 144*,125 146.1*,121 168 (ref. 125) | 69*125 | — | 100 (ref. 126) |
| Tm | X | 178.1*71 | 144.1*,71 147.2*121 | 68.8*71 | — | — |
| Yb | X | 160*125 | 129*,125 150*121 | 62*125 | — | 135 (ref. 126) |
| Lu | X | 192.1,71 210*125 | 152.8*,121 169.3,71 170*125 | 73.3,71 81*125 | 7.42 (ref. 71) | 155 (ref. 126) |
| Y | X | 145.5,71 224*,125 186 (ref. 127) | 132.4,71 144.4*,121 173*125 | 55.2,71 87*125 | 5.83 (ref. 71) | 95 (ref. 126) |
| Sc | X | 203,127 211*125 | 175.1*,121 140*125 | 84*125 | — | — |
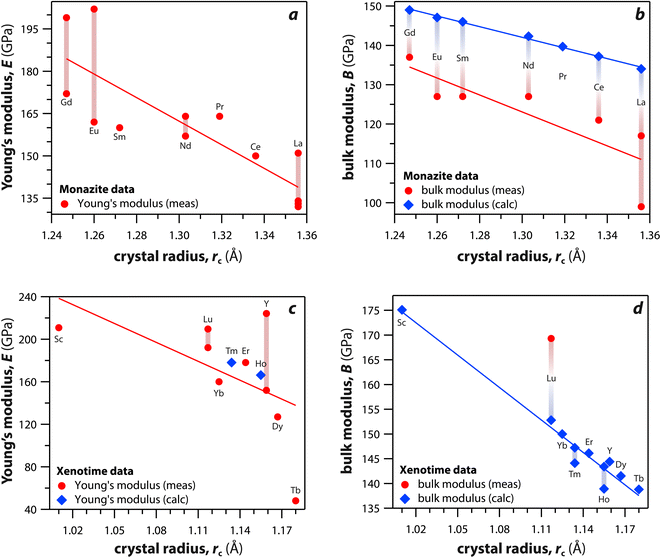 | ||
| Fig. 7 (a and c) Young's modulus and (b and d) bulk modulus values of (a and b) monazite and (c and d) xenotime compounds as functions of crystal radius of the RE cation (rc). | ||
Table 6 summarizes the thermal properties of monazite and xenotime including heat capacity (Cp), the CTE, thermal conductivity (k), thermal diffusivity (α), and melting temperatures (Tm). In general, the CTE values of monazite compounds seem to increase with smaller RE cations and RE–O distances in the structures. In general, the CTE values of monazite compounds seem to increase with the larger RE cations and RE–O distances in the structures. The CTE value is related to the inter-atomic potential and depends on the dissymmetry of the potential well.34 Examples of calculated CTE values for both monazites and xenotimes are shown in Fig. 8.121 The Cp values of monazite compounds are similar. The total heat capacity is the sum of the lattice component and an excess electronic term. The excess electronic heat capacity term increases for CePO4, PrPO4, NdPO4, SmPO4, and EuPO4 monazites but not for LaPO4 and GdPO4 due to empty and half-filled electron shell configurations, respectively, and this results in similar heat capacities among CePO4 → EuPO4, and slightly lower values for LaPO4 and GdPO4.34,117
| RE | Struct. | Cp (J mol−1 K−1) | CTE (×10−6 K−1) | k (W m−1 K−1) | α (mm2 s−1) | Tm (°C) |
|---|---|---|---|---|---|---|
| La | M | 101.28 (25 °C),128 101.28* (25 °C),128 106 (50 °C)34 | 7.78*,121 8.2 (25–1050 °C),118 8.894*,119 10 (20–1000 °C),123 10.3 (200–1000 °C)34 | 3.2 (25 °C),118 3.61 (25 °C),117 5.3 (50 °C)34 | 1.629 (25 °C)117 | 2072 (ref. 129) |
| Ce | M | 106.4 (25 °C),128 106.63* (25 °C),128 110 (50 °C)34 | 7.71*,121 9.029*,119 9.9 (20–1000 °C)123 | 3.14 (25 °C)117 | 1.334 (25 °C)117 | 2045 (ref. 129) |
| Pr | M | 106.04* (25 °C),128 108 (50 °C)34 | 7.66*,121 10.9 (200–1000 °C)34 | 3.4 (50 °C)34 | — | 1938 (ref. 129) |
| Nd | M | 104.8 (25 °C),128 104.92* (25 °C),128 108 (50 °C)34 | 7.61*,121 8.093*,119 9.4*,119 9.8 (20–1000 °C),123 10.7 (200–1000 °C)34 | 3.05 (25 °C),117 4.4 (50 °C)34 | 1.274 (25 °C)117 | 1975 (ref. 129) |
| Sm | M | 105.59* (25 °C),128 112 (50 °C)34 | 7.54*,121 9.7 (20–1000 °C),123 9.738*,119 11 (200–1000 °C)34 | 2.87 (25 °C),117 3.9 (50 °C)34 | 1.160 (25 °C)117 | 1916 (ref. 129) |
| Eu | M | 110 (50 °C),34 111.49 (25 °C)128 | 7.51*,121 8.303*,119 11.1 (200–1000 °C)34 | 2.99 (25 °C),117 5.8 (50 °C)34 | 1.135 (25 °C)117 | 2200 (ref. 119) |
| Gd | M | 102.21 (25 °C),128 102.21* (25 °C),128 105 (50 °C)34 | 7.47*,121 8.303*,119 11.4 (200–1000 °C)34 | 3.22 (25 °C),117 4.8 (50 °C)34 | 1.322 (25 °C)117 | 2200 (ref. 119) |
| Tb | X | 101.4* (25 °C)130 | 5.88*121 | — | — | 2150 (ref. 1) |
| Dy | X | 102.5* (25 °C)130 | 5.85*121 | — | — | 2150 (ref. 1) |
| Ho | X | 102.4* (25 °C)130 | 5.82*121 | — | — | — |
| Er | X | 102.3* (25 °C)130 | 5.79*,121 6 (1000 °C)126 | 12.01 (20 °C)126 | 0.5 (20 °C)126 | 1896 (ref. 129) |
| Tm | X | 102.7* (25 °C)130 | 5.78*121 | — | — | — |
| Yb | X | 102.8* (25 °C)130 | 5.75*,121 6 (1000 °C)126 | 11.71 (20 °C)126 | 0.5 (20 °C)126 | — |
| Lu | X | 100.2* (25 °C)130 | 5.72*,121 6.2 (1000 °C)126 | 11.97 (20 °C)126 | 0.5 (20 °C)126 | — |
| Y | X | 100.3* (25 °C)130 | 6.2 (1000 °C),126 6.7*121 | 12.02 (20 °C)126 | 0.6 (20 °C)126 | 1995 (ref. 129) |
| Sc | X | — | 6.95*121 | — | — | — |
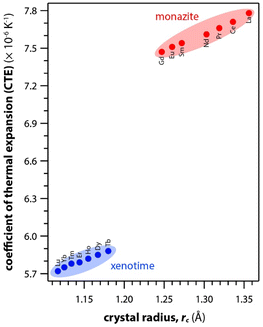 | ||
| Fig. 8 Summary of calculated CTE values for both monazite and xenotime REPO4 crystals from Li et al.121 as a function of RE rc. | ||
Du et al.117 synthesized polycrystalline monazite compounds of LaPO4, CePO4, NdPO4, SmPO4, EuPO4, and GdPO4 and pressed into pellets using a spark plasma sintering apparatus at 1350 °C and 40 MPa for 3 min. Young's modulus increased linearly from LaPO4 to GdPO4 as the RE rc values decreased. The specific heat values of all the monazites were similar at a given temperatures from 25 °C to 1000 °C and increased as the temperature increased except Gd monazite, which showed lower values at higher temperatures (>600 °C) compared to other monazites. The thermal conductivities of monazite compounds decreased as the temperature increased from 25 to 1000 °C, except EuPO4 and GdPO4 that showed increased thermal conductivities from 800 to 1000 °C. This is possibly due to the contribution of radiation transport effect, which becomes more important at higher temperatures. The thermal diffusivity values showed similar behavior as thermal conductivity with respect to temperature.
Perrière et al.34 investigated the structural dependence of the mechanical and thermal properties of monazite compounds including LaPO4, CePO4, PrPO4, NdPO4, SmPO4, EuPO4, and GdPO4. The synthesized monazite powders were pressed into pellets at 1500 °C and 65 MPa for 0.1–20 h. Both Young's modulus and shear modulus values increased with larger RE cations in the structure. The bending strengths of 94–122 MPa and fracture toughness around 1 MPa m1/2 showed the brittle behavior of monazite compounds, and this brittleness could cause inaccuracies when using micro-indentation analysis. The CTE values of monazites increased with smaller RE cations and RE–O distances in the structures and were in the 10–11.5 × 10−6 K−1 range. The heat capacities of all the synthesized monazites were ∼105–112 J mol−1 K−1 (with La and Gd having the lowest values). Controlling porosity during fabrication was important for achieving accurate measurements of both thermal and mechanical properties.
Li et al.121 calculated theoretical mechanical and thermal properties of monazite (La → Gd) and xenotime (Tb → Lu, Y, and Sc) compounds using the chemical bond theory of dielectric description. The CTE values increased with larger RE cations in the structures whereas the bulk moduli and lattice energies decreased. The CTE values were in the range of 7.78–7.47 × 10−6 K−1 for the La → Gd monazite compounds and 5.88–5.72 × 10−6 K−1 range for Tb → Lu xenotime compounds. The CTE and bulk modulus values were dependent on the RE–O bonds. The RE–O distances were ionically dominated and changed with different RE cations due to lanthanide contraction, and PO4 tetrahedra showed relatively high lattice energies and behaved nearly rigidly during deformation.
Kenges et al.118 synthesized pellet samples of LaPO4 monazite compounds with different sintering temperatures from 900 °C to 1500 °C and measured mechanical and thermal properties. The LaPO4 compounds contained a small amount of impurity phase La(PO3)3 (lanthanum metaphosophate). The LaPO4 monazite pellet sintered at 1100 °C showed the highest Young's modulus, toughness, and thermal conductivity. Increasing the sintering temperature increased the crystallite size and decreased the porosities of pellets. The LaPO4 monazite pellet sintered at 1100 °C had a Young's modulus of 132 GPa, a hardness of 4.6 GPa, a toughness of 1.6 MPa m1/2, a CTE of 8.2 × 10−6 K−1, and a thermal conductivity of 3.2 W m−1 K−1 at 25 °C.
Deepthi and Balamurugan131 compared the flexural strength and Young's modulus of LaPO4 and LaPO4 mixed with 20 mass% Y2O3. The LaPO4/Y2O3 pellets were sintered at 1000–1600 °C, and a pellet sintered at 1400 °C resulted in more uniform grain structure with less porosity. The LaPO4/Y2O3 pellet showed a reduction in flexural strength by 22% but increase of 1.05% in Young's modulus compared to the LaPO4 pellet.
Popa and Konings128 synthesized EuPO4 and SmPO4 monazite compounds and calculated their heat capacities. They used the enthalpy data of Sm and Eu monazites along with data from other La, Ce, Nd, and Gd monazites and calculated the heat capacity as a sum of lattice contributions and an excess electronic term. The calculated heat capacities of La → Gd monazites were in the range of 101.28–111.49 J mol−1 K−1 range, and these values were in good agreement with the experimental values.
Hay et al.93 investigated the phase transformations and deformation mechanisms of GdPO4, TbPO4, and DyPO4 compounds using scanning electron microscopy (SEM) and transmission electron microscopy (TEM) after indentation. The synthesized powders of TbPO4 and DyPO4 had xenotime structures whereas GdPO4 had a monazite structure. These materials were cold pressed at ∼300 MPa and sintered at 1600 °C for 20 h and 1700 °C for 1 h. The GdPO4, TbPO4, and DyPO4 compounds showed Young's moduli of 199, 48, and 127 GPa and hardness values of 7.8, 1.3, and 4.6 GPa, respectively. The authors observed stress-induced transformations from xenotime to monazite and suggested ferroelastic behavior under certain conditions.
Hikichi et al.126 measured the specific heats, thermal diffusivities, thermal conductivities, and bending strengths of xenotime pellets including ErPO4, YbPO4, LuPO4, and YPO4. The xenotime pellets were sintered at 700 °C to 1700 °C. The YbPO4 and LuPO4 pellets sintered above 1300 °C as well as YPO4 and ErPO4 pellets sintered above 1500 °C showed relative densities of ≥98%. The bending strengths increased with larger RE cations in the structures. The heat capacities of Er, Yb, Lu, and Y xenotime compounds were 0.40, 0.38, 0.38, and 0.48 J mol−1 K−1 at 20 °C, respectively. The CTE values were 6.0 × 10−6 K−1 for Er and Yb compounds and 6.2 × 10−6 K−1 for Lu and Y compounds.
Wilkinson et al.124 studied bulk modulus and hardness properties of EuPO4, GdPO4, TbPO4, and DyPO4 compounds using in situ nanoindentation for a range of loading rates and indentation depths. EuPO4 and GdPO4 formed monazite structures, and TbPO4 and DyPO4 formed xenotime structures. The bulk modulus values were decreasing in order of Gd, Eu, Dy, and Tb compounds. Both Eu and Gd compounds showed hardnesses of 8–9 GPa whereas Tb and Dy compounds showed hardnesses of 6–7 GPa. Hardnesses for all four compounds were not impacted by indentation depth or strain rate.
In addition to experimental methods, first principles calculations were also used to calculate the structural and physical properties of monazite and xenotime crystals. Kowalski and Li120 calculated elastic moduli of La, Ce, Pr, Nd, Pm, Sm, Eu, Gd, Tb, and Dy monazites using ab initio density functional theory (DFT). The Margules interaction parameters, which is related to excess enthalpy of mixing in a RE1xRE2(1−x)PO4 solid solution, and moduli were related to the mismatch in the endmember volumes of different RE cations within the structures. The computed Young's moduli, bulk moduli, and shear moduli increased with decreases in RE cation radii. The range of Young's moduli, bulk moduli, and shear moduli were 139–165 GPa, 110–129 GPa, and 54–65 GPa, respectively. Feng et al.119 calculated theoretical mechanical and thermal properties of monazite compounds using the results of local spin density approximation and compared to the experimental values. The Young's moduli, bulk moduli, and shear moduli of LaPO4, CePO4, NdPO4, SmPO4, EuPO4, and GdPO4 increased with smaller RE cations and shorter RE–O distances in the structures. The Young's modulus of monazite compounds showed high anisotropy. The calculated coefficients of linear thermal expansion were similar to experimental values, but the calculated thermal conductivities were higher than experimental values measured at >800 K.
Blanca-Romero et al.132 used the DFT + U method to calculate the structures and thermodynamic properties of monazite type crystals, with a goal to test the accuracy of the method for modeling f electron-containing systems such as RE-monazites. They found significant improvement both in terms of structures (lattice parameters, unit cell volumes, and RE–O distances for both RE oxides and phosphates) and properties (formation energies for RE phosphates and band gaps for RE oxides) of the DFT + U method as compared to the standard DFT in comparison to experimental values. Overall, the DFT + U method with the PBEsol (Perdew–Burke–Ernzerhof functional revised for solids) exchange correlation functional and Hubbard U parameters derived from linear response-based ab initio calculations was found to be a good choice for studying RE oxides and monazites.
Beridze et al.133 further investigated the DFT + U method for ab initio calculations of xenotime- and actinide-bearing complexes. The accuracy of the description of RE–O bond distances in xenotime was compared for two standard DFT xc functionals (PBEsol with f electrons in the core and f electrons in the valence shells) and the DFT + U (PBEsol + ULR, with the U values calculated from ab initio linear response). It was found that the DFT + U method has the best description of RE–O distances in xenotime crystals while both DFT + U and DFT (PBEsol with f electrons in the core) describe formation energies with good agreement with experiment, when accounting for the overestimation of P2O5 volume, similar to the case of monazites.132
4.2 Chemical durability
In general, the chemical durabilities of RE-phosphate and actinide-phosphate compounds documented in the literature are very high. Solubility product constants (Ksp) for hydrated actinide-phosphate (AnPO4·xH2O) and RE-phosphate (REPO4·xH2O) compounds, which cover rhabdophane, monazite, and xenotime compounds, have been found within the range of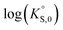 = −27.4 to −24.5 for LaPO4·0.5H2O134–136 to
= −27.4 to −24.5 for LaPO4·0.5H2O134–136 to 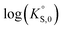 = −66.6 for Th2(PO4)2(HPO4)·H2O135,136 at 25 °C. Values for
= −66.6 for Th2(PO4)2(HPO4)·H2O135,136 at 25 °C. Values for 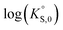 at 100 °C were reported at −26.0 for NdPO4·0.5H2O (rhabdophane), −25.7 for PrPO4-0.5H2O (rhabdophane), and −25.5 for ErPO4·nH2O (xenotime).46,134,136 Documented apparent activation energy (Ea) values fall within the 39–45 kJ mol−1 range.89,137 Oftentimes, the REPO4 compounds are used as surrogates for the actinide-equivalent analogs because they are easier and less costly to study than the actinide-containing phases.138,139 A summary of normalized release rate (NRi) data from the literature on these types of phosphate compounds is provided in Table 7.
at 100 °C were reported at −26.0 for NdPO4·0.5H2O (rhabdophane), −25.7 for PrPO4-0.5H2O (rhabdophane), and −25.5 for ErPO4·nH2O (xenotime).46,134,136 Documented apparent activation energy (Ea) values fall within the 39–45 kJ mol−1 range.89,137 Oftentimes, the REPO4 compounds are used as surrogates for the actinide-equivalent analogs because they are easier and less costly to study than the actinide-containing phases.138,139 A summary of normalized release rate (NRi) data from the literature on these types of phosphate compounds is provided in Table 7.
| Composition | Test conditions | NRi (g m−2 d−1) | Ref. |
|---|---|---|---|
| a ASTM denotes American Society for Testing and Materials International; DIW denotes deionized water; MCC denotes Materials Characterization Center; NRi denotes the i-th element normalized release rate; PTFE denotes polytetrafluoroethylene; RT denotes room temperature (i.e., ∼20–25 °C).b Natural monazite from Manangotry (Madagascar) listed with composition of (Ca0.04La0.21Ce0.43Pr0.05Nd0.15Sm0.02Gd0.01Th0.13)P0.90Si0.09O4 with a calculated (normalized) molecular weight of 248.85 g mol−1. | |||
| Ce0.5Pr0.5PO4 | MCC-1 (ASTM C1220); T = 90 °C, pH = 7, t = 42 days, PTFE, DIW | 5.7 × 10−6 [Ce] | 140 |
| 5.3 × 10−5 [Pr] | |||
| Naturalb | 50 °C < T < 229 °C; 1.62 < pH < 10.04; 50–100 μm particles | 8.13 × 10−7 [Ce] (70 °C, pH = 6) | 137 |
| 4.13 × 10−5 [Ce] (70 °C, pH = 1.6) | |||
| 9.29 × 10−7 [Ce] (50 °C, pH = 2) | |||
| 2.69 × 10−3 [Ce] (229 °C, pH = 2) | |||
| GdPO4 | 200 mg in 5 mL acidic solution; removed 100 μL for time resolved data points and replaced with fresh solution; 90 °C; 0.1 M HNO3 | 2.2 ± 0.7 × 10−5 [Gd] (RT) | 89 |
| 5.9 ± 2.1 × 10−4 [Gd] (90 °C) | |||
| (La,Nd,Pr)PO4 | Under saturation in either static tests (in HDPE with low leachate renewal) or dynamic tests (in PTFE with high leachate removal) | 10−3 to 10−7 | 136 |
| REPO4 | 25 °C < T < 90 °C | 1.17 × 10−3 [La] (90 °C) | 141 |
| 4.3 × 10−4 [Ce] (90 °C) | |||
| 1.01 × 10−3 [Nd] (90 °C) | |||
| 4.02 × 10−3 [Gd] (90 °C) | |||
| REPO4 | T = 90 °C; 0.1 M HNO3 | 1.4 × 10−3 [La] | 142 |
| 1.8 × 10−3 [Ce] | |||
| 1.0 × 10−3 [Nd] | |||
| 1.6 × 10−3 [Eu] | |||
| 1.0 × 10−3 [Gd] | |||
| REPO4 | 50% H2O vapor balanced with O2 at 0.3 cm s−1, 1500 °C, and 1 atm for 80 h. | 5.6 × 10−2 [Sc] | 125 |
| 6.0 × 10−2 [Y] | |||
| 9.8 × 10−2 [Er] | |||
| 1.0 × 10−1 [Yb] | |||
| 4.5 × 10−2 [Lu] | |||
In a study by Teng et al.,140 a mixed Ce0.5Pr0.5PO4 monazite sample set was produced from Pr6O11, Ce2(C2O4)3·10H2O, and ADP. Particles were ball milled in ethanol (4 h), dried at 60 °C (18 h), and calcined at 1000 °C (2 h). Calcined products were mixed with 5–10% polyvinyl alcohol (PVA). The calcined material was cold uniaxially pressed at 60 MPa, cold isostatically pressed at 200 MPa, and then calcined at 500 °C (6 h). Finally, samples were hot-pressed in evacuated graphite molds (<10 Pa of atmosphere, 30 MPa applied load) at temperatures of 1050–1250 °C for 0.5–4 h. A select set of samples (1150 °C for 2 h) were subjected to MCC-1 (ASTM C1220) chemical durability tests at a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 cm−1 surface-area-to-volume (sample
10 cm−1 surface-area-to-volume (sample![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) leachant) ratio at 90 °C in PTFE containers for different testing durations ranging from 3 d to 42 d where leachates were quantitatively measured using inductively coupled plasma mass spectrometry (ICP-MS). After 42 d of leaching, the NRi values were found to be 5.7 × 10−6 g m−2 d−1 for Ce and 5.3 × 10−5 g m−2 d−1 for Pr.
leachant) ratio at 90 °C in PTFE containers for different testing durations ranging from 3 d to 42 d where leachates were quantitatively measured using inductively coupled plasma mass spectrometry (ICP-MS). After 42 d of leaching, the NRi values were found to be 5.7 × 10−6 g m−2 d−1 for Ce and 5.3 × 10−5 g m−2 d−1 for Pr.
In a study by Oelkers and Poitrasson,137 dissolution tests were run on natural monazite from Manangotry (Madagascar) in open mixed flow reactors under different conditions of 50–229 °C (pH = 2) and 70 °C (pH = 1.6, 2.6, or 10) and closed reactors at 70 °C (pH = 2, 6, or 10). The starting material was ground to a 50–100 μm particle size fraction. The results showed a range of leach rates with the highest releases revealed for the highest test temperatures (≳200 °C).
In a study by Terra et al.,89 several monazites were made in the solid solution system of La(1−x)GdxPO4 (x = 0, 0.2, 0.3, 0.35, 0.4, 0.5, 0.6, 0.65, 0.7, 0.8, and 1.0). Starting materials included La(NO3)3·6H2O, LaCl3·7H2O, Gd(NO3)3·6H2O, GdCl3·6H2O, and H3PO4. An excess of H3PO4 was included to prevent RE2O3 formation during synthesis. Aqueous solutions of the RE reagents (i.e., 0.6–1.4 M) were prepared and these were added to 5 M H3PO4. Three different methods were used to synthesize the compounds. In the first approach, heat was applied in different steps: (1) samples were dried through direct evaporation using a sand bath, (2) dried material was ground to finer particle size and heated at 400 °C (14 h), and (3) heated at 1300 °C (10–14 h). In the second approach, the mixture was placed in a PTFE container at 150 °C in a sand bath for 1–2 weeks. The third approach utilized a hydrothermal synthesis process with additives in PTFE Parr autoclaves at 150–200 °C for 1–2 months. The GdPO4 compound was subjected to chemical durability testing as shown in Table 7.
In a study by Du Fou de Kerdaniel,136 AnPO4·xH2O compounds (An = Th, U) were produced using low-temperature methods based on procedures by Terra et al.143 and Clavier et al.144 or using dry chemistry routes by grinding mixtures and heating these mixtures to 1100–1400 °C where the target cations were Th, U, and REs. Leaching studies were performed under saturation in either static tests (in HDPE with low leachate renewal) or dynamic tests (in PTFE with high leachate removal) where solutions were analyzed with ICP-MS, time-resolved laser fluorescence spectroscopy, or α-scintillation counting. Dissolved solids were determined as mass loss and reported as RL(i) (i = element of interest) where RL(i) values ranged from 10−7 to 10−3 g m−2 d−1.
In a study by Hikichi et al.,126 the stabilities of RE elements of ErPO4, YbPO4, LuPO4, and YPO4 xenotime compounds in acidic or basic aqueous environments were investigated. The mass% losses of RE elements from xenotime compounds were measured using HCl, H2SO4, HNO3, NaOH, NH4OH solutions with concentrations of 6–36 N, and the test was conducted at 20 °C for 30 d. The results showed that the tested xenotime compounds were stable in these solutions, and the mass losses of RE elements were < 0.7 mass%.
In a study by Han et al.,125 xenotime powders including ErPO4, YbPO4, LuPO4, ScPO4, and YPO4 were cold pressed into pellets at 50 MPa and sintered at 1500 °C for 20 h in air. Chemical durability tests were performed using a vapor flow of 50% H2O balanced with O2 at 0.3 cm s−1 at 1500 °C and 1 atm for 80 h. The results showed dissolution rates of 5–10 × 10−2 g m−2 d−1 for xenotime compounds. However, the tests were performed in an alumina tube furnace, and formation of Al5RE3O12 compounds were observed.
Rafiuddin and Grosvenor145 investigated the room-temperature chemical durabilities of monazite-type, xenotime-type, and rhabdophane-type compounds on fine particles with specific surface areas ranging 1.3–15.1 m2 g−1. Two types of tests were run including dynamic tests over 84 d and static tests over 3 months. The tests revealed that the rhabdophane (GdPO4·H2O) structure released higher quantities of Gd and P ions in deionized water within the initial week of exposure. Analysis of the long-range and local structures of these materials indicates that the structures of these materials remained unchanged after seven months of leaching.
Wronkiewicz et al.146 studied the chemical durabilities of glass-crystal composites (GCCs) containing different crystalline phases, including apatite, monazite [(Ce,U)PO4], and spinel. The tests run included the product consistency test (PCT, t = 7 d, 28 d, and 91 d),147 the vapor hydration test (VHT),148 and the Toxicity Characteristic Leach Procedure (TCLP).149 The monazite was noted as having fewer elements (i.e., Ce, U, Th) compared to the apatite sample. The leachate from the PCTs (t = 7–91 d) was noted as being slightly acidic (pH ≈ 5.6–6.2). The apatite and monazite samples were noted as being 100–300× more durable than a glass waste form (i.e., SRL-202U) for U release.
Poitrasson et al.150 studied naturally formed magmatic monazites from European-based Paleozoic granites. Their studies showed that the hydrothermal alteration of these monazites was notably complex including a variety of mechanisms such as monoclinic → hexagonal crystal structure transitions, chemical exchanges, cation substitutions, selective Th removal, dissolution followed by precipitation, and dissolution with replacement by different minerals. They also noted that temperatures up to 300 °C likely occurred within the vicinity of the minerals.
Mikhailova et al.151 studied Pu-containing Eu-monazite and have documented Pu release being attributed to the formation of hydrated (rhabdophane) PuPO4 by storage in air. This calls into question the long-term disposal potential for actinides stored in REPO4 compounds if moisture is present in the atmosphere, which could be reduced if storage was performed in inert and dry conditions.
4.3 Radiation stability
The majority of naturally occurring monazites have been affected by radiation due to α decay of actinides within these minerals.152 This radiation has the potential to cause metamict alterations in the crystal structures of minerals, consequently elevating their solubility. In contrast to many radioactive minerals, monazite retains its crystalline structure under substantial cumulative radiation doses. Monazites are known to remain within the crystalline states by an α-healing mechanism through radiation-induced defects.153–155 Self-recovery of damaged structure was not observed in zircon minerals (isostructural to xenotime) with SiO4, but partial structural recovery was observed in xenotimes with PO4.156–158 Table 8 summarizes the critical amorphization dose of monazite and xenotime compounds.| Materials | Critical amorphization dose | Ref. |
|---|---|---|
| LaPO4 | 0.15 dpa (0 K) | 159 |
| Natural monazite | 7 × 1016 α mg−1 | 160 |
| Natural monazite | 0.13 dpa (0 K) | 159 |
| Synthetic monazite (La,Pu)PO4 | ∼(0.2–0.3) × 1016 α mg−1 | 161 |
| Natural xenotime with Th and U | (1.4–14) × 1016 α mg−1 | 160 |
| CePO4 | ∼0.35–0.47 dpa (∼298 K) | 162 |
| ErPO4 xenotime | (0.3–7.3) × 1016 α mg−1 | 163 |
| Nanocrystal phosphate Rb3Nd(PO4)2 | ∼0.52 dpa | 164 |
Meldrum et al.155 studied the effect of irradiation on monazite (LaPO4), xenotime (ScPO4), ZrSiO4, and ThSiO4 using 800 keV Kr+ ions. Recrystallization energies for the compounds were calculated to be 3.1–3.3 eV for the silicates and 1–1.5 eV for the phosphates. Radiation damage was monitored as a function of temperature, and above 700 °C, the amorphization of ZrSiO4 could not be induced as the recrystallization process was faster than damage accumulation. The critical temperature was calculated to be only 35 °C for LaPO4, and the monazite would not undergo phase decomposition at the tested conditions. In another study by the same group,159 monazite could not be amorphized when exposed to 800 keV Kr+ ions at temperatures surpassing 175 °C. On the contrary, zircon underwent amorphization at temperatures reaching up to 740 °C. It was found that materials with the zircon structure (i.e., ZrSiO4 and ScPO4) could be amorphized at slightly elevated temperatures compared to compounds with the monazite structure under equivalent irradiation conditions.
Seydoux-Guillaume et al.165 studied the healing of radiation damage in natural monazite with annealing at 500–1200 °C. The natural monazite contained two domains with distorted lattice areas with α-dose of 2.5 × 1016 α mg−1 accumulated since 474 Ma ago. From 500–900 °C, partial healing of the lattice occurred. At 900 °C after 10 days, only one domain remained, and a well-crystallized lattice was observed. The same group performed structural analysis using X-ray diffraction (XRD), TEM, SEM, and electron probe microanalysis and showed that monazites are not metamict despite the old ages of samples ranging from 24 to 1928 Ma.166
Bregiroux et al.167 synthesized monazite powders containing plutonium(III), plutonium(IV) and americium(III). They examined the response of the monazite structure to α self-irradiation using XRD. The results revealed a total amorphization of the crystalline structure after 300 days, reaching a cumulative dose of 1.65 × 1025 α m−3.
Picot et al.168 explored the impact of Au2+ and He+ ion irradiation on monazite to simulate α-decay effects. The Au2+ ion-irradiation induced significant alterations in the material properties. At a damage level of 6.7 dpa, monazite displayed an approximately 8.1% increase in volume, a 59% decrease in hardness, and complete structural amorphization. Conversely, no changes in the properties of these compounds were noted following He+ ion implantation.
Deschanels et al.169 investigated α-induced swelling in monazite and zirconolite ceramics. It was found that the macroscopic swelling and amorphization of monazite relied on the type of irradiation. Monazite samples irradiated externally with Au became amorphous and exhibited a maximum swelling of 8%. In contrast, the swelling in samples doped with 238Pu was significantly smaller, at approximately 1%.
Radiuddin and Grosvenor157 studied the structural stabilities of La1−xYbxPO4 materials implanted with Au ions. The long- and short-range order of La1−xYbxPO4 (x = 0, 0.3, 0.7, 1.0) are influenced by ion-implantation, indicating the materials are prone to structural damage. Interestingly, in certain members of the La1−xYbxPO4 series (x = 0.7 and 1.0), partial recovery of the structure was observed following high-dose Au ion implantation.
Sadhasivam and Rajesh38 studied the effect of γ-irradiation on the NdPO4 monazite compound using 60Co γ-cell source at a dose rate of 4.5 kGy h−1. Defect center, ionization, and charge trapping did not occur during irradiation, and no significant structural change was observed up to 150 kGy γ dose. The high level of γ dose did not affect the crystallinity and optical properties.
Rafiuddin et al.163 evaluated irradiation effects on the ErPO4 xenotime compound structure using high-energy dual ion-beam irradiation of 1.5 MeV Au2+ and 160 keV He+. The xenotime structure was found to undergo amorphization at a lower Au2+ ion-fluence than the monazite structure. Moreover, subsequential He+ ion-irradiation on the amorphized ErPO4 samples did not lead to the structural restoration of xenotime. Simultaneous ion-irradiation of Au2+ and He+ prevented the amorphization of ErPO4 as higher amounts of electronic energy was applied, similar to the α-healing mechanism in the monazite structures where high energies cause recrystallization faster than damage accumulation. However, the α-healing mechanism for xenotime required ∼4 times more energy compared to monazite.
Overstreet et al.170 investigated the structural stability of SmPO4 and TbPO4 under swift heavy ion irradiation using 1.1 GeV 197Au ions. Both SmPO4 monazite and TbPO4 xenotime structures experienced amorphization at comparable rates with increasing fluence, and complete amorphization occurred ∼5 × 1012 ions cm−2 for both compounds. No irradiation-induced recrystallization was observed at higher fluences for both compounds. Findings from this study differed from other radiation damage using relatively low-energy ions, where the monazite compounds were more resistant to amorphization compared to xenotime compounds. The results from this study suggested that the crystal chemistries and structures of monazite and xenotime will not greatly affect the radiation tolerance to highly energetic ions.
Tisdale et al.164 synthesized single crystals of Rb3RE(PO4)2 (RE = Y, La, Pr, Nd, and Sm→Lu) by high-temperature flux growth methods. The 1.2 MeV Xe3+ ions were used on the Rb3Nd(PO4)2 sample to investigate the radiation effect, and complete amorphization was observed by 0.22 dpa for a single crystal sample and ∼0.52 dpa for a polycrystalline sample. DFT calculations were performed for trivalent actinide analogs of Rb3M(PO4)2 (M = Am, Cm), and the results indicated high tolerance to radiation damage.
Burakov et al.161 studied radiation resistance effects, including amorphization, of different crystalline host phases on Pu storage to simulate the effects of long-term disposal. The study included Pu-doped cubic zirconia (Zr0.79Gd0.14Pu0.07O1.99), monazites [(La,Pu)PO4, PuPO4, and (Eu,Pu)PO4], zircon [(Zr,Pu)SiO4], and pyrochlore [(Ca,Gd,Hf,Pu,U)2Ti2O7]. The (La,Pu)PO4 and PuPO4 monazites remained crystalline until receiving cumulative doses of 1.19 × 1025 α m−3 and 4.2 × 1024 α m−3.
4.4 Optical properties and applications
Several studies have documented the study of optical properties of REPO4 compounds, including optical spectroscopy171,172 and Raman spectroscopy.173–175 Hernández and Martín172 studied the ultraviolet-visible-near-infrared (UV-Vis-NIR, i.e., 200–3000 nm) absorption spectra of EuPO4. Absorption spectra show low to medium absorption within the λ = 400–1700 nm region of the spectrum (Vis-NIR) but high absorptions in the UV (λ < 400 nm) and NIR (λ > 1700 nm). They noted that the absorption spectra remained unchanged, even after 18 kGy irradiation with 60Co. Studies have shown the utility of doped REPO4 compounds to function as scintillators when exposed to X-rays or γ-rays.1 Examples of these types of materials include LuPO4:Ce,176 LuPO4:Nd,177 YPO4:Nd,177 as well as Sm-doped or Eu-doped YPO4, ScPO4, and LuPO4.178 REPO4 compounds can also be used as thermophosphors to provide a remote-sensing probe for temperature determination, which was demonstrated using LuPO4: (Dy,Eu).24,25 An example of where this would have utility is where it is not practical to use metal thermocouples, e.g., remote sensors within a microwave environment.5 Future work and perspectives
After considering the wealth of data collected on the wide range of anhydrous REPO4 compounds discussed within this paper, more work is needed to fill in research gaps summarized within this section. Additional thoughts and perspectives are provided throughout where future work could be done.Regarding mechanical properties, extensive datasets are available for E, B, and G while several experimental gaps exist in datasets for H and FS (see Table 5). Many of the datasets from single studies do not correlate well with data from other studies or measured data fall far from calculated data (see Fig. 7), leading to difficulty in making accurate predictions in some cases. Gaps exist in the thermal properties for the different series (Table 6) and the data spread across literature values for single properties of a given REPO4 compound tends to be rather high in some cases. For one dataset of calculated CTE values, the spread was very low (see Fig. 8), but that was anomalous against the entire set of summarized data. Two of the most populated datasets include Cp and CTE. More work needs to be done to better elucidate the variabilities in these properties across the full RE dataset.
Since APO4 compounds are promising as stable options for long-term disposal of radionuclides, including rare earths and actinides, more detailed studies on their chemical durabilities are needed. The normalized release rates (NRi) for tested REPO4 compounds show very low values (Table 7) as compared to other nuclear waste forms, such as borosilicate glass. Understanding potential incongruent elemental release from these compounds is important, including comparisons between NRP and NRRE over long time scales under dilute conditions.
While some radiation stability tests have been documented in the literature for REPO4 compounds (see Table 8 for examples), additional studies are needed. This includes wider compositional ranges as well as more high-energy exposure studies (e.g., γ-rays). Several studies have demonstrated amorphization doses for a variety of REPO4 compounds and types of irradiations. A study by Nasdala et al.179 provided evidence that α-assisted annealing can prevent irradiation-induced amorphization in CePO4 monazite, but only above a specific damage level. Understanding how REPO4 compounds behave in potential geological repository environments and the transition of REPO4 compounds to the hydrated (i.e., rhabdophane or REPO4·xH2O) forms is very important from a waste form perspective for long-term disposal.
An overview of DFT-based first principles calculations on mechanical, structural, and thermodynamic properties was briefly covered due to the effectiveness of the method to predict the structures and properties of this class of materials. It was found that the usage of the DFT + U method180,181 to treat f electrons in RE elements was essential to improve the description of both structures and properties. More work can be done to study defect formation energies and mixing of RE elements in REPO4 compounds using first principles methods. First principles calculations can also be used to study high-entropy monazite-based or xenotime-based ceramics formation and properties through mixing of various RE elements. In addition, classical molecular dynamics (MD) simulations can be used to study radiation effects and thermomechanical behaviors.182 Recent advances using machine learning potentials183 based on first principles calculations can help to alleviate the bottleneck of interatomic potential availability. However, extensive testing and validation of these new potentials will be needed. Combining these techniques, one can expect computational methods to provide valuable information regarding the distribution of RE elements within the crystal lattice, the role of dopants in controlling properties, radiation induced structural change and amorphization, and the mechanisms governing phase transformations under extreme conditions.
With the rapid development of applying machine learning techniques in material science,184 the integration of predictive models and machine learning holds transformative potential across various applications of REPO4 compounds.185–187 These models can be utilized to predict properties such as phase stability, mechanical behavior, and chemical reactivity under various/extreme conditions. Future efforts, including constructing a more consistent dataset including trace elements, developing high-throughput parallel simulation routines, and standardizing characterization methods, would greatly benefit the implementation of machine learning in studying monazite and xenotime composition–structure–property relationships. By training models on experimental and/or simulation data, researchers can extrapolate insights beyond the limits of traditional analysis, guiding experimental design and hypothesis generation.
6 Summary and conclusions
The synthesis methods, crystal structures, and properties of anhydrous monazite and xenotime crystalline materials are summarized within this review. Monazite and xenotime compounds can be synthesized with a variety of different methods including flux-assisted, solid state, hydrothermal, aqueous, dehydration, and gel-based methods. For both monazite and xenotime structures, with larger and lighter RE cations in the crystal structure, the unit cell parameters (i.e., a, b, c) and volumes (V) increase linearly whereas the densities (ρ) decrease nonlinearly. Similar trends were observed for solid solution compounds containing mixed RE cations. Some solid solutions containing RE cations with large difference in sizes (e.g., La and Yb) showed the presence of both monazite and xenotime phases. For RE cations, the distortions of REOx polyhedra were greater in monazites when compared to xenotimes. Decreasing RE radii increased the Young's modulus, bulk modulus, and shear modulus, and this can be due to stronger interatomic bonding as the average RE–O distances decreased with smaller RE cations. Different modulus values from different studies are also affected by different sample preparation and sintering conditions for the pellets. In general, the CTE values of monazite compounds seem to increase with the larger RE cations and RE–O distances in the structures. The calculated CTE values usually followed the trends, but the experimental CTE values from different studies often varied greatly, and it was difficult to create a general trendline. First-principles DFT calculations have been shown to be a reliable predictive method for both the structures and properties of monazite and xenotime crystals, although care was needed in the description of the f-electrons and the DFT + U method was found to be reliable and computationally feasible approach for this purpose. The chemical and radiation resistance of monazite and xenotime are similar to that of zircon, and thus the natural minerals are often used in geochronology. Monazite compounds are generally more resistant to irradiation damage compared to the xenotime compounds.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The information, data, or work presented herein was funded in part by the Advanced Research Projects Agency-Energy (ARPA-E), U.S. Department of Energy, under Award Number DE-AR0001613. The views and opinions of authors expressed herein do not necessarily state or reflect those of the United States Government or any agency thereof. Pacific Northwest National Laboratory (PNNL) is operated by Battelle Memorial Institute for the DOE under contract DE-AC05-76RL01830. Authors thank John Vienna (PNNL) for helpful comments.References
- L. A. Boatner, Rev. Mineral. Geochem., 2002, 48, 87–121 CrossRef CAS
.
- R. P. Rapp and E. B. Watson, Contrib. Mineral. Petrol., 1986, 94, 304–316 CrossRef CAS
.
- A. Kumari, R. Panda, M. K. Jha, J. R. Kumar and J. Y. Lee, Miner. Eng., 2015, 79, 102–115 CrossRef CAS
.
- L. Richter, L. W. Diamond, P. Atanasova, D. A. Banks and J. Gutzmer, Geology, 2018, 46, 263–266 CrossRef CAS
.
- M. Rabiei, G. Chi, C. Normand, W. J. Davis, M. Fayek and N. J. Blamey, Econ. Geol., 2017, 112, 1483–1507 CrossRef
.
- H.-J. Förster, Am. Mineral., 1998, 83, 259–272 CrossRef
.
- C. J. Hetherington, D. E. Harlov and B. Budzyń, Mineral. Petrol., 2010, 99, 165–184 CrossRef CAS
.
- C. J. Hetherington, M. J. Jercinovic, M. L. Williams and K. Mahan, Chem. Geol., 2008, 254, 133–147 CrossRef CAS
.
- A. Berger, E. Gnos, E. Janots, A. Fernandez and J. Giese, Chem. Geol., 2008, 254, 238–248 CrossRef CAS
.
- R. G. Jonasson and E. R. Vance, Thermochim. Acta, 1986, 108, 65–72 CrossRef CAS
.
- B. Glorieux, M. Matecki, F. Fayon, J. P. Coutures, S. Palau, A. Douy and G. Peraudeau, J. Nucl. Mater., 2004, 326, 156–162 CrossRef CAS
.
- R. C. Ewing and W. Lutze, Ceram. Int., 1991, 17, 287–293 CrossRef CAS
.
- E. H. Oelkers and J.-M. Montel, Elements, 2008, 4, 113–116 CrossRef CAS
.
- N. Clavier, R. Podor and N. Dacheux, J. Eur. Ceram. Soc., 2011, 31, 941–976 CrossRef CAS
.
- L. A. Boatner, G. W. Beall, M. M. Abraham, C. B. Finch, P. G. Huray and M. Rappaz, in Scientific Basis for Nuclear Waste Management, ed. C. J. M. Northrup, Springer US, Boston, MA, 1980, DOI:10.1007/978-1-4684-3839-0_35, pp. 289–296
.
- A. I. Orlova, J. Nucl. Mater., 2022, 559, 153407 CrossRef CAS
.
- M. R. Rafiuddin, G. Donato, S. McCaugherty, A. Mesbah and A. P. Grosvenor, ACS Omega, 2022, 7, 39482–39490 CrossRef CAS PubMed
.
- S. Chong, B. J. Riley and Z. J. Nelson, J. Rare Earths, 2021, 40, 365–380 CrossRef
.
- B. J. Riley, Ind. Eng. Chem. Res., 2020, 59, 9760–9774 CrossRef CAS
.
- B. J. Riley, J. McFarlane, G. D. DelCul, J. D. Vienna, C. I. Contescu and C. W. Forsberg, Nucl. Eng. Des., 2019, 345, 94–109 CrossRef CAS
.
- Z. Wang, J. Kim, L. Magermans, F. Corbella, I. Florea, E. Larquet, J. Kim and T. Gacoin, Nanoscale, 2021, 13, 16968–16976 RSC
.
- N. Hashimoto, Y. Takada, K. Sato and S. Ibuki, J. Lumin., 1991, 48–49, 893–897 CrossRef CAS
.
- Y. I. Jeon, L. K. Bharat and J. S. Yu, J. Alloys Compd., 2015, 649, 531–536 CrossRef CAS
.
- S. W. Allison, L. A. Boatner and G. T. Gillies, Appl. Opt., 1995, 34, 5624–5627 CrossRef CAS PubMed
.
- S. W. Allison, M. R. Cates, L. A. Boatner and G. T. Gillies, High Temperature Thermometric Phosphors for Use in a Temperature Sensor, US Pat., 5730528A, 1998 Search PubMed
.
- D.-H. Kuo and W. M. Kriven, Mater. Sci. Eng., A, 1996, 210, 123–134 CrossRef
.
- P. E. D. Morgan, D. B. Marshall and R. M. Housley, Mater. Sci. Eng., A, 1995, 195, 215–222 CrossRef
.
- E. E. Boakye, P. Mogilevsky, T. A. Parthasarathy, R. S. Hay, J. Welter and R. J. Kerans, J. Am. Ceram. Soc., 2006, 89, 3475–3480 CrossRef CAS
.
- L. Boatner and B. Sales, in Radioactive Waste Forms for the Future, ed. R. C. Ewing and W. Lutze, North-Holland, New York, 1988, ch. 8, pp. 495–564 Search PubMed
.
- R. Feigelson, J. Am. Ceram. Soc., 1964, 47, 257–258 CrossRef CAS
.
- D. F. Mullica, W. O. Milligan, D. A. Grossie, G. W. Beall and L. A. Boatner, Inorg. Chim. Acta, 1984, 95, 231–236 CrossRef CAS
.
- M. Cao, C. Hu, Q. Wu, C. Guo, Y. Qi and E. Wang, Nanotechnology, 2005, 16, 282 CrossRef CAS PubMed
.
- X. Li and J. Ma, J. Lumin., 2011, 131, 1355–1360 CrossRef CAS
.
- L. Perrière, D. Bregiroux, B. Naitali, F. Audubert, E. Champion, D. S. Smith and D. Bernache-Assollant, J. Eur. Ceram. Soc., 2007, 27, 3207–3213 CrossRef
.
- A. Hirsch, P. Kegler, I. Alencar, J. Ruiz-Fuertes, A. Shelyug, L. Peters, C. Schreinemachers, A. Neumann, S. Neumeier, H. P. Liermann, A. Navrotsky and G. Roth, J. Solid State Chem., 2017, 245, 82–88 CrossRef CAS
.
- R. Khalili, A.-C. Larsson, V.-V. Telkki, P. Lantto and A. M. Kantola, J. Solid State Chem., 2022, 311, 123097 CrossRef CAS
.
- N. Adelstein, B. S. Mun, H. L. Ray, P. N. Ross, J. B. Neaton and L. C. De Jonghe, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 205104 CrossRef
.
- S. Sadhasivam and N. P. Rajesh, Mater. Res. Bull., 2016, 74, 117–123 CrossRef CAS
.
- Y. Wang, J. Li, J. Wang, S. Han and Y. Guo, J. Cryst. Growth, 2010, 312, 2779–2782 CrossRef CAS
.
- D. F. Mullica, D. A. Grossie and L. A. Boatner, J. Solid State Chem., 1985, 58, 71–77 CrossRef CAS
.
- J. M. Heuser, S. Neumeier, L. Peters, H. Schlenz, D. Bosbach and G. Deissmann, J. Solid State Chem., 2019, 273, 45–52 CrossRef CAS
.
- A. P. Gysi and D. Harlov, Chem. Geol., 2021, 567, 120072 CrossRef CAS
.
- A. P. Gysi, D. Harlov, D. C. Filho and A. E. Williams-Jones, Thermochim. Acta, 2016, 627–629, 61–67 CrossRef CAS
.
- L. A. Boatner, K. B. Helean, A. Navrotsky and S. V. Ushakov, J. Mater. Res., 2001, 16, 2623–2633 CrossRef
.
- D. F. Mullica, D. A. Grossie and L. A. Boatner, Inorg. Chim. Acta, 1985, 109, 105–110 CrossRef CAS
.
- F. Poitrasson, E. Oelkers, J. Schott and J.-M. Montel, Geochim. Cosmochim. Acta, 2004, 68, 2207–2221 CrossRef CAS
.
- A. Mesbah, N. Clavier, E. Elkaim, S. Szenknect and N. Dacheux, J. Solid State Chem., 2017, 249, 221–227 CrossRef CAS
.
- E. E. Boakye, P. Mogilevsky, R. S. Hay and G. E. Fair, J. Am. Ceram. Soc., 2008, 91, 3841–3849 CrossRef CAS
.
- R. D. Shannon, Acta Crystallogr., Sect. A, 1976, 32, 751–767 CrossRef
.
- F. Weigel, V. Scherer and H. Henschel, J. Am. Ceram. Soc., 1965, 48, 383–384 CrossRef CAS
.
- Y. Ni, J. M. Hughes and A. N. Mariano, Am. Mineral., 1995, 80, 21–26 CAS
.
- G. B. Callejas, M. Cabrera, S. Prieto, O. Luna, I. Choque and V. Crespo, Rev. Boliv. Quim., 2000, 17, 22–27 CAS
.
- K. Ghouse, Indian J. Pure Appl. Phys., 1968, 6, 265–268 CAS
.
- R. C. L. Mooney, J. Chem. Phys., 1948, 16, 1003 CrossRef CAS
.
- M. P. Kokkoros, Prakt. Akad. Athenon, 1942, 17, 163–174 Search PubMed
.
- T. Ueda, in Memoirs of the College of Science, University of Kyoto, Series B, 1953, vol. 20, pp. 227–246 Search PubMed
.
- T. Ueda, J. Jpn. Assoc. Mineral., Petrol. Econ. Geol., 1967, 58, 170–179 CrossRef
.
- M. M. Zaman and S. M. Antao, Minerals, 2021, 11, 16 CrossRef CAS
.
- G. W. Beall, L. A. Boatner, D. F. Mullica and W. O. Milligan, J. Inorg. Nucl. Chem., 1981, 43, 101–105 CrossRef CAS
.
- S. Bevara, K. K. Mishra, S. J. Patwe, T. R. Ravindran, M. K. Gupta, R. Mittal, P. S. R. Krishna, A. K. Sinha, S. N. Achary and A. K. Tyagi, Inorg. Chem., 2017, 56, 3335–3348 CrossRef CAS PubMed
.
- K. M. Kurbanov, V. A. Efremov and V. P. Orlovskij, Kristallografiya, 1986, 31, 800–802 CAS
.
- P. Halappa, A. Mathur, M.-H. Delville and C. Shivakumara, J. Alloys Compd., 2018, 740, 1086–1098 CrossRef CAS
.
- K. M. Heffernan, N. L. Ross, E. C. Spencer and L. A. Boatner, J. Solid State Chem., 2016, 241, 180–186 CrossRef CAS
.
- S. Rodriguez-Liviano, A. I. Becerro, D. Alcántara, V. Grazú, J. M. de la Fuente and M. Ocaña, Inorg. Chem., 2013, 52, 647–654 CrossRef CAS PubMed
.
- J. Coing-Boyat, F. Sayetat and A. Apostolov, J. Phys., 1975, 36, 1165–1174 CrossRef CAS
.
- W. O. Milligan, D. F. Mullica, G. W. Beall and L. A. Boatner, Inorg. Chim. Acta, 1983, 70, 133–136 CrossRef CAS
.
- J. López-Solano, P. Rodríguez-Hernández, A. Muñoz, O. Gomis, D. Santamaría-Perez, D. Errandonea, F. J. Manjón, R. S. Kumar, E. Stavrou and C. Raptis, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 144126 CrossRef
.
- W. Schäfer, Eine Apparatur für polarisierte Neutronen und Neutronenbeugungsuntersuchugen im System DyXO4 (X = P, V, As), Publikationen vor 2000, Kernforschungsanlage Jülich, Verlag Jülich, 1972 Search PubMed
.
- Z. Khadraoui, C. Bouzidi, K. Horchani-Naifer and M. Ferid, J. Alloys Compd., 2014, 617, 281–286 CrossRef CAS
.
- S. Skanthakumar, C. K. Loong, L. Soderholm, J. W. Richardson, M. M. Abraham and L. A. Boatner, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 5644–5648 CrossRef CAS PubMed
.
- O. Gomis, B. Lavina, P. Rodríguez-Hernández, A. Muñoz, R. Errandonea, D. Errandonea and M. Bettinelli, J. Phys.: Condens. Matter, 2017, 29, 095401 CrossRef CAS PubMed
.
- E. Patscheke, H. Fuess and G. Will, Chem. Phys. Lett., 1968, 2, 47–50 CrossRef CAS
.
- W. Milligan, D. Mullica, G. Beall and L. Boatner, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1983, 39, 23–24 CrossRef
.
- V. G. Lohmüller, G. Schmidt, B. Deppisch, V. Gramlich and C. Scheringer, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1973, 29, 141–142 CrossRef
.
- S. J. Patwe, S. N. Achary and A. K. Tyagi, Am. Mineral., 2009, 94, 98–104 CrossRef CAS
.
- W. O. Milligan, D. F. Mullica, G. W. Beall and L. A. Boatner, Inorg. Chim. Acta, 1982, 60, 39–43 CrossRef CAS
.
- M. Strada and G. Schwendimann, Gazz. Chim. Ital., 1934, 64, 662–674 CAS
.
- I. Krstanovic, Z. Kristallogr., 1965, 121, 315–316 CrossRef CAS
.
- L. Vegard, London, Edinburgh Dublin Philos. Mag. J. Sci., 1927, 4, 511–525 CrossRef CAS
.
- F. Angiuli, F. Mezzadri and E. Cavalli, J. Solid State Chem., 2011, 184, 1843–1849 CrossRef CAS
.
- R. Mooney, Acta Crystallogr., 1956, 9, 677–678 CrossRef CAS
.
- J.-E. Jørgensen, B. Lundtoft and S. E. Rasmussen, Powder Diffr., 1993, 8, 164–167 CrossRef
.
- R. Mi, J. Chen, Y.-g. Liu, M. Fang, L. Mei, Z. Huang, B. Wang and C. Zhaob, RSC Adv., 2016, 6, 28887–28894 RSC
.
- W. Baur, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1974, 30, 1195–1215 CrossRef CAS
.
- C. Giacovazzo, Fundamentals of Crystallography, Oxford university press, USA, 2002 Search PubMed
.
- R. Hoppe, Z. Kristallogr. - Cryst. Mater., 1979, 150, 23–52 CrossRef CAS
.
- R. Hoppe, S. Voigt, H. Glaum, J. Kissel, H. P. Müller and K. Bernet, J. Less-Common Met., 1989, 156, 105–122 CrossRef CAS
.
- R. De Biasi, A. Fernandes and J. Oliveira, J. Appl. Crystallogr., 1987, 20, 319–320 CrossRef
.
- O. Terra, N. Clavier, N. Dacheux and R. Podor, New J. Chem., 2003, 27, 957–967 RSC
.
- B. Van Emden, M. Thornber, J. Graham and F. Lincoln, Advances in X-Ray Analysis-The Proceedings of the Denver X-ray Conferences, 1996, pp. 2–15 Search PubMed
.
- A. Thust, Y. Arinicheva, E. Haussühl, J. Ruiz-Fuertes, L. Bayarjargal, S. C. Vogel, S. Neumeier and B. Winkler, J. Am. Ceram. Soc., 2015, 98, 4016–4021 CrossRef CAS
.
- Y. Arinicheva, A. Bukaemskiy, S. Neumeier, G. Modolo and D. Bosbach, Prog. Nucl. Energy, 2014, 72, 144–148 CrossRef CAS
.
- R. S. Hay, E. E. Boakye and P. Mogilevsky, J. Eur. Ceram. Soc., 2014, 34, 773–781 CrossRef CAS
.
- A. C. Strzelecki, M. Reece, X. Zhao, W. Yu, C. Benmore, Y. Ren, C. Alcorn, A. Migdisov, H. Xu and X. Guo, ACS Earth Space Chem., 2022, 6, 1375–1389 CrossRef CAS
.
- B. Xiao, H. Lösch, N. Huittinen and M. Schmidt, Chem.–Eur. J., 2018, 24, 13368–13377 CrossRef CAS PubMed
.
- M. R. Rafiuddin, E. Mueller and A. P. Grosvenor, J. Phys. Chem. C, 2014, 118, 18000–18009 CrossRef CAS
.
- R. Podor and M. Cuney, Am. Mineral., 1997, 82, 765–771 CAS
.
- D. B. Kitaev, Y. F. Volkov and A. I. Orlova, Radiochem, 2004, 46, 211–217 CrossRef CAS
.
- J.-M. Montel, J.-L. Devidal and D. Avignant, Chem. Geol., 2002, 191, 89–104 CrossRef CAS
.
- R. Podor, M. Cuney and T. C. Nguyen, Am. Mineral., 1995, 80, 1261–1268 CAS
.
- P. E. Raison, R. Jardin, D. Bouëxière, R. J. M. Konings, T. Geisler, C. C. Pavel, J. Rebizant and K. Popa, Phys. Chem. Miner., 2008, 35, 603–609 CrossRef CAS
.
- A. Tabuteau, M. Pagès, J. Livet and C. Musikas, J. Mater. Sci. Lett., 1988, 7, 1315–1317 CrossRef CAS
.
- O. Terra, N. Dacheux, N. Clavier, R. Podor and F. Audubert, J. Am. Ceram. Soc., 2008, 91, 3673–3682 CrossRef CAS
.
- E. Gardés, O. Jaoul, J.-M. Montel, A.-M. Seydoux-Guillaume and R. Wirth, Geochim. Cosmochim. Acta, 2006, 70, 2325–2336 CrossRef
.
- L. Schwarz, B. Finke, M. Kloss, A. Rohmann, U. Sasum and D. Haberland, J. Lumin., 1997, 72–74, 257–259 CrossRef CAS
.
- A. I. Orlova, D. B. Kitaev, N. G. Kazantsev, S. G. Samoilov, V. S. Kurazhkovskaya and E. N. Vopilina, Radiochem, 2002, 44, 326–331 CrossRef CAS
.
- A. T. Aldred, in Geochemical Behavior of Disposed Radioactive Waste, American Chemical Society, 1984, vol. 246, ch. 18, pp. 305–314 Search PubMed
.
- O. Muller and R. Roy, in The Major Ternary Structural Families, Springer, 1974, vol. 4, p. 143 Search PubMed
.
- O. Fukunaga and S. Yamaoka, Phys. Chem. Miner., 1979, 5, 167–177 CrossRef CAS
.
- J. P. Bastide, J. Solid State Chem., 1987, 71, 115–120 CrossRef CAS
.
- R. J. Finch and J. M. Hanchar, Rev. Mineral. Geochem., 2003, 53, 1–25 CrossRef CAS
.
- D. Errandonea and F. J. Manjón, Prog. Mater. Sci., 2008, 53, 711–773 CrossRef CAS
.
- M. K. Carron, M. E. Mrose and K. J. Murata, Am. Mineral., 1958, 43, 985–989 CAS
.
- B. J. Macey, Masters thesis, Virginia Tech, 1995
.
- R. S. Hay, P. Mogilevsky and E. Boakye, Acta Mater., 2013, 61, 6933–6947 CrossRef CAS
.
- U. Kolitsch and D. Holtstam, Eur. J. Mineral., 2004, 16, 117–126 CrossRef CAS
.
- A. Du, C. Wan, Z. Qu and W. Pan, J. Am. Ceram. Soc., 2009, 92, 2687–2692 CrossRef CAS
.
- K. Kenges, O. Proskurina, D. Danilovich, M. Aldabergenov and V. Gusarov, Russ. J. Appl. Chem., 2018, 91, 1538–1548 CrossRef CAS
.
- J. Feng, B. Xiao, R. Zhou and W. Pan, Acta Mater., 2013, 61, 7364–7383 CrossRef CAS
.
- P. M. Kowalski and Y. Li, J. Eur. Ceram. Soc., 2016, 36, 2093–2096 CrossRef CAS
.
- H. Li, S. Zhang, S. Zhou and X. Cao, Inorg. Chem., 2009, 48, 4542–4548 CrossRef CAS PubMed
.
- P. E. Morgan and D. B. Marshall, J. Am. Ceram. Soc., 1995, 78, 1553–1563 CrossRef CAS
.
- Y. Hikichi, T. Ota and T. Hattori, Mineral. J., 1997, 19, 123–130 CrossRef CAS
.
- T. M. Wilkinson, D. Wu, M. A. Musselman, N. Li, N. Mara and C. E. Packard, Mater. Sci. Eng., A, 2017, 691, 203–210 CrossRef CAS
.
- J. Han, Y. Wang, R. Liu and F. Wan, Sci. Rep., 2020, 10, 13681 CrossRef CAS PubMed
.
- Y. Hikichi, T. Ota, K. Daimon, T. Hattori and M. Mizuno, J. Am. Ceram. Soc., 1998, 81, 2216–2218 CrossRef CAS
.
- F. Zhang, J. Wang, M. Lang, J. Zhang, R. C. Ewing and L. A. Boatner, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 184114 CrossRef
.
- K. Popa and R. J. M. Konings, Thermochim. Acta, 2006, 445, 49–52 CrossRef CAS
.
- Y. Hikichi and T. Nomura, J. Am. Ceram. Soc., 1987, 70, C-252–C-253 Search PubMed
.
- Y. Ji, G. Beridze, D. Bosbach and P. M. Kowalski, J. Nucl. Mater., 2017, 494, 172–181 CrossRef CAS
.
- T. Deepthi and K. Balamurugan, Ceram. Int., 2019, 45, 18229–18235 CrossRef CAS
.
- A. Blanca Romero, P. M. Kowalski, G. Beridze, H. Schlenz and D. Bosbach, J. Comput. Chem., 2014, 35, 1339–1346 CrossRef PubMed
.
- G. Beridze, A. Birnie, S. Koniski, Y. Ji and P. M. Kowalski, Prog. Nucl. Energy, 2016, 92, 142–146 CrossRef CAS
.
- R. G. Jonasson, G. M. Bancroft and H. W. Nesbitt, Geochim. Cosmochim. Acta, 1985, 49, 2133–2139 CrossRef CAS
.
- N. Clavier, DSc thesis, Université Paris Sud-Paris XI, 2004
.
- E. Du Fou de Kerdaniel, N. Clavier, N. Dacheux, O. Terra and R. Podor, J. Nucl. Mater., 2007, 362, 451–458 CrossRef CAS
.
- E. H. Oelkers and F. Poitrasson, Chem. Geol., 2002, 191, 73–87 CrossRef CAS
.
- G. J. McCarthy, W. B. White and D. E. Pfoertsch, Mater. Res. Bull., 1978, 13, 1239–1245 CrossRef CAS
.
- B. C. Sales, C. W. White and L. A. Boatner, Nucl. Chem. Waste Manage., 1983, 4, 281–289 CrossRef CAS
.
- Y. Teng, P. Zeng, Y. Huang, L. Wu and X. Wang, J. Nucl. Mater., 2015, 465, 482–487 CrossRef CAS
.
- C. Gausse, S. Szenknect, A. Mesbah, N. Clavier, S. Neumeier and N. Dacheux, Appl. Geochem., 2018, 93, 81–93 CrossRef CAS
.
- E. Du Fou de Kerdaniel, DSc thesis, Université Paris Sud-Paris XI, 2007
.
- O. Terra, N. Dacheux, F. Audubert and R. Podor, J. Nucl. Mater., 2006, 352, 224–232 CrossRef CAS
.
- N. Clavier, N. Dacheux, G. Wallez and M. Quarton, J. Nucl. Mater., 2006, 352, 209–216 CrossRef CAS
.
- M. R. Rafiuddin and A. P. Grosvenor, J. Nucl. Mater., 2018, 509, 631–643 CrossRef CAS
.
- D. J. Wronkiewicz, S. F. Wolf and T. S. DiSanto, Mater. Res. Soc., 1995, 412, 345–352 CrossRef
.
- ASTM C1285-21, Standard Test Methods for Determining Chemical Durability of Nuclear, Hazardous, and Mixed Waste Glasses and Multiphase Glass Ceramics: The Product Consistency Test (PCT), 2021 Search PubMed
.
- ASTM C1663-18, Standard Test Method for Measuring Waste Glass or Glass Ceramic Durability by Vapor Hydration Test (VHT), 2018 Search PubMed
.
- EPA, SW-846 Test Method 1311: Toxicity Characteristic Leaching Procedure, 1992 Search PubMed
.
- F. Poitrasson, S. Chenery and T. J. Shepherd, Geochim. Cosmochim. Acta, 2000, 64, 3283–3297 CrossRef CAS
.
- P. Mikhailova, B. Burakov, N. Eremin, A. Averin and A. Shiryaev, Sustainab, 2021, 13, 1203 CrossRef CAS
.
- B. I. Omel’yanenko, T. S. Livshits, S. V. Yudintsev and B. S. Nikonov, Geol. Ore Deposits, 2007, 49, 173–193 CrossRef
.
- L. Nasdala, S. Akhmadaliev, A. Artac, C. Chanmuang N, G. Habler and C. Lenz, Phys. Chem. Miner., 2018, 45, 855–871 CrossRef CAS PubMed
.
- A.-M. Seydoux-Guillaume, X. Deschanels, C. Baumier, S. Neumeier, W. J. Weber and S. Peuget, Am. Mineral., 2018, 103, 824–827 CrossRef
.
- A. Meldrum, R. C. Ewing and L. A. Boatner, Mineral. Mag., 2000, 64, 185–194 CrossRef CAS
.
- L. Nasdala, M. Wenzel, G. Vavra, G. Irmer, T. Wenzel and B. Kober, Contrib. Mineral. Petrol., 2001, 141, 125–144 CrossRef CAS
.
- M. R. Rafiuddin and A. P. Grosvenor, J. Alloys Compd., 2015, 653, 279–289 CrossRef CAS
.
- V. S. Urusov, A. E. Grechanovsky and N. N. Eremin, Glass Phys. Chem., 2012, 38, 55–62 CrossRef CAS
.
- A. Meldrum, L. A. Boatner, W. J. Weber and R. C. Ewing, Geochim. Cosmochim. Acta, 1998, 62, 2509–2520 CrossRef CAS
.
- G. R. Lumpkin and T. Geisler-Wierwille, in Comprehensive Nuclear Materials, ed. R. J. M. Konings, Elsevier, Oxford, 2012, pp. 563–600, DOI: DOI:10.1016/B978-0-08-056033-5.00111-7
.
- B. E. Burakov, V. M. Garbuzov, A. A. Kitsay, M. A. Yagovkina and V. A. Zirlin, Mater. Res. Soc. Symp. Proc., 2004, 824, CC4 CrossRef
.
- F. Lu, Y. Shen, X. Sun, Z. Dong, R. C. Ewing and J. Lian, Acta Mater., 2013, 61, 2984–2992 CrossRef CAS
.
- M. R. Rafiuddin, A.-M. Seydoux-Guillaume, X. Deschanels, A. Mesbah, C. Baumier, S. Szenknect and N. Dacheux, J. Nucl. Mater., 2020, 539, 152265 CrossRef CAS
.
- H. B. Tisdale, M. S. Christian, G. Morrison, T. M. Besmann, K. Sun, G. S. Was and H.-C. zur Loye, Chem. Mater., 2022, 34, 3819–3830 CrossRef CAS
.
- A. M. Seydoux-Guillaume, R. Wirth, L. Nasdala, M. Gottschalk, J. M. Montel and W. Heinrich, Phys. Chem. Miner., 2002, 29, 240–253 CrossRef CAS
.
- A.-M. Seydoux-Guillaume, R. Wirth, A. Deutsch and U. Schärer, Geochim. Cosmochim. Acta, 2004, 68, 2517–2527 CrossRef CAS
.
- D. Bregiroux, R. Belin, P. Valenza, F. Audubert and D. Bernache-Assollant, J. Nucl. Mater., 2007, 366, 52–57 CrossRef CAS
.
- V. Picot, X. Deschanels, S. Peuget, B. Glorieux, A. M. Seydoux-Guillaume and R. Wirth, J. Nucl. Mater., 2008, 381, 290–296 CrossRef CAS
.
- X. Deschanels, A. M. Seydoux-Guillaume, V. Magnin, A. Mesbah, M. Tribet, M. P. Moloney, Y. Serruys and S. Peuget, J. Nucl. Mater., 2014, 448, 184–194 CrossRef CAS
.
- C. Overstreet, J. Cooper, E. O'Quinn, W. Cureton, R. Palomares, J. Leys, G. Deissmann, S. Neumeier, C.-H. Chen and M. Lang, Nucl. Instrum. Methods Phys. Res., Sect. B, 2022, 527, 34–39 CrossRef CAS
.
- A. N. Trukhin and L. A. Boatner, 13th Int. Conf. Defects Insul. Cryst. Mater. Sci. Forum, vol. 239–241, 1997 Search PubMed
.
- T. Hernández and P. Martín, J. Eur. Ceram. Soc., 2007, 27, 109–114 CrossRef
.
- G. M. Begun, G. W. Beall, L. A. Boatner and W. J. Gregor, J. Raman Spectrosc., 1981, 11, 273–278 CrossRef CAS
.
- P. C. Becker, N. Edelstein, G. M. Williams, J. J. Bucher, R. E. Russo, J. A. Koningstein, L. A. Boatner and M. M. Abraham, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 31, 8102–8110 CrossRef CAS PubMed
.
- P. C. Becker, G. M. Williams, N. M. Edelstein, J. A. Koningstein, L. A. Boatner and M. M. Abraham, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 5027–5030 CrossRef CAS PubMed
.
- A. Lempicki, E. Berman, A. J. Wojtowicz, M. Balcerzyk and L. A. Boatner, IEEE Trans. Nucl. Sci., 1993, 40, 384–387 CAS
.
- D. Wisniewski, S. Tavernier, A. J. Wojtowicz, M. Wisniewska, P. Bruyndonckx, P. Dorenbos, E. van Loef, C. W. E. van Eijk and L. A. Boatner, Nucl. Instrum. Methods Phys. Res., Sect. A, 2002, 486, 239–243 CrossRef CAS
.
- W. W. Moses, M. J. Weber, S. E. Derenzo, D. Perry, P. Berdahl and L. A. Boatner, IEEE Trans. Nucl. Sci., 1988, 45, 462–466 Search PubMed
.
- L. Nasdala, S. Akhmadaliev, B. E. Burakov, C. Chanmuang N and R. Škoda, Sci. Rep., 2020, 10, 14676 CrossRef CAS PubMed
.
- W. Sun and J. Du, Comput. Mater. Sci., 2017, 126, 326–335 CrossRef CAS
.
- J. Du, R. Devanathan, L. René Corrales and W. J. Weber, Comput. Theor. Chem., 2012, 987, 62–70 CrossRef CAS
.
- J. Du, M. Motorsi, S. Barbi and X. Lu, in Atomistic Simulations of Glasses Fundamentals and Applications, John Wiley & Sons Inc., 2022, pp. 367–438, DOI:10.1002/9781118939079.ch12
.
- A. M. Miksch, T. Morawietz, J. Kästner, A. Urban and N. Artrith, Mach. Learn.: Sci. Technol., 2021, 2, 031001 Search PubMed
.
- R. Ramprasad, R. Batra, G. Pilania, A. Mannodi-Kanakkithodi and C. Kim, npj Comput. Mater., 2017, 3, 54 CrossRef
.
- E. Di Napoli, X. Wu, T. Bornhake and P. M. Kowalski, Front. Appl. Math. Stat., 2024, 10, 1355726 CrossRef
.
- G. H. Alférez, O. A. Esteban, B. L. Clausen and A. M. M. Ardila, Earth Sci. Inform., 2022, 15, 1683–1698 CrossRef
.
- K. Itano, K. Ueki, T. Iizuka and T. Kuwatani, Geosci., 2020, 10, 63 CrossRef CAS
.
| This journal is © The Royal Society of Chemistry 2024 |