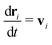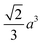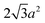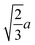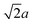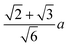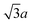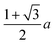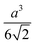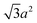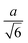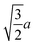Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Mesoscale simulations of diffusion and sedimentation in shape-anisotropic nanoparticle suspensions
Yashraj M.
Wani†
 a,
Penelope Grace
Kovakas†
a,
Penelope Grace
Kovakas†
 b,
Arash
Nikoubashman
b,
Arash
Nikoubashman
 *cd and
Michael P.
Howard
*cd and
Michael P.
Howard
 *b
*b
aInstitute of Physics, Johannes Gutenberg University Mainz, Staudingerweg 7, 55128, Mainz, Germany
bDepartment of Chemical Engineering, Auburn University, Auburn, Alabama 36849, USA. E-mail: mphoward@auburn.edu
cLeibniz-Institut für Polymerforschung Dresden e.V., Hohe Straße 6, 01069 Dresden, Germany. E-mail: anikouba@ipfdd.de
dInstitut für Theoretische Physik, Technische Universität Dresden, 01069 Dresden, Germany
First published on 26th April 2024
Abstract
We determine the long-time self-diffusion coefficient and sedimentation coefficient for suspensions of nanoparticles with anisotropic shapes (octahedra, cubes, tetrahedra, and spherocylinders) as a function of nanoparticle concentration using mesoscale simulations. We use a discrete particle model for the nanoparticles, and we account for solvent-mediated hydrodynamic interactions between nanoparticles using the multiparticle collision dynamics method. Our simulations are compared to theoretical predictions and experimental data from existing literature, demonstrating good agreement in the majority of cases. Further, we find that the self-diffusion coefficient of the regular polyhedral shapes can be estimated from that of a sphere whose diameter is the average of their inscribed and circumscribed sphere diameters.
I Introduction
The dynamics of nanoparticles (NPs) in suspensions play an important role in numerous applications, ranging from cellular transport1 to the fabrication of functional nanomaterials.2 For example, therapeutic agents can be encapsulated inside or attached to NPs for targeted drug delivery, and differences in NP dynamics in the body can affect their uptake and efficacy.3–5 Many factors impact the motion of NPs, including their size, interactions with each other, and interactions with their surroundings.6 This work focuses specifically on the effect of shape, which has emerged as an important factor for modulating the properties and function of NPs in many practical applications.7,8 For example, shape-anisotropic iron-oxide-based magnetic NPs were shown to enhance contrast for magnetic resonance imaging compared to spherical NPs,8 while quantum rods were shown to have enhanced diffusion compared to quantum dots in confined networks.9 Given that NPs with a variety of shapes can be readily synthesized10–12 and that many naturally occurring NPs (e.g., the rod-like tobacco mosaic virus13,14 and gibbsite platelets15) also exhibit pronounced shape anisotropy, it is important to develop a fundamental understanding of the relationship between shape and transport properties, such as diffusion coefficients, in order to engineer NPs for practical applications.Experimentally characterizing how NP dynamics depend on shape and concentration can be challenging. For example, dynamic light scattering is a common technique for measuring NP diffusion from fluctuations in scattered light intensity.16 However, knowledge about the distribution of NP sizes and/or shapes is needed to extract the diffusion coefficient from the raw measurement data,17,18 and it is difficult to perform this analysis for non-dilute solutions.19 Camera-based tracking of tagged NPs is an alternative approach that allows for the direct measurement of the NP diffusion coefficient,9,20 but this method has limited spatial and temporal resolution.20 NP properties may also be affected if labeling agents, such as fluorescent markers, are used.21 Further, it can be difficult to prepare NP suspensions with sufficiently low polydispersity and at high enough concentrations to accurately assess how the diffusion coefficient varies with both NP characteristics and concentration.
As a result, theory and simulations have proven to be useful approaches for studying the dynamics of NP suspensions. Early theories predominantly focused on spherical NPs, for which the single-particle translational and rotational diffusion coefficients can be calculated using the classical Stokes–Einstein and Stokes–Einstein–Debye relations, respectively. Theoretical predictions for the first-order concentration dependence of the long-time self-diffusion coefficient for suspensions of spherical NPs have also been derived.22,23 Beyond spherical NPs, pioneering works by Kuhn, Kirkwood, and others have led to estimates for the single-particle translational and rotational diffusion coefficients of rod-like particles.24–29 At finite concentration, the diffusive motion of the rods becomes more complex but can be split qualitatively into three regimes: at dilute concentrations, rods have essentially unrestricted motion in all directions; at semi-dilute concentrations, their motion is slightly hindered perpendicular to the long axis of the rod; and at high concentrations, the perpendicular diffusive motion is entirely suppressed.30 However, predicting the dynamics of rod-like NPs with quantitative accuracy still remains challenging because their anisotropic shape can lead to complex flow patterns around individual NPs and to non-trivial collective behavior such as nematic or smectic ordering. For more complicated NP shapes than rods, predicting even single-particle diffusion coefficients becomes challenging, and numerical approaches are often required.31,32 In general, fully analytic descriptions of NP dynamics in suspensions are challenging to construct due to the many-body hydrodynamic interactions (HIs) between NPs that are mediated by the solvent.
Computer simulations are highly useful tools for numerically investigating NP dynamics in suspensions. The main challenge is to construct models that capture the relevant physics while remaining computationally tractable. Explicitly resolving both the NPs and the solvent molecules they are suspended in using, e.g., classical molecular dynamics (MD) approaches, quickly becomes infeasible because NPs are typically much larger than solvent molecules. However, given the corresponding separation of time scales between the solvent dynamics and NP dynamics, it is often possible to overcome this difficulty using coarse-grained models having simplified or implicit treatments of the solvent.33 For example, Brownian dynamics (BD) is a well-known implicit-solvent technique that accounts for solvent-induced drag and fluctuating forces on the NPs,34 but which neglects HIs between the NPs in its most basic form. HIs can be introduced to BD through appropriate mobility tensors,35 such as the pairwise far-field Rotne–Prager–Yamakawa tensor for spherical particles.36,37 Stokesian dynamics, a gold-standard approach for simulating colloidal suspensions, additionally accounts for short-range lubrication forces between NPs within the BD framework.38,39 However, BD approaches that include HIs are often still computationally demanding to implement and require expressions for the mobility tensor, which may be difficult to obtain for complex NP shapes.
To circumvent issues determining inputs needed for a fully implicit treatment of the solvent, several mesoscale simulation methods, including multiparticle collision dynamics (MPCD),33,40,41 dissipative particle dynamics,42,43 and the lattice Boltzmann method,44,45 use simplified particle-based solvent models that are less demanding to simulate than an atomistic model but still have properties resembling that of real solvents. In this work, we will use MPCD because we have recently shown that MPCD can reasonably reproduce expected results for the long-time self-diffusion coefficient and sedimentation coefficient for suspensions of spherical NPs over a range of NP concentrations,46 and the same approach used to model the spherical NPs can be extended to NPs with other shapes. In MPCD, NPs are modeled as conventional MD particles that can be coupled to the solvent through different schemes to ensure HIs develop.46–52 The current state-of-the-art coupling scheme, first proposed by Poblete et al., uses a discrete particle model that represents an NP as a mesh of “vertex” particles interconnected via elastic springs.47 The solvent particles interact with the NPs only through stochastic collisions that are straightforward to compute. We used a discrete particle model to study the long-time self-diffusion of cubes,46 and similar models have been used to simulate the self-assembly of colloids with shape and/or interaction anisotropy.53–58 However, we are unaware of a systematic study using MPCD to characterize the long-time self-diffusion coefficients and sedimentation coefficients for suspensions of shape-anisotropic NPs at varying concentrations.
In this work, we use MPCD with a discrete particle model to study the long-time self-diffusion and sedimentation coefficients of octahedra, cubes, tetrahedra, and spherocylinders as a function of NP concentration. We investigate the effect of shape by comparing the results for the different NP shapes with each other and with spheres. We also assess the influence of solvent-mediated HIs by comparing the MPCD simulations with implicit-solvent Langevin dynamics (LD) simulations.
II Models
A. Multiparticle collision dynamics
In MPCD, the solvent consists of point particles that are propagated in alternating streaming and collision steps that occur at a regular time interval Δt. During the streaming step, the solvent particles move according to Newton's equations of motion,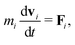 | (1) |
In the collision step, the solvent particles are sorted into cubic cells of edge length ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) , then exchange momentum with particles in the same cell according to a collision scheme. Here, we use the stochastic rotation dynamics (SRD) scheme without angular momentum conservation.40,41 SRD updates the velocity of particle i in cell j according to:
, then exchange momentum with particles in the same cell according to a collision scheme. Here, we use the stochastic rotation dynamics (SRD) scheme without angular momentum conservation.40,41 SRD updates the velocity of particle i in cell j according to:
| vi←uj + Ωj·(vi–uj), | (2) |
![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) /2, +
/2, +![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) /2] to ensure Galilean invariance,59,60 and a cell-level Maxwellian thermostat is used to maintain a constant temperature T.61
/2] to ensure Galilean invariance,59,60 and a cell-level Maxwellian thermostat is used to maintain a constant temperature T.61
The natural units for MPCD simulations are the length ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) of the collision cells, the mass m of the solvent particles, and the thermal energy kBT, where kB is the Boltzmann constant. The corresponding unit of time is
of the collision cells, the mass m of the solvent particles, and the thermal energy kBT, where kB is the Boltzmann constant. The corresponding unit of time is 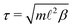 , where β = 1/(kBT). We adopted the standard SRD parameters Δt = 0.1τ, α = 130°, and average solvent number density 5
, where β = 1/(kBT). We adopted the standard SRD parameters Δt = 0.1τ, α = 130°, and average solvent number density 5![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) −3, which give a liquid-like Newtonian fluid with dynamic viscosity η0 = 3.95kBTτ/
−3, which give a liquid-like Newtonian fluid with dynamic viscosity η0 = 3.95kBTτ/![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) 3.62
3.62
B. Discrete particle model
A discrete particle model was used to represent the NPs and couple them to the solvent.46,47 The NP shapes we modeled were a sphere, an octahedron, a cube, a tetrahedron, and two spherocylinders with different aspect ratios (Fig. 1). Each NP consisted of Nv vertex particles on the surface of the shape, and each vertex particle had mass 5m. The vertex particles were bonded to their nearest neighbors with a harmonic potential,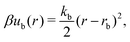 | (3) |
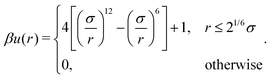 | (4) |
![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) −2 to make stiff bonds and σ =
−2 to make stiff bonds and σ = ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) , and we integrated eqn (1) using the velocity Verlet algorithm with time step 0.005τ. We visually confirmed that all NPs maintained a nearly rigid shape and that no NPs penetrated each other for the vertex-particle configurations chosen as described next.
, and we integrated eqn (1) using the velocity Verlet algorithm with time step 0.005τ. We visually confirmed that all NPs maintained a nearly rigid shape and that no NPs penetrated each other for the vertex-particle configurations chosen as described next.
 | ||
| Fig. 1 Discrete particle model for (a) sphere, (b) octahedron, (c) cube, (d) tetrahedron and (e) two spherocylinders (aspect ratios λ = 1 and 2). The Nv vertex particles are shown in orange, and the bonds to their nearest neighbors are shown in blue. To improve the clarity of these renderings, the size of the vertex particles has been decreased, and central particles and additional bonds used to maintain the shape have been omitted. These snapshots were rendered using visual molecular dynamics (version 1.9.3).64 | ||
Sphere.—We modeled a sphere having diameter d = 6![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) [Fig. 1(a)] as a reference point. To create the vertex particles, we subdivided the triangular faces of a regular icosahedron twice and scaled the positions of all vertices to lie on the surface of the sphere. This process resulted in Nv = 162 vertex particles with a typical nearest-neighbor distance between 0.83
[Fig. 1(a)] as a reference point. To create the vertex particles, we subdivided the triangular faces of a regular icosahedron twice and scaled the positions of all vertices to lie on the surface of the sphere. This process resulted in Nv = 162 vertex particles with a typical nearest-neighbor distance between 0.83![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) and 0.97
and 0.97![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) . Note that this model differs from the one we used in ref. 46 in two ways: (1) the number of vertex particles is larger and (2) the excluded volume is handled through the vertex particles rather than through the central particle. These choices were made in this work so that the spheres would have a comparable surface density of vertex particles and the same style of excluded-volume interactions as the anisotropic NPs we studied.
. Note that this model differs from the one we used in ref. 46 in two ways: (1) the number of vertex particles is larger and (2) the excluded volume is handled through the vertex particles rather than through the central particle. These choices were made in this work so that the spheres would have a comparable surface density of vertex particles and the same style of excluded-volume interactions as the anisotropic NPs we studied.
Octahedron and tetrahedron.—We modeled a regular octahedron and a regular tetrahedron, both having edge length a = 6![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) [Fig. 1(b) and (d)]. Because the faces of these polyhedra are equilateral triangles, we first created a three-dimensional triangulated model of each shape using computer-aided design software, then subdivided the faces 3 times to create a triangular mesh of vertex particles. This process resulted in 9 vertex particles per edge and distance a/8 = 0.75
[Fig. 1(b) and (d)]. Because the faces of these polyhedra are equilateral triangles, we first created a three-dimensional triangulated model of each shape using computer-aided design software, then subdivided the faces 3 times to create a triangular mesh of vertex particles. This process resulted in 9 vertex particles per edge and distance a/8 = 0.75![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) between all nearest-neighbor vertex particles for both shapes. The total number of vertex particles was Nv = 258 for the octahedron and Nv = 130 for the tetrahedron.
between all nearest-neighbor vertex particles for both shapes. The total number of vertex particles was Nv = 258 for the octahedron and Nv = 130 for the tetrahedron.
Cube.—We modeled a cube with edge length a = 6![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) [Fig. 1(c)] using a square mesh with 8 vertex particles per edge. The total number of vertex particles was Nv = 296, and the distance between nearest-neighbor vertex particles was a/7 ≈ 0.86
[Fig. 1(c)] using a square mesh with 8 vertex particles per edge. The total number of vertex particles was Nv = 296, and the distance between nearest-neighbor vertex particles was a/7 ≈ 0.86![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) . This is the same vertex particle configuration as in ref. 46, and the description here corrects a typographical error for the number of vertex particles per edge. Unlike in ref. 46, though, a central particle was used to maintain rigidity to keep consistency with the sphere, octahedron, and tetrahedron.
. This is the same vertex particle configuration as in ref. 46, and the description here corrects a typographical error for the number of vertex particles per edge. Unlike in ref. 46, though, a central particle was used to maintain rigidity to keep consistency with the sphere, octahedron, and tetrahedron.
Spherocylinder.—We modeled two types of spherocylinders: both had two hemispheres with diameter d = 6![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) , but one had a cylinder of length h = 6
, but one had a cylinder of length h = 6![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) while the other cylinder had the length h = 12
while the other cylinder had the length h = 12![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) [Fig. 1(e)]. Thus, the spherocylinders had aspect ratios λ ≡ d/h = 1 and 2, respectively. This degree of anisotropy is much smaller than that of many rod-like particles, such as those of biological origin like the fd virus65,66 and tobacco mosaic virus,13 that is often in the range λ ⪆ 10. Nanorods with smaller aspect ratios can be synthesized,67–69 but we found surprisingly little data on their transport coefficients. Hence, we chose to study spherocylinders with these smaller aspect ratios to begin to bridge the knowledge gap between spheres and long rod-like NPs. Discrete particle models for the spherocylinders were constructed through a multi-step process: First, a mesh of vertex particles for the hemispheres was created by slicing our discrete sphere model in half along a plane that exposed 20 evenly spaced vertex particles around its circumference and had 91 vertex particles in total. Then, vertex particles for the cylinder were generated from the ring of 20 exposed vertex particles by translating the ring by 0.75
[Fig. 1(e)]. Thus, the spherocylinders had aspect ratios λ ≡ d/h = 1 and 2, respectively. This degree of anisotropy is much smaller than that of many rod-like particles, such as those of biological origin like the fd virus65,66 and tobacco mosaic virus,13 that is often in the range λ ⪆ 10. Nanorods with smaller aspect ratios can be synthesized,67–69 but we found surprisingly little data on their transport coefficients. Hence, we chose to study spherocylinders with these smaller aspect ratios to begin to bridge the knowledge gap between spheres and long rod-like NPs. Discrete particle models for the spherocylinders were constructed through a multi-step process: First, a mesh of vertex particles for the hemispheres was created by slicing our discrete sphere model in half along a plane that exposed 20 evenly spaced vertex particles around its circumference and had 91 vertex particles in total. Then, vertex particles for the cylinder were generated from the ring of 20 exposed vertex particles by translating the ring by 0.75![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) and rotating it around the axis of the cylinder by 9° to stagger the particles on consecutive rings. This process was repeated until the entire cylinder surface was covered with vertex particles. The total number of vertex particles per spherocylinder was Nv = 322 for λ = 1 and Nv = 482 for λ = 2, with the nearest-neighbor distance between vertex particles ranging from 0.83
and rotating it around the axis of the cylinder by 9° to stagger the particles on consecutive rings. This process was repeated until the entire cylinder surface was covered with vertex particles. The total number of vertex particles per spherocylinder was Nv = 322 for λ = 1 and Nv = 482 for λ = 2, with the nearest-neighbor distance between vertex particles ranging from 0.83![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) to 0.97
to 0.97![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) .
.
C. Simulation details
We performed bulk simulations containing N NPs in a cubic simulation box with edge length L = 120![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) and periodic boundary conditions. We simulated a range of nominal NP volume fractions ϕ = Nv/L3, where v is the nominal volume of each NP (Table 1), by varying N. We created equilibrated configurations of NPs at the different volume fractions using LD simulations. LD simulations are faster to perform than MPCD simulations because they do not include HI, and we also chose the friction coefficient for the LD simulations to give faster NP dynamics than in the MPCD simulations in order to accelerate equilibration. Starting from these configurations, we measured the long-time self-diffusion coefficient as a function of ϕ using equilibrium simulations (Section IIIA) and the sedimentation coefficient as a function of ϕ using nonequilibrium simulations (Section IIIB). All simulations were conducted using HOOMD-blue70,71 (version 2.9.7) extended with azplugins72 (version 0.12.0).
and periodic boundary conditions. We simulated a range of nominal NP volume fractions ϕ = Nv/L3, where v is the nominal volume of each NP (Table 1), by varying N. We created equilibrated configurations of NPs at the different volume fractions using LD simulations. LD simulations are faster to perform than MPCD simulations because they do not include HI, and we also chose the friction coefficient for the LD simulations to give faster NP dynamics than in the MPCD simulations in order to accelerate equilibration. Starting from these configurations, we measured the long-time self-diffusion coefficient as a function of ϕ using equilibrium simulations (Section IIIA) and the sedimentation coefficient as a function of ϕ using nonequilibrium simulations (Section IIIB). All simulations were conducted using HOOMD-blue70,71 (version 2.9.7) extended with azplugins72 (version 0.12.0).
![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) (the edge length for all our polyhedral NPs) quoted in parentheses. The properties are the volume v, surface area A, sphericity ψ, inscribed-sphere diameter dI, circumscribed-sphere diameter dC, and mean of inscribed-sphere and circumscribed-sphere diameters
(the edge length for all our polyhedral NPs) quoted in parentheses. The properties are the volume v, surface area A, sphericity ψ, inscribed-sphere diameter dI, circumscribed-sphere diameter dC, and mean of inscribed-sphere and circumscribed-sphere diameters ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif)
For the spheres and regular polyhedra, we performed one equilibrium simulation of length 2 × 105τ and recorded the position of all central particles every 10τ. We performed one nonequilibrium simulation consisting of a warmup period of 0.5 × 105τ to reach steady state followed by a production period of length 1.5 × 105τ in which we recorded the average velocity of the NPs every 0.105τ and the average velocity of the solvent every 0.1τ. The different sampling frequencies for the NPs and solvent were chosen to account for acceleration of the NPs between solvent collisions.46 To estimate error bars, we subdivided these trajectories into three blocks and computed the standard error between blocks.
For the spherocylinders, we performed eight equilibrium simulations of length 105τ and recorded the position of enough vertex particles to reconstruct the center of mass of each NP every 2.5τ. We performed three nonequilibrium simulations consisting of a 0.5 × 105τ warmup period and 1 × 105τ production period with the velocities sampled in the same way as for the other shapes. Error bars were estimated as the standard error of the independent simulations.
III Results and discussion
A. Long-time self-diffusion coefficient
We computed the long-time self-diffusion coefficient D of the NPs from the time derivative of the average mean squared displacement 〈Δr2〉 of each NP,34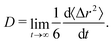 | (5) |
Due to the long-ranged nature of solvent-mediated HIs, self-diffusion coefficients measured in simulations with periodic boundary conditions can suffer from noticeable finite-size effects.75–77 For a cubic simulation box such as ours, the self-diffusion coefficient in an infinitely large box D∞ is related to D in a finite box with edge length L by76,77
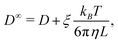 | (6) |
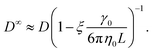 | (7) |
To apply eqn (7), γ0 must be determined for each NP shape. Experimental correlations81 for γ0 exist [e.g., eqn (9) below]; however, it is not guaranteed that the MPCD simulations are consistent with these. Instead, we noted that all diffusivities are corrected by the same factor in eqn (7) regardless of ϕ and that eqn (6) can be used directly when ϕ is sufficiently small that η ≈ η0. Accordingly, we linearly extrapolated our measured D to ϕ = 0, using the data from the smallest two values of ϕ that we simulated, to obtain a measured D0 with finite-size effects. We then applied eqn (6) with η = η0 to calculate D∞0 from D0 and used the ratio D∞0/D0 as the finite-size correction factor for all D. In the rest of the paper, all diffusion coefficients have been corrected for finite-size effects in this way, but we will still refer to them as D and D0 for notational simplicity.
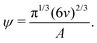 | (8) |
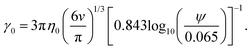 | (9) |
Based on eqn (9), a cube should diffuse more slowly than an octahedron, while an octahedron should diffuse more slowly than a tetrahedron when all have the same edge length a; a sphere with diameter d = a is predicted to have D0 between that of the octahedron and the tetrahedron (Table 2). Indeed, our simulation results for D0 were qualitatively consistent with these predictions. Quantitatively, D0 from the cube simulations was in excellent agreement with the value predicted using eqn (9), but D0 from the octahedron and tetrahedron simulations was 9% and 18% smaller, respectively. We calculated a similar deviation between the measured and predicted D0 for tetrahedra in recent experiments by Hoffmann and coworkers, who fabricated tetrahedral clusters from four spherical polystyrene NPs with diameter 154 nm; they measured a self-diffusion coefficient of D0= 1.72 × 10−12 m2 s−1 in water,82,83 which is 22% smaller than the predicted value of D0 = 2.2 × 10−12 m2 s−1 when using an edge length of a = 308 nm in eqn (9). These clusters are, however, not true tetrahedra so it is unclear whether this deviation from eqn (9) should be expected in the MPCD simulations too.
![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) given in Table 1. All values are in units of 10−3
given in Table 1. All values are in units of 10−3![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) 2/τ
2/τ
| Simulation | Using eqn (9) | Using ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) |
|
|---|---|---|---|
| Sphere | 4.32 | 4.48 | |
| Octahedron | 3.95 | 4.36 | 4.01 |
| Cube | 3.31 | 3.33 | 3.28 |
| Tetrahedron | 5.14 | 6.29 | 5.48 |
We and others previously found that D0 for a cube can also be reasonably well-approximated by D0 for a sphere with diameter ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) = (dI + dC)/2, the arithmetic mean of the diameters dI and dC of the spheres that inscribe and circumscribe it, respectively.32,46 We carried out the same calculation for the octahedron and tetrahedron, and we again found good agreement with our simulations (Table 2). Thus, using
= (dI + dC)/2, the arithmetic mean of the diameters dI and dC of the spheres that inscribe and circumscribe it, respectively.32,46 We carried out the same calculation for the octahedron and tetrahedron, and we again found good agreement with our simulations (Table 2). Thus, using ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) seems to provide a quick and reasonable estimate of D0 for regular polyhedra as an alternative to eqn (9).
seems to provide a quick and reasonable estimate of D0 for regular polyhedra as an alternative to eqn (9).
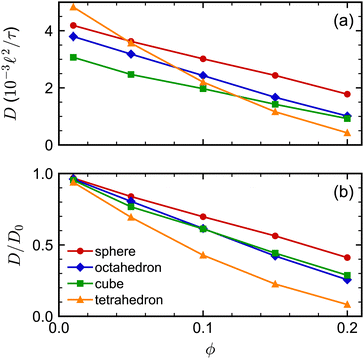
We next investigated the volume-fraction dependence of D [Fig. 2(a)]. Given that the different NP shapes had different D0, we report D/D0 to facilitate comparison between shapes [Fig. 2(b)]. The tetrahedra exhibited the strongest dependence on ϕ, the spheres exhibited the weakest dependence on ϕ, while both the cubes and octahedra exhibited a similar dependence on ϕ that was intermediate between the spheres and tetrahedra. In general, we expected D to decrease when ϕ increased because increased interactions between NPs usually slow their motion. At low NP volume fractions, long-ranged solvent-mediated HIs are important because short-ranged interactions are infrequent. Differences in the dependence of D/D0 on ϕ seen in Fig. 2 when ϕ is small are then likely caused by differences in HIs between shapes.
At higher NP volume fractions, direct interactions between NPs become more frequent and significant, particularly those due to excluded-volume between NPs. Indeed, we expect that eventually D/D0 → 0 when the NPs reach a freezing or jamming transition that essentially traps each NP in a local cage of surrounding NPs. Based on ϕ, the regular polyhedra we simulated were all expected to be fluids even at our largest concentration (ϕ = 0.20).84–87 However, we noted that the actual excluded volume vex of the NPs (and hence excluded-volume fraction ϕex) differs from the nominal volume v (and nominal volume fraction ϕ) because the vertex particles in our discrete model have a finite size. For example, the vertex particles on the surface of the cube [Fig. 1(c)] protrude roughly σ/2, so the edge length of the volume excluded by the cube is roughly σ longer than the nominal edge length. In general, we define the excluded volume as that of the regular polyhedron that contains the spheres with diameter σ on the surface of the nominal regular polyhedron. Geometric considerations give the edge length aex of our excluded-volume regular polyhedra as aex = a(1 + σ/dI). The ratio of the excluded volume to nominal volume is then vex/v ≈ (1 + σ/dI)3 and ϕex is proportionally larger than ϕ by the same factor. This larger excluded size aex is evident in the radial distribution function g(r) (Fig. 3) for all shapes.
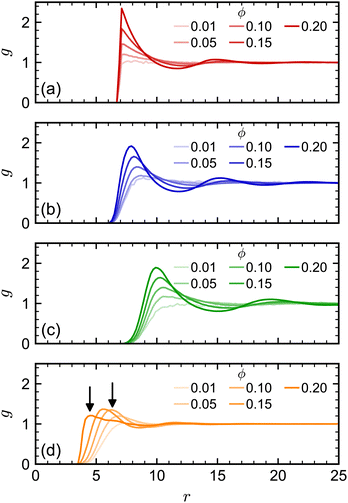 | ||
| Fig. 3 Radial distribution function for (a) spheres, (b) octahedra, (c) cubes, and (d) tetrahedra at different nominal volume fractions ϕ. The arrows in (d) denote signature peaks for the transition to pentagonal dipyramids at 0.55aex and 0.75aex.84,85 | ||
We attempted to assess the effect of this difference in nominal and excluded volume using the spherical NPs. We performed additional simulations where we implemented the excluded-volume interaction between spheres through a core-shifted Weeks–Chandler–Andersen potential between only their central particles, like in ref. 46. As expected, we found that there was less structuring in the fluid, measured through g(r), at a given nominal volume fraction ϕ due to the smaller excluded volume of each sphere [Fig. 4(a)]. However, we found little difference in the diffusivity over the range of volume fractions investigated [Fig. 4(b)]. Moreover, the simulation data for D/D0 agreed well with experimental data when plotted using ϕ. We observed similar agreement between MPCD simulations and experiments for cubes using the nominal volume fraction ϕ in our prior work46 [see also Fig. 5(c)]. Hence, at least over the range of volume fractions considered for the spheres, the nominal volume fraction ϕ seems to be a good description of the concentration.
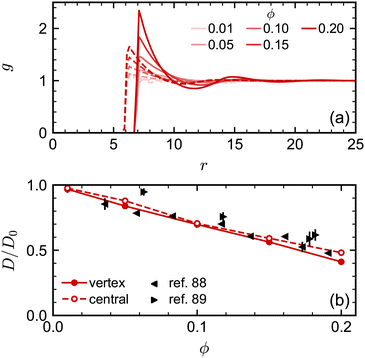 | ||
| Fig. 4 (a) Radial distribution function for spheres with excluded volume handled through either vertex particles (solid lines) or a central particle (dashed lines). (b) Long-time self-diffusion coefficient D (normalized by D0) for the same systems compared with experimental data.88,89 | ||
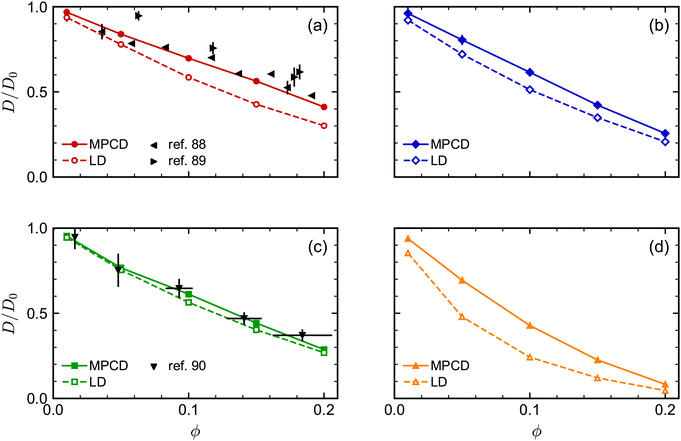 | ||
| Fig. 5 Comparison of long-time self-diffusion coefficient D (normalized by D0) of (a) spheres, (b) octahedra, (c) cubes, and (d) tetrahedra as a function of volume fraction ϕ from MPCD and LD simulations. Experimental data is included in (a) and (c) from multiple sources. The experimental values of D for the spheres88,89 were scaled by the Stokes–Einstein prediction for D0, while the experimental values of D for the cubes90 were scaled such that D/D0 = 1 for the lowest-concentration point in that data set (ϕ ≈ 0). | ||
We note, though, that structural effects caused by differences in nominal and excluded volume may still become significant at sufficiently high excluded volume fractions, particularly if a phase transition is approached. The tetrahedron, which has the largest vex/v ratio of our regular polyhedra, is an excellent example of this point. Previous simulations of hard tetrahedra84,85 revealed a transition to a fluid consisting of pentagonal dipyramids when the volume fraction was 0.47. That study found that g(r) showed a distinct signature of this transition: at low volume fractions where dipyramids did not form, g(r) had its first peak at r = 0.75a; whereas, at higher volume fractions where dipyramids formed, this original peak disappeared, and the first peak shifted to a much smaller distance r = 0.55a. Our largest nominal volume fraction ϕ = 0.20 is well below the reported transition to dipyramids, but if we instead consider the excluded volume fraction (ϕex = 0.56), then the system should have surpassed this transition. When we computed g(r) for the tetrahedra [Fig. 3(d)], we observed these signature peaks emerging at the reported r if aex was used rather than a. Thus, the tetrahedra appear to undergo a transition to dipyramids that is not expected using only ϕ. The more dramatic slowing down of the tetrahedra dynamics with ϕ compared to the other shapes could be partially due to this transition.
Finally, we assessed the influence of HIs between the NPs on their long-time self-diffusion by performing complementary LD simulations that do not have these interactions (Fig. 5). Due to the lack of long-ranged solvent-mediated HIs, we did not perform any finite-size corrections for the LD diffusion coefficients. Qualitatively, D/D0 had a similar dependence on ϕ both with and without HIs, with differences for the tetrahedra being most pronounced and differences for the cubes being least pronounced. However, there were clear quantitative differences between the MPCD simulations with HIs and the LD simulations without HIs. For all shapes, D/D0 was smaller for a given ϕ (had a stronger ϕ dependence) in the LD simulations compared to the MPCD simulations. Taken together, these differences support the established picture that solvent-mediated HIs and excluded-volume interactions between NPs that determine their fluid structure both play a role in determining the NP dynamics.
As an aside, we remark that the agreement between our MPCD simulations and experiments88,89 significantly improved for the spherical NPs compared to our previous study,46 which is likely due to the higher surface density of vertex particles used in this work. The accuracy of discrete particle models typically improves with increasing surface density,91 and the surface density of vertex particles on the sphere was roughly four times that of ref. 46. We note that Poblete et al. recommended a surface density of 0.53/![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) 2 in their study of spherical NPs to balance discretization and inertia effects,47 which lies between the value of 0.37/
2 in their study of spherical NPs to balance discretization and inertia effects,47 which lies between the value of 0.37/![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) 2 used in ref. 46 and 1.43/
2 used in ref. 46 and 1.43/![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) 2 used here. The surface density of vertex particles used for the other regular polyhedra was comparable to that of our spheres.
2 used here. The surface density of vertex particles used for the other regular polyhedra was comparable to that of our spheres.
In the isotropic phase, the translational diffusion of rod-like objects is the orientational average of their parallel and normal components. The self-diffusion coefficient of rods in the infinite dilution limit can be estimated as95
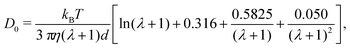 | (10) |
![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) 2/τ and 2.41 × 10−3
2/τ and 2.41 × 10−3![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) 2/τ for rods with λ = 1 and 2 in our MPCD solvent, respectively. Our simulated values D0 = 3.09 × 10−3
2/τ for rods with λ = 1 and 2 in our MPCD solvent, respectively. Our simulated values D0 = 3.09 × 10−3 ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 2/τ and 2.57 × 10−3
2/τ and 2.57 × 10−3 ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 2/τ were within 5% of eqn (10), showing the expected decrease of D0 with λ. We also note that eqn (10) underpredicts the diffusivity of a sphere (λ = 0) by about 5% compared to the classical Stokes–Einstein relation.
2/τ were within 5% of eqn (10), showing the expected decrease of D0 with λ. We also note that eqn (10) underpredicts the diffusivity of a sphere (λ = 0) by about 5% compared to the classical Stokes–Einstein relation.
The concentration dependence of D/D0 with ϕ was similar for both spherocylinders (Fig. 6). Indeed, D/D0 for the spherocylinders with λ = 1 was nearly indistinguishable from that for the spheres (λ = 0). The longer spherocylinders with λ = 2 showed some systematic differences, consistently having a slightly smaller value than for λ = 1 at a given ϕ. This result indicates that even a small amount of anisotropy may begin to have an effect on the diffusive dynamics, but the magnitude of this effect seems to be small. We also compared our simulation data to the parametric fit of ref. 97. Our simulations qualitatively agreed with the prediction that D/D0 should be smaller for a larger λ at a given ϕ, but the simulations consistently had smaller values of D/D0 than predicted. We note that ref. 97 used BD simulations that lacked HIs to develop this fit, so it is unclear to what extent we should expect agreement to simulations with HIs.
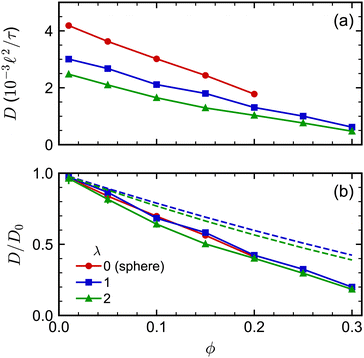 | ||
| Fig. 6 (a) Long-time self-diffusion coefficient D for spherocylinders with aspect ratios λ = 1 and 2 as a function of volume fraction ϕ. The sphere data from Fig. 2 is included as a reference point with λ = 0. (b) D normalized by its value extrapolated to infinite dilution D0. The dashed curves in (b) are D/D0 predicted from the fit of ref. 97. | ||
B. Sedimentation
After investigating the long-time self-diffusion coefficients of our shape-anisotropic NPs, we characterized their sedimentation coefficients. This complementary dynamic property of a suspension is important for understanding, e.g., how NPs settle under gravity. We defined the sedimentation coefficient K from the linear proportionality between the average velocity u of an NP under a sufficiently small applied force F,| u = Kγ−10F. | (11) |
![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) on all NPs, where
on all NPs, where ![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) is the unit vector in the x direction, and measured their average velocity ux = u·
is the unit vector in the x direction, and measured their average velocity ux = u·![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) . The applied forces were fx = 0.5kBT/
. The applied forces were fx = 0.5kBT/![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) and 1.0kBT/
and 1.0kBT/![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) per NP, which we distributed evenly among all the vertex and central particles in each NP. A balancing force was applied to the MPCD particles to ensure that the total force on the system was zero. We allowed the system to reach a steady state under the imposed forces, performed a production run where we measured ux, and extracted K from a linear regression of ux and fx.
per NP, which we distributed evenly among all the vertex and central particles in each NP. A balancing force was applied to the MPCD particles to ensure that the total force on the system was zero. We allowed the system to reach a steady state under the imposed forces, performed a production run where we measured ux, and extracted K from a linear regression of ux and fx.
As for diffusion coefficients, the sedimentation coefficients from our MPCD simulations must be corrected for finite-size effects from periodic boundary conditions. The sedimentation coefficient measured in an infinitely large box K∞ is related to the one measured in a finite box by98
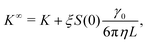 | (12) |
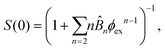 | (13) |
![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) n = Bn/vn−1 and Bn is the n-th virial coefficient. We used ϕex in eqn (13) because it should characterize the structure of the suspension better than ϕ (see discussion of Fig. 3). We used up to the 8th virial coefficient for the regular polyhedra99 and up to the 5th virial coefficient for the spherocylinders.100,101 Like eqn (6), eqn (12) also includes the suspension viscosity η so we made the same Stokes–Einstein-like approximation to eliminate this dependency,
n = Bn/vn−1 and Bn is the n-th virial coefficient. We used ϕex in eqn (13) because it should characterize the structure of the suspension better than ϕ (see discussion of Fig. 3). We used up to the 8th virial coefficient for the regular polyhedra99 and up to the 5th virial coefficient for the spherocylinders.100,101 Like eqn (6), eqn (12) also includes the suspension viscosity η so we made the same Stokes–Einstein-like approximation to eliminate this dependency,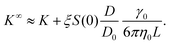 | (14) |
MPCD conserves linear momentum, so the sedimentation coefficients calculated directly from the simulation are in a frame of reference where the mass-averaged velocity of the NPs and solvent is zero. However, it is a common practice to consider suspensions in the frame of reference where the volume-averaged velocity is zero, i.e., 〈u〉 = ϕu + (1 − ϕ)u0 = 0 where u0 is the solvent velocity. Shifting from the mass-averaged to volume-averaged frame of reference amounts to a rescaling of K, which we implemented as in our previous work.46 All values of K are presented in the frame of reference where the volume-averaged velocity is zero.
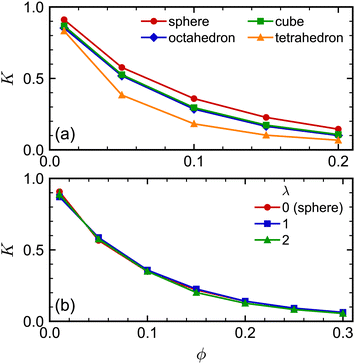
The sedimentation coefficients of the regular polyhedra [Fig. 7(a)] exhibited a qualitatively similar dependence on shape and concentration as the self-diffusion coefficients did. We consistently found that the spheres had the largest K, the tetrahedra had the smallest K, while the octahedra and cubes had an intermediate K. Moreover, all sedimentation coefficients decreased with increasing concentration, as expected, with the tetrahedra having the strongest concentration dependence. The sedimentation coefficients of both spherocylinders were highly similar to each other and to that of the sphere [Fig. 7(b)]. These behaviors are qualitatively similar to the self-diffusion coefficients, so we will not repeat that discussion here for brevity.
IV Conclusions
We investigated the long-time self-diffusion and sedimentation of NPs with anisotropic shapes. The anisotropic shapes we studied were an octahedron, a cube, a tetrahedron, and a spherocylinder. The NPs were represented with a discrete particle model and were hydrodynamically coupled to each other using the multiparticle collision dynamics method. Simulations were conducted across a range of volume fractions for each shape where the NPs remained in a fluid/isotropic phase. Our modeling approach can be easily extended to explore the dynamics of other NP shapes, e.g., irregular polyhedra and non-convex shapes.102For regular polyhedra having equal edge lengths, shape had a clear influence on their transport properties. Octahedra and cubes were slower diffusing than spheres with diameter equal to their edge length for all investigated volume fractions [Fig. 2(a)]. Tetrahedra diffused the fastest at small volume fractions but the slowest at larger volume fractions, which we partially attributed to the formation of pentagonal dipyramids. The simulated self-diffusion coefficients of all investigated NP shapes at infinite dilution were in good agreement with a correlation based on sphericity and also with an approximation using the mean diameter of the spheres that inscribed and circumscribed the shapes. After accounting for differences due to shape at infinite dilution [Fig. 2(b)], the self-diffusion coefficient of the spheres showed the weakest volume-fraction dependence, that of the tetrahedra showed the strongest volume-fraction dependence, while the octahedra and cubes showed intermediate behavior. Similar trends were found for the dependence of the sedimentation coefficients on volume fraction [Fig. 7(a)].
For small-aspect-ratio spherocylinders (λ = 1 and 2), the diffusion coefficients at infinite dilution showed a dependence on aspect ratio that was consistent with theoretical expectation, meaning that the spherocylinders diffused more slowly as aspect ratio increased [Fig. 6(a)]. However, after accounting for shape effects at infinite dilution, the self-diffusion coefficient [Fig. 6(b)] had a volume-fraction dependence that closely followed that of spheres having diameter equal to the spherocylinders, with only minor differences for the spherocylinder with λ = 2. The sedimentation coefficient [Fig. 7(b)] had essentially the same volume-fraction dependence for the spheres and both spherocylinders. We expect that the dynamics of spherocylinders should deviate more significantly from spheres as λ increases, and in principle, we can extend our spherocylinder model to study this regime. However, doing so incurs higher computational cost due to a substantial increase in the number of vertex particles per spherocylinder. Further, we would need larger simulation boxes to accommodate these spherocylinders and gather good statistics, thereby also increasing the number of solvent particles required. To mitigate these computational challenges, an alternative approach is to represent the spherocylinders as linear rods comprised of partially overlapping particles.103 However, establishing a connection between this model, our spherocylinder model, and experiments is still an open question, which we plan to explore.
Author contributions
Yashraj M. Wani: conceptualization, formal analysis, investigation, methodology, visualization, writing – original draft. Penelope Grace Kovakas: conceptualization, formal analysis, investigation, methodology, writing – review & editing. Arash Nikoubashman: conceptualization, funding acquisition, methodology, project administration, writing – review & editing. Michael P. Howard: conceptualization, data curation, formal analysis, funding acquisition, investigation, methodology, project administration, visualization, writing – review & editing.Data availability
The data that support the findings of this study are available from the authors upon reasonable request.Conflicts of interest
The authors have no conflicts to disclose.Acknowledgements
This material is based upon work supported by the National Science Foundation under Award No. 2223084 and by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) through Project No. 233630050, 405552959, 470113688, and 509039598. This work was completed with resources provided by the Auburn University Easley Cluster, the supercomputer Mogon at Johannes Gutenberg University Mainz (www.hpc.uni-mainz.de), and the Texas Advanced Computing Center (TACC) at The University of Texas at Austin.References
- R. P. Sear, Phys. Rev. Lett., 2019, 122, 128101 CrossRef CAS PubMed.
- M. A. Boles, M. Engel and D. V. Talapin, Chem. Rev., 2016, 116, 11220–11289 CrossRef CAS PubMed.
- C. Ding and Z. Li, Mater. Sci. Eng.: C, 2017, 76, 1440–1453 CrossRef CAS PubMed.
- P. T. Wong and S. K. Choi, Chem. Rev., 2015, 115, 3388–3432 CrossRef CAS PubMed.
- R. Toy, P. M. Peiris, K. B. Ghaghada and E. Karathanasis, Nanomedicine, 2014, 9, 121–134 CrossRef CAS PubMed.
- Dynamic Properties of Nanoparticles, ed. Z. L. Wang, Y. Liu and Z. Zhang, Springer, US, 2003, pp. 562–594 Search PubMed.
- L. Yang, Z. Zhou, J. Song and X. Chen, Chem. Soc. Rev., 2019, 48, 5140–5176 RSC.
- R. G. D. Andrade, S. R. S. Veloso and E. M. S. Castanheira, Int. J. Mol. Sci., 2020, 21, 2455 CrossRef CAS PubMed.
- K. A. Rose, N. Gogotsi, J. H. Galarraga, J. A. Burdick, C. B. Murray, D. Lee and R. J. Composto, Macromolecules, 2022, 55, 8514–8523 CrossRef CAS.
- Y. Sun and Y. Xia, Science, 2002, 298, 2176–2179 CrossRef CAS PubMed.
- L. Gou and C. J. Murphy, Nano Lett., 2002, 3, 231–234 CrossRef.
- E. C. Greyson, J. E. Barton and T. W. Odom, Small, 2006, 2, 368–371 CrossRef CAS PubMed.
- F. C. Bawden, N. W. Pirie, J. D. Bernal and I. Fankuchen, Nature, 1936, 138, 1051–1052 CrossRef.
- M. W. Beijerinck, Verhandelingen der Koninklijke Akademie van Wetensehappen te Amsterdam, Afd. Natuurkd., 1898, 5, 3–21 Search PubMed.
- F. M. van der Kooij, K. Kassapidou and H. N. W. Lekkerkerker, Nature, 2000, 406, 868–871 CrossRef CAS PubMed.
- B. J. Berne and R. Pecora, Dynamic Light Scattering With Applications to Chemistry, Biology and Physics, Dover publications, 2000 Search PubMed.
- W. Schärtl, Sample Preparation, Springer Berlin Heidelberg, 2007, pp. 43–50 Search PubMed.
- P. A. Hassan, S. Rana and G. Verma, Langmuir, 2015, 31, 3–12 CrossRef CAS PubMed.
- J. Stetefeld, S. A. McKenna and T. R. Patel, Biophys. Rev., 2016, 8, 409–427 CrossRef CAS PubMed.
- M. P. Lettinga, E. Barry and Z. Dogic, Europhys. Lett., 2005, 71, 692–698 CrossRef CAS.
- B. Kundukad, J. Yan and P. S. Doyle, Soft Matter, 2014, 10, 9721–9728 RSC.
- J. F. Brady, J. Fluid Mech., 1994, 272, 109–134 CrossRef CAS.
- M. Tokuyama and I. Oppenheim, Phys. Rev. E, 1994, 50, R16–R19 CrossRef CAS PubMed.
- W. Kuhn, Z. Phys. Chem., 1932, 161A, 1–32 CrossRef.
- W. Kuhn, Kolloid-Z., 1933, 62, 269–285 CrossRef CAS.
- W. Kuhn and H. Kuhn, Helv. Chim. Acta, 1945, 28, 1533–1579 CrossRef CAS PubMed.
- J. Riseman and J. G. Kirkwood, J. Chem. Phys., 1950, 18, 512–516 CrossRef CAS.
- M. M. Tirado and J. G. de la Torre, J. Chem. Phys., 1979, 71, 2581–2587 CrossRef CAS.
- M. M. Tirado and J. G. de la Torre, J. Chem. Phys., 1980, 73, 1986–1993 CrossRef CAS.
- M. P. B. van Bruggen, H. N. W. Lekkerkerker, G. Maret and J. K. G. Dhont, Phys. Rev. E, 1998, 58, 7668–7677 CrossRef CAS.
- G. K. Youngren and A. Acrivos, J. Fluid Mech., 1975, 69, 377–403 CrossRef.
- K. Okada and A. Satoh, Mol. Phys., 2020, 118, e1631498 CrossRef.
- M. P. Howard, A. Nikoubashman and J. C. Palmer, Curr. Opin. Chem. Eng., 2019, 23, 34–43 CrossRef.
- M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, Oxford University Press, 2017 Search PubMed.
- D. L. Ermak and J. A. McCammon, J. Chem. Phys., 1978, 69, 1352–1360 CrossRef CAS.
- J. Rotne and S. Prager, J. Chem. Phys., 1969, 50, 4831–4837 CrossRef CAS.
- H. Yamakawa, J. Chem. Phys., 1970, 53, 436–443 CrossRef CAS.
- J. F. Brady, R. J. Phillips, J. C. Lester and G. Bossis, J. Fluid Mech., 1988, 195, 257–280 CrossRef CAS.
- J. F. Brady and G. Bossis, Annu. Rev. Fluid Mech., 1988, 20, 111–157 CrossRef.
- A. Malevanets and R. Kapral, J. Chem. Phys., 1999, 110, 8605–8613 CrossRef CAS.
- G. Gompper, T. Ihle, D. M. Kroll and R. G. Winkler, in Multi-Particle Collision Dynamics: A Particle-Based Mesoscale Simulation Approach to the Hydrodynamics of Complex Fluids, Springer Berlin Heidelberg, 2009, pp. 1–87 Search PubMed.
- P. J. Hoogerbrugge and J. M. V. A. Koelman, Europhys. Lett., 1992, 19, 155–160 CrossRef.
- M. B. Liu, G. R. Liu, L. W. Zhou and J. Z. Chang, Arch. Comput. Methods Eng., 2015, 22, 529–556 CrossRef.
- B. Dünweg and A. J. C. Ladd, Lattice Boltzmann Simulations of Soft Matter Systems, Springer Berlin Heidelberg, 2009, pp. 89–166 Search PubMed.
- A. J. C. Ladd and R. Verberg, J. Stat. Phys., 2001, 104, 1191–1251 CrossRef CAS.
- Y. M. Wani, P. G. Kovakas, A. Nikoubashman and M. P. Howard, J. Chem. Phys., 2022, 156, 024901 CrossRef CAS PubMed.
- S. Poblete, A. Wysocki, G. Gompper and R. G. Winkler, Phys. Rev. E, 2014, 90, 033314 CrossRef PubMed.
- A. Malevanets and R. Kapral, J. Chem. Phys., 2000, 112, 7260–7269 CrossRef CAS.
- A. Nikoubashman, C. N. Likos and G. Kahl, Soft Matter, 2013, 9, 2603–2613 RSC.
- G. Batôt, V. Dahirel, G. Mériguet, A. A. Louis and M. Jardat, Phys. Rev. E, 2013, 88, 043304 CrossRef PubMed.
- V. Dahirel, X. Zhao, B. Couet, G. Batôt and M. Jardat, Phys. Rev. E, 2018, 98, 053301 CrossRef CAS.
- J. T. Padding and A. A. Louis, Phys. Rev. E, 2006, 74, 031402 CrossRef CAS PubMed.
- Y. Kobayashi, N. Arai and A. Nikoubashman, Langmuir, 2020, 36, 14214–14223 CrossRef CAS PubMed.
- Y. Kobayashi, N. Arai and A. Nikoubashman, Soft Matter, 2020, 16, 476–486 RSC.
- T. Yokoyama, Y. Kobayashi, N. Arai and A. Nikoubashman, Soft Matter, 2023, 19, 6480–6489 RSC.
- Y. Kobayashi and A. Nikoubashman, Langmuir, 2022, 38, 10642–10648 CrossRef CAS PubMed.
- B. R. Argun and A. Statt, Soft Matter, 2023, 19, 8081–8090 RSC.
- T. Ikeda, Y. Kobayashi and M. Yamakawa, Mol. Syst. Des. Eng., 2024, 9, 254–263 RSC.
- T. Ihle and D. M. Kroll, Phys. Rev. E, 2001, 63, 020201 CrossRef CAS PubMed.
- T. Ihle and D. M. Kroll, Phys. Rev. E, 2003, 67, 066705 CrossRef CAS PubMed.
- C. Huang, A. Chatterji, G. Sutmann, G. Gompper and R. Winkler, J. Comput. Phys., 2010, 229, 168–177 CrossRef CAS.
- A. Statt, M. P. Howard and A. Z. Panagiotopoulos, Phys. Rev. Fluids, 2019, 4, 043905 CrossRef.
- J. D. Weeks, D. Chandler and H. C. Andersen, J. Chem. Phys., 1971, 54, 5237–5247 CrossRef CAS.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- J. Newman, H. L. Swinney and L. A. Day, J. Mol. Biol., 1977, 116, 593–603 CrossRef CAS PubMed.
- M. P. Lettinga, J. K. G. Dhont, Z. Zhang, S. Messlinger and G. Gompper, Soft Matter, 2010, 6, 4556–4562 RSC.
- L. Scarabelli, M. Grzelczak and L. M. Liz-Marzán, Chem. Mater., 2013, 25, 4232–4238 CrossRef CAS.
- X. Ye, L. Jin, H. Caglayan, J. Chen, G. Xing, C. Zheng, V. Doan-Nguyen, Y. Kang, N. Engheta and C. R. Kagan, et al. , ACS Nano, 2012, 6, 2804–2817 CrossRef CAS PubMed.
- S. Seibt, J. Pearson, R. Nixon-Luke, H. Zhang, P. R. Lang, G. Bryant, H. Cölfen and P. Mulvaney, J. Phys. Chem. C, 2023, 127, 22336–22346 CrossRef CAS.
- J. A. Anderson, J. Glaser and S. C. Glotzer, Comput. Mater. Sci., 2020, 173, 109363 CrossRef CAS.
- M. P. Howard, A. Z. Panagiotopoulos and A. Nikoubashman, Comput. Phys. Commun., 2018, 230, 10–20 CrossRef CAS.
- https://github.com/mphowardlab/azplugins .
- J. Happel and H. Brenner, in The Motion of a Rigid Particle of Arbitrary Shape in an Unbounded Fluid, Springer, Netherlands, 1983, pp. 159–234 Search PubMed.
- M. Doi and S. F. Edwards, The Theory of Polymer Dynamics, Oxford University Press, 1988 Search PubMed.
- B. Dünweg and K. Kremer, Phys. Rev. Lett., 1991, 66, 2996–2999 CrossRef PubMed.
- B. Dünweg and K. Kremer, J. Chem. Phys., 1993, 99, 6983–6997 CrossRef.
- I.-C. Yeh and G. Hummer, J. Phys. Chem. B, 2004, 108, 15873–15879 CrossRef CAS.
- A. Einstein, Ann. Phys., 1906, 324, 289 CrossRef.
- A. Einstein, Ann. Phys., 1911, 339, 591 CrossRef.
- D. S. Bolintineanu, G. S. Grest, J. B. Lechman, F. Pierce, S. J. Plimpton and P. R. Schunk, Comput. Part. Mech., 2014, 1, 321–356 CrossRef.
- E. A. Pettyjohn and E. B. Christiansen, Chem. Eng. Prog., 1948, 44, 157–172 CAS.
- M. Hoffmann, C. S. Wagner, L. Harnau and A. Wittemann, ACS Nano, 2009, 3, 3326–3334 CrossRef CAS PubMed.
- R. Stuckert, C. S. Plüisch and A. Wittemann, Langmuir, 2018, 34, 13339–13351 CrossRef CAS PubMed.
- A. Haji-Akbari, M. Engel, A. S. Keys, X. Zheng, R. G. Petschek, P. Palffy-Muhoray and S. C. Glotzer, Nature, 2009, 462, 773–777 CrossRef CAS PubMed.
- A. Haji-Akbari, M. Engel and S. C. Glotzer, J. Chem. Phys., 2011, 135, 194101 CrossRef PubMed.
- U. Agarwal and F. A. Escobedo, Nat. Mater., 2011, 10, 230–235 CrossRef CAS PubMed.
- A. P. Gantapara, J. de Graaf, R. van Roij and M. Dijkstra, Phys. Rev. Lett., 2013, 111, 015501 CrossRef PubMed.
- W. van Megen and S. M. Underwood, J. Chem. Phys., 1989, 91, 552–559 CrossRef CAS.
- A. van Blaaderen, J. Peetermans, G. Maret and J. K. G. Dhont, J. Chem. Phys., 1992, 96, 4591–4603 CrossRef CAS.
- J. R. Royer, G. L. Burton, D. L. Blair and S. D. Hudson, Soft Matter, 2015, 11, 5656–5665 RSC.
- J. W. Swan and G. Wang, Phys. Fluids, 2016, 28, 011902 CrossRef.
- P. Bolhuis and D. Frenkel, J. Chem. Phys., 1997, 106, 666–687 CrossRef CAS.
- A. Milchev, S. A. Egorov, K. Binder and A. Nikoubashman, J. Chem. Phys., 2018, 149, 174909 CrossRef PubMed.
- M. Yetkin, Y. M. Wani, K. Kritika, M. P. Howard, M. Kappl, H.-J. Butt and A. Nikoubashman, Langmuir, 2024, 40, 1096–1108 CrossRef CAS PubMed.
- M. P. B. van Bruggen, H. N. W. Lekkerkerker and J. K. G. Dhont, Phys. Rev. E, 1997, 56, 4394–4403 CrossRef CAS.
- M. M. Tirado, C. L. Martínez and J. G. de la Torre, J. Chem. Phys., 1984, 81, 2047–2052 CrossRef.
- H. Löwen, Phys. Rev. E, 1994, 50, 1232–1242 CrossRef PubMed.
- G. Mo and A. S. Sangani, Phys. Fluids, 1994, 6, 1637–1652 CrossRef CAS.
- M. E. Irrgang, M. Engel, A. J. Schultz, D. A. Kofke and S. C. Glotzer, Langmuir, 2017, 33, 11788–11796 CrossRef CAS PubMed.
- P. Monson and M. Rigby, Chem. Phys. Lett., 1978, 58, 122–126 CrossRef CAS.
- B. Barboy and W. M. Gelbart, J. Chem. Phys., 1979, 71, 3053–3062 CrossRef CAS.
- C. Avendaño and F. A. Escobedo, Curr. Opin. Colloid Interface Sci., 2017, 30, 62–69 CrossRef.
- R. G. Winkler, K. Mussawisade, M. Ripoll and G. Gompper, J. Phys.: Condens. Matter, 2004, 16, S3941 CrossRef CAS.
Footnote |
| † These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2024 |