Effect of surface viscoelasticity on top jet drops produced by bursting bubbles
Zhengyu
Yang†
 a,
Sainath
Barbhai†
a,
Sainath
Barbhai†
 b,
Bingqiang
Ji
b,
Bingqiang
Ji
 *c and
Jie
Feng
*c and
Jie
Feng
 *ad
*ad
aDepartment of Mechanical Science and Engineering, University of Illinois at Urbana-Champaign, Urbana, Illinois 61801, USA. E-mail: jiefeng@illinois.edu
bDepartment of Aerospace Engineering, University of Illinois at Urbana-Champaign, Urbana, Illinois 61801, USA
cSchool of Astronautics, Beihang University, Beijing 100191, China. E-mail: bingqiangji@buaa.edu.cn
dMaterials Research Laboratory, University of Illinois at Urbana–Champaign, Urbana, Illinois 61801, USA
First published on 22nd April 2024
Abstract
Jet drops resulting from bubble bursting at a liquid surface play a key role in various mass transfer processes across the interface, including sea spray aerosol generation and pathogen transmission. However, the impact of structurally compound interfaces, characterized by complex surface rheology introduced by surface-active contaminants, on the jet drop ejection still remains unclear. Here, we experimentally investigate the influence of surface viscoelasticity on the size and velocity of the top jet drops from surface bubble bursting, examining both pure protein and mixed protein–surfactant solutions. We document that for bubble bursting at a pure-protein-laden surface where surface elasticity dominates, the increase in Ec, i.e. the interfacial elastocapillary number as the ratio between the effects of interfacial elasticity and capillarity, efficiently increases the radius and decreases the velocity of the top jet drop, ultimately inhibiting the jet drop ejection. On the other hand, considering the mixed protein–surfactant solution, we show that the top jet drop radius and velocity exhibit a different variation trend with Ec, which is attributed to the additional dissipation on the capillary waves as well as the retardation and resistance on the converging flow for jet formation from surface viscoelasticity. Our work may advance the understanding of bubble bursting dynamics at contaminated liquid surfaces and shed light on the potential influence of surface viscoelasticity on the generation of bubble bursting aerosols.
1 Introduction
Bursting of bubbles at a liquid surface is ubiquitous in a wide range of physical, biological, and geological phenomena. Specifically, the bursting dynamics results in the generation of film drops by cap disintegration,1 as well as jet drops by fragmentation of the upward liquid jet formed by cavity collapse.2,3 These droplets may remain suspended in the air, as a major source of sea spray aerosols, impacting global climate and atmosphere environment.4 In addition, they have received significant attention in recent years as an emission source for airborne transmission of bulk contaminants,5 pathogens,6 and even microplastics.7,8 Extensive studies have been conducted to characterize the bursting dynamics by experiments,1,3,9 theory1,10–15 and simulations.3,13,14,16–18 Most of these studies mainly focused on bubble bursting at clean liquid surfaces. However, in practice, liquid surfaces are inevitably contaminated. For example, rising bubbles scavenge surface-active substances on their surface from the water column due to flow conditions and physical chemistry,19 forming a structurally compound bubble surface. In addition, an organic-enriched interface known as the sea surface microlayer, containing biogenic molecules such as carbohydrates, lipids and proteinaceous materials, usually forms at the surface of oceans.5,20,21 It has been shown that the structurally compound gas–liquid interface can profoundly modify the bubble dynamics including formation, rising and bursting as well as the associated aerosol generation.22–27Recently, the complex interfacial rheology introduced by surface-active contaminants, such as surfactants, has attracted significant attention. It has been reported that the interfacial rheology profoundly modifies the bubble bursting dynamics, even if the bulk liquid still shows a Newtonian behavior. For instance, Constante-Amores et al.28 numerically investigated the bursting dynamics of a surfactant-laden bubble and demonstrated that the surfactant induces strong Marangoni stresses that retard the cavity collapse and produce shorter jets. Pierre et al.29 experimentally showed that the top jet drops (i.e., the first drop ejected from the upward jet produced from bubble bursting as shown in Fig. 1) at the surface of sodium dodecyl sulfate (SDS) solutions are faster and smaller than those at a surfactant-free solution surface. Interestingly, the jet drops disappeared at an SDS concentration of 0.4× critical micelle concentration (CMC), which was believed to be caused by the Marangoni stresses. On the other hand, the recent experiments by Vega and Monterano30 showed that at a dilute SDS solution (SDS concentration much smaller than the CMC), the top jet drop radius is almost constant while the top jet drop velocity is smaller than that in the surfactant-free case.
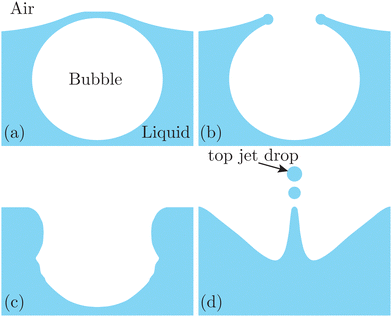 | ||
| Fig. 1 Schematics of jet drop ejection by bubble bursting: (a) bubble cap film drainage at the free surface; (b) cap film rupture; (c) cavity collapse; and (d) jet ejection and jet drop detachment. | ||
Compared with small-molecular surfactants, the adsorption of large-molecular proteins at the liquid surface introduces strong interfacial viscoelasticity, since globular protein molecules such as bovine serum albumin (BSA) and lysozyme at the surface can form a highly close-packed cross-linked network at the surface.31–33 Only recently has such a viscoelastic interface been shown to greatly influence the bubble bursting dynamics. Specifically, the interfacial elastocapillary number Ec = Ed/γ (ratio between the effects of interfacial elasticity and capillarity) has been found to play a crucial role. Here, Ed is the surface initial dilatation modulus, and γ is the surface tension. Tammaro et al.34 investigated the rupture of the bubble cap film of BSA solutions, and discovered a petal-like shape of the rupture film. They demonstrated that this phenomenon is caused by the cracks of the opening rim initiated by the strong surface elastic hoop stress when Ec ≥ 1. In addition, our prior work35 showed that when a bubble bursts at a viscoelastic surface of a BSA solution, a secondary bubble is entrapped with no subsequent jet drop ejection when Ec is larger than 1, contrary to the counterpart experimentally observed at a Newtonian surface. However, it is still unclear how the complex surface rheology affects the ejected top jet drop size and velocity. Additionally, since a viscoelasticity surface may exhibit surface elasticity and viscosity simultaneously, it remains an open question whether Ec is sufficient solely to describe the jetting dynamics.
Here we experimentally investigate the influence of surface viscoelasticity on the jetting dynamics from bursting bubbles, regarding the top jet drop ejection. Surface viscoelasticity is adjusted by adding protein or protein–surfactant mixtures in the bulk solution and modulating their concentrations. We describe the methods for solution preparation and experimental setups for bubble bursting dynamics and surface elasticity measurements in Section 2. In Section 3, we measure the size and velocity of the top jet drops at different protein and mixed protein–surfactant solutions, and discuss the effect of surface rheology on jet dynamics by considering the capillary wave focusing. Finally, we conclude our discoveries in Section 4.
2 Methods
2.1 Materials
Deionized (DI) water (resistivity = 18.2 MΩ cm) was obtained from a laboratory water purification system (Smart2Pure 3 UV/UF, Thermo Fisher Scientific). BSA (lyophilized powder, molecular weight (MW) = 66 kDa, Cat no. #A7906), Tween 80 (liquid, MW = 1310 g mol−1, CMC = 0.012 mM at 20–25 °C, Cat no. #P1754) and lysozyme (MW = 14.4 kDa, Cat no. #L4919, BioUltra, lyophilized powder) were all purchased from Sigma Aldrich. Sodium chloride (part no. SX0420-1) was purchased from EMD Millipore.We prepared 9 g L−1 NaCl solution by dissolving the appropriate amount of sodium chloride in DI water, utilizing a magnetic bar for stirring over an eight-hour period. All working solutions contained 9 g L−1 NaCl, which helps form a more compact configuration of adsorbed protein segments and boosts the surface elasticity.36 We prepared the working solutions by dissolving the appropriate amount of powders in 9 g L−1 NaCl solution, followed by gentle stirring with a stirring bar for at least 20 minutes. All the experiments were finished within 24 hours after the preparation of solutions. The experiments were performed at a controlled temperature of 20 °C and 1 atm. We note that the temperature is expected to affect the bubble lifetime by influencing the liquid properties such as surface tension and viscosity,37 as well as diffusivity of proteins,38 but the influence of the temperature is beyond the scope of the current study. Since all pure protein and mixed protein–surfactant solutions used in our experiments only exhibit Newtonian viscous behavior with a negligible variation in density and bulk viscosity,39–41 we use ρ = 1.0 × 103 kg m−3 as the density and μ = 1.0 mPa s as the viscosity for all solutions in the following discussion.
2.2 Experimental setup to observe bubble bursting
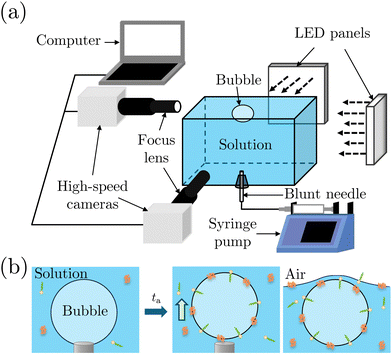
We performed bubble bursting experiments in the experimental apparatus sketched in Fig. 2(a). The experiment was conducted in a square transparent acrylic container of 28 × 28 × 12 mm3, with a dimension much larger than the equivalent bubble radius (R = 1.1 ± 0.1 mm) and the capillary length to eliminate the influence of the container walls and menisci on the bursting bubble. A blunt stainless needle (with an inner diameter of 0.26 mm) connected to a syringe pump (PHD ULTRA, 11 Pico Plus Elite, Harvard Apparatus) was plugged at the bottom of the container for bubble generation. We utilized two high-speed cameras (FASTCAM Mini AX200, Photron) to capture the bubble bursting dynamics simultaneously at a free liquid surface from the side view, under the illumination of two LED panels. The two cameras focused on the cavity collapse below the free surface and the jet evolution above the free surface, respectively. The cameras were tilted with an angle of ≈5° to avoid the influence of the meniscus on visualization.Before each experiment started, the container was carefully cleaned. We first filled up the container with the prepared solutions until a slightly convex meniscus formed above the container edge, which helped maintain the bubble location at the center of the container for visualization. A bubble attached to the needle was then generated by injecting 2.5 μL of air using a syringe pump with a flow rate of 1 mL min−1 in the step mode. After aging the attached bubble for the required aging time ta, the air was injected at a flow rate of 1 mL min−1 until the bubble detached from the needle (Fig. 2(b)). Bubbles usually burst right after they rested at the surface. For cases where bubbles didn't burst within seconds, we punctured the bubble cap with a sterile stainless needle immediately to avoid any deviation of ta. The bubble bursting dynamics were then recorded with a frame rate of 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 frames per second, a resolution of 640 × 480 pixels and a magnification of 3–4. The obtained images were post-processed with Fiji ImageJ and MATLAB 2019a. Specifically, we focus on the top jet drop, i.e., the first jet drop upon jet breakup, since it bounds the edge of the aerosol cloud and dominates the evaporation process as it is faster and usually bigger than the other jet drops.2,42 The radius rd and velocity vd of the top jet drop were measured right after it detached from the jet.
000 frames per second, a resolution of 640 × 480 pixels and a magnification of 3–4. The obtained images were post-processed with Fiji ImageJ and MATLAB 2019a. Specifically, we focus on the top jet drop, i.e., the first jet drop upon jet breakup, since it bounds the edge of the aerosol cloud and dominates the evaporation process as it is faster and usually bigger than the other jet drops.2,42 The radius rd and velocity vd of the top jet drop were measured right after it detached from the jet.
2.3 Measurement of surface tension and surface dilatational modulus
To determine the interfacial elastocapillary number Ec, we measured γ and Ed values of the solutions using a custom-built bubble tensiometer as sketched in Fig. 3(a). A blunt stainless needle (with an outer diameter of 1.83 mm) connected to a syringe pump was plugged into the bottom of the container for bubble generation. A high-speed camera (FASTCAM Mini AX200, Photron) was used to record the evolution of the shape profile of the pendant bubble at the needle under the illumination of an LED panel.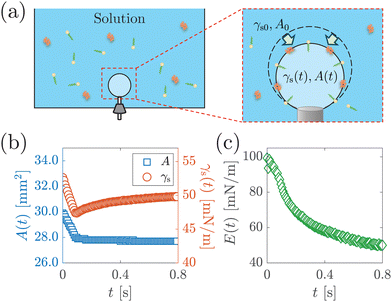 | ||
| Fig. 3 (a) Schematic of surface dilatational modulus measurement via a custom-built bubble tensiometer. A step compression is applied to the bubble at ta after bubble generation to measure the surface dilatational modulus. Surfactant molecules are depicted with yellow heads and green tails, and protein molecules are depicted with orange ribbons. (b) The area A(t) and surface stress γs(t) as a function of time t after step compression is applied, from the measurement of 1 g L−1 BSA solution with ta = 1200 s. (c) Surface dilatation modulus E(t) as a function of t calculated based on eqn (1). | ||
The measurement of the surface tension and dilatational modulus started by generating a bubble of 15 μL using a syringe pump with a flow rate of 1 mL min−1 in a step mode. After keeping the bubble attached to the needle for time ta, a 3 μL step volume compression at a flow rate of 1 mL min−1 was applied to withdraw air from the bubble. The evolution of the bubble shape over time after step compression was recorded using a high-speed camera for two minutes with a frame rate of 125 frames per second. The apparent surface tension γs of the solutions and the surface area A were obtained using the open-source software OpenDrop43 (Fig. 3(b)). The initial surface tension γs0 was obtained as γs before step compression was applied, which was also used as the surface tension γ. The surface dilatational modulus of the solutions at a time t after compression was calculated as44,45
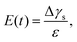 | (1) |
3 Results and discussion
3.1 Morphology and regime map of the top jet drop by bubble bursting
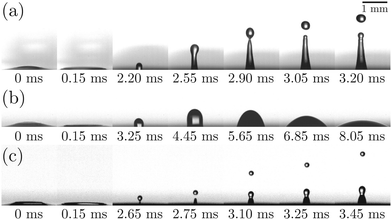
Fig. 4 illustrates the side views of jets produced by bubble bursting in different solutions. Compared to the bubble bursting jet at a pure NaCl solution surface (Fig. 4(a)), the jet from a protein solution is slower and wider (Fig. 4(b)). In Fig. 4(b) with a BSA concentration (CBSA) of 0.05 g L−1 and a ta value of 300 s, no jet drop is ejected as the wider and shorter jet fails to trigger the capillary instability13 necessary for the jet breakup. Such suppression of jet drops is observed at a low Ohnesorge number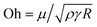 (ratio between viscocapillary and inertiocapillary effects) of 0.003–0.005 and a Bond number Bo = ρgR2/γ (ratio between gravity and capillary effects) of 0.1–0.3 in our experiments. However, for bubble bursting jets at a clean liquid surface with such a negligible gravity effect (Bo much smaller than a critical number of Boc ≈ 3), no jet drop is produced only when Oh is larger than a critical Ohnesorge number around 0.03–0.053,13,16,46 where viscous stresses suppress jet drop ejection. Here g represents gravitational acceleration. The deviation indicates the distinct dynamics of bubble bursting at a structurally compound surface. Interestingly, we further show that jet drop ejection is recovered when the above-mentioned BSA solutions are mixed with Tween 80 over a certain concentration, for example, in the 0.05 g L−1 BSA + 0.1 g L−1 Tween 80 solution (Fig. 4(c)). Both the jets produced in Fig. 4(b) and (c) arrive at the air–water level in a prolonged time after bursting compared to that in pure NaCl solutions, implying a smaller jet velocity when surface rheology exists, as we will discuss in the following sections.
(ratio between viscocapillary and inertiocapillary effects) of 0.003–0.005 and a Bond number Bo = ρgR2/γ (ratio between gravity and capillary effects) of 0.1–0.3 in our experiments. However, for bubble bursting jets at a clean liquid surface with such a negligible gravity effect (Bo much smaller than a critical number of Boc ≈ 3), no jet drop is produced only when Oh is larger than a critical Ohnesorge number around 0.03–0.053,13,16,46 where viscous stresses suppress jet drop ejection. Here g represents gravitational acceleration. The deviation indicates the distinct dynamics of bubble bursting at a structurally compound surface. Interestingly, we further show that jet drop ejection is recovered when the above-mentioned BSA solutions are mixed with Tween 80 over a certain concentration, for example, in the 0.05 g L−1 BSA + 0.1 g L−1 Tween 80 solution (Fig. 4(c)). Both the jets produced in Fig. 4(b) and (c) arrive at the air–water level in a prolonged time after bursting compared to that in pure NaCl solutions, implying a smaller jet velocity when surface rheology exists, as we will discuss in the following sections.
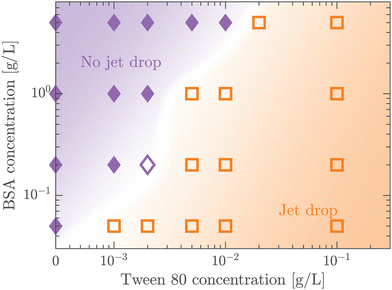
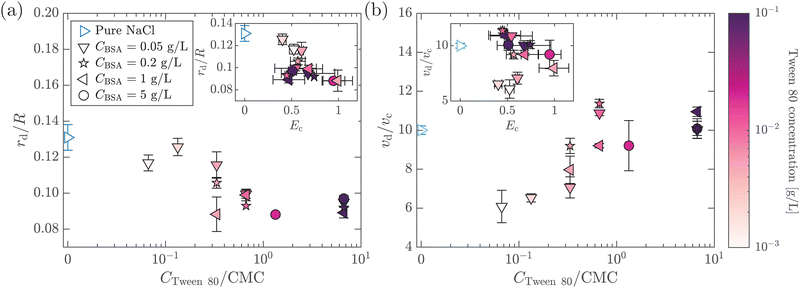
A protein-laden surface is expected to show significantly higher storage moduli due to its deformation capability under compression.34,47Fig. 5 demonstrates the regime map of jet drop production with BSA and Tween 80 concentrations, each spanning two orders of magnitude. The jet drop disappears at a large BSA concentration and a small Tween 80 concentration, when the surface elasticity is strong enough. Our regime map shows that the criterion of Ec ≤ 1 well describes the production of jet drops from bubble bursting in a BSA–Tween 80 mixture, implying that the competition between surface elasticity and surface tension effects plays an important role in jet drop ejection. We believe that for mixed protein–surfactant solutions, Ec is a key nondimensional parameter, which is widely applicable to characterize the interfacial flows where surface viscoelasticity is important.34,35 Additionally, we compare the bubble bursting dynamics in BSA solutions and mixed BSA–Tween 80 solutions with a similar range of γ values but different ranges of Ec values. For example, both 20–100 g L−1 BSA solutions35 and 0.05–5 g L−1 BSA + 0.1 g L−1 Tween 80 solutions have γ of 45–53 mN m−1 (ta = 300 s). However, Ec of the former BSA solutions has a range of 1.8–2.1 and jet drop production is suppressed,35 while Ec of the latter mixed BSA–Tween 80 solutions has a range of 0.4–0.8 and jet drops are produced. Therefore, we believe that it is the interplay between surface elasticity and capillary effects, instead of the capillary effects alone, that is mainly responsible for the inhibition of the jet drops. In the following, we will focus on the regime of Ec ≤ 1 with top jet drop ejection and discuss the experimental trend of the top jet drop radius and velocity with Ec in detail.
3.2 Top jet drop characteristics with pure protein solutions
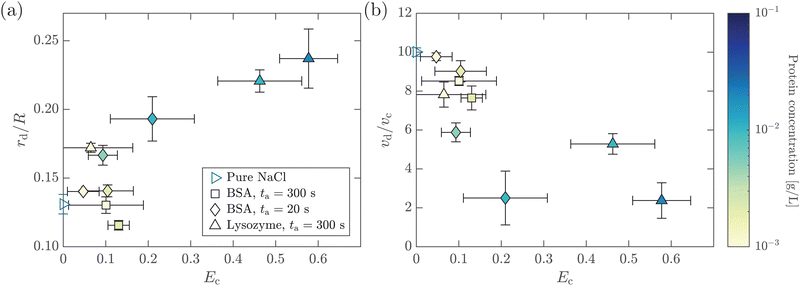
In this section, we study the effect of the surface elasticity of different pure protein solutions on the radius and velocity of the top jet drops in the jet drop ejection regime. We used BSA and lysozyme, which are well-studied model proteins with globular molecular shapes and produce strong surface elasticity.32,48,49 Jet drops are observed for lysozyme concentration CLysozyme ≤ 0.02 g L−1 at ta = 300 s, and for the BSA concentration CBSA ≤ 0.01 g L−1 at ta = 20 s and CBSA ≤ 0.002 g L−1 at ta = 300 s. As shown in Fig. 6(a), we observe a positive correlation between the dimensionless top jet drop radius rd/R and the interfacial elastocapillary number Ec. The correlation can be understood as an intermediate trend of rd/R between the thinner jets produced from bubble bursting in a Newtonian liquid with a clean surface (Fig. 4(a)) and the wider jets produced from that in a BSA solution with a highly viscoelastic surface (Fig. 4(b)). Correspondingly, the dimensionless velocity of the top jet drops vd/vc decreases with Ec as shown in Fig. 6(b). Here the inertia-capillary velocity,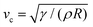 , is adopted as the characteristic velocity.12 Since the jetting results from the wave focusing during cavity collapse,3,16 we then focus on the difference of cavity shapes between bubble bursting in liquids without and with a protein-laden surface to interpret the influence of surface elasticity on the jet dynamics.
, is adopted as the characteristic velocity.12 Since the jetting results from the wave focusing during cavity collapse,3,16 we then focus on the difference of cavity shapes between bubble bursting in liquids without and with a protein-laden surface to interpret the influence of surface elasticity on the jet dynamics.
Fig. 7(a) presents the snapshots of cavity collapsing during bubble bursting at a pure NaCl solution surface. After the bubble cap ruptures (the panel at 0 ms in Fig. 7(a)), a train of capillary waves are initiated and propagate downwards along the cavity surface of the bubble (the panels between 0 and 1.65 ms in Fig. 7(a)). The wave train consists of the dominant wave (DW), which is the most energetic wave, and the precursor waves (PWs), which travel faster with shorter wavelengths. The PWs arrive at the cavity nadir first, disturbing the initially smooth bubble bottom (the panel at 1.40 ms in Fig. 7(a)), and then the DW focuses at the bubble bottom (the panel at 1.65 ms in Fig. 7(a)), producing an upward jet.9 For bubbles bursting at a protein solution surface (Fig. 7(b)), the waves are significantly damped compared to that at a pure NaCl solution surface (the panel at 1.00 ms in Fig. 7(b)), and sharp cusps form as the DW is about to collapse at the cavity bottom (the panel at 1.70 ms in Fig. 7(b)), with a curvature much larger than that at a pure NaCl solution surface. We further note that the cavity surface right in front of the DW demonstrates a concave geometry as the wave propagates to the cavity bottom right before the jet forms, distinct from the flat bottom shown in the pure NaCl case (Fig. 7(a)). The same features of such non-flat bottoms are observed in typical examples with significantly decelerated top jet drops as shown in Fig. 7(c and d).
The kinetics of a protein-laden surface must be considered to rationalize how a rigid surface yields jet drops that are larger and slower. Due to the short time scale of the bubble cavity collapse (∼1 ms), the diffusion of the protein molecules and the adsorption/desorption of protein molecules to/from the interface are negligible, as shown in our previous work.35 The surface elasticity dominates, and the adsorbed protein layer at the bubble surface acts as an insoluble viscoelastic layer, where the globular molecules are initially uniformly distributed and then undergo a redistribution dominated by surface convection upon bursting. The focusing capillary waves caused by the bubble cavity collapse sweep the protein molecules toward the cavity bottom, introducing compression on the protein layer and producing a gradient of the protein surface concentration toward the bottom. An elastic stress is thus produced and generates upward traction, which resists the wave propagation and retards the wave speed. Here, the surface elastic effect consists of two parts of contribution, including the Gibbs–Marangoni elasticity and the additional excess stress of the surface.35,50–52 Near the end of the cavity collapse, the highly protein-enriched cavity bottom surface, exhibiting a highly rigid and solid-like behavior, may wrinkle and form a concave bottom geometry, which breaks the symmetric self-similar focusing and sets a wider jet base as the jet forms, leading to a larger top jet drop. Additionally, the jet is significantly slowed due to the resisting elastic effect upon jet growth, which contributes to prolonged growth of the jet tip3 that finally pinches off as the top jet drop. Correspondingly, the top jet drop radius increases and the top jet drop velocity decreases with increasing Ec at a higher protein concentration. Since the rigid cavity bottom strongly weakens the focusing of the waves, we imply that the previously developed scaling laws, with the prerequisites that jet production is based on self-similar focusing,15,53 may need to be revisited to accurately predict rd/R when the cavity surface shows such strong surface elasticity. A detailed consideration of the surface viscoelastic model of a protein-laden surface is required in this case and beyond the scope of the current study.
3.3 Top jet drop characteristics with mixed protein–surfactant solutions
We further investigate the effect of additional low-molecular-weight surfactants on bubble bursting at a protein solution surface. Such surfactants (e.g. Tween 80) have been shown to displace proteins by competitive adsorption on the surface and affect the surface viscoelasticity.54 As shown in Fig. 8(a), with increasing Tween 80 concentration, the dimensionless top jet drop radius rd/R decreases. Notably, rd/R decreases with Ec for bubble bursting in the BSA–Tween 80 mixture at ta = 300 s (inset of Fig. 8(a)), different from the trends for those produced in pure BSA solutions (Fig. 6(a)). Previous research also documented top jet drops that have similarly smaller radii when they are produced from SDS solutions as opposed to from water.29 Additionally, the dimensionless velocity, vd/vc, is smaller in BSA–Tween 80 mixtures than in pure NaCl solution at small Tween 80 concentrations, but recovers at higher Tween 80 concentrations (Fig. 8(b)). No clear trend is shown between vd/vc and Ec (inset of Fig. 8(b)). Notably, when the Tween 80 concentration is as high as 0.1 g L−1 (6.7 CMC), rd/R and vd/vc do not strongly depend on CBSA. We attribute this to the strong displacement of protein by Tween 80. At a high concentration, Tween 80 strongly competes with proteins for surface coverage and prevents the proteins from forming a compact network on the bubble surface,34,54 which limits the effect of the BSA concentration.To understand the above-mentioned different trends between pure protein and mixed protein–surfactant solutions, we again observe the collapsing cavity before the formation of the jet. Fig. 9 displays representative collapsing cavities in the BSA–Tween 80 mixtures with different CBSA and CTween![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 80 values. When the bubble bursts at the surface of a 0.05 g L−1 BSA + 0.1 g L−1 Tween 80 solution (Fig. 9(a)), a similar wave train propagates toward the cavity bottom, with significantly weakened PWs (the panel at 1.20 ms in Fig. 9(a)) compared to those at a pure NaCl solution surface (Fig. 7(a)). The DW propagates downwards the cavity surface and finally collapses at the cavity bottom with a slightly longer period (the panel at 2.00 ms in Fig. 9(a)) compared to the case without proteins or surfactants. We note again that a jet drop is generated after the cavity collapses here. Different from the bottom of the collapsing cavity at a pure protein solution surface, we find that the cavity bottom becomes relatively flat right with the addition of Tween 80 before the waves focus at the cavity nadir. In other words, comparing Fig. 7(b–d) with Fig. 9, we note a significant difference in whether or not a concave geometry is formed at the cavity base when the DWs focus at the cavity bottom. In particular, the non-concave geometry with the DW focusing in mixed protein–surfactant solutions is similar to the experimental observations of cavity collapse in Newtonian liquids with clean surfaces (Fig. 7(a)). The same non-concave geometry of the cavity bottom is observed with a smaller Tween 80 concentration where jet drops are still ejected, as shown in Fig. 9(b and c). Evidently, the addition of small molecular surfactants affects the surface rheology and modifies the morphology of the collapsing cavity. This could be partly attributed to the displacement of protein molecules which reduces the surface elasticity. However, the effect of surface elasticity alone is insufficient to explain the observation of the non-concave geometry feature, because even with similar Ec values in pure protein solution, a concave cavity bottom geometry remains during DW focusing (Fig. 7(b)). In fact, previous experimental work showed that the addition of a small amount of Tween 80 in the protein solution can result in a significant decrease of surface elasticity but a minor decrease of surface viscosity.47 Therefore, the distinct features in the jet morphology and the collapsing cavity shape may suggest that both the surface elasticity and surface viscosity are required to be considered for the variation of the jet drop radius and velocity in a mixed protein–surfactant solution.
80 values. When the bubble bursts at the surface of a 0.05 g L−1 BSA + 0.1 g L−1 Tween 80 solution (Fig. 9(a)), a similar wave train propagates toward the cavity bottom, with significantly weakened PWs (the panel at 1.20 ms in Fig. 9(a)) compared to those at a pure NaCl solution surface (Fig. 7(a)). The DW propagates downwards the cavity surface and finally collapses at the cavity bottom with a slightly longer period (the panel at 2.00 ms in Fig. 9(a)) compared to the case without proteins or surfactants. We note again that a jet drop is generated after the cavity collapses here. Different from the bottom of the collapsing cavity at a pure protein solution surface, we find that the cavity bottom becomes relatively flat right with the addition of Tween 80 before the waves focus at the cavity nadir. In other words, comparing Fig. 7(b–d) with Fig. 9, we note a significant difference in whether or not a concave geometry is formed at the cavity base when the DWs focus at the cavity bottom. In particular, the non-concave geometry with the DW focusing in mixed protein–surfactant solutions is similar to the experimental observations of cavity collapse in Newtonian liquids with clean surfaces (Fig. 7(a)). The same non-concave geometry of the cavity bottom is observed with a smaller Tween 80 concentration where jet drops are still ejected, as shown in Fig. 9(b and c). Evidently, the addition of small molecular surfactants affects the surface rheology and modifies the morphology of the collapsing cavity. This could be partly attributed to the displacement of protein molecules which reduces the surface elasticity. However, the effect of surface elasticity alone is insufficient to explain the observation of the non-concave geometry feature, because even with similar Ec values in pure protein solution, a concave cavity bottom geometry remains during DW focusing (Fig. 7(b)). In fact, previous experimental work showed that the addition of a small amount of Tween 80 in the protein solution can result in a significant decrease of surface elasticity but a minor decrease of surface viscosity.47 Therefore, the distinct features in the jet morphology and the collapsing cavity shape may suggest that both the surface elasticity and surface viscosity are required to be considered for the variation of the jet drop radius and velocity in a mixed protein–surfactant solution.
Since the capillary waves in the mixed protein–surfactant solution cases (Fig. 9) focus on the cavity bottom in a way similar to those from Newtonian liquids with clean surfaces (Fig. 7(a)), we revisit the previously developed theory on the bubble bursting jet at a clean surface. For bubble bursting at the clean surface of a Newtonian liquid, it has been shown that during the collapse of the bubble cavity, the PW generated in front of the DW strongly affects the jet radius by weakening the final focusing of the DW.3,12,16 Appropriately enhanced viscous dissipation, signified by an increasing Oh, will attenuate the PWs without significantly affecting DW. With weaker perturbation from PWs, the DW focuses closer to the cavity nadir and undergoes a self-similar collapse closer to the singular limit, which finally results in thinner jets and therefore smaller jet drops. In this case, a function of rd/R = f(Oh) has been proposed by extensive prior work when the gravity effect is negligible,3,14,16,18 where Oh can be interpreted as the ratio between the characteristic wave dissipation rate td0−1 and the inverse of the characteristic bubble collapsing time scale tc−1 as Oh ∼ td0−1/(tc−1). Here, the characteristic dissipation rate of the capillary waves on the bubble surface in a Newtonian liquid with a clean interface can be estimated as td0−1 ∼ μ/(ρR2),9,12 and the characteristic bubble collapsing time scale is consistent with the inertio-capillary time scale as tc = (ρR3/γ)1/2.
Next, for the mixed protein–surfactant solution, considering a viscoelastic surface with an enhanced dissipation rate td−1, we define a revised Ohnesorge number Ohe ∼ td−1/(tc−1). We refer to the classical theories regarding the dissipation of capillary waves55,56 in a Newtonian liquid with the surface rheology characterized by the linear surface viscoelasticity model.50,52,55,56 A less mobile viscoelastic surface strengthens wave damping, with td−1 lying between td0−1 and a maximum dissipation rate 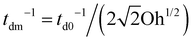 .55,56 Such a maximum dissipation rate is achieved with finite surface viscoelasticity that induces a resonance-like extra damping as the capillary ripples couple with longitudinal waves.55 With the wave damping enhanced, the perturbations at the bubble bottom will be further damped out to favor the collapse of DW closer to the cavity bottom, which finally decreases the size of the jet drop. The effect is indicated by an increasing revised Ohnesorge number. The maximum effective Ohnesorge number for a viscoelastic surface is then obtained as
.55,56 Such a maximum dissipation rate is achieved with finite surface viscoelasticity that induces a resonance-like extra damping as the capillary ripples couple with longitudinal waves.55 With the wave damping enhanced, the perturbations at the bubble bottom will be further damped out to favor the collapse of DW closer to the cavity bottom, which finally decreases the size of the jet drop. The effect is indicated by an increasing revised Ohnesorge number. The maximum effective Ohnesorge number for a viscoelastic surface is then obtained as 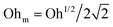 , and the minimum drop size produced by the most strongly damped waves is then predicted by rd/R = f(Ohm). With Ohe lying between Oh and Ohm, the drop size rd/R is also expected to lie between f(Oh) and f(Ohm). Fig. 10(a) shows the change in the drop size with Oh. The red dashed line represents the drop size function f proposed by Blanco-Rodríguez and Gordillo:18rd/R = f(Oh) = 0.22(1 − (Oh/0.031)1/2), and the experimental results of rd/R are smaller than the values predicted by the theory in Newtonian liquids. With the lower bound of rd/R = f(Ohm) also plotted as the black dotted line in Fig. 10(a), all the experimental data fall between f(Oh) and f(Ohm) as we expected, demonstrating that the surface viscoelasticity contributes to the decrease of rd/R by dissipating the capillary waves.
, and the minimum drop size produced by the most strongly damped waves is then predicted by rd/R = f(Ohm). With Ohe lying between Oh and Ohm, the drop size rd/R is also expected to lie between f(Oh) and f(Ohm). Fig. 10(a) shows the change in the drop size with Oh. The red dashed line represents the drop size function f proposed by Blanco-Rodríguez and Gordillo:18rd/R = f(Oh) = 0.22(1 − (Oh/0.031)1/2), and the experimental results of rd/R are smaller than the values predicted by the theory in Newtonian liquids. With the lower bound of rd/R = f(Ohm) also plotted as the black dotted line in Fig. 10(a), all the experimental data fall between f(Oh) and f(Ohm) as we expected, demonstrating that the surface viscoelasticity contributes to the decrease of rd/R by dissipating the capillary waves.
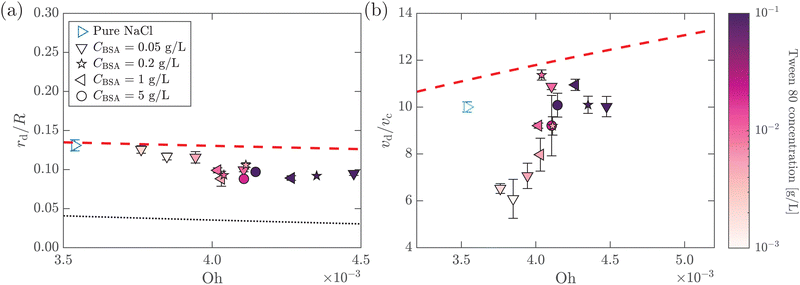 | ||
Fig. 10 (a) Dimensionless top jet drop size rd/R as a function of Ohnesorge number Oh for bubble bursting at the surface of mixed BSA–Tween solutions. The red dashed and the black dotted lines represent rd/R = f(Oh) and 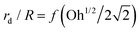 , respectively, where f(Oh) = 0.22(1 − (Oh/0.031)1/2) is the scaling law given by Blanco-Rodríguez and Gordillo.18 (b) Dimensionless top jet velocity vd/vc as a function of the Ohnesorge number Oh for bubble bursting at the surface of mixed BSA–Tween 80 solutions. The red dashed line represents the velocity scaling for the top jet drop, vd/vc = 1 + 31(Oh/0.033)1/2, for bubble bursting at a clean surface.13ta = 300 s in all cases. The marker color denotes the concentration of Tween 80. Error bars represent standard deviations of at least three measurements. , respectively, where f(Oh) = 0.22(1 − (Oh/0.031)1/2) is the scaling law given by Blanco-Rodríguez and Gordillo.18 (b) Dimensionless top jet velocity vd/vc as a function of the Ohnesorge number Oh for bubble bursting at the surface of mixed BSA–Tween 80 solutions. The red dashed line represents the velocity scaling for the top jet drop, vd/vc = 1 + 31(Oh/0.033)1/2, for bubble bursting at a clean surface.13ta = 300 s in all cases. The marker color denotes the concentration of Tween 80. Error bars represent standard deviations of at least three measurements. | ||
In addition, we further discuss the variation of the jet drop velocity in the mixed protein–surfactant solutions. When plotting vd/vcversus Oh, we observe a lower velocity of the top jet drop from mixed protein–surfactant solutions compared to the predicted values of top jet drop velocity from Newtonian liquids at the same Oh13 (Fig. 10(b)). Here, we note that the velocity of the top jet drop depends on not only the dissipation of the focusing capillary waves but also the flow flux into the jet during the jet growth.15 Since the surface elasticity effectively retards the propagation speed of the capillary waves,35 the jet is slowed due to the decreasing flow rate. In addition to the retardation effect of the surface elasticity, the surface viscosity could also produce shear traction that opposes the surface velocity gradient,57 decelerating the top jet drop ejection. Therefore, the lower vd/vc when the bubbles burst in mixed protein–surfactant solutions can be attributed to composite surface rheological effects, and further investigation is needed to rationalize the experimental observation.
4 Conclusions
In this paper, we study the top jet drops produced by bubble bursting at the viscoelastic surface of globular proteins (BSA, lysozyme) or mixed protein–surfactant (BSA–Tween 80) solutions. Using high-speed cameras, the dynamics of the top jet drops for a wide span of protein and surfactant concentrations are analyzed with controlled aging time. We show that the surface viscoelasticity introduced by these surface-active substances remarkably modifies the production of the top jet drops.In particular, we focus on the regime when the interfacial elastocapillary number Ec ≤ 1 in which the top jet drops are ejected. A significant difference is observed between the characteristics of the top jet drops from bubble bursting in protein solutions and mixed protein–surfactant solutions. For bubble bursting at an interface with strong surface elasticity, i.e., the protein solution surface in our study, the elasticity effectively weakens the top jet drop ejection by retarding the capillary wave propagation. Meanwhile, the capillary waves sweep the BSA molecules towards the cavity bottom, forming a highly rigid and solid-like elastic surface and thus triggering a concave geometry ahead of the dominant waves as the capillary waves focus at the cavity bottom, which prevents the waves from attaining an effective self-similar focusing. All these factors result in a larger and slower top jet drop.
Distinct from bubble bursting in pure protein solutions, bubble bursting in the mixed protein–surfactant solutions produces top jet drops with a smaller radius and lower velocity compared to the cases for clean surfaces. We observe that the bursting of such bubbles tends to produce cavities with flat bottoms without sharp cusps, and the dominant waves can effectively focus at the cavity bottom. In this case, in addition to the effect of the surface elasticity, the surface viscosity also plays a non-negligible role, decreasing the top jet drop size by damping the precursor waves. We describe the additional dissipation of capillary waves from the surface viscoelastic effect with a revised Ohnesorge number Ohe, which can contribute to the smaller top jet drop radius in mixed protein–surfactant solutions. Furthermore, we attribute the lower velocity of the top jet drop to the effect of surface viscoelasticity retarding the waves and resisting the formation and growth of the jet.
Our results not only advance the understanding of bubble bursting dynamics at viscoelastic interfaces, but also demonstrate that surface rheology can profoundly reshape free surface flows. In addition, the findings of this study may provide guidance for the prediction and control of the bursting bubble aerosols with a structurally compound surface in multiple natural and engineering configurations. Our experimental results could also serve as a benchmark for future theoretical and simulation studies to consider an appropriate surface rheological model to describe bubble bursting dynamics at a liquid surface laden with surface-active substances. Future close-up examinations for the effects of surface viscoelasticity on the self-similar dynamics of cavity collapse and jet growth would be helpful to revisit the scaling laws for the jet size and velocity developed for a Newtonian liquid accordingly.
Author contributions
Zhengyu Yang: data curation, formal analysis, investigation, visualization, writing – original draft, and writing – review & editing. Sainath Barbhai: formal analysis, investigation, and writing – review & editing. Bingqiang Ji: conceptualization, data curation, formal analysis, investigation, methodology, and writing – review & editing. Jie Feng: conceptualization, funding acquisition, formal analysis, investigation, project administration, resources, supervision, and writing – review & editing.Conflicts of interest
The authors declare no conflicts of interest.Notes and references
- H. Lhuissier and E. Villermaux, J. Fluid Mech., 2012, 696, 5 CrossRef CAS.
- E. Ghabache and T. Séon, Phys. Rev. Fluids, 2016, 1, 051901 CrossRef.
- C. F. Brasz, C. T. Bartlett, P. L. Walls, E. G. Flynn, Y. E. Yu and J. C. Bird, Phys. Rev. Fluids, 2018, 3, 074001 CrossRef.
- T. W. Wilson, L. A. Ladino, P. A. Alpert, M. N. Breckels, I. M. Brooks, J. Browse, S. M. Burrows, K. S. Carslaw, J. A. Huffman and C. Judd, et al. , Nature, 2015, 525, 234–238 CrossRef CAS PubMed.
- X. Wang, G. B. Deane, K. A. Moore, O. S. Ryder, M. D. Stokes, C. M. Beall, D. B. Collins, M. V. Santander, S. M. Burrows and C. M. Sultana, et al. , Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 6978–6983 CrossRef CAS PubMed.
- L. Bourouiba, Annu. Rev. Fluid Mech., 2021, 53, 473–508 CrossRef.
- D. B. Shaw, Q. Li, J. K. Nunes and L. Deike, Proc. Natl. Acad. Sci. U. S. A., 2023, 2, pgad296 Search PubMed.
- B. Ji, A. Singh and J. Feng, Nano Lett., 2022, 22, 5626–5634 CrossRef CAS PubMed.
- E. Ghabache, A. Antkowiak, C. Josserand and T. Séon, Phys. Fluids, 2014, 26, 121701 CrossRef.
- A. M. Gañán-Calvo, Phys. Rev. Lett., 2017, 119, 204502 CrossRef PubMed.
- A. M. Gañán-Calvo, Phys. Rev. Fluids, 2018, 3, 091601 CrossRef.
- J. Gordillo and J. Rodrguez-Rodrguez, J. Fluid Mech., 2019, 867, 556–571 CrossRef CAS.
- F. J. Blanco-Rodrguez and J. Gordillo, J. Fluid Mech., 2020, 886, R2 CrossRef.
- A. M. Gañán-Calvo and J. M. López-Herrera, J. Fluid Mech., 2021, 929, A12 CrossRef.
- J. M. Gordillo and F. J. Blanco-Rodrguez, Phys. Rev. Fluids, 2023, 8, 073606 CrossRef.
- L. Deike, E. Ghabache, G. Liger-Belair, A. K. Das, S. Zaleski, S. Popinet and T. Séon, Phys. Rev. Fluids, 2018, 3, 013603 CrossRef.
- A. Berny, L. Deike, T. Séon and S. Popinet, Phys. Rev. Fluids, 2020, 5, 033605 CrossRef.
- F. J. Blanco-Rodrguez and J. Gordillo, J. Fluid Mech., 2021, 916, A37 CrossRef.
- P. L. Walls, J. C. Bird and L. Bourouiba, Am. Zool., 2014, 54, 1014–1025 Search PubMed.
- R.-S. Tseng, J. T. Viechnicki, R. A. Skop and J. W. Brown, J. Geophys. Res.: Oceans, 1992, 97, 5201–5206 CrossRef CAS.
- S. M. Burrows, O. Ogunro, A. Frossard, L. M. Russell, P. J. Rasch and S. Elliott, Atmos. Chem. Phys., 2014, 14, 13601–13629 CrossRef.
- B. Ji, Z. Yang and J. Feng, Nat. Commun., 2021, 12, 1–10 CrossRef PubMed.
- B. Ji, Z. Yang and J. Feng, Phys. Rev. Fluids, 2021, 6, 033602 CrossRef.
- B. Ji, A. Singh and J. Feng, Phys. Fluids, 2021, 33, 103316 CrossRef CAS.
- B. Ji, L. Hong, J.-T. Kim, L. P. Chamorro and J. Feng, Phys. Rev. Fluids, 2022, 7, 033603 CrossRef.
- Z. Yang, B. Ji, J. T. Ault and J. Feng, Nat. Phys., 2023, 19, 884–890 Search PubMed.
- Z. Yang, B. Ji and J. Feng, J. Fluid Mech., 2023, 977, A10 Search PubMed.
- C. R. Constante-Amores, L. Kahouadji, A. Batchvarov, S. Shin, J. Chergui, D. Juric and O. K. Matar, J. Fluid Mech., 2021, 911, A57 Search PubMed.
- J. Pierre, M. Poujol and T. Séon, Phys. Rev. Fluids, 2022, 7, 073602 Search PubMed.
- E. J. Vega and J. M. Montanero, Exp. Therm. Fluid Sci., 2024, 151, 111097 CrossRef CAS.
- B. S. Murray and E. Dickinson, Food Sci. Technol. Int., Tokyo, 1996, 2, 131–145 CrossRef CAS.
- M. A. Bos and T. Van Vliet, Adv. Colloid Interface Sci., 2001, 91, 437–471 CrossRef CAS PubMed.
- E. M. Freer, K. S. Yim, G. G. Fuller and C. J. Radke, J. Phys. Chem. B, 2004, 108, 3835–3844 CrossRef CAS.
- D. Tammaro, V. Chandran Suja, A. Kannan, L. D. Gala, E. Di Maio, G. G. Fuller and P. L. Maffettone, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2105058118 CrossRef CAS PubMed.
- B. Ji, Z. Yang, Z. Wang, R. H. Ewoldt and J. Feng, Phys. Rev. Lett., 2023, 131, 104002 CrossRef CAS PubMed.
- B. Noskov, A. Mikhailovskaya, S.-Y. Lin, G. Loglio and R. Miller, Langmuir, 2010, 26, 17225–17231 CrossRef CAS PubMed.
- S. Poulain, E. Villermaux and L. Bourouiba, J. Fluid Mech., 2018, 851, 636–671 CrossRef CAS.
- A. K. Gaigalas, J. B. Hubbard, M. McCurley and S. Woo, J. Phys. Chem., 1992, 96, 2355–2359 CrossRef CAS.
- A. Jaishankar, V. Sharma and G. H. McKinley, Soft Matter, 2011, 7, 7623–7634 RSC.
- V. Sharma, A. Jaishankar, Y.-C. Wang and G. H. McKinley, Soft Matter, 2011, 7, 5150–5160 RSC.
- V. L. Dharmaraj, P. D. Godfrin, Y. Liu and S. D. Hudson, Biomicrofluidics, 2016, 10, 043509 CrossRef PubMed.
- M. Sakai, A. Tanaka, H. Egawa and G. Sugihara, J. Colloid Interface Sci., 1988, 125, 428–436 CrossRef CAS.
- E. Huang, A. Skoufis, T. Denning, J. Qi, R. R. Dagastine, R. F. Tabor and J. D. Berry, J. Open Source Softw., 2021, 6, 2604 CrossRef.
- G. L. Lin, J. A. Pathak, D. H. Kim, M. Carlson, V. Riguero, Y. J. Kim, J. S. Buff and G. G. Fuller, Soft Matter, 2016, 12, 3293–3302 RSC.
- A. Kannan, I. C. Shieh, D. L. Leiske and G. G. Fuller, Langmuir, 2018, 34, 630–638 CrossRef CAS PubMed.
- P. L. Walls, L. Henaux and J. C. Bird, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 021002 CrossRef PubMed.
- D. Grigoriev, S. Derkatch, J. Krägel and R. Miller, Food Hydrocoll., 2007, 21, 823–830 CrossRef CAS.
- O. Y. Milyaeva, R. A. Campbell, G. Gochev, G. Loglio, S.-Y. Lin, R. Miller and B. A. Noskov, J. Phys. Chem. B, 2019, 123, 4803–4812 CrossRef CAS PubMed.
- A. Javadi, S. Dowlati, S. Shourni, R. Miller, M. Kraume, K. Kopka and K. Eckert, Adv. Colloid Interface Sci., 2022, 301, 102601 CrossRef CAS PubMed.
- G. Narsimhan, Food Eng. Rev., 2016, 8, 367–392 CrossRef CAS.
- H. Manikantan and T. M. Squires, J. Fluid Mech., 2020, 892, P1 CrossRef CAS PubMed.
- X. Zhong and A. M. Ardekani, J. Fluid Mech., 2022, 935, A27 CrossRef CAS.
- C.-Y. Lai, J. Eggers and L. Deike, Phys. Rev. Lett., 2018, 121, 144501 CrossRef CAS PubMed.
- P. Wilde, A. Mackie, F. Husband, P. Gunning and V. Morris, Adv. Colloid Interface Sci., 2004, 108, 63–71 CrossRef PubMed.
- Interfacial Rheology, ed. R. Miller and L. Liggieri, CRC Press, London, 2009 Search PubMed.
- G. K. Rajan and D. M. Henderson, Phys. Fluids, 2018, 30, 072104 CrossRef.
- N. Singh and V. Narsimhan, J. Fluid Mech., 2022, 946, A24 CrossRef CAS.
Footnote |
| † These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2024 |