Accelerating the prediction of inorganic surfaces with machine learning interatomic potentials
Kyle
Noordhoek
 and
Christopher J.
Bartel
and
Christopher J.
Bartel
 *
*
Department of Chemical Engineering and Materials Science, University of Minnesota, Minneapolis, MN 55455, USA. E-mail: cbartel@umn.edu
First published on 6th March 2024
Abstract
The surface properties of solid-state materials often dictate their functionality, especially for applications where nanoscale effects become important. The relevant surface(s) and their properties are determined, in large part, by the material's synthesis or operating conditions. These conditions dictate thermodynamic driving forces and kinetic rates responsible for yielding the observed surface structure and morphology. Computational surface science methods have long been applied to connect thermochemical conditions to surface phase stability, particularly in the heterogeneous catalysis and thin film growth communities. This review provides a brief introduction to first-principles approaches to compute surface phase diagrams before introducing emerging data-driven approaches. The remainder of the review focuses on the application of machine learning, predominantly in the form of learned interatomic potentials, to study complex surfaces. As machine learning algorithms and large datasets on which to train them become more commonplace in materials science, computational methods are poised to become even more predictive and powerful for modeling the complexities of inorganic surfaces at the nanoscale.
Introduction
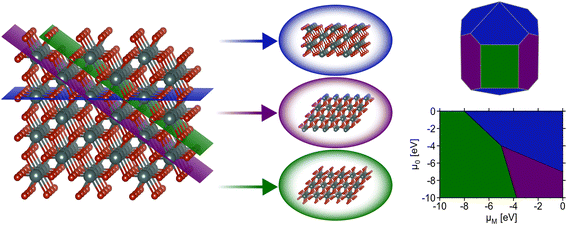
Surface science and nanoscale synthesis are key driving factors in many current technological applications including catalysis1 and microelectronics.2 For catalysis applications, surface reactivity is dictated by the structure of exposed surfaces on nanoparticles or thin films. Understanding the phase stability of relevant surfaces is therefore paramount for catalyst design. In thin-film devices, interfacial interactions between substrates and vapor-deposited materials dictate phase stability and, again, the observed properties are highly dependent upon the surface or interfacial structure. Hence, accurately capturing which surfaces are likely to be observed under relevant conditions plays an important role in the design of nanostructured solid-state materials.This review focuses on modeling inorganic surfaces with periodic boundary conditions (i.e., using slab models), but it should be noted that surface effects can also be captured with finite systems (e.g., using isolated nanoparticles).3,4 Using periodic boundary conditions, a typical inorganic surface is modeled as a slab – an infinite 2D sheet of material formed by slicing a bulk (3D) crystal using a particular 2D plane. The cleavage of the conventional unit cell through a designated Miller plane produces a single facet. Surface facets are nominally referred to using Miller index notation to indicate the plane used to perform the slice with respect to the conventional unit cell. A facet (Miller index) alone does not define a slab as the position along the vector normal to the plane defined by the Miller indices where the cut is made can lead to different “terminations” of the slab (i.e., different atomic species at the surface). It is typical for multiple possible terminations per facet to be generated when computing surface properties. For a more detailed description of how surface slabs with varying terminations can be systematically generated as a starting point for first-principles calculations, see the thorough explanation given by Sun and Ceder.5 After the generation of a facet with a particular termination, the “dangling bonds” formed by slicing the bulk material can induce a rearrangement of atomic positions at/near the surface. Surface rearrangements nominally fall under two categories: (1) relaxations, which result from subtle changes in atomic positions that do not drastically alter the surface structure, and (2) reconstructions, which result from significant changes producing a notably different structure than that which formed from the original cleavage of the bulk material. Reconstructions are often denoted using Wood's notation,6 which describes modifications of the surface unit cell compared with the bulk (e.g., the well-known 7 × 7 reconstruction of Si).7,8 Understanding the surface structure is critical for countless applications, and the relative energies of these various reconstructions, facets, and terminations determine which surface structures are likely to appear for a material at a given set of conditions (Fig. 1). This review focuses primarily on recent efforts to use machine learning to address the challenging problem of calculating the thermodynamics of solid-state, inorganic surfaces using first-principles methods.
Computational thermodynamics of surfaces
The surface (internal) energy, γ, of a slab in vacuum can be computed as the difference between the total internal energy of the slab, Eslab, and the total internal energy of the bulk, Ebulk, given the same number of atoms, N, as the slab. For the case where the upper and lower slab surfaces are identical, the surface free energy is calculated as: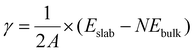 | (1) |
For real systems and applications, the temperature and environment (e.g., gas composition) play significant roles in dictating the structure and energetics of inorganic surfaces. This motivates the application of different thermodynamic potentials for computing the energies. Traditionally, mapping the DFT-calculated total internal energy (E) to the enthalpy at a given temperature, T, requires consideration of the zero-point energy correction as well as the integrated heat capacity (from 0 K to T). However, it has been shown that the DFT-calculated total internal energy alone is a reasonable approximation for the enthalpy of a solid at room temperature (because the pressure-volume contribution is small).14 Mapping these enthalpies to Gibbs energies with first-principles calculations is much more computationally intensive because this requires computing the vibrational (phonon) and configurational contributions to the free energies of all involved solids (including the slabs).15–19 A common approximation in computational surface science is that the entropic contribution of the involved gaseous species (e.g., O2 in air) is much larger than the entropic contribution from the involved solids.9 Thus, a typical approach is to compute grand canonical surface energies for slabs allowed to exchange species with their environment as:
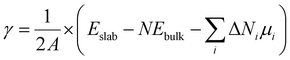 | (2) |
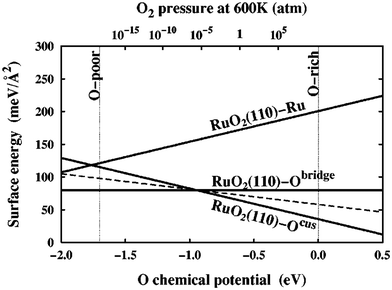 | ||
| Fig. 2 Surface free energies, γ(T, pO2), for three possible RuO2(110) terminations calculated over the allowed range of oxygen chemical potential, μO(T, pO2), as indicated by the vertical dashed lines. The sloped dashed line depicts the surface free energy of a RuO2(110)-Ocus termination with only every second Ocus site occupied. This figure has been reproduced from ref. 9 with permission from the American Physical Society, copyright 2001. | ||
This approach can also be generalized to more complex thermodynamic environments (e.g., aqueous electrochemical environments using the Pourbaix potential).20–23 An important consideration for the purposes of computational surface science is that these open systems introduce additional complexities as the surface composition (termination) can vary substantially depending on the temperature and environment.
While the aforementioned challenges are true for any particular facet (various terminations, restructuring), a further complication is that it is often critical to know the relative energies of many possible facets. Consider the Wulff construction, a prevalent method used to determine the equilibrium shape of a crystal of fixed volume, which is calculated by minimizing the total Gibbs free energy of the proposed system.24,25 The minimization is performed with respect to the weighted product of facet surface energies and facet surface areas. As such, changes in the relative energies of the facets (i.e. due to changes in temperature or environment) can manifest as modifications to the equilibrium crystal shape. In Fig. 3, we show how the computed equilibrium morphology of RuO2 nanoparticles changes due to the dependence of relative surface energies on the change in oxygen chemical potential, ΔμO.26 It is important to note that Wulff constructions produce size-independent particle morphologies while nanoparticles can exhibit dynamic surface structures under certain conditions.27 Even so, observed deviations from the computed equilibrium particle morphologies have been shown to be small outside of cases where particles experience large strains or edge/corner atoms are miscounted during morphology predictions.28,29
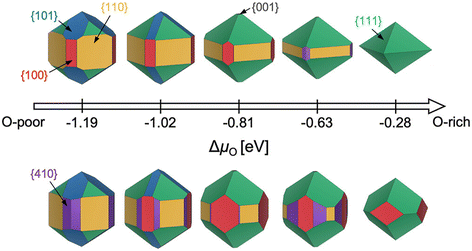 | ||
| Fig. 3 Equilibrium Wulff nanoparticle shapes computed from RuO2 surface energies of all low-index (up to (111)) facets and the (410) vicinal, using locally optimized structures (top) and global geometry optimized structures (bottom). The indicated changes in oxygen chemical potential, ΔμO, correspond to calcination pretreatment conditions used by Rosenthal et al.,30,31 Jirkovský et al.,32 Lee et al.,33 and Narkhede et al.,34 from left to right. Standard conditions (300 K, 1 bar, −0.28 eV) are also displayed. This figure has been reproduced from ref. 26 with permission from the American Chemical Society, copyright 2023. | ||
In an effort to cull the number of required calculations, many efforts have focused on a single facet9,35–40 or a (sub)set of low-Miller index facets (e.g., up to (111)).41–43 For some systems, this has led to good agreement with experimental measurements. For example, Reuter and Scheffler investigated the stability of the O-terminated, Ru-terminated, and stochiometric RuO2(110) facets as a function of ΔμO, ranging from −2.0 eV to 0.5 eV.9 They computed that a transition from the RuO2(110)-Ocus termination to the RuO2(110)-Obridge termination, where cus and bridge refer to specific locations of oxygen on the surface, occurs at T = 450 ± 50 K and pO2 = 10−12±2 atm. This agrees with temperature desorption spectroscopy (TDS) measurements that found an excess of Ocus atoms on the RuO2(0001) surface at temperatures between 300–550 K under ultra-high vacuum (p < 10−12 atm) conditions.44 RuO2(0001) has been found to form RuO2(110) domains under oxidizing conditions.11,45 The study of the RuO2 system was extended by Wang et al. to include all possible (1 × 1) terminations of the (100), (001), (110), (101) and (111) facets over the same range of ΔμO.42 These surface energies were used to compute equilibrium particle morphologies as a function of ΔμO. The particle morphologies were qualitatively compared to scanning electron microscopy (SEM) images of experimentally grown RuO2 nanoparticles,30,31,34 where the major features (overall shape, facet coverage) of the computed morphologies were found to agree with experiment. For other systems, the inclusion of only low-Miller index facets can be a substantial approximation, and many facets that are relevant to the application of a material can be missed by only looking at this subset. In the case of Pd and Rh, Mittendorfer et al. computed equilibrium particle morphologies with the inclusion of the (100), (110), (111), (211), (311), and (331) facets.46 They discovered that under UHV conditions a significant fraction of the nanoparticle surface is comprised of the high-Miller index surfaces (211), (311), and (331).
So far, we have discussed that surface structures of interest can be generated as inputs to DFT calculations, which perform a local relaxation of the structure and yield accurate estimates for the internal energies. Using the thermodynamic relations discussed previously, these internal energies can be mapped to more useful thermodynamic potentials. However, an intrinsic limitation of this approach is that the only surface structures that can appear in the resulting surface phase diagrams are those that were specified as inputs by the user. Enumerating all possible surfaces (facets, terminations, reconstructions) and computing their energies with DFT is intractable. This motivates the development of sampling approaches to rationally explore the landscape of plausible surface structures. These approaches make use of concepts from crystal structure prediction,47,48 optimization,49 statistical mechanics,16,17,19,50 and molecular dynamics simulations51 (among other techniques). A detailed description of these methods is outside the scope of this review, but the application of machine learning (ML) in the context of these methods will be discussed. The remainder of this review will focus on the role of ML methods in facilitating accurate predictions of inorganic surface structures and energies under thermochemically relevant conditions.
Machine learning interatomic potentials
The computational cost of energy evaluations with DFT scales approximately with the cube of the number of electrons in the system. This scaling means DFT calculations are often restricted to small numbers of structures, structures with less atoms, and very short timescales for molecular dynamics (MD). Interatomic potentials (IPs) are often used as surrogates for DFT and can scale approximately linearly with the number of atoms in the system. Historically, empirical IPs assume a particular functional form and fit parameters using higher fidelity data (e.g., from DFT) for some structures of interest. ML has recently emerged as a powerful tool for learning the relationship between crystal structures and DFT-calculated energies (and forces) that result. So-called machine learning interatomic potentials (MLIPs) have achieved remarkable performance as surrogates for DFT.52–54 For bulk crystals, there have been demonstrations of “universal” MLIPs that are trained to perform well on materials spanning the periodic table.55–58 Similarly, the Open Catalyst Project,59,60 a massive open data challenge, has shown that MLIPs trained on millions of structures relevant to heterogeneous catalysis can be effective surrogates for predicting the structures and energies of surfaces with adsorbates.61–67 Predicting the thermochemical stability of solid-state surfaces presents a different challenge, and MLIPs have not yet been shown to be effective “universal” surrogate models for solid-state surfaces. There have, however, been several examples of MLIPs dramatically accelerating the determination of surface phase diagrams within targeted materials spaces of interest.A thorough review of MLIPs is outside the scope of this work, so we will briefly introduce two classes of MLIPs that have been applied extensively for surface science. The first approach relies upon Gaussian Process Regression (GPR) to develop so-called Gaussian Approximation Potentials (GAPs).68–71 A typical procedure for fitting a GAP is shown in Fig. 4. Briefly, the method begins by collecting ground-truth energies and forces (usually from DFT) for structures of interest to populate a database of reference data. For efficient training, these crystal structures must be “represented” in a manner that maximizes the retention of information subject to common invariances and equivariances that should be exhibited by periodic crystals.72 GPR is then used to fit a probabilistic relationship between the target properties (energies, forces) in the reference data and the descriptors that result from the chosen representation.69 Once the model is trained, any new configuration (structure) of interest can be represented in the same manner and passed through the model to infer the energies and forces associated with that structure. It should be noted that any systematic inaccuracies present in the data used to populate the reference database will be learned by (and therefore translated to) the fitted model. In the context of populating a reference database with DFT-computed properties, it is therefore important to understand potential errors that may arise for a given system of interest and how, if at all, these errors can be corrected (e.g., through the use of a +U correction for systems with strongly localized electron states).73 GAPs can also be used as the “force field” to drive MD simulations. Because the underlying model (GPR) is probabilistic, the resulting uncertainties can be used to iteratively improve the model using active learning.74
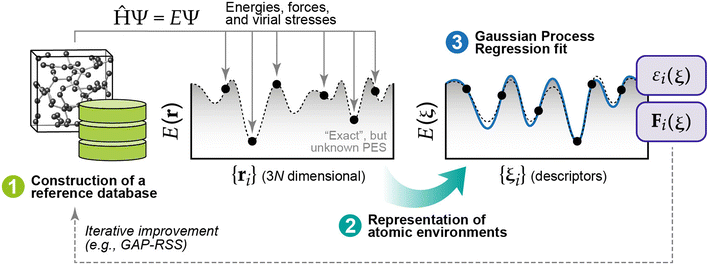 | ||
| Fig. 4 Three main components required for GAPs: (1) a robust reference database of quantum-mechanical data (usually generated with DFT), (2) a representation of the atomic environments associated with each reference point, and (3) the GPR model fit. This figure has been reproduced from ref. 69 with permission from the American Chemical Society, copyright 2021. | ||
Alternative MLIP fitting approaches and architectures make use of many of the same concepts (reference data, representing crystal structures, model training, active learning), but may vary the underlying model and associated structural representation. As one example, the GPR model can be replaced with a deep learning model in the form of neural network (NN) potentials. As one class of NN potentials, graph neural networks (GNNs) leverage a graph representation for each crystal structure, where each node is an atom in the structure and neighboring atoms (within some radial cutoff distance) are connected via edges.55–57,63 Aside from graphs, other well-known neural network potentials represent the crystal structure through equivariant descriptors, such as radial functions that are applied to and summed over distances from a central atom.75–79 There are many flavors of NN potentials and the interested reader is encouraged to see more thorough reviews of MLIPs.52,80–85 In the following sections, we review recent efforts to use MLIPs at various steps in the computational surface science pipeline.
Direct predictions of surface energy
MLIPs are capable of rapidly and directly predicting the surface energy of a given slab, provided they have been appropriately trained for the material system of interest. This approach enables the accelerated exploration of a selected materials system with the potential to more comprehensively understand the energetics that may be missed using only DFT. With the goal of more robustly exploring possible IrO2 surface structures, Timmermann and Reuter trained a GAP using 136 DFT-calculated structures.51 The training data included 78 low-index facets, 34 bulk structures, and 20 nonequilibrium surface structures taken from high temperature MD simulations of various nanoparticle sizes and shapes. The GAP predicts that reordered (101) and (111) (1 × 1) structures are most stable under simulated annealing conditions (ramping to T = 1000 K over 20 ps followed by slow cooling at 3 K per ps for 250 ps). This was further confirmed by DFT calculations as well as LEED and scanning-tunneling microscopy (STM) of annealed IrO2 crystals. These results show how data-driven approaches can be leveraged to identify important surface structures that may have been missed using typical low-throughput approaches.After previously identifying missed stable IrO2 structures, Timmermann et al. employed active learning in a two-stage framework for training GAPs to predict low-index surface structures of IrO2 and RuO2.86 An initial GAP model was trained on DFT-calculated energies of O2 dimers with varying O–O bond lengths, bulk unit cells of MO2 (M = Ir, Ru) at varying compressed, expanded, and optimized lattice parameters, and 21 low-Miller index (1 × 1) surfaces with M-, O-, stochiometric-, or peroxo-terminations. Sixteen of the low-Miller index surfaces, excluding the peroxo-terminations, were used as starting configurations for simulated annealing to generate 80 additional stable IrO2 structures and 63 RuO2 structures. The generated candidates were relaxed using DFT to assess differences in the GAP-predicted structures, which were measured as a function of the minimal similarity between two atoms within a structure, given by the Smooth Overlap of Atomic Positions (SOAP) kernel.79 For those GAP-predicted structures where there were significant differences, the DFT-relaxed structure was computed and used for training in place of the GAP-predicted structure. The authors ultimately identified 8 IrO2 and 7 RuO2 terminations that are more stable than terminations formed by cleaving the bulk oxides for −2.0 eV < ΔμO < 0 eV. In Fig. 5, we show 8 of these novel terminations compared to their conventional bulk cleaved counterparts.
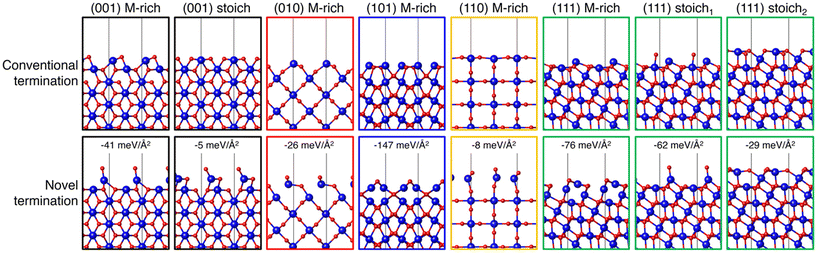 | ||
| Fig. 5 IrO2 (1 × 1) surface structures identified with DFT (conventional) or during GAP training and surface exploration (novel). The top row depicts a side view of the conventional terminations resulting from bulk truncation and DFT geometry optimization. The bottom row depicts a side view of the GAP identified most stable structure, with the relative difference in surface free energy stated explicitly. Ir atoms are drawn as larger blue spheres and O atoms are drawn as smaller red spheres. This figure was reproduced from ref. 86 with permission from AIP publishing, copyright 2021. | ||
Similar objectives have also been pursued using NN-based MLIPs rather than GAPs. Phuthi et al. used data from 4548 structures (bulk, bulk with defects, pristine surfaces, and surfaces with adsorbates) generated through the DPGen active learning framework87 to train NequIP88 and Deep Potential77 models for elemental Li.89 Surface energy and nanoparticle morphology predictions were compared directly to DFT calculations, as well as predictions from a popular modified embedded atom (MEAM) empirical potential90 and spectral neighbor analysis potential (SNAP).76 The authors show that both their NequIP and Deep Potential models achieve accuracies within 1 meV Å−2 of the surface energy computed by DFT for higher-Miller index facets (up to (332)) despite their models only explicitly using the (100), (110), and (111) facets as starting structures for the active learning framework.
Similarly, Gao and Kitchin constructed a NN potential for Pd using the Atomistic Machine-learning package (Amp).91,92 The NN architecture consisted of 2 hidden layers with 18 nodes each and was trained on ∼2700 DFT-calculated energies of bulk, slab, and defect structures. For the fcc(111) surface, the average surface energy was computed for supercells of size (2 × 2), (2 × 3), (3 × 3), (3 × 4), and (4 × 4). The average surface energy predicted by the model was in close agreement with DFT-computed average surface energies, with a mean absolute error (MAE) of <2 meV Å−2. Additionally, the surface vacancy energy was computed with DFT and the NN, where the authors found the NN to underestimate the DFT value by as much as 222 meV per atom, suggesting further tuning for defective surfaces would be needed. It is worth noting that the authors also compared the single point run time between DFT and their NN and found that the NN scaled linearly with the number of atoms and, on average, was four orders of magnitude faster than DFT.
From surface energies to nanoparticle morphologies
We have so far discussed the speed and accuracy with which GAPs and NN potentials are capable of directly evaluating surface energies. If the relative surface energies among various facets and terminations can be predicted accurately, this enables the efficient prediction of equilibrium nanoparticle morphologies. Lee et al. revisited the RuO2 system to explore feasible surface reconstructions and compare DFT-calculated Wulff constructions with those of an updated GAP model.26 Their updated model is an extension of the one previously trained by Timmermann et al.86 for the RuO2 (1 × 1) surface structures and now includes RuO2 c(2 × 2). The training for the new GAP potential added surface compositions with 25% and 75% additional oxygen coverage to the list of training data used for the initial (1 × 1) surface model. The inclusion of only 18 new surfaces with these new compositions enabled the model to predict critical reconstructions involving tetrahedral Ru4f motifs. The authors further utilized the GAP model to predict surface energies over the range −1.5 eV < ΔμO < 0 eV and computed the resulting equilibrium nanoparticle shapes. They noted that their particle morphologies resulting from GAP-predicted surface energies are qualitatively consistent with those reported by Wang et al., who calculated equilibrium shapes from surface energies computed strictly using DFT.42 However, Lee's computed morphologies, shown in Fig. 3, display a non-trivial percentage of the equilibrium particle morphology that is covered by the high-Miller index (410) facet, which was not shown by the previous low-Miller index studies.Returning to NN potentials, Shrestha et al. computed equilibrium particle morphologies as well as particle-size dependent phase diagrams for molybdenum and tungsten carbides.93 Similar to Gao and Kitchin,92 the authors utilized Amp91 to develop separate NN potentials for each carbide system. The training was performed using DFT-computed energies for a total of 5918 Mo–C and 5941 W–C structures. The 5918 Mo–C structures included 154 Mo metal, 49 bulk (MoxCy), and 5715 slabs with facets up to (111) and 49 high-Miller index facets for which the authors could find literature references. The 5941 W–C structures included 167 W metal, 46 bulk (WxCy), and 5728 slabs with facets up to (111) and 38 high-Miller index facets for which the authors could find literature references. Using these models, the authors predicted the surface energies of 1509 MoxCy and 1080 WxCy surfaces up to Miller index 5 before generating Wulff constructions for −0.5 eV < ΔμC < 0 eV. For facets found in the equilibrium nanoparticles at various points in the ΔμC range, the surface energy was computed using DFT. These DFT-computed surface energies of the NN-identified facets were then used to re-compute equilibrium particle morphologies. The resulting nanoparticle morphologies compared qualitatively well to transmission electron microscopy (TEM) and X-ray diffraction (XRD) measurements and are shown in Fig. 6 for the molybdenum carbide nanoparticles.94 The authors also determined particle-size dependent phase diagrams by utilized an alternative thermodynamic potential, following the work of Sun et al.,20 to compute grand potential energies for each equilibrium particle morphology as a function of the particle's diameter, d. The potential energies were computed for d > 2 nm and across the previously mentioned range of −0.5 eV < ΔμC < 0 eV. For both the Mo–C and W–C phase diagrams, the authors found good agreement between the computed and experimentally observed morphologies, with the only major exception being γ-MoC, which was computed to be stable only at d ≫ 10 nm but has been experimentally observed for 3 nm < d < 6 nm.95,96
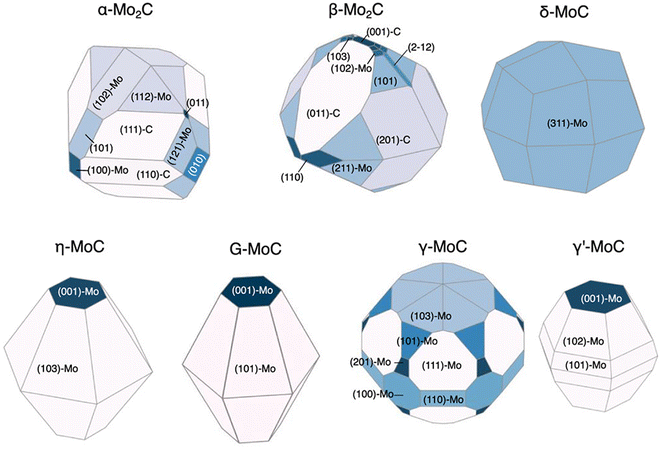 | ||
| Fig. 6 DFT-computed Wulff constructions of the equilibrium particle morphologies of different molybdenum carbide phases at ΔμC = −0.15 eV using NN-identified facets. This figure has been reprinted from ref. 93 with permission from the American Chemical Society, copyright 2021. | ||
Leveraging direct predictions of surface energies is not the only method of predicting equilibrium nanoparticle morphologies. Palizhati et al. utilized a crystal graph convolution neural network (CGCNN) to predict cleavage energies, or the energy required to break bonds along a specific plane, of bimetallic surfaces from which they compute Wulff constructions.97 The cleavage energies are equal to the surface energies provided that the terminations of the resulting slabs are identical. The CGCNN was trained on cleavage energies of 3033 intermetallic surfaces spanning 36 different elements. The training cleavage energies were computed using a linear extrapolation method, where the total DFT-computed slab energy was plotted as a function of slab thickness, and the cleavage energy is given by the y-intercept. The authors assessed their model's accuracy by comparing the DFT-calculated Wulff constructions with the CGCNN-predicted Wulff constructions for NiGa, CuAl, and CuAu. They show that their model's predictions of equilibrium particle morphologies capture the majority of high area facets, with the highest area fraction MAE for CuAu (MAE = 0.096).
Energy inputs to Monte Carlo simulations
Surface reconstruction can lead to complex equilibrium geometries under changing temperatures or environmental conditions, which drastically affect final surface properties. When a single facet is of particular interest, more extensive sampling of the feasible surface structures can lead to an improved understanding of the relative surface energies. Such extensive sampling leads to more realistic predictions of the final observed structure but comes with the drawback of significantly higher computational cost and is typically intractable when very many facets are relevant (e.g., in Wulff constructions).Sampling strategies are often based on Monte Carlo methods that can be used to explore the plausible reconstructions of a given surface under varying conditions. The rapid exploration of feasible reconstruction events is dependent on the speed and accuracy of the underlying surface energy calculator. Recently, Du et al. developed a high-throughput active learning framework, Automatic Surface Reconstruction (AutoSurfRecon), for end-to-end prediction of surface energetics and exploration of surface reconstructions.98 Their framework introduced a Virtual Surface Site Relaxation-Monte Carlo (VSSR-MC) method in the canonical and semi-grand canonical ensembles, which the authors showed can reproduce well known surface reconstructions of GaN(0001) (see Fig. 7a) and Si(111). Following the demonstration of VSSR-MC, the authors mapped a phase diagram for SrTiO3(100), shown in Fig. 7b. For the calculation of the SrTiO3(100) surface energies, the authors trained a neural network force field using the PaiNN67 architecture. The predicted surface energies over the range −10 eV < ΔμSr < 0 eV yielded a double layer TiO2 termination at low (more negative) ΔμSr and single layer TiO2 to single layer SrO terminations at increasing ΔμSr, all of which have been experimentally reported.99–105 The authors computed the phase diagram of SrTiO3(100) by also predicting the surface energies over the range −10 eV < ΔμO < 0 eV and note that their predicted phase diagram is qualitatively similar to that which was computed through DFT by Heifets et al.106
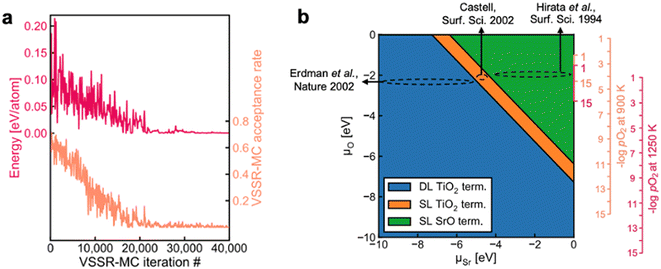 | ||
| Fig. 7 (a) A typical VSSR-MC run profile is depicted for high-temperature annealing of GaN(0001). (b) The NN-computed phase diagram of SrTiO3(100) showing the stable surface terminations at varying μSr and μO along with estimated positions of three experimental SrTiO3(001) surfaces, Erdman et al.,101 Castell,100 and Hirata et al.99 Four vertical axes are illustrated on the right. The smaller axes provide an abbreviated view of the larger axes. This figure has been reproduced/adapted from ref. 110 with permission from arXiv, copyright 2023. | ||
The previous investigation of surface reconstructions chose to avoid the computationally more expensive grand canonical Monte Carlo (GCMC), though in situations such as the study of oxidation processes, it may be necessary to use GCMC as it does not limit the interactions between the surface lattice and adsorbates. Therefore, Xu et al. developed a general framework for training NN potentials to be used with GCMC for exploring surface oxidation.107 They tested the framework by exploring the PtOx system. 52![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 448 DFT-computed energies were used to train an Embedded Atom Neural Network Potential (EANNP)108,109 to predict the surface and oxygen adsorption energies of the (111), (211), and (322) facets. Monte Carlo simulations were carried out using the EANNP and resulted in the discovery of formation mechanisms for the raised PtO4, minimal stripe Pt2O6, and edge PtO6 units, which were verified through replication by DFT calculations.
448 DFT-computed energies were used to train an Embedded Atom Neural Network Potential (EANNP)108,109 to predict the surface and oxygen adsorption energies of the (111), (211), and (322) facets. Monte Carlo simulations were carried out using the EANNP and resulted in the discovery of formation mechanisms for the raised PtO4, minimal stripe Pt2O6, and edge PtO6 units, which were verified through replication by DFT calculations.
Boes and Kitchin took a slightly different approach for predicting oxygen absorption on Pd surfaces. They utilize the Amp package91 to train a Behler-Parrinello (BP) NN111 for the Pd(111) surface.112 Their training data consisted of DFT calculations for 107 unique energy configurations of a 3 × 3 × 4 Pd slab. For each configuration, oxygen was placed at either the fcc, hcp, bridge, or top sites prior to relaxation. The authors used each step of the DFT-relaxation trajectories to provide 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 925 training data points to the model. GCMC was then performed with the BPNN as an energy calculator, where the authors predicted the relative potential energy barriers associated with oxygen migration across the Pd slab surface. Their results found good agreement with DFT and experimental energies, within 0.15 eV at any given site or nearest neighbor distance.113–115 Boes and Kitchin note that the BPNN could be expanded for use in ternary systems of interest, leading to Yang et al. training individual BPNNs for Pd, Au, and Cu.116 Training was performed on 5100 DFT-computed surface energies of fcc(111) slabs with random compositions of the three elements. The individual BPNNs were then combined to predict surface properties of the ternary Cu–Pd–Au fcc(111) alloy. MC simulations were performed across 24 bulk compositions to explore metal segregation at the fcc(111) surface. The framework was able to qualitatively depict trends in the AuPd, and CuAu portions of the ternary space though it falls short in predicting the CuPd portions when compared to cluster expansion results.117 The authors attribute this limitation to the use of ideal fcc(111) surfaces in generating their training data, as when fcc(110) surface data was incorporated the model was able to more consistently reproduce the CuPd behavior.
925 training data points to the model. GCMC was then performed with the BPNN as an energy calculator, where the authors predicted the relative potential energy barriers associated with oxygen migration across the Pd slab surface. Their results found good agreement with DFT and experimental energies, within 0.15 eV at any given site or nearest neighbor distance.113–115 Boes and Kitchin note that the BPNN could be expanded for use in ternary systems of interest, leading to Yang et al. training individual BPNNs for Pd, Au, and Cu.116 Training was performed on 5100 DFT-computed surface energies of fcc(111) slabs with random compositions of the three elements. The individual BPNNs were then combined to predict surface properties of the ternary Cu–Pd–Au fcc(111) alloy. MC simulations were performed across 24 bulk compositions to explore metal segregation at the fcc(111) surface. The framework was able to qualitatively depict trends in the AuPd, and CuAu portions of the ternary space though it falls short in predicting the CuPd portions when compared to cluster expansion results.117 The authors attribute this limitation to the use of ideal fcc(111) surfaces in generating their training data, as when fcc(110) surface data was incorporated the model was able to more consistently reproduce the CuPd behavior.
Alternative ML-based sampling strategies
So far, we have discussed the implementation of MLIPs to enable accurate equilibrium particle morphology estimation and efficient probabilistic simulation. The training of the described MLIPs has largely focused on structures generated through domain knowledge, literature surveys, or automated active learning approaches. The following section is set to introduce recent works in sampling more robust training sets through less conventional search approaches. The focus is again on those that leverage ML, though other sampling strategies (e.g., nested sampling16,118,119) have also been used.Zhu et al. returned to the well-studied RuO2 system to explore the structure of Ru/RuO2 interfaces.120 They used stochastic surface walking (SSW)121 to generate more than 107 (cluster, layered, and bulk) Ru–C–H–O structures. SSW is a Metropolis Monte Carlo122 based search method that smoothly manipulates a given structure to generate new configurations. DFT-computed internal energies for 46![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 731 select structures were used for training a NN potential. The authors used a modified version of the phenomenological theory of martensitic crystallography123 to generate plausible Ru/RuO2 interfaces before optimizing the atomic coordinates and predicting the interfacial energies with their NN. The five most stable interfaces are shown in Fig. 8. Three of the five most stable interfaces were matched with previous experimental results: RuO2(101) on Ru(1010), RuO2(101) on Ru(0001), and RuO2(100) on Ru(1010).12,124 The SSW-NN framework facilitated Chen et al. to develop an automated search for optimal surface phases (ASOP) in the grand canonical ensemble.125 The SSW-NN method was used to generate 50
731 select structures were used for training a NN potential. The authors used a modified version of the phenomenological theory of martensitic crystallography123 to generate plausible Ru/RuO2 interfaces before optimizing the atomic coordinates and predicting the interfacial energies with their NN. The five most stable interfaces are shown in Fig. 8. Three of the five most stable interfaces were matched with previous experimental results: RuO2(101) on Ru(1010), RuO2(101) on Ru(0001), and RuO2(100) on Ru(1010).12,124 The SSW-NN framework facilitated Chen et al. to develop an automated search for optimal surface phases (ASOP) in the grand canonical ensemble.125 The SSW-NN method was used to generate 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 131 (cluster, layered, and bulk) Ag–C–H–O structures and train a NN for exploring the surface oxide phases of Ag(111) and Ag(100). The authors reproduced the experimentally observed Ag(111) c(4 × 8),126 Ag(111) p(4 × 4),127–129 and Ag(100) (2√2 × √2)R45°130–132 surface structures together with unreported, but predicted-low-energy, Ag(111) (2 × 1) and Ag(100) (2√2 × 2√2)R45° surfaces.
131 (cluster, layered, and bulk) Ag–C–H–O structures and train a NN for exploring the surface oxide phases of Ag(111) and Ag(100). The authors reproduced the experimentally observed Ag(111) c(4 × 8),126 Ag(111) p(4 × 4),127–129 and Ag(100) (2√2 × √2)R45°130–132 surface structures together with unreported, but predicted-low-energy, Ag(111) (2 × 1) and Ag(100) (2√2 × 2√2)R45° surfaces.
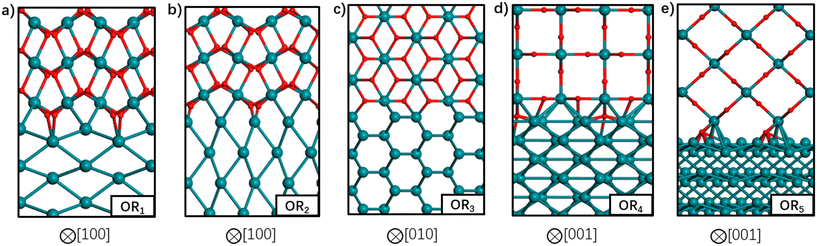 | ||
| Fig. 8 Atomic structures of the five most stable Ru-RuO2 interfaces with different orientation relationships (OR) in order of increasing interfacial energy from (a) to (e). Ru atoms are depicted by the green balls and O atoms by the red balls. The crystallographic direction in RuO2 bulk is indicated below each interface. This figure has been reprinted from ref. 120 with permission from the American Chemical Society, copyright 2021. | ||
Evolutionary strategies have also been utilized to generate candidate training structures. To explore possible TiOx overlay structures on SrTiO3, Wanzenböck et al. combined the covariance matrix adaptation evolution strategy (CMA-ES),133 which iteratively generates new overlay structures by perturbing existing surface atoms based on a normal distribution, and a NN potential.134 The NN was trained on 3000 DFT-computed surface energies for overlayer structures generated by CMA-ES with SrTiO3(110) (4 × 1) as the starting structure. The authors then performed a set of 50 CMA-ES runs using each of SrTiO3(110) (3 × 1), (4 × 1), and (5 × 1) as initial structures and the trained NN potential as the energy calculator. This approach generated stable SrTiO3(110) (3 × 1) overlay structures where TiO4 tetrahedron create six- and eight-membered rings, shown in Fig. 9, that were found to be consistent with STM images.135 Additionally, the SrTiO3(110) (4 × 1) seeded runs predicted six- and ten-membered rings of corner-sharing TiO4 tetrahedron, also observed by STM images.135–137 Finally, the SrTiO3(110) (5 × 1) seeded runs predicted an STM-observed six- and twelve-membered ring structure135 and a previously unobserved higher-energy eight- and ten-membered ring structure.
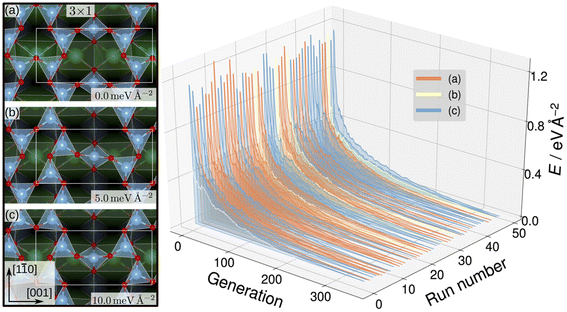 | ||
| Fig. 9 SrTiO3(110) (3 × 1) reconstruction overlayers (left) identified by performing sets of NN-backed CMA-ES runs and further refined by two subsequent optimizations. Structures show corner-sharing TiO4 tetrahedra in six- or eight-membered rings. The calculated energy minimum (a) is set to zero and the relative energies of the other arrangements, (b) and (c), are shown. The energy trajectories of the 50 CMA-ES runs (right) on the SrTiO3(110) (3 × 1) surface, with the calculated energy minimum set to zero. The labels (a), (b), (c) correspond to the overlayers shown on the left. This figure has been reproduced and adapted from ref. 134 with permission from the Royal Society of Chemistry, copyright 2022. | ||
In pursuit of further advancing evolutionary search approaches, Bisbo and Hammer developed the global optimization with first-principles energy expressions (GOFEE) strategy, which generates new candidate structures by perturbing atoms in a subset of structures from an initial population.138 The new candidate structures are relaxed using a GPR model, initially trained on a user-selected set of relevant structures. An acquisition function is used to assess which of the generated structures to select for DFT single-point energy evaluation. After evaluation, the structure is added to the initial training dataset and the process is repeated. In this way, the GPR model is improved while simultaneously exploring the energy landscape. The authors tested their method by reproducing a well-known SnO2(110) (4 × 1) surface reconstruction, observed both experimentally139 with LEED and computationally140 using evolutionary algorithms. Bisbo and Hammer also explored the intercalation of oxygen between graphene grown on Ir(111), an experimentally well-studied process.141–143 The authors find that an oxidized graphene edge lifts slightly from the Ir(111) surface, which may allow for intercalation. In pursuit of further improving the efficiency of GOFEE, Merte et al. modified the strategy to update the training set with subsets of the generated structures instead of a single structure.144 This improved strategy was used to explore the surface structure of Pt3Sn(111) with a (4 × 4) oxygen overlay. In conjunction with STM, LEED, X-ray photoelectron spectroscopy (XPS) and low-energy ion scattering (LEIS) data,145,146 the authors were able to propose and validate a surface composition of Sn11O12 and surface structure with Sn in 3-fold coordination with oxygen.
With the expansion of efficient search algorithms, a compact and flexible framework for training set generation and model production could further accelerate the development of accurate MLIPs. Here, Christiansen et al. developed the atomistic global optimization X (AGOX) package,147 which allows users to build their own dataset-generation pipelines based on flexible modules for performing random-structure search, basin-hopping, evolutionary-structure generation, and GOFEE.138,144 The AGOX package was built to train GPR models as energy calculators. The versatility of the package has been demonstrated by Rønne et al. who trained an Ag GPR model based on the SOAP79 representation by implementing parallel basin-hopping, which generates new structures using a stochastic perturbation of atoms in an initial structure.148 Twelve concurrent basin-hopping searches were performed from starting overlay structures with compositions AgxOy (x = 4, 5, or 6 and y = 2, 3, 4, or 5) on Ag(111). The concurrent searches generated structures that were subsequently fed into a shared database and used to train a single GPR. The model reproduced the stable Ag(111) c(4 × 8) structure.125
Aside from evolutionary and stochastic searches, alternative attempts applied learning strategies from fields such as computer vision for improving surface structure searches. Jørgensen et al. developed an atomistic structure learning algorithm (ASLA) that leverages convolutional neural networks (CNN) and reinforcement learning to construct 2D and planar structures atom-by-atom.149 Within reinforcement learning, a model is required to make decisions based on an expected “reward”, such as maximizing a chosen function. The ASLA is split between three stages: building, evaluation, and training. The building stage involves the placement of atoms by the model one-by-one on a real space grid to generate a structural candidate. The placement is restricted by a minimum distance between atoms and dictated by the CNN, which predicts the expected “reward” received by each atom placement. Within the ASLA framework, the reward is the minimization of the internal energy of a candidate structure, where the true energy is computed by DFT during the evaluation stage. The CNN is then updated based on the root mean square error between the expected energy of the generated structure and the DFT-computed energy. Through this iterative approach, the model learns to “build” structures of minimal energy without prior knowledge of the system of interest, at the potential cost of preforming many DFT calculations. The underlying grid that the structure is built upon can be empty or populated by atoms (e.g., for building overlay structures on a specific facet). The authors demonstrated the capabilities of this approach by building the p(4 × 4) oxygen overlay structure on an underlying Ag(111) surface, which was reproduced from experimental observation by the ASOP framework as discussed previously in this review.125 Meldgaard et al. expanded the ASLA framework to 3D predictions of surface reconstructions by increasing the dimensionality of the CNN.168 The method was verified by reproducing the minimum energy anatase TiO2(001) (1 × 4) reconstruction, as observed by STM imaging.150 Meldgaard then demonstrated the ability to apply transfer learning within the ASLA approach by reproducing the LEED-observed and DFT-predicted SnO2(110) (4 × 1) reconstruction,139 starting from the generation of stable SnO2(110) (1 × 1) reconstructions.
Conclusions and Perspective
Throughout the previous sections, we have reviewed the application of MLIPs for modeling inorganic surfaces. In several places, high-throughput or automated structure generation, model training, and analysis workflows were pivotal (e.g., DP-GEN,87 Amp,91 AutoSurfRecon,98 ASOP,125 AGOX147). Automated and publicly available frameworks have been a key aspect of accelerating the understanding of equilibrium particle morphologies and surface reconstruction mechanisms under different environments. Systematic workflow development has continued to be a focus of the community with examples including a recent semi-autonomous workflow, WhereWulff,151 which takes as input a stable bulk structure and performs the necessary bulk truncation, first-principles calculations, and surface optimization to compute Wulff constructions, generate Pourbaix diagrams, and preform reactivity analysis. Other examples exist for producing physics-based potentials152 performing model finetuning,153,154 and further exploring surface reconstructions155 bringing improved functionality to the fingertips of those working on surface science. In addition to lowering the barrier of entry for newcomers to this field, these (semi-)autonomous frameworks also enable the magnitude of systematic data generation required for efficient model training. These large, systematic datasets make open data repositories paramount for managing and compiling the generated data in a common format to foster more rapid model training and development and avoid duplication of efforts. Several projects including OCP,59,60 Crystalium,156–158 Colabfit,159 and NOMAD160 have begun to fill such roles for subsections of the surface science community. Even with open access to the data required to train MLIPs, exhaustive sampling (particularly in large-scale systems) becomes intractable due to computational costs.54 This motivates a push to further accelerate energy evaluations (e.g., lower the inference time of MLIPs).161 Beyond directly predicting the phase stabilities of inorganic surfaces, MLIPs open up new possibilities to explore complex problems such as materials synthesis prediction (where nanoscale effects may be important),20,162–164 catalyst degradation (which may involve a complex traversal of many surfaces),165 and heterogeneous surface interactions (which involve the direct simulation of inorganic surfaces with gas/liquid environments that are often relevant to catalysis and other applications).166,167 Overall, the continued improvement of MLIPs with more data, better model architectures, improved sampling strategies, and reduced inference times promises to open new possibilities for the computational modeling of inorganic surfaces.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge support from the University of Minnesota in the form of new faculty start-up and a student fellowship from the College of Science & Engineering Data Science Initiative.References
- H.-J. Freund, The Surface Science of Catalysis and More, Using Ultrathin Oxide Films as Templates: A Perspective, J. Am. Chem. Soc., 2016, 138(29), 8985–8996, DOI:10.1021/jacs.6b05565.
- P. R. Schwoebel and I. Brodie, Surface–science Aspects of Vacuum Microelectronics, J. Vac. Sci. Technol., B: Microelectron. Nanometer Struct.–Process., Meas., Phenom., 1995, 13(4), 1391–1410, DOI:10.1116/1.588219.
- L. Liu and A. Corma, Metal Catalysts for Heterogeneous Catalysis: From Single Atoms to Nanoclusters and Nanoparticles, Chem. Rev., 2018, 118(10), 4981–5079, DOI:10.1021/acs.chemrev.7b00776.
- S. M. Woodley and S. T. Bromley, Introduction to Modeling Nanoclusters and Nanoparticles. In: Frontiers of Nanoscience, ed. S. T. Bromley and S. M. Woodley, Computational Modelling of Nanoparticles, Elsevier, 2018, vol. 12, pp 1–54. DOI:10.1016/B978-0-08-102232-0.09991-7.
- W. Sun and G. Ceder, Efficient Creation and Convergence of Surface Slabs, Surf. Sci., 2013, 617, 53–59, DOI:10.1016/j.susc.2013.05.016.
- E. A. Wood, Vocabulary of Surface Crystallography, J. Appl. Phys., 1964, 35(4), 1306–1312, DOI:10.1063/1.1713610.
- D. E. Eastman, Geometrical and Electronic Structure of Si(001) and Si(111) Surfaces: A Status Report, J. Vac. Sci. Technol., 1980, 17(1), 492–500, DOI:10.1116/1.570492.
- G. Binnig, H. Rohrer, C. Gerber and E. Weibel, (7×7) Reconstruction on Si(111) Resolved in Real Space, Phys. Rev. Lett., 1983, 50(2), 120–123, DOI:10.1103/PhysRevLett.50.120.
- K. Reuter and M. Scheffler, Composition, Structure, and Stability of RuO2(110) as a Function of Oxygen Pressure, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 65(3), 035406, DOI:10.1103/PhysRevB.65.035406.
- A. Govender, D. Curulla Ferré and J. W. (Hans) Niemantsverdriet, A Density Functional Theory Study on the Effect of Zero-Point Energy Corrections on the Methanation Profile on Fe(100), ChemPhysChem, 2012, 13(6), 1591–1596, DOI:10.1002/cphc.201100733.
- H. Over, Y. D. Kim, A. P. Seitsonen, S. Wendt, E. Lundgren, M. Schmid, P. Varga, A. Morgante and G. Ertl, Atomic-Scale Structure and Catalytic Reactivity of the RuO(2)(110) Surface, Science, 2000, 287(5457), 1474–1476, DOI:10.1126/science.287.5457.1474.
- Y. D. Kim, H. Over, G. Krabbes and G. Ertl, Identification of RuO2 as the Active Phase in CO Oxidation on Oxygen-Rich Ruthenium Surfaces, Top. Catal., 2000, 14(1), 95–100, DOI:10.1023/A:1009063201555.
- K. Heinz, L. Hammer and S. Müller, The Power of Joint Application of LEED and DFT in Quantitative Surface Structure Determination, J. Phys.: Condens. Matter, 2008, 20(30), 304204, DOI:10.1088/0953-8984/20/30/304204.
- C. J. Bartel, A. W. Weimer, S. Lany, C. B. Musgrave and A. M. Holder, The Role of Decomposition Reactions in Assessing First-Principles Predictions of Solid Stability, npj Comput. Mater., 2019, 5(1), 1–9, DOI:10.1038/s41524-018-0143-2.
- R. P. Stoffel, C. Wessel, M.-W. Lumey and R. Dronskowski, Ab Initio Thermochemistry of Solid-State Materials, Angew. Chem., Int. Ed., 2010, 49(31), 5242–5266, DOI:10.1002/anie.200906780.
- M. Yang, L. B. Pártay and R. B. Wexler, Surface Phase Diagrams from Nested Sampling, arXiv, August 16, 2023,preprint, arXiv:2308.08509 DOI:10.48550/arXiv.2308.08509.
- M. Borg, C. Stampfl, A. Mikkelsen, J. Gustafson, E. Lundgren, M. Scheffler and J. N. Andersen, Density of Configurational States from First-Principles Calculations: The Phase Diagram of Al–Na Surface Alloys, ChemPhysChem, 2005, 6(9), 1923–1928, DOI:10.1002/cphc.200400612.
- Y. Zhou, C. Zhu, M. Scheffler and L. M. Ghiringhelli, Ab Initio Approach for Thermodynamic Surface Phases with Full Consideration of Anharmonic Effects: The Example of Hydrogen at Si(100), Phys. Rev. Lett., 2022, 128(24), 246101, DOI:10.1103/PhysRevLett.128.246101.
- Y. Zhou, M. Scheffler and L. M. Ghiringhelli, Determining Surface Phase Diagrams Including Anharmonic Effects, Phys. Rev. B, 2019, 100(17), 174106, DOI:10.1103/PhysRevB.100.174106.
- W. Sun, D. A. Kitchaev, D. Kramer and G. Ceder, Non-Equilibrium Crystallization Pathways of Manganese Oxides in Aqueous Solution, Nat. Commun., 2019, 10(1), 573, DOI:10.1038/s41467-019-08494-6.
- O. Vinogradova, D. Krishnamurthy, V. Pande and V. Viswanathan, Quantifying Confidence in DFT-Predicted Surface Pourbaix Diagrams of Transition-Metal Electrode–Electrolyte Interfaces, Langmuir, 2018, 34(41), 12259–12269, DOI:10.1021/acs.langmuir.8b02219.
- R. B. Wexler, J. M. P. Martirez and A. M. Rappe, Active Role of Phosphorus in the Hydrogen Evolving Activity of Nickel Phosphide (0001) Surfaces, ACS Catal., 2017, 7(11), 7718–7725, DOI:10.1021/acscatal.7b02761.
- X. Rong and A. M. Kolpak, Ab Initio Approach for Prediction of Oxide Surface Structure, Stoichiometry, and Electrocatalytic Activity in Aqueous Solution, J. Phys. Chem. Lett., 2015, 6(9), 1785–1789, DOI:10.1021/acs.jpclett.5b00509.
- G. Wulff, XXV. Zur Frage der Geschwindigkeit des Wachsthums und der Auflösung der Krystallflächen, Z. Kristallogr. - Cryst. Mater., 1901, 34(1–6), 449–530, DOI:10.1524/zkri.1901.34.1.449.
- C. Herring, Some Theorems on the Free Energies of Crystal Surfaces, Phys. Rev., 1951, 82(1), 87–93, DOI:10.1103/PhysRev.82.87.
- Y. Lee, J. Timmermann, C. Panosetti, C. Scheurer and K. Reuter, Staged Training of Machine-Learning Potentials from Small to Large Surface Unit Cells: Efficient Global Structure Determination of the RuO2(100)-c(2 × 2) Reconstruction and (410) Vicinal, J. Phys. Chem. C, 2023, 127(35), 17599–17608, DOI:10.1021/acs.jpcc.3c04049.
- E. Ringe, R. P. Van Duyne and L. D. Marks, Wulff Construction for Alloy Nanoparticles, Nano Lett., 2011, 11(8), 3399–3403, DOI:10.1021/nl2018146.
- L. D. Marks, Particle Size Effects on Wulff Constructions, Surf. Sci., 1985, 150(2), 358–366, DOI:10.1016/0039-6028(85)90652-1.
- J. C. Hamilton, F. Léonard, E. Johnson and U. Dahmen, Pb Nanoprecipitates in Al: Magic-Shape Effects Due to Elastic Strain, Phys. Rev. Lett., 2007, 98(23), 236102, DOI:10.1103/PhysRevLett.98.236102.
- D. Rosenthal, F. Girgsdies, O. Timpe, R. Blume, G. Weinberg, D. Teschner and R. Schlögl, On the CO-Oxidation over Oxygenated Ruthenium, Z. Phys. Chem., 2009, 223(1–2), 183–208, DOI:10.1524/zpch.2009.6032.
- D. Rosenthal, F. Girgsdies, O. Timpe, G. Weinberg and R. Schlögl, Oscillatory Behavior in the CO-Oxidation over Bulk Ruthenium Dioxide—the Effect of the CO/O2 Ratio, Z. Phys. Chem., 2011, 225(1), 57–68, DOI:10.1524/zpch.2011.5515.
- J. Jirkovský, H. Hoffmannová, M. Klementová and P. Krtil, Particle Size Dependence of the Electrocatalytic Activity of Nanocrystalline RuO2 Electrodes, J. Electrochem. Soc., 2006, 153(6), E111, DOI:10.1149/1.2189953.
- Y. Lee, J. Suntivich, K. J. May, E. E. Perry and Y. Shao-Horn, Synthesis and Activities of Rutile IrO2 and RuO2 Nanoparticles for Oxygen Evolution in Acid and Alkaline Solutions, J. Phys. Chem. Lett., 2012, 3(3), 399–404, DOI:10.1021/jz2016507.
- V. Narkhede, J. Aßmann and M. Muhler, Structure-Activity Correlations for the Oxidation of CO over Polycrystalline RuO2 Powder Derived from Steady-State and Transient Kinetic Experiments, Z. Phys. Chem., 2005, 219(7), 979–995, DOI:10.1524/zpch.219.7.979.67092.
- X.-G. Wang, W. Weiss, S. Shaikhutdinov, M. Ritter, M. Petersen, F. Wagner, R. Schlögl and M. Scheffler, The Hematite (α-Fe2O3) (0001) Surface: Evidence for Domains of Distinct Chemistry, Phys. Rev. Lett., 1998, 81(5), 1038–1041, DOI:10.1103/PhysRevLett.81.1038.
- X.-G. Wang, A. Chaka and M. Scheffler, Effect of the Environment on α−Al2O3 (0001) Surface Structures, Phys. Rev. Lett., 2000, 84(16), 3650–3653, DOI:10.1103/PhysRevLett.84.3650.
- P. Raybaud, M. Digne, R. Iftimie, W. Wellens, P. Euzen and H. Toulhoat, Morphology and Surface Properties of Boehmite (γ-AlOOH): A Density Functional Theory Study, J. Catal., 2001, 201(2), 236–246, DOI:10.1006/jcat.2001.3246.
- P. Havu, V. Blum, V. Havu, P. Rinke and M. Scheffler, Large-Scale Surface Reconstruction Energetics of Pt(100) and Au(100) by All-Electron Density Functional Theory, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82(16), 161418, DOI:10.1103/PhysRevB.82.161418.
- A. M. Kolpak, D. Li, R. Shao, A. M. Rappe and D. A. Bonnell, Evolution of the Structure and Thermodynamic Stability of the BaTiO3(001) Surface, Phys. Rev. Lett., 2008, 101(3), 036102, DOI:10.1103/PhysRevLett.101.036102.
- J. Rogal, K. Reuter and M. Scheffler, CO Oxidation on Pd(100) at Technologically Relevant Pressure Conditions: First-Principles Kinetic Monte Carlo Study, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77(15), 155410, DOI:10.1103/PhysRevB.77.155410.
- H. Perron, C. Domain, J. Roques, R. Drot, E. Simoni and H. Catalette, Optimisation of Accurate Rutile TiO2 (110), (100), (101) and (001) Surface Models from Periodic DFT Calculations, Theor. Chem. Acc., 2007, 117(4), 565–574, DOI:10.1007/s00214-006-0189-y.
- T. Wang, J. Jelic, D. Rosenthal and K. Reuter, Exploring Pretreatment–Morphology Relationships: Ab Initio Wulff Construction for RuO2 Nanoparticles under Oxidising Conditions, ChemCatChem, 2013, 5(11), 3398–3403, DOI:10.1002/cctc.201300168.
- J. Rogal, K. Reuter and M. Scheffler, Thermodynamic Stability of PdO Surfaces, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69(7), 075421, DOI:10.1103/PhysRevB.69.075421.
- A. Böttcher and H. Niehus, Oxygen Adsorbed on Oxidized Ru(0001), Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60(20), 14396–14404, DOI:10.1103/PhysRevB.60.14396.
- H. Madhavaram, H. Idriss, S. Wendt, Y. D. Kim, M. Knapp, H. Over, J. Aßmann, E. Löffler and M. Muhler, Oxidation Reactions over RuO2: A Comparative Study of the Reactivity of the (110) Single Crystal and Polycrystalline Surfaces, J. Catal., 2001, 202(2), 296–307, DOI:10.1006/jcat.2001.3281.
- F. Mittendorfer, N. Seriani, O. Dubay and G. Kresse, Morphology of Mesoscopic Rh and Pd Nanoparticles under Oxidizing Conditions, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76(23), 233413, DOI:10.1103/PhysRevB.76.233413.
- G. Schusteritsch and C. J. Pickard, Predicting Interface Structures: From SrTiO3 to Graphene, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90(3), 035424, DOI:10.1103/PhysRevB.90.035424.
- Q. Zhu, L. Li, A. R. Oganov and P. B. Allen, Evolutionary Method for Predicting Surface Reconstructions with Variable Stoichiometry, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87(19), 195317, DOI:10.1103/PhysRevB.87.195317.
- S. Chiriki, M.-P. V. Christiansen and B. Hammer, Constructing Convex Energy Landscapes for Atomistic Structure Optimization, Phys. Rev. B, 2019, 100(23), 235436, DOI:10.1103/PhysRevB.100.235436.
- R. B. Wexler, T. Qiu and A. M. Rappe, Automatic Prediction of Surface Phase Diagrams Using Ab Initio Grand Canonical Monte Carlo, J. Phys. Chem. C, 2019, 123(4), 2321–2328, DOI:10.1021/acs.jpcc.8b11093.
- J. Timmermann, F. Kraushofer, N. Resch, P. Li, Y. Wang, Z. Mao, M. Riva, Y. Lee, C. Staacke, M. Schmid, C. Scheurer, G. S. Parkinson, U. Diebold and K. Reuter, IrO2 Surface Complexions Identified through Machine Learning and Surface Investigations, Phys. Rev. Lett., 2020, 125(20), 206101, DOI:10.1103/PhysRevLett.125.206101.
- T. Mueller, A. Hernandez and C. Wang, Machine Learning for Interatomic Potential Models, J. Chem. Phys., 2020, 152(5), 050902, DOI:10.1063/1.5126336.
- J. Behler, Perspective: Machine Learning Potentials for Atomistic Simulations, J. Chem. Phys., 2016, 145(17), 170901, DOI:10.1063/1.4966192.
- Y. Zuo, C. Chen, X. Li, Z. Deng, Y. Chen, J. Behler, G. Csányi, A. V. Shapeev, A. P. Thompson, M. A. Wood and S. P. Ong, Performance and Cost Assessment of Machine Learning Interatomic Potentials, J. Phys. Chem. A, 2020, 124(4), 731–745, DOI:10.1021/acs.jpca.9b08723.
- C. Chen and S. P. Ong, A Universal Graph Deep Learning Interatomic Potential for the Periodic Tablev, Nat. Comput. Sci., 2022, 2(11), 718–728, DOI:10.1038/s43588-022-00349-3.
- B. Deng, P. Zhong, K. Jun, J. Riebesell, K. Han, C. J. Bartel and G. Ceder, CHGNet as a Pretrained Universal Neural Network Potential for Charge-Informed Atomistic Modelling, Nat. Mach. Intell., 2023, 5(9), 1031–1041, DOI:10.1038/s42256-023-00716-3.
- A. Merchant, S. Batzner, S. S. Schoenholz, M. Aykol, G. Cheon and E. D. Cubuk, Scaling Deep Learning for Materials Discovery, Nature, 2023, 1–6, DOI:10.1038/s41586-023-06735-9.
- K. Choudhary and B. DeCost, Atomistic Line Graph Neural Network for Improved Materials Property Predictions, npj Comput. Mater., 2021, 7(1), 1–8, DOI:10.1038/s41524-021-00650-1.
- L. Chanussot, A. Das, S. Goyal, T. Lavril, M. Shuaibi, M. Riviere, K. Tran, J. Heras-Domingo, C. Ho, W. Hu, A. Palizhati, A. Sriram, B. Wood, J. Yoon, D. Parikh, C. L. Zitnick and Z. Ulissi, Open Catalyst 2020 (OC20) Dataset and Community Challenges, ACS Catal., 2021, 11(10), 6059–6072, DOI:10.1021/acscatal.0c04525.
- R. Tran, J. Lan, M. Shuaibi, B. M. Wood, S. Goyal, A. Das, J. Heras-Domingo, A. Kolluru, A. Rizvi, N. Shoghi, A. Sriram, F. Therrien, J. Abed, O. Voznyy, E. H. Sargent, Z. Ulissi and C. L. Zitnick, The Open Catalyst 2022 (OC22) Dataset and Challenges for Oxide Electrocatalysts, ACS Catal., 2023, 13(5), 3066–3084, DOI:10.1021/acscatal.2c05426.
- Y.-L. Liao and T. Smidt, Equiformer: Equivariant Graph Attention Transformer for 3D Atomistic Graphs, arXiv, February 27, 2023, arxiv identifier : 2206.11990, DOI:10.48550/arXiv.2206.11990, (accessed 2023-07-20).
- Y.-L. Liao, B. Wood, A. Das and T. Smidt, EquiformerV2: Improved Equivariant Transformer for Scaling to Higher-Degree Representations, arXiv.org, 2023, arxiv identifier : 2306.12059v2, preprint, DOI:10.48550/arXiv.2306.12059.
- J. Gasteiger, F. Becker and S. Günnemann, GemNet: Universal Directional Graph Neural Networks for Molecules, arXiv.org, 2021, arxiv identifier : 2106.08903v9, preprint, DOI:10.48550/arXiv.2106.08903, (accessed 2023-12-05).
- K. T. Schütt, P.-J. Kindermans, H. E. Sauceda, S. Chmiela, A. Tkatchenko and K.-R. Müller, SchNet: A continuous-filter convolutional neural network for modeling quantum interactions, arXiv.org, 2017, arxiv identifier : 1706.08566v5, preprint, DOI:10.48550/arXiv.1706.08566(accessed 2023-12-05).
- J. Gasteiger, J. Groß and S. Günnemann, Directional Message Passing for Molecular Graphs, arXiv.org, 2020, arxiv identifier - 2003.03123v2, preprint, DOI:10.48550/arXiv.2003.03123, (accessed 2023-12-05).
- J. Gasteiger, S. Giri, J. T. Margraf and S. Günnemann, Fast and Uncertainty-Aware Directional Message Passing for Non-Equilibrium Molecules, arXiv.org, 2020, arxiv identifier - 2011.14115v3, preprint, DOI:10.48550/arXiv.2011.14115, (accessed 2023-12-05.
- K. T. Schütt, O. T. Unke and M. Gastegger, Equivariant message passing for the prediction of tensorial properties and molecular spectra, arXiv.org, 2021, arxiv identifier - 2102.03150v4, preprint, DOI:10.48550/arXiv.2102.03150(accessed 2023-12-05).
- A. P. Bartók, M. C. Payne, R. Kondor and G. Csányi, Gaussian Approximation Potentials: The Accuracy of Quantum Mechanics, without the Electrons, Phys. Rev. Lett., 2010, 104(13), 136403, DOI:10.1103/PhysRevLett.104.136403.
- V. L. Deringer, A. P. Bartók, N. Bernstein, D. M. Wilkins, M. Ceriotti and G. Csányi, Gaussian Process Regression for Materials and Molecules, Chem. Rev., 2021, 121(16), 10073–10141, DOI:10.1021/acs.chemrev.1c00022.
- J. Wang, An Intuitive Tutorial to Gaussian Processes Regression, arXiv.org, 2020, arxiv identifier - 2009.10862v4, preprint, DOI:10.48550/arXiv.2009.10862, (accessed 2023-12-05).
- D. Packwood, L. T. H. Nguyen, P. Cesana, G. Zhang, A. Staykov, Y. Fukumoto and D. H. Nguyen, Machine Learning in Materials Chemistry: An Invitation, Mach. Learn. Appl., 2022, 8, 100265, DOI:10.1016/j.mlwa.2022.100265.
- J. Damewood, J. Karaguesian, J. R. Lunger, A. R. Tan, M. Xie, J. Peng and R. Gómez-Bombarelli, Representations of Materials for Machine Learning, Annu. Rev. Mater. Res., 2023, 53(1), 399–426, DOI:10.1146/annurev-matsci-080921-085947.
- A. Wang, R. Kingsbury, M. McDermott, M. Horton, A. Jain, S. P. Ong, S. Dwaraknath and K. A. Persson, A Framework for Quantifying Uncertainty in DFT Energy Corrections, Sci. Rep., 2021, 11(1), 15496, DOI:10.1038/s41598-021-94550-5.
- G. Sivaraman, A. N. Krishnamoorthy, M. Baur, C. Holm, M. Stan, G. Csányi, C. Benmore and Á. Vázquez-Mayagoitia, Machine-Learned Interatomic Potentials by Active Learning: Amorphous and Liquid Hafnium Dioxide, npj Comput. Mater., 2020, 6(1), 1–8, DOI:10.1038/s41524-020-00367-7.
- A. V. Shapeev, Moment Tensor Potentials: A Class of Systematically Improvable Interatomic Potentials, Multiscale Model. Simul., 2016, 14(3), 1153–1173, DOI:10.1137/15M1054183.
- A. P. Thompson, L. P. Swiler, C. R. Trott, S. M. Foiles and G. J. Tucker, Spectral Neighbor Analysis Method for Automated Generation of Quantum-Accurate Interatomic Potentials, J. Comput. Phys., 2015, 285, 316–330, DOI:10.1016/j.jcp.2014.12.018.
- L. Zhang, J. Han, H. Wang, R. Car and E. Weinan, Deep Potential Molecular Dynamics: A Scalable Model with the Accuracy of Quantum Mechanics, Phys. Rev. Lett., 2018, 120(14), 143001, DOI:10.1103/PhysRevLett.120.143001.
- A. Musaelian, S. Batzner, A. Johansson, L. Sun, C. J. Owen, M. Kornbluth and B. Kozinsky, Learning Local Equivariant Representations for Large-Scale Atomistic Dynamics, Nat. Commun., 2023, 14(1), 579, DOI:10.1038/s41467-023-36329-y.
- A. P. Bartók, R. Kondor and G. Csányi, On Representing Chemical Environments, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87(18), 184115, DOI:10.1103/PhysRevB.87.184115.
- D. M. Anstine and O. Isayev, Machine Learning Interatomic Potentials and Long-Range Physics, J. Phys. Chem. A, 2023, 127(11), 2417–2431, DOI:10.1021/acs.jpca.2c06778.
- J. Behler, Four Generations of High-Dimensional Neural Network Potentials, Chem. Rev., 2021, 121(16), 10037–10072, DOI:10.1021/acs.chemrev.0c00868.
- J. Behler, Constructing High-Dimensional Neural Network Potentials: A Tutorial Review, Int. J. Quantum Chem., 2015, 115(16), 1032–1050, DOI:10.1002/qua.24890.
- F. Noé, A. Tkatchenko, K.-R. Müller and C. Clementi, Machine Learning for Molecular Simulation, Annu. Rev. Phys. Chem., 2020, 71(1), 361–390, DOI:10.1146/annurev-physchem-042018-052331.
- Y. Mishin, Machine-Learning Interatomic Potentials for Materials Science, Acta Mater., 2021, 214, 116980, DOI:10.1016/j.actamat.2021.116980.
- V. L. Deringer, M. A. Caro and G. Csányi, Machine Learning Interatomic Potentials as Emerging Tools for Materials Science, Adv. Mater., 2019, 31(46), 1902765, DOI:10.1002/adma.201902765.
- J. Timmermann, Y. Lee, C. G. Staacke, J. T. Margraf, C. Scheurer and K. Reuter, Data-Efficient Iterative Training of Gaussian Approximation Potentials: Application to Surface Structure Determination of Rutile IrO2 and RuO2, J. Chem. Phys., 2021, 155(24), 244107, DOI:10.1063/5.0071249.
- Y. Zhang, H. Wang, W. Chen, J. Zeng, L. Zhang, H. Wang and E. Weinan, DP-GEN: A Concurrent Learning Platform for the Generation of Reliable Deep Learning Based Potential Energy Models, Comput. Phys. Commun., 2020, 253, 107206, DOI:10.1016/j.cpc.2020.107206.
- S. Batzner, A. Musaelian, L. Sun, M. Geiger, J. P. Mailoa, M. Kornbluth, N. Molinari, T. E. Smidt and B. Kozinsky, E(3)-Equivariant Graph Neural Networks for Data-Efficient and Accurate Interatomic Potentials, Nat. Commun., 2022, 13(1), 2453, DOI:10.1038/s41467-022-29939-5.
- M. K. Phuthi, A. M. Yao, S. Batzner, A. Musaelian, B. Kozinsky, E. D. Cubuk and V. Viswanathan, Accurate Surface and Finite Temperature Bulk Properties of Lithium Metal at Large Scales Using Machine Learning, Interaction Potentials, arXiv, 2023, preprint arxiv:2305.06925, DOI:10.48550/arXiv.2305.06925.
- Y.-M. Kim, I.-H. Jung and B.-J. Lee, Atomistic Modeling of Pure Li and Mg–Li System, Model. Simul. Mater. Sci. Eng., 2012, 20(3), 035005, DOI:10.1088/0965-0393/20/3/035005.
- A. Khorshidi and A. A. Peterson, Amp: A Modular Approach to Machine Learning in Atomistic Simulations, Comput. Phys. Commun., 2016, 207, 310–324, DOI:10.1016/j.cpc.2016.05.010.
- T. Gao and J. R. Kitchin, Modeling Palladium Surfaces with Density Functional Theory, Neural Networks and Molecular Dynamics, Catal. Today, 2018, 312, 132–140, DOI:10.1016/j.cattod.2018.03.045.
- A. Shrestha, X. Gao, J. C. Hicks and C. Paolucci, Nanoparticle Size Effects on Phase Stability for Molybdenum and Tungsten Carbides, Chem. Mater., 2021, 33(12), 4606–4620, DOI:10.1021/acs.chemmater.1c01120.
- J. P. Hare, W. K. Hsu, H. W. Kroto, A. Lappas, K. Prassides, M. Terrones and D. R. M. Walton, Nanoscale Encapsulation of Molybdenum Carbide in Carbon Clusters, Chem. Mater., 1996, 8(1), 6–8, DOI:10.1021/cm950339y.
- G. He, Z. Yan, X. Ma, H. Meng, P. K. Shen and C. Wang, A Universal Method to Synthesize Nanoscale Carbides as Electrocatalyst Supports towards Oxygen Reduction Reaction, Nanoscale, 2011, 3(9), 3578–3582, 10.1039/C1NR10436E.
- X. Zhang, L. Huang, Y. Han, M. Xu and S. Dong, Nitrogen-Doped Carbon Encapsulating γ-MoC/Ni Heterostructures for Efficient Oxygen Evolution Electrocatalysts, Nanoscale, 2017, 9(17), 5583–5588, 10.1039/C7NR01027C.
- A. Palizhati, W. Zhong, K. Tran, S. Back and Z. W. Ulissi, Toward Predicting Intermetallics Surface Properties with High-Throughput DFT and Convolutional Neural Networks, J. Chem. Inf. Model., 2019, 59(11), 4742–4749, DOI:10.1021/acs.jcim.9b00550.
- X. Du, J. K. Damewood, J. R. Lunger, R. Millan, B. Yildiz, L. Li and R. Gómez-Bombarelli, Machine-Learning-Accelerated Simulations to Enable Automatic Surface Reconstruction, Nat. Comput. Sci., 2023, 1–11, DOI:10.1038/s43588-023-00571-7.
- A. Hirata, K. Saiki, A. Koma and A. Ando, Electronic Structure of a SrO-Terminated SrTiO3(100) Surface, Surf. Sci., 1994, 319(3), 267–271, DOI:10.1016/0039-6028(94)90593-2.
- M. R. Castell, Scanning Tunneling Microscopy of Reconstructions on the SrTiO3(001) Surface, Surf. Sci., 2002, 505, 1–13, DOI:10.1016/S0039-6028(02)01393-6.
- N. Erdman, K. R. Poeppelmeier, M. Asta, O. Warschkow, D. E. Ellis and L. D. Marks, The Structure and Chemistry of the TiO2-Rich Surface of SrTiO3 (001), Nature, 2002, 419(6902), 55–58, DOI:10.1038/nature01010.
- R. Herger, P. R. Willmott, O. Bunk, C. M. Schlepütz, B. D. Patterson and B. Delley, Surface of Strontium Titanate, Phys. Rev. Lett., 2007, 98(7), 076102, DOI:10.1103/PhysRevLett.98.076102.
- C. Hong, W. Zou, P. Ran, K. Tanaka, M. Matzelle, W.-C. Chiu, R. S. Markiewicz, B. Barbiellini, C. Zheng, S. Li, A. Bansil and R.-H. He, Anomalous Intense Coherent Secondary Photoemission from a Perovskite Oxide, Nature, 2023, 617(7961), 493–498, DOI:10.1038/s41586-023-05900-4.
- K. Szot and W. Speier, Surfaces of Reduced and Oxidized SrTiO3 from Atomic Force Microscopy, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60(8), 5909–5926, DOI:10.1103/PhysRevB.60.5909.
- T. Kubo and H. Nozoye, Surface Structure of SrTiO3(100), Surf. Sci., 2003, 542(3), 177–191, DOI:10.1016/S0039-6028(03)00998-1.
- E. Heifets, S. Piskunov, E. A. Kotomin, Y. F. Zhukovskii and D. E. Ellis, Electronic Structure and Thermodynamic Stability of Double-Layered SrTiO3(001) Surfaces: Ab Initio Simulations, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75(11), 115417, DOI:10.1103/PhysRevB.75.115417.
- J. Xu, W. Xie, Y. Han and P. Hu, Atomistic Insights into the Oxidation of Flat and Stepped Platinum Surfaces Using Large-Scale Machine Learning Potential-Based Grand-Canonical Monte Carlo, ACS Catal., 2022, 12(24), 14812–14824, DOI:10.1021/acscatal.2c03976.
- Y. Zhang, C. Hu and B. Jiang, Embedded Atom Neural Network Potentials: Efficient and Accurate Machine Learning with a Physically Inspired Representation, J. Phys. Chem. Lett., 2019, 10(17), 4962–4967, DOI:10.1021/acs.jpclett.9b02037.
- Y. Zhang, J. Xia and B. Jiang, REANN: A PyTorch-Based End-to-End Multi-Functional Deep Neural Network Package for Molecular, Reactive, and Periodic Systems, J. Chem. Phys., 2022, 156(11), 114801, DOI:10.1063/5.0080766.
- X. Du, J. K. Damewood, J. R. Lunger, R. Millan, B. Yildiz, L. Li and R. Gómez-Bombarelli, Machine-Learning-Accelerated Simulations Enable Heuristic-Free Surface Reconstruction, arXiv, May 12 2023, preprint, arxiv:2305.07251 DOI:10.48550/arXiv.2305.07251.
- J. Behler and M. Parrinello, Generalized Neural-Network Representation of High-Dimensional Potential-Energy Surfaces, Phys. Rev. Lett., 2007, 98(14), 146401, DOI:10.1103/PhysRevLett.98.146401.
- J. R. Boes and J. R. Kitchin, Neural Network Predictions of Oxygen Interactions on a Dynamic Pd Surface, Mol. Simul., 2017, 43(5–6), 346–354, DOI:10.1080/08927022.2016.1274984.
- M. K. Rose, A. Borg, J. C. Dunphy, T. Mitsui, D. F. Ogletree and M. Salmeron, Chemisorption of Atomic Oxygen on Pd(111) Studied by STM, Surf. Sci., 2004, 561(1), 69–78, DOI:10.1016/j.susc.2004.04.037.
- A. Markovits and C. Minot, On the Move of Strongly Chemisorbed Species on Metals: The Example of O Diffusion on Pd(111) Surface, Chem. Phys. Lett., 2008, 458(1), 92–95, DOI:10.1016/j.cplett.2008.04.100.
- K. Honkala and K. Laasonen, Ab Initio Study of O2 Precursor States on the Pd(111) Surface, J. Chem. Phys., 2001, 115(5), 2297–2302, DOI:10.1063/1.1384009.
- Y. Yang, Z. Guo, A. J. Gellman and J. R. Kitchin, Simulating Segregation in a Ternary Cu–Pd–Au Alloy with Density Functional Theory, Machine Learning, and Monte Carlo Simulations, J. Phys. Chem. C, 2022, 126(4), 1800–1808, DOI:10.1021/acs.jpcc.1c09647.
- P. Tanner, Ordering and Segregation in the PdAuCu System: Bulk vs. Surface. 2019 Search PubMed.
- G. Ashton, N. Bernstein, J. Buchner, X. Chen, G. Csányi, A. Fowlie, F. Feroz, M. Griffiths, W. Handley, M. Habeck, E. Higson, M. Hobson, A. Lasenby, D. Parkinson, L. B. Pártay, M. Pitkin, D. Schneider, J. S. Speagle, L. South, J. Veitch, P. Wacker, D. J. Wales and D. Yallup, Nested Sampling for Physical Scientists, Nat. Rev. Methods Primers, 2022, 2(1), 39, DOI:10.1038/s43586-022-00121-x.
- L. B. Pártay, G. Csányi and N. Bernstein, Nested Sampling for Materials, Eur. Phys. J. B, 2021, 94(8), 159, DOI:10.1140/epjb/s10051-021-00172-1.
- Z.-Y. Zhu, Y.-F. Li, C. Shang and Z.-P. Liu, Thermodynamics and Catalytic Activity of Ruthenium Oxides Grown on Ruthenium Metal from a Machine Learning Atomic Simulation, J. Phys. Chem. C, 2021, 125(31), 17088–17096, DOI:10.1021/acs.jpcc.1c04858.
- C. Shang and Z.-P. Liu, Stochastic Surface Walking Method for Structure Prediction and Pathway Searching, J. Chem. Theory Comput., 2013, 9(3), 1838–1845, DOI:10.1021/ct301010b.
- N. Metropolis, A. W. Rosenbluth, M. N. Rosenbluth, A. H. Teller and E. Teller, Equation of State Calculations by Fast Computing Machines, J. Chem. Phys., 2004, 21(6), 1087–1092, DOI:10.1063/1.1699114.
- E. C. Bain and N. Y. Dunkirk, The Nature of Martensite, Trans. AIME, 1924, 70, 25–46 Search PubMed.
- H. Over, Surface Chemistry of Ruthenium Dioxide in Heterogeneous Catalysis and Electrocatalysis: From Fundamental to Applied Research, Chem. Rev., 2012, 112(6), 3356–3426, DOI:10.1021/cr200247n.
- D. Chen, C. Shang and Z.-P. Liu, Automated Search for Optimal Surface Phases (ASOPs) in Grand Canonical Ensemble Powered by Machine Learning, J. Chem. Phys., 2022, 156(9), 094104, DOI:10.1063/5.0084545.
- J. Schnadt, J. Knudsen, X. L. Hu, A. Michaelides, R. T. Vang, K. Reuter, Z. Li, E. Lægsgaard, M. Scheffler and F. Besenbacher, Experimental and Theoretical Study of Oxygen Adsorption Structures on Ag(111), Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80(7), 075424, DOI:10.1103/PhysRevB.80.075424.
- J. Schnadt, A. Michaelides, J. Knudsen, R. T. Vang, K. Reuter, E. Lægsgaard, M. Scheffler and F. Besenbacher, Revisiting the Structure of the p(4×4) Surface Oxide on Ag(111), Phys. Rev. Lett., 2006, 96(14), 146101, DOI:10.1103/PhysRevLett.96.146101.
- G. Rovida, F. Pratesi, M. Maglietta and E. Ferroni, Chemisorption of Oxygen on the Silver (111) Surface, Surf. Sci., 1974, 43(1), 230–256, DOI:10.1016/0039-6028(74)90229-5.
- M. Schmid, A. Reicho, A. Stierle, I. Costina, J. Klikovits, P. Kostelnik, O. Dubay, G. Kresse, J. Gustafson, E. Lundgren, J. N. Andersen, H. Dosch and P. Varga, Structure of Ag(111)-p(4×4)-O: No Silver Oxide, Phys. Rev. Lett., 2006, 96(14), 146102, DOI:10.1103/PhysRevLett.96.146102.
- A. Stierle, I. Costina, S. Kumaragurubaran and H. Dosch, In Situ X-Ray Diffraction Study of Ag(100) at Ambient Oxygen Pressures, J. Phys. Chem. C, 2007, 111(29), 10998–11002, DOI:10.1021/jp0715631.
- M. Rocca, L. Savio, L. Vattuone, U. Burghaus, V. Palomba, N. Novelli, F. Buatier de Mongeot, U. Valbusa, R. Gunnella, G. Comelli, A. Baraldi, S. Lizzit and G. Paolucci, Phase Transition of Dissociatively Adsorbed Oxygen on Ag(001), Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61(1), 213–227, DOI:10.1103/PhysRevB.61.213.
- I. Costina, M. Schmid, H. Schiechl, M. Gajdoš, A. Stierle, S. Kumaragurubaran, J. Hafner, H. Dosch and P. Varga, Combined STM, LEED and DFT Study of Ag(100) Exposed to Oxygen near Atmospheric Pressures, Surf. Sci., 2006, 600(3), 617–624, DOI:10.1016/j.susc.2005.11.020.
- N. Hansen and A. Ostermeier, Completely Derandomized Self-Adaptation in Evolution Strategies, Evol. Comput., 2001, 9(2), 159–195, DOI:10.1162/106365601750190398.
- R. Wanzenböck, M. Arrigoni, S. Bichelmaier, F. Buchner, J. Carrete and G. K. H. Madsen, Neural-Network-Backed Evolutionary Search for SrTiO3(110) Surface Reconstructions, Digital Discovery, 2022, 1(5), 703–710, 10.1039/D2DD00072E.
- J. A. Enterkin, A. K. Subramanian, B. C. Russell, M. R. Castell, K. R. Poeppelmeier and L. D. Marks, A Homologous Series of Structures on the Surface of SrTiO3(110), Nat. Mater., 2010, 9(3), 245–248, DOI:10.1038/nmat2636.
- Z. Wang, X. Hao, S. Gerhold, M. Schmid, C. Franchini and U. Diebold, Vacancy Clusters at Domain Boundaries and Band Bending at the SrTiO3(110) Surface, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90(3), 035436, DOI:10.1103/PhysRevB.90.035436.
- M. Riva, M. Kubicek, X. Hao, G. Franceschi, S. Gerhold, M. Schmid, H. Hutter, J. Fleig, C. Franchini, B. Yildiz and U. Diebold, Influence of Surface Atomic Structure Demonstrated on Oxygen Incorporation Mechanism at a Model Perovskite Oxide, Nat. Commun., 2018, 9(1), 3710, DOI:10.1038/s41467-018-05685-5.
- M. K. Bisbo and B. Hammer, Efficient Global Structure Optimization with a Machine-Learned Surrogate Model, Phys. Rev. Lett., 2020, 124(8), 086102, DOI:10.1103/PhysRevLett.124.086102.
- L. R. Merte, M. S. Jørgensen, K. Pussi, J. Gustafson, M. Shipilin, A. Schaefer, C. Zhang, J. Rawle, C. Nicklin, G. Thornton, R. Lindsay, B. Hammer and E. Lundgren, Structure of the SnO2(110)-(4×1) Surface, Phys. Rev. Lett., 2017, 119(9), 096102, DOI:10.1103/PhysRevLett.119.096102.
- L. B. Vilhelmsen and B. Hammer, A Genetic Algorithm for First Principles Global Structure Optimization of Supported Nano Structures, J. Chem. Phys., 2014, 141(4), 044711, DOI:10.1063/1.4886337.
- E. Grånäs, J. Knudsen, U. A. Schröder, T. Gerber, C. Busse, M. A. Arman, K. Schulte, J. N. Andersen and T. Michely, Oxygen Intercalation under Graphene on Ir(111): Energetics, Kinetics, and the Role of Graphene Edges, ACS Nano, 2012, 6(11), 9951–9963, DOI:10.1021/nn303548z.
- R. Larciprete, S. Ulstrup, P. Lacovig, M. Dalmiglio, M. Bianchi, F. Mazzola, L. Hornekær, F. Orlando, A. Baraldi, P. Hofmann and S. Lizzit, Oxygen Switching of the Epitaxial Graphene–Metal Interaction, ACS Nano, 2012, 6(11), 9551–9558, DOI:10.1021/nn302729j.
- A. J. Martínez-Galera, U. A. Schröder, F. Huttmann, W. Jolie, F. Craes, C. Busse, V. Caciuc, N. Atodiresei, S. Blügel and T. Michely, Oxygen Orders Differently under Graphene: New Superstructures on Ir(111), Nanoscale, 2016, 8(4), 1932–1943, 10.1039/C5NR04976H.
- L. R. Merte, M. K. Bisbo, I. Sokolović, M. Setvín, B. Hagman, M. Shipilin, M. Schmid, U. Diebold, E. Lundgren and B. Hammer, Structure of an Ultrathin Oxide on Pt3Sn(111) Solved by Machine Learning Enhanced Global Optimization, Angew. Chem., Int. Ed., 2022, 61(25) DOI:10.1002/anie.202204244.
- A. Atrei, U. Bardi, G. Rovida, M. Torrini, M. Hoheisel and S. Speller, Test of Structural Models for the (4×4) Phase Formed by Oxygen Adsorption on the Pt3Sn(111) Surface, Surf. Sci., 2003, 526(1), 193–200, DOI:10.1016/S0039-6028(02)02650-X.
- M. Hoheisel, S. Speller, W. Heiland, A. Atrei, U. Bardi and G. Rovida, Adsorption of Oxygen on Pt3Sn(111) Studied by Scanning Tunneling Microscopy and x-Ray Photoelectron Diffraction, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66(16), 165416, DOI:10.1103/PhysRevB.66.165416.
- M.-P. V. Christiansen, N. Rønne and B. Hammer, Atomistic Global Optimization X: A Python Package for Optimization of Atomistic Structures, J. Chem. Phys., 2022, 157(5), 054701, DOI:10.1063/5.0094165.
- N. Rønne, M.-P. V. Christiansen, A. M. Slavensky, Z. Tang, F. Brix, M. E. Pedersen, M. K. Bisbo and B. Hammer, Atomistic Structure Search Using Local Surrogate Model, J. Chem. Phys., 2022, 157(17), 174115, DOI:10.1063/5.0121748.
- M. S. Jørgensen, H. L. Mortensen, S. A. Meldgaard, E. L. Kolsbjerg, T. L. Jacobsen, K. H. Sørensen and B. Hammer, Atomistic Structure Learning, J. Chem. Phys., 2019, 151(5), 054111, DOI:10.1063/1.5108871.
- M. Lazzeri and A. Selloni, Stress-Driven Reconstruction of an Oxide Surface: The Anatase TiO2(001) (1×4) Surface, Phys. Rev. Lett., 2001, 87(26), 266105, DOI:10.1103/PhysRevLett.87.266105.
- R. Y. Sanspeur, J. Heras-Domingo, J. R. Kitchin and Z. Ulissi, WhereWulff: A Semiautonomous Workflow for Systematic Catalyst Surface Reactivity under Reaction Conditions, J. Chem. Inf. Model., 2023, 63(8), 2427–2437, DOI:10.1021/acs.jcim.3c00142.
- M. Wen, Y. Afshar, R. S. Elliott and E. B. Tadmor, KLIFF: A Framework to Develop Physics-Based and Machine Learning Interatomic Potentials, Comput. Phys. Commun., 2022, 272, 108218, DOI:10.1016/j.cpc.2021.108218.
- J. Musielewicz, X. Wang, T. Tian and Z. Ulissi, FINETUNA: Fine-Tuning Accelerated Molecular Simulations, Mach. Learn.: Sci. Technol., 2022, 3(3), 03LT01, DOI:10.1088/2632-2153/ac8fe0.
- Y. Liu, S. Agarwal and S. Venkataraman, AutoFreeze: Automatically Freezing Model Blocks to Accelerate Fine-Tuning, arXiv, April 3 2021, identifier - 2102.01386, preprint, arxiv: 2102.01386 DOI:10.48550/arXiv.2102.01386 (accessed 2023-08-09).
- Y. Han, J. Wang, C. Ding, H. Gao, S. Pan, Q. Jia and J. Sun, Prediction of Surface Reconstructions Using MAGUS, J. Chem. Phys., 2023, 158(17), 174109, DOI:10.1063/5.0142281.
- R. Tran, X.-G. Li, J. H. Montoya, D. Winston, K. A. Persson and S. P. Ong, Anisotropic Work Function of Elemental Crystals, Surf. Sci., 2019, 687, 48–55, DOI:10.1016/j.susc.2019.05.002.
- R. Tran, Z. Xu, B. Radhakrishnan, D. Winston, W. Sun, K. A. Persson and S. P. Ong, Surface Energies of Elemental Crystals, Sci. Data, 2016, 3, 160080, DOI:10.1038/sdata.2016.80.
- H. Zheng, X.-G. Li, R. Tran, C. Chen, M. Horton, D. Winston, K. A. Persson and S. P. Ong, Grain Boundary Properties of Elemental Metals, arXiv, July 20 2019, arxiv:1907.08905 DOI:10.48550/arXiv.1907.08905.
- J. A. Vita, E. G. Fuemmeler, A. Gupta, G. P. Wolfe, A. Q. Tao, R. S. Elliott, S. Martiniani and E. B. Tadmor, ColabFit Exchange: Open-Access Datasets for Data-Driven Interatomic Potentials, J. Chem. Phys., 2023, 159(15), 154802, DOI:10.1063/5.0163882.
- M. Scheidgen, L. Himanen, A. N. Ladines, D. Sikter, M. Nakhaee, Á. Fekete, T. Chang, A. Golparvar, J. A. Márquez, S. Brockhauser, S. Brückner, L. M. Ghiringhelli, F. Dietrich, D. Lehmberg, T. Denell, A. Albino, H. Näsström, S. Shabih, F. Dobener, M. Kühbach, R. Mozumder, J. F. Rudzinski, N. Daelman, J. M. Pizarro, M. Kuban, C. Salazar, P. Ondračka, H.-J. Bungartz and C. Draxl, NOMAD: A Distributed Web-Based Platform for Managing Materials Science Research Data, J. Open Source Softw., 2023, 8(90), 5388, DOI:10.21105/joss.05388.
- S. R. Xie, M. Rupp and R. G. Hennig, Ultra-Fast Interpretable Machine-Learning Potentials, npj Comput. Mater., 2023, 9(1), 1–9, DOI:10.1038/s41524-023-01092-7.
- Y. Zeng, N. J. Szymanski, T. He, K. Jun, L. C. Gallington, H. Huo, C. J. Bartel, B. Ouyang and G. Ceder, Selective Formation of Metastable Polymorphs in Solid-State Synthesis, arXiv, September 11 2023, preprint, arxiv:2309.05800 DOI:10.48550/arXiv.2309.05800.
- E. Gerber, S. B. Torrisi, S. Shabani, E. Seewald, J. Pack, J. E. Hoffman, C. R. Dean, A. N. Pasupathy and E.-A. Kim, High-Throughput Ab Initio Design of Atomic Interfaces Using InterMatch, Nat. Commun., 2023, 14(1), 7921, DOI:10.1038/s41467-023-43496-5.
- H. Ding, S. S. Dwaraknath, L. Garten, P. Ndione, D. Ginley and K. A. Persson, Computational Approach for Epitaxial Polymorph Stabilization through Substrate Selection, ACS Appl. Mater. Interfaces, 2016, 8(20), 13086–13093, DOI:10.1021/acsami.6b01630.
- S. L. Scott, A Matter of Life(Time) and Death, ACS Catal., 2018, 8(9), 8597–8599, DOI:10.1021/acscatal.8b03199.
- H. Li, Y. Jiao, K. Davey and S.-Z. Qiao, Data-Driven Machine Learning for Understanding Surface Structures of Heterogeneous Catalysts, Angew. Chem., Int. Ed., 2023, 62(9), e202216383, DOI:10.1002/anie.202216383.
- B. B. Laird, R. L. Davidchack, Y. Yang and M. Asta, Determination of the Solid-Liquid Interfacial Free Energy along a Coexistence Line by Gibbs–Cahn Integration, J. Chem. Phys., 2009, 131(11), 114110, DOI:10.1063/1.3231693.
- S. A. Meldgaard, H. L. Mortensen, M. S. Jørgensen and B. Hammer, Structure prediction of surface reconstructions by deep reinforcement learning, J. Phys.: Condens. Matter, 2020, 32, 404005, DOI:10.1088/1361-648X/ab94f2.
| This journal is © The Royal Society of Chemistry 2024 |