Variation of topological surface states of nodal line semimetal MgB2 resulting from adsorption of hydrogen, hydroxide, and water molecules†
Received
11th June 2024
, Accepted 2nd September 2024
First published on 9th September 2024
Abstract
Topological semimetals have garnered significant interest due to their intrinsic topological physics and potential applications in devices. A crucial feature shared by all topological materials is the bulk-boundary correspondence, indicating the presence of unique topologically protected conducting states at the edges when non-trivial band topology exists in the bulk. Previous studies on surface states of topological materials predominantly focused on pristine surfaces, leaving the exploration of surface states in topological semimetals with adsorbates relatively uncharted. This work, based on ab initio calculations, examines variations in the topological surface states of MgB2, a well-known conventional superconductor and topological nodal line semimetal. We employ a thick slab model with Mg/B atoms as surface terminations to simulate its topological surface states. Subsequently, we investigate the adsorption of hydrogen (H), hydroxide (OH), and water (H2O) on the surface slabs to observe changes in the surface states. The pristine slab model gives the drumhead-like surface states inside the surface projected nodal lines, while the topological surface states change differently after adsorbing H, OH, and H2O, which can be understood systematically by combining the surface adsorption Gibbs free energy ΔG, surface terminations, and surface charge density distributions. Especially, our findings suggest that the Bader charge transfer value of surface atoms providing topological states is a key indicator for evaluating the variation in topological surface states after adsorption. This study provides a systematic understanding of the topological surface states of MgB2 with different adsorbates, paving the way for future theoretical and experimental investigations in related fields and shedding light on the potential device applications of topological materials.
Introduction
Topological materials, including topological insulators (TIs),1 topological superconductors (TSCs),2,3 and topological semimetals (TSMs)4 have been attracting significant research interest in recent years. The study of topological materials starts from the gapped TIs and TSCs, and then extends to gapless TSMs that hold topologically non-trivial band crossing points around the Fermi level (EF). The TSMs can be roughly classified into Weyl semimetals (WSMs)5–7 holding pairs of two-fold degenerate Weyl points with opposite chirality, Dirac semimetals (DSMs)8–10 with four-fold degenerate Dirac points, and nodal line semimetals (NLSMs) with continuous line of nodes11–23 inside the first Brillouin zone (BZ). A fascinating property shared by all topological materials is the so-called bulk-boundary correspondence,1,2 which means if there is non-trivial band topology in the bulk, we can expect topologically protected conducting states on the edge, such as the Dirac cone surface states for TIs,1 Majorana zero modes (MZMs) for TSCs,2 surface Fermi arc/loops for WSMs/DSMs,5,6,10 and drumhead-like surface states inside/outside the projected nodal lines for NLSMs.14,15 Generally, the topological surface states (TSSs) are topologically protected and robust against perturbations or disorders that do not change the protected symmetries.
Besides the comprehensive theoretical and materials studies, the applications of topological materials still need to be improved. In recent years, there has been a growing interest in investigating the potential use of topological materials for energy conversion and storage,24 closely related to surface adsorption in electrochemical processes. The earliest ab initio calculations on the catalytic properties of topological materials began with the topological insulator bismuth selenide (Bi2Se3) covered with a monolayer of golden (Au) atoms.25 The concept of “electron baths” was introduced in that work, which suggested that Bi2Se3 could not only modulate the adsorption energy of adsorbates, but also endow impart catalytically enhanced performances to the surface of Au atoms by endowing the Dirac cone bands of the topological surface states. Bi2Se3-covered monolayer ZnSe exhibited excellent catalytic performance for hydrogen evolution reaction (HER) on the surface.26 Research by Freitas et al. opens up a novel hydrogenated band gap of XBi (X = B, Al, Ga and In) monolayers, showing interesting electronic behavior in room-temperature applications of these two-dimensional materials.27 Moreover, Freitas et al. investigated the structural, electronic and topological insulation properties of XBi (X = B, Al, Ga and In) monolayers after halogenation. They lead to chemical tunability, produce apparent band inversion symmetry, and exhibit Rashba-type spin splitting in the valence bands of these systems.28
However, the low conductivity of the bulk phases in topological insulators can harm the catalytic kinetics. Given this, researchers have increasingly focused on topological semimetals because of their high chemical stability and relatively elevated conductivity. A series of WSMs (NbP, TaP, NbAs, TaAs, NiSi) were found to be good HER catalysts, and provided both theoretical and experimental evidence that the catalytic enhancement arises from the nontrivial Fermi arc surface states.29,30 In addition, the magnetic WSM Co3Sn2S2 was found to have high oxygen evolution reaction (OER) properties and it was concluded that the surface of bulk Co3Sn2S2 is more favorable for OH adsorption due to the presence of topological surface states.31 For the study of NLSMs, Li et al. first proposed that the TiSi family, which have the stable topologically non-trivial drumhead-like surface states, could serve as a platform for HER catalysis.32 In 2023, Zhang et al. investigated the HER performance of topological nodal net semimetals by using metal diboride MB2 (M = Ti, Sc, V, Zr, Hf, Nb, Ta, and Y).33 They found that the Gibbs free energy of hydrogen adsorption exhibited an excellent linear relationship with the density of states associated with the topological surface bands. For the applications of topological materials in an aqueous environment, exploring the effect of H, OH, and H2O adsorption on the surfaces of topological materials is necessary. However, previous studies on the surface states of NLSMs mainly focus on the pristine surface case or HER catalytic performance, while a systematical understanding of the variations of topological surface states after adsorbing different substances is still lacking. Generally, for NLSMs, the topological surface states have a strong dependence on the configurations of the surface terminations, and the drumhead-like surface states can be inside/outside the nodal lines when the surface terminations show a zigzag/beard type.18,20,34 In this work, we perform a systematical ab initio study on the variations of the topological surface states of MgB2, which is a well-known conventional superconductor with a high critical temperature Tc up to 39 K,35,36 and also a nodal line semimetal with straight band crossing lines on the edge of the first BZ.37,38 We build a thick slab model to simulate the topological surface states of MgB2. For the pristine MgB2 slab, the slab model gives a drumhead-like topological surface state inside the nodal lines, consistent with ref. 35. Then we add hydrogen (H), hydroxide (OH), and water (H2O) onto the slab models to see the variations of the surface states, and the surface states change differently with different surface adsorbates, which can be understood systematically by combining the surface adsorption free energy ΔG, the surface terminations, and the surface charge density distributions. Our work has provided a systematical understanding of the topological surface states of MgB2 with different surface adsorptions, which will also guide future theoretical studies and device applications of topological materials.
Computational method
We perform the ab initio calculations employing the Vienna Ab initio Simulation Package (VASP).39 The generalized gradient approximation (GGA) developed by Perdew, Burke, and Ernzerhof (PBE)40 is used as the exchange–correlation potential. The all-electron projector augmented wave (PAW)41 method is used and we set a plane-wave basis set with an energy cutoff of 500 eV. The BZ is sampled with an 8 × 8 × 10 Monkhorst–Pack k-point grid for the bulk system, and a 12 × 12 × 1 k-point grid for the slab systems. The vacuum layer of the slab system is set to 30 Å. The geometries are optimized with symmetry constraints until the remaining atomic forces are less than 10−5 eV Å−1 for the bulk system and 10−3 eV Å−1 for the slab system. The energy convergence criterion is set to be 10−6 eV for the bulk system, and 10−5 eV for the slab system. For the further exploration of the topological electronic properties of MgB2, we have built a tight-binding (TB) model using the maximally localized Wannier functions implemented in the Wannier90 package42,43 based on the s and p orbitals of Mg and B atoms, and searched all the nodal points and calculated the Berry phases with WannierTools package.44
Results and discussion
We firstly present the crystalline structure of MgB2. Fig. 1(a) shows the unit cell of MgB2. MgB2 has a hexagonal unit cell with one Mg atom and two B atoms in P6/mmm symmetry (D16h, space group No. 191). The optimized lattice parameters are a = b = 3.079 Å, and c = 3.505 Å, which are very close to the experimental values a = b = 3.083 Å, and c = 3.521 Å.45 The Mg atom occupies the 1a (0,0,0) Wyckoff position, while the B atoms occupy the 2d (2/3,1/3,1/2) Wyckoff positions. Fig. 1(b) shows the first BZ and the projected (010) surface BZ of MgB2, with some newly defined surface k points ![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) 0.15 (0.5,0.15),
0.15 (0.5,0.15), ![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) 0.218 (0.5,0.218),
0.218 (0.5,0.218), ![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) 0.27 (0.5,0.27),
0.27 (0.5,0.27), ![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) 0.3 (0.5,0.3),
0.3 (0.5,0.3), ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) 0.15 (0.0,0.15),
0.15 (0.0,0.15), ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) 0.218 (0.0,0.218),
0.218 (0.0,0.218), ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) 0.27 (0.0,0.27), and
0.27 (0.0,0.27), and ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) 0.3 (0.0,0.3).
0.3 (0.0,0.3).
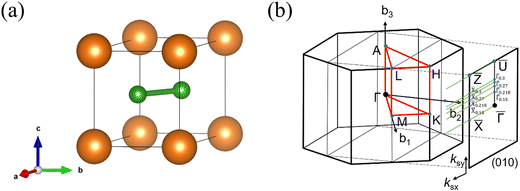 |
| | Fig. 1 (a) Crystal structure of MgB2 (orange ball: Mg; green ball: B), (b) The first BZ and projected (010) surface BZ of MgB2, with some newly defined surface k points ![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) 0.15 (0.5,0.15), 0.15 (0.5,0.15), ![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) 0.218 (0.5,0.218), 0.218 (0.5,0.218), ![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) 0.27 (0.5,0.27), 0.27 (0.5,0.27), ![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) 0.3 (0.5,0.3), 0.3 (0.5,0.3), ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) 0.15 (0.0,0.15), 0.15 (0.0,0.15), ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) 0.218 (0.0,0.218), 0.218 (0.0,0.218), ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) 0.27 (0.0,0.27), and 0.27 (0.0,0.27), and ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) 0.3 (0.0,0.3). 0.3 (0.0,0.3). | |
We compared the bulk phase band structure of MgB2 with and without SOC, and found that SOC had almost no effect on the band structure. In Fig. S2 of ESI† (ref. 46). Therefore, SOC was not considered in the subsequent study. Fig. 2(a) depicts the calculated band structures of MgB2 without considering the spin–orbit coupling (SOC). Here, we see that the bands are all doubly degenerate along the high-symmetric H–K edge, and the degenerate bands are contributed mainly by the p orbitals of B atoms. The detailed band structures analysis in the 3D BZ shows that MgB2 is a topological nodal line semimetal with six equivalent nodal lines along the high-symmetric H–K edges of the first BZ as shown in Fig. 2(b). The TB band structures and the distribution of band crossing nodes are shown in Fig. S1 of the ESI† (ref. 46). To confirm the topological origin of the nodal lines, we selected a closed loop around the nodal line and calculated the accumulated Berry phase ϕB, which are defined as:15
| | 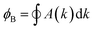 | (1) |
| | 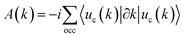 | (2) |
where,
A(
k) is the Berry connection, |
uc|(
k)〉 is the Bloch wave function, and
occ denotes the number of occupied bands. The calculated Berry phase is
ϕB =
π, thus confirming the topological origin and the robustness of these nodal lines.
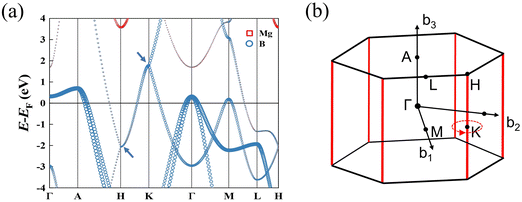 |
| | Fig. 2 (a) The calculated band structures of MgB2, the bands are all doubly degenerate along the high-symmetric H–K path without considering the spin–orbit coupling (SOC). The degenerate bands are contributed by B atoms; (b) the nodal lines of MgB2 in the first BZ, which are along the high-symmetric H–K edges (red line). The Berry phase associated with the nodal line is π. | |
TSSs analysis of multilayer structures are shown in Fig. S3 and S4 of ESI† (ref. 46). The 3-layer, 7-layer, 13-layer and 20-layer slab models are built to calculate the energy band structure, and found that the surface state of band structure reached the stable and clear result after the 13th layer. Considering the saving of computing resources and the improvement of scientific research efficiency, we do not employ the thicker slab than 20-layer. We have calculated (010) surface states of the 20-layer thick slab with Mg/B atoms as surface terminations as shown in Fig. 3. Because we aim to study the effect of adsorption of small molecules on the topological surface state of MgB2, we draw the distribution of the volume phase nodal lines of MgB2, and find that its topological surface state will appear on surface (010). Fig. 3(a) shows the estimated Mg-terminated surface states along the ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) –
–![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) –
–![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) ,
, ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) 0.15–
0.15–![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) 0.15–
0.15–![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) 0.15,
0.15, ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) 0.218–
0.218–![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) 0.218–
0.218–![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) 0.218, and
0.218, and ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) 0.3–
0.3–![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) 0.3–
0.3–![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) 0.3 paths as sketched in Fig. 1(b). The nearly flat topological surface bands are inside the projected nodal lines. Fig. 3(c) shows the Mg-terminated slab model we used and the band decomposed charge density for the topological surface bands at the projected
0.3 paths as sketched in Fig. 1(b). The nearly flat topological surface bands are inside the projected nodal lines. Fig. 3(c) shows the Mg-terminated slab model we used and the band decomposed charge density for the topological surface bands at the projected ![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) point, which confirms that the topological surface states are indeed from the surface B atoms. Fig. 3(b) shows the surface states given by the B-terminated slab models along the projected
point, which confirms that the topological surface states are indeed from the surface B atoms. Fig. 3(b) shows the surface states given by the B-terminated slab models along the projected ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) –
–![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) –
–![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) ,
, ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) 0.15–
0.15–![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) 0.15–
0.15–![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) 0.15,
0.15, ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) 0.27–
0.27–![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) 0.27–
0.27–![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) 0.27, and
0.27, and ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) 0.3–
0.3–![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) 0.3–
0.3–![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) 0.3 paths. The drumhead-like topological surface states can be seen along
0.3 paths. The drumhead-like topological surface states can be seen along ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) –
–![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) –
–![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) paths, while the topological surface bands tend to merge into the bulk along other paths. Fig. 3(d) gives the B-terminated slab model we used and also the band decomposed charge densities for the topological surface bands at the projected
paths, while the topological surface bands tend to merge into the bulk along other paths. Fig. 3(d) gives the B-terminated slab model we used and also the band decomposed charge densities for the topological surface bands at the projected ![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) point, also confirming that the topological surface states are indeed contributed by the surface B atoms. Remarkably, in both the Mg/B-terminated cases, the topological surface bands exclusively originate from the surface B atoms, as the bulk bands associated with the nodal lines are contributed by B atoms. Our findings align with those in ref. 37.
point, also confirming that the topological surface states are indeed contributed by the surface B atoms. Remarkably, in both the Mg/B-terminated cases, the topological surface bands exclusively originate from the surface B atoms, as the bulk bands associated with the nodal lines are contributed by B atoms. Our findings align with those in ref. 37.
 |
| | Fig. 3 (a) The Mg-terminated surface states along the projected ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) – –![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) – –![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) , , ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) 0.15– 0.15–![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) 0.15– 0.15–![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) 0.15, 0.15, ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) 0.218– 0.218–![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) 0.218– 0.218–![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) 0.218, and 0.218, and ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) 0.3– 0.3–![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) 0.3– 0.3–![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) 0.3 paths; (b) The B-terminated surface states along the projected 0.3 paths; (b) The B-terminated surface states along the projected ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) – –![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) – –![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) , , ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) 0.15– 0.15–![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) 0.15– 0.15–![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) 0.15, 0.15, ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) 0.27– 0.27–![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) 0.27– 0.27–![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) 0.27, and 0.27, and ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) 0.3– 0.3–![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) 0.3– 0.3–![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) 0.3 paths; (c) the slab model and the charge density associated with the surface bands for Mg-terminations at the projected 0.3 paths; (c) the slab model and the charge density associated with the surface bands for Mg-terminations at the projected ![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) point; (d) the slab model and the charge density associated with the surface bands for B-terminations at the projected point; (d) the slab model and the charge density associated with the surface bands for B-terminations at the projected ![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) point. The red line in (a) and (b) represents the drumhead-like topological surface states between two nodal points. point. The red line in (a) and (b) represents the drumhead-like topological surface states between two nodal points. | |
Notably, previous studies on the surface states of MgB2 have primarily focused on the pristine case.37,38 However, the surface adsorption is inevitable in real-world applications of topological materials, especially in aqueous environments. Therefore, we systematically studied on the variations of the surface states for MgB2 by introducing H, OH, and H2O onto the Mg/B-terminated slab models. In this section, we calculate the surface adsorption Gibbs free energies  to determine the most favorable adsorption sites for H, OH, and H2O adsorbed on the Mg/B-terminated slab models according to the following formulas:47
to determine the most favorable adsorption sites for H, OH, and H2O adsorbed on the Mg/B-terminated slab models according to the following formulas:47
| | 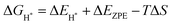 | (3) |
| | 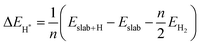 | (4) |
| | 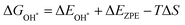 | (5) |
| | 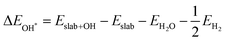 | (6) |
| | 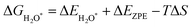 | (7) |
| | 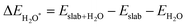 | (8) |
where, the * stands for the adsorption site on the surface,
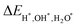
means the adsorption energies for H, OH, and H
2O, Δ
EZPE means the difference related to the zero-point energy between the gas phase and the adsorbed state,
T is the temperature and Δ
S is the change of the entropy.
47 The most favorable adsorption sites and their corresponding adsorption Gibbs free energies are presented in
Table 1. Additional details regarding the calculations for alternative sites can be found in the Tables S1–S3 of the ESI
† (ref.
46). Notably. The B-terminated slab exhibits a more pronounced adsorption effect on H, OH, and H
2O than the Mg-terminated slab. Furthermore, both H and OH exhibit significant negative values of

, respectively, indicating strong adsorption effects, while the adsorption effect of H
2O is relatively weak.
Fig. 4 illustrates the Mg/B-terminated slab models adsorbing H, OH, and H
2O onto their most favorable adsorption sites. The red dashed line represents the distance from the surface adsorbed atom to the surface atom, with specific distance values provided in
Table 1.
Table 1 The most favorable adsorption sites, the bond distance from the surface-adsorbed atom to the surface atom, the corresponding surface adsorption free energies (ΔG), and the charge gain and loss of the surface atoms derived from the Bader charge analysis for the Mg/B-terminated slab adsorbing H, OH, and H2O. “+” denotes a gain of charge, while “−” signifies a loss of charge (unit in e−)
| Systems |
Adsorbate |
Site |
Bond distance (Å) |
ΔG (eV) |
Δρ (e−) |
| Mg-terminated slab |
|
|
|
|
Adsorbate |
B |
Mg |
| H |
Hole |
2.370 |
−0.319 |
+0.900 |
−0.307 |
−0.011 |
| OH |
Bridge |
1.974 |
−0.347 |
+0.772 |
−0.183 |
−0.182 |
| H2O |
Top |
2.124 |
0.318 |
+0.224 |
−0.021 |
−0.114 |
| B-terminated slab |
|
|
|
|
Adsorbate |
B |
Mg |
| H |
Top |
1.211 |
−1.252 |
+0.361 |
−0.127 |
−0.017 |
| OH |
Top |
1.352 |
−1.442 |
+0.690 |
−0.228 |
−0.015 |
| H2O |
Top |
1.554 |
−0.170 |
+0.266 |
−0.082 |
−0.007 |
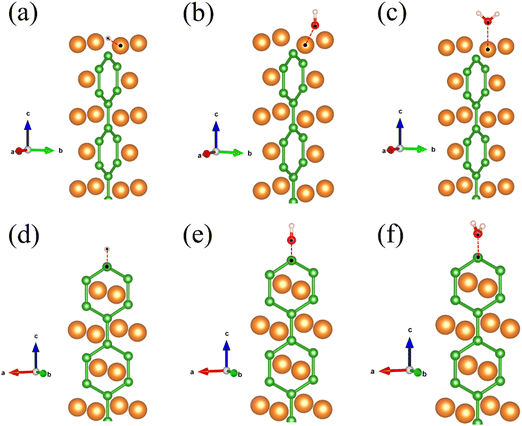 |
| | Fig. 4 (a) Mg-terminated slab adsorbing H on the hole site; (b) Mg-terminated slab adsorbing OH on the bridge site; (c) Mg-terminated slab adsorbing H2O on the top site; (d) B-terminated slab adsorbing H on the top site; (e) B-terminated slab adsorbing OH on the top site; (f) B-terminated slab adsorbing H2O on the top site. The red dashed lines represent the distance from the surface adsorbed atom to the surface atom, and the distance values are shown in Table 1. | |
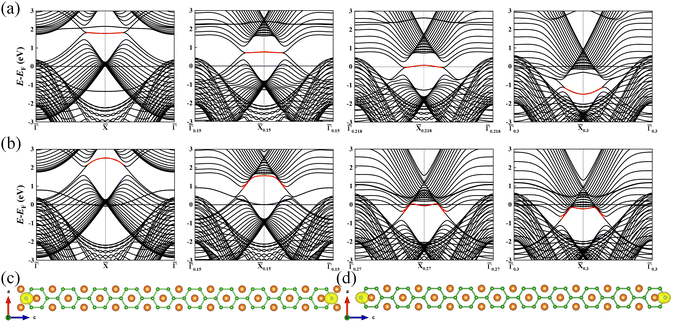
Subsequently, we discuss the surface states of the slab model adsorbing H and OH, represented in Fig. 5 and 6, respectively. Fig. 5(a) and 6(a) display the nearly flat drumhead-like topological surface states inside the nodal lines of the Mg-terminated pristine slab model along the projected ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) –
–![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) –
–![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) direction. Fig. 5(b) and 6(b) show the surface states adsorbing H and OH to the slab model on a single side, respectively, breaking the inversion symmetry of the slab model. Thus, the energy of one surface band is lower since the surface dangling bonds are saturated while another surface band is still there. Here, we propose ΔETSS as an index to describe the disturbance of adsorbates to the topological surface states, which is defined as:
direction. Fig. 5(b) and 6(b) show the surface states adsorbing H and OH to the slab model on a single side, respectively, breaking the inversion symmetry of the slab model. Thus, the energy of one surface band is lower since the surface dangling bonds are saturated while another surface band is still there. Here, we propose ΔETSS as an index to describe the disturbance of adsorbates to the topological surface states, which is defined as:
| | | ΔETSS = ΔETSSAds − ΔETSS0 | (9) |
Where the
ETSSAds is the energy of the topological surface state of the slab with adsorbate at the projected
![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif)
point,
ETSS0 means the topological surface state energy of pristine slab at the projected
![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif)
point. In addition,
Table 1 displays the Δ
ETSS values. It is evident that Δ
ETSS in
Fig. 5(b) has a more negative value (−0.936 eV) compared to
Fig. 6(b) (−0.322 eV). This fact indicates that the H has a more significant impact on the topological surface state on Mg-terminated slab than OH.
Fig. 5(c) and 6(c) depict the surface states with H and OH adsorbed on both sides of the slab model. The inversion symmetry of the slab model is restored, causing the surface bands are degenerate with lower energies. The changes in surface state energy in
Fig. 5(c) are more significant than those in
Fig. 6(c). In both cases, the surface states remain within the nodal lines. This is because the surface B atoms primarily contribute to the topological surface states. Adding H and OH atoms onto Mg atoms does not drastically alter the topological band structures contributed by the B atoms.
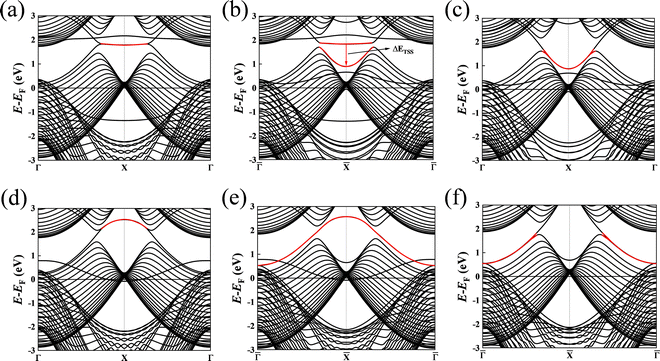 |
| | Fig. 5 (a) The (010) surface states from the pristine Mg-terminated slab; (b) the (010) surface states from the Mg-terminated slab adsorbing H on a single side; (c) the (010) surface states from the Mg-terminated slab adsorbing H on both sides; (d) the (010) surface states from the pristine B-terminated slab; (e) the (010) surface states from the B-terminated slab adsorbing H on a single side; (f) the (010) surface states from the B-terminated slab adsorbing H on both sides. The red line indicates the drumhead-like topological surface states between two nodal points. | |
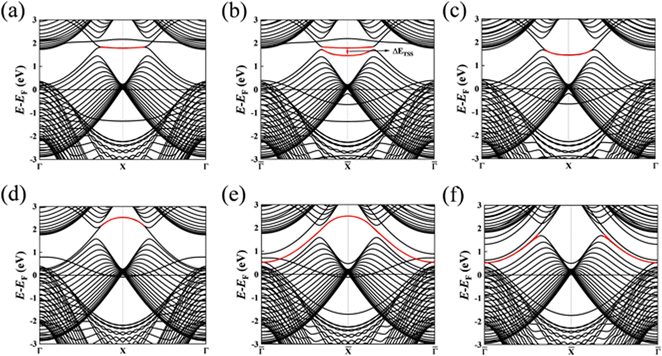 |
| | Fig. 6 (a) The (010) surface states from the pristine Mg-terminated slab; (b) the (010) surface states from the Mg-terminated slab adsorbing OH on a single side; (c) the (010) surface states from the Mg-terminated slab adsorbing OH on both sides; (d) the (010) surface states from the pristine B-terminated slab; (e) the (010) surface states from the B-terminated slab adsorbing OH on a single side; (f) the (010) surface states from the B-terminated slab adsorbing OH on both sides. The red line indicates the drumhead-like topological surface states between two nodal points. | |
Fig. 5(d) and 6(d) illustrate the surface states with the B-terminated pristine slab model along the projected ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) –
–![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) –
–![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) direction. These figures reveal the presence of nearly flat drumhead-like topological surface states situated within the nodal lines. Additionally, Fig. 5(e) and 6(e) showcase the surface states of the B-terminated slab with the adsorbates H and OH on a single side, respectively, breaking the inversion symmetry of the slab model. It is worth noting that the surface states are present inside and outside the nodal lines. This observation indicates a substantial alteration in the topological band structure resulting from the strong interaction between B atoms and H/OH. Fig. 5(f) and 6(f) show the surface states of B-terminated slab with the adsorbates H or OH on both sides, where the inversion symmetry of the slab model is restored, and the surface states are outside the nodal lines. Since B atoms mainly contribute to the topological surface states, adding H/OH onto B atoms changes the surface terminations from zigzag to beard types. This leads to the surface states outside the nodal lines, consistent with the previous works.18,20,34 Fig. S2 and S3 of the ESI† (ref. 46) show the determination of the surface state positions in the band analysis.
direction. These figures reveal the presence of nearly flat drumhead-like topological surface states situated within the nodal lines. Additionally, Fig. 5(e) and 6(e) showcase the surface states of the B-terminated slab with the adsorbates H and OH on a single side, respectively, breaking the inversion symmetry of the slab model. It is worth noting that the surface states are present inside and outside the nodal lines. This observation indicates a substantial alteration in the topological band structure resulting from the strong interaction between B atoms and H/OH. Fig. 5(f) and 6(f) show the surface states of B-terminated slab with the adsorbates H or OH on both sides, where the inversion symmetry of the slab model is restored, and the surface states are outside the nodal lines. Since B atoms mainly contribute to the topological surface states, adding H/OH onto B atoms changes the surface terminations from zigzag to beard types. This leads to the surface states outside the nodal lines, consistent with the previous works.18,20,34 Fig. S2 and S3 of the ESI† (ref. 46) show the determination of the surface state positions in the band analysis.
We also discuss the surface states of the slab model adsorbing H2O. Fig. 7(a) depicts the surface states from the Mg-terminated pristine slab model along the projected ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) –
–![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) –
–![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) direction as a reference. Fig. 7(b) illustrates the surface states when H2O is adsorbed onto a single side of the slab model, breaking the inversion symmetry of the slab model. Notably, the two surface bands exhibit a considerably weaker splitting compared to cases involving the adsorption of H/OH. The Mg-terminated slab shows a weak adsorption of H2O with the positive ΔG of 0.318 eV. Fig. 7(c) shows the surface states adsorbing H2O to the slab model on both sides, where the inversion symmetry of the slab model is restored and the surface bands are degenerate. Moreover, the topological surface bands also change slightly compared to the Fig. 7(a). Fig. 7(d) shows the surface states with a B-terminated pristine slab model along the projected
direction as a reference. Fig. 7(b) illustrates the surface states when H2O is adsorbed onto a single side of the slab model, breaking the inversion symmetry of the slab model. Notably, the two surface bands exhibit a considerably weaker splitting compared to cases involving the adsorption of H/OH. The Mg-terminated slab shows a weak adsorption of H2O with the positive ΔG of 0.318 eV. Fig. 7(c) shows the surface states adsorbing H2O to the slab model on both sides, where the inversion symmetry of the slab model is restored and the surface bands are degenerate. Moreover, the topological surface bands also change slightly compared to the Fig. 7(a). Fig. 7(d) shows the surface states with a B-terminated pristine slab model along the projected ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) –
–![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) –
–![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) direction as a benchmark and the nearly flat drumhead-like topological surface states can be seen inside the nodal lines. Fig. 7(e) shows the surface states adsorbing H2O to the slab model on a single side, breaking the inversion symmetry of the slab model. Notably though the H2O interacts with the B-terminated surface directly, H2O is a charge neutral molecule and the B-terminated surfaces show a very weak adsorption to it, the topological surface are states still inside the nodal lines. Fig. 7(f) shows the surface adsorbing H2O to the slab model on both sides, the inversion symmetry of the slab model is restored, and the surface bands are degenerate. Also, the surface bands change slightly compared with Fig. 7(d). In either case, the topological surface states are always inside the nodal lines since H2O is electric neutrality molecule and the surface slab has very weak adsorption for H2O. The determination of the surface states’ position is shown in Fig. S4 of ESI† (ref. 46).
direction as a benchmark and the nearly flat drumhead-like topological surface states can be seen inside the nodal lines. Fig. 7(e) shows the surface states adsorbing H2O to the slab model on a single side, breaking the inversion symmetry of the slab model. Notably though the H2O interacts with the B-terminated surface directly, H2O is a charge neutral molecule and the B-terminated surfaces show a very weak adsorption to it, the topological surface are states still inside the nodal lines. Fig. 7(f) shows the surface adsorbing H2O to the slab model on both sides, the inversion symmetry of the slab model is restored, and the surface bands are degenerate. Also, the surface bands change slightly compared with Fig. 7(d). In either case, the topological surface states are always inside the nodal lines since H2O is electric neutrality molecule and the surface slab has very weak adsorption for H2O. The determination of the surface states’ position is shown in Fig. S4 of ESI† (ref. 46).
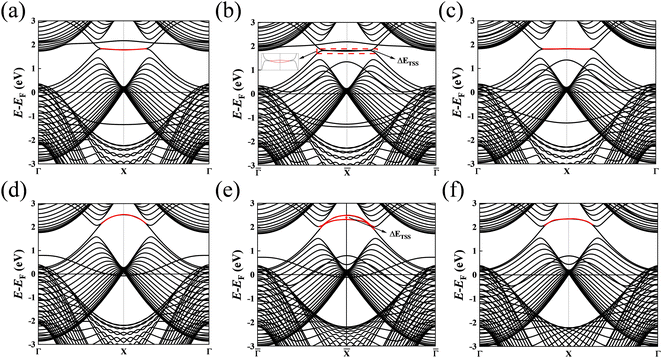 |
| | Fig. 7 (a) The (010) surface states given by the pristine Mg-terminated slab; (b) the (010) surface states exhibited by the Mg-terminated slab adsorbing H2O on a single side; (c) the (010) surface states shown by the Mg-terminated slab upon H2O adsorption on both sides; (d) the (010) surface states shown by the pristine B-terminated slab; (e) the (010) surface states displayed by the B-terminated slab following H2O adsorption on a single side; (f) the (010) surface states are depicted by the B-terminated slab after H2O adsorption on both sides. The red line represents the drumhead-like topological surface states between two nodal points. | |
From the results of the topological surface states changes ΔETSS of MgB2 with different adsorbates, we expect to propose a critical indicator with a positive correlation with the ΔETSS. Table 1 presents our calculations of Bader charge analysis48–51 to show the charge gain and loss of the surface atoms. It is evident that adsorbates H, OH, and H2O gain electrons, while the surface Mg/B-atoms tend to lose them. Simultaneously, the surface differential charge density calculations reveal this phenomenon, as depicted in Fig. S5 of the ESI† (ref. 46). It is noteworthy that there is a significant positive correlation between the Bader charge transfer of surface B atoms and the ΔETSS. We further investigated the relationship between the other significant parameters of surface adsorption, such as the bond lengths and adsorption Gibbs free energy, with the ΔETSS. However, they have a poor correlation, as illustrated in Fig. S6 of the ESI† (ref. 46). Thus, we can infer that the Bader charge transfer value of the surface atoms that provide the topological state is a crucial indicator for evaluating the variation in topological surface states after adsorption.
Conclusion
In summary, we have performed by ab initio calculations a systematical study on the variation of the (010) surface states of MgB2 after adding hydrogen (H), hydroxide (OH), and water (H2O). The most stable adsorption sites have been identified by calculating the surface adsorption free energies  . Meanwhile, it is shown that either Mg- or B-terminated surface has a very strong adsorption for OH, and then H, while has only weak adsorption for H2O, and the surface states have a crucial change after the adsorption for H, less change after the adsorption for OH, and only very slight change after the adsorption for H2O, which can be understood systematically by combining the surface adsorption free energies
. Meanwhile, it is shown that either Mg- or B-terminated surface has a very strong adsorption for OH, and then H, while has only weak adsorption for H2O, and the surface states have a crucial change after the adsorption for H, less change after the adsorption for OH, and only very slight change after the adsorption for H2O, which can be understood systematically by combining the surface adsorption free energies  , surface terminations, and surface charge density distributions. Particularly, we propose the value of the band structural change of topological surface state ΔETSS as an index to describe the disturbance of adsorbates to the topological surface states. Analyzing the relationships among Bader charge transfer, adsorption Gibbs free energy, and bond length to ΔETSS, we observed a high correlation solely between ΔETSS and the Bader charge transfer of the surface B atoms. The Bader charge transfer value of the surface B atoms providing the topological state should be a key indicator for evaluating the variation in topological surface states after adsorbing H, OH, and H2O adsorbates. Our work has provided a systematical understanding on the variation of topological surface states after surface adsorptions, and will also pave the way for future studies on the device applications of topological materials.
, surface terminations, and surface charge density distributions. Particularly, we propose the value of the band structural change of topological surface state ΔETSS as an index to describe the disturbance of adsorbates to the topological surface states. Analyzing the relationships among Bader charge transfer, adsorption Gibbs free energy, and bond length to ΔETSS, we observed a high correlation solely between ΔETSS and the Bader charge transfer of the surface B atoms. The Bader charge transfer value of the surface B atoms providing the topological state should be a key indicator for evaluating the variation in topological surface states after adsorbing H, OH, and H2O adsorbates. Our work has provided a systematical understanding on the variation of topological surface states after surface adsorptions, and will also pave the way for future studies on the device applications of topological materials.
Data availability
The data supporting this article have been included as part of the ESI.†
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
K. Bu acknowledges the support from the financial support from the National Natural Science Foundation of China (No. 12304087) and Natural Science Foundation of Shandong Province (ZR2023QA076). C. Wang acknowledges the financial support from the National Natural Science Foundation of China (No. 11804012), and the Urban Carbon Neutral Science and Technology Innovation Fund Project of Beijing University of Technology (048000514123695).
References
- M. Z. Hasan and C. L. Kane, Colloquium:Topological insulators, Rev. Mod. Phys., 2010, 82, 3045 CrossRef CAS.
- X. L. Qi and S. C. Zhang, Topological insulators and superconductors, Rev. Mod. Phys., 2011, 83, 1057 CrossRef CAS.
- C. K. Chiu, J. C. Y. Teo, A. P. Schnyder and S. Ryu, Classification of topological quantum matter with symmetries, Rev. Mod. Phys., 2016, 88, 035005 CrossRef.
- N. P. Armitage, E. J. Mele and A. Vishwanath, Weyl and Dirac semimetals in three-dimensional solids, Rev. Mod. Phys., 2018, 90, 015001 CrossRef CAS.
- X. Wan, A. M. Turner, A. Vishwanath and S. Y. Savrasov, Topological semimetal and Fermi-arc surface states in the electronic structure of pyrochlore iridates, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 205101 CrossRef.
- H. Weng, C. Fang, Z. Fang, B. Andrei. Bernevig and X. Dai, Weyl Semimetal Phase in Noncentrosymmetric Transition-Metal Monophosphides, Phys. Rev. X, 2015, 5, 011029 Search PubMed.
- G. Xu, H. Weng, Z. Wang, X. Dai and Z. Fang, Chern Semimetal and the Quantized Anomalous Hall Effect in HgCr2Se4, Phys. Rev. Lett., 2011, 107, 186806 CrossRef PubMed.
- Z. Wang, Y. Sun, X. Q. Chen, C. Franchini, G. Xu, H. Weng, X. Dai and Z. Fang, Dirac semimetal and topological phase transitions in A3Bi (A = Na, K, Rb), Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 195320 CrossRef.
- Z. Wang, H. Weng, Q. Wu, X. Dai and Z. Fang, Three dimensional Dirac semimetal and quantum transport in Cd3As2, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 125427 CrossRef.
- Q. D. Gibson, L. M. Schoop, L. Muechler, L. S. Xie, M. Hirschberger, N. P. Ong, R. Car and R. J. Cava, Three-dimensional Dirac semimetals: Design principles and predictions of new materials, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 205128 CrossRef.
- M. Phillips and V. Aji, Tunable line node semimetals, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 115111 CrossRef.
- Y. Kim, B. J. Wieder, C. L. Kane and A. M. Rappe, Dirac line nodes in inversion-symmetric crystals, Phys. Rev. Lett., 2015, 115, 036806 CrossRef PubMed.
- R. Yu, H. Weng, Z. Fang, X. Dai and X. Hu, Topological node-line semimetal and Dirac semimetal state in antiperovskite Cu3PdN, Phys. Rev. Lett., 2015, 115, 036807 CrossRef.
- C. Fang, Y. Chen, H. Y. Kee and L. Fu, Topological nodal line semimetals with and without spin-orbital coupling, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 081201(R) CrossRef.
- C. Fang, H. Weng, X. Dai and Z. Fang, Topological nodal line semimetals, Chin. Phys. B, 2016, 25, 117106 CrossRef.
- Q. Xu, R. Yu, Z. Fang, X. Dai and H. Weng, Topological nodal line semimetals in the CaP3 family of materials, Phys. Rev. B, 2017, 95, 045136 CrossRef.
- K. Bu, J. T. Wang, H. Weng and C. Chen, Topological semimetal in an sp2-sp3 hybridized carbon network with nodal rings, Phys. Rev. B, 2020, 101, 205104 CrossRef.
- K. Bu, Y. Qian, J. T. Wang and H. Weng, Hybrid Nodal Chain in an Orthorhombic Graphene Network, Phys. Rev. B, 2021, 103, L081108 CrossRef CAS.
- M. R. Khan, K. Bu and J. T. Wang, Topological nodal line semimetal in an all-sp2 monoclinic carbon, New J. Phys., 2022, 24, 043007 CrossRef CAS.
- Y. Tao, K. Bu and J. T. Wang, Orthorhombic C32: A topological semimetal with nodal ring, Phys. Lett. A, 2022, 451, 128397 CrossRef CAS.
- J. T. Wang, K. Bu, Y. Qian, H. Weng and C. F. Chen, Pentagraphite C8: An all-sp2 topological nodal-line semimetal, Phys. Rev. B, 2021, 104, 245143 CrossRef CAS.
- K. Bu and J. T. Wang, Topological nodal line semimetal with large nodal ring in an all-sp2 hybridized carbon network formed by all-ten-membered carbon rings, Phys. Rev. B, 2023, 107, 245111 CrossRef CAS.
- K. Bu and J. T. Wang, Topological states in the polymerized carbon nanotubes, Phys. Lett. A, 2023, 480, 128396 CrossRef.
- H. Luo, P. Yu, G. Li and K. Yan, Topological quantum materials for energy conversion and storage, Nat. Rev. Phys., 2022, 4, 611 CrossRef CAS.
- H. Chen, W. Zhu, D. Xiao and Z. Zhang, CO oxidation facilitated by robust surface states on Au-covered topological insulators, Phys. Rev. Lett., 2011, 107, 056804 CrossRef.
- L. Li, J. Zeng, W. Qin, P. Cui and Z. Zhang, Tuning the hydrogen activation reactivity on topological insulator heterostructures, Nano Energy, 2019, 58, 40 CrossRef CAS.
- R. R. Q. Freitas, R. Rivelino, F. de Brito Mota, C. M. C. de Castilho, A. Kakanakova-Georgieva and G. K. Gueorguiev, Topological Insulating Phases in Two-Dimensional Bismuth-Containing Single Layers Preserved by Hydrogenation, J. Phys. Chem. C, 2015, 119, 23599 CrossRef CAS.
- R. R. Q. Freitas, F. de Brito Mota, R. Rivelino, C. M. C. de Castilho, A. Kakanakova-Georgieva and G. K. Gueorguiev, Tuning band inversion symmetry of buckled III-Bi sheets by halogenation, Nanotechnology, 2016, 27, 055704 CrossRef CAS.
- C. R. Rajamathi, U. Gupta, N. Kumar, H. Yang, Y. Sun, V. Süβ, C. Shekhar, M. Schmidt, H. Blumtritt, P. Werner, B. H. Yan, S. Parkin, C. Felser and C. N. R. Rao, Weyl Semimetals as Hydrogen Evolution Catalysts, Adv. Mater., 2017, 29, 1606202 CrossRef PubMed.
- W. Liu, X. Zhang, W. Meng, Y. Liu, X. Dai and G. Liu, Theoretical realization of hybrid Weyl state and associated high catalytic performance for hydrogen evolution in NiSi, iScience, 2022, 25, 103543 CrossRef CAS.
- G. Li, Q. Xu, W. Shi, C. Fu, L. Jiao, M. E. Kamminga, M. Yu, H. Tüysüz, N. Kumar, V. Süβ, R. Saha, A. K. Srivastava, S. Wirth, G. Auffermann, J. Gooth, S. Parkin, Y. Sun, E. Liu and C. Felser, Surface states in bulk single crystal of topological semimetal Co3Sn2S2 toward water oxidation, Sci. Adv., 2019, 5, eaaw9867 CrossRef CAS.
- J. Li, H. Ma, Q. Xie, S. Feng, S. Ullah, R. Li, J. Dong, D. Li, Y. Li and X. Q. Chen, Topological quantum catalyst: Dirac nodal line states and a potential electrocatalyst of hydrogen evolution in the TiSi family, Sci. China Mater., 2018, 61, 23 CrossRef CAS.
- X. Zhang, L. Wang, M. Li, W. Meng, Y. Liu, X. Dai, G. Liu, Y. Gu, J. Liu and L. Kou, Topological surface state: Universal catalytic descriptor in topological catalysis, Mater. Today, 2023, 67, 23 CrossRef CAS.
- S. Ryu and Y. Hatsugai, Topological Origin of Zero-Energy Edge States in Particle-Hole Symmetric Systems, Phys. Rev. Lett., 2002, 89, 077002 CrossRef PubMed.
- J. Nagamatsu, N. Nakagawa, T. Muranaka, Y. Zenitani and J. Akimitsu, Superconductivity at 39 K in magnesium diboride, Nature, 2001, 410, 63 CrossRef CAS.
- C. Buzea and T. Yamashita, Review of the superconducting properties of MgB2, Supercond. Sci. Technol., 2001, 14, R115 CrossRef CAS.
- K. H. Jin, H. Huang, J. W. Mei, Z. Liu, L. K. Lim and F. Liu, Topological superconducting phase in high Tc superconductor MgB2 with Dirac nodal-line fermions, npj Comput. Mater., 2019, 5, 57 CrossRef.
- X. Zhou, K. N. Gordon, K. H. Jin, H. Li, D. Narayan, H. Zhao, H. Zheng, H. Huang, G. Cao, N. D. Zhigadlo, F. Liu and D. S. Dessau, Observation of topological surface states in the high-temperature superconductor MgB2, Phys. Rev. B, 2019, 100, 184511 CrossRef CAS.
- G. Kresse and J. Furthüller, Effcient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef PubMed.
- A. A. Mostofi, J. R. Yates, Y. S. Lee, I. Souza, D. Vanderbilt and N. Marzari, Wannier90: A tool for obtaining maximally-localised Wannier functions, Comput. Phys. Commun., 2008, 178, 685 CrossRef CAS.
- N. Marzari, A. A. Mostofi, J. R. Yates, I. Souza and D. Vanderbilt, Maximally localized Wannier functions:Theory and applications, Rev. Mod. Phys., 2012, 84, 1419 CrossRef CAS.
- Q. S. Wu, S. N. Zhang, H. F. Song, M. Troyer and A. A. Soluyanov, WannierTools: An open-source software package for novel topological materials, Comput. Phys. Commun., 2018, 224, 405 CrossRef CAS.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, The Materials Project: A materials genome approach to accelerating materials innovation, APL Mater., 2013, 1, 011002 CrossRef.
- See the Supplemental Materials for (1) the Wannier tight-binding model for MgB2; (2) the surface adsorption Gibbs free energies at all possible adsorption sites; (3) Fatband analysis for slab adsorbing H, OH, and H2O; (4) Differential charge density for most favorable adsorption sites; The Supplemental Materials include ref. 40 and 41.
- K. L. Zhou, Z. Wang, C. B. Han, X. Ke, C. Wang, Y. Jin, Q. Zhang, J. Liu, H. Wang and H. Yan, Platinum single-atom catalyst coupled with transition metal/metal oxide heterostructure for accelerating alkaline hydrogen evolution reaction, Nat. Commun., 2021, 12, 3783 CrossRef CAS.
- W. Tang, E. Sanville and G. Henkelman, A grid-based Bader analysis algorithm without lattice bias, J. Phys.: Condens. Matter, 2009, 21, 084204 CrossRef CAS PubMed.
- E. Sanville, S. D. Kenny, R. Smith and G. Henkelman, An improved grid-based algorithm for Bader charge allocation, J. Comp. Chem., 2007, 28, 899 CrossRef CAS PubMed.
- G. Henkelman, A. Arnaldsson and H. Jónsson, A fast and robust algorithm for Bader decomposition of charge density, Comput. Mater. Sci., 2006, 36, 354 CrossRef.
- M. Yu and D. R. Trinkle, Accurate and efficient algorithm for Bader charge integration, J. Chem. Phys., 2011, 134, 064111 CrossRef PubMed.
|
| This journal is © the Owner Societies 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  a and
Changhao
Wang
a and
Changhao
Wang
 *a
*a
![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) 0.15 (0.5,0.15),
0.15 (0.5,0.15), ![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) 0.218 (0.5,0.218),
0.218 (0.5,0.218), ![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) 0.27 (0.5,0.27),
0.27 (0.5,0.27), ![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) 0.3 (0.5,0.3),
0.3 (0.5,0.3), ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) 0.15 (0.0,0.15),
0.15 (0.0,0.15), ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) 0.218 (0.0,0.218),
0.218 (0.0,0.218), ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) 0.27 (0.0,0.27), and
0.27 (0.0,0.27), and ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) 0.3 (0.0,0.3).
0.3 (0.0,0.3).
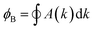
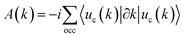
![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) –
–![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) –
–![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) ,
, ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) 0.15–
0.15–![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) 0.15–
0.15–![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) 0.15,
0.15, ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) 0.218–
0.218–![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) 0.218–
0.218–![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) 0.218, and
0.218, and ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) 0.3–
0.3–![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) 0.3–
0.3–![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) 0.3 paths as sketched in Fig. 1(b). The nearly flat topological surface bands are inside the projected nodal lines. Fig. 3(c) shows the Mg-terminated slab model we used and the band decomposed charge density for the topological surface bands at the projected
0.3 paths as sketched in Fig. 1(b). The nearly flat topological surface bands are inside the projected nodal lines. Fig. 3(c) shows the Mg-terminated slab model we used and the band decomposed charge density for the topological surface bands at the projected ![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) point, which confirms that the topological surface states are indeed from the surface B atoms. Fig. 3(b) shows the surface states given by the B-terminated slab models along the projected
point, which confirms that the topological surface states are indeed from the surface B atoms. Fig. 3(b) shows the surface states given by the B-terminated slab models along the projected ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) –
–![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) –
–![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) ,
, ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) 0.15–
0.15–![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) 0.15–
0.15–![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) 0.15,
0.15, ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) 0.27–
0.27–![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) 0.27–
0.27–![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) 0.27, and
0.27, and ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) 0.3–
0.3–![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) 0.3–
0.3–![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) 0.3 paths. The drumhead-like topological surface states can be seen along
0.3 paths. The drumhead-like topological surface states can be seen along ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) –
–![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) –
–![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) paths, while the topological surface bands tend to merge into the bulk along other paths. Fig. 3(d) gives the B-terminated slab model we used and also the band decomposed charge densities for the topological surface bands at the projected
paths, while the topological surface bands tend to merge into the bulk along other paths. Fig. 3(d) gives the B-terminated slab model we used and also the band decomposed charge densities for the topological surface bands at the projected ![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) point, also confirming that the topological surface states are indeed contributed by the surface B atoms. Remarkably, in both the Mg/B-terminated cases, the topological surface bands exclusively originate from the surface B atoms, as the bulk bands associated with the nodal lines are contributed by B atoms. Our findings align with those in ref. 37.
point, also confirming that the topological surface states are indeed contributed by the surface B atoms. Remarkably, in both the Mg/B-terminated cases, the topological surface bands exclusively originate from the surface B atoms, as the bulk bands associated with the nodal lines are contributed by B atoms. Our findings align with those in ref. 37. to determine the most favorable adsorption sites for H, OH, and H2O adsorbed on the Mg/B-terminated slab models according to the following formulas:47
to determine the most favorable adsorption sites for H, OH, and H2O adsorbed on the Mg/B-terminated slab models according to the following formulas:47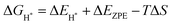
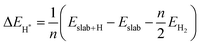
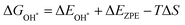
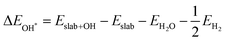
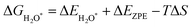
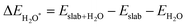
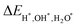 means the adsorption energies for H, OH, and H2O, ΔEZPE means the difference related to the zero-point energy between the gas phase and the adsorbed state, T is the temperature and ΔS is the change of the entropy.47 The most favorable adsorption sites and their corresponding adsorption Gibbs free energies are presented in Table 1. Additional details regarding the calculations for alternative sites can be found in the Tables S1–S3 of the ESI† (ref. 46). Notably. The B-terminated slab exhibits a more pronounced adsorption effect on H, OH, and H2O than the Mg-terminated slab. Furthermore, both H and OH exhibit significant negative values of
means the adsorption energies for H, OH, and H2O, ΔEZPE means the difference related to the zero-point energy between the gas phase and the adsorbed state, T is the temperature and ΔS is the change of the entropy.47 The most favorable adsorption sites and their corresponding adsorption Gibbs free energies are presented in Table 1. Additional details regarding the calculations for alternative sites can be found in the Tables S1–S3 of the ESI† (ref. 46). Notably. The B-terminated slab exhibits a more pronounced adsorption effect on H, OH, and H2O than the Mg-terminated slab. Furthermore, both H and OH exhibit significant negative values of  , respectively, indicating strong adsorption effects, while the adsorption effect of H2O is relatively weak. Fig. 4 illustrates the Mg/B-terminated slab models adsorbing H, OH, and H2O onto their most favorable adsorption sites. The red dashed line represents the distance from the surface adsorbed atom to the surface atom, with specific distance values provided in Table 1.
, respectively, indicating strong adsorption effects, while the adsorption effect of H2O is relatively weak. Fig. 4 illustrates the Mg/B-terminated slab models adsorbing H, OH, and H2O onto their most favorable adsorption sites. The red dashed line represents the distance from the surface adsorbed atom to the surface atom, with specific distance values provided in Table 1.

![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) –
–![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) –
–![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) direction. Fig. 5(b) and 6(b) show the surface states adsorbing H and OH to the slab model on a single side, respectively, breaking the inversion symmetry of the slab model. Thus, the energy of one surface band is lower since the surface dangling bonds are saturated while another surface band is still there. Here, we propose ΔETSS as an index to describe the disturbance of adsorbates to the topological surface states, which is defined as:
direction. Fig. 5(b) and 6(b) show the surface states adsorbing H and OH to the slab model on a single side, respectively, breaking the inversion symmetry of the slab model. Thus, the energy of one surface band is lower since the surface dangling bonds are saturated while another surface band is still there. Here, we propose ΔETSS as an index to describe the disturbance of adsorbates to the topological surface states, which is defined as:![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) point, ETSS0 means the topological surface state energy of pristine slab at the projected
point, ETSS0 means the topological surface state energy of pristine slab at the projected ![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) point. In addition, Table 1 displays the ΔETSS values. It is evident that ΔETSS in Fig. 5(b) has a more negative value (−0.936 eV) compared to Fig. 6(b) (−0.322 eV). This fact indicates that the H has a more significant impact on the topological surface state on Mg-terminated slab than OH. Fig. 5(c) and 6(c) depict the surface states with H and OH adsorbed on both sides of the slab model. The inversion symmetry of the slab model is restored, causing the surface bands are degenerate with lower energies. The changes in surface state energy in Fig. 5(c) are more significant than those in Fig. 6(c). In both cases, the surface states remain within the nodal lines. This is because the surface B atoms primarily contribute to the topological surface states. Adding H and OH atoms onto Mg atoms does not drastically alter the topological band structures contributed by the B atoms.
point. In addition, Table 1 displays the ΔETSS values. It is evident that ΔETSS in Fig. 5(b) has a more negative value (−0.936 eV) compared to Fig. 6(b) (−0.322 eV). This fact indicates that the H has a more significant impact on the topological surface state on Mg-terminated slab than OH. Fig. 5(c) and 6(c) depict the surface states with H and OH adsorbed on both sides of the slab model. The inversion symmetry of the slab model is restored, causing the surface bands are degenerate with lower energies. The changes in surface state energy in Fig. 5(c) are more significant than those in Fig. 6(c). In both cases, the surface states remain within the nodal lines. This is because the surface B atoms primarily contribute to the topological surface states. Adding H and OH atoms onto Mg atoms does not drastically alter the topological band structures contributed by the B atoms.
![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) –
–![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) –
–![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) direction. These figures reveal the presence of nearly flat drumhead-like topological surface states situated within the nodal lines. Additionally, Fig. 5(e) and 6(e) showcase the surface states of the B-terminated slab with the adsorbates H and OH on a single side, respectively, breaking the inversion symmetry of the slab model. It is worth noting that the surface states are present inside and outside the nodal lines. This observation indicates a substantial alteration in the topological band structure resulting from the strong interaction between B atoms and H/OH. Fig. 5(f) and 6(f) show the surface states of B-terminated slab with the adsorbates H or OH on both sides, where the inversion symmetry of the slab model is restored, and the surface states are outside the nodal lines. Since B atoms mainly contribute to the topological surface states, adding H/OH onto B atoms changes the surface terminations from zigzag to beard types. This leads to the surface states outside the nodal lines, consistent with the previous works.18,20,34 Fig. S2 and S3 of the ESI† (ref. 46) show the determination of the surface state positions in the band analysis.
direction. These figures reveal the presence of nearly flat drumhead-like topological surface states situated within the nodal lines. Additionally, Fig. 5(e) and 6(e) showcase the surface states of the B-terminated slab with the adsorbates H and OH on a single side, respectively, breaking the inversion symmetry of the slab model. It is worth noting that the surface states are present inside and outside the nodal lines. This observation indicates a substantial alteration in the topological band structure resulting from the strong interaction between B atoms and H/OH. Fig. 5(f) and 6(f) show the surface states of B-terminated slab with the adsorbates H or OH on both sides, where the inversion symmetry of the slab model is restored, and the surface states are outside the nodal lines. Since B atoms mainly contribute to the topological surface states, adding H/OH onto B atoms changes the surface terminations from zigzag to beard types. This leads to the surface states outside the nodal lines, consistent with the previous works.18,20,34 Fig. S2 and S3 of the ESI† (ref. 46) show the determination of the surface state positions in the band analysis.![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) –
–![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) –
–![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) direction as a reference. Fig. 7(b) illustrates the surface states when H2O is adsorbed onto a single side of the slab model, breaking the inversion symmetry of the slab model. Notably, the two surface bands exhibit a considerably weaker splitting compared to cases involving the adsorption of H/OH. The Mg-terminated slab shows a weak adsorption of H2O with the positive ΔG of 0.318 eV. Fig. 7(c) shows the surface states adsorbing H2O to the slab model on both sides, where the inversion symmetry of the slab model is restored and the surface bands are degenerate. Moreover, the topological surface bands also change slightly compared to the Fig. 7(a). Fig. 7(d) shows the surface states with a B-terminated pristine slab model along the projected
direction as a reference. Fig. 7(b) illustrates the surface states when H2O is adsorbed onto a single side of the slab model, breaking the inversion symmetry of the slab model. Notably, the two surface bands exhibit a considerably weaker splitting compared to cases involving the adsorption of H/OH. The Mg-terminated slab shows a weak adsorption of H2O with the positive ΔG of 0.318 eV. Fig. 7(c) shows the surface states adsorbing H2O to the slab model on both sides, where the inversion symmetry of the slab model is restored and the surface bands are degenerate. Moreover, the topological surface bands also change slightly compared to the Fig. 7(a). Fig. 7(d) shows the surface states with a B-terminated pristine slab model along the projected ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) –
–![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) –
–![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) direction as a benchmark and the nearly flat drumhead-like topological surface states can be seen inside the nodal lines. Fig. 7(e) shows the surface states adsorbing H2O to the slab model on a single side, breaking the inversion symmetry of the slab model. Notably though the H2O interacts with the B-terminated surface directly, H2O is a charge neutral molecule and the B-terminated surfaces show a very weak adsorption to it, the topological surface are states still inside the nodal lines. Fig. 7(f) shows the surface adsorbing H2O to the slab model on both sides, the inversion symmetry of the slab model is restored, and the surface bands are degenerate. Also, the surface bands change slightly compared with Fig. 7(d). In either case, the topological surface states are always inside the nodal lines since H2O is electric neutrality molecule and the surface slab has very weak adsorption for H2O. The determination of the surface states’ position is shown in Fig. S4 of ESI† (ref. 46).
direction as a benchmark and the nearly flat drumhead-like topological surface states can be seen inside the nodal lines. Fig. 7(e) shows the surface states adsorbing H2O to the slab model on a single side, breaking the inversion symmetry of the slab model. Notably though the H2O interacts with the B-terminated surface directly, H2O is a charge neutral molecule and the B-terminated surfaces show a very weak adsorption to it, the topological surface are states still inside the nodal lines. Fig. 7(f) shows the surface adsorbing H2O to the slab model on both sides, the inversion symmetry of the slab model is restored, and the surface bands are degenerate. Also, the surface bands change slightly compared with Fig. 7(d). In either case, the topological surface states are always inside the nodal lines since H2O is electric neutrality molecule and the surface slab has very weak adsorption for H2O. The determination of the surface states’ position is shown in Fig. S4 of ESI† (ref. 46). . Meanwhile, it is shown that either Mg- or B-terminated surface has a very strong adsorption for OH, and then H, while has only weak adsorption for H2O, and the surface states have a crucial change after the adsorption for H, less change after the adsorption for OH, and only very slight change after the adsorption for H2O, which can be understood systematically by combining the surface adsorption free energies
. Meanwhile, it is shown that either Mg- or B-terminated surface has a very strong adsorption for OH, and then H, while has only weak adsorption for H2O, and the surface states have a crucial change after the adsorption for H, less change after the adsorption for OH, and only very slight change after the adsorption for H2O, which can be understood systematically by combining the surface adsorption free energies  , surface terminations, and surface charge density distributions. Particularly, we propose the value of the band structural change of topological surface state ΔETSS as an index to describe the disturbance of adsorbates to the topological surface states. Analyzing the relationships among Bader charge transfer, adsorption Gibbs free energy, and bond length to ΔETSS, we observed a high correlation solely between ΔETSS and the Bader charge transfer of the surface B atoms. The Bader charge transfer value of the surface B atoms providing the topological state should be a key indicator for evaluating the variation in topological surface states after adsorbing H, OH, and H2O adsorbates. Our work has provided a systematical understanding on the variation of topological surface states after surface adsorptions, and will also pave the way for future studies on the device applications of topological materials.
, surface terminations, and surface charge density distributions. Particularly, we propose the value of the band structural change of topological surface state ΔETSS as an index to describe the disturbance of adsorbates to the topological surface states. Analyzing the relationships among Bader charge transfer, adsorption Gibbs free energy, and bond length to ΔETSS, we observed a high correlation solely between ΔETSS and the Bader charge transfer of the surface B atoms. The Bader charge transfer value of the surface B atoms providing the topological state should be a key indicator for evaluating the variation in topological surface states after adsorbing H, OH, and H2O adsorbates. Our work has provided a systematical understanding on the variation of topological surface states after surface adsorptions, and will also pave the way for future studies on the device applications of topological materials.






