Open Access Article
Open Access ArticleRevisiting Ce3Pt4Ge6 – crystal structure and physical properties†
Oliver
Janka
*ab,
Rolf-Dieter
Hoffmann
b,
Matthias
Eilers-Rethwisch
b,
Ute Ch.
Rodewald
b,
Oliver
Niehaus
bc and
Rainer
Pöttgen
b
aInstitut für Chemie, Carl von Ossietzky Universität, Carl-von-Ossietzky Strasse 9-11, D-26129 Oldenburg, Germany. E-mail: ocjanka@uni-muenster.de
bInstitut für Anorganische und Analytische Chemie, Universität Münster, Corrensstraße 30, D-48149 Münster, Germany
cNRW Graduate School of Chemistry, Universität Münster, Corrensstraße 30, D-48149 Münster, Germany
First published on 19th August 2016
Abstract
Structural reinvestigations of Ce3Pt4Ge6 on high quality single crystals revealed additional reflections contradicting the previously reported structure featuring half occupied crystallographic sites for this compound. The structure could be solved and refined in the orthorhombic (3 + 1)D superspace group Cmcm(α,0,0)0s0 with α = 0.5a* and lattice parameters of a = 441.17(2), b = 2618.26(14) and c = 441.33(2) pm using the super space approach. The description of the modulated structure as commensurate case allows for an ordering of the Ce2/Ge3 atoms and the respective voids caused by the 50% occupation. The corresponding approximant can be described in the orthorhombic crystal system with space group Pnma and lattice parameters of a = 2618.26(14), b = 441.33(2) and c = 882.34(2) pm. Investigations of the magnetic properties revealed a magnetic moment of μeff = 2.48(1)μB/Ce atom and a Weiss constant of θp = −39(5) K, indicating stable trivalent cerium. No clear magnetic ordering was evident from the susceptibility measurements. Heat capacity investigations showed a λ-shaped anomaly at T = 2.1(1) K. Resistivity measurements show values corresponding to Ce3Pt4Ge6 being a metal, however nearly temperature independent behavior is observed down to low temperatures. A shallow minimum and an abrupt drop suggest the title compound to be a Kondo material.
Introduction
The isothermal section of the Ce–Pt–Ge phase diagram at 873 K has carefully been studied by Gribanov et al.1 The phase analytical work, based on X-ray powder and single crystal diffraction as well as metallography in combination with electron microscopy revealed 12 ternary germanides. Most of the structures of these phases have been solved and preliminary physical property studies have been performed.2–23 To give some examples, CePtGe9,19 and CePt2Ge210 order antiferromagnetically at TN = 4 and 2.2 K, respectively. CePt5Ge3 is a low-dimensional magnetic material with an ordering temperature of 1.1 K.21In the original work, the structures of CePtGe3 and Ce3Pt4Ge611 were reported with mixed and partially occupied sites, respectively. Reinvestigation of the CePtGe structure18,19 revealed weak superstructure reflections, originating from platinum–germanium ordering. The single crystal data clearly stated the orthorhombic YPdSi structure type. The Ce3Pt4Ge6 structure11 was refined in space group Bmmb (non-standard setting of Cmcm) with half-occupied Ce2 (4c) and Ge3 (8g) sites. Similar composition, but different space group symmetry was observed for the RE3Pt4Ge6 representatives with the smaller rare earth (RE) elements.24–26 The Y3Pt4Ge6 structure24 as well as the silicide Yb∼3Pt∼4Si6−x (x = 0.3)26 were described in the monoclinic space group P21/m and the germanides RE3Pt4Ge6 (RE = Pr, Nd, Sm, Gd, Tb, Dy)25 were reported with space group Pnma which allows for an ordering of all atomic sites. Reinvestigation of the Ce3Pt4Ge6 structure by these authors gave hints for cerium–germanium ordering. Single crystals taken from a long-term annealed sample showed diffuse intensities.
We became interested in these order–disorder problems when solving the structure of a new monoclinic cerium–gold–germanide with an approximate composition Ce3Au∼5.5Ge∼4.527 and presumably Y3Pt4Ge6 structure. In the course of these systematic investigations we also synthesized new Ce3Pt4Ge6 samples and obtained well shaped single crystals upon annealing arc-melted precursors in a water-cooled sample chamber of an induction furnace. Herein we report on crystal chemical data on the ordered phase and the magnetic properties of Ce3Pt4Ge6. The order–disorder difficulty is discussed on the basis of a group–subgroup scheme.
Experimental
Synthesis
Ce3Pt4Ge6 was synthesized from the elements using cerium ingots (Sigma-Aldrich), platinum sheets (Agosi AG), and germanium lumps (Chempur), all with stated purities better than 99.9%. Pieces of cerium were first arc-melted under an argon pressure of 800 mbar in a water cooled copper heart.28 All starting materials were weighed in the ideal 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4
4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 ratio (Ce
6 ratio (Ce![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pt
Pt![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ge) and arc-melted under an argon pressure of 800 mbar. The obtained button was remelted and turned over several times to increase the homogeneity. In a subsequent step the ingot was heated to temperatures just below the melting point for 2 h in a high frequency furnace (Hüttinger Elektronik, Freiburg, Germany, Typ TIG 2.5/300).29 Afterwards the sample was slowly cooled to room temperature. The sample shows metallic luster and is stable in air over months.
Ge) and arc-melted under an argon pressure of 800 mbar. The obtained button was remelted and turned over several times to increase the homogeneity. In a subsequent step the ingot was heated to temperatures just below the melting point for 2 h in a high frequency furnace (Hüttinger Elektronik, Freiburg, Germany, Typ TIG 2.5/300).29 Afterwards the sample was slowly cooled to room temperature. The sample shows metallic luster and is stable in air over months.
X-ray diffraction
The polycrystalline sample was characterized by a Guinier pattern (imaging plate detector, Fujifilm BAS-1800 scanner) with CuKα1 radiation using α-quartz (a = 491.30, c = 540.46 pm, Riedel-de-Häen) as an internal standard.Correct indexing of the diffraction lines was ensured through an intensity calculation. The lattice parameters were obtained through least-squares fits30 with standard deviations smaller than ±0.1 pm for all axes.
Irregularly shaped crystals of Ce3Pt4Ge6 were obtained by mechanical fragmentation of the annealed arc-melted button. These fragments were glued to thin quartz fibers using beeswax. The crystal quality was tested by Laue photographs on a Buerger camera (white molybdenum radiation, image plate technique, Fuji film, BAS-1800). Intensity data sets of a suitable crystal were collected at room temperature by use of a Stoe IPDS II diffractometer (graphite-monochromatized MoKα radiation; oscillation mode). Numerical absorption correction was applied to the data set. All relevant crystallographic data and details of the data collections and evaluations are listed in Table 1.
| Empirical formula | Ce3Pt4Ge6 |
| Superspace group | Cmcm(α,0,0)0s0 |
| α = 1/2 a* | |
| Molar mass | 1636.2 g mol−1 |
| Unit cell dimensions | a = 441.17(2) pm |
| b = 2618.26(14) pm | |
| c = 441.33(2) pm | |
| V = 0.5098 nm3 | |
| Calculated density | 10.66 g cm−3 |
| Linear absorption coeff. | 85.0 mm−1 |
| Transm. ratio (min/max) | 0.096, 0.190 |
| F(000) | 1356 |
| Crystal size/μm | 30 × 30 × 35 |
| Diffractometer | IPDS-II |
| Wavelength | MoKα (71.073 pm) |
| Detector distance | 90 mm |
| Exposure time | 8 min |
| Integr. param./A, B, EMS | 9.9/1.5/0.012 |
| θ range | 2.4–30.7 ° |
| Range in hklm | ±6; ±37; ±6; ±1 |
| Total no. reflections | 23224 |
| Independent reflections | 1360 (Rint = 0.0519) |
| Reflections with I ≥ 3σ(I) | 930 (Rσ = 0.0112) |
| Main + satellite | 930 + 430 |
| Data/parameters | 1360/63 |
| Goodness-of-fit | 2.07 |
| Final R indices [I ≥ 3σ(I)] | R M = 0.0186/wRM = 0.0451 |
| R S = 0.0751/wRS = 0.1480 | |
| R indices for all data | R M = 0.0227/wRM = 0.0459 |
| R S = 0.1243/wRS = 0.1557 | |
| Extinction scheme | Lorentzian isotropic31 |
| Extinction coefficient | 222(12) |
| Largest diff. peak and hole/e Å−3 | 8.71, −3.64 |
Further details on the structure refinement are available from Fachinformationszentrum Karlsruhe, D-76344 Eggenstein-Leopoldshafen (Germany), E-mail: crysdata@fiz-karlsruhe.de, by quoting the Registry no. CSD 431566.
Physical property investigations
Results and discussion
Structure refinement
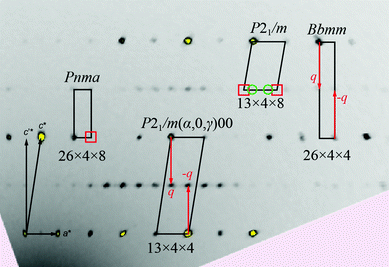
The obtained intensity data set of Ce3Pt4Ge6 was initially indexed in analogy to the structure solution of Pr3Pt4Ge6 in the orthorhombic space group Pnma (no. 62) with lattice parameters of a = 2625.4(8), b = 439.3(1) and c = 884.0(3) pm.25 However both, the monoclinic unit cell (a = 882.8(2), b = 441.24(8), c = 1325.5(3) pm and β = 99.62(2) °) in analogy to Y3Pt4Ge624 as well as an orthorhombic C-centered cell with space group Cmcm (a = 441.9(1), b = 2622.2(5), c = 442.2(1) pm) in analogy to the first report of Ce3Pt4Ge611 could be found using the automated indexing features. Fig. 1 shows a selected h1l area of the reconstructed diffraction patterns indicating the cells found in literature as well as our interpretation. A careful investigation of the reconstructed diffraction patterns indicated systematically extinct reflections (red square) needed in order to justify the P-centered orthorhombic cell (Fig. 1, left). For the C-centered orthorhombic cell (denoted as Bbmm here) additional reflections along 1/2 c* are found in our diffraction experiments making this interpretation as 3D structure obsolete (Fig. 1, right).Finally the description in the P-centered monoclinic cell lacks the interpretation of the additional reflections with 1/4 a* (green circles) and exhibits systematically absent reflection violations (red squares) for the interpretation as a primitive lattice (Fig. 1, top). A closer look at the reconstructed diffraction patterns reveals two possibilities to index all observed reflections. One possibility is to use the depicted Bbmm cell shown in Fig. 1 (right) along with a q-vector q = (0, 0, 1/2 c*), the other one is to use the depicted monoclinic cell with q = (1/4 a*, 0, 1/2 c*). Both possible cell settings have been integrated including all satellite reflections. The structure was subsequently solved by the program package Superflip,33 included in the Jana2006 package, which was used for the refinement.34,35 The corresponding superspace groups Cmcm(α,0,0)0s0 (SSG 63.1.13.2) and P21/m(α,0,γ)00 (SSG 11.1.2.1) have been identified. The notation of Stokes, Campbell and van Smaalen for the superspace groups was used.36,37 Since both refinements gave identical residuals, the higher symmetry was chosen and will be described in the following. The symmetry operations for the orthorhombic superspace group are listed in Table 2.
| x1 | x2 | x3 | x4 |
| −x1 | −x2 | x3 + 1/2 | −x4 |
| −x1 | x2 | −x3 + 1/2 | −x4 + 1/2 |
| x1 | −x2 | −x3 | x4 + 1/2 |
| −x1 | −x2 | −x3 | −x4 |
| x1 | x2 | −x3 + 1/2 | x4 |
| x1 | −x2 | x3 + 1/2 | x4 + 1/2 |
| −x1 | x2 | x3 | −x4 + 1/2 |
| x1 + 1/2 | x2 + 1/2 | x3 | x4 |
| −x1 + 1/2 | −x2 + 1/2 | x3 + 1/2 | −x4 |
| −x1 + 1/2 | x2 + 1/2 | −x3 + 1/2 | −x4 + 1/2 |
| x1 + 1/2 | −x2 + 1/2 | −x3 | x4 + 1/2 |
| −x1 + 1/2 | −x2 + 1/2 | −x3 | −x4 |
| x1 + 1/2 | x2 + 1/2 | −x3 + 1/2 | x4 |
| x1 + 1/2 | −x2 + 1/2 | x3 + 1/2 | x4 + 1/2 |
| −x1 + 1/2 | x2 + 1/2 | x3 | −x4 + 1/2 |
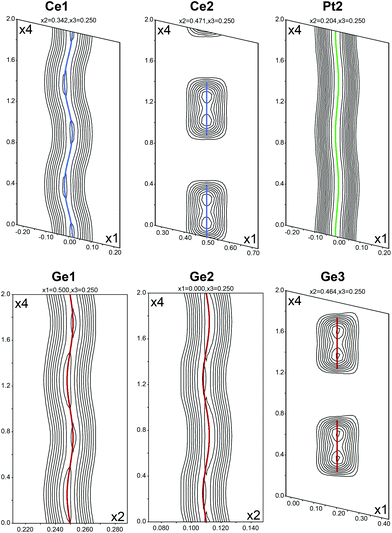
After refinement of the basic structure the satellites were added to the refinement and positional or occupational modulations for all atoms were applied. In addition, it was possible to refine modulated anisotropic atomic displacement parameters (ADP) for all atoms. The Fourier maps for all atoms showing significant modulations are depicted in Fig. 2. The space group allows for additional degrees of freedom, however some modulation components are very small (Table 3). While Ce1, Pt1, Pt2, Ge1 and Ge2 show positional modulations along x1/x4 and x3/x4, Ce2 and Ge3 exhibit occupational modulations along x3/x4. The occupational modulations were fitted using a crenel function; for the positional modulations simple harmonic functions were used. As a check for the correct composition, the occupancy parameters were refined in a separate series of least-squares cycles. All sites were fully occupied within three standard deviations. There was no indication of mixing on any site. The final difference electron-density synthesis was flat.
| Atom | Occ. | Wave | x | y | z | U eq |
|---|---|---|---|---|---|---|
| Ce1 | 1 | 0 | 0.34219(3) | 1/4 | 96(2) | |
| sin | 0.0174(3) | 0 | 0 | |||
| cos | 0 | 0.00002(5) | 0 | |||
| Ce2 | 0.5 | 1/2 | 0.47112(4) | 1/4 | 94(3) | |
| x40 = 0.25 | crenel | — | — | — | ||
| Pt1 | 1 | 1/2 | 0.06271(1) | 1/4 | 77(1) | |
| sin | 0.00094(17) | 0 | 0 | |||
| cos | 0 | −0.00009(3) | 0 | |||
| Pt2 | 1 | 0 | 0.20433(1) | 1/4 | 97(1) | |
| sin | −0.00671(19) | 0 | 0 | |||
| cos | 0 | −0.00259(3) | 0 | |||
| Ge1 | 1 | 1/2 | 0.24984(5) | 1/4 | 94(3) | |
| sin | 0.0061(5) | 0 | 0 | |||
| cos | 0 | −0.00197(9) | 0 | |||
| Ge2 | 0.5 | 0 | 0.11020(6) | 1/4 | 146(4) | |
| sin | 0.0003(5) | 0 | 0 | |||
| cos | 0 | −0.00203(10) | 0 | |||
| Ge3 | 1 | 0.2039(3) | 0.46437(6) | 1/4 | 120(4) | |
| x40 = 0.6 | crenel | — | — | — |
Due to the q-vector component α = 1/2 a*, the crystal structure can be refined as commensurate case in the corresponding orthorhombic superstructure with space group Pbnm and a doubled a axis. Standardization finally leads to space group Pnma and lattice parameters of a = 2618.26(14), b = 441.33(2) and c = 882.34(2) pm. This unit cell corresponds to the solution of the compounds in the RE3Pt4Ge6 (RE = Pr–Dy) series,25 however in our description all intensities were handled avoiding non-space group specific extinctions.
Crystal chemistry
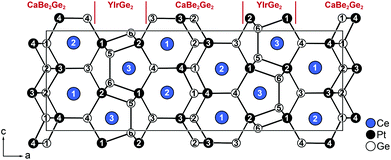
The building blocks and motifs obtained by the refinement are the same compared to those presented in the previous descriptions in the orthorhombic space groups Cmcm,11Pnma25 and the monoclinic description of Y3Pt4Ge6 in the space group P21/m.24 However one previous work needed half-occupied sites for Ce and Ge atoms in order to describe the structure.11 The other papers stated either the solution was achieved by “crystal chemical considerations”24 or mentioned that the unit cell was chosen under “consideration of the very weak reflections causing a doubling of the a axis”.25 These statements suggest that the diffraction patterns might have looked comparable to our investigations (vide supra), but were misinterpreted.Using the motifs highlighted by Venturini et al. for Y3Pt4Ge6, the structure can be described as an intergrowth between CaBe2Ge2- and YIrGe2-type slabs. The latter forms pentagonal prisms built by Ir and Ge (here Pt and Ge), which are linked alternatively (up/down) to form layers that are connected further over the pentagonal faces to form a three-dimensional framework. The pentagonal prisms are occupied by the Y3+ cations, here Ce2. The CaBe2Ge2 arrangements consist of tetrahedral [GeBe4/4] layers (here Pt and Ge), which are stacked along [100] and exhibit only Ge–Be bonds. The six-membered rings formed by the stacking of the layers are occupied by the Ca2+ cations, here Ce1. Due to the occupational modulation of the Ce2 and Ge3 atoms, the pentagonal prisms are allowed to order, facing either to the right or to the left along the a axis. In contrast to the description of Gribanov et al., no half occupied sites are needed in this description. The positional modulation can be easily understood since the orientation of the five membered rings influences the surrounding atoms of the remaining framework. The Pt1 atoms are the nearest neighbors of the five-membered rings, Ge2 is a part of the ring itself; therefore these atoms exhibit the strongest positional modulations along [100]. The remaining atoms follow the deformation of the framework, resulting in slightly lower amplitudes of the sin and cos functions (Table 3). In order to describe the crystal structure of Ce3Pt4Ge6 a commensurate description can be used, which is obtained via a doubling of the a axis followed by a standardization. The detailed group–subgroup relations will be discussed in the following paragraph (vide infra). The resulting orthorhombic 3D-approximant (Pnma, a = 2618.26(14), b = 441.33(2) and c = 882.34(2) pm) describes the crystal structure without the need of half-occupied sites.
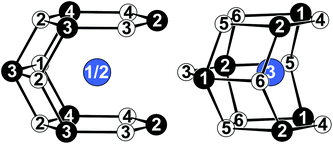
The crystallographic sites present in the modulated description split, resulting in three Ce, four Pt and six Ge sites. The structural elements described before are found as well in this model and are combined as shown in Fig. 3. In Fig. 4 the coordination polyhedra surrounding the Ce1/2 (left) and Ce3 (right) atoms are depicted. The refined anisotropic displacement parameters are listed in Table 4, interatomic distances in Table 5.
| Atom | U 11 | U 22 | U 33 | U 12 |
|---|---|---|---|---|
| Ce1 | 101(3) | 93(3) | 94(3) | 0 |
| Ce2 | 89(4) | 98(4) | 96(5) | 0 |
| Pt1 | 66(2) | 93(2) | 73(2) | 0 |
| Pt2 | 87(2) | 109(2) | 94(2) | 0 |
| Ge1 | 79(5) | 122(6) | 81(6) | 0 |
| Ge2 | 80(5) | 96(6) | 262(8) | 0 |
| Ge3 | 116(6) | 147(6) | 97(7) | −28(5) |
| Ce1 | 2 | Ge4 | 251.66(1) | Ce2 | 2 | Pt3 | 249.77(1) | Ce3 | 2 | Pt2 | 237.84(1) | Pt1 | 1 | Ce3 | 239.61(1) | Pt2 | 2 | Ce3 | 237.84(1) |
| 2 | Pt4 | 254.45(1) | 2 | Ge3 | 255.40(1) | 1 | Pt1 | 239.61(1) | 1 | Ge3 | 251.14(1) | 2 | Ge6 | 248.77(1) | |||||
| 1 | Ge1 | 325.20(1) | 1 | Ge1 | 327.63(1) | 2 | Ge5 | 307.05(1) | 1 | Ge4 | 255.34(1) | 1 | Ge3 | 251.13(1) | |||||
| 1 | Ge2 | 327.05(1) | 1 | Ge2 | 329.60(1) | 1 | Ge5 | 311.04(1) | 2 | Ge5 | 265.86(1) | 1 | Ge4 | 255.33(1) | |||||
| 1 | Ge6 | 343.50(2) | 1 | Ge5 | 333.86(2) | 2 | Ge3 | 375.68(1) | 1 | Ge6 | 272.66(1) | 1 | Ge5 | 288.73(1) | |||||
| 1 | Pt3 | 365.87(2) | 1 | Pt4 | 356.18(2) | 2 | Ge4 | 379.92(1) | 2 | Pt2 | 395.62(2) | 2 | Ge5 | 387.29(1) | |||||
| 2 | Ge2 | 394.54(1) | 2 | Ge2 | 392.41(1) | 2 | Pt1 | 395.62(2) | |||||||||||
| 2 | Ge1 | 396.19(1) | 2 | Ge1 | 393.96(1) | 2 | Ce2 | 395.99(1) | |||||||||||
| 2 | Pt2 | 396.25(1) | 2 | Pt2 | 395.99(1) | 2 | Ce1 | 396.25(1) | |||||||||||
| Pt3 | 1 | Ge3 | 245.44(1) | Pt4 | 1 | Ge4 | 247.52(1) | Ge1 | 2 | Ge2 | 220.70(1) | Ge2 | 2 | Ge1 | 220.70(1) | Ge3 | 1 | Pt3 | 245.44(1) |
| 2 | Ce2 | 249.77(1) | 1 | Ge2 | 249.99(1) | 1 | Pt4 | 250.38(1) | 1 | Pt4 | 249.99(1) | 1 | Pt2 | 251.13(1) | |||||
| 1 | Ge2 | 251.38(1) | 1 | Ge1 | 250.38(1) | 1 | Pt3 | 251.43(1) | 1 | Pt3 | 251.38(1) | 1 | Pt1 | 251.14(1) | |||||
| 1 | Ge1 | 251.43(1) | 2 | Ce1 | 254.45(1) | 1 | Ce1 | 325.20(1) | 1 | Ce1 | 327.05(1) | 2 | Ce2 | 255.40(1) | |||||
| 2 | Pt4 | 325.42(1) | 2 | Pt3 | 325.42(1) | 1 | Ce2 | 327.63(1) | 1 | Ce2 | 329.60(1) | 2 | Ge5 | 305.67(1) | |||||
| 2 | Ge1 | 337.29(1) | 2 | Ge1 | 331.25(1) | 2 | Pt4 | 331.25(1) | 2 | Pt4 | 331.48(1) | 2 | Ce3 | 375.68(1) | |||||
| 2 | Ge2 | 337.35(1) | 2 | Ge2 | 331.48(1) | 2 | Pt3 | 337.29(1) | 2 | Pt3 | 337.35(1) | 1 | Ge5 | 388.62(2) | |||||
| 1 | Ce1 | 365.87(2) | 1 | Ce2 | 356.18(2) | 2 | Ce2 | 393.96(1) | 2 | Ce2 | 392.41(1) | ||||||||
| 2 | Ce1 | 396.19(1) | 2 | Ce1 | 394.54(1) | ||||||||||||||
| Ge4 | 1 | Pt4 | 247.52(1) | Ge5 | 2 | Pt1 | 265.86(1) | Ge6 | 2 | Pt2 | 248.77(1) | ||||||||
| 2 | Ce1 | 251.66(1) | 1 | Pt2 | 288.73(1) | 1 | Pt1 | 272.66(1) | |||||||||||
| 1 | Pt2 | 255.33(1) | 2 | Ge3 | 305.67(1) | 2 | Ge4 | 324.63(1) | |||||||||||
| 1 | Pt1 | 255.34(1) | 2 | Ce3 | 307.05(1) | 1 | Ce1 | 343.50(2) | |||||||||||
| 2 | Ge6 | 324.63(1) | 1 | Ce3 | 311.04(1) | 2 | Ge5 | 363.54(1) | |||||||||||
| 2 | Ce3 | 379.92(1) | 1 | Ce2 | 333.86(2) | 2 | Ge6 | 389.56(1) | |||||||||||
| 2 | Ge5 | 340.39(1) | |||||||||||||||||
| 2 | Ge6 | 363.54(1) | |||||||||||||||||
| 2 | Pt2 | 387.29(1) | |||||||||||||||||
| 1 | Ge3 | 388.62(2) | |||||||||||||||||
The annealing temperature and the cooling rate are important parameters for the growth of high quality crystals. The structural details of Ce3Pt4Ge6 are comparable to the recently reported stannide Ce3Pt4Sn6.38 The stannide crystals showed smeared out reflections and disorder.
Group–subgroup relations
As mentioned before, the crystal structure of Ce3Pt4Ge6 can be derived from the published orthorhombic cell with space group Cmcm.11 The title compound, however, clearly shows additional reflections which were interpreted as satellite reflections, pointing towards an also C-centered orthorhombic (3 + 1)D superspace group. The according superspace group associated to the 3D space group is shown on the top left in Fig. 5. Due to α = 0.5 of the q-vector, the structure can be described as commensurately modulated. Therefore a description as approximant by a projection onto 3D space can be used. The corresponding 3D space group for this description is Pbnm. This is achieved by a transition of index a4 where a is introduced synonymously for approximant.39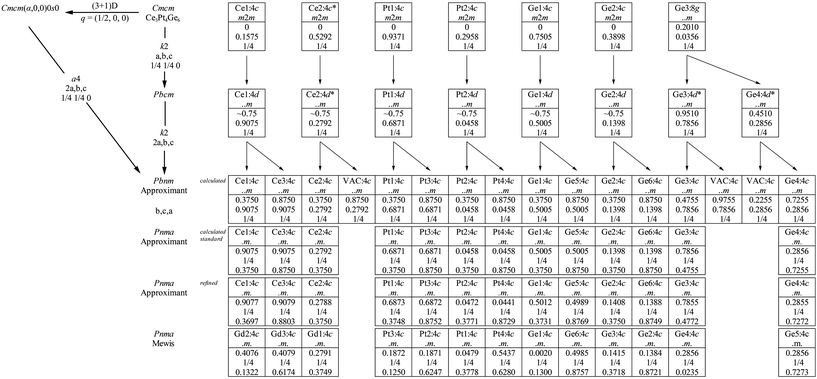 | ||
| Fig. 5 Relation of the (3 + 1)D and 3D space groups of the modulated structure of Ce3Pt4Ge6. Group–supgroup scheme in the Bärnighausen formalism40–43 for the subcell of Ce3Pt4Ge6 (*occupancy parameter listed as 50% in the literature24) and the supercell. The indices for the klassengleiche (k) symmetry reduction as well as the evolution of the atomic parameters are given. The index a is introduced for the formation of the approximant of the modulated structure.39 The last line gives the atomic coordinates for Gd3Pt4Ge6, published by Mewis in space group Pnma.25 | ||
Here two transitions are involved, a doubling of the a axis along with a loss of the centering and an origin shift of (1/4, 1/4, 0). The a4 transition is paralleled by two k2 transitions in 3D space. First a symmetry reduction from Cmcm to Pbcm by a klassengleiche transition of index 2 takes place, which is accompanied by an origin shift of (1/4, 1/4, 0). In the second step again a klassengleiche transition of index 2 takes place, allowing the doubling of the a axis. The final step is used to reach the standard setting of Pbnm, the orthorhombic space group Pnma. The group–supgroup scheme in the Bärnighausen formalism40–43 is shown in Fig. 5. The observed disorder and diffuse superstructure reflections of38 have their origin most likely in the occurrence of anti phase boundaries triggered by the klassengleiche transitions.
Magnetic properties
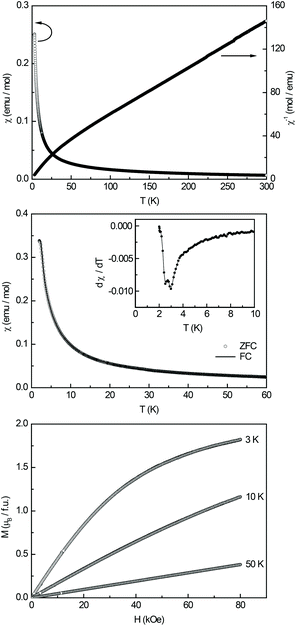
The magnetic properties of Ce3Pt4Ge6 were determined via susceptibility and magnetization experiments. Fig. 6 (top) shows the temperature dependence of the magnetic and inverse magnetic susceptibility (χ and χ−1 data) measured at 10 kOe. A fit of the χ−1 data in the region above 50 K using the Curie–Weiss law, revealed an effective magnetic moment of μeff = 2.48(1)μB/Ce atom and a Weiss constant of θp = −39(5) K. The effective magnetic moment matches well with the theoretical value of 2.54μB for a free Ce3+-ion indicating a stable trivalent ground state. The obvious negative value of the Weiss constant can be attributed to antiferromagnetic interactions in the paramagnetic regime, however crystal electric field splitting is a common feature in cerium intermetallics44–46 and also responsible for the curvatures in the low temperature region.To obtain more information about the magnetic ground state, a low-field measurement was performed in a zero-field- and field-cooled mode (ZFC/FC) which is shown in the middle graph of Fig. 6. No anomaly indicating clear magnetic ordering could be detected in this measurement, however in the low temperature region saturation effects can be observed, while the derivative dχ/dT shows a double feature at 2.5(1) K and 3.0(1) K (Fig. 6, inset). No bifurcation between the ZFC and FC curve is visible.
The bottom graph in Fig. 6 displays the magnetization isotherms of Ce3Pt4Ge6 measured at 3, 10, and 50 K. The isotherms at 10 and 50 K both display a linear field dependency of the magnetization as expected for a paramagnetic material. With respect to the 10 K isotherm less saturation effects are visible at 50 K. At 3 K a curvature of the magnetization isotherm can be observed with weak saturation effects towards higher fields. The magnetic moment at 3 K and 80 kOe is 0.61(5)μB/Ce atom which is significantly below the expected saturation magnetization of 2.14μB/Ce according to gJ × J. Magnetic susceptibility measurements reported in the literature1 found no ordering phenomena and a reduced magnetic moment of μeff = 2.19μB between 40 and 140 K and a moment of μeff = 1.86μB above 150 K. Between 140 and 150 K an anomaly is observed which is in agreement with their resistivity measurements (vide supra). A magnetization isotherm at 5.5 K shows a small hysteresis. Both, the reduced moment and the anomaly between 140–150 K, are in contrast to our investigations. However the authors report their sample to be “predominantly single phase”, which might be an explanation for the missing features in our investigations.
Heat capacity
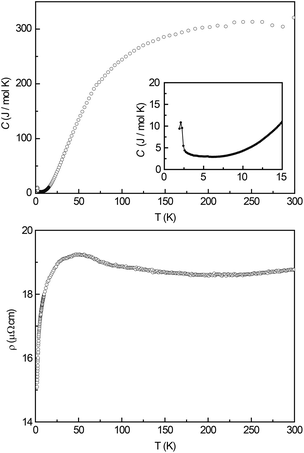
In order to check for magnetic phase transitions by a second method, heat capacity measurements were conducted in the temperature region between 1.9 and 300 K. Fig. 7 (top) depicts the full temperature scale, the inset displays the low temperature region between 1.9 and 15 K. Here a clear λ-shaped anomaly can be observed with a maximum at T = 2.1(1) K indicating a magnetic phase transition. This anomaly is in good agreement with the change of the slope of the ZFC/FC curve and its derivative.Electrical resistivity
Fig. 7 (bottom) shows the electrical resistivity of Ce3Pt4Ge6 between 2 K and 300 K. Down to about 75 K, the resistivity shows a nearly temperature independent behaviour. However a shallow minimum around 200 K is clearly visible. Below 75 K, the resistivity increases with a broad maximum centred at 50 K. When going to lower temperatures, a significant drop is observed. This behaviour is indicative of Kondo lattice systems. The upturn in the resistivity can be explained by the screening of the conduction electrons at the localized 4f1 electron from the Ce3+ ions.Conclusions
We have resynthesized Ce3Pt4Ge6 and reinvestigated its crystal structure. A commensurate modulated structure has been found. The structure can be solved and refined in the orthorhombic superspace group Cmcm(α,0,0)0s0 with α = 1/2 a*. The superspace group correlates with the orthorhombic description of Pr3Pt4Ge6 with space group Pnma, however the latter exhibits non space group specific extinction conditions. Magnetic investigations indicate that the cerium atoms are in the +3 oxidation state. Heat capacity measurements show a λ-anomaly at T = 2.1(1) K. Resistivity measurements confirmed the metallic nature, the temperature dependent behavior exhibits a broad maximum centered around 50 K followed by an abrupt drop below, suggesting Kondo behavior for the title compound.Acknowledgements
This work was supported by the Deutsche Forschungs-gemeinschaft. O. N. is indebted to the NRW Forschungsschule Molecules and Materials – A common Design Principle for a PhD stipend.Notes and references
- A. V. Gribanov, Y. D. Seropegin, O. I. Bodak, V. N. Nikiforov, A. A. Velikhovskii and J. Mirkovic, J. Phase Equilib., 1996, 17, 196–207 CrossRef CAS.
- D. Rossi, R. Marazza and R. Ferro, J. Less-Common Met., 1979, 66, P17–P25 CrossRef CAS.
- E. Hovestreydt, N. Engel, K. Klepp, B. Chabot and E. Parthé, J. Less-Common Met., 1982, 85, 247–274 CrossRef CAS.
- A. Dommann, F. Hulliger, H. R. Ott and V. Gramlich, J. Less-Common Met., 1985, 110, 331–337 CrossRef CAS.
- M. François, G. Venturini, E. McRae, B. Malaman and B. Roques, J. Less-Common Met., 1987, 128, 249–257 CrossRef.
- P. Rogl, B. Chevalier, M. J. Besnus and J. Etourneau, J. Magn. Magn. Mater., 1989, 80, 305–310 CrossRef CAS.
- G. Venturini, B. Malaman and B. Roques, J. Less-Common Met., 1989, 146, 271–278 CrossRef CAS.
- O. I. Bodak, Y. D. Seropegin, O. L. Sologub, V. K. Pecharsky and A. V. Gribanov, Abstr. Eur. Crystallogr. Meet. 12th, 1989, 2–39.
- L. Rebelsky, K. Reilly, S. Horn, H. Borges, J. D. Thompson and R. Caspary, J. Appl. Phys., 1990, 67, 5206–5208 CrossRef CAS.
- I. Das, E. V. Sampathkumaran, R. Nagarajan and R. Vijayaraghavan, Phys. Rev. B: Condens. Matter, 1991, 43, 13159–13163 CrossRef CAS.
- A. V. Gribanov, O. L. Sologub, P. S. Salamakha, O. I. Bodak, Yu. D. Seropegin and V. K. Pecharsky, J. Alloys Compd., 1992, 179, L7–L11 CrossRef CAS.
- A. V. Gribanov, O. L. Sologub, P. S. Salamakha, O. I. Bodak, Yu. D. Seropegin, V. V. Pavlyuk and V. K. Pecharsky, J. Alloys Compd., 1992, 189, L11–L13 CrossRef.
- A. V. Gribanov, O. L. Sologub, P. S. Salamakha, Yu. D. Seropegin and O. I. Bodak, Tez. Dokl. Sov. Kristallokhim. Koord. Soeden 6th, 1992, 172.
- A. V. Gribanov, Yu. D. Seropegin, O. I. Bodak, V. V. Pavlyuk, L. G. Akselrud, V. N. Nikiforov and A. A. Velikhovski, J. Alloys Compd., 1993, 202, 133–136 CrossRef CAS.
- O. Sologub, K. Hiebl, P. Rogl and O. I. Bodak, J. Alloys Compd., 1995, 227, 37–39 CrossRef CAS.
- Y. D. Seropegin, A. V. Gribanov and O. I. Bodak, Abstr. 6th Int. Conf. Crystal Chem. Intermet. Compd., 1995, 93.
- A. V. Morozkin, Yu. D. Seropegin, A. V. Gribanov and J. M. Barakatova, J. Alloys Compd., 1997, 256, 175–191 CrossRef CAS.
- D. Niepmann, R. Pöttgen, Yu. M. Prots’ and W. Jeitschko, Z. Kristallogr., 1998,(Suppl. 15), 49 Search PubMed.
- Yu. M. Prots’, R. Pöttgen, D. Niepmann, M. W. Wolff and W. Jeitschko, J. Solid State Chem., 1999, 142, 400–408 CrossRef.
- J. Sakurai, D. Huo, D. Kato, T. Kuwai, Y. Isikawa and K. Mori, Physica B, 2000, 281&282, 98–100 CAS.
- Z. Hossain, T. Takabatake, C. Geibel, P. Gegenwart, I. Oguro and F. Steglich, J. Phys.: Condens. Matter, 2001, 13, 4535–4542 CrossRef CAS.
- W. Hermes, U. Ch. Rodewald, B. Chevalier and R. Pöttgen, Z. Naturforsch., B: Chem. Sci., 2007, 62, 613–616 CAS.
- R. Gumeniuk, H. Borrmann, A. Ormeci, H. Rosner, W. Schnelle, M. Nicklas, Yu. Grin and A. Leithe-Jasper, Z. Kristallogr., 2010, 225, 531–543 CrossRef CAS.
- G. Venturini and B. Malaman, J. Less-Common Met., 1990, 167, 45 CrossRef CAS.
- A. Imre, A. Hellmann and A. Mewis, Z. Anorg. Allg. Chem., 2006, 632, 1145–1149 CrossRef CAS.
- A. Gribanov, P. Rogl, A. Grytsiv, Yu. Seropegin and G. Giester, J. Alloys Compd., 2013, 571, 93–97 CrossRef CAS.
- B. Heying and R. Pöttgen, unpublished results.
- R. Pöttgen, T. Gulden and A. Simon, GIT Labor-Fachz., 1999, 43, 133–136 Search PubMed.
- R. Pöttgen, A. Lang, R. D. Hoffmann, B. Künnen, G. Kotzyba, R. Müllmann, B. D. Mosel and C. Rosenhahn, Z. Kristallogr., 1999, 214, 143–150 Search PubMed.
- K. Yvon, W. Jeitschko and E. Parthé, J. Appl. Crystallogr., 1977, 10, 73–74 CrossRef.
- P. J. Becker and P. Coppens, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Cryst., 1974, 30, 129–147 CrossRef.
- L. J. van der Pauw, Philips Res. Repts., 1958, 13, 1–9 Search PubMed.
- L. Palatinus and G. Chapuis, J. Appl. Crystallogr., 2007, 40, 786–790 CrossRef CAS.
- V. Petříček, M. Dušek and L. Palatinus, Jana2006. The crystallographic computing system, Institute of Physics, Praha, Czech Republic, 2006 Search PubMed.
- V. Petříček, M. Dušek and L. Palatinus, Z. Kristallogr., 2014, 229, 345–352 Search PubMed.
- H. T. Stokes, B. J. Campbell and S. van Smaalen, Acta Crystallogr., Sect. A: Fundam. Crystallogr., 2011, 67, 45–55 CrossRef CAS PubMed.
- S. van Smaalen, B. J. Campbell and H. T. Stokes, Acta Crystallogr., Sect. A: Fundam. Crystallogr., 2013, 69, 75–90 CAS.
- W. Paschinger, K. Yubuta, Y. Saiga, T. Takabatake, G. Giester and P. Rogl, Solid State Sci., 2016, 55, 48–57 CrossRef CAS.
- O. Niehaus, R.-D. Hoffmann, S. Tencé, B. Chevalier and R. Pöttgen, Z. Kristallogr., 2015, 230, 579–591 CAS.
- H. Bärnighausen, Commun. Math. Chem., 1980, 9, 139–175 Search PubMed.
- H. Bärnighausen and U. Müller, Symmetriebeziehungen zwischen den Raumgruppen als Hilfsmittel zur straffen Darstellung von Strukturzusammenhängen in der Kristallchemie, Universität Karlsruhe und Universität-Gh Kassel, Germany, 1996 Search PubMed.
- U. Müller, Z. Anorg. Allg. Chem., 2004, 630, 1519–1537 CrossRef.
- U. Müller, Symmetry Relationships between Crystal Structures, Oxford University Press, 2013 Search PubMed.
- P. Javorský, L. Havela, V. Sechovský, H. Michor and K. Jurek, J. Alloys Compd., 1998, 264, 38–42 CrossRef.
- B. Chevalier and J. L. Bobet, Intermetallics, 2001, 9, 835–838 CrossRef CAS.
- W. Hermes, R. Mishra, U. C. Rodewald and R. Pöttgen, Z. Naturforsch., B: Chem. Sci., 2008, 63b, 537–542 Search PubMed.
Footnote |
| † Dedicated to Professor Mercouri G. Kanatzidis on the occasion of his 60th birthday. |
| This journal is © the Partner Organisations 2016 |