Benchmarking acetylthiophene derivatives: methyl internal rotations in the microwave spectrum of 2-acetyl-5-methylthiophene†
Christina
Dindić
a and
Ha Vinh Lam
Nguyen
 *bc
*bc
aInstitute of Physical Chemistry, RWTH Aachen University, Landoltweg 2, D-52074 Aachen, Germany
bUniv Paris Est Creteil and Université de Paris, CNRS, LISA, F-94010 Créteil, France. E-mail: lam.nguyen@lisa.ipsl.fr
cInstitut Universitaire de France (IUF), F-75231 Paris cedex 05, France
First published on 14th November 2022
Abstract
The microwave spectrum of 2-acetyl-5-methylthiophene (2A5MT) was recorded using a molecular jet Fourier transform microwave spectrometer working in the frequency range of 2 to 26.5 GHz. The spectrum was assigned to the syn-conformer of the molecule while that of anti-2A5MT was not observable. For the assignment of the spectrum of 2A5MT, adequate spectral analysis skill and quantum chemical benchmarking helped to significantly reduce the time required for recording survey scans. The rotational and centrifugal distortion constants were determined with high accuracy. The experimental values of the rotational constants are compared to those derived from quantum chemical calculations in the course of ongoing benchmarking effort. Splitting of each rotational transition into quintets due to internal rotations of the acetyl methyl and ring methyl groups could be resolved and analysed to yield barriers to internal rotations of 301.811(41) cm−1 and 157.2612(13) cm−1, respectively. These values are compared to those found in other thiophene and furan derivatives in order to understand the electronic effects transmitted through aromatic rings, as well as how different heteroatoms affect torsional barriers. The acetyl methyl group features torsional barriers of around 300 cm−1 if a thiophene derivative is attached at the other side of the carbonyl group. This finding allows the establishment of the so-called “thiophene class” for the acetyl group containing ketones.
1. Introduction
Almost a century ago, torsion oscillator rotation was treated for the first time quantum mechanically by Nielsen in 1932.1 Four years later, from calorimetric measurements, Kemp and Pitzer stated that the methyl torsion in ethane is hindered by a potential barrier, which opened up a new research subject on internal rotation.2 A significant number of studies on molecules containing one or more methyl rotors have been performed, but the barrier and its origin have not been fully understood yet from both experimental and theoretical perspectives.3–7 However, it is known that the height and shape of the torsional potential depend on the conformation of the molecule and the intramolecular interactions. Today, the method probably most accurate to determine the barrier to internal rotation is molecular jet Fourier transform microwave (FTMW) spectroscopy.8–10 Appropriate Hamiltonians accounting for the internal rotation of a methyl group attached onto an asymmetrical frame have been developed using several program codes such as BELGI-Cs,11 BELGI-C1,12 RAM3613 and aixPAM14 for one-top molecules, ERHAM15 for up to two-top molecules, BELGI-Cs-2Tops16 and PAM-C2v-2tops17 for two-top molecules, XIAM18 for up to three-top molecules and ntop for n-top molecules19 (currently tested at n = 4) to solve many internal rotation problems. Nevertheless, analysing the microwave spectra of molecules with multiple methyl rotors (n > 1) is still challenging due to their complexity. If in one-top molecules, A–E torsional doublets are observed for each rotational transition, they appear as quintets in two-top molecules if the rotors are inequivalent. The quintet components are called (σ1σ2) = (00), (01), (10), (11) and (12) species,20 corresponding to the A, E1, E2, E3 and E4 species, respectively, using the permutation–inversion formalism of the G18 group21 or to the AA, AE, EA, EE and EE* species in Dreizler's notation.22 The number of torsional components in the multiplets increases rapidly with the number of rotors present in the molecules.9 With the rapid development of quantum chemical calculations to compute not only the molecular geometries but also the torsional potentials with sufficient accuracy over last few decades, quantum chemistry has become a powerful supporting tool for FTMW spectroscopy to face challenges in analysing spectra with internal rotations.The FTMW results on 2-acetyl-3-methylthiophene (2A3MT)23 and 2-acetyl-4-methylthiophene (2A4MT)24 have been recently published. To further examine the effects of multiple methyl internal rotations, it was natural to continue with the two-top molecule 2-acetyl-5-methylthiophene (2A5MT), which is the last one in a series of 2-acetylmethylthiophenes. From our investigations on 2A3MT and 2A4MT and many further molecules,25–28 it is known that steric and electrostatic effects are the two main factors affecting the torsional barriers. In n-alkyl acetates, the same value of about 100 cm−1 is observed for the barrier to the internal rotation of the acetyl methyl group in different conformers.9,29,30 The value increases to 135 cm−1 or 150 cm−1 in α,β-unsaturated acetates.31–34 In tert-butyl acetates, the bulky tert-butyl group augments the methyl torsional barrier from 100 cm−1 to 111 cm−1.35 We were interested in exploring the torsional barriers in 2A5MT, and comparing them with the values found for 2A3MT23 and 2A4MT24 as well as related molecules to better understand the steric and electrostatic effects in thiophene containing molecules with methyl internal rotation(s).36 For aliphatic ketones containing an acetyl group CH3–CO, Andresen et al. proposed a classification to link the barrier height of the acetyl methyl group CH3– to the molecular structure.37,38 Linear aliphatic ketones were categorised into two classes: the C1 class with a barrier of about 240 cm−1 and the Cs class with a barrier of approximately 180 cm−1.37,39–41 α,β-Unsaturated ketones were grouped in the “mesomeric class” containing two sub-classes: antiperiplanar (ap) with a barrier of about 430 cm−1 and synperiplanar (sp) with a barrier of 350 cm−1.38 The categorisation was extended by Herbers et al. with the “phenyl class”.42 With data points from 2-acetylthiophene, 2A3MT, and 2A4MT, we proposed a “thiophene class” considering the torsional barriers of acetyl methyl groups in ketones which contain a thiophene ring on the other side of the carbonyl bond.24 The results of 2A5MT in the present work yielded a further important data point to establish this thiophene class. We will also compare the barrier height of the methyl top attached to the thiophene ring with that of methylthiophene and methylfuran derivatives to discuss the influence of the heteroatom in the aromatic ring on the methyl torsional barrier.
A classic resonator-based FTMW spectrometer was available for the investigation of 2A5MT, which is known for its high resolution but suffers from the time requirement for survey spectra. However, this drawback can be circumvented with the help of adequate spectral assignment skill and knowledge gained from quantum chemical benchmarking. From benchmarks on the rotational constants of the isomers 2A3MT23 and 2A4MT,24 it is known that the equilibrium rotational constants calculated at the MP2/6-31G(d,p) level of theory are very close to the experimentally determined values. With this gained knowledge, it can be inferred that only very small scan portions around the predicted frequencies of some transitions are needed. Furthermore, the benchmarks on 2A5MT also include the methyl torsional barriers of both methyl rotors. Predicting torsional barriers is challenging. Unlike for molecular geometries, benchmarking barriers to methyl internal rotation is only at an early stage due to the cost of the calculations.43 Recently, we have also started to benchmark the barrier heights of 2-acetylmethylthiophenes in our investigations on 2A3MT and 2A4MT, using the same levels used for benchmarking the molecular geometries, and we have continued this effort also for 2A5MT.
2. Quantum chemical calculations
2.1. Conformational analysis
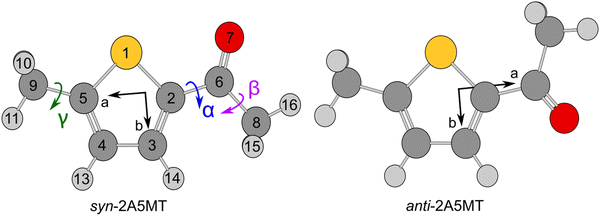
Since the thiophene ring is planar,44 the acetyl group is the only moiety in 2A5MT whose orientation changes create different conformers. In previous investigations on similar molecules containing an acetyl group, such as 2-acetylthiophene,45 2A3MT23 and 2A4MT,24 only two conformers are possible with the oxygen atom of the acetyl group being either in an anti or in a syn orientation relative to the sulphur atom. Therefore, the same situation is expected for 2A5MT. To analyse the conformational landscape, the dihedral angle α = ∠(S1–C2–C6![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O7) (for atom numbering see Fig. 1) was varied in 10° steps, while all other geometry parameters were optimised at the MP2/6-31G(d,p)46,47 level of theory using the Gaussian 16 program package.48 This level was chosen from our previous benchmarking experiences, as it predicted rotational constants that were very close to the experimentally determined ones for 2A3MT23 and 2A4MT,24 the two isomers of 2A5MT. The energy points obtained from these calculations were parameterised with a Fourier expansion using the coefficients given in Table S1 in the ESI.† The resulting potential energy curve shown in Fig. 2 shows that 2A5MT indeed possesses the two expected conformers, which correspond to the minima at α = 0° (syn-2A5MT) and α = 180° (anti-2A5MT). Subsequent full structure optimisations and frequency calculations confirmed both conformers (shown in Fig. 1) to be stable. The calculated rotational constants, dipole moment components, dihedral angles and energy differences between the two conformers are given in Table 1. The atomic coordinates of both the conformers are given in Table S2 in the ESI.†
O7) (for atom numbering see Fig. 1) was varied in 10° steps, while all other geometry parameters were optimised at the MP2/6-31G(d,p)46,47 level of theory using the Gaussian 16 program package.48 This level was chosen from our previous benchmarking experiences, as it predicted rotational constants that were very close to the experimentally determined ones for 2A3MT23 and 2A4MT,24 the two isomers of 2A5MT. The energy points obtained from these calculations were parameterised with a Fourier expansion using the coefficients given in Table S1 in the ESI.† The resulting potential energy curve shown in Fig. 2 shows that 2A5MT indeed possesses the two expected conformers, which correspond to the minima at α = 0° (syn-2A5MT) and α = 180° (anti-2A5MT). Subsequent full structure optimisations and frequency calculations confirmed both conformers (shown in Fig. 1) to be stable. The calculated rotational constants, dipole moment components, dihedral angles and energy differences between the two conformers are given in Table 1. The atomic coordinates of both the conformers are given in Table S2 in the ESI.†
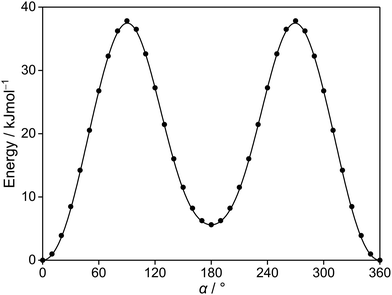 | ||
| Fig. 2 The potential energy curve of 2A5MT obtained by rotating the acetyl group about the C2–C6 bond (for atom numbering see Fig. 1). The calculations were performed at the MP2/6-31G(d,p) level of theory by varying the dihedral angle α in a grid of 10°. The relative energies are given with respect to the lowest energy conformation with EMP2 = −743.3683072 hartree. | ||
| Par. | Unit | syn | anti |
|---|---|---|---|
| a Energy differences including zero-point corrections relative to the more stable conformer syn-2A5MT with E = −743.2336782 hartree. | |||
| A e | MHz | 3425.2 | 3356.6 |
| B e | MHz | 927.6 | 928.8 |
| C e | MHz | 736.6 | 734.1 |
| |μa| | D | 2.33 | 3.55 |
| |μb| | D | 3.87 | 1.58 |
| |μc| | D | 0.00 | 0.00 |
| α | ° | 0.00 | 180.00 |
| β | ° | 0.00 | 0.00 |
| γ | ° | 179.86 | 179.98 |
| ΔEa | kJ mol−1 | 0.0 | 5.3 |
2.2. Basis set variations
In addition to the MP2/6-31G(d,p) level of theory, we also optimised the structure of the more stable conformer syn-2A5MT using various method/basis set combinations. The theoretical results are compared with the highly accurate set of rotational constants deduced from the experimental spectrum. This so-called basis set variation is a part of our benchmarking efforts to find the levels of theory allowing for cost-efficient, yet reasonably accurate predictions of rotational constants to guide the assignment of microwave spectra. In the present study, the basis set variation is a confirmation for the fruitful results of our previous benchmarks. Several exchange-correlation functionals from density functional theory (DFT) were selected, such as B3LYP49,50 with Grimme's distortion corrections51 and with or without Becke-Johnson damping52 as well as with the Coulomb-attenuating method (CAM-B3LYP),53 Truhlar's M06-2X,54 Head-Condon's ωB97X-D,55 as well as the ab initio Møller-Plesset perturbation theory of second order (MP2)46 and the coupled cluster (CCSD) methods.56 They are combined with different Pople47 and Dunning57 basis sets. The results of syn-2A5MT are summarized in Table S3 in the ESI.† An extract of Table S3 (ESI†) is shown in Table 2. For comparison, the corresponding tables for the two isomers 2A3MT23 and 2A4MT24 are also given in Table S3 (ESI†).| Level of theory | ΔA | ΔB | ΔC | ΔV3,1 | ΔV3,2 | ΔA | ΔB | ΔC | ΔV3,1 | ΔV3,2 |
|---|---|---|---|---|---|---|---|---|---|---|
| B3LYP-D3 | M06-2X | |||||||||
| 6-31G(d,p) | −29.3 | −8.6 | −7.1 | 19.3 | −62.2 | 0.7 | 0.4 | 0.0 | −33.5 | −48.4 |
| 6-31++G(d,p) | −31.7 | −11.6 | −9.0 | 86.9 | −58.0 | −0.7 | −1.9 | −1.5 | 24.5 | −46.7 |
| 6-311G(d,p) | −16.5 | −7.3 | −5.6 | 28.9 | −39.0 | 11.0 | 1.3 | 1.1 | −38.4 | −31.1 |
| 6-311++G(d,p) | −17.0 | −8.9 | −6.7 | 74.7 | −52.1 | 11.1 | −0.1 | 0.2 | −4.8 | −49.9 |
| cc-pVDZ | −42.0 | −10.3 | −8.6 | −33.1 | −38.4 | −9.0 | −0.8 | −1.1 | −61.0 | −29.5 |
| aug-cc-pVDZ | −39.0 | −12.5 | −9.9 | 65.8 | −37.8 | −6.3 | −2.8 | −2.3 | 4.5 | −31.6 |
| cc-pVTZ | 4.6 | −4.1 | −2.7 | 47.4 | −14.8 | 29.1 | 4.3 | 3.8 | −22.8 | −10.0 |
| aug-cc-pVTZ | 5.0 | −4.4 | −2.9 | 63.8 | −11.9 | 29.9 | 4.1 | 3.6 | −14.7 | −12.0 |
| B3LYP-D3BJ | MP2 | |||||||||
| 6-31G(d,p) | −28.9 | −5.2 | −4.9 | 52.8 | −43.1 | −22.4 | 0.6 | −0.9 | −57.2 | −8.2 |
| 6-31++G(d,p) | −30.9 | −8.1 | −6.8 | 122.0 | −39.2 | −28.1 | −2.1 | −2.9 | 39.6 | −36.9 |
| 6-311G(d,p) | −15.2 | −3.9 | −3.4 | 62.4 | −19.2 | −25.0 | −0.6 | −1.7 | −45.5 | −15.5 |
| 6-311++G(d,p) | −16.3 | −5.4 | −4.4 | 110.3 | −32.3 | −26.1 | −2.5 | −3.0 | 11.0 | −44.8 |
| 6-311G(df,pd) | −4.0 | −1.6 | −1.5 | 73.5 | −17.6 | 1.1 | 4.6 | 2.7 | −24.9 | −19.9 |
| 6-311++G(df,pd) | −4.2 | −3.0 | −2.4 | 125.8 | −20.7 | −1.9 | 2.8 | 1.5 | 31.2 | −36.9 |
| 6-311G(2d,2p) | 1.1 | −1.0 | −0.9 | 42.5 | 9.5 | −13.7 | 1.9 | 0.3 | −39.0 | 24.9 |
| 6-311++G(2d,2p) | −0.2 | −1.9 | −1.5 | 97.4 | 3.9 | −15.1 | 0.7 | −0.5 | 13.9 | 18.7 |
| 6-311G(2df,2pd) | 8.7 | 0.8 | 0.6 | 39.6 | 22.6 | 3.2 | 7.6 | 4.7 | −34.0 | 40.5 |
| 6-311++G(2df,2pd) | 7.7 | −0.4 | −0.2 | 93.6 | 15.1 | 1.2 | 6.0 | 3.6 | 20.2 | 29.4 |
| 6-311G(3df,3pd) | 13.8 | 1.3 | 1.1 | 55.6 | 29.0 | 7.0 | 7.3 | 4.6 | −37.4 | 59.9 |
| 6-311++G(3df,3pd) | 11.4 | 0.9 | 0.8 | 86.4 | 21.2 | 3.7 | 6.7 | 4.1 | 7.2 | 48.1 |
| cc-pVDZ | −41.3 | −6.8 | −6.3 | 0.5 | −18.7 | −64.8 | −7.9 | −8.1 | −104.5 | −9.5 |
| aug-cc-pVDZ | −38.2 | −8.9 | −7.6 | 103.2 | −17.7 | −73.8 | −10.6 | −10.2 | 30.6 | 5.3 |
| cc-pVTZ | 4.4 | −0.6 | −0.5 | 82.5 | 5.9 | −6.0 | 4.9 | 2.5 | 8.2 | 19.4 |
| aug-cc-pVTZ | 4.7 | −0.9 | −0.7 | 99.7 | 9.0 | |||||
| CCSD/cc-pVDZ | −56.4 | −15.0 | −12.2 | −101.9 | −4.0 | |||||
| CAM-B3LYP-D3BJ | ωB97X-D | |||||||||
| 6-311G(d,p) | 22.1 | 2.2 | 2.1 | 36.9 | −20.7 | 15.1 | −1.5 | −0.5 | 39.1 | −26.1 |
| 6-311++G(d,p) | 21.7 | 0.6 | 1.1 | 83.3 | −36.0 | 14.9 | −0.1 | 0.4 | 5.4 | −22.5 |
| cc-pVDZ | −3.4 | −0.9 | −0.9 | −16.7 | −24.9 | −9.1 | −3.4 | −2.7 | −32.6 | −19.2 |
| aug-cc-pVDZ | −0.3 | −3.1 | −2.2 | 80.0 | −24.8 | −6.6 | −5.2 | −3.8 | 21.4 | −17.3 |
| cc-pVTZ | 42.0 | 5.4 | 5.0 | 57.0 | 0.2 | 35.3 | 2.9 | 3.1 | 13.0 | 2.4 |
| aug-cc-pVTZ | 42.3 | 5.0 | 4.8 | 73.5 | 1.3 | 35.7 | 2.7 | 3.0 | 18.7 | 2.8 |
| Experiment | 3447.6 | 927.0 | 737.5 | 301.8 | 157.3 | |||||
2.3. Methyl internal rotations
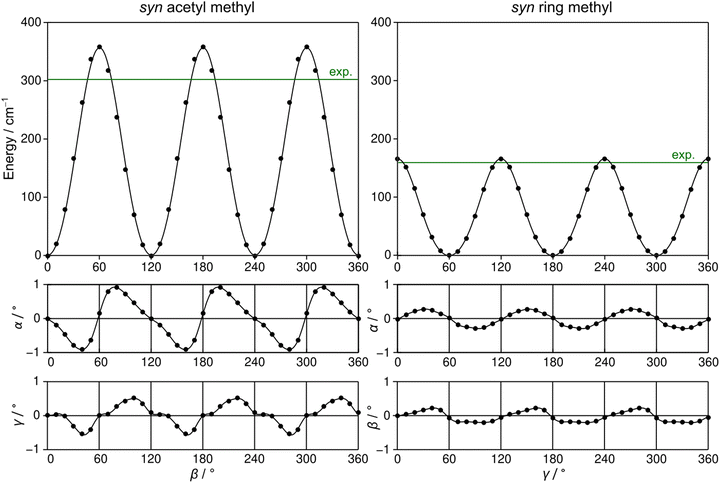
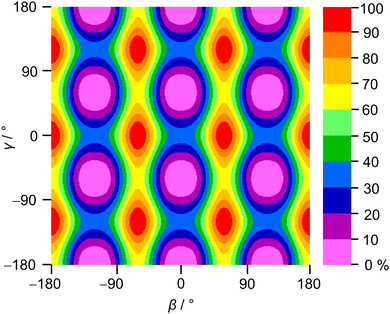
2A5MT possesses two inequivalent internal rotors, the acetyl methyl group and the ring methyl group. We expect the splitting of all rotational transitions into five torsional components (σ1σ2) = (00), (01), (10), (11), and (12).20 In order to predict the barriers to internal rotations, the respective dihedral angles β = ∠(O7–C6–C8–H16) and γ = ∠(S1–C5–C9–H10) were varied in 10° steps while all other geometry parameters were optimised at the MP2/6-31G(d,p) level of theory. The resulting potential energy curves of syn-2A5MT are shown in Fig. 3, and those of anti-2A5MT are shown in Fig. S1 in the ESI.† The Fourier coefficients utilised to plot the curves are given in Table S4 in the ESI.† We found the typical threefold symmetry expected for methyl groups in all cases. The predicted torsional barriers of syn-2A5MT are 359.0 cm−1 and 165.5 cm−1 for the acetyl methyl and the ring methyl groups, respectively. The torsional barriers of both rotors were also calculated for syn-2A5MT at all levels used for the geometry optimisations. The predicted values are included in Table 2 and Table S3 (ESI†). Fig. 3 also shows that the other rotor oscillates with an angle of less than 1°, indicating no coupling between the two rotors. The acetyl oscillation frequently observed in similar molecules23,24,45 is also absent.To check whether the coupling between the two rotors can be neglected, a two-dimensional potential energy surface (2D-PES) depending on the dihedral angles β and γ was calculated for syn-2A5MT, again at the MP2/6-31G(d,p) level of theory, in order to study the top–top interaction. Due to the symmetry, only data points in the range from 0° to 120° were necessary for both β and γ. The potential energies were parameterised with a Fourier expansion with the coefficients listed in Table S5 in the ESI.† The resulting 2D-PES is given in Fig. 4. We only achieved a deviation of 8.0% by fitting the data set but adding cross-coupling coefficients did not enhance the fit, since the values for these terms were negligibly small. Therefore, although the minima are slightly distorted and not circular as in the case of no top–top coupling, we expected no interaction between the acetyl methyl and the ring methyl groups.
3. Microwave spectroscopy
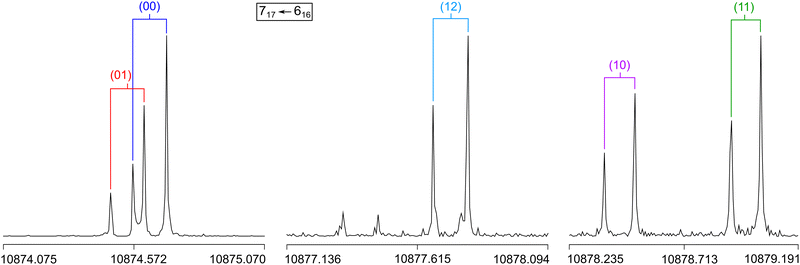
A molecular jet Fourier-transform microwave spectrometer operating in the frequency range of 2.0 to 26.5 GHz58 was used to record the spectrum of 2A5MT. The substance was purchased from TCI Europe, Zwijndrecht, Belgium, with a stated purity of >96.0% and used without further purification. Since 2A5MT is solid at room temperature with a melting point between 27 and 28 °C, we first heated the sample until the substance became liquid, and then added a few drops on a 5 cm piece of pipe cleaner. The pipe cleaner was placed in a metal tube upstream the nozzle heated to about 40 °C during measurements. Helium was flown as a carrier gas over the sample with a backing pressure of about 2 bar to transport the substance into the cavity.Unlike in many of our investigations, no broadband scan was recorded for 2A5MT. Instead, an approach similar to the investigation of 2-ethylfuran59 was employed. We only recorded very small scan portions of about 40 to 300 MHz around the predicted frequencies of some transitions with the highest expected intensities. This was only possible with the results from previous benchmarks for the isomers 2A3MT23 and 2A4MT,24 showing that the Be rotational constants calculated at the MP2/6-31G(d,p) level of theory are very close to the experimentally determined B0 values. Therefore, the spectrum of the more stable conformer syn-2A5MT was first predicted with the program XIAM18 using the values obtained at this level (see Table 1). The first transition that we searched for, 515 ← 404, was predicted at 9568.69 MHz, and we started the scan at 9532 MHz as a series of overlapping spectra with a step width of 0.25 MHz. We observed three strong lines very close to the expected frequency at 9569.25 MHz, 9573.25 MHz, and 9576.5 MHz, which were subsequently remeasured at a higher resolution with an experimental accuracy of 2 kHz.60 All three lines appear as Doppler pairs in the high resolution measurements due to the co-axial arrangement between the molecular beam and the resonator. They are three of the five torsional species expected for a two-top molecule. For torsional barriers of 165.5 and 359.0 cm−1 (see Fig. 3), the (00) and (01) species often appear as a doublet and the (10), (11) and (12) species appear as a triplet. Therefore, we suspected the three observed lines to be the (10), (11) and (12) species of the 515 ← 404 transition, although an assignment was not yet possible at this point.
Similarly, we searched for the 616 ← 505 and 717 ← 606 transitions and found the triplets red shifted from the predicted frequencies by less than 30 MHz. Further intense triplets could be found easily afterwards. The identification of all five torsional species was finally possible with the observation of quintets for the a-type R-branch 616 ← 515, 717 ← 616, 818 ← 717 due to the relatively small splittings between the species as shown in Fig. 5. We could then establish a first fit with the program XIAM which only incorporates the (00) species. This (00) fit was rapidly expanded with the (01) and (10) species into two separate one rotor fits and finally into a two-top fit taking all five torsional species into account. At this stage, transitions could be predicted with an accuracy of about 3 kHz, measured, and added to the fit. Ultimately, 427 transitions were included in a two-top fit shown in Table 3 with a standard deviation of 2.9 kHz. The standard deviation is very close to the estimated measurement accuracy of 2.7 kHz, corresponding to 1/10th of the average line width at half height (FWHH) of 27 kHz. The assigned transition frequencies are listed in Table S6 in the ESI.† All scan portions measured between 8000 and 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 MHz and the fitted spectrum of syn-2A5MT are shown in Fig. 6. The rotational barriers of the acetyl methyl and the ring methyl groups were experimentally determined to be 301.811(41) cm−1 and 157.2612(13) cm−1, respectively. The parameters F0,1 and F0,2, describing the moments of inertia of the two methyl internal rotors, could not be fitted and were fixed to 158 GHz, a value often found for methyl groups.
000 MHz and the fitted spectrum of syn-2A5MT are shown in Fig. 6. The rotational barriers of the acetyl methyl and the ring methyl groups were experimentally determined to be 301.811(41) cm−1 and 157.2612(13) cm−1, respectively. The parameters F0,1 and F0,2, describing the moments of inertia of the two methyl internal rotors, could not be fitted and were fixed to 158 GHz, a value often found for methyl groups.
| Par.a | Unit | XIAM | MP2b |
|---|---|---|---|
| a All parameters refer to the principal axis system. Watson's A reduction and Ir representation were used. b Calculated with the 6-31G(d,p) basis set. The ground state rotational constants and centrifugal distortion constants obtained from anharmonic frequency calculations are given. c Fixed due to symmetry. d Number of transitions. e Standard deviation of the fit. | |||
| A 0 | MHz | 3447.62273(27) | 3406.116 |
| B 0 | MHz | 927.022235(89) | 922.127 |
| C 0 | MHz | 737.533474(35) | 732.579 |
| Δ J | kHz | 0.02132(36) | 0.0200 |
| Δ JK | kHz | — | −0.0015 |
| Δ K | kHz | 0.3161(94) | 0.3279 |
| δ J | kHz | 0.00472(17) | 0.0046 |
| δ K | kHz | 0.0385(93) | 0.0330 |
| V 3,1 | cm−1 | 301.811(41) | 359.0 |
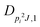
|
kHz | 18.33(59) | |
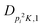
|
kHz | −214.6(51) | |
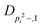
|
kHz | 8.36(61) | |
| ∠(i1,a) | ° | 44.338(31) | 47.9 |
| ∠(i1,b) | ° | 45.661(31) | 42.1 |
| ∠(i1,c) | ° | 90.0c | 90.0 |
| V 3,2 | cm−1 | 157.2612(13) | 165.5 |
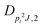
|
kHz | −3.641(63) | |
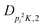
|
kHz | 165.64(55) | |
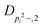
|
kHz | 0.775(67) | |
| ∠(i2,a) | ° | 16.2798(39) | 16.6 |
| ∠(i2,b) | ° | 73.7202(39) | 73.4 |
| ∠(i2,c) | ° | 90.0c | 90.0 |
| N | 427 | ||
| σ | kHz | 2.9 | |
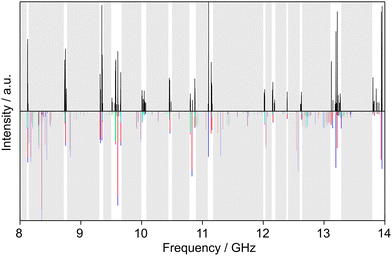 | ||
| Fig. 6 Partial scans between 8 and 14 GHz of 2A5MT. The experimental spectrum is shown in the upper trace. The lower trace displays the theoretical spectrum of syn-2A5MT predicted using the molecular parameters obtained from the fit given in Table 3. The grey sections were not scanned. The five torsional species are colour-coded according to Fig. 5. | ||
Finally, we attempted to assign the anti-conformer of 2A5MT in the same manner as syn-2A5MT. However, we only found two very weak lines that potentially belong to anti-2A5MT, even while using a higher number of 200 co-added decays per measurement to consider that anti-2A5MT is higher in energy than syn-2A5MT and may possess lines with a lower intensity.
4. Discussion
4.1 Conformational stability
Only the most stable of the two expected conformers was observed in the microwave spectrum of 2A5MT, confirming the higher energetic stability predicted for the syn form compared to the anti-form. The preference for the syn-conformer has already been established in other thiophene derivatives such as 2-thiophenecarboxaldehyde,61,62 2-acetylthiophene,45 and the isomer 2A4MT24 of 2A5MT. This was explained due to dipole–dipole interactions between the positively charged sulphur atom in the thiophene ring and the negatively charged oxygen of the carbonyl group,24,45,61 which also holds true for 2A5MT, as shown in the results of the NBO calculations63 given in Fig. 7. The only exception of thiophene derivatives where the anti-conformer is more stable is the isomer 2A3MT23 of 2A5MT due to steric interactions between the ring methyl group and the acetyl group.36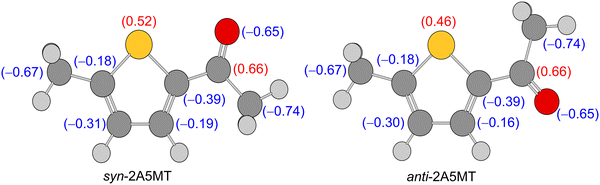 | ||
| Fig. 7 Charge distribution in syn- and anti-2A5MT obtained from NBO calculations at the MP2/6-31G(d,p) level of theory. | ||
In our previous investigations on thiophene derivatives,23,24,45,64 we often observed discrepancies while calculating the molecular structures at different levels of theory concerning the planarity. A number of MP2 calculations predicted the molecules to be non-planar due to an out-of-plane tilt of the acetyl group. In the case of syn-2A5MT, only the MP2/6-311++G(df,pd) level predicts a non-planar structure with a small tilt angle of about 3°; all other employed levels agree on a planar structure. Together with the inertial defect of 6.523 uÅ2, which is close to those of other planar molecules with four out-of-plane hydrogen atoms such as the cis–trans conformer of ethylnitrite (Δc = −6.422 uÅ2)65 and the Cs conformer of 2-ethylfuran (Δc = −6.483 uÅ2),59 the planarity question does not arise for syn-2A5MT.
4.2 Benchmarking 2-acetylthiophenes
The XIAM fit given in Table 3 includes 451 lines and reaches a standard deviation of 2.9 kHz, satisfactorily close to the measurement accuracy of 2.7 kHz. All the rotational and centrifugal distortion constants, except ΔJK which was finally not fitted, and the internal rotation parameters were determined with high accuracy.It is known that a comparison between the calculated rotational constants Be and the experimentally determined ones B0 is physically not meaningful, as the former refers to the equilibrium structure and the latter to the vibrational ground state. Nevertheless, our benchmarking efforts given in Section 2 are still helpful to determine the level of theory which deliver Be values close to the experimental ones. Even though this agreement is due to error compensations, this allows rapid spectral assignments of related molecules in future studies, as shown in the present case of 2A5MT. From the benchmarks carried out for 2A3MT23 and 2A4MT,24 we could significantly reduce the measurement time of 2A5MT by using Be rotational constants predicted at the MP2/6-31G(d,p) level of theory to guide the assignments. The benchmarking of syn-2A5MT shows that the B and C constants were predicted very accurately with deviations less than 1 MHz, but a larger deviation was found for the A constant (see Table 2 and Table S3, ESI†), though the difference is still quite acceptable. The values closest to the experimental ones were provided by the M06-2X/6-31G(d,p) level of theory. We note that the Pople's basis set 6-31G(d,p) is also involved here. Good results were also achieved when diffusion functions +(+) are added, as well as at the B3LYP-D3BJ/6-311(+)G(2d,2p) levels of theory that also performed very well for 2A3MT.23
The torsional barriers of the ring methyl group and the acetyl methyl group of syn-2A5MT were determined to be 301.811(41) cm−1 and 157.2612(13) cm−1, respectively. Compared to the calculated values (see Table 2 and Table S3, ESI†), the predictions are not very accurate, though generally the ring methyl barrier was better predicted than the acetyl methyl barrier. Currently, there are no obvious trends regarding methods or basis sets that can be recommended, except the few following points: (1) for the B3LYP method, either with D3 or D3BJ corrections or in the CAM-B3LYP variation, adding diffusion functions decreases the accuracy of calculations for the acetyl methyl group but not for the ring methyl group. (2) In most cases, adding Becke-Johnson damping decreases the accuracy of calculations for both methyl groups. (3) For the MP2, M06-2X and ωB97X-D methods, adding diffusion functions increases the accuracy of calculations for the acetyl methyl group. For the ring methyl group, there is no clear trend. Therefore, we only note two levels of theory, MP2/6-311+G(d,p) and B3LYP-D3/6-311G(2df,2dp), which predict values with less than 10 cm−1 deviation from the experimental value for both rotors. These two levels also perform well for the acetyl methyl rotors of 2A3MT23 and 2A4MT.24
4.3 Barriers to methyl internal rotations
Aromatic rings are of special interest while coupled with multiple methyl internal rotors as the conjugated double bond system is able to transfer electrostatic effects over a longer distance through the π-electrons, making the barrier to methyl torsion sometimes unpredictable.36 Heterocycles such as thiophene and furan additionally have the influence of the heteroatom on the torsional barrier. It was shown in the literature that changing from sulphur to oxygen increases the barrier, i.e., dimethyl sulfide (736 cm−1)66vs. dimethyl ether (944 cm−1),67trans-ethyl methyl sulfide (693 cm−1)68vs. trans-ethyl methyl ether (893 cm−1),69 conformer III of n-propyl sulfide (699 cm−1)70vs. trans–trans-methyl-n-propyl ether (1154 cm−1),71 and S-phenyl thioacetate (48 cm−1)72vs. phenyl acetate (137 cm−1).34 The same holds true for all methyl rotors attached to the thiophene and furan rings illustrated in Fig. 8, but interestingly not for the acetyl methyl rotors. Only two sulphur/oxygen analogue pairs possessing an acetyl methyl rotor have been studied so far, 2-acetylthiophene (molecule (1) in Fig. 8)45 and 2-acetylfuran (5)73 as well as syn-2A5MT (11) and 2-acetyl-5-methylfuran (12),74 where the lower torsional barrier of the acetyl methyl group was observed for the syn-conformers of furans. The question of why only the acetyl methyl group of the syn conformers and not of the anti-ones shows this different behaviour, is still lacking an answer. To better understand this phenomenon, investigations on 2-acetyl-3-methylfuran and 2-acetyl-4-methylfuran, as well as the 3-acetylmethylthiophene isomers would be helpful and interesting.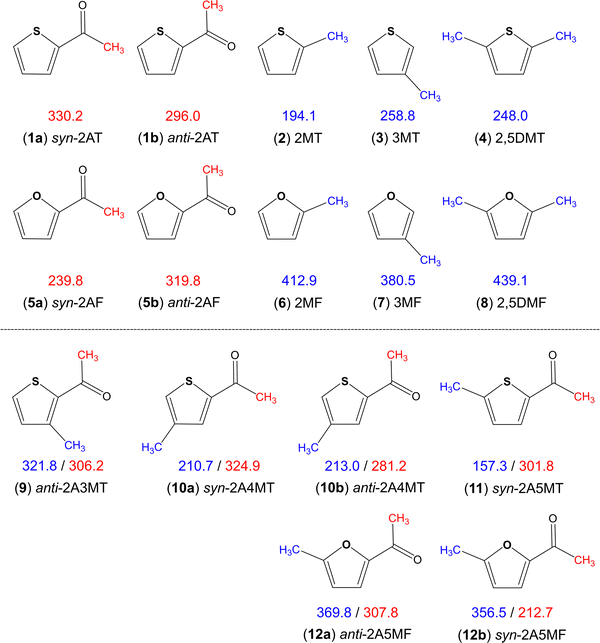 | ||
| Fig. 8 Comparison of barriers to internal rotations (in cm−1) of the acetyl (red) and ring (blue) methyl groups in thiophene and furan derivatives: (1) 2-acetylthiophene,45 (2) 2-methylthiophene,75 (3) 3-methylthiophene,76 (4) 2,5-dimethylthiophene,77 (5) 2-acetylfuran,73 (6) 2-methylfuran,78 (7) 3-methylfuran,79 (8) 2,5-dimethylfuran,80 (9) anti-2-acetyl-3-methylthiophene,23 (10) 2-acetyl-4-methylthiophene,24 (11) syn-2-acetyl-5-methylthiophene (this work) and (12) 2-acetyl-5-methylfuran.74 | ||
The various thiophenes and furans shown in Fig. 8 possess either a ring methyl group, an acetyl methyl group, or both. The influence of electrostatic effects can be shown by comparing the barriers in 2-methylthiophene (2) (194.1 cm−1)75 and 2,5-dimethylthiophene (4) (248.0 cm−1)77 as well as in their oxygen analogues 2-methylfuran (6) (412.9 cm−1)78 and 2,5-dimethylfuran (8) (439.1 cm−1).80 The presence of a second methyl group causes an increase of the torsional barrier in both cases. As the methyl groups at the 2- and the 5-positions cannot interact by steric effects, electrostatic effects have to be the reason. The comparison of the ring methyl barriers in syn-2A5MT (11) (157.3 cm−1) and 2-methylthiophene (2) (194.1 cm−1)75 demonstrates that the negative inductive and mesomeric effects of the carbonyl group decrease the methyl torsional barrier. Only in anti-2A3MT (9),23 the presence of an acetyl substituent increases the barrier to 321.8 cm−1 compared to the value of 258.8 cm−1 found for 3-methylthiophene (3).76 The reason was steric hindrance between the acetyl group at the second substitution position and the methyl group at the third substitution position. The barrier of the ring methyl rotor is independent of the orientation of the acetyl group, as demonstrated by the almost unchanged value found for syn-2A4MT (10a) (210.7 cm−1) and anti-2A4MT (10b) (213.0 cm−1).24
The ring methyl group also affects the barrier to the internal rotation of the acetyl methyl group. Comparing the values observed for anti-2-acetylthiophene (1b) (296.0 cm−1) and syn-2-acetylthiophene (1a) (330.2 cm−1) to those of 2A3MT (9), 2A4MT (10) and 2A5MT (11), we found that the barrier decreases with the presence of a methyl group on the thiophene ring at the 4- or the 5-position,24 but increases if the methyl group is at the 3-position.23 The comparison between 2-acetylfuran (5)73 and 2-acetyl-5-methylfuran (12)74 leads to the same observation. In previous studies on a series of acetyl group containing linear aliphatic ketones, the chain-length effect has been introduced, stating that if the molecular shape is more prolate, the torsional barrier of the acetyl methyl group becomes lower.37 This effect can explain the above-mentioned observation. The addition of a methyl group at the 4- and the 5-position of the thiophene ring makes the molecule more prolate compared to 2-acetylthiophene or 2-acetylfurane and decreases the barrier, while the addition of a methyl group at the 3-position makes the molecule more globular and increases the barrier.36
Overall, it is noticeable that the barriers of the acetyl methyl group fall into a much wider range for furan derivatives (212.7 cm−1 to 319.8 cm−1) than that for thiophene derivatives (281.2 cm−1 to 330.2 cm−1). In ref. 24, we proposed a “thiophene class”, as an extension to the classification system proposed by Andresen et al.37,38 and Herbers et al.42 for the acetyl methyl torsional barrier. We found that the barrier heights of acetylthiophene derivatives are 300 cm−1, and the present study on syn-2A5MT firmly supports this hypothesis.
5. Conclusion
Previous benchmarking efforts on similar molecules allowed for the very rapid assignment of the syn-conformer of 2A5MT where only small scan portions of the microwave spectrum were required. The barrier heights were determined for the two inequivalent rotors, the acetyl methyl and the ring methyl groups, to be 301.811(41) cm−1 and 157.2612(13) cm−1, respectively. A comparison with other thiophene derivatives possessing either an acetyl group, a ring methyl group, or both indicates that electrostatic effects influencing the torsional barriers are transferred through the π-electron system of the heteroaromatic ring. It was also observed that the chain length effects reported for α,β-saturated ketones hold true for 2-acetylthiophene derivatives, i.e., the more prolate the molecular frame, the lower the torsional barrier of the acetyl methyl rotor. The effect of the heteroatom in the ring on methyl torsion was also investigated by comparing the barrier heights in thiophene and furan derivatives. The usual observation that the torsional barrier is higher in oxygen analogues compared to that in equivalent sulphur analogues is no longer the case for the syn-conformers of 2-acetylfuran vs. 2-acetylthiophene and 2-acetyl-5-methylfuran vs. 2A5MT. The torsional barriers of acetyl methyl groups in molecules with a thiophene ring attached at the other side of the carbonyl bond are always around 300 cm−1 and can thus be grouped together in the so-called “thiophene class”.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Agence Nationale de la Recherche ANR (project ID ANR-18-CE29-0011). Simulations were performed with computing resources granted by the RWTH Aachen University under the projects rwth0369 and rwth0506.References
- H. H. Nielsen, Phys. Rev., 1932, 40, 445–456 CrossRef CAS.
- J. D. Kemp and K. S. Pitzer, J. Chem. Phys., 1936, 4, 749–750 CrossRef CAS.
- A. M. Halpern and E. D. Glendening, J. Chem. Phys., 2003, 119, 11186–11191 CrossRef CAS.
- V. Pophristic and L. Goodman, Nature, 2001, 411, 565–586 CrossRef CAS PubMed.
- R. F. W. Bader, J. R. Cheeseman, K. E. Laidig, K. B. Wiberg and C. Breneman, J. Am. Chem. Soc., 1990, 112, 6530–6536 CrossRef CAS.
- T. Kundu, B. Pradhan and B. P. Singh, J. Chem. Sci., 2002, 114, 623–638 CrossRef CAS.
- S. Liu, N. Govind and L. G. Pedersen, J. Chem. Phys., 2008, 129, 094104 CrossRef PubMed.
- D. G. Lister, J. N. Macdonald and N. L. Owen, Internal Rotation and Inversion, Academic Press, London, 1978 Search PubMed.
- H. V. L. Nguyen and I. Kleiner, Phys. Sci. Rev., 2022, 7, 679–726 Search PubMed.
- J.-U. Grabow, Fourier Transform Microwave Spectroscopy Measurement and Instrumentation. in Handbook of High-Resolution Spectroscopy, ed. M. Quack and F. Merkt, Wiley, Chichester, UK, 2011, ch. 1, vol. 2 Search PubMed.
- J. T. Hougen, I. Kleiner and M. Godefroid, J. Mol. Spectrosc., 1994, 163, 559–586 CrossRef CAS.
- I. Kleiner and J. T. Hougen, J. Chem. Phys., 2003, 119, 5505–5509 CrossRef CAS.
- V. V. Ilyushin, Z. Kisiel, L. Pszczolkowski, H. Mäder and J. T. Hougen, J. Mol. Spectrosc., 2010, 259, 26–38 CrossRef CAS.
- L. Ferres, W. Stahl and H. V. L. Nguyen, J. Chem. Phys., 2018, 148, 124304 CrossRef PubMed.
- P. Groner, J. Chem. Phys., 1997, 107, 4483–4498 CrossRef CAS.
- M. Tudorie, I. Kleiner, J. T. Hougen, S. Melandri, L. W. Sutikdja and W. Stahl, J. Mol. Spectrosc., 2011, 269, 211–225 CrossRef CAS.
- V. V. Ilyushin and J. T. Hougen, J. Mol. Spectrosc., 2013, 289, 41–49 CrossRef CAS.
- H. Hartwig and H. Dreizler, Z. Naturforsch., 1996, 51a, 923–932 CrossRef.
- L. Ferres, W. Stahl and H. V. L. Nguyen, J. Chem. Phys., 2019, 151, 104310 CrossRef PubMed.
- L. Ferres, J. Cheung, W. Stahl and H. V. L. Nguyen, J. Phys. Chem. A, 2019, 123, 3497–3503 CrossRef CAS PubMed.
- P. R. Bunker and P. Jensen, Molecular Symmetry and Spectroscopy, NRC Research Press, Ottawa, Ontario, Canada, 2nd edn, 2006 Search PubMed.
- H. Dreizler, Z. Naturforsch., 1961, 16a, 1354–1367 CrossRef CAS.
- C. Dindić and H. V. L. Nguyen, Chem. Phys. Chem., 2021, 22, 2420–2428 CrossRef PubMed.
- C. Dindić, M. Barth and H. V. L. Nguyen, Spectrochim. Acta, Part A, 2022, 280, 121505 CrossRef PubMed.
- S. Khemissi, A. Pérez Salvador and H. V. L. Nguyen, J. Phys. Chem. A, 2021, 125, 8542–8548 CrossRef CAS PubMed.
- K. P. R. Nair, S. Herbers, J.-U. Grabow and H. V. L. Nguyen, J. Mol. Struct., 2021, 1246, 131096 CrossRef CAS.
- J. Mélan, S. Khemissi and H. V. L. Nguyen, Spectrochim. Acta, Part A, 2021, 253, 119564 CrossRef PubMed.
- K. Eibl, W. Stahl, I. Kleiner and H. V. L. Nguyen, J. Chem. Phys., 2018, 149, 144306 CrossRef PubMed.
- L. Sutikdja, W. Stahl, V. Sironneau, H. V. L. Nguyen and I. Kleiner, Chem. Phys. Lett., 2016, 663, 145–149 CrossRef CAS.
- T. Attig, R. Kannengießer, I. Kleiner and W. Stahl, J. Mol. Spectrosc., 2014, 298, 47–53 CrossRef CAS.
- H. V. L. Nguyen, A. Jabri, V. Van and W. Stahl, J. Phys. Chem. A, 2014, 118, 12130–12136 CrossRef CAS PubMed.
- A. Jabri, V. Van, H. V. L. Nguyen, W. Stahl and I. Kleiner, Chem. Phys. Chem., 2016, 17, 2660–2665 CrossRef CAS PubMed.
- H. V. L. Nguyen and W. Stahl, J. Mol. Spectrosc., 2010, 264, 120–124 CrossRef CAS.
- L. Ferres, L. Evangelisti, A. Maris, S. Melandri, W. Caminati, W. Stahl and H. V. L. Nguyen, Molecules, 2022, 27, 2730 CrossRef CAS PubMed.
- Y. Zhao, H. Mouhib, G. Li, I. Kleiner and W. Stahl, J. Mol. Spectrosc., 2016, 322, 38–42 CrossRef CAS.
- H. V. L. Nguyen, W. Caminati and J.-U. Grabow, Molecules, 2022, 27, 3948 CrossRef CAS PubMed.
- M. Andresen, D. Schöngen, I. Kleiner, M. Schwell, W. Stahl and H. V. L. Nguyen, Chem. Phys. Chem., 2020, 21, 2206–2216 CrossRef CAS PubMed.
- M. Andresen, M. Schwell and H. V. L. Nguyen, J. Mol. Struct., 2022, 1247, 131337 CrossRef CAS.
- M. Andresen, I. Kleiner, M. Schwell, W. Stahl and H. V. L. Nguyen, J. Phys. Chem. A, 2018, 122, 7071–7078 CrossRef CAS PubMed.
- M. Andresen, I. Kleiner, M. Schwell, W. Stahl and H. V. L. Nguyen, Chem. Phys. Chem., 2019, 20, 2063–2073 CAS.
- M. Andresen, I. Kleiner, M. Schwell, W. Stahl and H. V. L. Nguyen, J. Phys. Chem. A, 2020, 124, 1353–1361 CrossRef CAS PubMed.
- S. Herbers, S. M. Fritz, P. Mishra, H. V. L. Nguyen and T. S. Zwier, J. Chem. Phys., 2020, 152, 074301 CrossRef PubMed.
- K. G. Lengsfeld: Van-der-Waals-Wechselwirkungen: Präzise Struktur und Dynamik von Molekülen, PhD thesis, Gottfried Wilhelm Leibniz Universität Hannover, 2022 Search PubMed.
- V. L. Orr, Y. Ichikawa, A. R. Patel, A. M. Kougias, K. Kobayashi, J. F. Stanton, B. J. Esselman, R. C. Woods and R. J. McMahon, J. Chem. Phys., 2021, 154, 244310 CrossRef CAS PubMed.
- C. Dindić, J. Ludovicy, V. Terzi, A. Lüchow, N. Vogt, J. Demaison and H. V. L. Nguyen, Phys. Chem. Chem. Phys., 2022, 24, 3804–3815 RSC.
- C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618–622 CrossRef.
- M. J. Frisch, J. A. Pople and J. S. Binkley, J. Chem. Phys., 1984, 80, 3265–3269 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision B.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. Lee, W. Yang and R. G. Paar, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- G. E. Scuseria, A. C. Scheiner, T. J. Lee, J. E. Rice and H. F. Schaefer III, J. Chem. Phys., 1987, 86, 2881–2890 CrossRef CAS.
- T. H. Dunning Jr., J. Chem. Phys., 1989, 90, 1007–1023 CrossRef.
- J.-U. Grabow, W. Stahl and H. Dreizler, Rev. Sci. Instrum., 1996, 67, 4072–4084 CrossRef CAS.
- H. V. L. Nguyen, J. Mol. Struct., 2020, 1208, 127909 CrossRef CAS.
- J.-U. Grabow and W. Stahl, Z. Naturforsch., 1990, 45a, 1043–1044 CrossRef.
- R. Hakiri, N. Derbel, W. C. Bailey, H. V. L. Nguyen and H. Mouhib, Mol. Phys., 2020, 118, e1728406 CrossRef.
- W. Li, M. Li, Y. Jan, Q. Gou, J.-U. Grabow and G. Feng, J. Chem. Phys., 2019, 151, 164307 CrossRef PubMed.
- E. D. Glendening, C. R. Landis and F. Weinhold, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 1–42 CAS.
- C. Dindic, W. Stahl and H. V. L. Nguyen, Phys. Chem. Chem. Phys., 2020, 22, 19704 RSC.
- N. Hansen, F. Temps, H. Mäder and N. W. Larsen, Phys. Chem. Chem. Phys., 1999, 1, 3219–3233 RSC.
- A. Jabri, V. Van, H. V. L. Nguyen, H. Mouhib, F. Kwabia Tchana, L. Manceron, W. Stahl and I. Kleiner, Astron. Astrophys., 2016, 589, A127 CrossRef.
- W. Neustock, A. Guarnieri, J. Demaison and G. Wlodarczak, Z. Naturforsch., 1990, 45a, 702–706 CrossRef.
- M. Hayashi, M. Adachi and J. Nakagawa, J. Mol. Spectrosc., 1981, 86, 129–135 CrossRef CAS.
- M. Hayashi and K. Kuwada, J. Mol. Struct., 1975, 28, 147–161 CrossRef CAS.
- L. Tulimat, H. Mouhib, H. V. L. Nguyen and W. Stahl, J. Mol. Spectrosc., 2020, 373, 111356 CrossRef CAS.
- H. Kato, J. Nakagawa and M. Hayashi, J. Mol. Spectrosc., 1980, 80, 272–278 CrossRef CAS.
- L. Ferres, Quantum Chemical and Microwave Spectroscopic Investigations on Phenyl Ring Containing Molecules, PhD thesis, RWTH Aachen University, 2019 Search PubMed.
- C. Dindić, A. Lüchow, N. Vogt, J. Demaison and H. V. L. Nguyen, J. Phys. Chem. A, 2021, 125, 4986–4997 CrossRef PubMed.
- V. Van, W. Stahl and H. V. L. Nguyen, Chem. Phys. Chem., 2016, 17, 3223–3228 CrossRef CAS PubMed.
- N. M. Posdeev, L. N. Gunderova and A. A. Shapkin, Opt. Spektrosk., 1970, 28, 254 Search PubMed.
- T. Ogata and K. Kozima, J. Mol. Spectrosc., 1972, 42, 38–46 CrossRef CAS.
- V. Van, W. Stahl and H. V. L. Nguyen, Phys. Chem. Chem. Phys., 2015, 17, 32111–32114 RSC.
- I. A. Finneran, S. T. Shipman and S. L. Widicus Weaver, J. Mol. Spectrosc., 2012, 280, 27–33 CrossRef CAS.
- T. Ogata and K. Kozima, Bull. Chem. Soc. Jpn., 1971, 44, 2344–2346 CrossRef CAS.
- V. Van, J. Bruckhuisen, W. Stahl, V. Ilyushin and H. V. L. Nguyen, J. Mol. Spectrosc., 2018, 343, 121–125 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp03897h |
| This journal is © the Owner Societies 2023 |