Alloying effect on the lattice thermal conductivity of MNiSn half-Heusler alloys
Received
6th October 2022
, Accepted 25th November 2022
First published on 8th December 2022
Abstract
The lattice thermal conductivity of MNiSn (M = Ti, Zr, Hf) half-Heusler (HH) alloys was studied. Ab initio DFT calculations were used for the calculation of the material physical properties. A combination of the Slack model and Klemens analytical alloying model was used to simulate the lattice thermal conductivity as a function of composition and temperature. Our results emphasize the major role of point defect scattering in a single-phase state of HH alloys because of the mixing of elements in the M-sub-lattice, especially at the high working temperature of the thermoelectric material. We performed a series of calculations from pure unalloyed compounds to multicomponent compositions with five elements in the M sub-lattice of (Ti, Zr, Hf, Al, Sc)NiSn.
1. Introduction
MNiSn (M = Ti, Zr, Hf) half-Heusler (HH) alloys are well-known n-type materials1 used in thermoelectric (TE) devices. Their crystallographic structure contains four interpenetrating face-centered cubic sub-lattices, where one of them is empty. Each sub-lattice can be doped or alloyed separately, thus changing the electronic and mechanical properties of the material. The efficiency of thermoelectric (TE) materials is defined by the figure-of-merit, 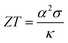 , which is the ratio between the product of the squared Seebeck coefficient, α, and the electrical conductivity, σ, with the thermal conductivity, κ. The thermal conductivity contains the electronic part and lattice (phonon) part. Among these two the lattice thermal conductivity gives the major contribution in HH alloys and therefore its reduction is essential for further optimization of the thermoelectric figure of merit.
, which is the ratio between the product of the squared Seebeck coefficient, α, and the electrical conductivity, σ, with the thermal conductivity, κ. The thermal conductivity contains the electronic part and lattice (phonon) part. Among these two the lattice thermal conductivity gives the major contribution in HH alloys and therefore its reduction is essential for further optimization of the thermoelectric figure of merit.
Different scattering mechanisms are usually considered for phonon scattering: alloying elements as point defects, grain boundaries, inclusions of a second phase, etc.2,3 As the M sub-lattice can be alloyed to a high level with different isoelectronic elements (Ti, Zr, Hf) the phonon scattering mechanism has special importance in these HH alloys. As an extension, in our previous work, the alloy with five different elements on the M sub-lattice was studied4 to analyze the thermodynamic stability of the alloy using the high entropy alloys (HEA) methodology, and to determine a new HEA parameter for multi-component alloying in only one sub-lattice of the compound.
The work of Eliassen et al.5 was devoted to the examination of the lattice thermal conductivity of MNiSn alloys using DFT calculations. The alloying in the M sub-lattice included the isoelectronic elements (Ti, Zr, Hf) in the whole composition range. To model the alloying in the sub-lattice the virtual crystal approximation (VCA) was used. Here, the electronic nature of the alloy assumes to be like the pure compounds. This allows direct calculation of the phonon parameters of the material, including phonon density of states. In our previous work,6 we examined the lattice thermal conductivity of (Ti, Al)NiSn alloys using DFT calculations combined with the Slack model.7–9 Other several semi-empirical works10–13 used the analytical model of Klemens14–16 to study the lattice thermal contribution in HH and MNiSn alloys. Although all these works include important insights on the influence of the mixing elements in the M sub-lattice on the thermal conductivity, a comprehensive comparative analysis for alloying elements (isoelectronic and non-isoelectronic) in a single-phase state of HH was not performed. Moreover, the multicomponent alloying on one sub-lattice in the single-phase state of HH material was never studied to the best of our knowledge.
In the current work, the lattice thermal conductivity of MNiSn alloy was studied, as a function of element composition M = Ti/Zr/Hf/Al/Sc, from pure compound to multi-component alloy. The same ab initio density functional theory (DFT) approach was used to calculate the physical properties of the material. The thermal conductivity as a function of temperature was calculated using the Slack model,8,9 for the pure compounds and low amount of alloying. The alloying model of Klemens14–16 was used for alloys in the whole composition range.
2. Computational details
DFT using the full potential method with the linearized augmented plane waves (FP-LAPW) formalism, as implemented in the WIEN2k code,17 was applied in all calculations. The DFT calculations included the generalized gradient approximation (GGA). The full description of the calculation details can be found in our previous work.18 For the pure MNiSn compounds, a unit cell containing 3 atoms was used. For cases where the (M, Al/Sc)NiSn alloys properties were directly calculated the 2 × 2 × 2 cubic supercell with 96 atoms was used. The accuracy in the total energy calculations for all considered cases was not less than ∼10−4 Ryd.
3. Lattice thermal conductivity
3.1 Slack model
The model of Slack7–9 was used for the lattice thermal conductivity calculation| | 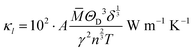 | (1) |
where a primitive unit cell is considered and n is the number of atoms in this cell, (for TiNiSn, n = 3); ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) is the average mass of the atom in atomic mass units; δ is the volume per atom; ΘD is the Debye temperature in K; γ is the Grüneisen parameter and the constant A is given by the expression
is the average mass of the atom in atomic mass units; δ is the volume per atom; ΘD is the Debye temperature in K; γ is the Grüneisen parameter and the constant A is given by the expression 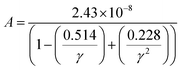 .9 All the other physical parameters are given by the following equations:19,20
.9 All the other physical parameters are given by the following equations:19,20| | 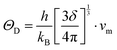 | (2) |
| | 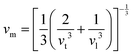 | (3) |
| | 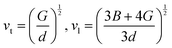 | (4) |
where h is the Planck constant, kB is the Boltzmann constant, vm is the mean sound velocity, vt and vl are transverse and longitudinal sound velocity, B is the bulk modulus, G is the shear modulus and d is the density. The relation G = 0.59B was applied, as discussed in ref. 21 for TiNiSn. This relation dictates (see ref. 6 for an extended discussion) the following expression for the Grüneisen parameter:| | 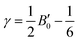 | (5) |
By substitution of one from 32 atoms in the M sub-lattice in a supercell, a direct calculation of the M0.97(Al/Sc)0.03NiSn is achieved, assuming that the number of atoms in the sub-lattice is enough to simulate random distribution. In this way, a direct calculation of the low alloying amount is possible.6 Nevertheless, the higher composition of the alloying element cannot be calculated this way as it is difficult to consider a “random” distribution in supercell calculations. For this purpose, we use the following complementary analytical alloying model. Note, that due to the time-consuming WIEN2k-based DFT calculations in 96 atom supercells, this type of calculation was performed only for Al or Sc substitution, and the alloying of Ti/Zr/Hf was studied only with the analytical alloying model.
By using the Slack model, we take into account only the acoustic phonon modes. This approach was successfully applied for many materials, with simple structures (rocksalt, zinc blende and wurtzite),22 for complex thermoelectric materials23 and for HH compounds.24 Recently, this method was used for high-throughput computational evaluation for large set of 353 materials.25 The acoustic modes have an important role in the lattice thermal conductivity, using the basic model of Slack will allow us to examine the influence of alloying element on this physical property. It worth mentioning here that the most successful models for calculations of lattice thermal conductivity (with Umklapp scattering only) of crystalline solids were developed by Slack7 and by Snyder et al.26 Both models are based on a linear phonon dispersion of Debye for acoustic phonons. The difference between them is that Slack considers only the contribution of acoustic phonons while Snyder assumes that all optical phonons have the cut-off frequency of the acoustic branch. Usually, these models overestimate the lattice thermal conductivity, while other models that reduce the role of acoustic phonons by decreasing the group velocity or by including optical bands in consideration may significantly decrease kl. This is especially important in the low temperature region below the Debye temperatures of materials and for low dimensionalities like 1D nano-wires,27 2D single-layer materials,28 in the superlattices29,30 and heterostructures.31 In the superlattices phonon band gaps can be created through constructive interference by Bragg reflection, which reduces the phonon group velocity. A nice review on strategies of phonon engineering may be found in ref. 32. Orientation of bonding connections may have a crucial role in ionic compounds. For example, in perovskite oxides like SrTiO3 the degeneracy of the polar modes is broken if a tetragonal distortion is applied to a cubic phase. The softening of the c axis polar mode and the change in the acoustic bands’ dispersion reduce the thermal conductivity as demonstrated by ab initio Molecular Dynamics and DFT calculations in ref. 33. It is clear that all these examples are not relevant to our case of low band gap HH compounds, and for our estimations we decided to use the Slack model.
Our calculated results for lattice thermal conductivity in pure HH compounds for relatively high temperatures above the Debye temperatures are all well inside the intervals reported from the measurements (see Table 2 of the paper) encouraging the application of relatively simple formalism used in our manuscript. This is supported also by the main aim of the paper – to study the trends of alloying on lattice thermal conductivity in the working conditions of devices based on these materials. In this case the fine peculiarities of the phonon spectra are less important, and are mainly determined by integral elastic and thermodynamic properties of materials which are much less sensitive to the details of behavior of the branches of electronic or phonon spectra (see, for example, ref. 34).
3.2 Alloying model
An analytical approach for assessing the thermal conductivity of alloys based on the Klemens point-defect scattering model14 is applied. It was lately presented by Gurunathan et al.15 (see also ref. 16) and was used for MNiSn and other HH-based alloys.10–13 The lattice thermal conductivity of the alloy (κl) is calculated by using the lattice thermal conductivity of the pure compounds (κ0) and the average volume per atom, δ, with a scattering parameter (Γ)| | 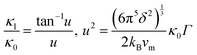 | (6) |
The scattering parameter considers the influence of alloying elements in the lattice. It is composed of two parts (Γ = ΓM + ΓS): the mass variance and the stain field variance. The first is a function of the mass change and the second is a function of the atomic radius change. For an MNiSn alloy, where there is a substitution of different elements only in the M sub-lattice of a compound with 3 lattices, the mass and strain variance parameters are defined as15
| | 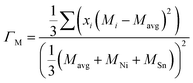 | (7) |
| | 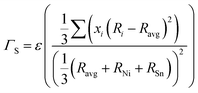 | (8) |
where
x is the site fraction of an element in the M sub-lattice of MNiSn,
Mi/
Ri are the mass/atomic radius of an element in the M sub-lattice and
Mavg/
Ravg are the average mass/radius of the elements in the M sub-lattice. In the strain field variance
ε is a phenomenological parameter that can be used for fitting experimental results.
ε can also be defined theoretically from elastic properties,
35 we use the following definition
36,37| | 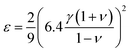 | (9) |
where
ν is the Poisson parameter, that can be found from the relation
21| | 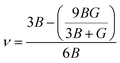 | (10) |
The combination of DFT calculations for the pure compounds (eqn (1)) and the analytical alloying model (eqn (6)) enables the assessment of the lattice thermal conductivity in the whole temperature and composition range in the M sub-lattice.
4. Results and discussion
4.1 Slack model calculations
Table 1 summarizes the results of the DFT calculations for the physical parameters; a comparison with other calculated and experimental values shows a generally good fit. Note that the lattice thermal conductivity model of Slack that we use here is accurate enough for temperatures above the Debye temperature. This is in line with the working temperature of HH materials, here we consider it as 700 K. Calculations for room temperature (300 K) will be used for comparison with other works or experimental results. Fig. 1 presents the lattice thermal conductivity of the pure (Ti/Zr/Hf)NiSn compounds and the (M, Al, Sc)NiSn (M = Ti, Zr, Hf) alloys as a function of temperature. Table 2 shows the lattice thermal conductivity at 300 K and 700 K of the pure compounds in comparison with other calculations and experimental measurements. It may be seen, that there is some deviation in the results of different theoretical works and there is no specific trend (see ref. 5) in the order of the lattice thermal conductivity value in accordance with the type of pure compound. In general, the theoretical lattice thermal conductivity is much higher than the experimentally measured. This is since the real compound has more inherent phonon scattering defects (grain boundaries, inclusions of a second phase)2,3,5 than only point defects that are taken into account in our calculations. Furthermore, the temperature dependence of the lattice thermal conductivity in the considered real pure compounds is relatively weak. The differences between the calculated and measured values are decreasing with the temperature (see the calculated values at 700 K). Moreover, the calculations for different (M0.97Al/Sc0.03)NiSn alloys show neither a significant reduction in the thermal conductivity nor a trend between the different M = Ti/Zr/Hf elements.
Table 1 DFT calculated parameters for MNiSn (M = Ti, Zr, Hf, Al, Sc) alloys in the HH structure, other calculated and experimental values are presented for comparison
|
|
a
0 [Å] |
B
o [GPa] |
Θ
D [K] |
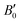
|
γ
|
v
m [m s−1] |
| TiNiSn6 |
5.943 |
127.24 |
413.4 |
4.03 |
1.85 |
3604 |
| Cal 5.94,38 exp 5.9339 |
Exp 124.940 |
Cal 370,41 exp 335,41 41742 |
| Ti0.97Al0.03NiSn6 |
5.941 |
127.23 |
413.9 |
4.14 |
1.90 |
3607 |
| Ti0.97Sc0.03NiSn |
5.944 |
127.40 |
413.6 |
4.24 |
1.95 |
3607 |
| ZrNiSn |
6.137 |
121.96 |
377.3 |
4.25 |
1.96 |
3397 |
| Cal 6.15,38 exp 6.1139 |
Exp 124.640 |
Cal 372,41 exp 32342 |
| Zr0.97Al0.03NiSn |
6.136 |
120.54 |
376.5 |
4.32 |
1.99 |
3389 |
| Zr0.97Sc0.03NiSn |
6.139 |
120.68 |
376.3 |
4.30 |
1.98 |
3389 |
| HfNiSn |
6.103 |
129.47 |
336.2 |
4.12 |
1.89 |
3010 |
| Cal 6.11,38 exp 6.0839 |
Exp 96.940 |
Cal 320,41 exp 30742 |
| Hf0.97Al0.03NiSn |
6.102 |
128.15 |
336.7 |
4.20 |
1.93 |
3014 |
| Hf0.97Sc0.03NiSn |
6.105 |
128.28 |
336.6 |
4.19 |
1.93 |
3015 |
| AlNiSn |
5.942 |
100.58 |
385.8 |
4.61 |
2.14 |
3363 |
| ScNiSn |
6.158 |
94.28 |
359.8 |
4.31 |
1.99 |
3250 |
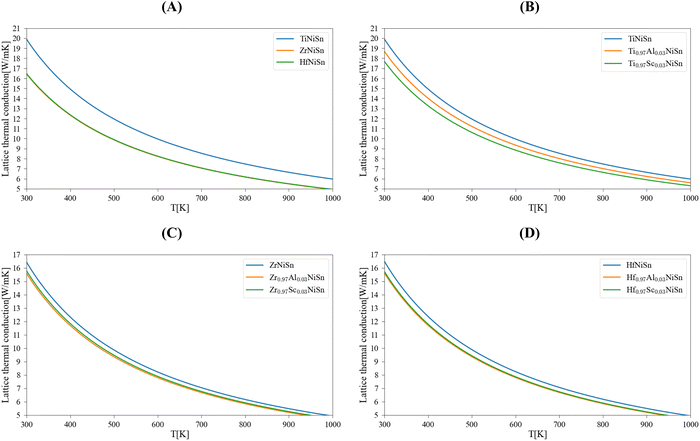 |
| | Fig. 1 Calculated lattice thermal conductivity of MNiSn (M = Ti, Zr, Hf): (A) pure compounds, the substitution of 3 atm% Al/Sc in the M sub-lattice – (B) (Ti, Al/Sc)NiSn, (C) (Zr, Al/Sc)NiSn, (D) (Hf, Al/Sc)NiSn. | |
Table 2 Lattice thermal conductivity of MNiSn compounds
| Composition |
κ
l@300 K |
κ
l@700 K, this work |
| This work |
Other calculations (Table I in ref. 5) |
Experimental (Table I in ref. 5) |
| TiNiSn |
19.9 |
12.8–17.9 |
7.5–9.3 |
8.5 |
| ZrNiSn |
16.4 |
13.4–19.6 |
4.75–10.1 |
7.0 |
| HfNiSn |
16.5 |
14.6–19.5 |
4.8–12 |
7.1 |
| AlNiSn |
10.7 |
— |
— |
4.6 |
| ScNiSn |
11.7 |
— |
— |
5.0 |
4.2 Analytical alloying model combined with the Slack model
The lattice thermal conductivity of the MNiSn alloys (Table 2) was calculated with eqn (6)–(8) from the Slack model and the physical parameter which were calculated using DFT (Table 1). For the scattering parameter, the molar mass and atomic radii of the pure elements are given in Table 3. To use the strain field parameter (eqn (8)), the magnitude of ε is needed. It is obtained by using eqn (9) and (10) with the calculated bulk modulus (B) and Grüneisen parameter (γ) from the DFT calculations (Table 1). The ε parameter for (M0.97, Al/Sc0.03)NiSn (M = Ti, Zr, Hf) alloys yields values in the range of 88–117, and similar to that for pure compounds. Also, the difference between the value of ε parameter from average composition using the pure compounds values to a specific composition is small. For example for (Ti0.97,Al0.03)NiSn versus (0.97·TiNiSn + 0.03·AlNiSn)) it is ∼10%. Thus, to simplify the model and to spare calculation for each composition, the round fixed ε = 90 was chosen. An example of the application of a fixed value of ε from fitting to experimental measurements of HH alloy can be found in ref. 11.
Table 3 Molar mass and atomic radius of the pure elements
| Element |
Molar mass [g mole−1] |
Atomic radius [Å] |
| Ti |
47.867 |
1.46 |
| Zr |
91.224 |
1.60 |
| Hf |
178.486 |
1.58 |
| Ni |
58.6934 |
1.25 |
| Sn |
118.710 |
1.55 |
| Al |
26.982 |
1.43 |
| Sc |
44.956 |
1.64 |
A comparison between the calculations for an alloy at 300 K for a specific composition with Al/Sc alloying carried out in the framework of the Slack model versus the alloying model is presented in Table 4. In the analytical alloying model, the substitution of Al or Sc in the M sub-lattice has a larger influence on the reduction of the thermal conductivity. As we compare calculations for an alloy from DFT and from an analytical model, this kind of deference is expected. Moreover, the scattering parameters (Γ = ΓM + ΓS) in the alloying model for (Ti0.97Al0.03)NiSn and (Zr0.97Sc0.03)NiSn are one order of magnitude smaller than in other compositions. As a result, these two compositions show the smallest differences between the two models. The analytical alloying model results are more reasonable, as the experimental measurements show a notable change in the thermal conductivity even for alloying of just a few percentages of an element. For example, see the influence of Sc alloying in ZrNiSn HH alloy43 where the alloying with 1 at% of Sc leads to ∼21% decrease of the thermal conductivity due to phonon scattering reported.
Table 4 Comparison of calculations of lattice thermal conductivity at 300 K for a specific composition – Slack model versus analytical alloying model
| Composition |
Slack model |
Analytical alloying model |
Γ
M
|
Γ
S
|
Γ
|
| (Ti0.97Al0.03)NiSn |
18.7 |
18.5 |
0.0008 |
0.0011 |
0.0019 |
| (Ti0.97Sc0.03)NiSn |
17.7 |
12.8 |
0.0000(1) |
0.0140 |
0.0140 |
| (Zr0.97Al0.03)NiSn |
15.6 |
10.3 |
0.0051 |
0.0118 |
0.0169 |
| (Zr0.97Sc0.03)NiSn |
15.8 |
14.2 |
0.0026 |
0.0006 |
0.0032 |
| (Hf0.97Al0.03)NiSn |
15.6 |
8.8 |
0.0162 |
0.0092 |
0.0254 |
| (Hf0.97Sc0.03)NiSn |
15.7 |
10.5 |
0.0126 |
0.0015 |
0.0141 |
Table 5 summarizes lattice thermal conductivity calculations and experimental measurements of representative compositions for MNiSn (M = Ti, Zr, Hf, Al, Sc) alloys. This table will be referred to in the following paragraphs. To examine the analytical alloying model, including the specific ε parameter value, the lattice thermal conductivity was calculated at 300 K and 700 K using the mass variance with and without the strain variance (Fig. 2). The general U-like shape of the thermal conductivity as a function of composition was obtained: a large sharp reduction following a plateau and a sharp increase back to the value of the pure compound. We used the CALPHAD model of Berche44 to define the maximal solubility limit (for 700 K) in each binary system in the M sub-lattice. This is important because the model we use here considers the solubility of each element in the M sub-lattice. There is a significant difference between the three quasi-binary systems: while the (Zr1−x–Hfx)NiSn shows total solubility of components on the M sub-lattice of the HH alloy, the (Zr1−x–Tix)NiSn and (Hf1−x–Tix)NiSn are only partially soluble and have a trend to decomposition. Looking at the calculated scattering parameters, we can see that on one hand, the stain field variance in the (Zr1−x–Tix)NiSn is the major one, while the mass variance in (Hf1−x–Tix)NiSn has the majority. On the other hand, the total scattering parameter in (Zr1−x–Hfx)NiSn is rather small. This makes physical sense of the fact that (Zr/Hf1−x–Tix)NiSn has a miscibility gap while (Zr1−x–Hfx)NiSn is fully soluble. The solubility limit of Ti indicated that it interferes in the host lattice due to a large mass/volume difference.
Table 5 Lattice thermal conductivity calculations and experimental measurements for several MNiSn (M = Ti, Zr, Hf, Al, Sc) alloy compositions
| Composition κl |
κ
l@300 K |
κ
l@700 K |
Γ
M
|
Γ
S
|
Γ
|
| Combined model |
Experimental |
Combined model |
Experimental |
| (Ti0.99Al0.01)NiSn |
19.4 |
4.7@353 K6 |
8.4 |
3.1@703 K6 |
0.0003 |
0.0001 |
0.0004 |
| (Zr0.5Hf0.5)NiSn |
6.6 |
2.3 @323 K47 |
3.8 |
1.6@722 K47 |
0.0586 |
0.0014 |
0.0600 |
| (Ti0.3Zr0.35Hf0.35)NiSn, * phase separation occurs |
4.7 |
2.4@352 K48,49 |
2.9 |
1.7@702 K48,49 |
0.1070 |
0.0516 |
0.1586 |
| (Ti0.3Zr0.3Hf0.3Al0.005Sc0.005)NiSn, * phase separation occurs |
4.5 |
2.6@3254 |
2.7 |
1.8@7054 |
0.1110 |
0.0551 |
0.1661 |
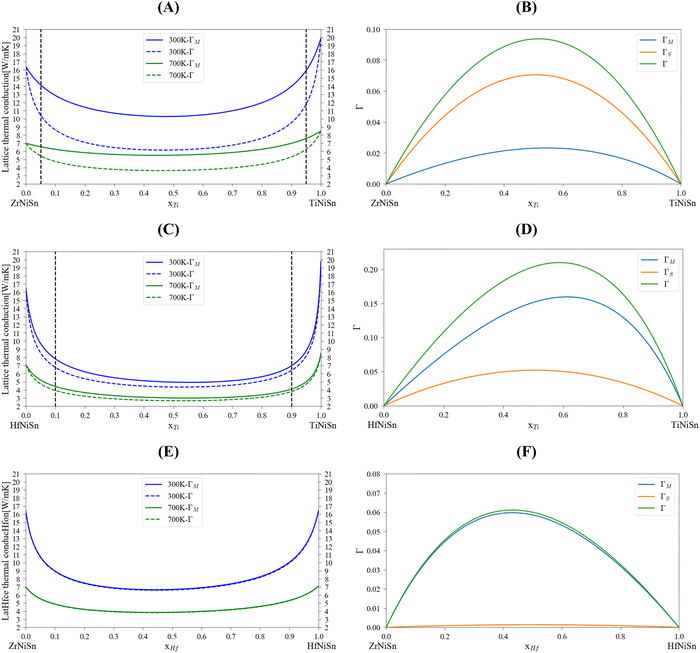 |
| | Fig. 2 Calculated lattice thermal conductivity and scattering parameters for MNiSn (M = Ti, Zr, Hf) alloys using the analytical alloying model: (A and B) (Zr1−x,Tix)NiSn, (C and D) (Hf1−x,Tix)NiSn, (E and F) (Zr1−x, Hfx)NiSn. The dashed black line represents the maximal solubility of each element at 700 K.44 | |
A comparison of the calculated lattice thermal conductivity of (Zr1−x–Hfx)NiSn alloys with experimental measurements is displayed in Fig. 3. Note that the measurements of Liu et al.45 include some alloying of Sb in the Sn sub-lattice. There is a noticeable difference between the calculation and the measurements, which is highest in the non-alloyed compounds and becomes smaller with the addition of an alloying element or increase of the temperature. As was mentioned above, the pure compound includes phonon scattering defects which are not simulated in the current calculation. As the composition of the alloy change and another element enter the M sub-lattice a new phonon scattering mechanism takes place and the difference between the calculation and the measurements is reduced. As the temperature rises, the phonon–phonon scattering mechanism (which the Slack model considers) is more significant while the other defects mechanisms (inclusion, grain boundaries) are temperature independent (at least in the considered temperature range), so the difference between the calculation and measurements is also reduced. Similar findings were presented also in our previous work6 and the work of Eliassen et al.5 As was mentioned in Section 3, the Slack model (eqn (1)) allows the calculation of the lattice thermal conductivity in pure compounds in all temperature range. Thus, when combined with the analytical alloying model (eqn (6)), the lattice thermal conductivity for a specific alloy composition can be calculated as a function of temperature. Fig. 4 presents the calculated and measured lattice thermal conductivity of the Zr0.5Hf0.5NiSn alloy. This is a composition in which the HH is stable, and the alloying scattering parameter is maximal. The trend of temperature dependence can be seen here more clearly.
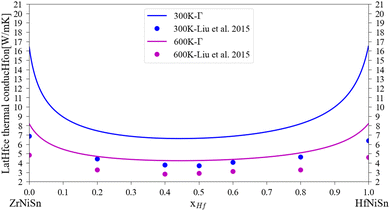 |
| | Fig. 3 Lattice thermal conductivity for (Zr1−x, Hfx)NiSn at 300 K and 600 K: the solid lines represent the current calculation, the dots are experimental measurements for Zr1−xHfxNiSn0.985Sb0.015.45 | |
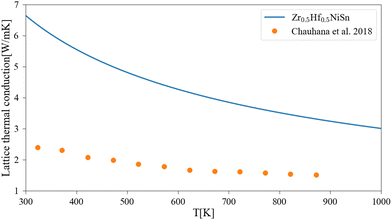 |
| | Fig. 4 Lattice thermal conductivity for Zr0.5Hf0.5NiSn as a function of temperature: the solid lines represent the current calculation, and the dots are experimental measurements.47 | |
The application of the analytical alloying model enables the calculation of multi-component alloying in the M sub-lattice. The addition of Ti to Zr1−xHfxNiSn alloy is used to reduce lattice thermal conductivity without changing the electronic behavior of the material. Fig. 5 shows how the Ti addition up to the solubility limit into Zr0.5Hf0.5NiSn alloy enables the reduction of the lattice thermal conductivity by only alloying scattering. A comparison with the measured values of the (Ti0.3Zr0.35Hf0.35)NiSn is given in Table 5. Although we assume full solubility in this calculation the calculated value is still larger than the measured one. It is worth mentioning that the addition of other described above scattering mechanisms should be taken into consideration. In addition, the phase separation that occurs at this composition results in smaller grains which further reduces the lattice thermal conductivity. Another interesting composition is the HEA in the M sub-lattice (Ti, Zr, Hf, Al, Sc)NiSn, where five elements are mixed to achieve maximal entropy while persevering single phase state.4 Thus, phonon scattering by the alloying element can be maximized. The maximal solubility limit of Al and Sc was assessed there using the HEA parameter for alloying in a single sub-lattice of a compound, the estimated value is 20 at%. This is of course an overestimation that shows the potential of alloying with these elements in MNiSn. For example, the solubility limit on the Ti sub-lattice in TiNiSn was reported at ∼1 at% for Al18 and ∼5 at% for Sc.46Fig. 6 shows the calculated lattice thermal conductivity and scattering parameters of (Ti0.333Zr0.3335Hf0.333)1−x(Al0.5Sc0.5)xNiSn. The rather high value of Γ rises as the Al and Sc composition increases because the mass or atomic radius of these two elements is very different than the Ti/Zr/Hf elements. As a result, further reduction in the lattice thermal conductivity is achieved in values smaller than the suggested solubility limit. It can be seen from Table 5 that this composition has the maximal value of Γ and calculated lattice thermal conductivity, as expected from this HEA composition. Fig. 7 presents the lattice thermal conductivity of the Ti0.333Zr0.333Hf0.333Al0.05Sc0.05NiSn as a function of temperature, showing once again the difference between calculation and measured values that decreases as the temperature rises. Note that all the calculations for the (Ti, Zr, Hf, Al, Sc)NiSn system with the analytical alloying model can be carried out only using the ab initio method. The reason is that the AlNiSn and ScNiSn compounds are not stable in the HH structure:18,46 the AlNiSn composition separates into two phases (Sn + NiAl) and the ScNiSn composition is stable in the TiNiSi structure. So, the thermal conductivity of these compositions in the HH structure cannot be measured directly.
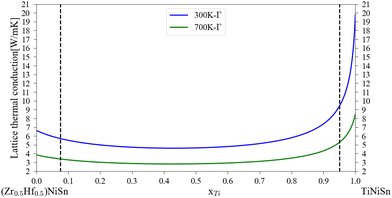 |
| | Fig. 5 Calculated lattice thermal conductivity of (Zr0.5Hf0.5)1−xTixNiSn at 300 K and 700 K. The dashed black line represents the maximal solubility of each element at 700 K.44 | |
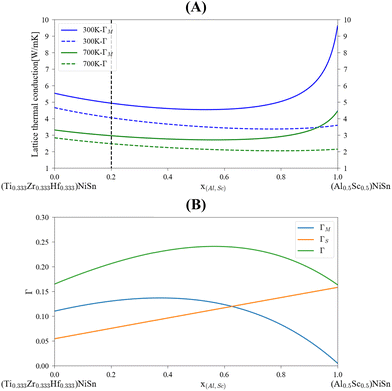 |
| | Fig. 6 Calculated lattice thermal conductivity, (A), and scattering parameters, (B) for (Ti0.333Zr0.3335Hf0.333)1−x(Al0.5Sc0.5)xNiSn. The dashed black line represents the maximal assessed solubility.4 | |
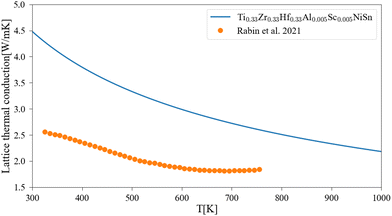 |
| | Fig. 7 Lattice thermal conductivity of Ti0.333Zr0.333Hf0.333Al0.05Sc0.05NiSn as a function of temperature: the solid line represents the current calculation, and the dots are experimental measurements.4 | |
5. Conclusions
Lattice thermal conductivity of MNiSn (M = Ti, Zr, Hf) based alloys was investigated using ab initio DFT calculation combined with an analytical alloying model. This method enabled the application of relatively simple DFT calculations with only three atoms per unit cell for the non-doped compounds with an additional mixing model in the M sub-lattice. Thus, the phonon scattering by mixing in a single sub-lattice is simulated. The method was used for calculations of multi-component alloying with the addition of Al and Sc in the M sub-lattice.
Our investigation demonstrates how the different mixed elements in the alloyed sub-lattice cause phonon scattering, resulting in a reduction of the lattice thermal conductivity. The calculated values are well above the measured values, as expected. This is since the real material includes defects that cause phonon scattering due to other mechanisms (e.g. inclusion, grain boundaries). The difference between the calculations and measured values decreased as the alloying element composition increased or the temperature rises, where the phonon–phonon and point-defect scattering mechanisms are more significant.
The calculations showed the potential of multi-component alloy with the Al and Sc addition to MNiSn for lattice thermal conductivity reduction. Here it was demonstrated how the ab initio DFT facilitates the calculation for an alloying element that is not stable in a ternary compound in the HH structure.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
The work was supported by the Israel Science Foundation (ISF), Grant no. 326/20. One of the authors (YG) is the incumbent of the Samuel Ayrton Chair in Metallurgy at BGU.
References
- T. Graf, C. Felser and S. S. P. Parkin, Simple rules for the understanding of Heusler compounds, Prog. Solid State Chem., 2011, 39(1), 1–50 CrossRef CAS
 .
.
- S. Bhattacharya, M. J. Skove, M. Russell, T. M. Tritt, Y. Xia, V. Ponnambalam, S. J. Poon and N. Thadhani, Effect of boundary scattering on the thermal conductivity of TiNiSn-based half-Heusler alloys, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77(18), 184203 CrossRef
 .
.
- R. He, T. Zhu, Y. Wang, U. Wolff, J. C. Jaud, A. Sotnikov, P. Potapov, D. Wolf, P. Ying, M. Wood and Z. Liu, Unveiling the phonon scattering mechanisms in half-Heusler thermoelectric compounds, Energy Environ. Sci., 2020, 13(12), 5165–5176 RSC
 .
.
- D. Rabin, A. Meshulam, D. Fuks and Y. Gelbstein, High entropy alloy on single sub-lattice in MNiSn compound: Stability and thermoelectric properties, J. Alloys Compd., 2021, 874, 159940 CrossRef CAS
 .
.
- S. N. H. Eliassen, A. Katre, G. K. H. Madsen, C. Persson, O. M. Løvvik and K. Berland, Lattice thermal conductivity of TixZryHf1-x-yNiSn half-Heusler alloys calculated from first principles: Key role of nature of phonon modes, Phys. Rev. B, 2017, 95(4), 045202 CrossRef
 .
.
- D. Rabin, T. Kyratsi, D. Fuks and Y. Gelbstein, Thermoelectric transport properties of (Ti1-cAlc)NiSn half-Heusler alloy, Phys. Chem. Chem. Phys., 2020, 22(3), 1566–1574 RSC
 .
.
- G. A. Slack, Nonmetallic crystals with high thermal conductivity, J. Phys. Chem. Solids, 1973, 34(2), 321–335 CrossRef CAS
 .
.
- G. A. Slack, The Thermal Conductivity of Nonmetallic Crystals, Solid State Phys., 1979, 34(C), 1–71 CAS
 .
.
-
D. T. Morelli and G. A. Slack, High lattice thermal conductivity solids, High Thermal Conductivity Materials, Springer, New York, 2006 Search PubMed
 .
.
- J. Yang, G. P. Meisner and L. Chen, Strain field fluctuation effects on lattice thermal conductivity of ZrNiSn-based thermoelectric compounds, Appl. Phys. Lett., 2004, 85(7), 1140–1142 CrossRef CAS
 .
.
- M. Zhou, L. Chen, W. Zhang and C. Feng, Disorder scattering effect on the high-temperature lattice thermal conductivity of TiCoSb-based half-Heusler compounds, J. Appl. Phys., 2005, 98(1), 013708 CrossRef
 .
.
- H. Geng and H. Zhang, Effects of phase separation on the thermoelectric properties of (Ti, Zr, Hf)NiSn half-Heusler alloys, J. Appl. Phys., 2014, 116(3), 033708 CrossRef
 .
.
- K. Yadav, S. Singh, O. Muthuswamy, T. Takeuchi and K. Mukherjee, Unravelling the phonon scattering mechanism in half-Heusler alloys ZrCo1-xIrxSb (x = 0, 0.1 and 0.25), J. Phys.: Condens. Matter, 2022, 34(3), 6 CrossRef PubMed
 .
.
- P. G. Klemens, Thermal resistance due to point defects at high temperatures, Phys. Rev., 1960, 119(2), 507–509 CrossRef CAS
 .
.
- R. Gurunathan, R. Hanus and G. J. Snyder, Alloy scattering of phonons, Mater. Horiz., 2020, 7(6), 1452–1456 RSC
 .
.
-
R. Gurunathan, Phonon-Defect Interactions in Thermoelectric Materials, Doctoral dissertation, Northwestern University, 2021
 .
.
- P. Blaha, K. Schwarz, F. Tran, R. Laskowski, G. K. H. Madsen and L. D. Marks, WIEN2k: An APW+lo program for calculating the properties of solids, J. Chem. Phys., 2020, 152(7), 074101 CrossRef CAS PubMed
 .
.
- D. Rabin, D. Fuks and Y. Gelbstein, Al solubility in (Ti1−cAlc)NiSn half-Heusler alloy, Phys. Chem. Chem. Phys., 2019, 21, 7524–7533 RSC
 .
.
- G. Leibfried and W. Ludwig, Theory of Anharmonic Effects in Crystals, Solid State Phys., 1961, 12(C), 275–444 CAS
 .
.
- O. L. Anderson, A simplified
method for calculating the Debye temperature from elastic constants, J. Phys. Chem. Solids, 1963, 24(7), 909–917 CrossRef CAS
 .
.
- M. Hichour, D. Rached, R. Khenata, M. Rabah, M. Merabet, A. H. Reshak, S. B. Omran and R. Ahmed, Theoretical investigations of NiTiSn and CoVSn compounds, J. Phys. Chem. Solids, 2012, 73(8), 975–981 CrossRef CAS
 .
.
- T. Jia, G. Chen and Y. Zhang, Lattice thermal conductivity evaluated using elastic properties, Phys. Rev. B, 2017, 95(15), 155206 CrossRef
 .
.
- S. K. Saha and G. Dutta, Elastic and thermal properties of the layered thermoelectrics BiOCuSe and LaOCuSe, Phys. Rev. B, 2016, 94(12), 125209 CrossRef
 .
.
- S. Singh and R. Kumar, Ab-initio calculations of elastic constants and thermodynamic properties of LuAuPb and YAuPb half-heusler compounds, J. Alloys Compd., 2017, 722, 544–548 CrossRef CAS
 .
.
- G. Qin, A. Huang, Y. Liu, H. Wang, Z. Qin, X. Jiang, J. Zhao, J. Hu and M. Hu, High-throughput computational evaluation of lattice thermal conductivity using an optimized Slack model, Mater. Adv., 2022, 3(17), 6826–6830 RSC
 .
.
- E. S. Toberer, A. Zevalkink and G. J. Snyder, Phonon engineering through crystal chemistry, J. Mater. Chem., 2011, 21(40), 15843–15852 RSC
 .
.
- C. Marchbanks and Z. Wu, Reduction of heat capacity and phonon group velocity in silicon nanowires, J. Appl. Phys., 2015, 117(8), 084305 CrossRef
 .
.
- J. Li, P. F. Liu, C. Zhang, X. Shi, S. Jiang, W. Chen, H. Yin and B. T. Wang, Lattice vibrational modes and phonon thermal conductivity of single-layer GaGeTe, J. Mater., 2020, 6(4), 723–728 Search PubMed
 .
.
- S. I. Tamura, Y. Tanaka and H. J. Maris, Phonon group velocity and thermal conduction in superlattices, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60(4), 2627–2630 CrossRef CAS
 .
.
- K. Imamura, Y. Tanaka, N. Nishiguchi, S. Tamura and H. J. Maris, Lattice thermal conductivity in superlattices: Molecular dynamics calculations with a heat reservoir method, J. Phys.: Condens. Matter, 2003, 15(50), 8679–8690 CrossRef CAS
 .
.
- E. P. Pokatilov, D. L. Nika and A. A. Balandin, Phonon spectrum and group velocities in AlN/GaN/AlN and related heterostructures, Superlattices Microstruct., 2003, 33(3), 155–171 CrossRef CAS
 .
.
- W. Kim, Strategies for engineering phonon transport in thermoelectrics, J. Mater. Chem. C, 2015, 3(40), 10336–10347 RSC
 .
.
- A. O. Fumega, Y. Fu, V. Pardo and D. J. Singh, Understanding the lattice thermal conductivity of SrTiO3 from an ab initio perspective, Phys. Rev. Mater., 2020, 4(3), 033606 CrossRef CAS
 .
.
- H. Ehrenreich and L. M. Schwartz, The Electronic Structure of Alloys, Solid State Phys., 1976, 31(C), 149–286 CAS
 .
.
- H. Wang, A. D. Lalonde, Y. Pei and G. J. Snyder, The criteria for beneficial disorder in thermoelectric solid solutions, Adv. Funct. Mater., 2013, 23(12), 1586–1596 CrossRef CAS
 .
.
- C. L. Wan, W. Pan, Q. Xu, Y. X. Qin, J. D. Wang, Z. X. Qu and M. H. Fang, Effect of point defects on the thermal transport properties of (LaxGd1-x)2Zr2O7: Experiment and theoretical model, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74(14), 144109 CrossRef
 .
.
- Q. Zhang, P. Xie, C. Liu, S. Li, X. Lei, L. Huang, G. Yuan and F. Cai, Enhanced thermoelectric performance of Hafnium free n-type ZrNiSn half-Heusler alloys by isoelectronic Si substitution, Mater. Today Phys., 2022, 1(24), 100648 CrossRef
 .
.
- L. Andrea, G. Hug and L. Chaput,
Ab initio phonon properties of half-Heusler NiTiSn, NiZrSn and NiHfSn, J. Phys.: Condens. Matter, 2015, 27(42), 425401 CrossRef PubMed
 .
.
- H. Hohl, A. P. Ramirez, C. Goldmann, G. Ernst, B. Wölfing and E. Bucher, Efficient dopants for ZrNiSn-based thermoelectric materials, J. Phys.: Condens. Matter, 1999, 11(7), 1697–1709 CrossRef CAS
 .
.
- G. Rogl, A. Grytsiv, M. Gürth, A. Tavassoli, C. Ebner, A. Wünschek, S. Puchegger, V. Soprunyuk, W. Schranz, E. Bauer and H. Müller, Mechanical properties of half-Heusler alloys, Acta Mater., 2016, 107, 178–195 CrossRef CAS
 .
.
- A. Page, C. Uher, P. F. Poudeu and A. Van Der Ven, Phase separation of full-Heusler nanostructures in half-Heusler thermoelectrics and vibrational properties from first-principles calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92(17), 174102 CrossRef
 .
.
- R. Kuentzler, R. Clad, G. Schmerber and Y. Dossmann, Gap at the Fermi level and magnetism in RMSn ternary compounds (R = Ti, Zr, Hf and M = Fe, Co, Ni), J. Magn. Magn. Mater., 1992, 104–107(PART 3), 1976–1978 CrossRef CAS
 .
.
- J. Schmitt, Z. M. Gibbs, G. J. Snyder and C. Felser, Resolving the true band gap of ZrNiSn half-Heusler thermoelectric materials, Mater. Horiz., 2015, 2(1), 68–75 RSC
 .
.
- A. Berche, J. C. Tédenac and P. Jund, Phase separation in the half-Heusler thermoelectric materials (Hf, Ti, Zr)NiSn, Scr. Mater., 2017, 139, 122–125 CrossRef CAS
 .
.
- Y. Liu, H. Xie, C. Fu, G. J. Snyder, X. Zhao and T. Zhu, Demonstration of a phonon-glass electron-crystal strategy in (Hf, Zr)NiSn half-Heusler thermoelectric materials by alloying, J. Mater. Chem. A, 2015, 3(45), 22716–22722 RSC
 .
.
- M. Kaller, D. Fuks and Y. Gelbstein, Sc solubility in p-type half-Heusler (Ti1-cScc)NiSn thermoelectric alloys, J. Alloys Compd., 2017, 729, 446–452 CrossRef CAS
 .
.
- N. S. Chauhan, S. Bathula, A. Vishwakarma, R. Bhardwaj, K. K. Johari, B. Gahtori, M. Saravanan and A. Dhar, Compositional tuning of ZrNiSn half-Heusler alloys: Thermoelectric characteristics and performance analysis, J. Phys. Chem. Solids, 2018, 123, 105–112 CrossRef CAS
 .
.
-
T. Zaharoni, O. Appel and Y. Gelbstein, Development of advanced half-Heusler materials for Thermoelectric application, Ben Gurion University of the Negev, 2018.
- O. Appel, T. Zaharoni, G. Breuer, O. Beeri and Y. Gelbstein, Thermoelectric properties of Ti0.3Zr0.35Hf0.35Ni1.005Sn half-Heusler alloy, J. Appl. Phys., 2019, 126(8), 085110 CrossRef
 .
.
|
| This journal is © the Owner Societies 2023 |
Click here to see how this site uses Cookies. View our privacy policy here.  *a,
David
Fuks
b and
Yaniv
Gelbstein
*a,
David
Fuks
b and
Yaniv
Gelbstein
 b
b
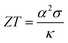 , which is the ratio between the product of the squared Seebeck coefficient, α, and the electrical conductivity, σ, with the thermal conductivity, κ. The thermal conductivity contains the electronic part and lattice (phonon) part. Among these two the lattice thermal conductivity gives the major contribution in HH alloys and therefore its reduction is essential for further optimization of the thermoelectric figure of merit.
, which is the ratio between the product of the squared Seebeck coefficient, α, and the electrical conductivity, σ, with the thermal conductivity, κ. The thermal conductivity contains the electronic part and lattice (phonon) part. Among these two the lattice thermal conductivity gives the major contribution in HH alloys and therefore its reduction is essential for further optimization of the thermoelectric figure of merit.
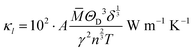
![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) is the average mass of the atom in atomic mass units; δ is the volume per atom; ΘD is the Debye temperature in K; γ is the Grüneisen parameter and the constant A is given by the expression
is the average mass of the atom in atomic mass units; δ is the volume per atom; ΘD is the Debye temperature in K; γ is the Grüneisen parameter and the constant A is given by the expression 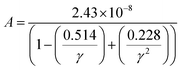 .9 All the other physical parameters are given by the following equations:19,20
.9 All the other physical parameters are given by the following equations:19,20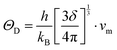
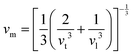
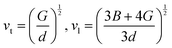
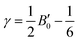
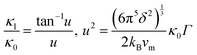
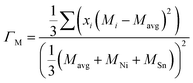
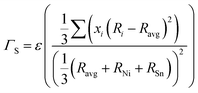
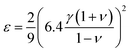
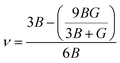






.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.