Open Access Article
Open Access ArticleMachine learning to tame divergent density functional approximations: a new path to consensus materials design principles†
Chenru
Duan
 ab,
Shuxin
Chen
ab,
Michael G.
Taylor
ab,
Shuxin
Chen
ab,
Michael G.
Taylor
 a,
Fang
Liu
a,
Fang
Liu
 a and
Heather J.
Kulik
a and
Heather J.
Kulik
 *a
*a
aDepartment of Chemical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA. E-mail: hjkulik@mit.edu; Tel: +1-617-253-4584
bDepartment of Chemistry, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
First published on 2nd September 2021
Abstract
Virtual high-throughput screening (VHTS) with density functional theory (DFT) and machine-learning (ML)-acceleration is essential in rapid materials discovery. By necessity, efficient DFT-based workflows are carried out with a single density functional approximation (DFA). Nevertheless, properties evaluated with different DFAs can be expected to disagree for cases with challenging electronic structure (e.g., open-shell transition-metal complexes, TMCs) for which rapid screening is most needed and accurate benchmarks are often unavailable. To quantify the effect of DFA bias, we introduce an approach to rapidly obtain property predictions from 23 representative DFAs spanning multiple families, “rungs” (e.g., semi-local to double hybrid) and basis sets on over 2000 TMCs. Although computed property values (e.g., spin state splitting and frontier orbital gap) differ by DFA, high linear correlations persist across all DFAs. We train independent ML models for each DFA and observe convergent trends in feature importance, providing DFA-invariant, universal design rules. We devise a strategy to train artificial neural network (ANN) models informed by all 23 DFAs and use them to predict properties (e.g., spin-splitting energy) of over 187k TMCs. By requiring consensus of the ANN-predicted DFA properties, we improve correspondence of computational lead compounds with literature-mined, experimental compounds over the typically employed single-DFA approach.
1. Introduction
Virtual high-throughput screening (VHTS)1–8 with direct physics-based simulation and aided by machine learning (ML)9–13 is essential in the accelerated discovery of new molecules and materials. Approximate density functional theory (DFT) has become indispensable for both property prediction in VHTS and for generating training data for ML models. Although the favorable combination of cost and accuracy in DFT has motivated its use in screening workflows, the failures of DFT are prominent for the cases where chemical discovery efforts are most needed (e.g., open-shell radicals, transition-metal-containing systems, and strained bonds).14–18 One solution to overcome these limits is to climb up a “Jacob's ladder”19 of density functional approximations (DFAs), where functionals on higher rungs include greater complexity such as higher-order derivatives of the density, Hartree–Fock exchange, and correlation from perturbation theory (i.e., MP2). Doing so has been shown to increase accuracy for organic molecules with a modest increase in computational cost, but simply climbing up to higher rungs does not always guarantee improvements in challenging systems.20,21 Furthermore, choosing the “right” rung a priori in computational materials discovery efforts is impractical if benchmarks are unavailable, and, instead, a single low-cost, heavily-tested DFA (e.g., PBE or B3LYP) is usually employed.Transition-metal complexes (TMCs) exemplify such challenges in single-DFA-based high-throughput screening. While TMCs are of interest for discovery due their widespread applications in catalysis4,22–28 and energy utilization (e.g., in redox flow batteries,29 solar cells,30 and molecular switches31), their electronic structure is challenging to describe accurately.16 The variable nature of metal, oxidation state, and spin of TMCs introduces combinatorial explosion in design spaces11,32 that cannot be exhaustively explored by either first-principles methods or experiments, motivating ML acceleration.33–39 Open-shell TMCs are particularly difficult to study due to their near-degenerate d orbitals that may introduce significant multireference (MR) character.40–44 Furthermore, many properties are highly sensitive to the choice of DFA and the resulting biases will be passed down to and encoded in ML models trained on this data. For example, ML-accelerated discovery based on semi-local DFT will identify lead TMCs targeted for specific spin state properties (i.e., spin-crossover or SCO) with weaker field ligands than those found by hybrid-DFT-derived ML models.37
When careful studies of smaller data sets have been carried out, they have revealed DFA dependence (e.g., including fraction of Hartree–Fock, HF, exchange) of property evaluations for both organic molecules45–47 and TMCs.48–52 To address this issue, some have tried to optimize a DFA for specific properties with respect to the experimental or correlated wavefunction theory (WFT) reference data53–55 or suggest DFAs in a system- and property-specific manner.56,57 Recently, we have built an ML decision engine58,59 at DFT cost that classifies systems with strong MR character and thus identifies regions of chemical space that are safe to make predictions in with DFT.60 One may expect single-reference WFT and DFAs with high HF exchange fractions to fail when strong MR character is present, but high errors may not be present for all DFAs in these cases.14,15,18 Bayesian inference has been used to analyze errors from different DFAs and design new DFAs for systems that potentially contain strong static correlation (i.e., MR character).61–64 It remains to be thoroughly investigated how the systematic biases in a dataset resulting from the behavior of the chosen DFA influence ML model training and the nature of the lead compounds in chemical discovery.
Here, we carry out the first large-scale study on over 2000 TMCs of 23 DFAs from numerous rungs of “Jacob's ladder” (i.e., from semi-local DFT to double hybrids) for three distinct chemical properties. We show that while absolute properties computed by different DFAs disagree, good linear correlations are generally observed between DFA pairs. We show how design rules obtained from the most important features in feature-selected ML models are invariant to DFA choice or basis set, providing a robust tool for materials screening. We introduce a fine-tuning strategy to train multiple artificial neural networks (ANNs) to approximate predictions of different DFAs while maintaining comparable latent spaces. We show how exploiting the consensus among 23 ANNs to discover complexes (e.g., SCOs) results in improved agreement with experiment over a single-DFA approach.
2. Results and discussion
2.1 Statistical analysis of properties derived with different DFAs
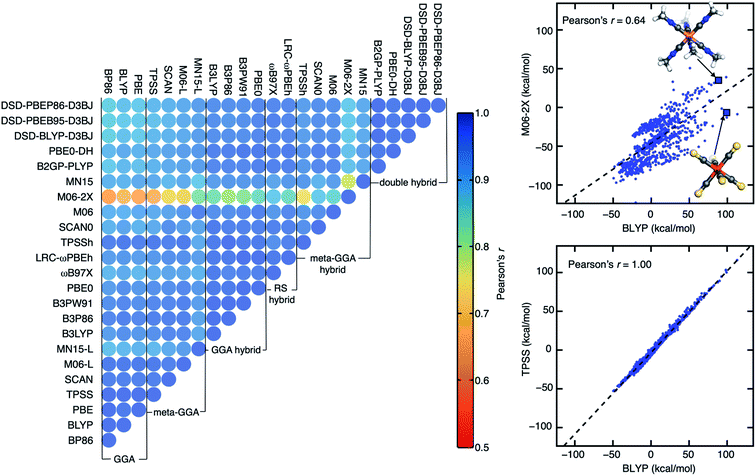
We study a broad range of 23 density functional approximations (DFAs) that are distributed among multiple rungs of “Jacob's ladder”19 (ESI Table S1†). We employ three popular semi-local generalized gradient approximations (GGAs) that are widely used to study both molecular and solid-state systems (i.e., BLYP,65,66 BP86,67,68 and PBE69) and their corresponding global GGA hybrids (B3LYP,70–72 B3P86,67,70 B3PW91,70,73 and PBE0 (ref. 74)). We include two few-parameter, meta-GGAs (TPSS75 and SCAN76) and two more highly parameterized ones (M06-L77 and MN15-L78) that have been empirically tuned to improve performance on a range of benchmark properties,77,78 such as bond energies, reaction barrier heights, and noncovalent interactions. We also include popular hybrid variants of these meta-GGAs (i.e., TPSSh,75 SCAN0,79 M06,80 M06-2X,80 and MN15 (ref. 81)). In addition to the GGA and meta-GGA hybrids, we employ two range-separated hybrids (i.e., LRC-ωPBEh82 and ωB97X83) that consist of GGA hybrids in the short range and full non-local exchange in the long range. Lastly, we incorporate both non-empirical, double hybrids (B2GP-BLYP84 and PBE0-DH85) and parameterized, spin-component-scaled double hybrids that were formulated with empirical dispersion corrections (DSD-BLYP-D3BJ,86 DSD-PBEB95-D3BJ,86 and DSD-PBEP86-D3BJ86). This set of DFAs covers a number of semi-local exchange or correlation functional families, an extended range of HF exchange fractions (0.100 to 0.710) in hybrids, and a large range of MP2 correction fractions (0.125 to 1.000) in double hybrids (ESI Table S1†).To evaluate the relative agreement among these DFAs, we focus on three properties that depend either on multiple geometries, charges, or spin states calculated for a large set of transition-metal complexes (TMCs, see Section 4). These include: (i) the adiabatic high-spin (HS) to low-spin (LS) splitting energy, ΔEH–L; (ii) the vertical ionization potential, IP, of the complex; and (iii) the frontier orbital gap from the Δ-SCF87 approach (hereafter, the Δ-SCF gap) obtained as the difference between the vertical IP and vertical electron affinity (EA) of the TMC. We selected ΔEH–L because it is known48,88–96 to be strongly sensitive to DFA choice. We selected the Δ-SCF87 evaluation of the HOMO–LUMO gap and vertical IP evaluated from total energy differences because they are expected to be less sensitive to the lack of piecewise linearity97,98 in a DFA in comparison to the same properties obtained from frontier orbital energies.14 All properties are evaluated with the single parent functional and basis set choice (B3LYP/LACVP*) we typically employ for its efficiency in high-throughput screening (see Section 4). By using a consistent geometry and developing a strategy for preserving the qualitative description of the wavefunction across DFAs (see Section 4), we isolate the role of the DFA parameterization in altering predicted energetic properties.
Although the absolute computed values differ by DFA for each of the three properties, the obtained values from different DFAs generally have high linear correlations, as quantified by Pearson's correlation coefficients (Fig. 1, ESI Fig. S1 and Table S2†). To put this in context, the range of ΔEH–L values can differ strongly by functional (M06-2X: −122.8 to 50.7 kcal mol−1vs. M06-L: −59.2 to 100.4 kcal mol−1) as can, to a lesser extent, vertical IP (M06-L: 0.9 to 28.4 eV vs. M06-2X: 1.2 to 29.6 eV). We observe strong positive correlations between all pairs of DFAs, even for DFAs from different rungs of “Jacob's ladder”, and for properties (i.e., ΔEH–L) that can be expected to be strongly functional-dependent. Across all functionals, the correlations for vertical IP are consistently high (i.e., 0.99–1.00) so we focus further analysis on the Δ-SCF gap and especially on the most DFA-sensitive property ΔEH–L (ESI Fig. S1†).
Despite strong DFA sensitivity for ΔEH–L, three GGAs have near-perfect linear correlations (Pearson's r > 0.99) with each other (Fig. 1). For this property, most of the meta-GGAs also have extremely high (Pearson's r > 0.98) linear correlation with GGAs, with MN15-L being the sole exception (e.g., Pearson's r of 0.89 with BLYP, ESI Fig. S2†). One might expect a functional like the SCAN meta-GGA that has been demonstrated to make more accurate predictions of formation enthalpy99 and reaction energy100 to correlate poorly with less accurate semi-local GGA functionals, but SCAN-computed Δ-SCF gaps and ΔEH–L values correlate just as highly to the GGAs as other few-parameter meta-GGAs and better than the more highly parameterized MN15-L (Fig. 1 and ESI Fig. S1†). Although the family of double hybrids has lower correlations with pure GGAs in comparison to their correlation with hybrids (i.e., GGA or meta-GGA) for both Δ-SCF gap and ΔEH–L, even the low correlations are still relatively high (Pearson's r = 0.8–0.9, Fig. 1 and ESI Fig. S1†). These good correlations likely benefit from our workflow that ensures qualitative correspondence and limited spin contamination of the converged electronic state with change of DFA (see Section 4).
As could be expected, HF exchange influences ΔEH–L correlations significantly: within the LYP correlation family, B3LYP and B2GP-PLYP are more highly correlated with one another than the latter is with BLYP (ESI Fig. S2†). This behavior of ΔEH–L extends to the more highly parameterized Minnesota (e.g., M06) functionals, e.g., Pearson's r coefficients are lowest between the pure meta-GGA M06-L and M06-2X with high HF exchange (ESI Table S3†). Overall, DFA agreement, as quantified by Pearson's r values, is surprisingly strong across our data set with the 23 distinct functionals regardless of property. When deviations occur between functionals (e.g., for Δ-SCF gap or ΔEH–L), they appear to be due most to HF exchange fraction rather than to pure DFA parameter or correlation family choice.
Among all possible DFA pairings in our set, we observe the lowest Pearson's r for ΔEH–L the pure GGA BLYP and the highly parameterized meta-GGA hybrid M06-2X (Pearson's r: 0.64, Fig. 1). This pair of DFAs is also among the most poorly correlated for Δ-SCF gap (Pearson's r ca. 0.8, ESI Fig. S1†). As an example of this disagreement, differences between the two DFAs of over 100 kcal mol−1 are observed for ΔEH–L (BLYP: 98 kcal mol−1, M06-2X: −6 kcal mol−1) for Fe(II)(CS)6. While BLYP predicts a low-spin (LS) ground state expected for the strong-field CS ligand, M06-2X predicts a likely incorrect high-spin (HS) ground state. For another TMC with similarly strong-field ligands, Co(III)(C2H3N)6, BLYP and M06-2X both predict a LS ground state, albeit with large variations in the ΔEH–L (BLYP: 88 kcal mol−1, M06-2X: 35 kcal mol−1) predicted.
For the cases where pairs of DFAs demonstrate low linear correlations for specific properties (i.e., ΔEH–L and Δ-SCF gap), we note large differences in the distributions of the computed property (Fig. 2 and ESI Fig. S3–S5†). For example, two peaks are observed in the M06-2X ΔEH–L distribution in comparison to only one for M06 and M06-L (Fig. 2). In contrast to the two DFA-sensitive properties, vertical IPs computed with different DFAs tend to differ by a small rigid shift in value with a preserved distribution (Fig. 2 and ESI Fig. S4†). A qualitative difference in the ΔEH–L distributions is associated with more disagreement between functionals (e.g., M06-L and M06-2X in Fig. 2). M06-L and M06-2X predict strong-field Fe(II)(HNO)6 to have the same ΔEH–L of 51 kcal mol−1, but they differ strongly in their predictions for the mixed ligand field of Mn(II)(CO)4(I−)2. In this case, different ground states are obtained with M06-L (LS; ΔEH–L: 32 kcal mol−1) and M06-2X (HS; ΔEH–L: −61 kcal mol−1), and the predicted spin-splitting values differ by 93 kcal mol−1. Returning to the vertical IP for the same pair of DFAs, consistent distributions are instead observed, with HF exchange in M06-2X rigidly shifting the IP up by around 5% (i.e., 1–2 eV over a 30 eV range, Fig. 2). The greatest disagreement, which is observed for LS Co(II)(H2O)4(NH3)2, is only twice this amount (i.e., 4 eV) when comparing M06-L (17.1 eV) to M06-2X (21.4 eV, Fig. 2).
The ranking of compounds by ΔEH–L and Δ-SCF properties varies with DFA choice, but little variation is observed for the vertical IP percentile ranks (Fig. 3 and ESI Fig. S6†). For ΔEH–L, the TMCs with the strongest (e.g., Co(III)(CO)6) and weakest ligand fields (e.g., Mn(II)(H2O)5(C5H5N)) have values at the extremes of the distributions and correspondingly their percentile ranks obtained with the 23 DFAs have the smallest standard deviations (ESI Table S4†). Complexes with moderate ligand field strengths instead have the largest standard deviation of percentile ranks, suggesting that the ordering of TMCs with moderate ligand field strengths for ΔEH–L is most strongly functional dependent. For example, Mn(II)(CO)4(H2O)(C5H5N) is an intermediate-rank ΔEH–L complex (average across the 23 DFAs: 49th percentile) but has a percentile rank ranging from the 20th (e.g., 20 for M06-2X or 26 for DSD-BLYP-D3BJ) to the 73rd percentile (e.g., 73 for BP86 and 65 for M06-L) depending on the DFA (ESI Table S4†). Generally, the pure GGAs and pure meta-GGAs predict this compound to have the highest percentile rank while double hybrids predict it to have among the lowest. Thus, DFAs can broadly be expected to agree at extremes but have divergent behavior for these compounds that have intermediate ΔEH–L properties arising from a mixture of strong-field and weak-field axial ligands (Fig. 3 and ESI Table S4†).
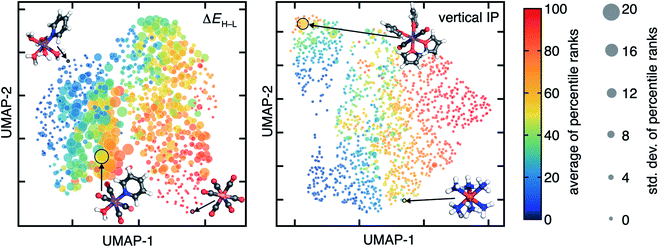 | ||
| Fig. 3 Uniform manifold approximation and projection (UMAP)101 2D visualization of the latent space of a B3LYP/LACVP* ANN (see Section 4) for ΔEH–L (left) and vertical IP (right). Each TMC is shown as a circle colored by the average percentile rank of the property (ΔEH–L (left) and vertical IP (right)) obtained over all 23 DFAs and is scaled by the std. dev. of the percentile rank over the DFAs. Representative TMCs from left to right in the left pane: Mn(II)(H2O)5(C5H5N), Mn(II)(CO)4(H2O)(C5H5N), Co(III)(CO)6, and in the right pane: HS Mn(II)(C4H4O)4(CO)2 and LS Fe(II)(NH3)6. Atoms are colored as follows: orange for Fe, purple for Mn, pink for Co, blue for N, red for O, gray for C, and white for H. | ||
In contrast to ΔEH–L, the ranking of vertical IPs of TMCs remains nearly constant across all 23 DFAs, including for those complexes that have intermediate values (e.g., LS Fe(II)(NH3)6 in Fig. 3, ESI Table S4†). This result is expected because variation in the functional was qualitatively observed to rigidly shift the vertical IP distribution (Fig. 2). Still, there are a few exceptions with large percentile rank standard deviations among the DFAs for vertical IP. In one extreme example, HS Mn(II)(C4H4O)4(CO)2 has a low percentile rank (i.e., <40) for most pure GGAs (e.g., 36 for BLYP) and meta-GGAs but a higher percentile rank (i.e., >60) for hybrids (e.g., 66 for SCAN0) and double hybrids (ESI Table S4†).
For a given functional, the basis set can also be expected102–105 to influence property predictions. We therefore repeated our analysis with a larger triple-ζ (i.e., def2-TZVP) basis set in addition to the double-ζ LACVP* basis set that is more amenable to high-throughput screening. Over each of the three properties and 23 DFAs, we observe that properties computed using the small and large basis sets display both high linear correlation (Pearson's r > 0.98) and absolute property prediction agreement (ESI Table S5 and Fig. S7†). Although one may expect vertical IP to be more dependent on basis set, e.g., for complexes with strongly negatively charged ligands,35,106 we observe little basis set dependence even for this property (ESI Fig. S8†). Therefore, we conclude that DFA dependence outweighs basis dependence for evaluation of the properties considered here, and subsequent discussions focus on results obtained with the VHTS-relevant LACVP* basis set.
2.2 Universal design rules invariant to DFA choices
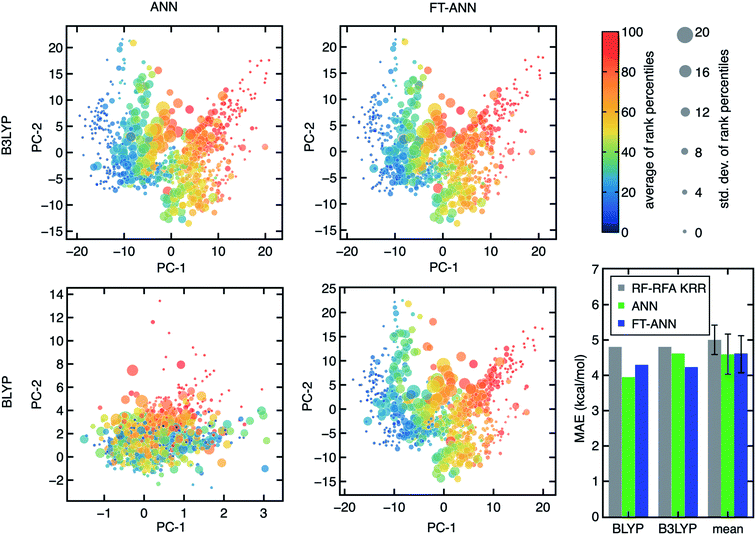
Feature analysis of ML models provides valuable abstractions of learned design principles that can be used to guide materials design.37 For transition-metal chemistry, a series of revised autocorrelations (RAC-155)35 that are products and differences on the molecular graph of heuristic properties (e.g., electronegativity, χ; nuclear charge, Z; topology, T; covalent radius, S; and identity, I) have been used to train predictive ML (e.g., kernel ridge regression, KRR, or artificial neural network, ANN) models (see Section 4). Feature selection to determine the relative importance of individual RACs in terms of distance to the metal on the molecular graph as well as their electronic (i.e., Z or χ) versus geometric (i.e., S, T, or I) nature has been used to reveal design principles for individual properties.35 For example, ΔEH–L has been shown35 to be strongly metal-local and electronic in nature, whereas frontier orbital and vertical-IP-related properties are known107 to depend more on the overall size and shape of the TMC. Nevertheless, such feature-selection-derived design principles have been exclusively obtained with a single DFA. To identify sensitivity of design principles to the DFA used to generate ML model training data, we perform random-forest-ranked recursive feature addition (RF-RFA) from RAC-155 with KRR models following our previously established procedure60,107 for all 23 DFAs (see Section 4).Across this wide set of DFAs, the RF-RFA/KRR-selected features are insensitive to the functional choice for each of the three properties studied (Fig. 4 and ESI Fig. S9–S14†). This observation holds both for the DFA-sensitive ΔEH–L and DFA-insensitive vertical IP (Fig. 4). When quantitative differences are observed, they occur for functionals and properties that had poor correlation, e.g., differences in the fraction of metal-coordinating atom features for M06-2X and ΔEH–L (Fig. 4). Even when small quantitative differences are observed between features selected for each of the DFAs, these differences are significantly smaller than the magnitude of differences among the selected features for each of the three properties within a DFA.
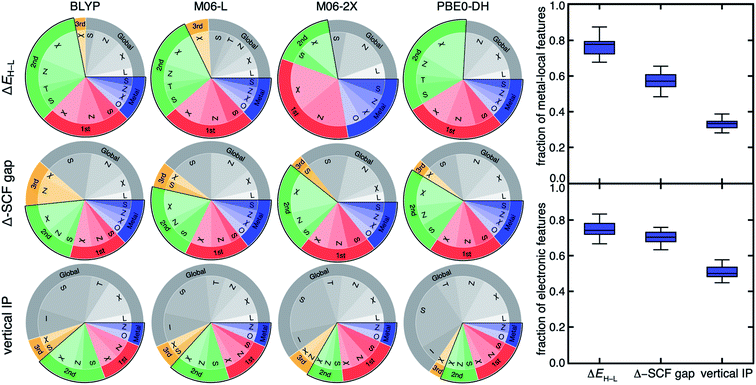 | ||
| Fig. 4 (Left) pie charts of the RF-RFA/KRR-selected RAC-155 features for ΔEH–L (top), Δ-SCF gap (middle), and vertical IP (bottom) for the DFAs indicated (top). Features are grouped by the most metal-distal atoms: metal in blue, first coordination sphere in red, second coordination sphere in green, third coordination sphere in orange, and more distant, global features in gray. A black outline groups the first three categories (i.e., within two bond paths to the metal) as metal-local features. Within each connectivity distance category, the property (i.e., χ, S, T, Z, or I) is also indicated, with the oxidation/spin state (O) assigned as metal-local and the ligand charge (L) assigned as global. (Right) box plot for the fraction of metal-local features (top) and the fraction of electronic features (bottom) for all 23 DFAs at each property. Following our previous work,60,107 we have categorized χ, Z, O, and L as electronic features, with all remaining features categorized as geometric. | ||
For example, RF-RFA/KRR on ΔEH–L from either of the poorly correlated pair of GGA BLYP and meta-GGA hybrid M06-2X DFAs selects a feature set with a comparably high fraction of metal-local features (BLYP: 0.72, M06-2X: 0.72) and electronic (i.e., electronegativity, nuclear charge, oxidation state, see Section 4) features (BLYP: 0.78, M06-2X: 0.83, Fig. 4). The observation of the invariance of selected features for ΔEH–L also holds for M06-L and M06-2X (Fig. 4). Thus, the feature-derived design rules are insensitive to the significant differences in the distributions of ΔEH–L obtained with each of the DFAs, despite this difference leading to variations in percentile rank or low correlations among functionals (Fig. 2).
Although higher-rung double hybrids have been shown96 in some cases to yield more accurate property prediction for spin state ordering, feature selection for all three properties on the PBE0-DH double hybrid yields very similar selected features to DFAs from lower rungs (Fig. 4 and ESI Fig. S9–S14†). Notably, semi-local DFAs that often yield unphysically small or closed HOMO–LUMO gaps give nearly the same selected features as range-separated functionals that contain asymptotically correct, non-local (i.e., 1/r) exchange, even for the vertical IP and Δ-SCF gap (ESI Fig. S9–S14†). Consistent with the correlation analysis, we also observe weak dependence of the selected features on basis set for a given property-DFA combination, reinforcing the utility of small basis sets for computational high throughput screening (ESI Fig. S15†). Taken together, these observations provide powerful support for the design rules revealed through RF-RFA/KRR; such design features are robust to DFA choice and basis set to a much greater extent than absolute or even relative (i.e., rank ordering) property prediction across diverse properties.
A related, open question is the extent to which observations of design rules we have made are sensitive to the nature of the compounds in and the size of the data set on which the models are trained. Consistent with prior work using B3LYP on modest data sets,35,107 the ΔEH–L, Δ-SCF gap, and vertical IP demonstrate decreasing dependence on metal-local and electronic features across representative DFAs from our broader 23 DFA set (Fig. 4). Importantly, the RF-RFA/KRR-selected features are quantitatively comparable, even when considering distinct data sets. The current set contains both smaller complexes with considerably more diverse metal-local chemistry (i.e., both P/S/Cl- and C/N/O-coordinating) and a greater number of ligand types and sizes relative to the set in previous work35,107 that had only five unique ligands with a narrow range (i.e., C/N/O) of metal-coordinating atoms (Fig. 5 and ESI Fig. S16†). Thus, not only is the RF-RFA/KRR feature map insensitive to method choice, but the design rules are likely insensitive to data set choice as long as sufficient variation (e.g., metal identity and ligand field strength) is included in the set.108
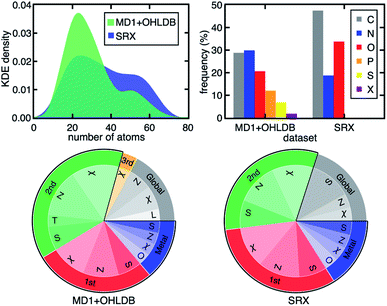 | ||
| Fig. 5 (Top, left) kernel density estimation (KDE) of the size distribution of complexes in two subsets of data from prior work (MD1 + OHLDB) used in this study and the small redox set (SRX) of only five small ligand types from previous work.35,107 (Top, right) clustered bar graph for the connecting atom identity (X indicates any halide) in the two sets. (Bottom) pie charts of the features selected by RF-RFA/KRR for ΔEH–L with B3LYP/LACVP* for MD1 + OHLDB (left) and SRX (right). The pie chart labels follow the format of those in Fig. 4. | ||
Overall, the robustness of RF-RFA/KRR-selected features to data set, basis set, and DFA suggests an efficient approach for materials design. To reveal design rules for new properties in materials spaces that have twin challenges of combinatorial explosion and method accuracy such as open-shell transition-metal chemistry, low-cost DFAs (e.g., GGAs) and small basis sets (i.e., double-ζ) on modest data sets of small, representative complexes can be used to efficiently reveal design principles even when they would be insufficient for individual property predictions.
2.3 Robust chemical discovery using the consensus among multiple DFAs
To enable the exploration of a large chemical space for discovery, we also trained artificial neural network (ANN) models. ANNs have been shown to generalize better than kernel-based models38 on data sets (e.g., hundreds of open-shell TMCs) similar to those studied here. Given the large space of hyperparameters involved in training ANN models, independently trained ANNs for each DFA could differ due to the training procedure while exhibiting similar performance. Indeed, we observe that small differences in weight initialization and the stochastic nature of model optimization lead to distinct architectures (e.g., numbers of nodes or hidden layers) even when the essential features from RF-RFA/KRR indicate the structure–property mapping should be similar (Fig. 6).We next aimed to screen hypothetical compounds with ANNs trained on all 23 DFAs to identify trends of agreement and disagreement among DFAs with ANN models that had comparable confidence (i.e., as judged through latent space distance uncertainty quantification109) and predictive accuracy. To overcome the challenge of inequivalent ANN latent spaces, we use the weights of the ANN trained with B3LYP data as a starting point to train fine-tuned ANNs (FT-ANNs) on properties obtained with each of the 23 DFAs (Fig. 6 and see Section 4 and ESI Table S6†). The FT-ANNs trained through this procedure have comparable latent spaces for different DFAs without sacrificing prediction accuracy in comparison to alternative (i.e., RF-RFA/KRR or standard ANN) models (Fig. 6). This is true regardless of whether the DFA-calculated properties are well correlated with each other or with the parent B3LYP DFA used to obtain the initial ANN model weights and architecture (ESI Fig. S17–S19 and Tables S7–S9†). Despite having similar latent spaces, each of the 23 ANNs predicts distinct properties approximating a unique DFA, enabling us to understand in the context of large-scale chemical discovery how ML models differing in DFA data sources will influence absolute or relative property prediction performance.
Leveraging the 23 FT-ANNs trained on all of the DFAs, we next investigate how ML-approximated knowledge of DFA predictions will influence the design of lead compounds in comparison to the more common approach of using an ML model trained on a single DFA. We first define a target property and then identify consensus lead TMCs as the set of materials in which a majority (i.e., ≥12) of the ML models each trained on a distinct DFA are in agreement about the target property value. Because we have selected a wide-ranging set of DFAs that include semi-local functionals, meta-GGAs, and range-separated hybrids along with varied HF exchange and MP2 correlation fractions, the consensus lead TMCs cannot be chosen simply due to the dominance of a single family of closely related functionals (ESI Tables S1 and S10†). In our procedure, we also perform discovery using latent-space-distance-derived uncertainty quantification,109 restricting our chemical discovery task to regions of chemical space with high ML model confidence (ESI Fig. S20 and Table S11†).
We apply our consensus-based approach in the screening of a large space of 187![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 TMCs obtained from ref. 60. This enumerated space consists of HS and LS M(II/III) midrow metals (M = Cr, Mn, Fe, or Co) with 36 unique ligands in heteroleptic and homoleptic mononuclear octahedral TMCs (ESI Tables S12–S14†). The diverse chemistry, metal-coordinating atom types, symmetry of the complexes, and sizes of the ligands produce a large space of smaller TMCs along with those with up to 200 atoms (ESI Fig. S21 and Tables S12–S13†).
200 TMCs obtained from ref. 60. This enumerated space consists of HS and LS M(II/III) midrow metals (M = Cr, Mn, Fe, or Co) with 36 unique ligands in heteroleptic and homoleptic mononuclear octahedral TMCs (ESI Tables S12–S14†). The diverse chemistry, metal-coordinating atom types, symmetry of the complexes, and sizes of the ligands produce a large space of smaller TMCs along with those with up to 200 atoms (ESI Fig. S21 and Tables S12–S13†).
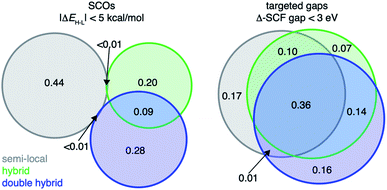
Screening complexes with targeted Δ-SCF gaps <3 eV in this design space is motivated by their relative rarity (ca. 0.1%) in the original set of data from the 23 DFAs (ESI Fig. S22†). We find that lead TMCs for the targeted Δ-SCF gap are robust to the choice of DFA (Fig. 7 and ESI Table S15†). Even DFA pairs with weak linear correlations among our 23-DFA set, such as BLYP and M06-2X (Δ-SCF gap Pearson's r = 0.80), still recommend similar (21% overlap for compounds favored by either functional) lead complexes (ESI Fig. S23†). Although the original data set contains few complexes with the targeted (i.e., <3 eV) Δ-SCF gaps, the ML models generalize well on the 187![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 complex design space, yielding fruitful candidate lead complexes for this design objective. As would be observed with a single DFA, the consensus targeted Δ-SCF gap lead complexes favor large or bidentate N- or O-coordinating ligands with no significant metal preference, an observation that follows the expected trend of smaller Δ-SCF gap with increasing system size (Fig. 8 and ESI Fig. S24†). Because of the robustness of the Δ-SCF gap, this observation does not change if we only employ a single DFA or single family of DFAs (ESI Fig. S25†). When different DFAs were used to train ML models to predict band gaps in solid state materials, it was observed that the ML models sometimes failed to preserve the rank ordering of band gaps that would have been otherwise preserved by lower-level DFAs.110 In our FT-ANN training approach for predicting Δ-SCF gaps of different DFAs, we do not observe this effect. Over the 187.2k compounds, high rank correlation (Spearman's r = 0.86 to 0.99) is observed between all 23 FT-ANN models (ESI Fig. S26†).
200 complex design space, yielding fruitful candidate lead complexes for this design objective. As would be observed with a single DFA, the consensus targeted Δ-SCF gap lead complexes favor large or bidentate N- or O-coordinating ligands with no significant metal preference, an observation that follows the expected trend of smaller Δ-SCF gap with increasing system size (Fig. 8 and ESI Fig. S24†). Because of the robustness of the Δ-SCF gap, this observation does not change if we only employ a single DFA or single family of DFAs (ESI Fig. S25†). When different DFAs were used to train ML models to predict band gaps in solid state materials, it was observed that the ML models sometimes failed to preserve the rank ordering of band gaps that would have been otherwise preserved by lower-level DFAs.110 In our FT-ANN training approach for predicting Δ-SCF gaps of different DFAs, we do not observe this effect. Over the 187.2k compounds, high rank correlation (Spearman's r = 0.86 to 0.99) is observed between all 23 FT-ANN models (ESI Fig. S26†).
To validate our approach on a more challenging property, we next target discovery of SCOs with |ΔEH–L| < 5 kcal mol−1 because SCO chemistry is known to be strongly sensitive to DFA choice (e.g., HF exchange fraction35,37). We identify the consensus (i.e., majority) leads selected by family of functional. We find that discovered complexes are indeed very sensitive to HF exchange fraction, resulting in a limited number (<1%) of leads identified by consensus of the pure semi-local DFAs also selected by the consensus of the HF-exchange-containing hybrid DFAs or double-hybrid DFAs (Fig. 7 and ESI Fig. S27†). Although the GGA-hybrid and double-hybrid family of functionals are expected to be more similar to each other than to those classified as pure GGAs, their consensus-suggested lead complexes differ significantly, with only 9% overlap between leads favored by the consensus of either family of functionals (Fig. 7). Additionally, lead SCO complexes can differ even when we compare DFAs within the same rung of “Jacob's ladder” that were observed to have strong linear correlation with each other for ΔEH–L. For example, within the meta-GGA hybrid group, SCAN0 and TPSSh (ΔEH–L Pearson's r = 0.97) recommend vastly different lead SCO complexes (i.e., only 3% in common), likely due to a rigid shift of ΔEH–L values between the two DFAs (ESI Fig. S27†). That different design objectives result in divergent behavior with respect to DFA sensitivity of the predicted leads suggests that the conventional workflow of only considering a single DFA for chemical discovery may work for some design targets but not others.
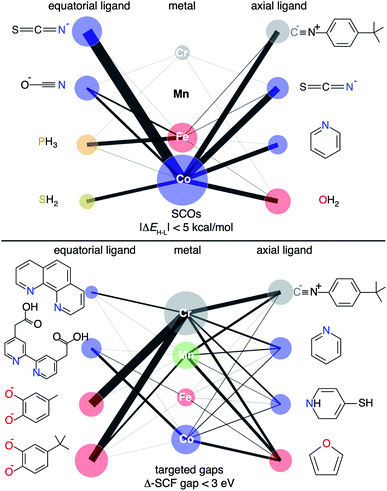
Specific examples illustrate how the large DFA sensitivity of ΔEH–L values results in DFA-dependent chemistry for the SCO candidates. As expected,37,48,49,55 we find that GGAs (e.g., BLYP) have a low-spin bias and favor O-coordinating weak-field ligands, whereas hybrid functionals (e.g. B3LYP) favor N-coordinating intermediate-field ligands in SCO candidates (ESI Fig. S28†). When requiring a majority of 23 DFAs to agree, consensus lead SCO complexes are mostly Fe/Co complexes with weak/moderate-field ligands, matching expectations from experimentally characterized SCOs111 (Fig. 8). Specifically, the consensus lead SCO complexes exclude C-coordinating strong-field ligands or extremely weak field ligands such as small anions (e.g., S2−, F−, and I−). We observe few Cr or Mn SCO complexes, indicating no consensus designs for SCOs containing these metals. Importantly, both sets of discrete lead complexes (i.e., SCO and targeted Δ-SCF gap) identified by the ANNs follow the design rules revealed by RF-RFA/KRR, i.e., that ΔEH–L depends much more on metal-local features than the Δ-SCF gap (Fig. 4 and 8).
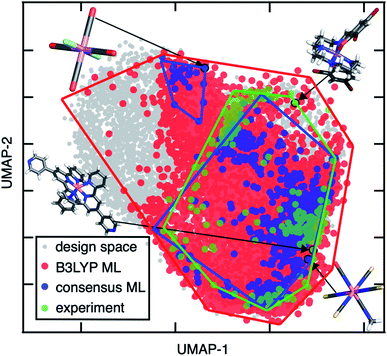
To demonstrate the distinct advantages of our consensus-based workflow for chemical discovery, we mined experimentally observed SCO complexes from the Cambridge Structural Database (CSD)112 following slight modifications to the procedure used in prior work95,113 and compared them to our ML lead complexes (ESI Text S1†). We observe significant overlap between the experimentally identified SCO complexes and those discovered by our consensus ML approach by visualizing both sets of compounds in the latent space of the B3LYP ANN (Fig. 9). For example, Co(II)(NCS−)4(NCO−)(C2H3N), a SCO complex predicted by our consensus ML approach, is close to an experimentally observed Co(II), N-coordinating SCO complex (CSD refcode: JUMPEO, Fig. 9). When qualitative differences between the experimentally observed SCO complexes and our consensus ML leads are seen, they likely result from differences between the composition of our design space and the experimentally studied SCO compounds.114 For example, a hexadentate Mn(II) complex with mixed N and O coordinating atoms is an experimentally observed SCO complex (CSD refcode: YANLAC), but we do not have any hexadentate TMCs in our design space and therefore do not predict any similar Mn(II) compounds to be SCOs.
In comparison to the consensus-based approach, when we apply our conventional workflow of using a single DFA (e.g., B3LYP) to discover lead SCO complexes, we find that the candidate SCOs occupy a much larger region of the B3LYP ANN latent space than the experimental SCO complexes (Fig. 9). This suggests that many of the lead compounds obtained from an ANN trained on the single B3LYP DFA are likely false positives (Fig. 9). This comparison demonstrates the power of using DFA consensus to constrain ML-identified lead complexes to reasonable chemical spaces during discovery. While the consensus-based approach naturally increases the risk of false negatives in comparison of the single DFA, false negatives are observed primarily for the experimental SCO cases where average model confidence is low (ESI Fig. S29†). Thus, the good performance of the consensus-based approach could be improved even further by incorporating more known experimental SCOs absent from the original training data. Notably, use of converged wavefunctions and structures from the parent DFA to derive properties with other DFAs as well as ANN model weights both improves consistency in the consensus-based approach and limits the computational overhead in comparison to the best available alternatives (e.g., correlated wavefunction theory or experiments).
Due to their widespread study, Fe metal centers with N-coordinating ligands dominate our set of experimentally studied SCO complexes111 (ESI Table S16†). The robustness of our consensus-based approach motivates us to make recommendations for other regions of chemical space to explore beyond these well-studied Fe/N SCOs. Because Co(II) and Co(III) complexes appear frequently in the consensus leads and lie near experimental Fe SCO complexes in the latent space of the B3LYP ANN model, our studies suggest their potential for experimental or theoretical validation in SCO complex design (Fig. 8, ESI Fig. S30†). The most likely candidate ligand chemistry suggested by the consensus screen is Co in combination with N-coordinating intermediate-field ligands such as isothiocyanate, cyanate, and pyridine or higher-denticity analogues.
3. Conclusions
While the limited accuracy of density functional approximations in challenging materials spaces is well established, the use of a single DFA in virtual high-throughput screening and machine learning has remained commonplace. To understand the potential biases that choice of a single DFA introduces in discovery campaigns, we computed three properties, ΔEH–L, Δ-SCF gap, and vertical IP, for over 2000 open-shell TMCs with 23 DFAs. For DFAs distributed over multiple rungs of “Jacob's ladder” (e.g., semi-local to double-hybrids), absolute properties were observed to differ, but linear correlations between predictions from different DFAs were high. Over the three properties studied, the degree of dependence on DFA ranged from low (i.e., vertical IP) to intermediate (i.e., frontier orbital Δ-SCF gap) or high (i.e., ΔEH–L) sensitivity. Sensitivity to DFA choice was observed to be greater than to the change from an affordable double-ζ basis set (i.e., LACVP*) to a larger, triple-ζ (i.e., def2-TZVP) one.Feature selection revealed design rules for each property that were invariant over the 23 DFAs tested, even those DFAs that showed poor linear and rank correlations with other predictions. In addition, the selected features were strikingly similar between data sets that contained different metal-coordinating chemistry and system sizes. The robustness of RF-RFA/KRR selected features suggests that universal design rules for new properties can be uncovered with low-cost DFAs and small basis sets on small, representative complexes. Such design rules can then guide more targeted exploration for refinement of properties at higher levels of theory.
To enable large-scale chemical discovery informed by the 23 DFAs, we developed a fine-tuning procedure to obtain a set of comparably performing ANNs trained each trained on data from a single DFA. Using these models to explore a large space of 187![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 TMCs, we obtained design principles for SCO complexes and complexes with a targeted Δ-SCF gap. Lead targeted-gap complexes were robust to the choice of DFA, whereas lead SCO complexes were very sensitive to both the choice of DFA family and HF exchange fraction. This observation suggests that the conventional use of a single DFA in VHTS and ML workflows is appropriate for only specific types of properties.
200 TMCs, we obtained design principles for SCO complexes and complexes with a targeted Δ-SCF gap. Lead targeted-gap complexes were robust to the choice of DFA, whereas lead SCO complexes were very sensitive to both the choice of DFA family and HF exchange fraction. This observation suggests that the conventional use of a single DFA in VHTS and ML workflows is appropriate for only specific types of properties.
By requiring consensus among more than half of the DFAs for a chosen property in a discovery workflow, we overcame the limitations of single DFA. While the single-DFA and consensus approaches both recapitulated RF-RFA/KRR design principles and produced consistent leads for DFA-insensitive properties, the consensus-based approach was critical to identifying lead SCO complexes. These consensus leads overlapped significantly in the ANN model latent space with experimentally observed SCO complexes from the CSD. In contrast, lead SCO complexes identified by a single DFA (e.g., B3LYP) occupied a much larger region of chemical space, indicating many single-DFA leads to be false positives. Thus, using DFA consensus with the approach described here to constrain ML-identified leads during chemical discovery is a promising method to improve prediction robustness without resorting to higher computational cost (i.e., correlated wavefunction theory) methods.
4. Computational details
4.1 Data sets and calculation details
We employ two subsets of data, as curated in prior work60 from five prior studies33–35,107,115 that originally corresponded to a total of 2828 mononuclear octahedral transition-metal complexes in equilibrium geometries obtained with gas-phase density functional theory (DFT). In comparison to the prior curation60 (i.e., where the sets were referred to as MD1 and OHLDB), we refined the data further by de-duplicating structures with identical molecular graph, charge, and spin state across the two sets. This final filtering step followed the procedure for molecular graph identification described in ref. 95 and resulted in a data set of 2639 unique complexes. Details of all complexes are provided in the ESI. As in the original studies,33–35,107,115 the complexes contain M(III)/M(II) (M = Cr, Mn, Fe, or Co) centers with high-spin (HS) and low-spin (LS) multiplicities defined as: quintet-singlet for d4 Mn(III)/Cr(II) and d6 Co(III)/Fe(II), sextet-doublet for d5 Fe(III)/Mn(II), and quartet-doublet d3 Cr(III) and d7 Co(II).For all DFT geometry optimizations carried out in the original work, TeraChem,116 as automated by molSimplify117,118 and molSimplify automatic design (mAD),107 was employed. These calculations used the B3LYP70–72 hybrid functional with the LACVP* basis set, which corresponds to the LANL2DZ119 effective core potential for transition metals (i.e., Cr, Mn, Fe, Co) and heavier elements (i.e., I or Br) and the 6-31G* basis for all remaining elements. All non-singlet states were calculated with an unrestricted formalism and singlet states with a restricted formalism. In all these calculations, level shifting of 1.0 Ha on virtual majority-spin orbitals and 0.1 Ha on virtual minority-spin orbitals was employed.
We developed an approach to maximize correspondence between B3LYP and the 22 additionally studied DFAs that also reduced computational cost (ESI Table S1†). We carried out single-point energy evaluations on B3LYP/LACVP* structures with 23 total DFAs with a LACVP* basis and with a larger, triple-ζ def2-TZVP basis set. To automate these single-point energy calculations, we interfaced molSimplify with a developer version of Psi4 (ref. 15) (1.4a2.dev723). This step was necessary in part because meta-GGAs, double-hybrids, and Minnesota functionals and the larger basis set were unavailable in TeraChem. The 23 functionals included in our study are described in Section 2, and they were used with all default definitions applied in Psi4, as indicated in ESI Table S1.†
In our accelerated workflow, we used the previously converged33–35,107,115 B3LYP/LACVP* TeraChem wavefunction molecular orbital coefficients as an initial guess for a Psi4 B3LYP/LACVP* SCF calculation. The converged Psi4 B3LYP/LACVP* wavefunction was used as an initial guess to obtain self-consistent single-point energies in Psi4 for all other functionals with the LACVP* basis set using the recommended grid size120,121 with 99 radial points and 590 spherical points (ESI Fig. S31 and Table S17†). We also carried out single-point energy calculations with the larger def2-TZVP122 basis set for all combinations of functionals and complexes (ESI Fig. S31†). For these larger-basis calculations, we first carried out basis set projection to obtain the B3LYP/def2-TZVP converged wavefunction from the B3LYP/LACVP* result in Psi4. These calculations were run with a maximum of 50 SCF iterations to reach SCF convergence with both the energy and density convergence thresholds being 3.0 × 10−5 Ha (ESI Fig. S32 and Table S17†). Some pure GGA and meta-GGA calculations did not initially converge. In these cases, we performed calculations with a hybrid form of the pure GGA or meta-GGA, sequentially reducing the percentage of HF exchange and extrapolating to the 0% HF (i.e., pure GGA) total energy (ESI Fig. S33–S34 and Text S2†).
The three primary properties computed (i.e., ΔEH–L, vertical IP, and Δ-SCF gap) were all evaluated on B3LYP/LACVP* geometries obtained with TeraChem. For vertical IP and Δ-SCF gap evaluated on the N-electron reference system, we adopted a consistent spin state convention: we removed a majority-spin electron from the N-electron reference for the N − 1-electron calculation (i.e., for IP) and added a minority-spin electron for the N + 1-electron case (i.e., for EA), in each case starting the Psi4 calculation with an initial guess for the (N − 1/N + 1)-electron calculation from the converged B3LYP/LACVP* TeraChem result (ESI Fig. S31 and S35†).
The filtering procedure applied in previous work60 required that all B3LYP/LACVP* wavefunctions had limited spin contamination (i.e., 〈S2〉 deviations from the expected S(S + 1) value <1.0μB2). The number of calculations excluded by this filtering threshold is sensitive to the choice of functional (ESI Fig. S36†). In this work, we increased the cutoff for inclusion to 1.1μB2 (ESI Fig. S36†). Finally, complexes were retained in the data set only if properties could be converged below this cutoff from all 23 functionals (ESI Tables S18–S19†).
4.2 ML models
As in prior work,60 we use revised auto-correlations35 (RACs) as descriptors for all our machine learning models. RACs are sums of products and differences of five atom-wise heuristic properties (i.e., topology, identity, electronegativity, covalent radius, and nuclear charge) on the 2D molecular graph. As motivated previously,35 we applied the maximum bond depth of three and eliminated RACs that were invariant over the mononuclear octahedral transition-metal complexes, leaving 151 RACs in total (ESI Text S3†). Along with three overall complex features33,35 (i.e., oxidation state, spin multiplicity, and total ligand charge), we obtained a feature set of 154 descriptors in total. For both kernel ridge regression (KRR) and artificial neural network (ANN) models, the hyperparameters were selected using Hyperopt123 with 200 evaluations on a range of hyperparameters, using a random 80%/20% train/test split and 20% of the training data (i.e., 16% overall) used as the validation set (ESI Tables S20–S21†). As in prior work,60,107 recursive feature addition (RFA) was carried out on random-forest-ranked features (i.e., RF-RFA) to obtain the selected feature set that gives the best-performing KRR model with the lowest mean absolute error. All KRR models were implemented in scikit-learn124 with a radial basis function kernel. Details of all models and selected features are provided in the ESI.†All ANN models were trained using Keras125 with Tensorflow126 as the backend and Hyperopt123 for hyperparameter selection (ESI Table S20†). To avoid randomness in the weight initialization and to increase the consistency between ANN models trained with DFT data derived from different functionals, we fine-tuned the B3LYP ANN model with a reduced (i.e., 1 × 10−5) learning rate for each of the 23 functionals, which produced 23 fine-tuned ANN (FT-ANN) models at each property and basis set combination (ESI Table S6†). All ANN models were trained with the Adam optimizer up to 2000 epochs, and dropout, batch normalization, and early stopping were applied to avoid over-fitting (ESI Table S20†).
Data availability
The datasets supporting this article have been uploaded as part of the ESI.†Author contributions
Chenru Duan: data curation, conceptualization, writing – original draft preparation, visualization; Shuxin Chen: data curation; Michael G. Taylor: data curation; Fang Liu: data curation; Heather J. Kulik: writing – reviewing and editing, supervision, conceptualization.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
The authors acknowledge primary support by the Office of Naval Research under Grant Numbers N00014-17-1-2956, N00014-18-1-2434, and N00014-20-1-2150 (to C. D., M. G. T., and H. J. K.). The machine learning effort was also supported by DARPA (grant number DE18AP00039). F. L. was partially supported by the Department of Energy under Grant Number DE-SC0018096 and a MolSSI fellowship (Grant No. ACI-1547580). M. G. T. was supported by the Department of Energy under Grant Number DE-SC0012702. S. C. was supported by an MIT Energy Initiative Fund for Undergraduate Research. This work made use of Department of Defense HPCMP computing resources. This work was also carried out in part using computational resources from the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation Grant Number ACI-1548562. H. J. K. holds a Career Award at the Scientific Interface from the Burroughs Wellcome Fund, an AAAS Marion Milligan Mason Award, and an Alfred P. Sloan Fellowship in Chemistry, which supported this work. The authors thank Adam H. Steeves, Aditya Nandy, and Vyshnavi Vennelakanti for providing a critical reading of the manuscript.References
- Y. N. Shu and B. G. Levine, Simulated Evolution of Fluorophores for Light Emitting Diodes, J. Chem. Phys., 2015, 142(10), 104104 CrossRef PubMed.
- R. Gomez-Bombarelli, J. Aguilera-Iparraguirre, T. D. Hirzel, D. Duvenaud, D. Maclaurin, M. A. Blood-Forsythe, H. S. Chae, M. Einzinger, D. G. Ha and T. Wu, et al., Design of Efficient Molecular Organic Light-Emitting Diodes by a High-Throughput Virtual Screening and Experimental Approach, Nat. Mater., 2016, 15(10), 1120 CrossRef CAS PubMed.
- I. Y. Kanal, S. G. Owens, J. S. Bechtel and G. R. Hutchison, Efficient Computational Screening of Organic Polymer Photovoltaics, J. Phys. Chem. Lett., 2013, 4(10), 1613 CrossRef CAS.
- K. D. Vogiatzis, M. V. Polynski, J. K. Kirkland, J. Townsend, A. Hashemi, C. Liu and E. A. Pidko, Computational Approach to Molecular Catalysis by 3d Transition Metals: Challenges and Opportunities, Chem. Rev., 2018, 119, 2453 CrossRef PubMed.
- M. Foscato and V. R. Jensen, Automated in silico Design of Homogeneous Catalysts, ACS Catal., 2020, 10(3), 2354 CrossRef CAS.
- S. Curtarolo, G. L. Hart, M. B. Nardelli, N. Mingo, S. Sanvito and O. Levy, The High-Throughput Highway to Computational Materials Design, Nat. Mater., 2013, 12(3), 191 CrossRef CAS PubMed.
- S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Python Materials Genomics (pymatgen): A Robust, Open-Source Python Library for Materials Analysis, Comput. Mater. Sci., 2013, 68, 314 CrossRef CAS.
- J. K. Nørskov and T. Bligaard, The Catalyst Genome, Angew. Chem., Int. Ed., 2013, 52(3), 776 CrossRef PubMed.
- B. Meredig, A. Agrawal, S. Kirklin, J. E. Saal, J. Doak, A. Thompson, K. Zhang, A. Choudhary and C. Wolverton, Combinatorial Screening for New Materials in Unconstrained Composition Space with Machine Learning, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89(9), 094104 CrossRef.
- P. O. Dral, Quantum Chemistry in the Age of Machine Learning, J. Phys. Chem. Lett., 2020, 11(6), 2336 CrossRef CAS PubMed.
- J. P. Janet, C. Duan, A. Nandy, F. Liu and H. J. Kulik, Navigating Transition-Metal Chemical Space: Artificial Intelligence for First-Principles Design, Acc. Chem. Res., 2021, 54(3), 532 CrossRef CAS PubMed.
- K. T. Butler, D. W. Davies, H. Cartwright, O. Isayev and A. Walsh, Machine Learning for Molecular and Materials Science, Nature, 2018, 559(7715), 547 CrossRef CAS PubMed.
- A. Chen, X. Zhang and Z. Zhou, Machine learning: accelerating materials development for energy storage and conversion, InfoMat, 2020, 2(3), 553 CrossRef CAS.
- A. J. Cohen, P. Mori-Sánchez and W. Yang, Challenges for Density Functional Theory, Chem. Rev., 2012, 112(1), 289 CrossRef CAS PubMed.
- A. D. Becke, Perspective: Fifty Years of Density-Functional Theory in Chemical Physics, J. Chem. Phys., 2014, 140(18), 18A301 CrossRef PubMed.
- C. J. Cramer and D. G. Truhlar, Density Functional Theory for Transition Metals and Transition Metal Chemistry, Phys. Chem. Chem. Phys., 2009, 11(46), 10757 RSC.
- C. Duan, F. Liu, A. Nandy and H. J. Kulik, Putting Density Functional Theory to the Test in Machine-Learning-Accelerated Materials Discovery, J. Phys. Chem. Lett., 2021, 12(19), 4628 CrossRef CAS.
- H. Y. S. Yu, S. H. L. Li and D. G. Truhlar, Perspective: Kohn-Sham Density Functional Theory Descending a Staircase, J. Chem. Phys., 2016, 145(13), 130901 CrossRef PubMed.
- J. P. Perdew and K. Schmidt, Density Functional Theory and Its Application to Materials, 2001, p. 1 Search PubMed.
- F. Tran, J. Stelzl and P. Blaha, Rungs 1 to 4 of DFT Jacob's Ladder: Extensive Test on the Lattice Constant, Bulk Modulus, and Cohesive Energy of Solids, J. Chem. Phys., 2016, 144(20), 204120 CrossRef PubMed.
- B. G. Janesko, Replacing Hybrid Density Functional Theory: Motivation and Recent Advances, Chem. Soc. Rev., 2021, 50(15), 8470 RSC.
- P. Huo, C. Uyeda, J. D. Goodpaster, J. C. Peters and T. F. Miller III, Breaking the Correlation Between Energy Costs and Kinetic Barriers in Hydrogen Evolution via a Cobalt Pyridine-Diimine-Dioxime Catalyst, ACS Catal., 2016, 6(9), 6114 CrossRef CAS.
- L. Grajciar, C. J. Heard, A. A. Bondarenko, M. V. Polynski, J. Meeprasert, E. A. Pidko and P. Nachtigall, Towards Operando Computational Modeling in Heterogeneous Catalysis, Chem. Soc. Rev., 2018, 47(22), 8307 RSC.
- P. B. Arockiam, C. Bruneau and P. H. Dixneuf, Ruthenium(II)-Catalyzed C-H Bond Activation and Functionalization, Chem. Rev., 2012, 112(11), 5879 CrossRef CAS PubMed.
- D. M. Schultz and T. P. Yoon, Solar Synthesis: Prospects in Visible Light Photocatalysis, Science, 2014, 343(6174), 985 CrossRef CAS.
- D. W. Shaffer, I. Bhowmick, A. L. Rheingold, C. Tsay, B. N. Livesay, M. P. Shores and J. Y. Yang, Spin-State Diversity in a Series of Co(II) PNP Pincer Biomide Complexes, Dalton Trans., 2016, 45(44), 17910 RSC.
- C. Tsay and J. Y. Yang, Electrocatalytic Hydrogen Evolution under Acidic Aqueous Conditions and Mechanistic Studies of a Highly Stable Molecular Catalyst, J. Am. Chem. Soc., 2016, 138(43), 14174 CrossRef CAS PubMed.
- M. Schilling, G. R. Patzke, J. Hutter and S. Luber, Computational Investigation and Design of Cobalt Aqua Complexes for Homogeneous Water Oxidation, J. Phys. Chem. C, 2016, 120(15), 7966 CrossRef CAS.
- B. Dunn, H. Kamath and J. M. Tarascon, Electrical Energy Storage for the Grid: A Battery of Choices, Science, 2011, 334(6058), 928 CrossRef CAS PubMed.
- A. Yella, H. W. Lee, H. N. Tsao, C. Y. Yi, A. K. Chandiran, M. K. Nazeeruddin, E. W. G. Diau, C. Y. Yeh, S. M. Zakeeruddin and M. Gratzel, Porphyrin-Sensitized Solar Cells with Cobalt(II/III)-Based Redox Electrolyte Exceed 12 Percent Efficiency, Science, 2011, 334(6056), 629 CrossRef CAS PubMed.
- S. Goswami, K. Aich, S. Das, A. K. Das, D. Sarkar, S. Panja, T. K. Mondal and S. Mukhopadhyay, A Red Fluorescence ‘Off-On’ Molecular Switch for Selective Detection of Al3+, Fe3+ and Cr3+: Experimental and Theoretical Studies along with Living Cell Imaging, Chem. Commun., 2013, 49(91), 10739 RSC.
- A. M. Virshup, J. Contreras-García, P. Wipf, W. Yang and D. N. Beratan, Stochastic Voyages into Uncharted Chemical Space Produce a Representative Library of All Possible Drug-Like Compounds, J. Am. Chem. Soc., 2013, 135(19), 7296 CrossRef CAS PubMed.
- C. Duan, J. P. Janet, F. Liu, A. Nandy and H. J. Kulik, Learning from Failure: Predicting Electronic Structure Calculation Outcomes with Machine Learning Models, J. Chem. Theory Comput., 2019, 15(4), 2331 CrossRef CAS PubMed.
- J. P. Janet, L. Chan and H. J. Kulik, Accelerating Chemical Discovery with Machine Learning: Simulated Evolution of Spin Crossover Complexes with an Artificial Neural Network, J. Phys. Chem. Lett., 2018, 9, 1064 CrossRef CAS PubMed.
- J. P. Janet and H. J. Kulik, Resolving Transition Metal Chemical Space: Feature Selection for Machine Learning and Structure-Property Relationships, J. Phys. Chem. A, 2017, 121(46), 8939 CrossRef CAS.
- J. P. Janet and H. J. Kulik, Predicting Electronic Structure Properties of Transition Metal Complexes with Neural Networks, Chem. Sci., 2017, 8(7), 5137 RSC.
- J. P. Janet, F. Liu, A. Nandy, C. Duan, T. H. Yang, S. Lin and H. J. Kulik, Designing in the Face of Uncertainty: Exploiting Electronic Structure and Machine Learning Models for Discovery in Inorganic Chemistry, Inorg. Chem., 2019, 58(16), 10592 CrossRef CAS PubMed.
- J. P. Janet, S. Ramesh, C. Duan and H. J. Kulik, Accurate Multiobjective Design in a Space of Millions of Transition Metal Complexes with Neural-Network-Driven Efficient Global Optimization, ACS Cent. Sci., 2020, 6(4), 513 CrossRef CAS.
- A. Nandy, J. Z. Zhu, J. P. Janet, C. Duan, R. B. Getman and H. J. Kulik, Machine Learning Accelerates the Discovery of Design Rules and Exceptions in Stable Metal-Oxo Intermediate Formation, ACS Catal., 2019, 9(9), 8243 CrossRef CAS.
- N. J. DeYonker, K. A. Peterson, G. Steyl, A. K. Wilson and T. R. Cundari, Quantitative Computational Thermochemistry of Transition Metal Species, J. Phys. Chem. A, 2007, 111(44), 11269 CrossRef CAS PubMed.
- W. Jiang, N. J. DeYonker and A. K. Wilson, Multireference Character for 3d Transition-Metal-Containing Molecules, J. Chem. Theory Comput., 2012, 8(2), 460 CrossRef CAS PubMed.
- J. Wang, S. Manivasagam and A. K. Wilson, Multireference Character for 4d Transition-Metal-Containing Molecules, J. Chem. Theory Comput., 2015, 11(12), 5865 CrossRef CAS PubMed.
- C. A. Gaggioli, S. J. Stoneburner, C. J. Cramer and L. Gagliardi, Beyond Density Functional Theory: The Multiconfigurational Approach to Model Heterogeneous Catalysis, ACS Catal., 2019, 9(9), 8481 CrossRef CAS.
- K. Boguslawski, P. Tecmer, O. Legeza and M. Reiher, Entanglement Measures for Single-and Multireference Correlation Effects, J. Phys. Chem. Lett., 2012, 3(21), 3129 CrossRef CAS PubMed.
- L. Goerigk, A. Hansen, C. Bauer, S. Ehrlich, A. Najibi and S. Grimme, A Look at the Density Functional Theory Zoo with the Advanced GMTKN55 Database for General Main Group Thermochemistry, Kinetics and Noncovalent Interactions, Phys. Chem. Chem. Phys., 2017, 19(48), 32184 RSC.
- S. P. Veccham and M. Head-Gordon, Density Functionals for Hydrogen Storage: Defining the H2Bind275 Test Set with Ab Initio Benchmarks and Assessment of 55 Functionals, J. Chem. Theory Comput., 2020, 16(8), 4963 CrossRef CAS PubMed.
- N. Mardirossian and M. Head-Gordon, How Accurate Are the Minnesota Density Functionals for Noncovalent Interactions, Isomerization Energies, Thermochemistry, and Barrier Heights Involving Molecules Composed of Main-Group Elements?, J. Chem. Theory Comput., 2016, 12(9), 4303 CrossRef CAS.
- S. R. Mortensen and K. P. Kepp, Spin Propensities of Octahedral Complexes from Density Functional Theory, J. Phys. Chem. A, 2015, 119(17), 4041 CrossRef CAS PubMed.
- O. S. Siig and K. P. Kepp, Iron(II) and Iron(III) Spin Crossover: Toward an Optimal Density Functional, J. Phys. Chem. A, 2018, 122(16), 4208 CrossRef CAS PubMed.
- M. Bursch, A. Hansen, P. Pracht, J. T. Kohn and S. Grimme, Theoretical Study on Conformational Energies of Transition Metal Complexes, Phys. Chem. Chem. Phys., 2021, 23(1), 287 RSC.
- M. Radon, Benchmarking Quantum Chemistry Methods for Spin-State Energetics of Iron Complexes against Quantitative Experimental Data, Phys. Chem. Chem. Phys., 2019, 21(9), 4854 RSC.
- D. Coskun, S. V. Jerome and R. A. Friesner, Evaluation of the Performance of the B3LYP, PBE0, and M06 DFT Functionals, and DBLOC-Corrected Versions, in the Calculation of Redox Potentials and Spin Splittings for Transition Metal Containing Systems, J. Chem. Theory Comput., 2016, 12(3), 1121 CrossRef CAS PubMed.
- Z. M. Williams, T. C. Wiles and F. R. Manby, Accurate Hybrid Density Functionals with UW12 Correlation, J. Chem. Theory Comput., 2020, 16(10), 6176 CrossRef CAS PubMed.
- Y. X. Chen, L. F. Zhang, H. Wang and E. D. P. K. S. Weinan, A Comprehensive Data-Driven Approach toward Chemically Accurate Density Functional Theory, J. Chem. Theory Comput., 2021, 17(1), 170 CrossRef CAS PubMed.
- D. Y. Zhang and D. G. Truhlar, Spin Splitting Energy of Transition Metals: A New, More Affordable Wave Function Benchmark Method and Its Use to Test Density Functional Theory, J. Chem. Theory Comput., 2020, 16(7), 4416 CrossRef CAS PubMed.
- A. Mitrofanov, V. Korolev, N. Andreadi, V. Petrov and S. Kalmykov, Simple Automatized Tool for Exchange-Correlation Functional Fitting, J. Phys. Chem. A, 2020, 124(13), 2700 CrossRef CAS PubMed.
- S. McAnanama-Brereton and M. P. Waller, Rational Density Functional Selection Using Game Theory, J. Chem. Inf. Model., 2018, 58(1), 61 CrossRef CAS PubMed.
- C. Duan, F. Liu, A. Nandy and H. J. Kulik, Data-Driven Approaches Can Overcome the Cost-Accuracy Trade-Off in Multireference Diagnostics, J. Chem. Theory Comput., 2020, 16(7), 4373 CrossRef CAS PubMed.
- C. Duan, F. Liu, A. Nandy and H. J. Kulik, Semi-Supervised Machine Learning Enables the Robust Detection of Multireference Character at Low Cost, J. Phys. Chem. Lett., 2020, 11(16), 6640 CrossRef CAS PubMed.
- F. Liu, C. Duan and H. J. Kulik, Rapid Detection of Strong Correlation with Machine Learning for Transition-Metal Complex High-Throughput Screening, J. Phys. Chem. Lett., 2020, 11(19), 8067 CrossRef CAS PubMed.
- J. J. Mortensen, K. Kaasbjerg, S. L. Frederiksen, J. K. Norskov, J. P. Sethna and K. W. Jacobsen, Bayesian Error Estimation in Density-Functional Theory, Phys. Rev. Lett., 2005, 95(21), 216401 CrossRef CAS PubMed.
- J. Wellendorff, K. T. Lundgaard, K. W. Jacobsen and T. Bligaard, mBEEF: An Accurate Semi-Local Bayesian Error Estimation Density Functional, J. Chem. Phys., 2014, 140(14), 144107 CrossRef PubMed.
- J. Wellendorff, K. T. Lundgaard, A. Mogelhoj, V. Petzold, D. D. Landis, J. K. Norskov, T. Bligaard and K. W. Jacobsen, Density Functionals for Surface Science: Exchange-Correlation Model Development with Bayesian Error Estimation, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85(23), 235149 CrossRef.
- E. A. Walker, D. Mitchell, G. A. Terejanu and A. Heyden, Identifying Active Sites of the Water-Gas Shift Reaction over Titania Supported Platinum Catalysts under Uncertainty, ACS Catal., 2018, 8(5), 3990 CrossRef CAS.
- F. J. Devlin, J. W. Finley, P. J. Stephens and M. J. Frisch, Ab-Initio Calculation of Vibrational Absorption and Circular-Dichroism Spectra Using Density-Functional Force-Fields – A Comparison of Local, Nonlocal, and Hybrid Density Functionals, J. Phys. Chem., 1995, 99(46), 16883 CrossRef CAS.
- B. Miehlich, A. Savin, H. Stoll and H. Preuss, Results Obtained with the Correlation-Energy Density Functionals of Becke and Lee, Yang and Parr, Chem. Phys. Lett., 1989, 157(3), 200 CrossRef CAS.
- J. P. Perdew, Density-Functional Approximation for the Correlation-Energy of the Inhomogeneous Electron-Gas, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33(12), 8822 CrossRef PubMed.
- A. D. Becke, Density-Functional Exchange-Energy Approximation with Correct Asymptotic-Behavior, Phys. Rev. A, 1988, 38(6), 3098 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77(18), 3865 CrossRef CAS PubMed.
- A. D. Becke, Density-Functional Thermochemistry. III. The Role of Exact Exchange, J. Chem. Phys., 1993, 98(7), 5648 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS PubMed.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields, J. Phys. Chem., 1994, 98(45), 11623 CrossRef CAS.
- J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Atoms, Molecules, Solids, and Surfaces – Applications of the Generalized Gradient Approximation for Exchange and Correlation, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46(11), 6671 CrossRef CAS PubMed.
- C. Adamo and V. Barone, Toward Reliable Density Functional Methods without Adjustable Parameters: The PBE0 Model, J. Chem. Phys., 1999, 110(13), 6158 CrossRef CAS.
- J. M. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Climbing the Density Functional Ladder: Nonempirical Meta-Generalized Gradient Approximation Designed for Molecules and Solids, Phys. Rev. Lett., 2003, 91(14), 146401 CrossRef PubMed.
- J. W. Sun, A. Ruzsinszky and J. P. Perdew, Strongly Constrained and Appropriately Normed Semilocal Density Functional, Phys. Rev. Lett., 2015, 115(3), 036402 CrossRef PubMed.
- Y. Zhao and D. G. Truhlar, A New Local Density Functional for Main-Group Thermochemistry, Transition Metal Bonding, Thermochemical Kinetics, and Noncovalent Interactions, J. Chem. Phys., 2006, 125(19), 194101 CrossRef PubMed.
- H. S. Yu, X. He and D. G. Truhlar, MN15-L: A New Local Exchange-Correlation Functional for Kohn-Sham Density Functional Theory with Broad Accuracy for Atoms, Molecules, and Solids, J. Chem. Theory Comput., 2016, 12(3), 1280 CrossRef CAS PubMed.
- K. Hui and J. D. Chai, SCAN-based Hybrid and Double-Hybrid Density Functionals from Models without Fitted Parameters, J. Chem. Phys., 2016, 144(4), 044114 CrossRef PubMed.
- Y. Zhao and D. G. Truhlar, The M06 Suite of Density Functionals for Main Group Thermochemistry, Thermochemical Kinetics, Noncovalent Interactions, Excited States, and Transition Elements: Two New Functionals and Systematic Testing of Four M06-Class Functionals and 12 Other Functionals, Theor. Chem. Acc., 2008, 120(1–3), 215 Search PubMed.
- H. Y. S. Yu, X. He, S. H. L. Li and D. G. Truhlar, MN15: A Kohn-Sham Global-Hybrid Exchange-Correlation Density Functional with Broad Accuracy for Multi-Reference and Single-Reference Systems and Noncovalent Interactions, Chem. Sci., 2016, 7(9), 6278 RSC.
- M. A. Rohrdanz, K. M. Martins and J. M. Herbert, A Long-Range-Corrected Density Functional That Performs Well for Both Ground-State Properties and Time-Dependent Density Functional Theory Excitation Energies, Including Charge-Transfer Excited States, J. Chem. Phys., 2009, 130(5), 054112 CrossRef PubMed.
- J. D. Chai and M. Head-Gordon, Systematic Optimization of Long-Range Corrected Hybrid Density Functionals, J. Chem. Phys., 2008, 128(8), 084106 CrossRef PubMed.
- A. Karton, A. Tarnopolsky, J. F. Lamere, G. C. Schatz and J. M. L. Martin, Highly Accurate First-Principles Benchmark Data Sets for the Parametrization and Validation of Density Functional and Other Approximate Methods. Derivation of a Robust, Generally Applicable, Double-Hybrid Functional for Thermochemistry and Thermochemical Kinetics, J. Phys. Chem. A, 2008, 112(50), 12868 CrossRef CAS.
- E. Bremond and C. Adamo, Seeking for Parameter-Free Double-Hybrid Functionals: The PBE0-DH Model, J. Chem. Phys., 2011, 135(2), 024106 CrossRef PubMed.
- S. Kozuch and J. M. L. Martin, Spin-Component-Scaled Double Hybrids: An Extensive Search for the Best Fifth-Rung Functionals Blending DFT and Perturbation Theory, J. Comput. Chem., 2013, 34(27), 2327 CAS.
- T. Ziegler, A. Rauk and E. J. Baerends, On the Calculation of Multiplet Energies by the Hartree-Fock-Slater Method, Theor. Chim. Acta, 1977, 43(3), 261 CrossRef CAS.
- H. J. Kulik, M. Cococcioni, D. A. Scherlis and N. Marzari, Density Functional Theory in Transition-Metal Chemistry: A Self-Consistent Hubbard U Approach, Phys. Rev. Lett., 2006, 97(10), 103001 CrossRef PubMed.
- G. Ganzenmuller, N. Berkaine, A. Fouqueau, M. E. Casida and M. Reiher, Comparison of Density Functionals for Differences between the High-(5T2g) and Low-(1A1g) Spin States of Iron(II) Compounds. IV. Results for the Ferrous Complexes [Fe(L)(‘NHS4’)], J. Chem. Phys., 2005, 122(23), 234321 CrossRef PubMed.
- A. Droghetti, D. Alfe and S. Sanvito, Assessment of Density Functional Theory for Iron(II) Molecules across the Spin-Crossover Transition, J. Chem. Phys., 2012, 137(12), 124303 CrossRef CAS PubMed.
- E. I. Ioannidis and H. J. Kulik, Towards Quantifying the Role of Exact Exchange in Predictions of Transition Metal Complex Properties, J. Chem. Phys., 2015, 143(3), 034104 CrossRef PubMed.
- E. I. Ioannidis and H. J. Kulik, Ligand-Field-Dependent Behavior of Meta-GGA Exchange in Transition-Metal Complex Spin-State Ordering, J. Phys. Chem. A, 2017, 121(4), 874 CrossRef CAS PubMed.
- G. Prokopiou and L. Kronik, Spin-State Energetics of Fe Complexes from an Optimally Tuned Range-Separated Hybrid Functional, Chem.–Eur. J., 2018, 24(20), 5173 CrossRef CAS PubMed.
- F. Liu, T. H. Yang, J. Yang, E. Xu, A. Bajaj and H. J. Kulik, Bridging the Homogeneous-Heterogeneous Divide: Modeling Spin for Reactivity in Single Atom Catalysis, Front. Chem., 2019, 7, 219 CrossRef CAS PubMed.
- M. G. Taylor, T. Yang, S. Lin, A. Nandy, J. P. Janet, C. Duan and H. J. Kulik, Seeing Is Believing: Experimental Spin States from Machine Learning Model Structure Predictions, J. Phys. Chem. A, 2020, 124(16), 3286 CrossRef CAS PubMed.
- L. Wilbraham, C. Adamo and I. Ciofini, Communication: evaluating non-empirical double hybrid functionals for spin-state energetics in transition-metal complexes, J. Chem. Phys., 2018, 148(4), 041103 CrossRef PubMed.
- J. P. Perdew, R. G. Parr, M. Levy and J. L. Balduz, Density-Functional Theory for Fractional Particle Number – Derivative Discontinuities of the Energy, Phys. Rev. Lett., 1982, 49(23), 1691 CrossRef CAS.
- L. J. Sham and M. Schluter, Density-Functional Theory of the Energy-Gap, Phys. Rev. Lett., 1983, 51(20), 1888 CrossRef.
- Y. B. Zhang, D. A. Kitchaev, J. L. Yang, T. N. Chen, S. T. Dacek, R. A. Sarmiento-Perez, M. A. L. Marques, H. W. Peng, G. Ceder and J. P. Perdew, et al., Efficient first-principles prediction of solid stability: towards chemical accuracy, npj Comput. Mater., 2018, 4, 9 CrossRef.
- C. J. Bartel, A. W. Weimer, S. Lany, C. B. Musgrave and A. M. Holder, The role of decomposition reactions in assessing first-principles predictions of solid stability, npj Comput. Mater., 2019, 5, 4 CrossRef.
- L. McInnes, J. Healy and J. Melville, UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction, arXiv:1802.03426, 2018.
- F. Jensen, How Large Is the Elephant in the Density Functional Theory Room?, J. Phys. Chem. A, 2017, 121(32), 6104 CrossRef CAS PubMed.
- S. R. Jensen, S. Saha, J. A. Flores-Livas, W. Huhn, V. Blum, S. Goedecker and L. Frediani, The Elephant in the Room of Density Functional Theory Calculations, J. Phys. Chem. Lett., 2017, 8(7), 1449 CrossRef CAS PubMed.
- F. Jensen, Method Calibration or Data Fitting?, J. Chem. Theory Comput., 2018, 14(9), 4651 CrossRef CAS PubMed.
- D. Feller and D. A. Dixon, Density Functional Theory and the Basis Set Truncation Problem with Correlation Consistent Basis Sets: Elephant in the Room or Mouse in the Closet?, J. Phys. Chem. A, 2018, 122(9), 2598 CrossRef CAS PubMed.
- M. C. Kim, E. Sim and K. Burke, Communication: avoiding unbound anions in density functional calculations, J. Chem. Phys., 2011, 134(17), 171103 CrossRef PubMed.
- A. Nandy, C. Duan, J. P. Janet, S. Gugler and H. J. Kulik, Strategies and Software for Machine Learning Accelerated Discovery in Transition Metal Chemistry, Ind. Eng. Chem. Res., 2018, 57(42), 13973 CrossRef CAS.
- S. M. Moosavi, A. Nandy, K. M. Jablonka, D. Ongari, J. P. Janet, P. G. Boyd, Y. Lee, B. Smit and H. J. Kulik, Understanding the diversity of the metal-organic framework ecosystem, Nat. Commun., 2020, 11(1), 4068 CrossRef CAS PubMed.
- J. P. Janet, C. Duan, T. H. Yang, A. Nandy and H. J. Kulik, A Quantitative Uncertainty Metric Controls Error in Neural Network-Driven Chemical Discovery, Chem. Sci., 2019, 10(34), 7913 RSC.
- C. J. Bartel, A. Trewartha, Q. Wang, A. Dunn, A. Jain and G. Ceder, A critical examination of compound stability predictions from machine-learned formation energies, npj Comput. Mater., 2020, 6(1), 1 CrossRef.
- M. A. Halcrow, Structure:Function Relationships in Molecular Spin-Crossover Complexes, Chem. Soc. Rev., 2011, 40(7), 4119 RSC.
- C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, The Cambridge Structural Database, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171 CrossRef CAS PubMed.
- M. E. Rose and J. R. Kitchin, pybliometrics: Scriptable Bibliometrics Using a Python Interface to Scopus, SoftwareX, 2019, 10, 100263 CrossRef.
- X. W. Jia, A. Lynch, Y. H. Huang, M. Danielson, I. Lang’at, A. Milder, A. E. Ruby, H. Wang, S. A. Friedler and A. J. Norquist, et al., Anthropogenic Biases in Chemical Reaction Data Hinder Exploratory Inorganic Synthesis, Nature, 2019, 573(7773), 251 CrossRef CAS PubMed.
- S. Gugler, J. P. Janet and H. J. Kulik, Enumeration of de novo Inorganic Complexes for Chemical Discovery and Machine Learning, Mol. Syst. Des. Eng., 2020, 5(1), 139 RSC.
- S. Seritan, C. Bannwarth, B. S. Fales, E. G. Hohenstein, C. M. Isborn, S. I. L. Kokkila-Schumacher, X. Li, F. Liu, N. Luehr and J. W. Snyder Jr, et al., TeraChem: a graphical processing unit-accelerated electronic structure package for large-scale ab initio molecular dynamics, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 11(2), e1494 CAS.
- E. I. Ioannidis, T. Z. H. Gani and H. J. Kulik, molSimplify: A Toolkit for Automating Discovery in Inorganic Chemistry, J. Comput. Chem., 2016, 37, 2106 CrossRef CAS.
- KulikGroup, molSimplify documentation, 2020, accessed June 24, 2021, http://molsimplify.mit.edu.
- P. J. Hay and W. R. Wadt, Ab Initio Effective Core Potentials for Molecular Calculations. Potentials for the Transition Metal Atoms Sc to Hg, J. Chem. Phys., 1985, 82(1), 270 CrossRef CAS.
- Y. Wang, X. S. Jin, H. Y. S. Yu, D. G. Truhlar and X. He, Revised M06-L Functional for Improved Accuracy on Chemical Reaction Barrier Heights, Noncovalent Interactions, and Solid-State Physics, Proc. Natl. Acad. Sci. U. S. A., 2017, 114(32), 8487 CrossRef CAS PubMed.
- Psi4, Psi4 manual, accessed June 24, 2021, https://psicode.org/psi4manual/master/dft.html.
- F. Weigend and R. Ahlrichs, Balanced Basis Sets of Split Valence, Triple Zeta Valence and Quadruple Zeta Valence Quality for H to Rn: Design and Assessment of Accuracy, Phys. Chem. Chem. Phys., 2005, 7(18), 3297 RSC.
- J. Bergstra, D. Yamins and D. D. Cox, Proceedings of the 12th Python in Science Conference, 2013, p. 13 Search PubMed.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss and V. Dubourg, Scikit-learn: machine learning in Python, Journal of Machine Learning Research, 2011, 12, 2825 Search PubMed.
- F. Chollet, Keras, accessed June 24, 2021, https://keras.io.
- M. Abadi, A. Agarwal, P. Barham, E. Brevdo, Z. Chen, C. Citro, G. S. Corrado, A. Davis, J. Dean and M. Devin, et al., TensorFlow: Large-scale machine learning on heterogeneous systems, 2021, https://tensorflow.org/ Search PubMed.
Footnote |
† Electronic supplementary information (ESI) available: Summary of 23 DFAs; statistics of properties obtained by 23 DFAs; Pearson's r matrix and parity plots for ΔEH–L, vertical IP, and Δ-SCF gap; distributions of ΔEH–L, vertical IP, and Δ-SCF gap at different DFAs; UMAP 2D visualization of Δ-SCF gap data; percentile ranks at each DFA for example complexes; statistics and parity plots for basis set comparison; pie charts of RF-RFA KRR selected features at different DFAs; RF-RFA KRR selected features for vertical IP for difference datasets; hyperparameters for FT-ANN models; MAEs, R2, and scaled MAEs of all 23 functionals for three properties; uncertainty quantification metric and its cutoff; possible metal, oxidation, spin state, and ligand combinations in the 187![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 complex space; size distribution of the 187 200 complex space; size distribution of the 187![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 complexes design space; histograms of Δ-SCF gap grouped by system size; Venn diagrams of lead Δ-SCF gap complexes and lead SCO complexes; network graph of lead Δ-SCF gap and lead SCO complexes; procedure of isolating of candidate SCO complexes; statistics of experimental SCO complexes; UMAP visualization of selected lead SCO complexes; computational workflow and DFT parameters used therein; Hartree–Fock linear extrapolation scheme; statistics of SCF iterations for convergence and failed calculations before and after HF extrapolation; electron configuration diagram of electron addition/removal convention; extended description of RAC featurization; range of hyperparameters sampled during Hyperopt for KRR and ANN models. See DOI: 10.1039/d1sc03701c 200 complexes design space; histograms of Δ-SCF gap grouped by system size; Venn diagrams of lead Δ-SCF gap complexes and lead SCO complexes; network graph of lead Δ-SCF gap and lead SCO complexes; procedure of isolating of candidate SCO complexes; statistics of experimental SCO complexes; UMAP visualization of selected lead SCO complexes; computational workflow and DFT parameters used therein; Hartree–Fock linear extrapolation scheme; statistics of SCF iterations for convergence and failed calculations before and after HF extrapolation; electron configuration diagram of electron addition/removal convention; extended description of RAC featurization; range of hyperparameters sampled during Hyperopt for KRR and ANN models. See DOI: 10.1039/d1sc03701c |
| This journal is © The Royal Society of Chemistry 2021 |