Controlling the reactions of 1-bromogalactose acetate in methanol using ionic liquids as co-solvents

Abstract

The reactions of an acetobromogalactose in mixtures of methanol and one of seven different ionic liquids with varying constituent ions were studied. In general, small amounts of ionic liquid in the reaction mixture led to increases in the rate constant compared to methanol, whilst large amounts of ionic liquid led to decreases in the rate constant; this outcome differs significantly from previous reactions proceeding through this mechansim. Temperature dependent kinetic studies indicated that the dominant interaction driving these changes was between the ionic liquid and the transition state of the process. Through considering solvent parameters of ionic liquids, a relationship was found between the changes in the rate constant and both the hydrogen bond accepting ability and polarisability of the solvent, indicating that the interactions affecting reaction outcome are both specific and non-specific in nature; once more, these interactions were different to those observed in previous similar reactions. By changing the amount of ionic liquid in the reaction mixture, additional products not seen in the molecular solvent case were observed, the ratios of which are dependent on the anion of the ionic liquid and the proportion of ionic liquid in the reaction mixture. This demonstrates the importance of considering solvent effects on both the rate and product determining steps and the potential application of such changes is discussed.

---

Introduction

The search for alternatives to traditional organic solvents has led to significant interest in ionic liquids.¹ Ionic liquids are arbitrarily defined as salts with a melting point below 100 °C,² and are composed of bulky, often asymmetric, cations and anions of low coordinating strength.³ The structures of the ions frustrate crystallisation, leading to their low melting points, while the electrostatic interactions between the ions result in useful properties, such as negligible vapour pressure⁴ and low flammability.⁵ In addition, ionic liquids have the potential to be recyclable⁶ and their properties (such as viscosity and miscibility) can be altered, and selected for, by changing the constituent ions.⁷ For this reason, they have been classified as ‘designer solvents’.⁸

A hinderance to the use of ionic liquids as alternative solvents is the fact that their effects on organic reactions, including changing both the rate of reaction and preference for certain products, have not been readily predictable.⁹ In order to better understand, and potentially predict, these effects a significant amount of research has focussed on the use of ionic liquids as solvents for organic reactions that proceed through well-known mechanisms.^3,10–13 A particular group of reactions that have received relatively limited attention are those that proceed through a unimolecular nucleophilic substitution (S_N1) mechanism.

Reactions that proceed through both localised and delocalised carbocation intermediates have previously been studied in mixtures of ionic liquids and traditional solvents;^14–19 it was shown that changing the amount of ionic liquid in the reaction mixture can lead to different effects on the rate constant for the process. The unimolecular rate constant, k₁, for the process increased when a small amount of ionic liquid was present in the reaction mixture compared to the molecular solvent. It is important to note that the effects of large proportions of ionic liquid in the reaction mixture were found to be dependent on the nature of the carbocation intermediate; k₁ either decreased below that of the molecular solvent (localised carbocation intermediate^14,15,17) or remained higher than that of the molecular solvent (delocalised carbocation intermediate^16,18,19). Therefore, it is clear that by changing the nature of the intermediate, which in this mechanism correlates with a significant degree of charge development in the transition state, the ionic liquid effect can change dramatically and understanding these changes is key if ionic liquids are to be used in a rational fashion to control reaction outcome. These studies have also attempted to identify the interactions responsible for the observed changes in the rate constant through determining both the activation enthalpies and entropies of the processes,^15,16 and correlating solvent properties to the rate constant data;^18,19 this information can in turn allow for the prediction of the effects of other ionic liquids on these systems. Notably, the interactions responsible in each case vary with the substrate of the reaction and understanding the relationship between the interactions and the substrate is necessary for rational choice of ionic liquid components.

Given the above, it was of interest to investigate an S_N1 reaction specifically chosen because it proceeds through a carbocation intermediate that is stabilised by the presence of a heteroatom; Scheme 1 shows the solvolysis of the galactose 1 in methanol, which proceeds through an oxocarbenium intermediate.²⁰ Not only does this reaction allow for the study of any effects an ionic liquid may have on a reaction that proceeds through an oxocarbenium ion, but it also allows for the study of a substrate similar to those commonly found in nature as ionic liquids have been extensively studied in the dissolution of biomass^21,22 and related carbohydrate chemistry,²³ with some examples of studies using ionic liquids as catalysts for carbohydrate-related conversions.^24,25

Scheme 1 The methanolysis of the sugar derivative 1 to give the β-isomer 2.

Therefore, the aim of this study was to analyse the effects of ionic liquids on the reaction shown in Scheme 1 and to correlate any changes observed with solvent properties, particularly comparing to other related systems to highlight the differences. Such a correlation would facilitate an understanding of how ionic liquids affect this reaction and potentially enable prediction of the effects that further ionic liquids would have on reactions of this type. Overall, this study will allow for further understanding of, and perhaps a more widespread use of, ionic liquids as solvents for S_N1 processes.

Results and discussion

Kinetic analysis

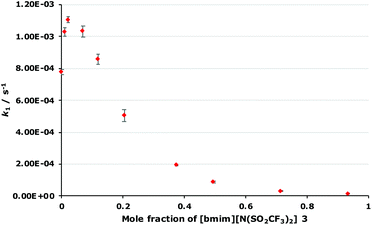
As outlined in the Introduction, the solvolysis of the bromogalactose 1 in methanol (Scheme 1) typically proceeds through a unimolecular nucleophilic substitution mechanism. This mechanism was confirmed using nucleophile dependence studies in which changing the amount of methanol in the reaction mixture did not affect the rate constant for the process (see Fig. S1 in ESI†). In addition, only the β-isomer 2 was formed in these mixtures; no other products were observed.

In order to study the effects of using an ionic liquid as the solvent for this reaction, the rate constant for the process was initially measured in mixtures containing different proportions of [bmim][N(SO₂CF₃)₂] 3 (Fig. 1) in methanol. This ionic liquid 3 was selected as it is readily prepared and purified,²⁶ and has been used widely in mechanistic studies,^11,27 particularly for reactions that proceed through the same mechanism as the reaction shown in Scheme 1.^14,16,28 The results of these experiments are summarised as a plot showing the mole fraction dependence of the rate constant (Fig. 2).

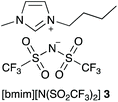Fig. 1 The ionic liquid 1-butyl-3-methylimidazolium bis(trifluoromethanesulfonyl)imide ([bmim][N(SO₂CF₃)₂], 3) used in this study. It should be noted that this anion might also be named as a secondary (sulfonyl)amide.⁵⁷ However, imide nomenclature is also reasonable⁵⁸ and serves to emphasise the two substituents, along with being consistent with previous work and what is used by the community in, for example, chemical catalogues.

Fig. 2 The dependence of the unimolecular rate constant (k₁) of the reaction of the acetobromogalactose 1 on the mole fraction of [bmim][N(SO₂CF₃)₂] 3 () in methanol at 315 K. Uncertainties reported are the standard deviation of triplicate measurements; some uncertainties fall within the size of the markers used.

This plot is generally the same shape as has been observed for some,^14,16,18 though not all,¹⁹ related S_N1 reactions; the rate constant increases at low mole fractions of the salt 3 compared to the molecular solvent and then decreases at higher mole fractions of the salt 3. However, it is the differences between this and previous cases that are significant. In this case, the maximum rate constant increase occurs at χ₃ = 0.02 and is approximately 1.5 times the rate constant in the methanol case, which is similar to an alkyl chloride example¹⁴ but notably different to a case with a delocalised benzhydrylium intermediae.^16,18 Additionally, at χ₃ > 0.1, k₁ is lower than in the methanol case to the point where k₁ is only 2% that of the methanol case at χ₃ = 0.93; such a significant decrease in rate constant for this reaction type has not been reported before. Importantly, this demonstrates the effects of the proportion of salt 3 in the reaction mixture for reactions with this type of reagent, allows contrast with previous cases, and hence selection of the proportion of ionic liquid to get a desired reaction outcome.

Temperature dependence studies were used to determine the activation parameters for this process in order to identify the underlying interactions responsible for these changes in k₁ when using an ionic liquid solvent. These studies were carried out in methanol and mixtures containing either χ₃ = 0.02 or χ₃ = 0.50. The low mole fraction of the salt 3 was selected as this corresponds to the reaction mixture where the maximum increase in k₁ occurs; the higher mole fraction was selected so that the origin of the rate constant decrease could be evaluated, particularly comparing these origins to those for the previously considered S_N1 system that proceeds through a localised carbocation.^14,15 The activation parameters determined are shown in Table 1.

Table 1 The activation parameters determined for the reaction of acetobromogalactose 1 in either methanol or mixtures of [bmim][N(SO₂CF₃)₂] 3 in methanol at the proportion of ionic liquid 3 shown

Solvent	χ 3	ΔH^‡/kJ mol^−1 ^a	ΔS^‡/J K^−1 mol^−1 ^a
a Uncertainties reported were obtained from the fit of the linear regression for the respective Eyring plots.
Methanol	0	72.1 ± 0.9	−76 ± 3
[bmim][N(SO2CF3)2] 3	0.02	65.9 ± 1.3	−92 ± 4
[bmim][N(SO2CF3)2] 3	0.49	69.7 ± 2.0	−101 ± 6

---

In both cases in which the ionic liquid 3 is present, there is a measurable decrease in the entropy of activation compared to the methanol case as well as a decrease in the enthalpy of activation at the χ₃ = 0.02 case. Significantly, this is the first example of a measurable change in both activation parameters between the molecular solvent case and the case with a low mole fraction of ionic liquid present for this type of reaction mechanism.

In the reaction mixture containing a small amount of the salt 3, these changes indicate that the ionic liquid is stabilising the transition state of the process as shown by the lowered enthalpy of activation; in doing so, the ionic liquid orders about the transition state, hence lowering the entropy of activation (that is, making it more negative). The change in the enthalpy of activation dominates the change in the entropy of activation with the result being an increase in the observed rate constant at χ₃ = 0.02.

While the larger uncertainties associated with the activation parameters for the χ₃ca. 0.50 case mean that no change in the enthalpy of activation from the methanol case can be seen, the significant decrease in the entropy of activation suggests that the dominant interaction involves ordering of the ionic liquid about the transition state of the reaction. Such organisation is not unexpected given the high degree of charge development in the transition state for this reaction and is consistent with what has been observed previously.^15,16 These activation parameters also show that the decrease in k₁ observed at higher mole fractions of the ionic liquid is due to significant ordering of the solvent around the transition state; that is, the change in k₁ from a small to large amount of ionic liquid 3 in the reaction mixture is a delicate balance between an enthalpic benefit (stabilising the transition state – occurs at low mole fractions of the salt 3) and an entropic cost (ordering around the transition state – occurs at higher mole fractions of the salt 3).

In order to better understand how the ionic liquid 3 is interacting with the transition state for this process, a series of ionic liquids were selected that differ from salt 3 in either the cation or the anion (Fig. 3). Ionic liquids 4–6, which differ in the cation while having the same [N(SO₂CF₃)₂]⁻ anion, were selected due to differences in both localisation of the charge and accessibility of the charged centre(s) compared to the [bmim]⁺ cation. Ionic liquids 7–9, which differ in the anion while keeping the [bmim]⁺ cation constant, have anions that vary in both coordinating ability and size. Any changes in the effects of an ionic liquid on k₁ when using these ionic liquids as solvents (cf. salt 3) could indicate how the ionic liquid is interacting with the transition state.

Fig. 3 The ionic liquids used to study the effect of varying the constituents: 1-butyl-2,3-dimethylimidazolium bis(trifluoromethanesulfonyl)imide ([bm₂im][N(SO₂CF₃)₂], 4), N-butyl-N-methylpyrrolidinium bis(trifluoromethanesulfonyl)imide ([bmpyr][N(SO₂CF₃)₂], 5), methyltrioctylammonium bis(trifluoromethanesulfonyl)imide ([mtoa][N(SO₂CF₃)₂], 6), 1-butyl-3-methylimidazolium hexafluorophosphate ([bmim][PF₆], 7), 1-butyl-3-methylimidazolium tetrafluoroborate ([bmim][BF₄], 8) and 1-butyl-3-methylimidazolium tricyanomethanide ([bmim][C(CN)₃], 9).

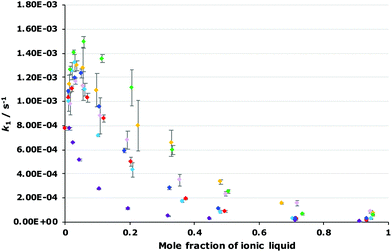
The dependence of the rate constant for the reaction shown in Scheme 1 on the proportion of each of the ionic liquids 4–9 was determined to evaluate how varying the constituents of the ionic liquid affects k₁ (Fig. 4; see Fig. S2–S7 in ESI† for mole fraction dependence plots of each ionic liquid 4–9 individually). Immediately obvious is that the general shape of all of the plots are the same, irrespective of the ionic liquid used, however the maximum increase in k₁ differs, as does the proportion of salt in the reaction mixture at which this maximum occurs. Importantly, these results indicate that changing each of the constituents of the ionic liquid affects k₁. Such changes have been seen previously,^18,19 though the effect is more marked in the case seen here.

Fig. 4 The dependence of the unimolecular rate constant (k₁) of the reaction of the acetobromogalactose 1 on the mole fraction of on the mole fraction of either [bmim][N(SO₂CF₃)₂] 3 (), [bm₂im][N(SO₂CF₃)₂] 4 (), [bmpyr][N(SO₂CF₃)₂] 5 (), [mtoa][N(SO₂CF₃)₂] 6 (), [bmim][PF₆] 7 (), [bmim][BF₄] 8 () or [bmim][C(CN)₃] 9 () in methanol at 315 K. Uncertainties reported are the standard deviation of triplicate measurements; some uncertainties fall within the size of the markers used.

Focusing first on the effects of changing the cation of the ionic liquid, both of the ionic liquids [bm₂im][N(SO₂CF₃)₂] 4 and [bmpyr][N(SO₂CF₃)₂] 5 display a maximum increase in k₁ at χ ca. 0.02 with a similar magnitude to that seen for [bmim][N(SO₂CF₃)₂] 3. In addition, the rate constant at any mole fraction is generally similar for both of these ionic liquids and again, comparable to the equivalent [bmim][N(SO₂CF₃)₂] 3 case.

In contrast, the largest k₁ observed in mixtures containing [mtoa][N(SO₂CF₃)₂] 6 occurs at χ₆ = 0.01 and is the same magnitude as in methanol; there is no measurable increase. As the mole fraction of the salt 6 in the reaction mixture increases, k₁ steadily decreases. These differences show that access to the charged centre(s) of the cation is necessary to increase the rate constant for this reaction, irrespective of whether the charge is delocalised (as in [bmim]⁺ and [bm₂im]⁺) or localised (as in [bmpyr]⁺). Whilst the addition of a methyl group to [bmim]⁺ to give the [bm₂im]⁺ cation does introduce a slight steric effect, clearly this effect is not great enough to negatively affect k₁ in this case unlike the much more significantly sterically hindered [mtoa]⁺ cation.

Moving to the effects of changing the anion of the ionic liquid, the mole fraction dependence plot (Fig. 4) shows that k₁ increases at χ = 0.02 in the following order: [bmim][N(SO₂CF₃)₂] 3 < [bmim][C(CN)₃] 9 < [bmim][BF₄] 8 < [bmim][PF₆] 7. As the mole fraction of salt increases, the k₁ observed for both [bmim][BF₄] 8 and [bmim][C(CN)₃] 9 is always greater than the other ionic liquids studied (k₁ is approximately five times greater at χ = 0.95 for the tetrafluoroborate salt 8 relative to the parent salt 3). Interestingly, mixtures containing [bmim][PF₆] 7 up to χ₇ = 0.2 show the greatest increase in k₁ of all of the ionic liquids studied; beyond this proportion of salt 7, the rate constant gradually decreases such that the rate constant is below that seen for [bmim][BF₄] 8 mixtures and at the highest mole fraction of salt 7 the rate constant is three times greater than that seen for the parent ionic liquid 3. Irrespective, this analysis shows that the ionic liquid solvent effects on k₁ are also dependent on the anion.

It is of interest to consider the microscopic origin of this anion dependence. The coordinating abilities of [N(SO₂CF₃)₂]⁻ and [PF₆]⁻ are similar,²⁹ and the coordinating abilities of [BF₄]⁻ and [C(CN)₃]⁻ are similar,³⁰ so clearly this property does not explain the order of the solvent effect. As such, the size and shape of each anion can be considered; both [BF₄]⁻ and [PF₆]⁻ anions are highly symmetric. The result might be that the ions pack more efficiently about the transition state, resulting in greater interactions. Additionally, the larger size of the [PF₆]⁻ anion compared to [BF₄]⁻ might explain why this ionic liquid does not give the highest increase in k₁ at higher mole fractions as any entropic cost may become significant with more ionic liquid in the reaction mixture.

In order to further understand the changes in k₁ for the reaction shown in Scheme 1 observed for the series of ionic liquids 4–9, temperature dependence studies were performed at χ = 0.02 and ca. 0.50. These parameters are shown in Table 2, along with those for both the methanol case and the salt 3 cases. For ease of comparison, after each activation parameter, an indication of the change relative to the methanol case is shown.

Table 2 The activation parameters determined for the reaction of acetobromogalactose 1 in either methanol or mixtures of the ionic liquids 3–9 in methanol. After each activation parameter, the symbol in brackets indicates the change relative to methanol case: (—): no change, (↑): increase, (↓): decrease

Solvent	χ salt	ΔH^‡/kJ mol^−1  ^a	ΔS^‡/J K^−1 mol^−1 ^a
a Uncertainties reported were obtained from the fit of the linear regression for the respective Eyring plots.
Methanol	0	72.1 ± 0.9	−76 ± 3
[bmim][N(SO2CF3)2] 3	0.02	65.9 ± 1.3 (↓)	−92 ± 4 (↓)
[bm2im][N(SO2CF3)2] 4	0.02	68.7 ± 2.8 (—)	−84 ± 9 (—)
[bmpyr][N(SO2CF3)2] 5	0.02	66.7 ± 1.0 (↓)	−90 ± 3 (↓)
[mtoa][N(SO2CF3)2] 6	0.02	75.0 ± 0.8 (↑)	−68 ± 3 (↑)
[bmim][PF6] 7	0.02	64.3 ± 1.4 (↓)	−96 ± 5 (↓)
[bmim][BF4] 8	0.02	70.6 ± 1.9 (—)	−77 ± 6 (—)
[bmim][C(CN)3] 9	0.02	75.3 ± 1.6 (↑)	−63 ± 5 (↑)
[bmim][N(SO2CF3)2] 3	0.49	69.7 ± 2.0 (—)	−101 ± 6 (—)
[bm2im][N(SO2CF3)2] 4	0.48	58.6 ± 3.1 (↓)	−137 ± 10 (↓)
[bmpyr][N(SO2CF3)2] 5	0.48	70.0 ± 1.0 (↓)	−99 ± 3 (↓)
[mtoa][N(SO2CF3)2] 6	0.45	30.4 ± 1.4 (↓)	−237 ± 4 (↓)
[bmim][PF6] 7	0.51	56.5 ± 3.3 (↓)	−135 ± 10 (↓)
[bmim][BF4] 8	0.48	66.5 ± 2.7 (↓)	−101 ± 9 (↓)
[bmim][C(CN)3] 9	0.50	77.2 ± 2.2 (↑)	−71 ± 7 (—)

---

The activation parameters determined for ionic liquids [bm₂im][N(SO₂CF₃)₂] 4, [bmpyr][N(SO₂CF₃)₂] 5 and [bmim][PF₆] 7 show that on moving from the methanol case to χ ca. 0.02 there is a decrease in both the enthalpy and entropy of activation, as described above for [bmim][N(SO₂CF₃)₂] 3. Therefore, it is clear that for these cases, the origin of the rate constant enhancement is stabilisation of the transition state of this reaction. This is not the situation, however, for all cases; [bmim][BF₄] 8 shows no change within uncertainty for either parameter compared to methanol (this outcome is consistent with a previous case¹⁵) and both [mtoa][N(SO₂CF₃)₂] 6 and [bmim][C(CN)₃] 9 show an increase in both the enthalpy and entropy of activation relative to the molecular solvent. Importantly, these changes with the nature of the constituent ions in the ionic liquid differ from previous examples,^18,19 showing the importance of the nature of the reagent (and hence the transition state) in determining ionic liquid solvent effects.

Previous examples^31,32 have demonstrated that an increase in both activation parameters is likely due to stabilisation of the starting material through ordering of the solvent about it (as opposed to less interaction with and ordering about the transition state); this ordering is disrupted as the reaction proceeds, causing an increase in the disorder of the system. For this reaction, given that the changes in activation parameters seen in each ionic liquid case at χ = 0.02 compared to the methanol case are quite small, there is the possibility that both significant starting material–ionic liquid and transition state–ionic liquid interactions are introduced in each case; by changing the constituents of the ionic liquid, the dominant interaction driving the rate constant change can vary. It is evident here that either a more coordinating anion (as are present in salts 8 and 9) or a less accessible charge on the cation (allowing the anion to be more free to interact, in the case of [mtoa][N(SO₂CF₃)₂] 6) leads to starting material interactions becoming more dominant.‡

At a higher mole fraction of salt in the reaction (χ ca. 0.50), both the enthalpy and entropy of activation decrease compared to the methanol case for each of the ionic liquids 4–8. These data indicate that by increasing the amount of each of these ionic liquids in the system, transition state interactions dominate. As mentioned previously, this results in a large decrease in k₁ in all cases compared to both the methanol case and cases where small amounts of ionic liquid are present, as the ionic liquid orders significantly about the transition state.

The exception to the above trend is the [bmim][C(CN)₃] 9 which, as mentioned above, shows an increase in the enthalpy of activation and no change within uncertainty for the entropy of activation compared to the methanol case at χ₉ = 0.50. The parameters determined are the same as those at χ₉ = 0.02, indicating that the dominant interactions driving the rate constant change for this particular ionic liquid do not change as significantly as in the case of ionic liquids 3–8, even though k₁ decreases in a similar fashion to that seen for the other ionic liquids. This may be a result of the same features that result in the low viscosity of ionic liquid 9 compared to the other ionic liquids studied,³³ which may cause a change in these interactions.

Kamlet–Taft parameter analysis

In order to further understand these key interactions that are driving the rate constant change, and to potentially allow for the prediction of effects additional ionic liquids would have on this reaction, Kamlet–Taft solvent parameters were considered. These parameters, while not specific to ionic liquids, have been used previously to correlate reaction outcome with solvent descriptors and can be used to establish which constituents of the ionic liquid are involved in the key interactions responsible for rate constant changes.^{18,19,34–38} The parameters include α (the hydrogen bond donating ability; often associated with the cation of the ionic liquid),³⁹β (the hydrogen bond accepting ability of the solvent; often associated with the anion of the ionic liquid),⁴⁰ and π* (the polarizability of the solvent; relating to both the cation and anion of the ionic liquid).⁴¹

Initial attempts to correlate the natural log of the rate constant to each individual parameter showed poor correlations§ (see Fig. S9–S35 in ESI†). Therefore, it was of interest to determine whether a combination of these parameters would result in a good correlation. Multiple regression analysis is useful for this as it allows for identification of any existing correlation between multiple parameters and changes in reaction outcome. This method has been used previously with ionic liquid systems to identify these correlations,^34,42 by using the following equation:

ln(k₁) = intercept + aα + bβ + cπ*

where a, b and c are coefficients of each parameter and indicate the relative contribution of each parameter to any observed correlation. A p-value of <0.05 indicates a good correlation. These analyses were performed across each mole fraction for the series of ionic liquids. Including all parameters in the analysis, as well as a combination of either α and β or α and π* showed no correlations with significant p-values, indicating that a correlation was poor for these combinations. However, analyses that contained a combination of β and π* across each mole fraction showed good to very good correlations (Table 3 and Fig. 5 for a representative example, which shows this relationship at the proportion of ionic liquid 3 that showed the maximum increase in k₁; see ESI† for all analyses). Notably the importance of both β and π* parameters contrasts markedly with the previous correlations of these solvent parameters with unimolecular processes on different substrates,^18,19 again showing the importance of the structure of the reagent.

Fig. 5 The relationship between the natural logarithm of the rate constant and a combination of the β and π* Kamlet–Taft parameters for the reaction of the galactose 1 for each of the ionic liquids 3–9 at χ ca. 0.02. Uncertainties are calculated from the standard deviation of triplicate measurements and transformed on calculating the natural logarithm.

Table 3 The correlation between ln(k₁) and the Kamlet–Taft parameters β and π* across each mole fraction of ionic liquids 3–9

Mole fraction (ca.)	ln(k1)^a	R ^2  ^b
a In all cases, p < 0.05 for all variables, indicating a significant contribution with the exception of the β parameter for the χ ca. 0.73 case. b Adjusted R^2, which takes into account the number of variables contributing to the fit.
0.01	−8.49–3.38β + 3.65π*	0.84
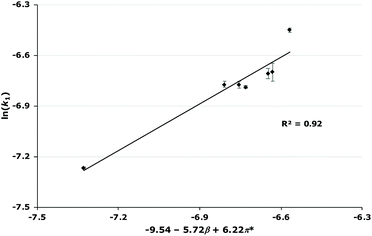
0.02	−9.54–5.72β + 6.22π*	0.88
0.05	−10.53–7.72β + 8.36π*	0.88
0.10	−12.77–11.36β + 12.55π*	0.84
0.20	−16.53–15.74β + 18.68π*	0.86
0.35	−20.56–16.89β + 23.07π*	0.77
0.50	−22.25–14.44β + 22.85π*	0.79
0.73	−23.77–8.19β + 20.19π*	0.74
0.95	−24.34–13.61β + 23.23π*	0.72

---

Immediately clear from these relationships is that both the β and π* parameters are important but that the coefficients for these parameters vary as the mole fraction varies. This trend is of note as it has not been observed previously to such a significant degree. Generally, the effect of the mole fraction of ionic liquid has not been studied extensively when looking at these relationships;^34,42,43 where it has been, either there was no significant relationship as the mole fraction of ionic liquid was increased,⁴⁴ or where there was a significant relationship, the co-solvent was acetonitrile¹⁹ (which has similar solvent parameters to the ionic liquids studied in those cases). Therefore, it is clear that the changes in the coefficients across mole fractions are likely due to interactions involving the methanol also having a significant effect. This is not unexpected as methanol is a polar, hydrogen bonding solvent and therefore the Kamlet–Taft parameters are generally higher than those seen for acetonitrile, particular the α and β parameters.⁴⁵ Ideally Kamlet–Taft parameters for the solvent mixtures considered would be used, but these are unavailable. Attempts to find relationships involving contributions from methanol to the solvent parameters at each solvent composition (based on observed correlations for both aprotic^46,47 and protic⁴⁸ systems, see ESI† for full analyses) showed no improvement. For this reason, the relationships shown in Table 3 will be discussed from this point.

As mentioned, these correlations show that both the hydrogen bond accepting ability and the polarizability of the ionic liquid are important in affecting the rate constant.¶ In this case, the two parameters have opposite effects; the coefficient for π* is always positive, indicating that an increase in k₁ is favoured when the solvent has a higher polarizability; whereas the coefficient for β is always negative, meaning that a solvent that is more able to accept hydrogen bonds will decrease the rate constant for this reaction. Additionally, as the mole fraction of the ionic liquid in the reaction mixture increases, both of these effects become larger but the favourable π* effect becomes more pronounced. These features are apparent in the plots of rate constant against the mole fraction of ionic liquid (Fig. 4, Fig. S2–S7†): (i) at lower proportions of salt in the reaction mixture, the [bmim][PF₆] 7, [bmim][BF₄] 8 and [bmim][C(CN)₃] 9 cases gave the highest rate constants out of the series as each of these ionic liquids have high polarizability values; (ii) at higher mole fractions of salt in the reaction mixture, k₁ values in the [bmim][PF₆] 7 cases decrease compared to both [bmim][BF₄] 8 and [bmim][C(CN)₃] 9 cases even though both [bmim][BF₄] 8 and [bmim[C(CN)₃] 9 have high β values compared to [bmim][PF₆] 7 – at these solvent compositions, the higher π* values for both ionic liquids 8 and 9 outweigh any detrimental hydrogen bond accepting effects, leading to high k₁ values across each mole fraction.

These correlations can be used to clarify the microscopic interactions in solution that result in the changes in reaction outcome in ionic liquids; the positive coefficient for π* for each solvent composition indicates that the dominant interactions responsible for the changes in k₁ for each ionic liquid are favourable non-specific interactions, likely charge–charge interactions. This further supports the proposition that the ionic liquid components are stabilising the developing charges in the transition state as indicated by the trends observed in the enthalpies of activation. The negative β coefficient indicates that hydrogen bond acceptance from the ionic liquid is detrimental to k₁; again, looking at the trends in activation parameters indicates that starting material interactions, where hydrogen bond acceptance by the ionic liquid is likely to be occurring, are more pronounced in the cases of ionic liquids 6, 8 and 9 (with higher β values). The interaction responsible for this feature is not immediately clear, given that hydrogen bond acceptance might be expected to favour the formation of the transition state. As such, interaction with the starting material 1 is implied. Importantly, these interactions are different to those that have been implicated in the solvent effects of ionic liquids on other similar reactions.

Product analysis

As shown earlier in Scheme 1, product 2 is the only observable species when the reaction is performed in methanol. However, multiple products were observed throughout the mole fraction dependence experiments described above when using ionic liquids 3–9. These products are shown in Scheme 2.|| As shown, product 2 is present alongside a mixture of isomers 10 and 11** (resulting from interaction of a neighbouring acetate group with the C2, as shown in the intermediate in Scheme 2, which is then attacked by the nucleophile), as well as product 12 which is produced through loss of a proton from the intermediate (a base, triethylamine, is present in the reaction mixture). Interestingly, the presence of these products and the ratios between them differ when changing both the ionic liquid and the proportion of salt in the reaction mixture; importantly, the effect of the ionic liquid is thus demonstrated on both the rate and product determining steps. Table 4 gives a summary of product ratios at representative key solvent compositions (for ratios for all solvent compositions see Tables S2–S6†).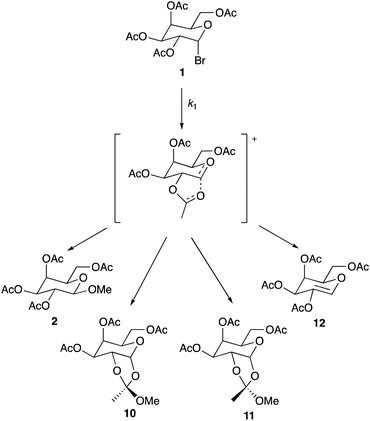

Scheme 2 The reaction of the galactose 1 with methanol through the proposed intermediate to give the products 2, 10–12. The ratio of these products differs when changing the solvent composition.

Table 4 The ratio of products observed for the reaction of the galactose 1 in different solvent compositions

Entry	Ionic liquid	χ salt	t/h^a	%2^b^,^c	%10^b^,^c	%11^b^,^c	%12^b^,^c
a Each reaction was followed to completion. b Percentages were obtained from the ratio of the integrals of representative signals of each product against an internal standard. c Uncertainties reported were obtained from the standard deviation of triplicate measurements. d Not detected using ^1H NMR spectroscopy.
1	—	0	2	100	—^d	—^d	—^d
2	3	0.02	1	100	—^d	—^d	—^d
3	7	0.02	1	100	—^d	—^d	—^d
4	8	0.02	1	100	—^d	—^d	—^d
5	3	0.37	5	93 ± 2	5 ± 1	2 ± 1	—^d
6	7	0.33	2	100	—^d	—^d	—^d
7	3	0.73	37	63 ± 4	20 ± 1	9 ± 3	9 ± 4
8	5	0.72	37	55 ± 6	25 ± 6	13 ± 2	7 ± 1
9	7	0.74	17	100	—^d	—^d	—^d
10	3	0.93	65	—^d	46 ± 5	18 ± 9	36 ± 14
11	5	0.93	45	—^d	56 ± 1	25 ± 3	20 ± 3
12	7	0.95	20	—^d	51 ± 5	31 ± 7	18 ± 4

---

Several general comments can be made about the ratio of products observed in different solvent compositions: as the amount of ionic liquid is increased in the reaction mixture the amount of product 2 decreases. This change suggests that the relative ease of nucleophilic attack at C2 decreases with the proportion of ionic liquid present, and implies significant interactions of the ionic liquid constituents with the intermediate. In cases where the isomers 10 and 11 are observed, the amount of isomer 10 is always greater than 11; this preference is likely, at least in part, due to a steric effect of the sugar portion of the molecule. However, differences between the ratios of these two products in cases where different ionic liquids are used again suggest interactions of the constituents of the ionic liquid with the intermediate; in this case, these interactions may hinder attack from one face of the intermediate. Product 12, likely resulting from elimination involving the triethylamine present in solution acting as a base, is only seen at higher mole fractions of ionic liquid in the reaction mixture. This outcome is consistent with a decrease in the rate of formation of those products 2, 10 and 11 that require nucleophilic attack of methanol on the intermediate as the amount of methanol in the reaction mixture decreases. Importantly though, elimination is not the major reaction pathway at any solvent composition.

Focussing on more specific cases, entries 2–4 show that using a small amount of ionic liquid (χ ca. 0.02) gives the same product 2 as seen in the methanol case but at a faster rate; this is representative of all ionic liquid cases studied. These examples suggest that this proportion of ionic liquid is insufficient to result in interactions with the intermediate that change the product ratio. This outcome is significant because it reinforces that the amounts of ionic liquid required to affect the rate determining and product determining steps are different.

As the amount of ionic liquid is increased in the reaction mixture, additional products are observed. Entries 5 and 7 show that the two dioxal isomers 10 and 11 are formed to a small and then moderate extent as the mole fraction of ionic liquid is increased to 0.37 and 0.73 for salt 3, demonstrating that the formation of these two isomers is favoured as more ionic liquid is present in the reaction mixture. Entries 7, 8, 10 and 11 show that changing the cation of the ionic liquid does not influence these product ratios; the same ratios of each product across all mole fractions are observed for ionic liquids 4–6 within uncertainty, suggesting that the cation is not involved in the interactions that affect the product determining step. That product formation is dependent on the anion of the ionic liquid is indicated in entries 6, 9 and 12 as the use of [bmim][PF₆] 7 only produces product 2 up until a solvent composition of χ = 0.95 where the additional products 10–12 are observed.††

This effect of the anion of the ionic liquid on product formation in this reaction is not unexpected given the indication from the Kamlet–Taft analysis, which showed that the anion is involved in the interactions affecting the rate constant of the reaction, and the activation parameter data, which suggested that these interactions are with the transition state towards the intermediate at high proportions of ionic liquid. It should be noted, of course, that the product forming step of this reaction does not affect k₁, however the importance of the anion in both steps is logical and suggests that the organisation of the solvent about the intermediate is key to the changes in outcome seen in both steps on moving to mixtures containing an ionic liquid. Importantly, there is the potential for rational solvent choice to not only control the rate determining step of the reaction, but also the product determining step, yielding products not readily available in molecular solvents.

Isolation studies

Due to the different products that were observed to form using different solvent mixtures, it was of interest to attempt to isolate these products from the reaction mixtures. Several solvent compositions were selected:

• χ_IL = 0, that is where methanol is the solvent alone. It was expected that this case would be easy to isolate the product 2.

• χ_IL = 0.02 using [bmim][BF₄] 8 to compare the isolated yields between this and the methanol case. This ionic liquid was selected as it is water soluble and was thought that the product 2 would be relatively easily isolated.

• χ_IL = 0.02 using [bmim][N(SO₂CF₃)₂] 3 to compare the isolated yields between two different ionic liquids that give the same product 2 at this low mole fraction.

• χ_IL = 0.32 using [bmim][N(SO₂CF₃)₂] 3 where products 2, 10 and 11 were observed in the kinetic studies.

• χ_IL = 0.75 using [bmim][N(SO₂CF₃)₂] 3 where all products 2 and 10–12 were observed in the kinetic studies.

Initial attempts at scales ca. 2.5 times those for the kinetics experiments (ca. 10 mg of substrate 1) gave good, reproducible yields for the methanol and χ_IL = 0.02 cases. However, at higher mole fractions, isolating the products on such a small scale proved difficult, likely due to the large amount of ionic liquid present and difficulty separating small amounts of product. For this reason, both the χ_IL = 0.32 and χ_IL = 0.75 cases were scaled up in terms of substrate 1 (ca. 100 mg) but the total volume of the system was reduced to avoid issues noted at smaller scales, resulting in a smaller proportion of methanol in the reaction mixture in order to ensure the mole fraction of the ionic liquid remained consistent. Due to this change, product ratios differed from those seen originally. However, the products observed were still found to be the same. These ratios, as well as the yields of each are outlined in Table 5. Product 2 was readily isolated from the mixture of products while products 10–12 were isolated as a mixture. Initial separation of this mixture was attempted but proved difficult so the data reported are for the unseparated mixture.

Table 5 A summary of the isolation studies completed for the solvolysis of the galactose 1 at 42 °C in different solvent compositions showing both the extent of conversion and yields of products 2 and 10–12

Solvent	χ IL	t/h	Extent of conversion^a				Yield
			2	10	11	12	2	10	11	12
a Extent of conversion determined by ^1H NMR spectroscopy after the time listed for each case. b Isolated yield determined from the mass recovered after isolation. c Determined from the mass recovered after isolation as a mixture of products. Uncertainties are determined from the standard deviation of triplicate experiments.
Methanol	0	2	>95	0	0	0	91 ± 3	0	0	0
8	0.02	1	>95	0	0	0	92 ± 4	0	0	0
3	0.02	1	>95	0	0	0	86 ± 10	0	0	0
3	0.32	5	35 ± 3	46 ± 1	19 ± 3	0	22 ± 4	25 ± 6	11 ± 3	0
3	0.76	45	6 ± 3	71 ± 2	19 ± 2	4 ± 1	4 ± 2	29 ± 8	10 ± 3	3 ± 1

---

Experimental

The galactose 1 was commercially available and was recrystallised from 1 : 1 hexane/diethyl ether and stored at 253 K until use. Analytical grade deuterated methanol was dried over 3 Å molecular sieves before use. Triethylamine was distilled and stored over 3 Å molecular sieves at 253 K until use. The ionic liquids 3–5 and 7–9 were prepared according to modified literature procedures,^26,49–52 by alkylating the appropriate heterocycle and performing a salt metathesis with the appropriate anion. Ionic liquid 6 was prepared from the corresponding bromide salt through a salt metathesis with Li[N(SO₂CF₃)₂]. All ionic liquids were dried under reduced pressure (<0.3 mbar) for at least 7 hours and found to have <200 ppm water using the Karl Fischer titration method. Ion chromatography was used to determine residual halide content as <20 ppm in each ionic liquid. All synthetic procedures are completely described in the ESI.†

Kinetic analyses were carried out in solutions containing the electrophile 1 (ca. 0.005 mol L⁻¹), triethylamine (ca. 0.02 mol L⁻¹) and the desired solvent mixture of methanol and one of the ionic liquids 3–9. Nucleophile dependence studies were carried out with the same proportions of both the electrophile 1 and triethylamine as above with varying concentrations of methanol (ca. 0.1, 0.2, 0.3 and 0.4 mol L⁻¹) in acetonitrile. An aliquot (0.5 mL) of each stock solution was placed in an NMR tube and the reactions followed using ¹H NMR spectroscopy at the appropriate temperature (mole fraction dependence studies, 315 K; temperature dependence studies, over the range 306–331 K). Rate constants were determined by following the integration of the signal due to the H1 on the electrophile 1 over time. Each rate constant was measured in triplicate. Activation enthalpies and entropies were determined by fitting the obtained rate constants to the Eyring equation.⁵³ Further details of kinetic experiments, including rate constants and stock solution compositions, can be found in the ESI.†

Microsoft Excel (version 16.34) was used for multivariate regression analyses of Kamlet–Taft parameters and the natural logarithm of the obtained rate constants. All analyses can be found in the ESI.†

Isolation studies were carried out in triplicate for each case. Full experimental details and characterisation of products are outlined in the ESI.†

Conclusions

The work described has studied the effect of using ionic liquids as solvents for the reaction of the galactose 1, including through solvolysis. It was found, using mole fraction dependence studies, that a low proportion of ionic liquid in the reaction mixture leads to an increase in the rate constant compared to the molecular solvent methanol. This effect decreases significantly at higher mole fractions and is dependent on both constituents of the ionic liquid. Significantly, the dependence on the proportion of salt in the reaction mixture differed from previous cases that proceed through the same mechanism, demonstrating the importance of the structure of the reagent in determining ionic liquid solvent effects. An ionic liquid with a more coordinating anion gave a greater increase in k₁ overall.

Temperature dependence studies indicated that the dominant interaction driving these changes in k₁ was between the ionic liquid and the transition state of the process but that starting material interactions are important in some cases, showing that there is a balance between the two types of interactions. Whilst different from what has been seen with other reactions that proceed through this mechanism,^16,18,19 this outcome has been seen for reactions that proceed through a different mechanism.^54,55 Importantly, it also shows the complexity in the balance of interactions and the resultant effects on reaction outcome that can occur in mixtures containing ionic liquids.

Multiple regression analyses were used to better understand these interactions; a relationship between the natural logarithm of the rate constant and both the hydrogen bond accepting ability and the polarizability of the solvent across each mole fraction was found. This relationship showed that non-specific, likely charge–charge interactions, are favourable for this reaction, whereas specific hydrogen bonding interactions are disfavoured. In all cases, an ionic liquid with greater polarizability but less able to accept a hydrogen bond would lead to an increase in the rate constant. This relationship sheds light on the dominant interactions affecting k₁ and can allow for the rational selection of an ionic liquid for this process. Of note is that the correlation of the parameters found was different to the correlations found for previous related systems, once again indicating the importance of the nature of the reagent in solvent effects for these systems.

Finally, it was found that the product determining step of the reaction was also affected by the use of ionic liquids. At proportions of salt in the reaction mixture, additional products were observed that are not seen under these conditions without the presence of an ionic liquid. This difference is likely due to a change in the solvation of the intermediate carbocation, resulting in different energies for the subsequent pathways. At the highest mole fractions of ionic liquids in the reaction, elimination was also observed, potentially due to there being less methanol in the reaction mixture available to react. The ratios of these products were found to be dependent on the anion of the ionic liquid. These results are significant as they not only show new reactivity but also allow for control of reaction outcome when using ionic liquids.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

AG acknowledges the support of the Australian Government through the receipt of a Research Training Program Scholarship. JBH acknowledges financial support from the Australian Research Council Discovery Project Funding Scheme (Project DP180103682). The authors also acknowledge the NMR facility and the Bioanalytical Mass Spectrometry facility, both within the Mark Wainwright Analytical Centre at the University of New South Wales; the former for NMR support and the latter for carrying out mass spectrometric analysis.

Notes and references

1. M. J. Earle and K. R. Seddon, Pure Appl. Chem., 2000, 72, 1391.
2. T. Welton, Chem. Rev., 1999, 99, 2071–2084.
3. J. P. Hallett and T. Welton, Chem. Rev., 2011, 111, 3508–3576.
4. S. Mallakpour and M. Dinari, in Green Solvents II: Properties and Applications of Ionic Liquids, ed. A. Mohammad and D. Inamuddin, Springer Netherlands, Dordrecht, 2012,  DOI:10.1007/978-94-007-2891-2_1, pp. 1–32.
5. H.-J. Liaw, C.-C. Chen, Y.-C. Chen, J.-R. Chen, S.-K. Huang and S.-N. Liu, Green Chem., 2012, 14, 2001–2008.
6. K. Ghandi, Green Sustainable Chem., 2014, 4, 44–53.
7. J. G. Huddleston, H. D. Willauer, R. P. Swatloski, A. E. Visser and R. D. Rogers, Chem. Commun., 1998, 1765–1766.
8. M. Freemantle, Chem. Eng. News, 1998, 76, 32–37.
9. M. J. Earle, S. P. Katdare and K. R. Seddon, Org. Lett., 2004, 6, 707–710.
10. C. Chiappe and D. Pieraccini, J. Phys. Org. Chem., 2005, 18, 275–297.
11. A. Gilbert, R. S. Haines and J. B. Harper, in Reference Module in Chemistry, Molecular Sciences and Chemical Engineering, Elsevier, 2018,  DOI:10.1016/B978-0-12-409547-2.14212-X.
12. R. R. Hawker and J. B. Harper, in Advances in Physical Organic Chemistry, ed. I. H. Williams and N. H. Williams, Academic Press, 2018, vol. 52, pp. 49–85.
13. S. T. Keaveney, R. S. Haines and J. B. Harper, in Encyclopedia of Physical Organic Chemistry, Wiley, New Jersey, 2017, vol. 2.
14. B. Y. W. Man, J. M. Hook and J. B. Harper, Tetrahedron Lett., 2005, 46, 7641–7645.
15. H. M. Yau, S. A. Barnes, J. M. Hook, T. G. A. Youngs, A. K. Croft and J. B. Harper, Chem. Commun., 2008, 3576–3578.
16. S. T. Keaveney, B. P. White, R. S. Haines and J. B. Harper, Org. Biomol. Chem., 2016, 14, 2572–2580.
17. E. Kochly, N. Lemon and A. Deh-Lee, Molecules, 2016, 21, 60.
18. A. Gilbert, R. S. Haines and J. B. Harper, Org. Biomol. Chem., 2019, 17, 675–682.
19. A. Gilbert, G. Bucher, R. S. Haines and J. B. Harper, Org. Biomol. Chem., 2019, 17, 9336–9342.
20. M. Miljkovic, Carbohydrates: Synthesis, Mechanisms, and Stereoelectronic Effects, Springer-Verlag, New York, 2009.
21. A. Brandt, J. Gräsvik, J. P. Hallett and T. Welton, Green Chem., 2013, 15, 550–583.
22. A. S. Amarasekara, Isr. J. Chem., 2019, 59, 789–802.
23. O. A. El Seoud, A. Koschella, L. C. Fidale, S. Dorn and T. Heinze, Biomacromolecules, 2007, 8, 2629–2647.
24. S. Marullo, C. Rizzo and F. D'Anna, Front. Chem., 2019, 7, 134.
25. J. Song, B. Zhang, J. Shi, H. Fan, J. Ma, Y. Yang and B. Han, RSC Adv., 2013, 3, 20085–20090.
26. H. Srour, H. Rouault, C. C. Santini and Y. Chauvin, Green Chem., 2013, 15, 1341–1347.
27. H. M. Yau, S. T. Keaveney, B. J. Butler, E. E. L. Tanner, M. S. Guerry, S. R. D. George, M. H. Dunn, A. K. Croft and J. B. Harper, Pure Appl. Chem., 2013, 85, 1979.
28. X. Creary, E. D. Willis and M. Gagnon, J. Am. Chem. Soc., 2005, 127, 18114–18120.
29. B. B. Hurisso, K. R. J. Lovelock and P. Licence, Phys. Chem. Chem. Phys., 2011, 13, 17737–17748.
30. S. Spange, R. Lungwitz and A. Schade, J. Mol. Liq., 2014, 192, 137–143.
31. H. M. Yau, A. K. Croft and J. B. Harper, Faraday Discuss., 2012, 154, 365–371.
32. H. M. Yau, A. G. Howe, J. M. Hook, A. K. Croft and J. B. Harper, Org. Biomol. Chem., 2009, 7, 3572–3575.
33. I. Y. López-Cortés, G. A. Iglesias-Silva, M. Ramos-Estrada and J. L. Rivera-Rojas, Fluid Phase Equilib., 2020, 514, 112543.
34. R. Bini, C. Chiappe, V. L. Mestre, C. S. Pomelli and T. Welton, Org. Biomol. Chem., 2008, 6, 2522–2529.
35. B. J. Butler and J. B. Harper, J. Phys. Org. Chem., 2018, 31, e3819.
36. J. Alarcón-Espósito, R. Contreras, R. A. Tapia and P. R. Campodónico, Chem. – Eur. J., 2016, 22, 13347–13351.
37. P. Pavez, D. Millán, J. I. Morales, E. A. Castro, C. A. López and J. G. Santos, J. Org. Chem., 2013, 78, 9670–9676.
38. S. T. Keaveney, R. S. Haines and J. B. Harper, ChemPlusChem, 2017, 82, 449–457.
39. R. W. Taft and M. J. Kamlet, J. Am. Chem. Soc., 1976, 98, 2886–2894.
40. M. J. Kamlet and R. W. Taft, J. Am. Chem. Soc., 1976, 98, 377–383.
41. M. J. Kamlet, J. L. Abboud and R. W. Taft, J. Am. Chem. Soc., 1977, 99, 6027–6038.
42. M. A. Ab Rani, A. Brant, L. Crowhurst, A. Dolan, M. Lui, N. H. Hassan, J. P. Hallett, P. A. Hunt, H. Niedermeyer, J. M. Perez-Arlandis, M. Schrems, T. Welton and R. Wilding, Phys. Chem. Chem. Phys., 2011, 13, 16831–16840.
43. P. Pavez, D. Millan, C. Cocq, J. G. Santos and F. Nome, New J. Chem., 2015, 39, 1953–1959.
44. R. R. Hawker, R. S. Haines and J. B. Harper, Org. Biomol. Chem., 2018, 16, 3453–3463.
45. P. G. Jessop, D. A. Jessop, D. Fu and L. Phan, Green Chem., 2012, 14, 1245–1259.
46. R. Rinaldi, Chem. Commun., 2011, 47, 511–513.
47. Y. Dong, T. Takeshita, H. Miyafuji, T. Nokami and T. Itoh, Bull. Chem. Soc. Jpn., 2018, 91, 398–404.
48. D. Yalcin, A. J. Christofferson, C. J. Drummond and T. L. Greaves, Phys. Chem. Chem. Phys., 2020, 22, 10995–11011.
49. L. Cammarata, S. G. Kazarian, P. A. Salter and T. Welton, Phys. Chem. Chem. Phys., 2001, 3, 5192–5200.
50. S. N. Baker, E. B. Brauns, T. M. McCleskey, A. K. Burrell and G. A. Baker, Chem. Commun., 2006, 2851–2853.
51. E. E. L. Tanner, R. R. Hawker, H. M. Yau, A. K. Croft and J. B. Harper, Org. Biomol. Chem., 2013, 11, 7516–7521.
52. I. S. Molchan, G. E. Thompson, R. Lindsay, P. Skeldon, V. Likodimos, G. E. Romanos, P. Falaras, G. Adamova, B. Iliev and T. J. S. Schubert, RSC Adv., 2014, 4, 5300–5311.
53. H. Eyring, J. Chem. Phys., 1935, 3, 107–115.
54. R. R. Hawker, R. S. Haines and J. B. Harper, Chem. Commun., 2018, 54, 2296–2299.
55. K. S. Schaffarczyk McHale, R. R. Hawker and J. B. Harper, New J. Chem., 2016, 40, 7437–7444.
56. C.-W. Li, K.-W. Hon, B. Ghosh, P.-H. Li, H.-Y. Lin, P.-H. Chan, C.-H. Lin, Y.-C. Chen and K.-K. T. Mong, Chem. – Asian J., 2014, 9, 1786–1796.
57. IUPAC, Compendium of Chemical Terminology, 2nd ed. (the “Gold Book”), Compiled by A. D. McNaught and A. Wilkinson, Blackwell Scientific Publications, Oxford, 1997. Online version (2019-) created by S. J. Chalk. ISBN 0-9678550-9-8. DOI:  DOI:10.1351/goldbook.
58. IUPAC, Compendium of Chemical Terminology, 2nd ed. (the “Gold Book”), Compiled by A. D. McNaught and A. Wilkinson, Blackwell Scientific Publications, Oxford, 1997. Online version (2019-) created by S. J. Chalk, ISBN 0-9678550-9-8. DOI:  DOI:10.1351/goldbook.

---

Footnotes

† Electronic supplementary information (ESI) available: Synthesis of ionic liquids and their precursors, experimental details for kinetic analyses, nucleophile dependence plot for the reaction shown in Scheme 1, Eyring plot for reaction shown in Scheme 1, correlation of rate constant data with solvent parameters (including multivariate regression analyses), product analyses for the reaction shown in Scheme 1 in different ionic liquids, experimental details for isolation studies, rate data for all the plots presented, ¹H NMR spectra of prepared compounds. See DOI: 10.1039/d0ob01198c

‡ It can also be argued that ionic liquids containing a more coordinating cation (such as those with a less coordinating anion that would make the cation more available) would result in transition state interactions becoming more dominant.

§ Correlations between ln(k₁) and α were fair with R² values up to 0.61, however better correlations were subsequently sought.

¶ It is important to note that in the χ ca. 0.7 case the coefficient for the β parameter gave a p-value of 0.14, indicating this is not a significant fit. An additional analysis showed a significant relationship of ln(k₁) = −20.86 + 12.46π*. This observation further supports the indication that favourable non-specific interactions dominate at higher mole fractions.

|| It should be noted that the product determining step occurs after the rate determining step, so the argument presented in the earlier sections is valid, irrespective of the product ratio.

** These isomers have been synthesised previously but under different conditions; an additional molecular solvent is needed, likely to avoid formation of product 2. These syntheses also require the use of a salt such as tetrabutylammonium bromide.⁵⁶

†† Product ratios of both [bmim][BF₄] 8 and [bmim][C(CN)₃] 9 are not discussed as in both cases an additional product was observed at mole fraction >0.35; it was found that adventitious water was reacting in an irreproducible manner. See ESI† for more detail.

---