Slow relaxation of the magnetization, reversible solvent exchange and luminescence in 2D anilato-based frameworks†‡
Samia
Benmansour
 *a,
Antonio
Hernández-Paredes
*a,
Antonio
Hernández-Paredes
 a,
Arpan
Mondal
a,
Arpan
Mondal
 b,
Gustavo
López Martínez
a,
Josep
Canet-Ferrer
b,
Gustavo
López Martínez
a,
Josep
Canet-Ferrer
 a,
Sanjit
Konar
a,
Sanjit
Konar
 b and
Carlos J.
Gómez-García
b and
Carlos J.
Gómez-García
 *a
*a
aInstituto de Ciencia Molecular, Departamento de Química Inorgánica, Universidad de Valencia, C/Catedrático José Beltrán, 2, 46980 Paterna (Valencia), Spain. E-mail: sam.ben@uv.es; carlos.gomez@uv.es
bDepartment of Chemistry, Indian Institute of Science Education and Research Bhopal, India
First published on 20th July 2020
Abstract
A series of multifunctional 2D frameworks prepared with Dy(III) and the bromanilato ligand, formulated as: [Dy2(C6O4Br2)3(G)n]·nG with G = H2O, dimethylformamide (dmf) and dimethylsulfoxide (dmso), can exchange the coordinated and non-coordinated solvent molecules (G) in a reversible way. These multifunctional frameworks show field induced slow relaxation of the magnetization and luminescence that can be easily and reversibly modified by solvent exchange.
In the last two decades, the synthesis of coordination networks with lanthanoid metal ions and different bridging ligands has become a source of multifunctional networks with interesting catalytic, optical and/or magnetic properties.1–4 The inclusion of porosity in these networks allows the possibility to insert, remove and exchange guest molecules which may play two important roles: (i) controlling and tuning these properties and (ii) triggering or cancelling them.5,6 This double role allows the preparation of functional networks with the desired properties that can act as sensors or switchers by simple guest-exchange.7 Although this strategy has been used to prepare some Ln(III)-based examples with guest-dependent luminescence that can be used as sensors,8,9 its use for magnetic probes is less common.
In recent years, the use of anilato-type ligands (Scheme S1, ESI‡) with Ln(III) ions has led to the synthesis of several two-dimensional10–20 and a few three-dimensional lattices,10,20 besides a few examples of discrete clusters (mainly anilato-bridged dimers).14,21
The magnetic properties of these Ln(III)-based networks are those expected for almost isolated Ln(III) ions since the anilato ligands are known to give rise to very weak magnetic coupling even with transition metals.22–24
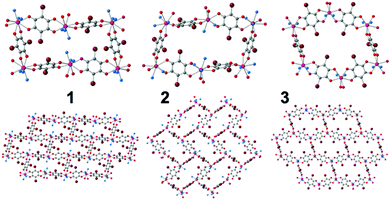
Here we present three similar two-dimensional (2D) networks: [Dy2(C6O4Br2)3(H2O)6]·8H2O (1), [Dy2(C6O4Br2)3(dmf)6] (2) and [Dy2(C6O4Br2)3(dmso)4]·2dmso·2H2O (3) prepared with bromanilato (Scheme S1, ESI‡), Dy(III) and three different solvents with high coordinating capacity towards Ln(III) ions.25 In these compounds the Dy(III) ions are coordinated to three bromanilato ligands and to three (in 1 and 2) or two (in 3) solvent molecules. Additionally, these layered materials may contain solvent molecules inserted between the layers (in 1 and 3). Here we show that these three compounds present field induced slow relaxation of the magnetization at low temperatures and can easily and reversibly exchange the solvent molecules (including the coordinated ones) leading to important changes in the magnetic parameters of the relaxation process. As far as we know, this is the first observation of both phenomena (slow relaxation of the magnetization and solvent exchange) in an anilato-based lattice.
Compounds 1–3 were prepared as polycrystalline samples by direct one-pot reaction of bromanilic acid and Dy(NO3)3·5H2O in the corresponding solvents (H2O, dmf or dmso for 1–3, respectively). Single crystals of these compounds were obtained by carefully layering, in long thin tubes, a methanolic solution of bromanilic acid on top of a solution of Dy(NO3)3·5H2O in the corresponding solvent (ESI‡). Interestingly, the kinetics of the crystallization process leads to a different phase for the compound prepared in water.26 Thus, the fast one-pot crystallization leads to a phase containing eight water molecules: [Dy2(C6O4Br2)3(H2O)6]·8H2O (1) whereas the slow diffusion leads to a solvate containing twelve water molecules: [Dy2(C6O4Br2)3(H2O)6]·12H2O (1′), as shown by the X-ray powder diffraction (ESI‡). Fortunately, the phase containing eight water molecules can be obtained as single crystals by slow diffusion for the two smaller Ln(III) ions: Yb(III) and Tm(III) and, therefore, here we will describe the structure of the Yb(III) derivative (1-Yb) which is isostructural to compound 1.
The single crystal X-ray diffraction (ESI‡) of the three compounds shows that they are similar but not isostructural (indicating that the solvent molecules play an important structural role). Note that the structure of 3 was recently reported by some of us,13 but not its capacity to exchange solvent molecules, its luminescence or the presence of a field induced slow relaxation of the magnetization. The asymmetric unit of compounds 1–3 contains one Dy(III) ion, three halves of bromanilato ligands (one complete and a half in 2), three coordinated solvent molecules (two in 3) and four crystallization water molecules in 1 and one water and one dmso molecule in 3. The Dy(III) ions are nonacoordinated in 1 and 2 and octacoordinated in 3 with coordination geometries of tricapped trigonal prism for 1, capped square antiprism for 2 and triangular dodecahedron in 3 as shown by Shape analysis (ESI‡).27 The differences in the coordination geometries are due to the different sizes and steric hindrances of the solvent molecules, as already observed in other reacted lattices.11,19 Each Dy(III) is connected to three Dy(III) through a bis-bidentate bromanilato ligand, generating layers with distorted hexagonal cavities with a 6,3-topology, that look like rectangles in 1 and 2 (Fig. 1). The disposition of these cavities can be described as brick-wall, spike-like and distorted honeycomb in 1–3, respectively (Fig. 1). These differences are due to the different orientations of the planes of the anilato rings with respect to the plane of the cavity which, in turn, depend on the sites occupied by the anilato oxygen atoms in the coordination sphere of the Dy(III) ions (ESI‡).11,19
One of the most interesting properties of these frameworks is their capacity to reversibly exchange the crystallization and coordinated solvents by simple immersion, allowing the synthesis of any of the three compounds starting from any of the other two (ESI‡). The exchanged compounds have been fully characterized with elemental analysis, IR spectroscopy and thermogravimetric measurements (ESI‡).
The solid-state luminescence spectra of compounds 1–3 show a main peak (P1 in Fig. 2a) centred around 500 nm, typical of the Dy(III) 4F9/2 → 6H15/2 transition, suggesting that they are mainly dominated by the antenna effect of the ligands.28 The light absorbed by the surrounding of the Dy(III) ions through the coordinated bromanilato ligand is transferred to the Dy(III) excited states from the bromanilato ligand by intramolecular energy transfer, and finally, luminescence is generated from the lanthanide ions, as can be concluded by comparison with the absorption of the free bromanilic acid in solution (ESI‡).29
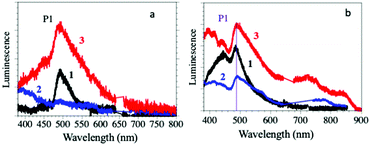 | ||
| Fig. 2 (a) Luminescence emission spectra of compounds 1–3 in the solid state. (b) Luminescence emission spectra of suspensions of compounds 1–3 in H2O, dmf and dmso, respectively. | ||
The intensity of the P1 peak decreases when the coordinated solvent changes from dmso (3) to H2O (1) and dmf (2) (where the peak has almost completely disappeared and the emission spectrum is almost identical to the free bromanilic acid in the solid state, see the ESI‡). This result indicates that the luminescence of the Dy(III) centres in compounds 1–3 is solvent-dependent and it is almost completely quenched by the coordination of dmf.
The emission spectra for suspensions of compounds 1–3 in their corresponding solvents (Fig. 2b) are similar to those obtained in the solid state, except for compound 2, since it loses dmf molecules upon drying. Thus, they show the P1 peak at around 500 nm with the same trends in intensity and linewidth to those of the solid-state ones, confirming: (i) that the Dy(III) coordination environment is stable in the solid and (ii) that the emission is due to the Dy(III) centres rather than to the bromanilato ligand since bromanilic acid dissolved in H2O, dmf or dmso gives much weaker emissions (ESI‡). This fact confirms the important role of the coordination of the bromanilato ligand and the solvent molecules in the luminescence of compounds 1–3.
The magnetic properties of the three compounds indicate that the Dy(III) ions are magnetically isolated since the magnetic coupling through anilato bridges is negligible when connecting lanthanoid ions.11–13,15,19 Compounds 1–3 show at room temperature χmT values of ca. 28.5 cm3 K mol−1 per two Dy(III) ions, which is close to the expected value for two isolated Dy(III) ions with a ground state 6H15/2.30 When the temperature is lowered, the three compounds show a continuous decrease in the χmT value, reaching a value close to 16 cm3 K mol−1 at 2 K (ESI‡) due to the depopulation of the sublevels generated by the ligand field, rather than to a noticeable antiferromagnetic coupling.
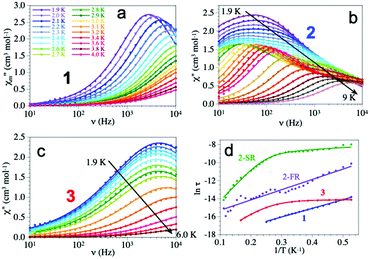
The magnetic isolation provided by the bromanilato bridges prompted us to perform AC susceptibility measurements to check for the presence of a slow relaxation of the magnetization at low temperatures. These measurements show the presence of frequency dependent in-phase (χm′) and out-of-phase (χm′′) signals at low temperatures and very high frequencies (10 kHz) in compounds 2 and 3 (but not in 1, ESI‡). In contrast, when a DC field is applied, the three compounds show clear frequency-dependent χm′ and χm′′ signals. Since the χm′′ vs. DC field plot shows maxima of χm′′ at ca. 1000 Oe (ESI‡), we have performed AC measurements at low temperatures with a DC field of 1000 Oe for the three compounds in the frequency range 10 Hz to 10 kHz. These measurements show quite different thermal dependences for compounds 1–3 (ESI‡): (i) a maximum in χm′′ at low temperatures that shifts to higher temperatures as the frequency increases in 1, (ii) up to three different maxima in the χm′′ plot at high frequencies (3–10 kHz), two at intermediate frequencies (700–1500 Hz) and only one with a divergence at low temperatures at low frequencies (<400 Hz) in 2 and (iii) a divergence at low temperatures at any frequency in 3.
The frequency dependence shows different behaviours for the three compounds (Fig. 3). Compound 1 shows a maximum at around 3 kHz at 1.9 K that shifts to ca. 10 kHz at 2.4 K. Compound 2 shows a broad maximum at ca. 50 Hz at 1.9 K that shifts to higher frequencies as the temperature increases. The large width of the maximum and its temperature dependence indicate that the AC signal is due to at least two different relaxation processes as clearly seen at intermediate temperatures. Compound 3 shows a temperature independent maximum at ca. 4 kHz in the 1.9–3.0 K range that shifts to higher frequencies above ca. 3.0 K (ESI‡).
Accordingly, we have used a Debye model to reproduce the frequency dependence of compounds 1 and 3 (solid lines in Fig. 3). These fits show α values in the range of 0.14–0.29 in 1 and slightly higher, in the range of 0.28–0.43 in 3 (ESI‡) indicative of a distribution of the relaxation processes. Compound 2, in contrast, shows two different relaxation processes overlapping at very low temperatures. When the temperature is increased the fast relaxation process (FR, τ2) shifts to higher frequencies faster that the slow relaxation one (SR, τ1) and, thus, at intermediate temperatures, the FR process appears as a shoulder of the SR one (Fig. 3). Accordingly, we have used a Debye model for two relaxation processes to reproduce the frequency dependence of χm′′ (solid lines in Fig. 3)31 Note that this double relaxation process has been observed in other Dy(III) containing compounds32 and has been attributed to the presence of two relaxation pathways via excited states,33 since there is only one independent Dy(III) ion in 2. The relaxation times obtained at high temperatures in 1 and 3 and at low temperatures in 2 have to be taken with caution since the maxima in the χm′′ plot cannot be observed.
The Arrhenius plot of the relaxation times in compounds 1–3 (Fig. 3d) shows straight lines for 1 and for the FR process of 2, typical of an Orbach relaxation mechanism. In contrast, compound 3 and the SR process in 2 both deviate from the linear behaviour at low temperatures, indicative of one or more additional relaxation mechanisms. In order to fit the relaxation times we have used the general model including all the possible mechanisms: quantum tunnelling (QTM, first term), direct (second term), Raman (third term) and Orbach (fourth term):34
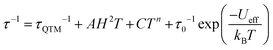 | (1) |
Compounds 1 and 2 (FR) can be fit using only the last term (Orbach mechanism) with τ0 = 6.1(3) × 10−10 and 7(1) × 10−8 s and Ueff = 9.6(1) and 11.4(6) K, respectively. Compound 2 (SR) can be fit with Orbach and direct mechanisms with AH2 = 2.09(9) × 103 K−1, τ0 = 1.7(3) × 10−8 s and Ueff = 36(1) K and finally compound 3 can only be fit if a quantum tunnelling term is added to the Orbach and Direct ones, with τQTM = 8.5(4) × 10−7 s, AH2 = 1.0(3) × 105 K−1, τ0 = 2.0(1) × 10−9 s and Ueff = 22.8(4) K (solid lines in Fig. 3d).
The computed ab initio energy spectrum, g tensor, and wave function composition for the eight Kramer's doublets (KDs) originating from the spin–orbit coupled ground state term 6H15/2 are listed in Tables S17–S21 (ESI‡). It was found that compound 2 possesses higher axial anisotropy (gx = 0.004, gy = 0.005 and gz = 19.83) in the ground state as compared to 1 (gx = 0.114, gy = 0.198 and gz = 19.12) and 3 (gx = 0.017, gy = 0.031 and gz = 19.57) (ESI‡). The wave function composition of the ground state KDs of 2 reveals that it is purer (mj = ±15/2) than the other two compounds (1 and 3) (Tables S19–S21, ESI‡). To further unify our statement, we have also analyzed the computed crystal field parameters (CFPs) which disclose the negative diagonal and axial terms in all three compounds (Table S22, ESI‡). The corresponding crystal field Hamiltonian can be expressed by the following equation, where ôkq and Bkq are the Stevens operator and crystal field parameters, respectively:
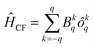 | (2) |
It was found that the axial term (B02) (−1.3, −3.1 and −2.2 in 1–3, respectively, Table S21, ESI‡) follows the order 1 < 3 < 2, confirming that the extent of mixing in the ground state decreases in the same order as observed in the wave function composition analysis (Tables S19–S21, ESI‡). However, the ground ranked extra diagonal non-axial terms are non-negligible, which may lead to the mixing in the ground state KDs in all the compounds. Additionally, the higher-ranked extra diagonal terms with higher magnitude (which are smaller in 2 as compared to 1 and 3) may contribute to larger QTM and transverse anisotropy in the ground state; therefore, none of the compounds displays a slow relaxation process under zero field. The local magnetic anisotropy axis of the ground states is found to be oriented towards a particular direction (Fig. S43, ESI‡) to minimize the electrostatic repulsion of the β electron density and can be understood from LoProp charges obtained from the CASSCF wave function.35 To explain the relaxation dynamics, we have plotted the quantitative mechanism for slow magnetic relaxation (Fig. S44–S46, ESI‡). The calculated barriers (120 cm−1 for 1, 193 cm−1 for 2 and 141 cm−1 for 3) for all the compounds are well above the observed energy barriers (6.7 cm−1 for 1, 25.0 cm−1 for 2 and 15.8 cm−1 for 3) of the magnetization reversal process. This can be understood by some other relaxation processes which follow the shortcut pathways (QTM, Raman and direct) and are not considered in the ab initio calculated energy barriers. It was observed that the QTMs in the ground state for compounds 1 and 3 are relatively higher as compared to 2. Therefore, the relaxation process through the ground state KDs becomes faster in 1 and 3 than in 2. On the other hand, the QTM between the ground state KDs is much higher in 1, compared to 3. Therefore, the energy barrier for the slow magnetic relaxation process increases as we move from compound 1 to 3 to 2, in agreement with the experimental data. However, both the experimental and theoretical observations suggest that the relaxation mainly occurs through the ground state (QTM) or some virtual states (Raman or direct processes), as the first excited states are of much higher energy in all compounds.
Compounds 1–3 constitute a unique series of multifunctional frameworks showing luminescence, slow relaxation of the magnetization and solvent exchange. The ease of the solvent exchange and the solvent-dependence of both the magnetic and optical properties opens the way to prepare novel layered materials that may act as magnetic and optical sensors simultaneously.
We thank the Spanish MINECO (project CTQ2017-87201-P AEI/FEDER, UE and grant to A. H.) and the Generalidad Valenciana (Prometeo/2019/076) for financial support.
Conflicts of interest
There are no conflicts to declare.Notes and references
- S. Fordham, X. Wang, M. Bosch and H. Zhou, Struct. Bonding, 2015, 163, 1–27 CAS.
- Y. Hasegawa and T. Nakanishi, RSC Adv., 2015, 5, 338–353 RSC.
- C. Pagis, M. Ferbinteanu, G. Rothenberg and S. Tanase, ACS Catal., 2016, 6, 6063–6072 CrossRef CAS.
- M. L. Mercuri, F. Congiu, G. Concas and S. A. Sahadevan, Magnetochemistry, 2017, 3, 17 CrossRef.
- S. Roy, A. Chakraborty and T. K. Maji, Coord. Chem. Rev., 2014, 273, 139–164 CrossRef.
- Y. Cui, Y. Yue, G. Qian and B. Chen, Chem. Rev., 2012, 112, 1126–1162 CrossRef CAS PubMed.
- L. Wang, G. Fan, X. Xu, D. Chen, L. Wang, W. Shi and P. Cheng, J. Mater. Chem. A, 2017, 5, 5541–5549 RSC.
- M. L. Cable, J. P. Kirby, H. B. Gray and A. Ponce, Acc. Chem. Res., 2013, 46, 2576–2584 CrossRef CAS PubMed.
- B. Yan, Acc. Chem. Res., 2017, 50, 2789–2798 CrossRef CAS PubMed.
- B. F. Abrahams, J. Coleiro, K. Ha, B. F. Hoskins, S. D. Orchard and R. Robson, J. Chem. Soc., Dalton Trans., 2002, 1586–1594 RSC.
- S. Benmansour, I. Pérez-Herráez, G. López-Martínez and C. J. Gómez García, Polyhedron, 2017, 135, 17–25 CrossRef CAS.
- P. Gómez-Claramunt, S. Benmansour, A. Hernández-Paredes, C. Cerezo-Navarrete, C. Rodríguez-Fernández, J. Canet-Ferrer, A. Cantarero and C. J. Gómez-García, Magnetochemistry, 2018, 4, 6 CrossRef.
- S. Benmansour, A. Hernández-Paredes and C. J. Gómez-García, J. Coord. Chem., 2018, 71, 845–863 CrossRef CAS.
- A. Hernández-Paredes, C. Cerezo-Navarrete, C. J. Gómez García and S. Benmansour, Polyhedron, 2019, 170, 476–485 CrossRef.
- S. Benmansour, A. Hernández-Paredes and C. J. Gómez-García, Magnetochemistry, 2018, 4, 58 CrossRef CAS.
- S. A. Sahadevan, N. Monni, A. Abhervé, G. Cosquer, M. Oggianu, G. Ennas, M. Yamashita, N. Avarvari and M. L. Mercuri, Inorg. Chem., 2019, 58, 13988–13998 CrossRef CAS PubMed.
- F. Artizzu, M. Atzori, J. Liu, D. Mara, K. Van Hecke and R. Van Deun, J. Mater. Chem. C, 2019, 7, 11207–11214 RSC.
- C. J. Kingsbury, B. F. Abrahams, J. E. Auckett, H. Chevreau, A. D. Dharma, S. Duyker, Q. He, C. Hua, T. A. Hudson, K. S. Murray, W. Phonsri, V. K. Peterson, R. Robson and K. F. White, Chem. – Eur. J., 2019, 25, 5222–5234 CrossRef CAS.
- S. Benmansour, I. Pérez-Herráez, C. Cerezo-Navarrete, G. López-Martínez, C. Martínez Hernandez and C. J. Gómez-García, Dalton Trans., 2018, 47, 6729–6741 RSC.
- K. Bondaruk and C. Hua, Cryst. Growth Des., 2019, 19, 3338–3347 CrossRef CAS.
- S. Benmansour, G. López-Martínez, J. Canet-Ferrer and C. J. Gómez-García, Magnetochemistry, 2016, 2, 32 CrossRef.
- M. Atzori, S. Benmansour, G. Mínguez Espallargas, M. Clemente-León, A. Abhervé, P. Gómez-Claramunt, E. Coronado, F. Artizzu, E. Sessini, P. Deplano, A. Serpe, M. L. Mercuri and C. J. Gómez García, Inorg. Chem., 2013, 52, 10031–10040 CrossRef CAS PubMed.
- S. Benmansour, A. Abhervé, P. Gómez-Claramunt, C. Vallés-García and C. J. Gómez-García, ACS Appl. Mater. Interfaces, 2017, 9, 26210–26218 CrossRef CAS PubMed.
- S. Benmansour and C. J. Gómez-García, Gen. Chem., 2020, 6, 190033 Search PubMed.
- R. Diaz-Torres and S. Alvarez, Dalton Trans., 2011, 40, 10742–10750 RSC.
- G. López-Martínez, PhD thesis, University of Valencia, 2017.
- M. Llunell, D. Casanova, J. Cirera, J. M. Bofill, P. Alemany, S. Alvarez, M. Pinsky and D. Avnir, SHAPE 2.3. 2013.
- V. R. Panse, A. N. Yerpude, N. S. Kokode and S. J. Dhoble, Optik, 2016, 127, 4778–4779 CrossRef CAS.
- X. Li, Z. Gao and Q. Zeng, Chin. Sci. Bull., 2012, 57, 1659–1664 CrossRef CAS.
- L. Sorace and D. Gatteschi, in Electronic Structure and Magnetic Properties of Lanthanide Molecular Complexes, ed. R. A. Layfield and M. Murugesu, 2015, pp. 1–25 Search PubMed.
- M. Dolai, M. Ali, J. Titis and R. Boca, Dalton Trans., 2015, 44, 13242–13249 RSC.
- J. Ruiz, A. J. Mota, A. Rodriguez-Dieguez, S. Titos, J. M. Herrera, E. Ruiz, E. Cremades, J. P. Costes and E. Colacio, Chem. Commun., 2012, 48, 7916–7918 RSC.
- R. J. Blagg, L. Ungur, F. Tuna, J. Speak, P. Comar, D. Collison, W. Wernsdorfer, E. J. L. McInnes, L. F. Chibotaru and R. E. P. Winpenny, Nat. Chem., 2013, 5, 673–678 CrossRef CAS PubMed.
- S. Demir, J. M. Zadrozny and J. R. Long, Chem. – Eur. J., 2014, 20, 9524–9529 CrossRef CAS PubMed.
- A. B. Canaj, S. Dey, E. R. Martí, C. Wilson, G. Rajaraman and M. Murrie, Angew. Chem. Int. Ed., 2019, 58, 14146–14151 CrossRef CAS PubMed.
Footnotes |
| † In memory of Professor Peter Day, an excellent researcher and a better person. |
| ‡ Electronic supplementary information (ESI) available: Details of the synthesis and crystal structures; FT-IR, TGA, magnetic and optical characterization and ab initio theoretical calculations. CCDC 1565283 (1-Yb), 1579873 (2) and 2005220 (3). For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0cc03964k |
| This journal is © The Royal Society of Chemistry 2020 |