Solvent effects on the second harmonic responses of donor–acceptor Stenhouse adducts: from implicit to hybrid solvation models†
Angela
Dellai
 a,
Isabella
Krismer
a,
Giacomo
Prampolini
a,
Isabella
Krismer
a,
Giacomo
Prampolini
 b,
Benoît
Champagne
b,
Benoît
Champagne
 c,
Tárcius N.
Ramos
c,
Tárcius N.
Ramos
 *c and
Frédéric
Castet
*c and
Frédéric
Castet
 *a
*a
aUniv. Bordeaux, CNRS, Bordeaux INP, Institut des Sciences Moléculaires, UMR 5255, F-33400 Talence, France. E-mail: frederic.castet@u-bordeaux.fr
bConsiglio Nazionale delle Ricerche, CNR-ICCOM, Pisa, Italy
cUnité de Chimie Physique Théorique et Structurale, Chemistry Department, Namur Institute of Structured Matter, University of Namur, Belgium. E-mail: tarcius.nascimento@unamur.be
First published on 4th December 2024
Abstract
The effect of conformational dynamics and solvent interactions on the second-order nonlinear optical (NLO) responses of the open and closed forms of a donor–acceptor Stenhouse adduct (DASA) are investigated by a mixed quantum/classical computational approach, which couples molecular dynamics (MD) simulations and time-dependent density functional theory (TD-DFT) calculations. The latter are further combined with various solvation schemes, including polarizable continuum models, hybrid QM/MM approaches using either non polarizable or polarizable electrostatic embedding, and QM/QM′ schemes with explicit treatment of a few molecules of the first solvation shell. The performances of the different solvation models are discussed in the context of comparisons with experimental data obtained from hyper-Rayleigh scattering measurements.
Introduction
Organic photochromes that isomerize with large variations in their second-harmonic (SH) optical responses are of growing interest for photonic applications, as they are the active elements of all-optical input/output devices in which UV or visible wavelengths are used to trigger the photo-switching, while lower-energy NIR wavelengths are used for readout. A plethora of molecular nonlinear optical switches (NLOs) have been designed over the past 20 years, mostly by chemically tuning well-known photochromic patterns.1–4 Among this wide variety of systems, reverse photochromes triggered using visible-light such as donor–acceptor Stenhouse adducts (DASAs) offer advantages over more conventional UV-activated photoswitches, as their lower isomerization energies increase their fatigue resistance and can therefore help improve device lifetimes.5–18 As shown in Fig. 1 for a representative system incorporating a N-methylbenzylamine donor and a barbituric acid acceptor group, DASAs reversibly isomerize from a π-conjugated (open) form to a non-π-conjugated cyclic (closed) one upon exposure to visible light, and thermally revert to the initial form in the dark. Recent works combining NIR-range hyper-Rayleigh scattering (HRS) experiments and quantum chemical calculations demonstrated that DASA derivatives behave as highly efficient NLO switches, the π-conjugated form displaying large first hyperpolarizability (β) which cancels out upon cyclization due to the breakdown of the π-electron conjugation.19,20 | ||
| Fig. 1 Photo-switching between the open and zwitterionic closed forms of the investigated DASA derivative, labeled BA4 according to the nomenclature used in ref. 20. | ||
The quest of optimal NLO photoswitches with tailored specifications in terms of wavelength control, photoconversion rates, relative stability of isomeric forms and β contrast, relies heavily on computational chemistry. One of the benefits offered by a computer-aided rational design, consists in the possibility to straightforwardly disentangle the complex interplay among the different factors that may concur to the efficiency of the switches. Such contributions can be either intrinsic to the chromophore molecular structure (e.g. arising from symmetry, chemical substitution or π-electron delocalization), or also induced by external parameters, as the laser probe or environment effects. Given the size of the chromophores of interest for practical applications, the range of first principles methods to calculate first hyperpolarizabilities is in practice restricted to time-dependent density functional theory (TD-DFT) and the related quadratic response methods.21 As a result of the intrinsic nonlocal character of electric field effects and of the fact that the β response of push–pull π-conjugated compounds is associated with excitation-induced/field-induced charge transfer, several benchmark studies have demonstrated that adequate exchange–correlation functionals (XCFs) should contain a substantial amount of Hartree–Fock (HF) exchange, as it displays the correct −1/r asymptotic behavior.22–26 In this regard, the M06-2X global hybrid,27 which contains 54% of HF exchange, has been shown to well reproduce both experimental data and reference ab initio values for a large set of systems including highly dipolar merocyanines.26 Alternatively, range-separated hybrids like CAM-B3LYP,28 in which the Coulomb operator is split into a short-range part associated with local/semilocal exchange and a long-range part associated with HF exchange, have also been shown to predict reliable β values.29–34
Beside the choice of the appropriate DFT approximation, two major challenges still remain for achieving accurate comparisons between computed and experimental results. The first is to take into account the influence of the conformational dynamics of the molecule on the NLO responses. Since in π-conjugated systems NLO responses are largely sensitive to fluctuations in the molecular geometry, quantitative estimates not only require a fine description of the molecular structure, but also, to extract reliable averaged properties, the complete sampling of the conformational space spanned during their dynamics. As shown in recent works,35–38 the most straightforward and computationally affordable strategy for achieving this goal is to combine classical molecular dynamics (MD) simulations with TD-DFT calculations, in so-called “sequential MD + QM” procedures.39–43 Using the system schematized in Fig. 1 as a working example (labeled as BA4 according to the nomenclature used in ref. 20), we recently showed that taking structural dynamics into account considerably increases the first hyperpolarizability of the NLO-active open form compared with TD-DFT calculations performed on the equilibrium structure, and provides an average β value in better agreement with experimental data.43 We also showed that this large enhancement is correlated with the changes in the bond order alternation along the π-conjugated triene bridge linking the amine donor and the barbituric acid acceptor. Concretely, structural distortions take the molecule out of its cyanine-type equilibrium geometry, move the bond order alternation away from its zero value and therefore increase the second-order NLO response.
The second computational challenge stands in the accurate description of environment effects. Since HRS experiments are performed in solution and not in vacuo, the interactions between the NLO chromophore and the solvent need to be appropriately addressed. Most often, solute–solvent interactions are treated by using polarizable continuum models (PCM),44 in which the solvent is approximated as a structureless polarizable continuum, only characterized by its macroscopic dielectric permittivity ε, which depends on the frequency of the applied electric field. These models have the advantage to be computationally efficient and to reliably describe the polarization effects due to the surrounding solvent molecules. However, the lack of an explicit treatment of weak yet specific noncovalent interactions might be detrimental to quantitative predictions of the NLO responses of solvated chromophores. In this work, we further investigate the NLO responses of the photochromic system sketched in Fig. 1, focusing on the effects of solute–solvent interactions. Implicit approaches, which are discussed in a first part, are compared to hybrid solvation schemes based on either QM/MM or QM/QM′ methodologies. The relevance of the approximations inherent in these different calculation schemes is discussed in the context of comparisons with experimental data. In particular, we decipher the relevance of introducing local field corrections in the calculation and/or in the experimental determinations of the NLO responses.
Investigated NLO properties and computational methods
Second harmonic responses of molecules in solution
The molecular electronic structure is strongly affected by the embedding solvent, which can significantly alter the properties of solvated molecules. Indeed, solute–solvent interactions might lead to a reorganization of the electron densities of both the solute and, mainly, the nearest solvent molecules. This topic has been widely studied over many decades within several approximations.45–50 Such electronic reorganization can be conceptually understood using a simple model, which approximates the solvent as an isotropic continuum (with a given dielectric constant) around a cavity hosting the solute. For the sake of simplicity, the following discussion assumes that the solute reduces to a point dipole (in the center of a spherical cavity), but the scheme can be straightforwardly generalized to a solute having electronic and nuclear distributions (in a molecular shape cavity). The solute–solvent interaction is described using a classical electrostatic formalism, leading to the so-called reaction field (![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) R0), which depends on the dipole moment of the solute in the solution (
R0), which depends on the dipole moment of the solute in the solution (![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) solute):
solute):![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) R0 = fR0 R0 = fR0![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) solute solute | (1) |
![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) M) oscillating at a frequency ω interacts with the solute–solvent system, the local field (
M) oscillating at a frequency ω interacts with the solute–solvent system, the local field (![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) L) acting on the solute includes three contributions: (i)
L) acting on the solute includes three contributions: (i) ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) R0, which is always present, but also (ii) the induced reaction field originating from the induced dipole moment oscillating at the fundamental and harmonic frequencies of the Maxwell field (
R0, which is always present, but also (ii) the induced reaction field originating from the induced dipole moment oscillating at the fundamental and harmonic frequencies of the Maxwell field (![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) RI = fRI
RI = fRI![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) solute, with fRI the induced-reaction field tensor), and (iii) a contribution due to the screening of
solute, with fRI the induced-reaction field tensor), and (iii) a contribution due to the screening of ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) M, which creates the so-called “cavity field” (
M, which creates the so-called “cavity field” (![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) C = fC
C = fC![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) M, with fC the cavity field tensor). So, this local field has been historically expressed in different ways, e.g., by collecting the reaction field factors, fR = fR0 + fRI, and adding the cavity contribution fC, or by simply assuming a general fL tensor:
M, with fC the cavity field tensor). So, this local field has been historically expressed in different ways, e.g., by collecting the reaction field factors, fR = fR0 + fRI, and adding the cavity contribution fC, or by simply assuming a general fL tensor: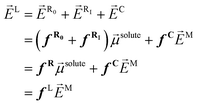 | (2) |
On this basis, the molecular optical properties of the solute have been obtained using perturbation theory by expanding the molecular polarization in terms of the electric field ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) X, where X = L, C, M:
X, where X = L, C, M:
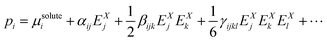 | (3) |
![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) M are often referred to as “effective” properties (αeff,βeff,γeff,⋯). From a computational point of view, self-consistent reaction field (SCRF) methods expand the molecular polarization in terms of
M are often referred to as “effective” properties (αeff,βeff,γeff,⋯). From a computational point of view, self-consistent reaction field (SCRF) methods expand the molecular polarization in terms of ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) C, as the reaction field contributions (
C, as the reaction field contributions (![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) R0 +
R0 + ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) RI) are intrinsically included in the self-consistent procedure. Thus, the corresponding properties have been labeled “cavity” properties (αcav,βcav,γcav,⋯) and they relate to the effective properties by fC. Besides, “solute” properties (αsol,βsol,γsol,⋯) were defined by Wortmann51 by considering the perturbation of the static reaction field associated with the permanent dipole moment.
RI) are intrinsically included in the self-consistent procedure. Thus, the corresponding properties have been labeled “cavity” properties (αcav,βcav,γcav,⋯) and they relate to the effective properties by fC. Besides, “solute” properties (αsol,βsol,γsol,⋯) were defined by Wortmann51 by considering the perturbation of the static reaction field associated with the permanent dipole moment.
The (hyper)polarizabilities and the local field factors all depend on the oscillating frequency of the Maxwell field, which, for simplicity, has not yet been explicitly introduced in the equations. A detailed derivation of the relationships between the effective and cavity responses can be found in ref. 47, 48, and 51. Alternatively, the harmonic contributions of eqn (3) can be collected [pi(t) = p0i + pωi![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ωt) + p2ωi
cos(ωt) + p2ωi![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(2ωt) + ⋯] and associated with the optical responses. Truncating the pnωi harmonic responses up to the first order allows51 for expressing the second harmonic generation (SHG) first hyperpolarizability tensor [β(−2ω;ω,ω)] as:
cos(2ωt) + ⋯] and associated with the optical responses. Truncating the pnωi harmonic responses up to the first order allows51 for expressing the second harmonic generation (SHG) first hyperpolarizability tensor [β(−2ω;ω,ω)] as:
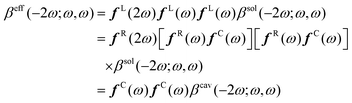 | (4) |
Second harmonic responses as determined by hyper-Rayleigh scattering measurements
For a two-component chromophore/solvent (here BA4/chloroform) system, the intensity of the harmonic scattered light (IVV2ω) is proportional to the sum of both contributions. Considering a linear polarization of the incident laser beam at a given angle Ψ and a scattered light collection perpendicular to the incident direction with a vertical (V) polarization (i.e. at 90° along the laboratory Z axis), it yields:53–55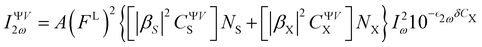 | (5) |
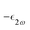 is the molar extinction coefficient at frequency 2ω, δ the optical path length, and CX the concentration) accounts for possible absorption losses at the second harmonic wavelength. FL is a local field correction that implicitly contains both reaction and cavity field effects. In experimental works, it is usually approximated using the Lorentz–Lorenz spherical cavity expression, which involves the refractive index of the solvent at the optical frequencies ω and 2ω:
is the molar extinction coefficient at frequency 2ω, δ the optical path length, and CX the concentration) accounts for possible absorption losses at the second harmonic wavelength. FL is a local field correction that implicitly contains both reaction and cavity field effects. In experimental works, it is usually approximated using the Lorentz–Lorenz spherical cavity expression, which involves the refractive index of the solvent at the optical frequencies ω and 2ω: | (6) |
C ΨVS and CΨVX in eqn (5) correspond to the orientational averages of the spherical components of the molecular first hyperpolarizability tensor of the solvent and solute, respectively.
In practice, the chromophore contribution to the harmonic light intensity ((FL)2|βX|2CΨVX) can be determined by using either the so-called internal or external reference method.53,55 The former consists in using a series of different solute concentrations NX and a solvent whose contribution is known. The chromophore contribution is then determined from the slope of the quadratic coefficient IΨV2ω/Iω2 as a function of NX. In the cases where the solvent has negligible or no quadratic NLO response, the external reference method is applied, which uses as reference an additional chromophore with known hyperpolarizability in the same solvent. Because of the presence of the local field correction in eqn (5), the chromophore contribution can be interpreted as an effective response. However, it is important to note that, when relying to the internal reference method, the experimental protocol used to determine the chromophore's NLO response in HRS experiments leads to the cancellation of this local field correction (see ESI† for details). Nevertheless, regardless of the reference (internal or external) method used, HRS experiments are calibrated with respect to an absolute reference. The nature of the response measured for the chromophore thus depends on the nature of the response of the reference system used for calibration. In the present case, HRS experiments were calibrated based on the incoherent NLO response of liquid chloroform, which is itself calibrated with respect to the β value of liquid carbon tetrachloride used as absolute reference (see the ESI†), and can be assumed to provide effective quantities.
Furthermore, using different polarization angles Ψ gives access to different orientational invariants. Using Ψ = 90° (i.e. a Vertical–Vertical geometry) allows to determine |βX|2CVVX ≡ 〈βZZZ2〉, while using Ψ = 0° (i.e. a Horizontal–Vertical geometry) provides |βX|2CHVX ≡ 〈βZXX2〉. Ultimately, these two quantities are used to define the total HRS hyperpolarizability βHRS and the depolarization ratio DR:
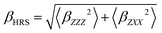 | (7) |
| DR = 〈βZZZ2〉/〈βZXX2〉 | (8) |
The relations between 〈βZZZ2〉 and 〈βZXX2〉 and the calculated molecular β-tensor components, first derived by Bersohn et al.,56 are provided in ESI.† All β values reported in this study are given in atomic units (1 a.u. of β = 3.63 × 10−42 m4 V−1 = 3.2063 × 10−53 C3 m3 J−2 = 8.641 × 10−33 esu) and assume a Taylor series expansion (T convention57) of the molecular induced dipoles with respect to the external electric fields, as done in eqn (3). Since it is important for the forthcoming discussions, more details on the experimental determination of βHRS and DR for the BA4 derivative are given in the ESI.†
Computational methods
The equilibrium geometries of the open and closed forms of BA4 were optimized at the DFT level using the M06-2X XCF with the aug-cc-pVDZ basis set. Dispersion effects were accounted for by means of the Grimmes D3 correction58 and solvent effects (here chloroform) by using the solvation model based on density (SMD).59 As described in our previous work,43 the influence of the thermalized conformational dynamics on the HRS responses (βHRS and DR, eqn (7) and (8)) was addressed by performing TD-DFT calculations on structural snapshots saved at regular time intervals of classical MD trajectories. Specifically-tailored force fields were parameterized and validated according to the Joyce protocol60–62 in order to finely reproduce the geometrical features, potential energy surfaces and NLO responses of both isomers in chloroform solution. For more details, the reader is referred to ref. 43. In the present work, the NLO responses of the open and closed isomers were calculated both in the gas phase and in solution, based either on their equilibrium structures or on the statistical set of structures provided by MD runs, in order to address the interplay between structural dynamics and solvent effects. Average values and standard deviations of the NLO responses are calculated from the distributions generated by the sequential MD + QM procedure. The standard deviation represents the fluctuations of the computed property over time due to the different geometrical arrangements and surrounding of the chromophore. It can be directly related to the spectral broadening of the responses and is associated with the statistical error of the mean by a factor of , where N is the number of sampled configurations (N = 1000 in this study).63–65
, where N is the number of sampled configurations (N = 1000 in this study).63–65
Calculations of the NLO responses were carried out at the M06-2X or CAM-B3LYP level, in association with the 6-311+G(d) basis set. An incident wavelength of 1300 nm was used as in the experiments.20 Solvent effects were described using the three different computational strategies described below, namely (i) polarizable continuum models, (ii) hybrid schemes combining quantum chemistry and classical (non)polarizable embedding (QM/MM), and (iii) hybrid schemes combining two different QM levels (QM/QM′) within the own N-layered integrated molecular orbitals and molecular mechanics (ONIOM)66 approach. PCM-like and ONIOM calculations were performed with the Gaussian16 package.67 QM/MM calculations were carried out with the Dalton program.68
In the frame of PCM, a set of apparent surface charges (ASC)44 self-consistently computed during the optimization of the solute wavefunction gives rise to ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) R0 (always present) and
R0 (always present) and ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) RI (present only in the case of an
RI (present only in the case of an ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) perturbation). Therefore, PCM provides cavity properties which intrinsically include reaction field effects, so that the PCM values do not require any further correction using fR0 or fRI factors. In addition, cavity field effects (CFEs) can also be taken into account when calculating response properties of solvated molecules using continuum models. The evaluation of CFEs has been introduced in the PCM framework and implemented in Gaussian16 by Cammi and coworkers,47,72 as an additional apparent surface charge distribution at the cavity surface that leads to an effective dipole moment entering in the solute Hamiltonian. These effects can be switched on in Gaussian16 by using the CavityFieldEffects option. In that case, the CFEs are included on top of
perturbation). Therefore, PCM provides cavity properties which intrinsically include reaction field effects, so that the PCM values do not require any further correction using fR0 or fRI factors. In addition, cavity field effects (CFEs) can also be taken into account when calculating response properties of solvated molecules using continuum models. The evaluation of CFEs has been introduced in the PCM framework and implemented in Gaussian16 by Cammi and coworkers,47,72 as an additional apparent surface charge distribution at the cavity surface that leads to an effective dipole moment entering in the solute Hamiltonian. These effects can be switched on in Gaussian16 by using the CavityFieldEffects option. In that case, the CFEs are included on top of ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) R0 and
R0 and ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) RI, and therefore, effective responses are calculated. In order to address the magnitude of CFEs on the HRS responses of the two isomeric forms of BA4, TD-DFT calculations were performed with and without using the CavityFieldEffects option.
RI, and therefore, effective responses are calculated. In order to address the magnitude of CFEs on the HRS responses of the two isomeric forms of BA4, TD-DFT calculations were performed with and without using the CavityFieldEffects option.
Hereafter, the nomenclature METHOD[SOLV] is used to indicate the level of calculation, where METHOD is either DFT (i.e. the calculations are performed on the equilibrium structure only) or MD + DFT (i.e. the calculations are performed on the snapshots extracted from the MD runs). SOLV is either IEF-PCM (abbreviated as PCM) or SMD, while SOLV + CFE indicates that cavity field effects have been taken into account. Gas phase calculations (METHOD[gas]) are also reported for comparison purpose. Note that, as the MD simulations were carried out in the presence of solvent, the MD + DFT[gas] calculations include the mechanical effects due to the solvent molecules. The aim of these calculations is, by comparison with MD + DFT[SOLV] calculations, to assess the electronic polarization effects on the NLO responses of the chromophore, using the same set of geometries.
In addition, the polarization of the solvent molecules due to their interaction with the external electric field can be included in the PE model by using the effective external field (EEF) approximation.50 The expansion in eqn (3) is now written as a function of ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) EEF, which represents the external electric field acting on the isolated supermolecule (composed by the solute molecule surrounded by a shell of classical solvent sites) screened by the solvent molecules. The obtained properties of the solute molecule are, therefore, labeled with EEF (αEEF, βEEF, γEEF, …) and are not directly comparable with those presented at eqn (4). This extension of the PE model is included in Dalton as a modification of the electric dipole moment operator.
EEF, which represents the external electric field acting on the isolated supermolecule (composed by the solute molecule surrounded by a shell of classical solvent sites) screened by the solvent molecules. The obtained properties of the solute molecule are, therefore, labeled with EEF (αEEF, βEEF, γEEF, …) and are not directly comparable with those presented at eqn (4). This extension of the PE model is included in Dalton as a modification of the electric dipole moment operator.
QM/MM calculations were performed here at the CAM-B3LYP/6-311+G(d) level on the structural snapshots extracted from the MD trajectories. The surrounding chloroform molecules were described by using atomic point charges (q) and point polarizabilities (α) as defined by the solvent embedding potential74 (see Table S2 for the parameters, ESI†) and interacting with the solute electronic density through both the EE, PE and PE + EEF schemes. Additionally, convergence tests as a function of the embedding size and number of sampled configurations from the MD trajectory have been addressed in ESI.† Briefly, the reported values were obtained for embeddings comprising all chloroform molecules within a 20 Å radius sphere centered at the center-of-mass of the conformers, and averaged over 1000 configurations.
The QM′ (low) level was selected from benchmark calculations using a small set of snapshots for both the open and closed forms. Reference results were obtained by describing the solvent shell at the same level of approximation as the one used for the inner layer, i.e. M06-2X/6-311+G(d). Then, keeping the M06-2X XCF, the number of Gaussian basis functions has been progressively reduced from 6-311G+(d) to 6-311G(d), 6-31+G(d), 6-31G(d), 6-31G, and to 4-31G. As detailed in ESI,† the best time/accuracy compromise was obtained with the 6-31G(d) basis set, so that the M06-2X/6-31G(d) approximation was selected as the low level in all ONIOM calculations. The ONIOM βijk tensor components are calculated as follows:
| βONIOMijk = βmodelijk(high) + [βrealijk(low) − βmodelijk(low)] | (9) |
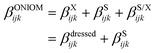 | (10) |
 | (11) |
 | (12) |
Results and discussion
Solvent effects using polarizable continuum models
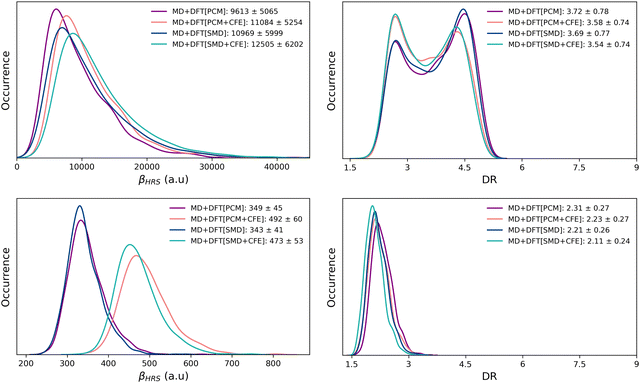
Table 1 reports the βHRS and DR values of the open and closed isomers, calculated using the M06-2X and CAM-B3LYP XCFs on the basis of equilibrium structures (DFT) and snapshots extracted from the MD simulations (MD + DFT). Solvent effects are either ignored [gas] or taken into account using IEF-PCM or SMD schemes. The statistical distributions of the NLO responses calculated with M06-2X using the various MD + DFT[SOLV] schemes are illustrated in Fig. 3 (see Fig. S4 for the CAM-B3LYP distributions, ESI†).| Method | M06-2X | CAM-B3LYP | ||
|---|---|---|---|---|
| Open form | β HRS | DR | β HRS | DR |
| DFT[gas] | 3987 | 4.33 | 3578 | 3.99 |
| DFT[PCM] | 4030 | 2.55 | 4357 | 2.57 |
| DFT[PCM + CFE] | 5301 | 2.57 | 5691 | 2.59 |
| DFT[SMD] | 4860 | 2.69 | 5368 | 2.81 |
| DFT[SMD + CFE] | 6082 | 2.63 | 6635 | 2.72 |
| MD + DFT[gas] | 5423 ± 2334 | 4.20 ± 0.68 | 4991 ± 2129 | 3.97 ± 0.72 |
| MD + DFT[PCM] | 9613 ± 5056 | 3.72 ± 0.78 | 9413 ± 4762 | 3.61 ± 0.75 |
| MD + DFT[PCM + CFE] | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 084 ± 5254 084 ± 5254 |
3.58 ± 0.74 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 947 ± 4940 947 ± 4940 |
3.46 ± 0.70 |
| MD + DFT[SMD] | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 969 ± 5999 969 ± 5999 |
3.69 ± 0.77 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 822 ± 5709 822 ± 5709 |
3.60 ± 0.74 |
| MD + DFT[SMD + CFE] | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 505 ± 6202 505 ± 6202 |
3.54 ± 0.74 | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 417 ± 5903 417 ± 5903 |
3.45 ± 0.70 |
| Closed form | β HRS | DR | β HRS | DR |
|---|---|---|---|---|
| DFT[gas] | 290 | 3.72 | 283 | 3.61 |
| DFT[PCM] | 291 | 2.45 | 285 | 2.38 |
| DFT[PCM + CFE] | 418 | 2.33 | 407 | 2.26 |
| DFT[SMD] | 292 | 2.38 | 287 | 2.33 |
| DFT[SMD + CFE] | 408 | 2.18 | 399 | 2.13 |
| MD + DFT[gas] | 355 ± 72 | 3.60 ± 0.43 | 350 ± 69 | 3.59 ± 0.42 |
| MD + DFT[PCM] | 349 ± 45 | 2.31 ± 0.27 | 345 ± 45 | 2.32 ± 0.27 |
| MD + DFT[PCM + CFE] | 492 ± 60 | 2.23 ± 0.27 | 486 ± 59 | 2.23 ± 0.27 |
| MD + DFT[SMD] | 343 ± 41 | 2.21 ± 0.26 | 340 ± 41 | 2.21 ± 0.25 |
| MD + DFT[SMD + CFE] | 473 ± 53 | 2.11 ± 0.24 | 467 ± 53 | 2.11 ± 0.25 |
One first observes that M06-2X and CAM-B3LYP provide globally similar results. Next, whatever the level of approximation, and whether or not dynamics or solvent effects are taken into account, the βHRS value of the open form is one order of magnitude larger than that of the closed form. For the latter, and with both XCFs, the βHRS values calculated at the DFT[gas], DFT[PCM] and DFT[SMD] levels are very similar. Therefore, while solvent effects have proved to be essential in accurately describing the stability of the closed form10,14,20 (both relative to the non-zwitterionic closed isomer and the open form), they have negligible impact on its NLO response, as far as an implicit solvation model is used. The inclusion of dynamic structural effects does not alter this conclusion, as shown by the quite similar βHRS values calculated at the MD + DFT[gas], MD + DFT[PCM] and MD + DFT[SMD] levels.
Turning to the open form, βHRS values calculated with M06-2X using the equilibrium geometry in the gas phase (DFT[gas]) and using the IEF-PCM solvation scheme (DFT[PCM]) are quasi identical, while the DFT[SMD] value is significantly larger. When using CAM-B3LYP, the solvent effects are more pronounced: with respect to gas phase calculations, βHRS increases by 22% and 50% when using IEF-PCM and SMD, respectively. However, these differences between XCFs cancel out when dynamic effects are taken into account: both XCFs predict a strong increase of βHRS of the solvated chromophore with respect to those of the isolated one. Indeed, MD + DFT[PCM] values are larger than MD + DFT[gas] values by ∼77% with M06-2X and ∼88% with CAM-B3LYP. In addition, both XCFs predict DFT[SMD] βHRS values larger (by ∼20%) than the DFT[PCM] ones, indicating that the difference in the cavity shape between the two solvation models has a sizeable impact on the NLO response of the π-conjugated form. When including structural dynamics effects, the difference in the βHRS values provided by the two solvation models is reduced to ∼15%.
Moreover, as far as cavity field effects are concerned, comparing DFT[SOLV] and DFT[SOLV + CFE] results shows that including them increases the βHRS values of the open form (by ∼30% with PCM and by ∼25% with SMD), regardless of the functional used in the calculations. This enhancement is reduced to ∼15% when including structural dynamics effects. Note that CFEs have even a larger impact on the NLO response of the closed form, βHRS being enhanced by up to ∼40%.
Dynamics and solvent effects also impact the amplitude of the βHRS variation upon the photochemical reaction. For instance, the calculated βHRS(open)/βHRS(closed) ratios using the M06-2X XCF amount to ≈14, 15, and 32 for DFT[gas], MD + DFT[gas], and MD + DFT[SMD], respectively. Finally, solvent effects tend to decrease the depolarization ratio of both the open and closed forms with both tested functionals, SMD providing slightly smaller values than PCM. Contrary to what is found for βHRS, cavity field effects slightly reduce the DR values, with the exception of DFT[PCM] calculations for the open form.
Overall, the results reported in Table 1 allow for disentangling the relative impact of dynamics and solvent effects (labeled as D.E. and S.E., respectively) on the NLO responses of the two isomers. Comparing DFT[gas] to MD + DFT[gas] provides an estimate of the impact of the structural dynamics on the two isomers in the absence of environment. Results computed with M06-2X and CAM-B3LYP are very similar, and show that geometrical fluctuations increase by a factor f(D.E.) = 1.36–1.39 the βHRS value of the conjugated open form, while their impact is less marked (∼22% increase) for the more rigid closed isomer. As mentioned in the introduction, the increase of βHRS with the conformational dynamics was rationalized in our previous work.43βHRS is minimum when the DASA is in its equilibrium geometry because it has a cyanine-type electronic structure; any geometrical distortion thus increases the NLO response. Comparing DFT[gas] to DFT[SOLV] calculations allows to measure the impact of the solvent environment on a fixed (equilibrium) geometry of the chromophores. As discussed above, solvent effects are negligible for the closed form, while for the open form their magnitude depends on the choice of the functional and solvation model. Considering DFT[SMD] calculations, solvent effects tend to enlarge βHRS by a factor f(S.E.) ranging from 1.22 (with M06-2X) to 1.50 (with CAM-B3LYP). Finally, comparing DFT[gas] to MD + DFT[SOLV] calculations allows to size up the combination of environment and structural dynamics effects on the NLO responses. Nevertheless, these f(S.E.) and f(D.E.) factors depend on the order according to which they are taken into account (i.e., S.E. then D.E. or the reverse). Indeed, from DFT[SMD] to MD + DFT[SMD] and employing the M06-2X XCF, βHRS increases by a factor f(D.E.) ≈ 2.3 while from MD + DFT[gas] to MD + DFT[SMD], βHRS is enhanced by f(S.E.) ≈ 2.0. The various scenarios are graphically illustrated in Fig. 4 for M06-2X calculations on the open form (see Fig. S7 for the closed form, ESI†), where the dynamic and solvent effects are quantified by the enhancement factors in the HRS first hyperpolarizability.
Solvent effects using hybrid QM/MM models
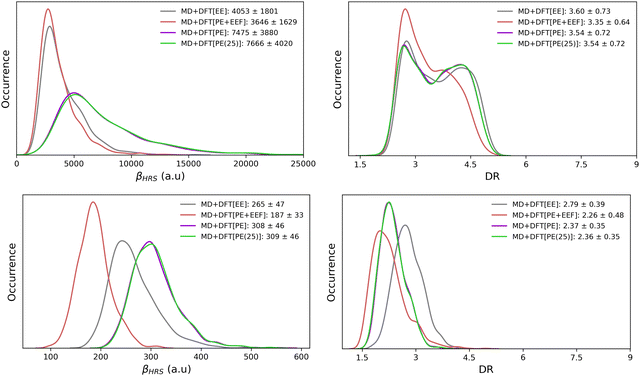
Table 2 reports the βHRS and DR values of the open and closed isomers, calculated at the QM/MM level with QM = CAM-B3LYP/6-311+G(d). Calculations were performed on the snapshots extracted from the MD simulations with different solvation schemes (MD + DFT[SOLV] with SOLV = EE, PE or PE + EEF). The distributions of the calculated NLO responses are illustrated in Fig. 5.| Model | Open | Closed | ||
|---|---|---|---|---|
| β HRS | DR | β HRS | DR | |
| MD + DFT[gas] | 4991 ± 2129 | 3.97 ± 0.72 | 350 ± 69 | 3.59 ± 0.42 |
| MD + DFT[EE] | 4053 ± 1801 | 3.60 ± 0.73 | 265 ± 47 | 2.79 ± 0.39 |
| MD + DFT[PE] | 7475 ± 3878 | 3.54 ± 0.72 | 309 ± 46 | 2.37 ± 0.35 |
| MD + DFT[PE(25)] | 7666 ± 4018 | 3.54 ± 0.72 | 309 ± 46 | 2.36 ± 0.35 |
| MD + DFT[PE + EEF] | 3646 ± 1629 | 3.35 ± 0.64 | 189 ± 32 | 2.25 ± 0.46 |
It is easier to disentangle the different contributions of the solvent onto the solute NLO responses by using QM/MM approaches than by using continuum models. Turning on only the electrostatic embedding (MD + DFT[EE]) accounts for a partial polarization of the solute, while the polarizable embedding (MD + DFT[PE]) includes a self-consistent polarization of both solute and solvent. The βHRS contrast upon photo-switching, i.e. βHRS(open)/βHRS(closed), equals to 15 when using the MD + DFT[gas] and MD + DFT[EE] models, and increases to 25 at the MD + DFT[PE] level. While the surrounding effects on βHRS are qualitatively similar for both isomers, their amplitude is weaker for the closed form. Conversely, the DR value of the open form is less sensitive to the solvation choice, showing variations of at most 0.6.
Let's now focus on how the embedding effects affect βHRS and DR of the open form. The inclusion of a discrete electrostatic embedding (MD + DFT[EE]) leads to a βHRS decrease of about 20% relative to MD + DFT[gas]. The solute polarization due to the MD + DFT[EE] embedding also reduces the ratio between the dipolar and octupolar NLO contributions, as indicated by the 10% decrease of DR. With a polarizable embedding (MD + DFT[PE]), βHRS increases by a factor of 1.5 with respect to MD + DFT[gas] (or by a factor of 1.84 with respect to MD + DFT[EE]). Thus, although weak solute–solvent interactions are expected, the solvent polarization ability (associated with fRI) creates stronger electric fields on the solute, enhancing its first hyperpolarizability responses. However, the DR values are similar to that obtained for MD + DFT[EE], indicating that the stronger intensity of the electric fields in MD + DFT[PE] does not change the directionality of the NLO response. Note that, βHRS values calculated using a slightly extended PE model (MD + DFT[PE(25)]) encompassing solvent molecules up to R = 25 Å differs by less than 3% compared to MD + DFT[PE] (R = 20 Å), indicating that the NLO properties are converged with respect to the size of the environment.
Finally, using the effective external field approach (MD + DFT[PE + EEF]) leads to a decrease of βHRS by about 25% compared to MD + DFT[gas]. In comparison to MD + DFT[PE], MD + DFT[PE + EEF] predicts a decrease of βHRS by about 50%. These opposite effects are related to the definition of the electric field used in the expansion of eqn (3) (see the discussion above). Interestingly, a quasi linear correlation between MD + DFT[PE] and MD + DFT[PE + EEF] βHRS values is obtained by using a linear least-squares fitting for the open form (Fig. S8, ESI†), while the correlation is more diffusive for the closed form (Fig. S8, ESI†). The variations in the βHRS values of the open form are summarized in Fig. 6.
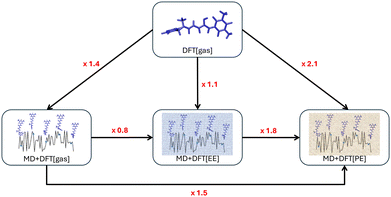 | ||
| Fig. 6 Enhancement factors (in red) of the HRS first hyperpolarizability of the open form computed at the CAM-B3LYP level due to the inclusion of structural dynamic and solvent effects. | ||
Solvent effects using hybrid QM/QM′ models
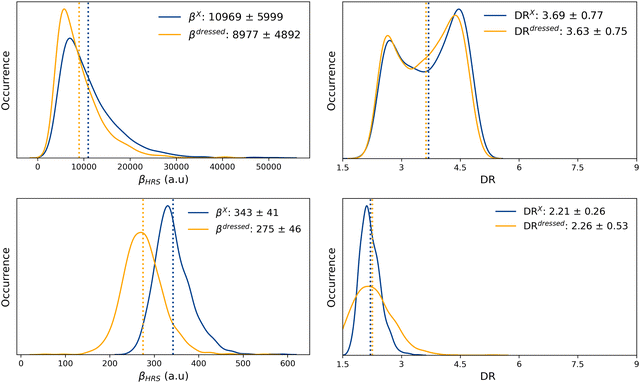
The probability distributions of the total ONIOM hyperpolarizability (βONIOMHRS) calculated for the open and closed isomers using 1000 MD snapshots, as well as the chromophore (βXHRS) and solvent (βSHRS) contributions, are reported in Fig. S17 and S18 (ESI†) together with the corresponding depolarization ratios. The average value and standard deviation of all the NLO responses, as well as of the dressed quantities (eqn (11) and (12)) are reported in Table 3.Despite the distributions of βSHRS values show different patterns for the open and closed forms, their average values as well as their standard deviations remain quite similar. As expected, the average solvent contribution is thus independent from the open or closed state of the chromophore. Moreover, although four times weaker, 〈βSHRS〉 is of the same order of magnitude as the “dressed” contribution of the closed chromophore (〈βdressedHRS〉), consistently with the fact that the SHG signal of the closed form is not detectable experimentally. Reversely, the solvent contribution is negligible compared to the contribution of the open isomer. Interestingly, the ratio Rβ = 〈βdressedHRS〉/〈βXHRS〉 is equal to ∼0.8 for both the closed and open forms, suggesting that solute–solvent interactions reduce by about 20% the NLO responses of the solute in both cases. On the contrary, solute–solvent interactions hardly impact the average DR values, as indicated by the value close to 1.0 of the ratio RDR = 〈DRdressed〉/〈DRX〉 for both open and closed isomers. Moreover, the 〈βONIOMHRS〉 contrast between the open and closed form amounts to ≈30.
Discussion and comparison with experiments
In this last section, the NLO responses obtained using the MD + DFT scheme with various solvation models are discussed and compared to experimental data. The βHRS and DR values of interest are gathered in Table 4, with indication of the type of response they are associated with. Only methods that include a full (self-consistent) treatment of polarization effects between solute and solvent are discussed hereafter.| Model | Response | Open | Closed | |||
|---|---|---|---|---|---|---|
| β HRS | DR | β HRS | DR | η | ||
| MD + DFT[PCM] | Cavity | 9613 ± 5056 | 3.72 ± 0.78 | 349 ± 45 | 2.31 ± 0.27 | 27.5 |
| MD + DFT[PCM + CFE] | Effective | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 084 ± 5254 084 ± 5254 |
3.58 ± 0.74 | 492 ± 60 | 2.23 ± 0.27 | 22.5 |
| MD + DFT[SMD] | Cavity | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 969 ± 5999 969 ± 5999 |
3.69 ± 0.77 | 343 ± 41 | 2.21 ± 0.26 | 32.0 |
| MD + DFT[SMD + CFE] | Effective | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 505 ± 6202 505 ± 6202 |
3.54 ± 0.74 | 473 ± 53 | 2.11 ± 0.24 | 26.4 |
| MD + DFT[PE(25)] | Cavity | 7666 ± 4018 | 3.54 ± 0.72 | 309 ± 46 | 2.36 ± 0.35 | 24.8 |
| MD + DFT[PE + EEF] | EEF | 3646 ± 1629 | 3.35 ± 0.64 | 189 ± 32 | 2.25 ± 0.46 | 19.3 |
| MD + DFT[ONIOM] | Cavity | 8977 ± 4892 | 3.63 ± 0.75 | 275 ± 46 | 2.26 ± 0.53 | 32.6 |
| HRS experiments | Effective | 8600 ± 390 | 5.0 ± 0.3 | — | — | — |
As mentioned above, experimental data considered in this study can be interpreted as effective responses. Therefore, according to the above discussions, they are in principle strictly comparable only with quantities calculated using the MD + DFT[PCM + CFE] and MD + DFT[SMD + CFE] levels, which respectively overestimate βHRS by 29 and 45%. However, the old saying that every situation is more complicated than it seems also applies to HRS experiments. Indeed, coming back to eqn (5), the same local field correction using the Lorentz–Lorenz spherical cavity expression is applied to both the chromophore and solvent contributions, which is a quite crude approximation. Moreover, if a spherical cavity correction can be assumed as reasonable for the closed DASA form which has a compact shape, it is certainly not adapted to the extended open form. Thus, any quantitative comparison between effective theoretical and experimental responses are questionable owing to the dependence of the latter on the models used to account for local field effects. In addition, although eqn (4) clearly establishes the different ways in which the NLO responses can be defined, i.e. as effective, solute or cavity responses, the approximations inherent in the calculation levels and in the models used to convert measured second harmonic intensities into hyperpolarizabilities make this distinction somewhat inoperative. Therefore, all levels of calculation listed in Table 4 are hereafter compared with experimental data. In this regard, it is remarkable that most of the theoretical levels provide βHRS values for the open form within a good range, with the experimental value within the standard deviation of the calculated data. Nevertheless, it should be stressed here that, although compiled in Table 4, the computed standard deviations cannot be compared with the experimental errors. As previously indicated, standard deviations provided by MD + DFT calculations measure the amplitude of the fluctuations of the NLO responses resulting from changes in the conformation and environment of the chromophore during the dynamics, and as such can be related to the spectral broadening of the response, whereas experimental errors, if not systematic, are due to fluctuations in the experimental measurements.
The βHRS values of the open form calculated using implicit solvation at the MD + DFT[PCM] and MD + DFT[SMD] levels overestimate the experimental value by 12% and 26%, respectively. QM/MM calculations at the MD + DFT[PE(25)] level provide smaller first hyperpolarizabilities than the continuum model for both open and closed isomers, as well as a slightly reduced NLO contrast upon switching. This finding is consistent with the results of a previous study of a dithienylethene-indolinooxazolidine biphotochrome, showing that, at optical frequencies, first hyperpolarizabilities calculated with IEF-PCM are larger than those obtained with a QM/MM approach.76 However, both approaches predict similar contrasts, indicating that implicit solvation models such as IEF-PCM are well-suited to describe the variations in the NLO responses of molecular switches. The QM/MM βHRS value of the open form is nevertheless in much better agreement with the experimental data, with an underestimation of only 11%. On the other hand, MD + DFT[PE + EEF] provides a much smaller βHRS value than all other calculation levels, and strongly underestimates the experimental value, suggesting that this approximation is not adequate to reproduce HRS data. However, further studies on other systems are needed to make this conclusion general.
Reversely, the dressed MD + DFT[ONIOM] βHRS response of the open form (βdressedHRS = 8977 ± 4892 a.u.) is in quantitative agreement with experimental measurements (βexpHRS = 8600 ± 390 a.u.). This βdressedHRS value of the open form is ∼20% smaller than the value calculated using a dielectric continuum (βHRS = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 969 ± 5999 a.u.). Nevertheless, explicit solute–solvent interactions also reduce the NLO response of the closed form, leading to a very similar βopenHRS/βclosedHRS contrast as that predicted by the MD + DFT[SMD] approach.
969 ± 5999 a.u.). Nevertheless, explicit solute–solvent interactions also reduce the NLO response of the closed form, leading to a very similar βopenHRS/βclosedHRS contrast as that predicted by the MD + DFT[SMD] approach.
Regarding DR, the distributions of values for the open and closed DASA reported in Fig. 3, 5 and 7 display similar shapes, regardless of the level of calculation. In particular, the DR distributions for the open form exhibit two clear maxima, one centered at ∼2.8 and the other at ∼4.5. The average values also barely depend on the solvent model used. Interestingly, DR distributions obtained from MD + DFT calculations in the gas phase show a much lower peak at DR ∼ 2.8 (Fig. S5, ESI†), and therefore provide significantly larger average values than those predicted using solvated approaches (4.2 ± 0.7 vs. ∼3.6 ± 0.7 at the M06-2X level, see Table 1). This result indicates that the bimodal distributions of DR do not only originate from structural effects but also from solvent polarization effects, which impact the amplitude of the intramolecular charge transfer within the solute. However, further analyses detailed in ESI† do not show any correlation between structural parameters and NLO properties.
Noticeably, whatever the level of approximation, the average DR value calculated for the open form is significantly underestimated compared to the experimental value of 5.0, which indicates that the elongated form of BA4 behaves as an ideal 1D NLO chromophore. One can nevertheless observe that, in the case of MD + DFT[ONIOM] calculations, the peak centered at ∼4.5 in the DR distribution, closer to the experimental value, has a larger intensity than the first peak, which is not the case in the MD + DFT[SMD] and MD + DFT[PE] distributions. Increasing the number of explicit solvent molecules in the MD + DFT[ONIOM] scheme could further accentuate the asymmetry between the two peaks, and improve the agreement with the measured DR by shifting the average toward a larger value. These calculations are however still difficult to perform owing to the large computational needs.
Conclusions
The role of solute–solvent interactions on the NLO responses of the open and closed isomers of a DASA derivative has been investigated using a mixed quantum-classical approach that integrates TD-DFT calculations with classical MD simulations. This computational scheme allows for sampling all representative fluctuations in the molecular conformations at room temperature. TD-DFT calculations were performed in combination with various solvation models of increasing complexity, starting from a comparison of the IEF-PCM and SMD polarizable continuum models. Although the βHRS values computed for the NLO-active open form are in the same range, SMD provides βHRS values ∼20% larger than the PCM ones, which is ascribed to the difference in the cavity shape. Moreover, including cavity field effects in the simulations is shown to increase the βHRS values of the open form by 25–30%, regardless of the solvation model.The performance of more accurate approaches based on a discrete modeling of the environment was then addressed. In a first part, hybrid QM/MM schemes differing by the treatment of the solvent in the MM region were considered, including the simple electrostatic embedding (EE) approximation, which assumes the surrounding molecules as fixed point charges, and the polarizable embedding (PE) model, which includes mutual solute–solvent polarization effects using a self-consistent process. Compared to the PE model, the EE model is shown to significantly underestimate the NLO responses of both open and closed forms of the chromophore, as well as the NLO contrast. This evidences that a complete description of reaction field effects, including the back reaction of the solvent to the electronic polarization of the solute, is necessary for a reliable description of the NLO responses of chromophores in solution. Finally, a further refinement of solvent effects was considered by means of hybrid QM/QM′ calculations, in which implicit solvation models are combined with the explicit QM treatment of a few molecules within the first solvent shell. Compared to pure implicit solvation schemes, including explicit solvent molecules lowers the amplitude of the NLO response, and provides βHRS values lying between those provided by PCM and QM/MM calculations.
This work also highlights the difficulty of comparing computational results to experimental data. The necessary treatments made to extract the first hyperpolarizability of a chromophore from the measured intensity of the second harmonic light scattered by a binary solution, which imply the use of local field corrections based on classical electrostatic and assuming the same spherical shape for the solute and solvent, hampers any quantitative comparisons with calculated values. Nevertheless, it is striking to observe that the sequential MD + DFT scheme provides βHRS distributions that include the experimental value within their standard deviation, regardless of the solvation model, as long as the latter includes mutual polarization effects between the chromophore and its surrounding. Although a finer description of solvent effects may be required in the case of solvents developing specific local interactions with the solute, simple implicit solvation schemes therefore prove reliable for predicting the magnitude and contrast of the NLO responses of solvated photoswitches in non-protic solution, provided that structural fluctuations are taken into account.
Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are indebted to Prof. Vincent Rodriguez for his help in understanding the technical aspects of HRS experiments. F. C. thanks Dr Claudine Katan for helpful discussions. T. N. R. thanks the Fonds de la Recherche Scientifique – FNRS for his postdoctoral researcher position. This work was supported by the French National Research Agency (grant number ANR-20-CE29-0009-01). G. P. thanks the financial support from ICSC – Centro Nazionale di Ricerca in High Performance Computing, Big Data and Quantum Computing, funded by European Union – NextGenerationEU – PNRR, Missione 4 Componente 2 Investimento 1.4. Calculations were performed using the computing facilities provided by the Mésocentre de Calcul Intensif Aquitain (MCIA) of Université de Bordeaux and Université de Pau et des Pays de l’Adour. Computational resources of the Consortium des Équipements de Calcul Intensif (CÉCI, https://www.ceci-hpc.be) were also used, and particularly those of the Technological Platform of High-Performance Computing of UNamur, for which the authors gratefully acknowledge the financial support of the FNRS-FRFC, of the Walloon Region, and of the University of Namur (Conventions no. U.G006.15, U.G018.19, U.G011.22, RW1610468, RW/GEQ2016, and RW2110213). The present research also benefited from computational resources made available on Lucia, the Tier-1 supercomputer of the Walloon Region, infrastructure funded by the Walloon Region under the grant agreement no RW1910247.References
- B. J. Coe, Nonlinear Optical Properties Responses in Molecular Materials, Chem. – Eur. J., 1999, 5, 2464–2471 CrossRef CAS.
- F. Castet, V. Rodriguez, J. L. Pozzo, L. Ducasse, A. Plaquet and B. Champagne, Design and characterization of molecular nonlinear optical switches, Acc. Chem. Res., 2013, 46, 2656–2665 CrossRef CAS PubMed.
- P. Beaujean, F. Bondu, A. Plaquet, J. Garcia-Amorós, J. Cusido, F. M. Raymo, F. Castet, V. Rodriguez and B. Champagne, Oxazines: A New Class of Second-Order Nonlinear Optical Switches, J. Am. Chem. Soc., 2016, 138, 5052–5062 CrossRef CAS PubMed.
- C. Tonnelé and F. Castet, Nonlinear optical properties of spirocyclohexadine photochromes: Insights from DFT calculations, Photochem. Photobiol. Sci., 2019, 18, 2759–2765 CrossRef.
- J. R. Hemmer, S. O. Poelma, N. Treat, Z. A. Page, N. D. Dolinski, Y. J. Diaz, W. Tomlinson, K. D. Clark, J. P. Hooper, C. Hawker and J. Read De Alaniz, Tunable Visible and Near Infrared Photoswitches, J. Am. Chem. Soc., 2016, 138, 13960–13966 CrossRef CAS.
- M. M. Lerch, S. J. Wezenberg, W. Szymanski and B. L. Feringa, Unraveling the Photoswitching Mechanism in Donor–Acceptor Stenhouse Adducts, J. Am. Chem. Soc., 2016, 138, 6344–6347 CrossRef CAS.
- N. Mallo, P. T. Brown, H. Iranmanesh, T. S. C. MacDonald, M. J. Teusner, J. B. Harper, G. E. Ball and J. E. Beves, Photochromic switching behaviour of donoracceptor Stenhouse adducts in organic solvents, Chem. Commun., 2016, 52, 13576–13579 RSC.
- M. Di Donato, M. M. Lerch, A. Lapini, A. D. Laurent, A. Iagatti, L. Bussotti, S. P. Ihrig, M. Medved’, D. Jacquemin, W. Szymański, W. J. Buma, P. Foggi and B. L. Feringa, Shedding Light on the Photoisomerization Pathway of Donor–Acceptor Stenhouse Adducts, J. Am. Chem. Soc., 2017, 139, 15596–15599 CrossRef CAS.
- M. M. Lerch, W. Szymański and B. L. Feringa, The (photo)chemistry of Stenhouse photoswitches: guiding principles and system design, Chem. Soc. Rev., 2018, 47, 1910–1937 RSC.
- M. M. Lerch, M. Di Donato, A. D. Laurent, M. Medved’, A. Iagatti, L. Bussotti, A. Lapini, W. J. Buma, P. Foggi, W. Szymański and B. L. Feringa, Solvent Effects on the Actinic Step of Donor–Acceptor Stenhouse Adduct Photoswitching, Angew. Chem., Int. Ed., 2018, 57, 8063–8068 CrossRef CAS.
- R. F. A. Gomes, J. A. S. Coelho and C. A. M. Afonso, Synthesis and Applications of Stenhouse Salts and Derivatives, Chem. – Eur. J., 2018, 24, 9170–9186 CrossRef CAS PubMed.
- J. R. Hemmer, Z. A. Page, K. D. Clark, F. Stricker, N. D. Dolinski, C. J. Hawker and J. Read De Alaniz, Controlling Dark Equilibria and Enhancing Donor–Acceptor Stenhouse Adduct Photoswitching Properties through Carbon Acid Design, J. Am. Chem. Soc., 2018, 140, 10425–10429 CrossRef CAS.
- C. García-Iriepa, M. Marazzi and D. Sampedro, From Light Absorption to Cyclization: Structure and Solvent Effects in Donor–Acceptor Stenhouse Adducts, ChemPhotoChem, 2019, 3, 866–873 CrossRef.
- H. Zulfikri, M. A. J. Koenis, M. M. Lerch, M. Di Donato, W. Szymański, C. Filippi, B. L. Feringa and W. J. Buma, Taming the complexity of donor–acceptor stenhouse adducts: Infrared motion pictures of the complete switching pathway, J. Am. Chem. Soc., 2019, 141, 7376–7384 CrossRef CAS PubMed.
- M. Ugandi and M. Roemelt, An Ab Initio Computational Study of Electronic and Structural Factors in the Isomerization of Donor–Acceptor Stenhouse Adducts, J. Phys. Chem. A, 2020, 124, 7756–7767 CrossRef CAS PubMed.
- D. M. Sanchez, U. Raucci, K. N. Ferreras and T. J. Martínez, Putting Photomechanical Switches to Work: An Ab Initio Multiple Spawning Study of Donor–Acceptor Stenhouse Adducts, J. Phys. Chem. Lett., 2020, 11, 7901–7907 CrossRef CAS.
- C. Xiong, G. Xue, L. Mao, L. Gu, C. He, Y. Zheng and D. Wang, Carbon Spacer Strategy: Control the Photoswitching Behavior of Donor–Acceptor Stenhouse Adducts, Langmuir, 2021, 37, 802–809 CrossRef CAS PubMed.
- S. W. Connolly, R. Tiwari, S. J. Holder and H. J. Shepherd, A simple strategy to overcome concentration dependence of photoswitching properties in donor–acceptor Stenhouse adducts, Phys. Chem. Chem. Phys., 2021, 23, 2775–2779 RSC.
- C. Tonnelé, B. Champagne, L. Muccioli and F. Castet, Second-order nonlinear optical properties of Stenhouse photoswitches: insights from density functional theory, Phys. Chem. Chem. Phys., 2018, 20, 27658–27667 RSC.
- S. Dubuis, A. Dellai, C. Courdurié, J. Owona, A. Kalafatis, L. Vellutini, E. Genin, V. Rodriguez and F. Castet, Nonlinear Optical Responses of Photoswitchable Donor–Acceptor Stenhouse Adducts, J. Am. Chem. Soc., 2023, 145, 10861–10871 CrossRef CAS PubMed.
- T. Helgaker, S. Coriani, P. Jørgensen, K. Kristensen, J. Olsen and K. Ruud, Recent Advances in Wave Function-Based Methods of Molecular-Property Calculations, Chem. Rev., 2012, 112, 543–631 CrossRef CAS.
- B. Champagne, E. A. Perpète, D. Jacquemin, S. J. A. van Gisbergen, E.-J. Baerends, C. Soubra-Ghaoui, K. A. Robins and B. Kirtman, Assessment of Conventional Density Functional Schemes for Computing the Dipole Moment and (Hyper)polarizabilities of Push-Pull π-Conjugated Systems, J. Phys. Chem. A, 2000, 104, 4755–4763 CrossRef CAS.
- F. A. Bulat, A. Toro-Labbé, B. Champagne, B. Kirtman and W. Yang, Density functional theory (hyper)polarizabilities of push-pull π-conjugated systems: Treatment of exact exchange and role of correlation, J. Chem. Phys., 2005, 123, 014319 CrossRef PubMed.
- K. Y. Suponitsky, S. Tafur and A. E. Masunov, Applicability of hybrid density functional theory methods to calculation of molecular hyperpolarizability, J. Chem. Phys., 2008, 129, 044109 CrossRef.
- L. E. Johnson, L. R. Dalton and B. H. Robinson, Optimizing Calculations of Electronic Excitations and Relative Hyperpolarizabilities of Electrooptic Chromophores, Acc. Chem. Res., 2014, 47, 3258–3265 CrossRef CAS PubMed.
- L. Lescos, S. Sitkiewicz, P. Beaujean, M. Blanchard-Desce, B. Champagne, E. Matito and F. Castet, Performance of DFT Functionals for Calculating the Second-Order Nonlinear Optical Properties of Dipolar Merocyanines, Phys. Chem. Chem. Phys., 2020, 22, 16579–16594 RSC.
- Y. Zhao and D. G. Truhlar, The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other function, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- T. Yanai, D. P. Tew and N. C. Handy, A new hybrid exchange–correlation functional using the Coulomb-attenuating method (CAM-B3LYP), Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- D. Jacquemin, E. A. Perpète, M. Medved’, G. Scalmani, M. J. Frisch, R. Kobayashi and C. Adamo, First hyperpolarizability of polymethineimine with long-range corrected functionals, J. Chem. Phys., 2007, 126, 191108 CrossRef.
- P. A. Limacher, K. V. Mikkelsen and H. P. Lüthi, On the accurate calculation of polarizabilities and second hyperpolarizabilities of polyacetylene oligomer chains using the CAM-B3LYP density functional, J. Chem. Phys., 2009, 130, 194114 CrossRef PubMed.
- S. Borini, P. A. Limacher and H. P. Lüthi, A systematic analysis of the structure and (hyper)polarizability of donor–acceptor substituted polyacetylenes using a Coulomb attenuating density functional, J. Chem. Phys., 2009, 131, 124105 CrossRef.
- V. Parthasarathy, R. Pandey, M. Stolte, S. Ghosh, F. Castet, F. Würthner, P. K. Das and M. Blanchard-Desce, Combination of Cyanine Behaviour and Giant Hyperpolarisability in Novel Merocyanine Dyes: Beyond the Bond Length Alternation (BLA) Paradigm, Chem. – Eur. J., 2015, 21, 14211–14217 CrossRef CAS PubMed.
- V. Parthasarathy, R. Pandey, P. K. Das, F. Castet and M. Blanchard-Desce, Linear and Nonlinear Optical Properties of Tricyanopropylidene-Based Merocyanine Dyes: Synergistic Experimental and Theoretical Investigations, ChemPhysChem, 2018, 19, 187–197 CrossRef CAS PubMed.
- C. Naim, F. Castet and E. Matito, Impact of van der Waals interactions on the structural and nonlinear optical properties of azobenzene switches, Phys. Chem. Chem. Phys., 2021, 23, 21227–21239 RSC.
- K. Pielak, C. Tonnelé, L. Sanguinet, E. Cariati, S. Righetto, L. Muccioli, F. Castet and B. Champagne, Dynamical Behavior and Second Harmonic Generation Responses in Acido-Triggered Molecular Switches, J. Phys. Chem. C, 2018, 122, 26160–26168 CrossRef CAS.
- F. Castet, C. Tonnelé, L. Muccioli and B. Champagne, Predicting the Second-Order Nonlinear Optical Responses of Organic Materials: the Role of Dynamics, Acc. Chem. Res., 2022, 55, 3716–3726 CrossRef CAS.
- C. Naim, R. Vangheluwe, I. Ledoux-Rak, B. Champagne, C. Tonnelé, M. Blanchard-Desce, E. Matito and F. Castet, Electric-field induced second harmonic generation responses of push–pull polyenic dyes: experimental and theoretical characterizations, Phys. Chem. Chem. Phys., 2023, 25, 13978–13988 RSC.
- C. Bouquiaux, P. Beaujean, T. N. Ramos, F. Castet, V. Rodriguez and B. Champagne, First hyperpolarizability of the di-8-ANEPPS and DR1 nonlinear optical chromophores in solution. An experimental and multi-scale theoretical chemistry study, J. Chem. Phys., 2023, 159, 174307 CrossRef PubMed.
- K. J. de Almeida, K. Coutinho, W. B. de Almeida, W. R. Rocha and S. Canuto, A Monte Carlo–quantum mechanical study of the solvatochromism of pyrimidine in water and in carbon tetrachloride, Phys. Chem. Chem. Phys., 2001, 3, 1583–1587 RSC.
- K. Coutinho and S. Canuto, The sequential Monte Carlo-quantum mechanics methodology. Application to the solvent effects in the Stokes shift of acetone in water, J. Mol. Struct. THEOCHEM, 2003, 632, 235–246 CrossRef CAS.
- K. Coutinho, R. Rivelino, H. C. Georg and S. Canuto, The Sequential qm/mm Method and its Applications to Solvent Effects in Electronic and Structural Properties of Solutes, Springer, Dordrecht, 2008, pp. 159–189 Search PubMed.
- N. De Mitri, S. Monti, G. Prampolini and V. Barone, Absorption and Emission Spectra of a Flexible Dye in Solution: A Computational Time-Dependent Approach, J. Chem. Theory Comput., 2013, 9, 4507–4516 CrossRef CAS.
- A. Dellai, C. Naim, J. Cerezo, G. Prampolini and F. Castet, Dynamic effects on the nonlinear optical properties of donor acceptor stenhouse adducts: insights from combined MD + QM simulations, Phys. Chem. Chem. Phys., 2024, 26, 13639–13654 RSC.
- J. Tomasi, B. Mennucci and R. Cammi, Quantum mechanical continuum solvation models, Chem. Rev., 2005, 105, 2999–3093 CrossRef CAS PubMed.
- H. A. Lorentz, The theory of electrons and its applications to the phenomena of light and radiant heat, Reprinted Dover, New York, 1952, edn, 1916 Search PubMed.
- L. Onsager, Electric Moments of Molecules in Liquids, J. Am. Chem. Soc., 1936, 58, 1486–1493 CrossRef CAS.
- R. Cammi, B. Mennucci and J. Tomasi, On the Calculation of Local Field Factors for Microscopic Static Hyperpolarizabilities of Molecules in Solution with the Aid of Quantum-Mechanical Methods, J. Phys. Chem. A, 1998, 102, 870–875 CrossRef CAS.
- P. Macak, P. Norman, Y. Luo and H. Ågren, Modeling of dynamic molecular solvent properties using local and cavity field approaches, J. Chem. Phys., 2000, 112, 1868–1875 CrossRef CAS.
- B. Champagne and B. Kirtman, Handbook of Advanced Electronic and Photonic Materials and Devices, Elsevier, 2001, vol. 9, pp. 63–126 Search PubMed.
- N. H. List, H. J. A. Jensen and J. Kongsted, Local electric fields and molecular properties in heterogeneous environments through polarizable embedding, Phys. Chem. Chem. Phys., 2016, 18, 10070–10080 RSC.
- R. Wortmann and D. M. Bishop, Effective polarizabilities and local field corrections for nonlinear optical experiments in condensed media, J. Chem. Phys., 1998, 108, 1001–1007 CrossRef CAS.
- R. W. Munn, Y. Luo, P. Macák and H. Ågren, Role of the cavity field in nonlinear optical response in the condensed phase, J. Chem. Phys., 2001, 114, 3105–3108 CrossRef CAS.
- E. Hendrickx, K. Clays and A. Persoons, Hyper-Rayleigh Scattering in Isotropic Solution, Acc. Chem. Res., 1998, 31, 675–683 CrossRef CAS.
- F. Castet, E. Bogdan, A. Plaquet, L. Ducasse, B. Champagne and V. Rodriguez, Reference molecules for nonlinear optics: A joint experimental and theoretical investigation, J. Chem. Phys., 2012, 136, 024506 CrossRef PubMed.
- T. Verbiest, K. Clays and V. Rodriguez, Second-Order Nonlinear Optical Characterization Techniques: An Introduction, Taylor & Francis, 2009 Search PubMed.
- R. Bersohn, Y. Pao and H. L. Frisch, Double-Quantum Light Scattering by Molecules, J. Chem. Phys., 1966, 45, 3184–3198 CrossRef CAS.
- H. Reis, Problems in the comparison of theoretical and experimental hyperpolarizabilities revisited, J. Chem. Phys., 2006, 125, 014506 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104 CrossRef.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed.
- I. Cacelli and G. Prampolini, Parametrization and Validation of Intramolecular Force Fields Derived from DFT Calculations, J. Chem. Theory Comput., 2007, 3, 1803–1817 CrossRef CAS PubMed.
- J. Cerezo, G. Prampolini and I. Cacelli, Developing accurate intramolecular force fields for conjugated systems through explicit coupling terms, Theor. Chem. Acc., 2018, 137, 80 Search PubMed.
- G. Prampolini, L. G. D. Silveira, J. G. Vilhena and P. R. Livotto, Predicting Spontaneous Orientational Self-Assembly: In Silico Design of Materials with Quantum Mechanically Derived Force Fields, J. Phys. Chem. Lett., 2022, 13, 243–250 CrossRef CAS PubMed.
- J. P. Bergsma, P. H. Berens, K. R. Wilson, D. R. Fredkin and E. J. Heller, Electronic spectra from molecular dynamics: a simple approach, J. Phys. Chem., 1984, 88, 612–619 CrossRef CAS.
- K. J. de Almeida, K. Coutinho, W. B. de Almeida, W. R. Rocha and S. Canuto, A Monte Carlo–quantum mechanical study of the solvatochromism of pyrimidine in water and in carbon tetrachloride, Phys. Chem. Chem. Phys., 2001, 3, 1583–1587 RSC.
- J. Cerezo, F. Santoro and G. Prampolini, Comparing classical approaches with empirical or quantum-mechanically derived force fields for the simulation electronic lineshapes:application to coumarin dyes, Theor. Chem. Acc., 2016, 135, 143 Search PubMed.
- L. W. Chung, W. M. C. Sameera, R. Ramozzi, A. J. Page, M. Hatanaka, G. P. Petrova, T. V. Harris, X. Li, Z. Ke, F. Liu, H.-B. Li, L. Ding and K. Morokuma, The ONIOM Method and Its Applications, Chem. Rev., 2015, 115, 5678–5796 CrossRef CAS PubMed.
- M. J. Frisch, et al., Gaussian 16 Revision C.01, Gaussian Inc., Wallingford CT, 2016 Search PubMed.
- K. Aidas, et al., The Dalton quantum chemistry program system, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 269–284 CAS.
- F. Castet, A. Gillet, F. Bureš, A. Plaquet, V. Rodriguez and B. Champagne, Second-order nonlinear optical properties of Λ-shaped pyrazine derivatives, Dyes Pigm., 2021, 184, 108850 CrossRef CAS.
- A. Dellai, C. Courdurié, S. Dubuis, K. S. Kaka, B. Champagne, L. Vellutini, E. Genin, V. Rodriguez and F. Castet, Second harmonic responses of clickable azobenzenes in solution: Comparative Hyper-Rayleigh scattering and density functional theory studies, Dyes Pigm., 2023, 220, 111744 CrossRef CAS.
- V. Postils, Z. Burešová, D. Casanova, B. Champagne, F. Bureš, V. Rodriguez and F. Castet, Second-order nonlinear optical properties of X-shaped pyrazine derivatives, Phys. Chem. Chem. Phys., 2024, 26, 1709–1721 RSC.
- R. Cammi, C. Cappelli, S. Corni and J. Tomasi, On the Calculation of Infrared Intensities in Solution within the Polarizable Continuum Model, J. Phys. Chem. A, 2000, 104, 9874–9879 CrossRef CAS.
- J. M. Olsen, K. Aidas and J. Kongsted, Excited states in solution through polarizable embedding, J. Chem. Theory Comput., 2010, 6, 3721–3734 CrossRef CAS.
- M. T. P. Beerepoot, A. H. Steindal, N. H. List, J. Kongsted and J. M. H. Olsen, Averaged Solvent Embedding Potential Parameters for Multiscale Modeling of Molecular Properties, J. Chem. Theory Comput., 2016, 12, 1684–1695 CrossRef CAS PubMed.
- T. Vreven, B. Mennucci, C. Silva, K. Morokuma and J. Tomasi, The ONIOM-PCM method: Combining the hybrid molecular orbital method and the polarizable continuum model for solvation. Application to the geometry and properties of a merocyanine in solution, Chem. Phys., 2001, 115, 62–72 CAS.
- J. Quertinmont, B. Champagne, F. Castet and M. Hidalgo Cardenuto, Explicit versus Implicit Solvation Effects on the First Hyperpolarizability of an Organic Biphotochrome, J. Phys. Chem. A, 2015, 119, 5496–5503 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Details on experimental and computational methodologies; additional results obtained using the PCM, QM/MM and QM/QM′ solvation models. See DOI: https://doi.org/10.1039/d4cp03674c |
| This journal is © the Owner Societies 2025 |