Mechanical properties and thermal stability of ultrathin molybdenum nanowires

Abstract

The most stable structures of three ultrathin molybdenum (Mo) nanowires were predicted by the simulated annealing basin-hopping method (SABH) with the penalty algorithm. The predicted structures of Mo nanowires indicate that, at this small scale, they do not possess the BCC configuration found in bulk Mo material. Mechanical properties including the Young's modulus, yielding stress, and strength of these wires were determined by a tensile test after the analysis of the stress–strain profiles. In addition, in order to understand the feasibility of application of these Mo nanowires in nano-devices, their thermal stability was also investigated at room temperature (300 K) by MD simulation.

---

1. Introduction

Nanotechnology has rapidly developed in recent years, with one-dimensional nanostructures being investigated widely because they possess broad applications in different areas, such as for nano-mechanical^1,2 and nano-electronic devices.³ Metallic nanowires with well-defined structures of several nanometers have been fabricated by using different methods. As the scale decreases to nanometer size, the nature of physical and transport phenomena will dramatically change due to the surface effect, small size effect and quantum effect.^4–6 Recently, numerous metal one-dimensional nanostructures have been produced experimentally by new nanomaterial fabrication techniques; the Mo nanowire is one such novel material utilizing this nanotechnology generation process. Bulk Mo is a brittle metal which possesses high tensile strength, excellent mechanical properties,^1,4,7,8 thermal stability,^9,10 and chemical and electronic^3,11,12 properties such that it could be used in many different applications. Michael et al.¹³ employed electrodeposition to build metallic Mo nanowires with a diameter of 15 nm to 1 mm, and experiments on the conductivity, mechanical flexibility, and resiliency produced results similar to the bulk material. Kim et al.¹⁴ used Mo nano-pillars of 1 μm to examine the tension and compressive behaviour at an orientation of 〈001〉, and found that the Mo nano-pillars have an entangled dislocation substructure after deformation. Andrej et al.¹⁵ utilized directional solidification and subsequent electrochemical processing to synthesize Mo nanowires, showing that the Mo nanowire had high aspect ratios such that they can be applied to sensor and field emission devices. As shown in these studies mentioned above, the advantageous properties of Mo materials allow for use in many different applications; accordingly, the Mo nanowires have also been investigated in simulation studies to understand their structural and mechanical properties. Peng et al.¹ performed the deformation mechanisms of Mo nanowires by MD simulation, and they found that both the orientation and lateral size will affect plastic deformation in the nanowires. In addition, Wang et al.¹⁶ observed single-crystalline Mo nanowires that demonstrate two phase transitions during the uniaxial tensile process. Furthermore, Li et al.¹⁷ found two kinds of structure transformations during the stress deformation process of polycrystalline Mo nanowires. One is the BCC configuration transforming into other configurations then changing into the FCC or HCP configuration; another is the FCC configuration converting into other configurations then changing into the BCC or HCP configuration. These excellent natural properties allow for better energy storage and applications than current smart materials.

In Mo material research, some thermal dynamics studies have investigated the physical properties of metallic nanowires. For example, Shibuta et al.⁹ found that different cooling rates will form Mo nanoparticles of different crystalline structures. Kim et al.¹⁰ used oxidation enthalpies to indicate the thermal stabilities of Mo nanoclusters and estimate the corresponding bulk value. Although the mechanical properties of the Mo nanowire have been reviewed, research on their thermal properties is still lacking. Therefore, the feasibility of the Mo nanowire is also a main discussion point in this work.

As described above, the Mo nanowires have excellent characteristics and have been widely investigated in different applications. To the best of our knowledge, the mechanical properties of ultrathin molybdenum nanowires have not been studied in previous experimental or theoretical studies. In order to understand the structural and thermal properties of molybdenum nanowires, the SABH method was first used to predict possible configurations of Mo nanowires and nanotubes. In this study, we construct different sized nanowires and analyze their mechanical properties by MD simulation.

2. Simulation model

So far, many global optimization algorithms had been successfully developed to obtain such a favourable configuration, such as genetic algorithms (GA),¹⁸ the big-bang method (BB),¹⁹ and the simulated annealing basin-hopping (SABH)²⁰ global optimization algorithm. In the present study, the multi-shell structures of the ultrathin Mo nanowires were constructed by SABH. In the traditional basin-hopping method, a conjugate gradient method was used to reach the local minimum, where a new geometry was generated. In our SABH method, the conjugate gradient method was replaced by the limited memory BFGS method (LBFGS),²¹ which can be used to simulate a system consisting of a large number of atoms. Furthermore, using the LBFGS method in the BH method is faster than the conjugate gradient method for a larger system. Furthermore, the simulated annealing²¹ (SA) method was also implemented with the BH method to become a SABH method, which includes a wider searching domain within the potential energy surface. Therefore, we adopt the LBFGS method to stabilize the system and reach the local minimum in the SABH method. Because the searched configurations are near-spherical in geometry in three-dimensional space, the penalty function should be added and combined with SABH to construct the one-dimensional nanowire structures.

To describe the interaction between Mo atoms, we need employ the potential function to construct nanowire structures. The EAM²² and tight-binding potentials²³ are two popular functions to describe the transition function, and these two potentials are also developed to simulate alloy systems. Some material properties have been predicted through simulations of the alloy systems, and those simulations have presented dramatic results.²⁴ However, the tight-binding many-body potential²³ uses a simple formula that can save more computational time. The interaction between two Mo atoms depends not only on the distance between them, but also on their local environment. The tight-binding potential was originally derived by Slater from the method of linear combination of atomic orbital (LCAO), or tight-binding (TB) method.²⁵ Consequently, Slater first named this form the tight-binding potential, which can model the interaction between the atoms without directly considering the electronic interaction. The prediction of some properties by the TB method has proven to be more accurate for some transient metals in past studies.^23,26 This model commences by summing the band energy, which is characterized by the second moment of the d-band density of state, and a pair wise potential energy of the Born–Mayer type and is expressed in the following form:

where ξ is an effective hopping integral, r_ij is the distance between atom i and j, and r₀ is the first-neighbour distance. The parameters of the tight-binding potential relating to Mo in current simulation are listed in Table 3. Furthermore, the interaction force on atom i is given by

It is known that the potential function parameters are very important for the accuracy of construction. In this paper, we try to fit the tight-binding potential parameters. The force-matching method (FMM) was used to determine the potential function parameters. FMM is based on the variable optimization process of an objective function, which is constructed by the summation of squares of differences between the atomic forces obtained by a potential function and the corresponding atomic forces by ab initio or density functional theory (DFT) calculations. The original FMM minimizes the following objective function, Z(α):

where α, M and N_k are the entire set of potential parameters, the number of atomic configurations, and the number of atoms in a configuration k, respectively. F_ki(α) is the force acting on atom i of the configuration k, which is computed from the potential parameter α. F⁰_ki is the corresponding referenced force calculated from the ab initio or density functional theory (DFT) calculation approach. Except for atomic forces of all optimized structures, the binding energy, bulk moduli, and elastic constants of crystal reference structures were also included in our object function. The crystal configurations including pure element systems were used to prepare the reference data for FMM. All required reference data were directly prepared by the DFT calculation. For the binding energies, the Dmol³ package was used, and the elastic constants and bulk moduli were prepared by the CASTEP package. The generalized gradient approximation (GGA) with the parameterization of Perdew–Wang generalized-gradient approximation (PW91) was used for both Dmol³ and CASTEP. For Dmol³ settings, all electron calculations with a double numeric plus polarization basis set DND were used. The energy tolerance in the self-consistent field calculations was 1 × 10⁻⁶ eV, and the energy, force and atomic displacement tolerances for the ionic step were 1 × 10⁻⁵ eV, 2 × 10⁻³ eV Å⁻¹ and 5.00 × 10⁻³ Å. For the settings of CASTEP, the energy tolerance in the self-consistent field calculations was 5 × 10⁻⁷ eV per atom and the convergence conditions for the ionic step were set as 1 × 10⁻⁶ eV per atom for the energy change, 2 × 10⁻³ eV per Å for the force change, 1 × 10⁻⁴ Å for the atomic displacement, and 490 eV for the plane-wave cutoff energy. To ensure the accuracy in the DFT calculations of Mo crystal structures, Table 1 lists the lattice constants as well as the cohesive energies by DFT calculations and from the corresponding measured data. It can be seen that the lattice constants and binding energies obtained by Dmol³ are very close to the experimental values.²⁷ Table 2 illustrates the elastic constants, bulk moduli, and shear moduli of Mo unit cells after the CASTEP geometry optimization, and the corresponding experimental data are very similar. The calculated lattice constants by the Dmol³ calculation and the elastic constants for the CASTEP calculation results are good enough to obtain the mechanical properties of Mo systems to prepare the FMM reference data.

Table 1 The comparisons of the lattice constant and binding energy between experiment and DFT calculation results for bulk Mo

Element	Methods	Lattice constant (Å)	Error (%)	Cohesive energy (eV per atom)	Error (%)
Mo	Exp.^27	3.15		6.82
	DFT	3.17	0.77%	6.81	−0.18%
	MS (bulk parameter)^28	3.12	−0.99%	7.08	3.74%
	MS (fitting parameter)	3.17	0.72%	6.83	0.09%

---

Table 2 The experiment and DFT calculation values (by CASTEP) of lattice constant (a), elastic constants (C₁₁, C₁₂, C₄₄), bulk modulus (B) and shear modulus (S) for Mo unit cells

Element	Property	Exp.^27	DFT	Error (%)
Mo	a (Å)	3.15	3.15	0.11%
	C11 (GPa)	450	493.10	9.58%
	C12 (GPa)	173	114.77	33.66%
	C44 (GPa)	125	168.42	34.74%
	B (GPa)	230	275.50	19.78%
	S (GPa)	126	130.00	3.18%

---

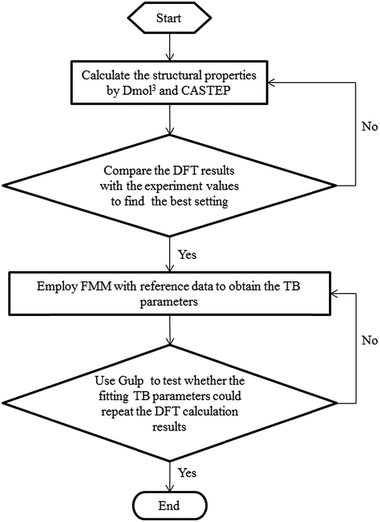
In the fitting process, the TB parameters of Mo were modified by FMM to minimize the discrepancies between the reference data and the data calculated by using the fitted parameters. For improving the many-body effect in the TB potential, the binding energies of Mo structures with one-atom defects were also included. During the fitting process, the object function optimization was conducted by the general utility lattice program (GULP). The BB method was used to randomly change the values of TB parameters after each optimization process. The Monte Carlo method was adopted to find the parameter set which can obtain the global minimal value of the objective function. After the fitting process, a set of potential parameters can be obtained, which can be seen in Table 3 for TB potentials. In addition, the parameters of the tight-binding potential fitting process framework are shown in Fig. 1. To make certain that our fitting parameters are more appropriate than the bulk parameters which had been fitted in a former study by Karolewski,²⁸ the lattice constant and cohesive energy of bulk Mo were examined with the relative parameters by molecular statics simulation. In Table 1, the results with fitting parameters of lattice constant and cohesive energy in this work are shown as 3.173 Å and 6.826 Å, which are both consistent with the experimental data of 3.15 Å and 6.82 Å,²⁷ respectively. A comparison of the two sets of parameters indicates that our fitting parameters are closer to experimental results and can be adapted to describe the interaction in Mo materials.

Table 3 The bulk and fitting tight-binding potential parameters

	A (eV)	ξ (eV)	p	q	r0 (Å)
Mobulk^28	0.21	2.50	10.01	2.05	2.72
Mofitting	0.62	4.04	8.74	3.70	2.70

---

Fig. 1 The fitting process flow chart.

Because the structures which are searched in the SABH method are prone to spherical symmetry, we need to employ the penalty function to constrain all atoms within a cylindrical space with a specific cross-section radius in the process of the structure search. The formula of the penalty method is shown as follows:

p_i = [x_i² + y_i² − r₀²]² (5)

where E_i is the energy of atom i calculated by the TB potential, and p_i is the penalty potential; p_i is applied to atom i only if atom i is located outside the radius of the nanowire (r₀). The terms x_i and y_i are the coordinate of atom i in x and y directions, and c is defined to discriminate whether the atom is in the wire radius range. The value c = 200 was adopted in this SABH calculation. In fact, c is independent of final structure as long as the c value is large enough. The formula of the penalty potential can be defined as any form which provides a constraint condition of the simulation model.

In summary, we combine SABH with a penalty method to construct the ultrathin nanowires by different initial conditions. Next, optimizations are implemented by the DFT calculations, and three global minimum structures are finally obtained in this calculation process. Nanowires consisting of 140, 196, and 432 Mo atoms are optimized with 250 000 steps by LBFGS method and are used to search the stable Mo nanowire structures. Then the ordered segment of Mo nanowires obtained by SABH method is used to estimate the information of its unit cell. The structures of these ultrathin Mo nanowires appear to consist of coaxial tubes with n, n′, n′′, n′′′ atom rows, where n is the atom number of outer shell, n′ is of the first shell, and n′′ is second shell. The radii of multi-shell Mo nanowires range from 3.0 Å to 5.0 Å. The three types of nanowires are named 6-1, 10-4, and 10-5-1 Mo nanowires, and are shown in Fig. 2(a–c). At a diameter of 3.0 Å, the 6-1 multi-shell configuration has a single central strand of Mo atoms and a tube structure formed of the atom wires coiled around the axis of the tube. The 4.2 Å diameter 10-4 multi-shell configuration has two tube structures forming the atom wires coiled around the axis of the tube. The 5.0 Å diameter 10-5-1 multi-shell configuration has a single central strand of Mo atoms and two tube structures forming the atom wires coiled around the axis of the tube.

Fig. 2 The three types of Mo nanowires: (a) 6-1, (b) 10-4, and (c) 10-5-1.

The MD simulation was performed by the large-scale atomic/molecular massively parallel simulator (LAMMPS) developed by Plimpton and co-workers.²⁹ During MD simulation, the loading state of the tensile test was as follows: the loading is applied along the axis, and the axial direction is set with periodic boundary condition at a strain rate of 1% ps⁻¹. The equilibration step allows the lattice to reach a temperature of 300 K, and the Nosé–Hoover method is adopted to ensure a constant system temperature during the simulation process.

The normal strain in the axial direction ε is calculated as:

where l_z(t) is the instantaneous length in the axial direction and l_z(o) is its initial length. Thus, the stress–strain relationship of the ultrathin Mo nanowires is determined by means of eqn (6).

3. Results and discussion

In this work, three types of multi-shell nanowires with different diameters were constructed by the simulated annealing basin-hopping method with tight-binding potential. This study addresses tensile tests of ultrathin Mo nanowires with 6-1, 10-4, and 10-5-1 structures. To understand the width effect on the mechanical property and the deformation mechanism in this work, three different widths of Mo nanowires are held at equilibrium at 300 K for 50 ps. The calculated results of radius, cohesive energy, Young's modulus, yielding stress, yielding strain, and maximum strain for three types of nanowires are listed in Table 4.^30,31 The radii of 6-1, 10-4, and 10-5-1 structures are 3.0 Å, 4.2 Å, and 5.0 Å, respectively. The stress–strain relationship is studied to understand the effects of stress on nanowire structure. For clarity, the corresponding stress–strain profiles for the tensile process for different types of nanowires are shown in Fig. 3(a–c). It is clear that as wire width decreases, the maximum stress and the slope of stress–strain curve increase. In the first stage, the stress increases linearly with slight fluctuation until the yielding occurs at yielding strain. The Young's modulus can be determined from the results of tensile test for the strain of 2% using linear regression. The calculated results of Young's modulus for three types of nanowires are listed in Table 4. When the area cross-section is smaller, the Young's modulus and the yielding stress are higher. This tendency variation of the mechanical property as a function of the width of an Au nanowire has been verified by our previous study.³²

Table 4 Mechanical properties of different Mo nanowire under tensile test

	Radius (Å)	Cohesive energy (eV)	Young's modulus (GPa)	Yielding stress (GPa)	Yielding strain	Maximum strain
6-1	3.0	5.85	466.58	35.45	0.10	0.3
10-4	4.2	6.13	341.58	16.50	0.07	0.6
10-5-1	5.0	5.81	233.59	18.60	0.13	0.6
Bulk		6.82^29	329^30

---

Fig. 3 (a–c) Stress–strain relationship for (a) 6-1, (b) 10-4, and (c) 10-5-1 multi-shell structures.

The elongation deformations of morphology for the three Mo nanowires are shown in Fig. 3. All structures show an initial decreasing slope with increasing strain. Fig. 3(a) shows the structure does not present significant deformation before approaching the maximum stress of 35.45 GPa. As the tensile progress continues, the nanowire breaks suddenly. Fig. 3(b) shows the variation of stress–strain distribution of 10-4 multi-shell structure at loading as well as a decrease in the ultimate stress with increasing strain. After approaching the maximum stress of 16.50 GPa, the stress fluctuation also exhibits an increase in the frequency and a decrease in the amplitude depending on the strain variation. When the strain reaches 0.51, the nanowire forms a multi-shell structure as in a 6-1 nanowire, and then breaks rapidly. In Fig. 3(c), the stress of the largest size 10-5-1 nanowire reaches 18.60 GPa during the tensile progress, showing a local peak where the nanowire forms a 6-1 multi-shell structure and then breaks. Among the three types of Mo nanowire, it can be observed that 10-4 and 10-5-1 nanowire possess excellent ductility when the strain increases and the necking region of the multi-shell structures gradually grows.

In order to ensure the feasibility of Mo nanowires for nano-device applications, an examination of their thermal stabilities is necessary. Fig. 4(a)–(c) shows the relative energy of the three types of Mo nanowires at 300 K as temperature increases, performed by MD simulation in the canonical ensemble (NVT). The equilibration step is maintained for 50 ps at 300 K to obtain the stable structure. The Nosé–Hoover method is adopted to ensure a constant system temperature during the simulation process. Temperature was elevated from 300 to 3000 K with a heating rate of 2 K ps⁻¹. To indicate the temperature at which the nanowires underwent a serious structural deformation, the parameter ΔR was used, and is defined as:

where r_ij ≠ r_cut, r_ij is the distance between atoms i and j, and n is the total number of atoms. The value of r_cut is the half of the box length in the axial direction. The variation of this parameter is very sensitive to the structural change and any distinct increase or decrease in ΔR indicates the structure is undergoing a considerable deformation. In Fig. 4(a), the relative energy of the 6-1 nanowire increases with increasing temperature, and ΔR fluctuates at an average value until about 1230 K. At this temperature range, the 6-1 nanowire undergoes thermal vibration without any structural damage. When the temperature is continuously elevated higher than 1230 K, ΔR displays a prominent drop, indicating that the 6-1 nanowire begins to display structural damage.

Fig. 4 The variations in relative energy and ΔR during the temperature elevation process for (a) 6-1, (b) 10-4, and (c) 10-5-1 multi-shell structures.

The same heating process was adopted to examine the thermal stability of the 10-4 nanowire, and the results are shown in Fig. 4(b). The parameter of ΔR shows a distinct decrease once the temperature is higher than 1530 K, indicating the occurrence of nanowires deformation. The structure undergoes serious deformation when the temperature is elevated further. Furthermore the thermal property of 10-5-1 structure is represented in Fig. 4(c); it shows that the 10-5-1 multi-shell structure is not more stable than the other types in the heating process. At 2090 K, the significant deformation of the nanowire is confirmed by heating process. After the thermal stability examination of the 6-1 and 10-5-1 nanowires, these findings imply that these two wires are still very stable at temperatures higher than room temperature and can be further considered for their potential use. Snapshots of the 6-1, 10-4, and 10-5-1 multi-shell structures at their respective melting points are shown in Fig. 5(a)–(c).

Fig. 5 Snapshots of the 6-1, 10-4, and 10-5-1 multi-shell structures at their respective melting points.

4. Conclusions

This work fits a set of tight-binding potential parameters to accurately describe the interactions of Mo materials. Furthermore, the SABH method with the fitting parameters is employed to construct three types of Mo nanowires. Significantly, the structures of the ultrathin Mo nanowires are different from BCC crystal in their mechanical, electronic and thermal properties. The results indicate that the nanowire possess a multi-shell configuration under a radius of 5.0 Å. Furthermore, we use MD to simulate the mechanical properties including the Young's modulus, yielding stress, and the strength of these wires was determined by the tensile test after the analyses of the stress–strain profiles. The Young's moduli of two sizes of Mo nanowires are larger than the bulk result, decreasing in the larger nanowire. To understand the stability of the ultrathin Mo nanowire, thermal analyses are investigated by MD simulation; the results indicate melting points are distributed over 1230–2090 K. Although the melting point temperatures are smaller than bulk value, the feasibility of ultrathin Mo nanowires still possesses advantages in the applications of industry and other heat-resistant elements. We hope these simulation results support the study of Mo nanowire structural and mechanical properties and provides a perspective for future experiments.

Acknowledgements

The authors would like to thank the (1) Ministry of Science and Technology of Taiwan, under Grant no. NSC 101-2221-E-492-006-MY3, NSC 101-2628-E-110-003-MY3, and MOST 103-2221-E-239-012, (2) National Center for High-performance Computing, Taiwan, and (3) National Center for Theoretical Sciences, Taiwan.

References

1. P. Wang, W. Chou, A. Nie, Y. Huang, H. Yao and H. Wang, Molecular dynamics simulation on deformation mechanisms in body-centered-cubic molybdenum nanowires, J. Appl. Phys., 2011, 110, 093521.
2. Y.-H. Wen, R. Huang, Z.-Z. Zhu and Q. Wang, Mechanical properties of platinum nanowires: An atomistic investigation on single-crystalline and twinned structures, Comput. Mater. Sci., 2012, 55, 205–210.
3. Y. Shen, S. Deng, Y. Zhang, F. Liu, J. Chen and N. Xu, Highly conductive vertically aligned molybdenum nanowalls and their field emission property, Nanoscale Res. Lett., 2012, 7, 463.
4. J.-Y. Kim and J. R. Greer, Size-dependent mechanical properties of molybdenum nanopillars, Appl. Phys. Lett., 2008, 93, 101916.
5. A. S. Schneidera, C. P. Frickb, E. Arztc, W. J. Cleggd and S. Korte, Philos. Mag. Lett., 2013, 93, 331–338.
6. H. Liang, M. Upmanyu and H. Huang, Size-dependent elasticity of nanowires: Nonlinear effects, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 241403.
7. J.-Y. Kim, D. Jang and J. R. Greer, Tensile and compressive behavior of tungsten, molybdenum, tantalum and niobium at the nanoscale, Acta Mater., 2010, 58, 2355–2363.
8. S. J. Wang, H. Wang, K. Du, W. Zhang, M. L. Sui and S. X. Mao, Deformation-induced structural transition in body-centred cubic molybdenum, Nat. Commun., 2014, 5, 3433.
9. Y. Shibuta, A Molecular Dynamics Study of Effects of Size and Cooling Rate on the Structure of Molybdenum Nanoparticles, J. Therm. Sci. Technol., 2012, 7, 45–57.
10. H. K. Kim, S. H. Huh, J. W. Park, J. W. Jeong and G. H. Lee, The cluster size dependence of thermal stabilities of both molybdenum and tungsten nanoclusters, Chem. Phys. Lett., 2001, 354, 165–172.
11. Y. Shen, N. Xu, S. Deng, Y. Zhang, F. Liu and J. Chen, A Mo nanoscrew formed by crystalline Mo grains with high conductivity and excellent field emission properties, Nanoscale, 2014, 6, 4659–4668.
12. V. Meunier, H. Muramatsu, T. Hayashi, Y. A. Kim, D. Shimamoto and H. Terrones, et al., Properties of One-Dimensional Molybdenum Nanowires in a Confined Environment, Nano Lett., 2009, 9, 1487–1492.
13. M. P. Zach, K. H. Ng and R. M. Penner, Molybdenum Nanowires by Electrodeposition, Science, 2000, 290, 2120–2123.
14. J.-Y. Kim and J. R. Greer, Tensile and compressive behavior of gold and molybdenum single crystals at the nano-scale, Acta Mater., 2009, 57, 5245–5253.
15. A. Kovic, A. Znidarsic, A. Jesih, A. Mrzel, M. Gaberscek and A. Hassanien, A novel facile synthesis and characterization of molybdenum nanowires, Nanoscale Res. Lett., 2012, 7, 567.
16. J. Wang, W. Hu, X. Li, S. Xiao and H. Deng, Strain-driven phase transition of molybdenum nanowire under uniaxial tensile strain, Comput. Mater. Sci., 2010, 50, 373–377.
17. X. Li, W. Hu, S. Xiao and W.-Q. Huang, Stress-induced phase transformation and strain rate effect in polycrystalline Mo nanowires, Phys. E, 2011, 43, 1131–1139.
18. D. E. Goldberg and J. H. Holland, Mach. Learn., 1988, 3, 95–99.
19. J. Ellis, J. S. Hagelin, D. V. Nanopoulos, K. Olive and M. Srednicki, Nucl. Phys. B, 1984, 238, 453–476.
20. M. Iwamatsu and Y. Okabe, Chem. Phys. Lett., 2004, 399–400.
21. D. C. Liu and J. Nocedal, Math. Program., 1989, 45, 503–528.
22. M. S. Daw and M. I. Baskes, Phys. Rev. Lett., 1983, 50, 1285–1288.
23. V. Rosato, M. Guillope and B. Legrand, Philos. Mag. A, 1989, 59, 321–326.
24. X. Zhou, J. Zimmerman, B. Wong and J. Hoyt, An embedded-atom method interatomic potential for Pd–H alloys, J. Mater. Res., 2008, 23, 704–718.
25. J. C. Slater and G. F. Koster, Simplified LCAO method for periodic potential problem, Phys. Rev., 1954, 94, 1498–1524.
26. F. Cleri and V. Rosato, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 22–33.
27. C. Kittel, Introduction to Solid State Physics, 2005.
28. M. A. Karolewski, Tight-binding potentials for sputtering simulations with fcc and bcc metals, Radiat. Eff. Defects Solids, 2001, 153, 239–255.
29. S. Plimpton, Fast parallel algorithms for short-range molecular dynamics, J. Comput. Phys., 1995, 117, 1–9.
30. B. Johansson and N. Mårtensson, Phys. Rev. B: Condens. Matter Mater. Phys., 1980, 21, 4427.
31. C. Durkan, A. Ilie, M. S. M. Saifullah and M. E. Welland, Appl. Phys. Lett., 2002, 80, 4244.
32. S.-P. Ju, J.-S. Lin and W.-J. Lee, Nanotechnology, 2004, 15, 1221–1225.

---