Probing adsorption interactions of lignin derivatives in industrial zeolite catalysts through combining vibrational spectroscopy and ab initio calculations

Abstract

Understanding the adsorption interactions of lignin derivatives within established industrial zeolite catalysts is crucial for optimising the catalytic conversion of more sustainable, non-fossil, lignin-based feedstocks into value-added fuels and chemicals using established infrastructure. The adsorption of key lignin pyrolysis oil derivatives (p-cresol, m-cresol, o-cresol, anisole and guaiacol) within commercial samples of zeolite catalysts relevant to lignin conversion (HY, H-Beta, H-ZSM-5) was investigated using a combination of inelastic neutron spectroscopy (INS) and density functional theory (DFT) calculations. A wide range of adsorption energies were calculated (−97 to −157 kJ mol⁻¹), with stronger adsorption observed in the smaller pored zeolites, correlated to the increased stabilising interactions with the pore walls. The observed variations in adsorption strengths among lignin derivatives were attributed to the specific adsorption geometries influenced by their functional groups, and the molecular shape relative to the pore topography at the location of the acid site, with each derivative, except anisole, favouring a configuration involving two hydrogen bonds via a five-membered ring structure. Using DFT phonon calculations to directly reproduce the INS spectra, we assigned vibrational modes for each structure within the 200–1200 cm⁻¹ range. Changes in peak positions, intensities, and widths between the INS spectra of the pure compounds and those dosed in the zeolite catalysts were explained through comparisons with the phonon calculated spectra. Specific peaks attributed to H-bonding group vibrations showed the most significant shifts in H-ZSM-5, followed by H-Beta and HY, correlated with a breaking of adsorbate–adsorbate interactions in the smaller-pored zeolites due to strong interactions with the acidic sites and pore walls. In contrast, the larger HY supercages facilitated increased adsorbate–adsorbate interactions, resulting in spectra more similar to those of the pure compound systems. Where the pure compound contained no H-bonding groups, in the case of anisole, the vibrations attributed to the methoxy group bend decreased in intensity upon adsorption. This effect was due to H-bonding to acid sites, and was amplified in the smaller pores of H-ZSM-5. The study brings insights into factors governing the interactions fundamental to the conversion of biomass based feedstocks with established catalytic technologies.

---

Sustainability spotlight

The sustainable transformation of lignin-based biomass into value-added fuels and chemicals is critical for reducing dependency on fossil fuels and advancing a circular bioeconomy. Our work provides key insights into the adsorption interactions of lignin derivatives within industrial zeolite catalysts, enabling the optimisation of catalytic processes for biomass conversion using existing infrastructure. By elucidating the role of pore topology and functional group interactions, we help to lay groundwork for improving catalyst design and efficiency, contributing to the transition to sustainable energy and chemical systems. This research aligns with UN Sustainable Development Goals 7 (Affordable and Clean Energy), 12 (Responsible Consumption and Production), and 13 (Climate Action) by promoting renewable feedstocks, reducing waste, and advancing technologies that mitigate environmental impacts.

1 Introduction

Lignin-based feedstocks have the potential to play a significant role in decarbonising the chemical industry by replacing fossil sources for the production of higher value chemicals or fuels. However, their high O : C and C : H ratios must first be reduced to improve their processability (where a high oxygen content leads to increased polarity and reactivity, making the feedstock more prone to degradation, side reactions and polymerisation) and energy density.¹ Deoxygenation of lignin is hindered by high aromaticity, with the C–OH bond in phenolic species being approximately 84 kJ mol⁻¹ stronger than in aliphatic compounds.² A promising solution involves acidic zeolite catalysts, which can reduce oxygen content under milder conditions and are part of an established infrastructure from their long standing use in the petrochemical industry.^3–5

Oxygen-containing functional groups often form hydrogen bonds (H-bonds) with zeolite Brønsted acid sites (BASs) and these are typically the first to be removed during lignin conversion. However, zeolites are prone to deactivation as lignin-based compounds, such as phenol, strongly adsorb to zeolite acid sites, reducing catalytic activity and micropore volume.^6–8 This leads to coke formation through re-polymerisation reactions influenced by the zeolite pore size. Phenolic compounds with two oxygen atoms, such as guaiacol, are more resistant to hydrodeoxygenation (HDO) and prone to coke formation.⁹ Therefore, understanding how the presence and nature of oxygen-containing functional groups, coupled with how the differing molecular shapes of lignin derivatives controls their adsorption and selectivity within the zeolite catalyst pores, is crucial for developing more effective lignin conversion processes.

Infra-red (IR) spectroscopy is frequently employed to study the nature of such adsorption. The adsorption of benzene in ZSM-5 was investigated by IR, which found that BASs were the most common adsorption site.¹⁰ Even in siliceous ZSM-5, adsorption to the framework oxygen was observed instead of adsorbate clustering, which was also observed with cresol adsorption in Na–X.¹¹ IR spectral peaks, representing the hydroxy asymmetric stretching and deformation modes of cresol molecules, showed major shifts upon adsorption into the zeolite, increasing for the p-isomer over the m-isomer due to stronger interactions with the framework. In contrast, adsorption studies of xylene isomers (containing no hydroxy groups) in zeolite Beta showed an increase in uptake for m-xylene over p-xylene, attributed to increasing polarity and increasing kinetic diameters.¹² Vibrational spectroscopy has also been used to study guaiacol vibrational bands pre- and post-loading into shape-selective clay catalysts, which showed shifting of several vibrational modes to lower energies indicating the presence of significant adsorption interactions.⁹

In recent years, ab initio modelling techniques have become increasingly accurate in predicting adsorption energies of aromatics and lignin derivatives in zeolite catalysts,^13,14 displaying significant transferability and allowing the inclusion of important dispersion/non-bonding interactions with the zeolite which profoundly impact the energetics.¹⁵ For example, benzene adsorption onto HY gave a binding energy of −63 kJ mol⁻¹, compared to an experimental value of −64 kJ mol⁻¹.¹⁶ Adsorption energies are strongly dependent on the molecule/pore shape relationship and resulting adsorption configurations, based on electronic (mesomeric and inductive) and steric (local zeolite topography and molecule shape and size) effects.⁸ In siliceous zeolites, adsorption of aromatic molecules through their ring hydrogen atoms or π-interactions, observed for phenol (−62 kJ mol⁻¹), toluene (−55 kJ mol⁻¹) and benzene, is far weaker than adsorption through H-bonding interactions with the phenol hydroxy group (−115 kJ mol⁻¹), with the hydroxy group giving shorter H-bonding distances also.^16,17 Even stronger H-bonding interactions were observed for phenol and catechol to BASs in acidic zeolites through the formation of two simultaneous H-bonds.^18–20 Comparing the adsorption of different functional groups, guaiacol exhibited preferential bonding to BASs through its hydroxy group, rather than its methoxy group.²¹ The adsorption selectivity can also be tuned upon variation of the Si/Al ratio, with stronger adsorption of anisole observed upon additional interactions with a second, nearby BAS.²²

Beyond the effects of molecular species and their associated functional groups, the zeolite pore shape and diameter greatly affect adsorption strengths.²³ More negative adsorption energies are typically observed in smaller-pored zeolites due to the ‘confinement effect’ or ‘nest effect’.²⁴ This phenomenon has been observed both experimentally^25,26 and computationally,^27,28 where the catalytic properties may be improved through optimising the pore environment in terms of the shape, bonding configuration, and electronic structure of the adsorbate.²⁶ The bonding strength increases as the molecular size approaches that of the zeolite pore or with molecules of sufficient polarisability, demonstrated by the increasing adsorption strengths of n-butanol within the smaller pores of H-ZSM-5 compared to HY,²⁹ or when at sufficient loadings to fill the zeolite pores.²⁸ Isomer shape effects are also important to consider, shown for xylene isomers where the E_ads varied by 150 kJ mol⁻¹ due to differences in steric constraints, which in turn, controlled the selectivity of their disproportionation products.³⁰

Neutron spectroscopy techniques are particularly suited to both probing the catalyst structure/active sites³¹ and the behaviour of adsorbed molecules in the catalyst micropores, the unique sensitivity of neutron spectroscopy to ¹H allows for deep penetration of the neutron into the inorganic zeolite catalyst structure to interact only with the organic adsorbates.³² Inelastic neutron scattering (INS, vibrational spectroscopy with neutrons) differs from photon-based techniques in that they do not exhibit cut-offs due to lattice absorption, and are not subject to selection rules meaning all modes are allowed and the entire vibrational range is accessible (0–4000 cm⁻¹).³³ The technique has been shown to be particularly revealing in probing H-bonding species interacting with acidic sites in zeolite catalysts, and how this changes with zeolite framework.³⁴ Direct interpretation of INS spectra may be achieved through the quantitative comparison between vibrational bands obtained using static density functional theory lattice dynamics calculations,³⁵ either carried out using period boundary conditions or with more recently developed QM/MM based methodologies.³⁶ As INS measurements are typically taken at base temperatures (<10 K), they are particularly suited to comparisons with low energy configurations calculated by DFT, as opposed to higher temperature experiments which may benefit more from dynamic sampling of potential energy surfaces. At lower temperatures, entropic contributions are less significant due to reduced configurational mobility, making static energy considerations more critical, and the free energy more closely resembles the electronic energy.¹⁵

In this study, we capitalise on the strong complementarity of INS and QM modelling to analyse the vibrational modes and adsorption energies of cresol isomers, anisole and guaiacol when adsorbed in industrial samples of acidic zeolites HY (Si/Al = 15), H-Beta (Si/Al = 12.5) and H-ZSM-5 (Si/Al = 11.5), where significant differences in diffusivity of the proposed lignin derivatives have been observed.^37,38 The combination gives us significant insight into the adsorption interactions of the different derivatives in the differing pore systems, verified by the experimentally observed changes in vibrational bands at low energy, which were directly reproduced by the QM modelling.

2 Experimental

2.1 Inelastic neutron scattering experiments

Zeolite HY (Si/Al = 15), NH₄-beta (Si/Al = 12.5) and NH₄-ZSM-5 (Si/Al = 11.5) were obtained from Zeolyst International (CBV720, CP814E* and CBV2314 respectively). These industrial reference materials have been extensively characterised in the literature and we have compiled a table of their textural properties including the internal/external surface areas along with micropore and mesopore volume in Table S1 in Section S1.† The ammonium form zeolites were calcined in air by heating from room temperature to 523 K at a rate of 2 K min⁻¹ and then to 823 K at 5 K min⁻¹ and held for 4 hours. The zeolites were dried under vacuum at 523 K for ca. 18 hours.³⁹ After cooling, zeolite samples which were to be studied for lignin derivative adsorption were loaded gravimetrically with either 10% wt. of each cresol isomer, guaiacol or anisole (each obtained from Sigma-Aldrich) under an argon atmosphere. The lignin derivative liquids were applied drop-wise to the zeolite powders and the mixtures were ground using a pestle and mortar. The loaded samples were then heated at 353 K for ca. 18 hours in an airtight container sealed with copper rings to allow diffusion into the zeolite pores.⁴⁰ Then, under an argon atmosphere, 10 g of each zeolite sample without the presence of adsorbate was transferred after the drying step, and 11 g of each organic dosed sample was then loaded into large, flat, aluminium cans sealed with indium wire. 1 g of the pure lignin derivatives (cresol isomers, guaiacol and anisole) were loaded by the same method into smaller cells.

The INS measurements were carried out at base temperature (<20 K) and were performed on the TOSCA instrument, an indirect geometry spectrometer at the ISIS Pulsed Neutron and Muon Source, Rutherford Appleton Laboratory.^41,42 MANTID⁴³ neutron scattering analysis software was used to convert the neutron time-of-flight data to energy transfer values and sort the data to generate the presented spectra.

2.2 Density functional theory calculations

2.2.1 Building and testing the zeolite framework models. For each different zeolite, the unit cell was obtained from the results of a single crystal X-ray study and optimised, with the cell parameters (Å) listed in Table S2.†^44–48 For zeolite HY, to minimise the calculation expense, rather than use the larger cubic crystal system with a Fd3m space group, the primitive triclinic crystal system of 144 atoms was used. For zeolite H-Beta, a primitive unit cell of polymorph A composed of 192 atoms was used, with tetragonal symmetry (P4₁22), shown in Fig. 1(b). For H-ZSM-5 the primitive monoclinic unit cell formed below 340 K⁴⁹ with P2₁/n11 symmetry, containing 288 atoms was used. The structures are shown with their non-equivalent T-sites (T = Si or Al) labelled in Fig. 1, there is only one unique T-site in HY.

Fig. 1 Primitive unit cells of HY, H-Beta and H-ZSM-5 and their labelled O/T-sites (T = Si or Al). Si shown in blue, oxygen in red.

The experimental systems had high acid site densities (Si/Al from 11.5–15.0) and relatively high adsorbate loadings (10% wt.) with the aim of better representing catalytic systems and increasing the scattering signal. There were more acid sites present compared to adsorbates, with 1.13, 1.33 and 1.45 acid sites available per cresol/anisole molecule in HY, H-Beta and H-ZSM-5 and 1.30, 1.53 and 1.66 acid sites available per guaiacol molecule.

Brønsted acid sites (BASs) are heterogeneously distributed in zeolites. The most common Al T-site positions in each structure vary with synthesis conditions^50–52 and with the experimental⁵³ and theoretical techniques applied, as well as complications related to thermodynamic or kinetic control,^50,52 with some evidence even suggesting that protons can hop between adjacent oxygen atoms.^54–56 It is important to note that the density of acid sites in specific confining regions of each framework may vary with zeolite structure. However, to match the experimental Si/Al ratios in the simulations, the primitive cell systems of HY, H-Beta and H-ZSM5 would require approximately 3, 4, and 7 BASs, respectively. When designing the systems for each zeolite structure, a range of potential T-sites were assessed and the configurations giving the best agreement between simulated and experimental vibrational spectra were selected. The precise nature of how we generate the simulated spectra is described in detail in the next section, as well as in the ESI.† However, these modelled spectra take into account the neutron scattering cross-section, resolution effects and combination/overtone bands that are present in the experimental spectra. A detailed discussion including assessment of differing combinations/locations of acid sites and the agreement with experimental INS spectra can be found in Section S3.† In zeolite Y, all T-sites are crystallographically equivalent and the proton placed at O1, protruding into the super cage^55,57–59 showed good agreement with the experimental spectra as shown in Fig. 2. It is of course important to note that HY catalysts with Si/Al = 15 will contain significant defects related to extra-framework aluminium (EFAL) or silanol nests⁶⁰ due to the dealumination process necessary to achieve this composition in FAU zeolites. Indeed, recent characterisation of our exact material revealed 11.2% of the Al in the sample was octahedral EFAL.⁶¹ Given the majority of Al is found to remain as framework Al, and given the acceptable agreement of the theoretical and experimental INS spectra, we consider our approximation of the unit cell for HY to be adequate.

Fig. 2 Simulated spectra of each zeolite containing a single acid site (dashed lines) and their matches to the corresponding experimental INS spectra (solid lines).

The BAS placed at T1 in both H-Beta^50,62–64 and H-ZSM-5 (ref. 49 and 65) gave the best match to the INS experiment, where the comparison between the calculated and experimental INS spectra are shown in Fig. 2. The phonon calculated INS spectra sampling a range of different acid site locations are displayed and detailed in Section S3.†

Based on the zeolite unit cell structures, a loading of 10% wt. Corresponds to 2–3, 3–4 and 5–6 cresol molecules loaded into HY, H-Beta and H-ZSM-5, respectively. Hence, we tested our DFT modelled systems to assess the impact of increasing the loading of cresol molecules on the reproduction of experimental INS spectra as discussed in Section S3.3.† In our preliminary calculations comparing the phonon calculated INS spectra as a function of p-cresol loading in each zeolite, we observed good agreement between the experiment and the simulations which contain a single acid site bound to a single cresol molecule. We could therefore confidently proceed by modelling a single adsorbate per zeolite unit cell.

The acid sites and adsorbates were added into the unit cells using Materials Studio⁶⁶ and viewed in VESTA,⁶⁷ with all images taken from VESTA. The simulated vibrational spectra were produced using the AbINS plug-in in MANTID^43,68 and the dynamics were viewed using Jmol.⁶⁹

2.2.2 Running the simulations. The calculations were performed using the VASP code,^70–72 applying the PAW method.⁷³ As with previous work looking into molecular adsorption onto zeolite BASs,⁵⁷ the PBE exchange correlation density functional⁷⁴ with the D3 dispersion correction⁷⁵ was applied, which has been shown to reproduce trends in adsorption energies with zeolite topology.⁷⁶ Functional choice showed little difference to the modelled vibrational spectra, as discussed in Section S3.4 and shown in Fig. S6.† The cut-off energy was set to 850 eV, sampling the Brillouin zone at the Γ-point only, considering both the simulation convergence and computational expense, as shown in Fig. S1.† The use of Γ-point grids is consistent with previous works studying large zeolite systems in recent years.^77,78

In an attempt to find the global ground state structures before calculating the adsorption energies, a simulated annealing process was carried out using ab initio MD simulations, ramping them up to temperatures of 80–180 K in an NVT ensemble, as detailed by Abatal et al.⁷⁹ The temperature was then ramped down to 0 K, which gave lower energy structures than those obtained through placing the molecules manually. This was followed by a geometry optimisation, applying an electron smearing method of σ with 0.05 eV. The convergence criteria was set to 10⁻⁸ eV for the total energy, and 0.02 eV Å⁻¹ in force.

The vibrational frequencies of all atoms were obtained by computing the second order derivatives of the total energy concerning the ion positions by applying the finite differences method. The adsorption energies (E_ads) were also calculated applying eqn (1) using the final energies of the empty zeolite (E_zeolite), isolated adsorbate (E_adsorbate) and the system with the adsorbate adsorbed within the zeolite (E_{adsorbate+zeolite}).

E_ads = E_{adsorbate+zeolite} − (E_adsorbate + E_zeolite) (1)

All of the simulated vibrational spectra show the fundamental vibrations, with the first overtones and second-order combinations present in the shaded regions of the spectra. All of the spectra intensities (S(Q, ω)) in this report have been scaled and offset to allow for a clear comparison of the data.

3 Results and discussion

3.1 Inelastic neutron scattering

INS can directly probe the vibrational modes of hydrogenous species with enhanced clarity, particularly for low energy modes, due to the very large incoherent scattering cross-section of ¹H. It is therefore uniquely powerful for probing molecules encapsulated within inorganic zeolite frameworks and observing changes to the spectra obtained from the pure compound upon adsorption. These changes are shown for each lignin derivative upon adsorption into H-ZSM-5 in Fig. 3 where the most significantly affected adsorption bands are highlighted with an asterisk. The spectra of all compounds adsorbed into each zeolite catalyst are shown and discussed in Section S5.2.†

Fig. 3 INS spectra (a) p-cresol, m-cresol and o-cresol and (b) guaiacol and anisole, each as a pure compound, and then when loaded into H-ZSM-5. Example bands exhibiting more notable changes when dosed into the zeolite have been identified (*).

All vibrational modes have been assigned through direct comparison with DFT phonon calculated spectra, as detailed in Section 3.3 and comprehensive identification of the peaks observed in the INS spectra, alongside delineation of changes in each band upon adsorption in the zeolite catalysts, are listed in Tables S4–S8.†

The adsorption of each derivative into each zeolite induces common changes in the INS spectra across all samples, including broadened and less distinct peaks at low wavenumbers (approximately <400 cm⁻¹). Many peaks in the spectra of the pure (solid) compounds indicate frustrated translational and rotational (lattice) modes of the molecule.^9,80 The broadening and shifting of these peaks in the zeolite samples indicate significant adsorption interactions of each lignin derivative in the catalyst frameworks, leading to lower symmetry structures.⁹

Adsorbed molecules can occupy a range of environments, including H-bonding to zeolite BASs of varying acidities, the formation of weaker van der Waals interactions with the framework, or interactions with one or more adsorbate molecules in the pore system.⁸¹ Such broadening effects were observed for loosely adsorbed water,⁸² and methanol^34,83 due to interactions that manifest in various configurations and were shown to have significant effects on the mobility of both species.^84,85 Intermolecular bonding interactions between adsorbates can feature varied bond lengths and angles owing to the differing environments within the zeolite, such as straight and sinusoidal channels, channel intersections, and cages/windows of differing dimensions or indeed at defect sites.⁸⁶ In contrast, the pure compounds that have a solid, typically crystalline structure at 20 K exhibit higher symmetry and fewer unique molecular positions, leading to sharper, well-defined peaks.

Comparing zeolite-encapsulated samples to their bulk counterparts reveals numerous peak red-shifts towards lower wavenumbers, with varying magnitudes, alongside reductions in the intensities of specific peaks (detailed in Tables S4–S8†). The red-shifts can be partially attributed to decreased geometrical constraints in the zeolite pores compared to the severely restricted solid crystal structures. Similar observations were made at very low wavenumbers for confined water, where the faujasite pore system offered more vibrational freedom and resulted in fewer H-bonds per molecule than in ice.⁸²

In Fig. 3(a), the labelled cresol vibrational bands (*), which show a broadening and decrease in the intensity of the relative peak heights upon adsorption into each zeolite framework, all involve oop (out of plane) bends of the cresol hydroxy group. In anisole, Fig. 3(b), the labelled peaks all involve a vibration of the methoxy group, and guaiacol (Fig. 3(b)) typically shows concerted motions of both the hydroxy and methoxy groups (as listed in Tables S7 and S8†). The methoxy-related peaks in anisole show much more broadening and decreases in intensity compared to hydroxy-related peaks in the cresol samples. This is because in anisole no hydrogen bonding occurs in the pure compound, unlike the other samples, but does occur when H-bonds form with the zeolite acid sites. This is present in guaiacol but to a lesser degree.

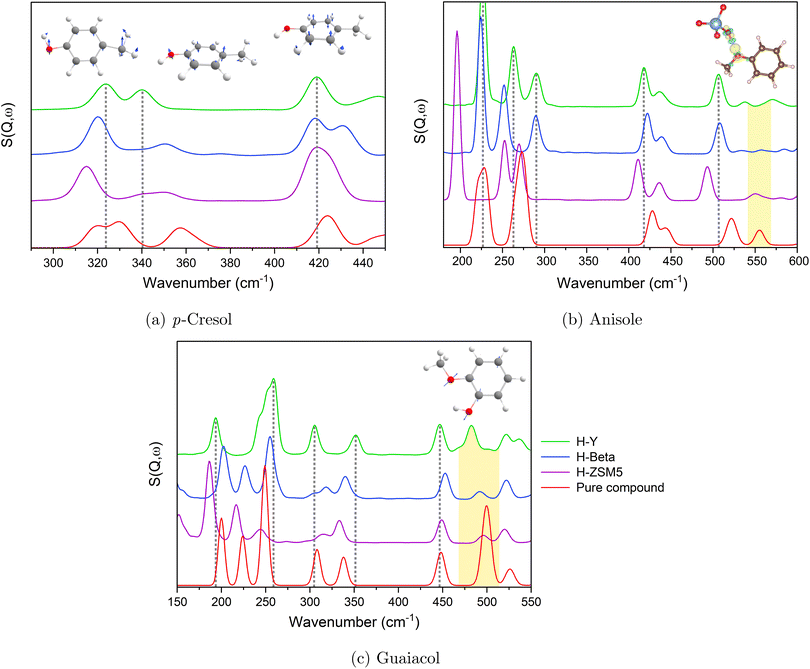
More subtle changes were observed upon comparing each molecule adsorbed into the different zeolites, as shown for p-cresol, anisole and guaiacol in Fig. 4.

Fig. 4 Vibrational spectra of (a) p-cresol, (b) anisole and (c) guaiacol in zeolites HY, H-Beta, and H-ZSM-5 compared to the pure compounds, with selected vibrational modes pictured.

Between the different zeolite frameworks, more subtle differences in peak shifts and broadenings are observed for each compound, particularly for larger magnitude motions (e.g. symmetrical methyl and hydroxy bending modes) and those involving the H-bonding functional groups. Modes that show little to no shift typically involve smaller magnitude motions - such as ring atom vibrations - that do not involve changes upon H-bonding, suggesting that the local energy surface around their energetic minima is relatively unaffected by such perturbations. This is shown by the changes in charge density upon H-bonding, primarily involving the hydroxy groups, discussed further in Section 3.2.

Increased spectral red-shifting for each compound is generally observed with the decreasing zeolite pore size of HY > H-Beta > H-ZSM-5. In the case of the cresols, there are slightly more acid sites available compared to the number of molecules as the pore size decreases in each sample (1.13 in HY, 1.33 in H-Beta and 1.45 in H-ZSM-5 acid sites per molecule), but the larger, more cage-like pore structure of HY (∼14 Å supercages) is more able to accommodate adsorbate–adsorbate interactions, perhaps leading to spectra more similar to those of the pure compounds. The peak at 343 cm⁻¹ in Fig. 4(a), representing OH bending, particularly decreases in intensity from HY to H-ZSM-5. The H-Beta and H-ZSM-5 channel structures are more conducive to adsorbates strongly interacting with the pore walls as opposed to adsorbate–adsorbate interactions⁸⁷ (discussed in more detail in Section 3.2).

Anisole and guaiacol show slightly differing relationships between peak broadening/intensity losses and the zeolite framework. Anisole (Fig. 4(b)) shows significant peak shifts from 227–283 cm⁻¹ from HY to H-ZSM-5, representing changes in the methoxy methyl torsions. The lower energy methoxy methyl rotational modes have previously been shown to be very sensitive to their local environment,⁸⁸ and such red-shifts were also observed for methyl acetate in H-ZSM-5.⁸⁹ Guaiacol (Fig. 4(c)), shows less shifting of this methyl torsion peak as the zeolite topology changes. It is however noted that the internal H-bonding between the hydroxy and methoxy groups may affect the interactions with the acidic sites (probed further in Section 3.2) and the resulting shifts.

The loss of intensity and broadening of the in-plane methoxy bending modes of both anisole (∼550 cm⁻¹) and guaiacol (∼500 cm⁻¹ - concerted with a ring deformation) is highlighted in yellow in Fig. 4(b) and (c), respectively, and the increase in the level of shifting as the zeolite framework changes is particularly clear. Notably, no bonds occur between methoxy groups in the crystalline pure compounds (Section S5.1†) and van der Waals forces dominate the interactions of these groups. Upon dosing either compound into the zeolites, the potential formation of H-bonds between the methoxy groups and the zeolite acid sites leads to larger changes in this bending mode (Fig. 4(b)). The following sections examine the varying adsorption strengths and configurations across different samples and assess the extent of shifting in the DFT-calculated INS spectra to rationalise the spectral changes for each compound upon adsorption into each zeolite framework.

3.2 Adsorption energies and bonding configurations

From the DFT adsorption calculations performed for each lignin derivative in each zeolite framework, some general trends for the adsorption energies and H-bonding configurations were identified. The adsorption energies are listed in Table S3,† ranging between −97.4 and −156 kJ mol⁻¹. The lowest energy zeolite-adsorbate configurations (shown in Fig. S7–S9†) always involved the formation of H-bonding interactions⁹⁰ between the adsorbate oxygen (present in methoxy or hydroxy functional groups) and the zeolite BAS (H_BAS–O_ads), with associated O_BAS–H_BAS–O_ads angles.

The most energetically favourable configuration for molecules containing a hydroxy group (excluding anisole) was observed when it adopted a configuration with two H-bonds, creating a pseudo-6-membered ring (6-MR), as depicted in the images for p-cresol to guaiacol at the top of Fig. 5, with all of the configurations shown in Fig. S7–S9.† The adsorbate hydroxy group exhibits a preference for bonding to a framework oxygen atom adjacent to the aluminium atom due to its increased electron density (illustrated by the listed changes in the H_ads–O_zeo bond and O_ads–H_ads–O_zeo angle in Fig. S10 and S11† respectively). Similar bonding configurations have been reported previously for hydroxy-aromatic compounds adsorbed onto H-ZSM-5,^8,18 with lower energy configurations of guaiacol-to-acid site bonding through its hydroxy, rather than the methoxy group.²¹ However, an exception is observed with m-cresol in H-ZSM-5, where an 8-MR structure is adopted (see Fig. S9†) and will be discussed in more detail later.

Fig. 5 The adsorption energies for each lignin monomer H-bonded to an acid site in zeolite HY (green), H-Beta (blue), and H-ZSM-5 (purple). At the top are the bonding configurations of each monomer in H-Beta.

In the case of guaiacol, which features adjacent methoxy and hydroxy groups, the molecule was able to form additional intramolecular interactions (H_ads–O_OMe), with the hydroxy group H-bonding to the zeolite framework oxygen and the methoxy group oxygen concurrently (Fig. S7(d)–S9(d)†), thereby further stabilising its structure. This arrangement resulted in guaiacol's lowest-energy configuration in H-Beta and H-ZSM-5, but not in HY, where the specific geometry of the pore structure causes steric hindrance that makes this configuration less favourable, though this is also dependent on the acid site location.

The trends in adsorption energy with zeolite and adsorbate type are shown in Fig. 5. The values associated with these parameters are listed in Table S3,† and where the adsorbates formed 6-MR (or 8-MR) structures, or intramolecular H-bonding in the case of guaiacol, the lengths and angles of the additional bonds formed are also given.

A wide range of adsorption energies were observed, from −97 to −157 kJ mol⁻¹, with stronger adsorption energies obtained as the zeolite pore size decreases (i.e. from HY to H-Beta to H-ZSM-5). These values align with those reported for analogous systems, such as phenol adsorption in Brønsted acidic H-ZSM-5 (−105 kJ mol⁻¹)¹⁸ and and other studies probing phenol (−100 to −109 kJ mol⁻¹), anisole (−106 to −118 kJ mol⁻¹) and cresols (−108 to −124 kJ mol⁻¹) in H-ZSM-5 with acid sites situated at T-11 and T-12 respectively.⁸ The H_BAS–O_ads bond lengths showed minimal variation, ranging from 1.46–1.57 Å (defined as strong H-bonding).⁹⁰ Additional H_ads–O_zeo H-bonds were observed in all systems except anisole, ranging from 1.81–2.35 Å, comparable to the previously observed bonding structure of phenol adsorption onto H-ZSM-5 with two H-bonds of lengths 1.53 and 1.80 Å.¹⁸ Interestingly, the H_ads–O_zeo bond lengths increase from HY to H-ZSM-5 (Fig. S10(b)†), which contrasts the trend of stronger adsorption energies. This suggests that minor bond length variations have little effect on adsorption strength, or that in smaller-pore systems, enhanced van der Waals interactions with the framework may pull the adsorbate away from the acid site, with the overall gain in framework interactions outweighing the loss of interaction at the acid site, discussed next.

The bond angles exhibit some deviation from an optimal linear H-bonding configuration, with O_BAS–H_BAS–O_ads angles ranging from 154–178°, though no consistent trends are observed across zeolite frameworks. Compared to structures where only a single H-bond can form (e.g. anisole-to-zeolite interactions), allowing for near-linear bonding angles, structures with two H-bonds between the molecule and the zeolite exhibit more constrained geometries. The molecules adopt conformations that appear to maximise the linearity of both H-bonds.

Despite the lack of a clear trend in adsorbate-to-zeolite H-bond lengths and angles, the zeolite framework structure significantly influences adsorption strengths. We largely attribute the increased adsorption strengths observed with decreasing zeolite pore size to the enhanced ‘confinement effect’ of smaller-pored zeolites, as discussed in Section 1.²⁴Fig. 6 illustrates this ‘confinement effect’, showing an increase in the number of zeolite framework oxygen atoms in proximity (within 5 Å) to adsorbate hydrogen atoms, progressing from HY to H-Beta to H-ZSM-5. This demonstrates a clear correlation between the adsorbate-to-zeolite contact and adsorption energy.

Fig. 6 The number of H_ads–O_zeo pairs within 5 Å of one another, supporting the hypothesis of a stabilising confinement effect of zeolite HY (green), H-Beta (blue), and H-ZSM-5 (purple).

The charge difference plot in Fig. 7 shows large changes in the charge density of all atoms involved directly in H-bonds, but also the surrounding atoms. Locally, these changes facilitate H-bonding; however, the changes on the non-interacting atoms (such as the benzyl hydrogen in closest proximity to the framework) may be due to longer-range interactions with the adjacent pore walls. This intricate balance of short-range H-bonding and longer-range excess charge/van der Waals interactions is greatly dependent on the adsorbate species, the local acid site geometry and the longer-range geometry of the pore walls. Therefore, tailoring acid site placement to improve molecule-zeolite compatibility can accommodate stronger adsorption.

Fig. 7 Example charge density difference plot of p-cresol in H-ZSM-5, with areas of increased and decreased electron density shown in yellow and blue, respectively, relative to unbonded p-cresol and H-ZSM-5.

The adsorption energies, however, vary less between the different aromatic lignin derivative species than between the zeolite topologies, appearing to depend less on longer-range adsorbate-zeolite contacts and more on the shorter–range interactions of the functional groups present and the H-bonding interactions formed. Most notably, weaker adsorption of anisole to the BASs in each framework is evident (see Fig. 5), with only a single H-bond formed between the molecule and zeolite (Fig. S7–S9†). This is primarily attributed to the absence of the hydroxy group, which is present in every other monomer, so a second H-bonding interaction cannot form, but allows for a more optimal linear bonding angle of the single H-bond formed (Table S3†).

The remaining derivatives show greater similarities in their adsorption energies, with complex differences in the charge densities, depending on the configurations adopted. When comparing the cresol isomers, a trend in adsorption strength is observed as p-cresol > m-cresol > o-cresol in HY and H-Beta. For o-cresol, we observe slightly longer H_BAS–O_ads bonds (1.46–1.57 Å compared to 1.46–1.47 Å) and less linear bonding angles (154–165° compared to 161–173°). In o-cresol, short-range repulsive interactions between the methyl group and zeolite framework cause the neighbouring H-bond to lengthen and weaken, relative to the other cresol isomers where the methyl group is positioned further from the hydroxy group. The effect is evident in the reduced electron density of the H_BAS–O_ads bond for o-cresol, as shown in Fig. 8, compared to the other cresols.

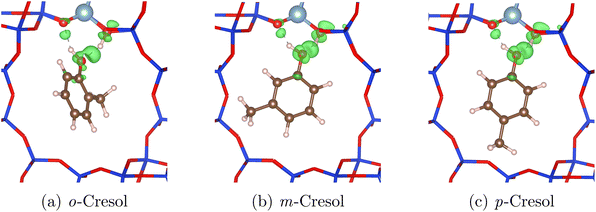Fig. 8 Charge difference models showing increased electron density (green) in the different cresol isomers H-bonded to an acid site in HY, relative to the unbonded cresol isomers and zeolites.

In contrast, in H-ZSM-5, the meta cresol isomer exhibits the weakest adsorption due to a less stable 8-MR configuration, shown in Fig. 9. While the 6-MR configuration is typically more stable, m-cresol adopting such a conformation in H-ZSM-5 raises the system's energy as the methyl group would come into very close contact with the zeolite framework atoms, resulting in repulsive interactions. In the 8-MR configuration, the methyl group orients into the sinusoidal channel opening, reducing repulsion and stabilising this configuration. In the case of o-cresol, although the presence of the methyl group slightly increases the length of the H-bonds formed in the 6-MR configuration, the methyl group is positioned towards the sinusoidal channel, avoiding short-range repulsive interactions with the framework. p-Cresol forms the most stable structure in H-ZSM-5 by adopting an unperturbed 6-MR configuration, with the methyl group pointing down the H-ZSM-5 straight channel (Fig. S9†).

Fig. 9 8-MR structure formed by m-cresol in H-ZSM-5.

Comparatively, guaiacol exhibits weaker adsorption in HY compared to the cresol isomers, but stronger adsorption in the other two zeolites despite exhibiting longer bonding lengths and less linear bonding angles of both the H_BAS–O_ads and H_ads–O_zeo interactions, due to greater steric hindrance of the larger methoxy group in the ortho position. Repulsive interactions involving the bulkier methoxy group explain the weaker adsorption in HY, however, stronger adsorption of guaiacol in H-Beta and H-ZSM-5 is attributed to the ability of guaiacol to form three H-bonds as shown in Fig. S8 and S9.† The same stabilised structure with intramolecular H-bonding was also observed in previous work probing lignin derivative interactions and diffusion.^37,38,91,92 When guaiacol is optimally H-bonded to the acid site in HY, which involves forming simultaneous intramolecular H-bonds, the methoxy group comes into close contact with the zeolite framework. Guaiacol, therefore, flips its intramolecular configuration such that the hydroxy group points away from the methoxy (6-MR structure, Fig. S7(d)†). The penalty for guaiacol forming its more standard intramolecular H-bonding in HY is therefore too great in comparison to the stabilisation effect of optimal H-bonds formed between its hydroxy group and the zeolite acid site.

We have demonstrated that the zeolite topology and local framework environment significantly impact the adsorption energies of small aromatic species due to the ‘confinement effects’ they impose, along with orientational variations depending on the local channel structure. Additionally, the functional groups present on each molecule and the resulting H-bonding interactions they can form with the zeolite BASs also impact adsorption energies, albeit to a lesser extent, as seen in the case of anisole when compared to other molecules. The impact of minor variations in molecular shape on the strengths of the calculated interactions formed is highly dependent on the shape-compatibility between adsorbate and zeolite pore, affecting the H-bonds, long-range van der Waals, and short-range repulsive interactions. Therefore, the lower energy configurations that form and the strength of interactions are also highly dependent on the acid site location. In reality, zeolites exhibit diverse distributions of acid sites located across many T-sites, which are strongly dependent on the synthesis conditions.⁵¹ Hence, different lignin derivatives adsorbed to BASs in varying locations throughout the zeolite frameworks will form H-bonds of many different strengths,⁹³ and potentially even form adsorbate–adsorbate interactions at higher loadings. A 6-MR bonding configuration, where molecular shape allows, has been highlighted as a generally more favourable configuration for monocyclic aromatics containing a hydroxy group, when adsorbed onto zeolite BASs.

3.3 Comparison of experimental and theoretical vibrational spectra

Phonon calculations were carried out to generate modelled vibrational spectra for direct comparison to the experimental INS spectra observed in Section 3.1. Here, the overtones have been removed to simplify the spectra. Generally, close agreement between the INS and corresponding simulated spectra was observed as shown for p-cresol, anisole and guaiacol in H-ZSM-5 (Fig. 10). Modelled spectra for all derivatives across all zeolites (in comparison with their experimental counterparts) are shown in Fig. S18–S22.† Close agreement between the simulated and experimental spectra of the pure compounds was also achieved as shown in Fig. S12–S16,† (no crystal structure was available for guaiacol, so the modelled spectrum of a single molecule was employed). Using all the available spectra, we compared the relative positions and amplitudes of the simulated and experimental spectra to provide the most likely peak assignment for each mode between 200–1200 cm⁻¹, listed in Tables S4–S8† and discussed in Sections 3.1, S3.1 and S3.2.† Assigning peaks below 200 cm⁻¹ proved challenging owing to the extraordinarily weak forces driving low-frequency dynamics, rendering accurate reproduction difficult without employing higher accuracy methods⁹⁴ deemed unnecessary here.

Fig. 10 Simulated spectra of p-cresol, anisole and guaiacol in H-ZSM-5 (dashed lines) and the corresponding experimental INS spectra (solid lines).

A phonon calculation of each single-molecule generally provides a good description of the experimental spectra of the pure compounds (Fig. S12–S16†). However, the single-molecule calculations consistently show shifts to higher wavenumbers. As discussed in Section 3.1, higher energy vibrations occur in solid-state environments because the vibrational modes are constrained by steric effects, intermolecular adsorbate–adsorbate interactions and the prevalence of H-bonding (recently shown for vibrations of confined versus bulk water⁹⁵). Additionally, the single molecule spectrum of each cresol isomer displays a strong peak attributed to the hydroxy bend at 390 cm⁻¹ (shown in Fig. S12–S14†), with a similar such mode at 498 cm⁻¹ in the case of guaiacol (shown in Fig. S16†). These peaks are not present in the experimental or simulated crystal spectra. We can attribute the disappearance of this mode to the strong directionality of the adsorbate–adsorbate H-bonding through the hydroxy group. As expected, the full crystal calculations typically provide a better experimental fit of the vibrational spectra, particularly at lower frequencies, which are affected more by collective motions and the non-local energy landscape.

A range of red-shifts, intensity losses and peak broadenings observed in the spectra of each molecule upon adsorption into each catalyst, observed in the experiment (see Fig. 3 and 4) are also observed in the modelled spectra, with some of the more significant cases shown in Fig. 11.

Fig. 11 Simulated spectra of p-cresol, anisole and guaiacol in zeolites HY, H-Beta, and H-ZSM-5 compared to the pure compounds. For (b) and (c), the bands attributed to the methoxy bend are highlighted in yellow.

While the simulated spectra do reproduce a number of red-shifts when comparing the pure compound modelled spectra to those of zeolite adsorbed systems, they do not always replicate the more subtle shifts seen between different zeolite topologies. This suggests that the differences between zeolites depend less on the specific BAS-adsorbate H-bonding interactions reproduced by the model and more on the bulk properties of the experimental samples containing higher loadings of derivatives adsorbed into each zeolite. It is important to note that the increasing occurrence of adsorbate–adsorbate interactions allowed in the pores of HY in the experiment could produce spectra more similar to those of the solid pure compound samples observed with the INS, as discussed in Section 3.1.

The simulated spectra do reproduce trends in decreasing peak intensities/peak broadenings for hydroxy and methoxy bends as zeolite pore size decreases/adsorption energies increase (shown in Fig. 11), as observed with INS. For the cresol isomers, where p-cresol is used as an example in Fig. 11(a), the peak intensity of the OH/ring out-of-plane bend decreases and broadens as we move from HY to H-Beta to HZSM-5. It is important to note that this band occurs at a lower wavenumber in the phonon calculation of the pure compound system (Fig. S12†) due to the extensive directional H-bonding in this crystalline system.

The simulated spectra also show how methoxy related modes spread when the adsorbate is dosed into the zeolite due to changes in the interactions of this group from the pure compound to within each zeolite. In anisole, the peak highlighted in yellow at 554 cm⁻¹ in Fig. 11(b) is attributed to a vibration involving a large methoxy oxygen bend, suggesting that changes in the peak heights are due to differences in bonding interactions with the zeolite BASs as opposed to in the crystal. Other peaks attributed to modes involving methoxy oxygen motions, such as that at 781 cm⁻¹ for anisole, also show decreased intensities (see Table S7†). Changes in vibrational modes due to changes in bonding interactions may be more apparent with anisole because there are no H-bonds present in the solid structure, compared to the H-bonds that form with zeolite BASs. With careful examination of the phonon calculations of the zeolite adsorbed anisole systems, this 554 cm⁻¹ mode is still present but in much lower proportions and at a greater number of frequencies, suggesting that the heterogeneous nature of the zeolite structure causes some degree of broadening alongside a decrease in the peak intensity. One could conclude that the experimental system exhibits even greater heterogeneity through the presence of many acid site locations, and would thus smear the vibrational density of states further, causing it to all but disappear. For guaiacol, the simulated combined methoxy/hydroxy out-of-plane bend at 515 cm⁻¹ (also highlighted in yellow) shows a significant loss of intensity in HY compared to the pure compound. This loss of intensity is more significant in H-Beta and H-ZSM-5, indicative of stronger H-bonding to the zeolite framework and the breaking of adsorbate–adsorbate interactions, which are facilitated to a greater degree in the larger pore HY framework.

In general, the decrease in the simulated peak intensities largely follows the same experimentally observed trend from HY to H-Beta to H-ZSM-5, which may suggest that peak intensity decreases are due to stronger bonding interactions with the zeolite acid sites, as shown in Section 3.2, as opposed to a large contribution from a decrease in adsorbate–adsorbate bonding in smaller-pored zeolites, as this would not be replicated by the simulations that only model one-to-one bonding. These case studies of lignin derivative adsorption within different zeolites highlight how both confinement within zeolites of differing pore shapes and sizes and the specific bonding interactions that can occur, subtly influence the nature of the vibrational dynamics of the adsorbed molecules.

4 Conclusions

In this study, we combined experiment and theory to analyse and quantify the interactions of the lignin pyrolysis oil derivatives anisole, guaiacol and the three cresol isomers in industrial samples of zeolite catalysts HY, H-Beta and H-ZSM-5 (Si/Al = 11.5–15) using INS and DFT techniques.

INS spectral bands of each derivative could be accurately assigned thanks to our DFT phonon calculations, and many spectral features in the lower energy region (200–1200 cm⁻¹) of the pure compounds showed significant changes in the form of peak broadenings and red-shifts upon loading into the zeolite catalysts. For most lignin derivatives, increased red-shifts were observed in modes involving H-bonding groups (hydroxy or methoxy species) or neighbouring groups to these (methoxy/methyl groups) as the zeolite pore size decreased from HY > H-Beta > H-ZSM-5. Less shifting in the larger pores of HY benchmarked against the spectra of the pure compounds, was attributed to a greater proportion of adsorbate–adsorbate H-bonding allowed in the larger HY supercages, leading to structures more similar to the pure (solid/crystalline) compound which have highly ordered crystal structures and therefore more restricted bending modes (apart from anisole). Decreases in relative peak intensities were also observed as zeolite pore size decreased, particularly for methoxy related bending modes in anisole and guaiacol. Such intensity decreases with framework topology still occurred, but to a lesser extent for the hydroxy groups of the cresol isomers.

DFT calculated adsorption energies gave values ranging from −97 to −157 kJ mol⁻¹. All lignin derivatives gave E_ads values in the order of HY < H-Beta < H-ZSM-5, increasing in magnitude as the zeolite pore size decreased. The trend was attributed to the ‘confinement effect’, supported by the increased number of zeolite-adsorbate short-range interactions as the pore size decreased. Less variation in E_ads was observed between the different lignin derivatives compared to the different zeolite structures. Most derivatives (excluding anisole) favoured an optimal bonding configuration involving two H-bonds through a 6-MR structure with the zeolite acid site. Guaiacol in H-ZSM-5 displayed the strongest adsorption, facilitated by the formation of three H-bonds involving the OH and OMe groups; notably this orientation could not occur in HY, hence guaiacol showed the largest gulf in E_ads between larger and smaller pore zeolites. Among the cresol isomers, o-cresol showed slightly weaker H-bonding because the ortho methyl group physically hindered the bonding of its adjacent hydroxy group. Weaker adsorption was also observed for m-cresol in H-ZSM-5 where the combination of the local zeolite topography and molecular shape inhibited the formation of a low energy 6-MR structure. The observations clearly demonstrated the dependence of the adsorption strength on the interplay between the zeolite-adsorbate shape compatibility, short-range H-bonding, and the longer-range van der Waals interactions able to form without incurring an energy penalty from short-range repulsion.

The modelled INS spectra obtained from the DFT simulations closely matched the experimental data, enabling confident assignment of most vibrational modes between 200–1200 cm⁻¹. The modelled spectra also revealed consistent trends in red-shifts, peak broadening, and intensity changes upon adsorption, with some stronger effects observed in smaller-pored zeolites, giving an intensity loss trend of H-ZSM-5 > H-Beta > HY. The simulations successfully replicated experimentally observed decreases in peak intensity for hydroxy and methoxy bending modes with decreasing pore size, corroborating the relationship between zeolite-adsorbate interactions and adsorption strength. However, the shifting of vibrational bands between zeolite topologies was less accurately captured, indicating a significant contribution from adsorbate–adsorbate interactions in the experiment, particularly in the larger-pored HY.

For anisole and guaiacol, vibrational changes directly reflected their specific bonding interactions within the zeolites. Anisole's methoxy bending modes and guaiacol's combined methoxy/hydroxy out-of-plane bends showed pronounced peak intensity losses in the smaller-pored zeolites, reflecting the stronger binding to Brønsted acid sites. The cresol isomers exhibited trends such as peak broadening in the hydroxy out-of-plane bending modes, further highlighting how zeolite topology influences vibrational dynamics. These findings illustrate the interplay of confinement effects and direct adsorbate–framework interactions that govern the nuanced vibrational behaviour of each lignin derivative along with its adsorption energy.

In the context of catalysis, this study highlights the importance of considering both zeolite confinement effects and the specific hydrogen-bonding interactions of lignin derivatives with zeolite Brønsted acid sites. These interactions govern the adsorption strengths and localised vibrational dynamics which are directly tied to catalytic activity and selectivity. Through assessing how molecular structure, zeolite topology, and confinement effects influence the interaction strength of biomass-derived compounds in industrial zeolite catalysts, this work has aimed to contribute fundamental insights to the design of catalysts tailored to lignin valorisation. Improved understanding of these interactions enables the development of more selective and efficient microporous catalysts for upgrading lignin pyrolysis oils—an essential step toward replacing fossil-derived feedstocks with renewable carbon sources. Such advances support broader sustainability goals, including lowering greenhouse gas emissions and increasing the viability of bio-based chemical production.

Data availability

Experimental data for this article are fully available at https://doi.org/10.5286/ISIS.E.RB2000224. Simulation data may be found at https://doi.org/10.17172/NOMAD/2025.04.25-1. The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the UK Engineering and Physical Sciences Research Council (EPSRC) grant EP/T518013/1 for the University of Bath as part of a studentship with the STFC and the EPSRC Network Engineering Porous Materials at Multiple Scales EP/X013065/1. Experiments at the ISIS Pulsed Neutron and Muon Source were supported by beamtime allocation from the Science and Technology Facilities Council (data available at: https://doi.org/10.5286/ISIS.E.RB2000224), with preliminary sample characterisation carried out with the aid of the Materials Characterisation Laboratory. The authors thank the Computing resources provided by the STFC Scientific Computing Department's SCARF cluster (simulation data available at: https://doi.org/10.17172/NOMAD/2025.04.25-1). A. J. O'Malley acknowledges Roger and Sue Whorrod for the funding of a Whorrod Fellowship and IChemE for the provision of the Andrew Fellowship. We extend our gratitude to Carlos Hernandez-Tamargo for generously providing initial zeolite DFT configurations and for his invaluable advice. The resources and support provided by the UK Catalysis Hub via membership of the UK Catalysis Hub consortium are gratefully acknowledged.

References

1. R. Rinaldi and F. Schüth, Energy Environ. Sci., 2009, 2, 610.
2. E. Furimsky, Appl. Catal., A, 2000, 199, 147–190.
3. M. Zhang and A. Moutsoglou, Energy Fuels, 2014, 28, 1066–1073.
4. H. Ben and A. J. Ragauskas, ACS Sustain. Chem. Eng., 2013, 1, 316–324.
5. P. A. Jacobs, M. Dusselier and B. F. Sels, Angew. Chem., Int. Ed., 2014, 53, 8621–8626.
6. I. Graça, J.-D. Comparot, S. Laforge, P. Magnoux, J. Lopes, M. Ribeiro and F. R. Ribeiro, Appl. Catal., A, 2009, 353, 123–129.
7. I. Graça, A. Fernandes, J. Lopes, M. Ribeiro, S. Laforge, P. Magnoux and F. Ramôa Ribeiro, Appl. Catal., A, 2010, 385, 178–189.
8. N. Pichot, J. Hounfodji, M. Badawi, V. Valtchev, S. Mintova, J.-P. Gilson, A. Dufour and L. Pinard, Appl. Catal., A, 2023, 665, 119352.
9. I. B. Adilina, N. Rinaldi, S. P. Simanungkalit, F. Aulia, F. Oemry, G. B. G. Stenning, I. P. Silverwood and S. F. Parker, J. Phys. Chem. C, 2019, 123, 21429–21439.
10. N. Sivasankar and S. Vasudevan, J. Phys. Chem. B, 2004, 108, 11585–11590.
11. E. Titus, A. K. Kalkar and V. G. Gaikar, Sep. Sci. Technol., 2002, 37, 105–125.
12. A. Song, J. Ma, D. Xu and R. Li, Catalysts, 2015, 5, 2098–2114.
13. J. Vercammen, M. Bocus, S. Neale, A. Bugaev, P. Tomkins, J. Hajek, S. Van Minnebruggen, A. Soldatov, A. Krajnc, G. Mali, V. Van Speybroeck and D. E. De Vos, Nat. Catal., 2020, 3, 1002–1009.
14. G. Collinge, S. F. Yuk, M.-T. Nguyen, M.-S. Lee, V.-A. Glezakou and R. Rousseau, ACS Catal., 2020, 10, 9236–9260.
15. V. Van Speybroeck, M. Bocus, P. Cnudde and L. Vanduyfhuys, ACS Catal., 2023, 13, 11455–11493.
16. S. Kasuriya, J. Catal., 2003, 219, 320–328.
17. I. Khalil, H. Jabraoui, S. Lebègue, W. J. Kim, L.-J. Aguilera, K. Thomas, F. Maugé and M. Badawi, Chem. Eng. J., 2020, 402, 126264.
18. S. Javadian and F. Ektefa, RSC Adv., 2015, 5, 100799–100808.
19. C. Hernandez-Tamargo, A. O'Malley, I. P. Silverwood and N. H. de Leeuw, Catal. Sci. Technol., 2019, 9, 6700–6713.
20. C. Hernandez-Tamargo, I. P. Silverwood, A. J. O’malley and N. H. d. Leeuw, Top. Catal., 2021, 64, 707–721.
21. H. Zhang, C. Yang, Y. Tao, M. Chen and R. Xiao, Fuel Process. Technol., 2022, 238, 107512.
22. N. Pichot, J. Hounfodji, H. El Siblani, M. Badawi, V. Valtchev, S. Mintova, J.-P. Gilson, A. Dufour and L. Pinard, Appl. Catal., A, 2024, 671, 119565.
23. H. Stach, U. Lohse, H. Thamm and W. Schirmer, Zeolites, 1986, 6, 74–90.
24. E. DEROUANE, J. Catal., 1986, 100, 541–544.
25. E. G. Derouane and C. D. Chang, Microporous Mesoporous Mater., 2000, 35–36, 425–433.
26. M. Pera-Titus and J. Llorens, Appl. Surf. Sci., 2010, 256, 5305–5310.
27. Y. Chai, W. Dai, G. Wu, N. Guan and L. Li, Acc. Chem. Res., 2021, 54, 2894–2904.
28. E. Grifoni, G. Piccini, J. A. Lercher, V.-A. Glezakou, R. Rousseau and M. Parrinello, Nat. Commun., 2021, 12, 2630.
29. C. M. Nguyen, M.-F. Reyniers and G. B. Marin, J. Catal., 2015, 322, 91–103.
30. T. Demuth, J. Catal., 2004, 222, 323–337.
31. M. E. Potter, S. Chapman, A. J. O'Malley, A. Levy, M. Carravetta, T. M. Mezza, S. F. Parker and R. Raja, ChemCatChem, 2017, 9, 1897–1900.
32. A. J. O'Malley, S. F. Parker and C. R. A. Catlow, Chem. Commun., 2017, 53, 12164–12176.
33. B. S. F. Parker and P. Collier, Johnson Matthey Technol. Rev., 2016, 60, 132–144.
34. A. J. O'Malley, S. F. Parker, A. Chutia, M. R. Farrow, I. P. Silverwood, V. García-Sakai and C. R. A. Catlow, Chem. Commun., 2016, 52, 2897–2900.
35. J. Armstrong, A. J. O'Malley, M. R. Ryder and K. T. Butler, J. Phys. Commun., 2020, 4, 072001.
36. J. Guan, Y. Lu, K. Sen, J. Abdul Nasir, A. W. Desmoutier, Q. Hou, X. Zhang, A. J. Logsdail, G. Dutta, A. M. Beale, R. W. Strange, C. Yong, P. Sherwood, H. M. Senn, C. R. A. Catlow, T. W. Keal and A. A. Sokol, Philos. Trans. R. Soc., A, 2023, 381, 20220234.
37. K. S. C. Morton, A. J. Porter, J. Armstrong and A. J. O’Malley, Catal. Sci. Technol., 2024, 14, 3756–3770.
38. K. Morton, M. Appel, C. Woodward, J. Armstrong and A. O'Malley, Microporous Mesoporous Mater., 2025, 383, 113388.
39. R. Warringham, D. Bellaire, S. F. Parker, J. Taylor, R. A. Ewings, C. M. Goodway, M. Kibble, S. R. Wakefield, M. Jura, M. P. Dudman, R. P. Tooze, P. B. Webb and D. Lennon, J. Phys.: Conf. Ser., 2014, 554, 012005.
40. S. Chapman, A. J. O'Malley, I. Miletto, M. Carravetta, P. Cox, E. Gianotti, L. Marchese, S. F. Parker and R. Raja, Chem.–Eur. J., 2019, 25, 9938–9947.
41. A. Perrichon, C. Bovo, S. F. Parker, D. Raspino, J. Armstrong and V. G. Sakai, Nucl. Instrum. Methods Phys. Res. A, 2023, 1047, 167899.
42. S. F. Parker, F. Fernandez-Alonso, A. J. Ramirez-Cuesta, J. Tomkinson, S. Rudic, R. S. Pinna, G. Gorini and J. Fernández Castañon, J. Phys.: Conf. Ser., 2014, 554, 012003.
43. O. Arnold, J. Bilheux, J. Borreguero, A. Buts, S. Campbell, L. Chapon, M. Doucet, N. Draper, R. F. Leal, M. Gigg, V. Lynch, A. Markvardsen, D. Mikkelson, R. Mikkelson, R. Miller, K. Palmen, P. Parker, G. Passos, T. Perring, P. Peterson, S. Ren, M. Reuter, A. Savici, J. Taylor, R. Taylor, R. Tolchenov, W. Zhou and J. Zikovsky, Nucl. Instrum. Methods Phys. Res. A, 2014, 764, 156–166.
44. D. H. Olson, G. T. Kokotailo, S. L. Lawton and W. M. Meier, J. Phys. Chem., 1981, 85, 2238–2243.
45. H. G. C. Baerlocher, L. B. McCusker and B. Marler, Database of Zeolite Structures, http://www.iza-structure.org/databases, Accessed: June 2024.
46. D. Olson, J. Catal., 1969, 13, 221–231.
47. J. Higgins, R. LaPierre, J. Schlenker, A. Rohrman, J. Wood, G. Kerr and W. Rohrbaugh, Zeolites, 1988, 8, 446–452.
48. H. Vankoningsveld, J. Jansen and H. Vanbekkum, Zeolites, 1990, 10, 235–242.
49. A. R. Ruiz-Salvador, R. Grau-Crespo, A. E. Gray and D. W. Lewis, J. Solid State Chem., 2013, 198, 330–336.
50. A. Vjunov, J. L. Fulton, T. Huthwelker, S. Pin, D. Mei, G. K. Schenter, N. Govind, D. M. Camaioni, J. Z. Hu and J. A. Lercher, J. Am. Chem. Soc., 2014, 136, 8296–8306.
51. J. Dědeček, E. Tabor and S. Sklenak, ChemSusChem, 2018, 12, 556–576.
52. J. Bae and M. Dusselier, Chem. Commun., 2023, 59, 852–867.
53. E. Dib, T. Mineva, E. Veron, V. Sarou-Kanian, F. Fayon and B. Alonso, J. Phys. Chem. Lett., 2017, 9, 19–24.
54. M. Sierka and J. Sauer, J. Phys. Chem. B, 2001, 105, 1603–1613.
55. A. J. Jones and E. Iglesia, ACS Catal., 2015, 5, 5741–5755.
56. Z.-s. Mo, Q. Li, Y.-c. Qin, L.-h. Duan, X.-t. Zhang and L.-j. Song, Mol. Simul., 2016, 42, 986–992.
57. L. Wei, H. Yang, P. Ren, Y. Yang, Y.-W. Li, R. Li, X.-D. Wen and H. Jiao, Microporous Mesoporous Mater., 2022, 344, 112184.
58. M. Czjzek, H. Jobic, A. N. Fitch and T. Vogt, J. Phys. Chem., 1992, 96, 1535–1540.
59. K. Suzuki, N. Katada and M. Niwa, J. Phys. Chem. C, 2006, 111, 894–900.
60. Z. Yu, A. Zheng, Q. Wang, L. Chen, J. Xu, J.-P. Amoureux and F. Deng, Angew. Chem., Int. Ed., 2010, 49, 8657–8661.
61. S. Singh, J. Martínez-Ortigosa, N. Ortuño, V. Polshettiwar and J. García-Martínez, Chem. Sci., 2024, 15, 20240–20250.
62. S. Li, Z. Zhao, R. Zhao, D. Zhou and W. Zhang, ChemCatChem, 2017, 9, 1494–1502.
63. C. Li, X. Dong, H. Yu and Y. Yu, Phys. Chem. Chem. Phys., 2023, 25, 24547–24562.
64. R. Zhao, Z. Zhao, S. Li and W. Zhang, J. Phys. Chem. Lett., 2017, 8, 2323–2327.
65. J. Holzinger, P. Beato, L. F. Lundegaard and J. Skibsted, J. Phys. Chem. C, 2018, 122, 15595–15613.
66. M. Meunier and S. Robertson, Mol. Simul., 2021, 47, 537–539.
67. K. Momma and F. Izumi, J. Appl. Crystallogr., 2008, 41, 653–658.
68. K. Dymkowski, S. F. Parker, F. Fernandez-Alonso and S. Mukhopadhyay, Phys. B, 2018, 551, 443–448.
69. A. Herraez, How to Use Jmol to Study and Present Molecular Structures, Lulu.com, Barking, England, 2008, vol. 1.
70. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
71. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
72. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561.
73. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
74. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396.
75. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
76. K. Stanciakova, J. N. Louwen, B. M. Weckhuysen, R. E. Bulo and F. Göltl, J. Phys. Chem. C, 2021, 125, 20261–20274.
77. D. R. Galimberti and J. Sauer, J. Chem. Theory Comput., 2021, 17, 5849–5862.
78. I. Karamanis, A. Daouli, H. Monnier, M.-A. Dziurla, G. Maurin and M. Badawi, Mol. Syst. Des. Eng., 2023, 8, 1165–1181.
79. M. Abatal, A. R. Ruiz-Salvador and N. C. Hernández, Microporous Mesoporous Mater., 2020, 294, 109885.
80. A. P. Hawkins, A. J. O'Malley, A. Zachariou, P. Collier, R. A. Ewings, I. P. Silverwood, R. F. Howe, S. F. Parker and D. Lennon, J. Phys. Chem. C, 2018, 123, 417–425.
81. R. Schenkel, A. Jentys, S. F. Parker and J. A. Lercher, J. Phys. Chem. B, 2004, 108, 7902–7910.
82. H. Jobic, Spectrochim. Acta, Part A, 1992, 48, 293–312.
83. A. J. O'Malley, A. J. Logsdail, A. A. Sokol and C. R. A. Catlow, Faraday Discuss., 2016, 188, 235–255.
84. C. H. Botchway, R. Tia, E. Adei, A. J. O’malley, N. Y. Dzade, C. Hernandez-Tamargo and N. H. de Leeuw, Catalysts, 2020, 10, 1342.
85. A. Porter, S. McHugh, T. Omojola, I. Silverwood and A. O'Malley, Microporous Mesoporous Mater., 2023, 348, 112391.
86. A. J. Porter and A. J. O'Malley, J. Phys. Chem. C, 2021, 125, 11567–11579.
87. B. Smit and T. L. M. Maesen, Chem. Rev., 2008, 108, 4125–4184.
88. A. Zachariou, A. P. Hawkins, P. Collier, R. F. Howe, D. Lennon and S. F. Parker, ACS Omega, 2020, 5, 2755–2765.
89. A. Zachariou, A. P. Hawkins, P. Collier, R. F. Howe, S. F. Parker and D. Lennon, Catal. Sci. Technol., 2023, 13, 1976–1990.
90. G. A. Jeffrey, An Introduction to Hydrogen Bonding, Oxford University Press, New York, NY, 1997.
91. R. Wu and B. Brutschy, Chem. Phys. Lett., 2004, 390, 272–278.
92. C. Cheng, F. Bian, C. Lu, Q. Wang, D. Shen and X. Jiang, JIE, 2024, 112, 101460.
93. N. Katada, K. Suzuki, T. Noda, G. Sastre and M. Niwa, J. Phys. Chem. C, 2009, 113, 19208–19217.
94. E. M. Kleist and M. T. Ruggiero, Cryst. Growth Des., 2021, 22, 939–953.
95. P. K. Verma, A. Kundu, M. S. Puretz, C. Dhoonmoon, O. S. Chegwidden, C. H. Londergan and M. Cho, J. Phys. Chem. B, 2017, 122, 2587–2599.

---

Footnote

† Electronic supplementary information (ESI) available: data includes a full description of the testing of different models to obtain the global minimum structures for the phonon and adsorption energy calculations. It also shows all of the simulated spectra for each model and the assignments of all experimental vibrational modes when at sufficient resolution. See DOI: https://doi.org/10.1039/d5su00024f

---