Theoretical insights into single-atom catalysts for improved charging and discharging kinetics of Na–S and Na–Se batteries

Abstract

Dissolution of poly-sulfide/selenides (p-S/Ses) intermediates into electrolytes, commonly known as the shuttle effect, has posed a significant challenge in the development of more efficient and reliable Na–S/Se batteries. Single-atom catalysts (SACs) play a crucial role in mitigating the shuttling of Na–pS/Ses and in promoting Na₂S/Se redox processes at the cathode. In this work, single transition metal atoms Co, Fe, Ir, Ni, Pd, Pt, and Rh supported in nitrogen-deficient graphitic carbon nitride (rg-C₃N₄) are investigated to explore the charging and discharging kinetics of Na–S and Na–Se batteries using Density Functional Theory calculations. We find that SAs adsorbed on reduced g-C₃N₄ monolayers are substantially more effective in trapping higher-order Na₂X_n than pristine g-C₃N₄ surfaces. Moreover, our ab initio molecular dynamics calculations indicate that the structure of X₈ (X = S, Se) remains almost intact when adsorbed on Fe, Co, Ir, Ni, Pt, and Rh SACs, suggesting that there is no significant S or Se poisoning in these cases. Additionally, SACs reduce the free energies of the rate-determining step during discharge and present a lower decomposition barrier of Na₂X during charging of Na–X electrode. The underlying mechanisms behind this fast kinetics are thoroughly examined using charge transfer, bonding strength, and d-band center analysis. Our work demonstrates an effective strategy for designing single-atom catalysts and offers solutions to the performance constraints caused by the shuttle effect in sodium–sulfur and sodium–selenium batteries.

---

1. Introduction

The increased interest in electric vehicles and the widespread use of portable devices have prompted extensive research to develop more efficient energy storage technologies. While lithium-ion batteries currently dominate the battery market,¹ their continued expansion faces challenges related to raw materials supply, safety concerns linked to organic electrolytes, and high cost, among other factors.^2,3 At the same time, sodium (Na)-ion batteries are drawing more attention due to the low cost and abundance of Na compared to Li.^4–6 Sodium chalcogen batteries, specifically Na–S batteries, have been extensively studied and show promising potential for applications in next-generation sustainable energy storage systems.^7–9 While sulfur (S) and selenium (Se) are promising cathode materials due to their abundance and impressive volumetric capacities of 3467 mA h cm⁻³ and 3268 mA h cm⁻³, respectively.^10–12 These battery technologies still face various challenges for practical applications. Some of these challenges are sluggish reaction kinetics, complex reaction mechanisms, and significant volume expansion during charge/discharge cycles.^13,14 To address these concerns, especially in preventing the shuttle effect, extensive research has focused on the idea of physical confinement and chemical adsorption that can effectively immobilize soluble intermediates.^15,16 Various low-dimensional materials have been incorporated to serve as the framework for the chalcogen (S, Se) cathode system such as carbon nanotubes,¹⁷ graphene,^8,18 porous carbon,^9,19 polymers,²⁰ and other low-dimensional materials.¹⁰ However, enhancing the affinity between the anchoring materials and both low (Na₂X_n; n ≤ 2) and high order (Na₂X_n; n > 2) Na–poly-sulfide/selenides (Na–pS/Ses) is not sufficient to notably diminish the shuttle effect arising from the sluggish kinetics of immobilized Na₂S/Se. Hence, there has been a recent focus on accelerating conversion kinetics by optimizing the compounds involved in these reactions through the shift from insoluble Na₂S/Se to soluble extended-chain Na–pXs (X = S, Se).^21–23

Single atom catalysts (SACs) have been studied as efficient catalysts for electrochemical reactions within metal–S/Se batteries as they exhibit homogeneous active sites, a high catalytic activity, and an optimal catalyst utilization compared to conventional nanocatalysts.²⁴ In order to prevent the aggregation of single atoms (SAs), a substrate that offers effective anchoring sites to trap these SAs is needed. Presently, SACs consisting of transition metal atoms supported on N-doped defective graphene is the most studied model for electrocatalysis in Li–S batteries to suppress the shuttle effect and improve the electrode electrochemical performance.^25–28

Besides N-doped graphene, metal-free graphitic carbon nitride sheets (g-C₃N₄) have attracted attention owing to their unique porous structure and abundant sites for confinement of metal atoms facilitated by their high nitrogen concentration.^29–32 In fact, there have been several reports about utilizing SAs supported by g-C₃N₄ as reliable electrocatalysts for different reactions such as HER,³³ OER,³⁴ and Co₂RR.³⁵ Moreover, few results are also reported with N-coordinated Fe³⁶ and Ni³⁷ adsorbed on two-dimensional g-C₃N₄ for applications in Li–S batteries. However, due to the lack of the special anchoring sites, pristine g-C₃N₄ encounters some challenges in preventing the single metal atoms from aggregation. It has been reported that a stronger metal–support interaction can be achieved by introducing N-vacancies in the g-C₃N₄ monolayer to boost photocatalytic H₂ production,³⁸ nitrogen fixation,³⁹ and in bifunctional oxygen electrocatalyst applications.³⁴ To the best of our knowledge, there is no literature studying SACs in N-deficient graphitic carbon nitride for Na–S and Na–Se batteries.

This study systematically investigates the effect of SACs in the charging and discharging kinetics of Na–S and Na–Se cathodes through Density Functional Theory (DFT) calculations. To this end, we choose seven SA (Co, Fe, Ir, Ni, Pd, Pt, and Rh) adsorbed on a N-deficient graphitic carbon nitride (rg-C₃N₄) monolayer as SACs model systems. We also perform ab initio molecular dynamics (AIMD) simulations for X₈ (X = S, Se) species adsorbed on SACs models and discuss the interaction mechanism between the SAC and Na–pXs. Our calculations indicate that SACs can accelerate the discharging kinetics of sulfur and selenium reduction reaction and we also compare their effectiveness in the Na–S and Na–Se systems. Furthermore, an exploration of decomposition energy barriers and integrated crystal orbital Hamilton populations (ICOHPs) is conducted to compare the charging performance of the SACs models. In both, Na–S and Na–Se systems, SACs demonstrate a significantly improve charging and discharging performance. These findings can guide experimental investigations for exploration and implementation of SACs in energy storage systems.

2. Computational methods

Spin-polarized DFT calculations are performed using the Vienna Ab initio Simulation Package (VASP).^40,41 The exchange–correlation interactions are described using the gradient-corrected Perdew–Burke–Ernzerhof (GGA-PBE) functional⁴² and the projector augmented-wave (PAW) method.⁴³ In addition, van der Waals interactions are included utilizing the Grimme DFT-D3 correction scheme.⁴⁴ For the plane-wave expansion, the cutoff energy is set to 520 eV. The SAC models are built by adsorbing single atom (SA) on a 2 × 2 × 1 supercell of a reduced graphitic carbon nitride monolayer (rg-C₃N₄). Monkhorst–Pack meshes with 3 × 3 × 1 k-points are used for geometric relaxation following previous theoretical studies of SA supported on g-C₃N₄.^45–47 During the geometric optimization of Na–pXs within the SACs models, relaxation of atomic positions is carried out with a constant cell shape until the residual force reaches a threshold of less than 0.01 eV Å⁻¹. A 20 Å vacuum space along the z-direction is considered to prevent interactions with adjacent periodic images. Our ab initio molecular dynamics (AIMD) simulations are conducted using the Nose–Hoover thermostat at room temperature (300 K) for X₈ (X = S, Se) species on the SACs models. The climbing image-nudged elastic-band (CI-NEB) method is used to calculate the decomposition energies of Na₂X.^48,49 Bader charge analysis is carried out to analyze the charge transfer between Na₂X and the SA.⁵⁰ Phonon dispersion curves are obtained using DFPT (density functional perturbation theory) and the PHONONPY packages.^51,52 The chemical bond analyses based on the Crystal Orbital Hamilton Population (COHP) method were conducted using the LOBSTER package.⁵³ The d-band center and Gibbs free energy correction is calculated using vaspkit.⁵⁴ The VESTA code was used for the visualization of geometric configurations and charge density differences.⁵⁵

The adsorption energies (E_ads) of Na–pXs on the rg-C₃N₄ substrate was evaluated using the following equation^56,57

E_ads = E_Na–pXs + E_Substrate − E_Total

where E_Total, E_Substrate, and E_Na–pXs are the energies of the Na–pXs (X = S, Se) adsorbed on the rg-C₃N₄ substrate, the isolated rg-C₃N₄ substrate, and an isolated Na–pXs molecule, respectively. According to this definition, a positive E_ads indicates a stable binding between molecule and substrate. Details on the Gibbs free energy calculations procedure are presented in ESI.†

3. Results and discussion

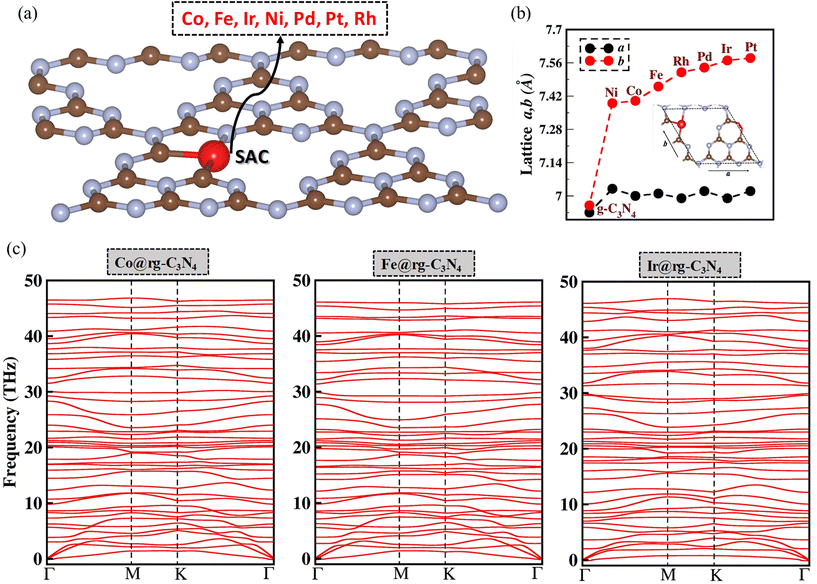
As shown in Fig. 1(a), SACs are modeled by embedding a SA on a N-deficient graphitic carbon nitride (SA@rg-C₃N₄) monolayer. The metals selected as SACs are Co, Fe, Ir, Ni, Pd, Pt, and Rh as they have been identified as the are most robust SACs based on their high thermodynamic, electrochemical, and thermal stability.⁵⁸ As depicted in Fig. 1(b), the lattice parameters (a and b for a 1 × 1 unit cell) of the SA@rg-C₃N₄ systems exhibit a significant increase compared to the pristine (a = 6.93 Å, b = 6.95 Å) and reduced (a = 6.91 Å, b = 5.94 Å) g-C₃N₄ monolayers. This volume expansion can be attributed to the large van der Waals radii of the SAs incorporated in the manolayer.⁵⁹ Additionally the optimized configuration and electronic band structure of g-C₃N₄ and rg-C₃N₄ monolayers are presented in Fig. S1.† In order to verify the dynamic stability of the SA@rg-C₃N₄ systems, we conducted an analysis of the phonon dispersion spectra. As illustrated in Fig. 1(c) for Co, Fe, and Ir, and Fig. S2† for the remaining SAs, no noticeable imaginary phonon modes are detected in the spectra, indicating the overall dynamic stability of all seven SA@rg-C₃N₄ systems.

Fig. 1 (a) Perspective view of a SA adsorbed on the rg-C₃N₄ support. (b) Lattice constant of the SA@rg-C₃N₄ monolayer for a 1 × 1 unit cell as represented in the inset. (c) Phonon spectra curves of SA@rg-C₃N₄ for SA = Co, Fe, Ir.

3.1. Adsorption of X₈

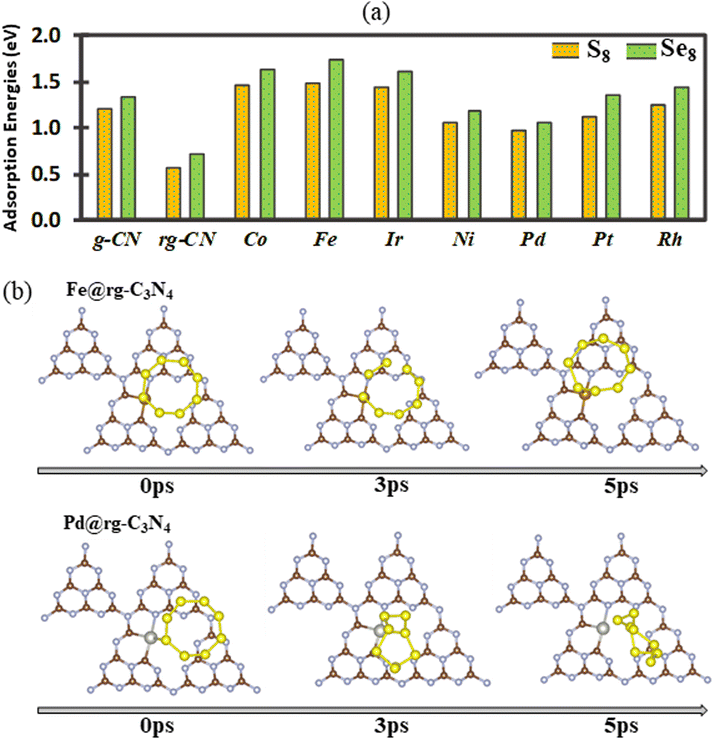
Initially, the adsorption of X₈ (with X = S and Se) species is examined on pristine and reduced g-C₃N₄ as well as SA@rg-C₃N₄. The calculated adsorption energies are shown in Fig. 2(a), where we observe that the adsorption on all substrates is slightly stronger for Se₈ than for S₈, even though the overall trends are similar for the two cases. In both cases, the highest adsorption energy is obtained for the Fe catalyst and can be correlated to the shortest bond lengths Fe–S (2.16 Å) and Fe–Se (2.29 Å) among all SAC substrates. With the exception of Pd and Ni, the adsorption energies on the SAC surfaces of both S₈ and Se₈ structures are notably higher than on pristine and reduced g-C₃N₄ indicating that the incorporation of SACs can boost the capacity of g-C₃N₄ to load S and Se active materials. To further elucidate the adsorption mechanism of X₈ on the SAC substrates, the charge transfer between the X₈ molecules and the substrates is obtained (Fig. S4†). In the case of Pd and Pt catalysts there is a small charge transfer of approximately 0.016 electrons from S₈ to the substrate. For Fe, Co, Ir, Ni, and Rh SACs, the charge transfer is also small but occurs in the opposite direction, with approximately in the range from 0.047 to 0.13 electrons transferred from the substrate to S₈.

Fig. 2 (a) The adsorption energies of X₈ (X = S and Se) adsorbed on the surface of pristine, reduced g-C₃N₄, and SA@rg-C₃N₄ (SA = Co, Fe, Ir, Ni, Pd, Pt, and Rh). (b) Snapshot at 5 ps of AIMD simulations of the adsorption of S₈ on SA@rg-C₃N₄ for SA = Fe and Pd.

In order better understand the adsorption behaviour of S₈ and Se₈ at the early stages of discharge, AIMD simulations starting at the optimized adsorption configurations on various substrates are performed. After 5 ps, all adsorption configurations of S₈ and Se₈ on the SAC substrates (except on the Pd SAC) remain intact without any apparent migration or deformation (S₈ on the Fe SAC is shown as an example in Fig. 2(b)). However, our calculations indicate that for X₈ adsorption on substrates without metal atom catalysts (pristine and reduced g-C₃N₄ substrates), there is a substantial surface reconstruction and deformation of the X₈ molecule. The AIMD snapshots of S₈ and Se₈ on various substrates are presented in Fig. S5 and S6,† respectively. The apparent migration and rotation of S₈ from the hollow cavity shown in Fig. 2(b) can be correlated to the lower adsorption energy of S₈ on Pd-based SAC compared to other SA catalysts. Our AIMD calculations indicate that up to 5 ps, the structure of X₈ remains almost intact when adsorbed on Fe, Co, Ir, Ni, Pt, and Rh SACs, suggesting that there is no significant occurrence of sulfur or selenium poisoning in these substrates.^28,60

3.2. Adsorption of Na–pXs (X = S, Se)

During the discharge process, the interaction of Na cations with the X cathode can generate a series of intermediate compounds from Na₂X₈ to Na₂X (Na₂X₈, Na₂X₆, Na₂X₄, Na₂X₂, and Na₂X). Therefore, we also investigated the interaction between both insoluble species (Na₂X_n; n = 1, 2) and soluble species (Na₂X_n; n = 4, 6, 8) and the substrates to elucidate the role of the SAC in mitigating the poly-sulfide and selenide shuttle effect in Na–S and Na–Se electrodes. The optimized geometric configurations of all the Na₂X_n; n = 1, 2, 4, 6, 8 species are provided in Fig. S7† and the obtained X–X and Na–X bond distance agrees well with previous studies (Table S2†).^61–63Fig. 3(a) shows the adsorption energies of Na₂X_n (n = 1, 4, 8) species on the surface of pristine (g-C₃N₄), reduced (rg-C₃N₄) and seven SA@rg-C₃N₄ catalysts. The most stable configurations of Na–pSs and Na–pSes adsorbed on various substrates are presented in Fig. S8 and S9,† respectively. The adsorption configurations of Na–pXs for SACs are very similar. Both X and Na atoms contribute to their adsorption via SA–X and Na–N interactions, while the adsorption on pristine and reduced g-C₃N₄ primarily results only from the interaction between Na and N, which is further confirmed by the charge density analysis in section 3.4. Taking Fe SAC as a representative example, Fig. 3(b) shows that the Fe–S bond length is shortened from 2.18 Å (Na₂S₈) to 2.16 Å (Na₂S), suggesting an enhanced interaction in low-order Na–pXs. Moreover, the adsorption energies of insoluble Na₂X on the surface of SACs are in the range of 3.0–3.8 eV, significantly larger than on pristine and reduced g-C₃N₄ (2.5–2.8 eV), which indicates that the introduction of SAs can enhance the interaction of Na–pXs and rg-C₃N₄. For comparison, it is worth noting that Na–pSs (Na₂S_n; n = 1, 2, 4, 6) exhibit stronger adsorption energies than Na–pSes. However, Na₂Se₈ exhibits a larger adsorption energies than Na₂S₈. Among the SACs studied in this work, Fe@rg-C₃N₄ presents the strongest interaction for both Na–pSs and Na–pSes, with adsorptions energies surpassing numerous previously reported 2D sulfur hosts like graphene,⁶⁴ MXenes,⁶⁵ VS₂,⁶⁶ and As₂S₃.⁶⁷ Additionally, we have also computed the adsorption energy for Na₂X₃ species on pristine, reduced g-C₃N₄, and Fe SAC as shown in Fig. S10.† The observed trend of adsorption strength, with Na₂X₃ exhibiting greater affinity than Na₂X₄ and lesser affinity than Na₂X, closely mirrors findings reported in the literature for Li₂S₃.⁶⁸ It is interesting to compare the Na–pXs binding strengths on these substrates with the interaction energies of these species in commonly used electrolyte solvents such as 1,3-dioxolane (DOL) and 1,2 dimethoxymethane (DME).⁶⁹ The optimized configurations of DOL and DME with Na–pXs (X = S, Se) are shown in Fig. S11.† The interaction energies (0.58–0.81 eV)⁶⁵ between Na–pXs and DOL/DME are significantly lower than the adsorption energies (1.65–3.83 eV) of Na–pXs on SACs, suggesting that these SACs can effectively preclude Na–pXs shuttling in Na–S and Na–Se batteries.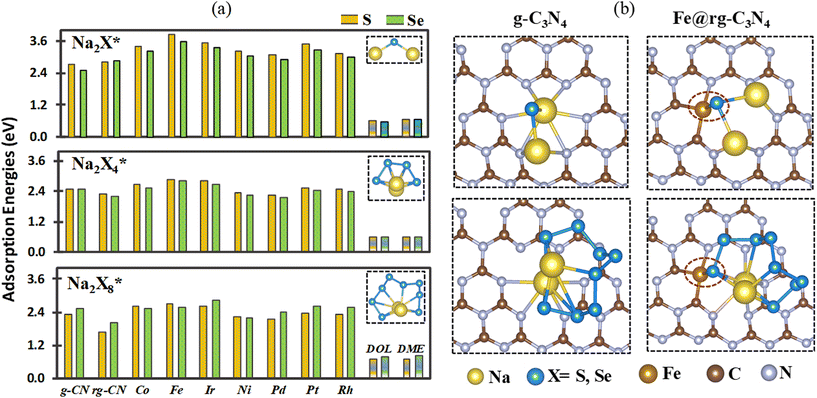

Fig. 3 (a) The adsorption energies of Na₂X_n (n = 1, 4, 8) adsorbed on SA@rg-C₃N₄. (b) Geometrical structures of Na₂X_n (n = 1, 8) adsorbed on a pristine g-C₃N₄ and Fe@rg-C₃N₄ monolayer.

In order to further understand the underlying physical mechanisms governing the interaction between Na–pXs and SAC, we examined the charge transfer of the adsorbed Na–pXs using Bader charge analysis. Our results (see Table S3†) indicate that overall, as sodiation progresses from Na₂X₈ to Na₂X, there is a gradual increase in the amount of charge transferred between the Na–pXs and the substrate. This result indicates that the interaction between each SAC substrate and Na–pXs becomes more robust with increased sodiation, which in turn could explain their greater adsorption affinity for lower Na–pXs. However, when comparing different substrates, we note that the charge transfer between Na–pXs and substrates is, in general, larger in pristine and reduced g-C₃N₄ than in the SACs substrates. As the binding energies of Na–pXs are significantly larger in the SACs substrates, it is then expected that the SACs substrates increase the covalency of the interactions compared to pristine and reduced g-C₃N₄.

3.3. Discharging performance of Na–S and Na–Se electrodes

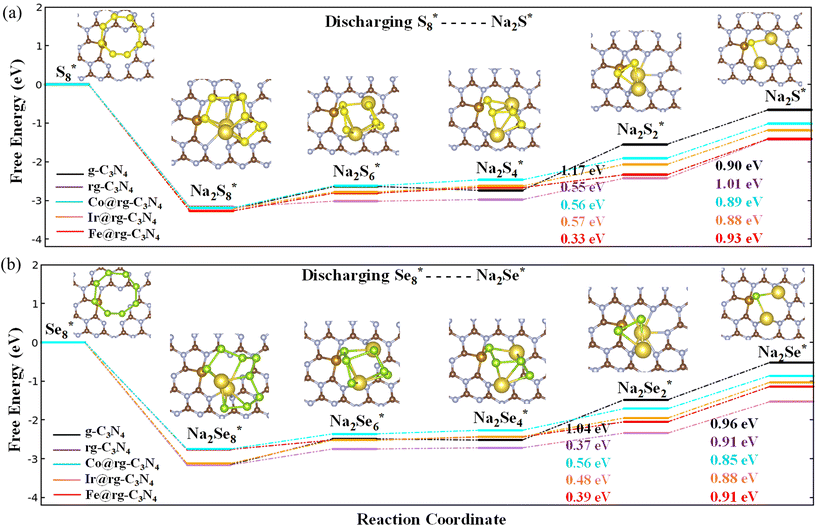
To analyze the discharging performance of the electrodes, we next explore the sulfur and selenium reduction reactions on various g-C₃N₄ substrates. During the initial discharge process of a Na–S electrode, the solid-phase S₈ undergoes a transformation into a series of soluble Na–pSs (Na₂S_n; 4 ≤ n ≤ 8), which are subsequently further reduced into insoluble Na–pSs (Na₂S_n; 1 ≤ n ≤ 3).⁷⁰ As discussed previously, the electrochemical reaction mechanisms of Na–Se batteries is similar to that of Na–S batteries, with the formation of Na–pSes as intermediate products and Na₂Se as the final discharge product.¹⁰ The Gibbs free energy of each intermediate reaction step from S₈* to Na₂S* and from Se₈* to Na₂Se* over g-C₃N₄, rg-C₃N₄ and SA@rg-C₃N₄ (with SA = Co, Ir, and Fe) are shown in Fig. 4(a) and (b), respectively. The remaining Gibbs free energy plots for the reduction of Na–pSs and Na–pSes on SA@g-C₃N₄ (with SA = Rh, Ni, Pd, and Pt) are presented in ESI (Fig. S12†). Following current literature notation, * represents an active site on the catalytic substrate.

Fig. 4 Energy profiles for the reduction of (a) Na–pSs and (b) Na–pSes on g-C₃N₄, rg-C₃N₄ and SA@rg-C₃N₄ (SA = Co, Fe, Ir) monolayer. The inset images are the top view of Na–pXs adsorbed on the substrates.

For both battery systems, the initial step corresponding to the reduction of X₈ to Na₂X₈ is an exothermic reaction regardless of the substrate, indicating the spontaneous nature of this conversion. All the following four reactions steps are endothermic reactions. Our calculations indicate that for g-C₃N₄, the limiting step corresponds to the transition from Na₂X₄ to Na₂X₂, and from Na₂X₂ to Na₂X in the rg-C₃N₄ substrate. A similar trend of limiting steps is observed in graphene and N-doped graphene for Li–S battery systems.⁷¹ For Ir, Co, Fe, and Rh SACs, the last transition from Na₂X₂ to Na₂X is associated with a notably high positive Gibbs free energy barrier compared to other steps indicating the last reaction step as the rate determining (RD) step in the whole process. On the other hand, for SACs containing Ni, Pd, and Pt, the transition from a soluble Na₂X₄ to an insoluble Na₂X₂ is found to be the RD step as they present the highest energy barrier. In comparison to Na–S, Na–Se shows a superior reaction kinetics due to the lower RD step barrier for selenium reduction reactions on SACs. The RD step on the surface of SACs is significantly reduced, falling within the range of 0.68 to 1.0 eV, compared to the 1.17 eV and 1.01 eV for pristine g-C₃N₄ and rg-C₃N₄, respectively. The obtained RD step barriers for Ni, and Co, Ir, Fe, Rh are lower than for the reported highly active MXenes for Na–S batteries (0.85–1.23 eV)⁷² and Na–Se batteries (0.80–1.4 eV).⁶¹ Overall, the presence of a SA in conjunction with a rg-C₃N₄ support significantly enhances the discharging performance for the sulfur and selenium reduction reactions.

3.4. Charging performance of Na–S and Na–Se electrodes

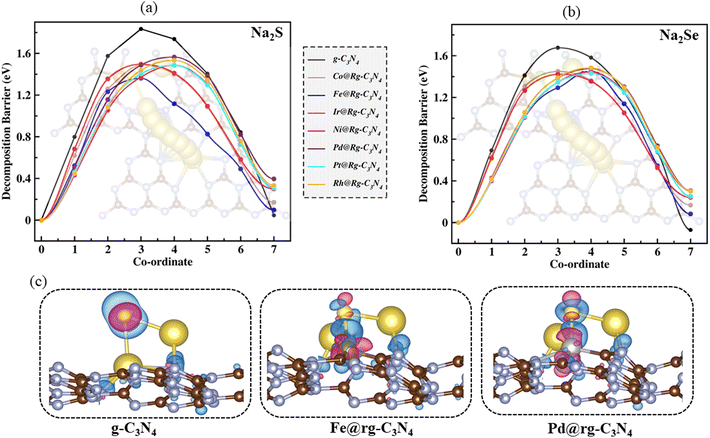
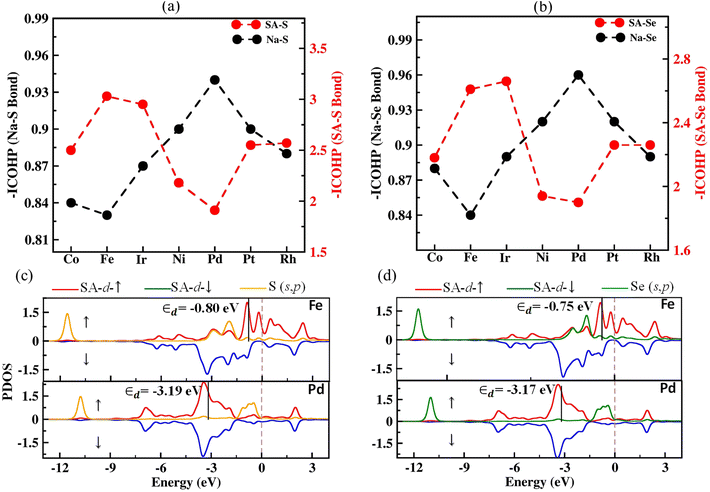
The reaction kinetics during the charging process of Na–S and Na–Se electrodes are primarily governed by the decomposition of Na₂S and Na₂Se, respectively.¹¹ Therefore, reducing the decomposition barriers of Na₂X can significantly enhance the oxidation reaction kinetics and prolong the life cycle of the electrodes. We investigated the decomposition mechanisms of Na₂X oxidation (Na₂X* → NaX* + Na⁺ + e⁻) using the CI-NEB method.^48,49 The energy profiles along the optimal reaction pathways for Na₂X decomposition are illustrated in Fig. 5(a) and (b). The barriers for the Na₂X decomposition on the SACs substrates (1.44–1.56 eV for Na₂S and 1.42–1.48 eV for Na₂Se) are significantly lower than in both g-C₃N₄ (1.83 eV for Na₂S and 1.68 eV for Na₂Se) and rg-C₃N₄ substrate (2.69 eV for Na₂S and 2.53 eV for Na₂Se). Furthermore, in Fig. 5(c) we show the charge density difference, defined as Δρ = ρ_total − ρ_substrate − ρ_Na–pXs,⁷³ where ρ_total, ρ_substrate, and ρ_Na–pXs stand for the charge densities of the Na–pXs (X = S, Se) molecule adsorbed on the SA@rC₃N₄ substrate, the SA@rC₃N₄ substrate, and the isolated Na–pXs molecule, respectively. Fig. 5c, indicates that in the case of pristine g-C₃N₄, the charge transfer occurs predominantly between Na atoms and the substrate. However, for the SAC substrates, in addition to electron transfer from Na to the substrate, there is also a substantial flow of electrons between S and the metal atom (SA). It is worth noting that the electron transfer is more pronounced in Fe–S than in Pd–S bonds. This increased electron transfer between S and the SA atom can lead to the formation of a S–SA bond and a weakening the Na–S bond.

Fig. 5 Decomposition paths and decomposition energies of (a) Na₂S and (b) Na₂Se on the pristine g-C₃N₄ and SA@rg-C₃N₄ monolayers. (c) The charge density differences of Na₂S adsorbed on the pristine g-C₃N₄ and SA@rg-C₃N₄ monolayer. The blue regions represent electron accumulation, and magenta regions represent depletion.

To further investigate the Na₂X decomposition mechanism on different SAC substrates, the intensity of Na–X and SA–X on various SACs substrates is evaluated using the Integrated of Crystal Orbital Hamilton Population (ICOHP) analysis.^74,75 For clarity, on Fig. 6(a) and (b), we present the negative values of the ICOHP results, –ICOHP, in units of eV per bond. Therefore, larger values of –ICOHP represent stronger inter-atomic interactions. The results shown in Fig. 6(a) and (b) suggest that the strength of both the SA–S and SA–Se bonds is largest for Fe among all other SACs, in agreement with our previous analysis. Conversely, for Na–X bonds, –ICHOP results reveal the opposite trend, i.e., this interaction is weakest for Fe. Additionally, the Na–X bond strength (–ICOHP = 0.95 eV for Na₂S and 0.96 eV for Na₂Se) is larger in pristine g-C₃N₄ than in SACs based substrates, in agreement with the decomposition barriers results. The bonding interactions are further explored by plotting the partial density of states (PDOS) for SACs to reveal the electronic states of the SA and X (S, Se) atom. The strength of the SA–X interaction can be correlated to the position of the antibonding state (relative to the Fermi level), where a closer position of the antibonding state to the Fermi level can indicate a stronger SA–X interaction. The d-band model is extensively utilized to elucidate bond formation and reactivity patterns observed in transition metals.⁷⁶ Results presented in Fig. 6(c) and (d) show that the d-band centers (ε_d) of Fe are closer to the Fermi level than in other SACs. This proximity results in a stronger interaction between X and Fe, in agreement with the calculated decomposition barriers and binding strengths and the consequent weakening of the Na–X bonds in Na₂X. The remaining PDOS for Na₂X–SAC (SAC = Co, Ir, Rh, Ni, and Pt) are presented in Fig. S13.†

Fig. 6 The strength of (a) Na–S and SA–S bonds and (b) Na–Se and SA–Se evaluated using the integrated COHP (–ICOHP) for the Na₂X–SAC system. (Here, the depicted bond strength (–ICOHP) is the sum of the spin-up and spin-down –ICOHP values in eV per bond.) (c and d) The calculated partial density of states (PDOS) of Na₂X–SAC (SAC = Fe, Pd) systems. The up-spin d-band center values are illustrated on the PDOS plot, measured with respect to the Fermi level set at zero.

4. Conclusions

In summary, first-principles calculations are performed to elucidate the charging and discharging kinetics of SACs embedded on reduced g-C₃N₄ for Na–S and Na–Se electrodes. Through an analysis of Na–pS/Ses adsorption energies, the anchoring functionality of rg-C₃N₄ monolayer is found to be enhanced through the incorporation of SACs. AIMD simulations are performed to better understand the adsorption behaviour of S₈ and Se₈ species at the early stages of discharge and indicate no significant occurrence of sulfur or selenium poisoning on the surface of Fe, Co, Ir, Ni, Pt, and Rh SACs.

During the discharge process, the Gibbs free energy of the rate-limiting step of S/Se reduction reactions on the SACs is greatly reduced compared to the pristine g-C₃N₄ and rg-C₃N₄ surfaces, indicating a higher catalytic activity in the SACs substrates.

For the charging of S and Se electrodes, our results indicate that SACs substrates present a lower decomposition energy barrier for Na₂S and Na₂Se indicating a faster charging process of Na–S and Na–Se electrodes. These results are further supported by our ICOHP, PDOS, and d-band center analysis of Na₂S and Na₂Se adsorbed on SAC substrates.

This study offers solutions to the performance limitations caused by the shuttle effect and proposes an effective approach for optimizing single-atom catalysts to enhance the efficiency of sodium–sulfur and sodium–selenium electrodes.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge the support of the Automotive Research Center (ARC), Cooperative Agreement W56HZV-19-2-0001 U.S. Army DEVCOM GVSC. DISTRIBUTION STATEMENT A. Approved for public release; distribution is unlimited. OPSEC#8405. We acknowledge the computational resources and services provided by the Institute for Cyber-Enabled Research at Michigan State University.

References

1. J. Bi, Z. Du, J. Sun, Y. Liu, K. Wang, H. Du, W. Ai and W. Huang, Adv. Mater., 2023, 35, 2210734.
2. Y.-K. Liu, C.-Z. Zhao, J. Du, X.-Q. Zhang, A.-B. Chen and Q. Zhang, Small, 2023, 19, 2205315.
3. J. Neumann, M. Petranikova, M. Meeus, J. D. Gamarra, R. Younesi, M. Winter and S. Nowak, Adv. Energy Mater., 2022, 12, 2102917.
4. N. T. Aristote, X. Deng, K. Zou, X. Gao, R. Momen, F. Li, W. Deng, H. Hou, G. Zou and X. Ji, J. Alloys Compd., 2022, 913, 165216.
5. R. Wang, D. Wang, Y. Dong, B. Xie, X. Wu, Q. Wu, S. Zhu, G. Diao and M. Chen, J. Alloys Compd., 2023, 952, 169980.
6. L. Jingjing, L. Hongji, H. Qiang and C. Zhe, Prog. Chem., 2022, 34, 857.
7. P. Chen, C. Wang and T. Wang, Mater. Res. Lett., 2022, 10, 691–719.
8. P. Hu, F. Xiao, Y. Wu, X. Yang, N. Li, H. Wang and J. Jia, Chem. Eng. J., 2022, 443, 136257.
9. G. Wang, Y. Chen, S. Yuan and P. Ge, Molecules, 2022, 27, 5880.
10. Z. Huang, P. Jaumaux, B. Sun, X. Guo, D. Zhou, D. Shanmukaraj, M. Armand, T. Rojo and G. Wang, Electrochem. Energy Rev., 2023, 6, 21.
11. J. Xu, Y. Qiu, J. Yang, H. Li, P. Han, Y. Jin, H. Liu, B. Sun and G. Wang, Adv. Funct. Mater., 2024, 34, 2306206.
12. Z. Wu, X. Lin, J. Zhang, X. Chu, J. Xu, J. Li, Y. Liu, H. Yu, L. Yan and L. Zhang, et al. , Chem. Eng. J., 2023, 454, 140433.
13. C. Wu, Y. Lei, L. Simonelli, D. Tonti, A. Black, X. Lu, W.-H. Lai, X. Cai, Y.-X. Wang and Q. Gu, et al. , Adv. Mater., 2022, 34, 2108363.
14. Z. Yan, L. Zhao, Y. Wang, Z. Zhu and S.-L. Chou, Adv. Funct. Mater., 2022, 32, 2205622.
15. Y. Wang, D. Zhou, V. Palomares, D. Shanmukaraj, B. Sun, X. Tang, C. Wang, M. Armand, T. Rojo and G. Wang, Energy Environ. Sci., 2020, 13, 3848–3879.
16. R. Fang, J. Xu and D.-W. Wang, Energy Environ. Sci., 2020, 13, 432–471.
17. L. Wang, X. Zhang, L. Deng, J. Tang, H. Deng, W. Hu and Z. Liu, ACS Appl. Mater. Interfaces, 2019, 11, 4995–5002.
18. J. Ding, H. Zhou, H. Zhang, T. Stephenson, Z. Li, D. Karpuzov and D. Mitlin, Energy Environ. Sci., 2017, 10, 153–165.
19. Q. Xu, H. Liu, W. Du, R. Zhan, L. Hu, S. Bao, C. Dai, F. Liu and M. Xu, Electrochim. Acta, 2018, 276, 21–27.
20. X. L. Huang, Y.-X. Wang, S.-L. Chou, S. X. Dou and Z. M. Wang, Energy Environ. Sci., 2021, 14, 3757–3795.
21. M. S. Nahian, R. Jayan and M. M. Islam, ACS Catal., 2022, 12, 7664–7676.
22. F. Jin, B. Wang, J. Wang, Y. Wang, Y. Ning, J. Yang, Z. Zhang, P. Liu, Y. Zhou and D. Wang, et al. , Matter, 2021, 4, 1768–1800.
23. C. Wang, T. Li, X. Hou, M. Jiang, Q. Zheng and X. Li, Chem. Eng. J., 2023, 451, 139062.
24. H. Tian, A. Song, H. Tian, J. Liu, G. Shao, H. Liu and G. Wang, Chem. Sci., 2021, 12, 7656–7676.
25. Z. Du, X. Chen, W. Hu, C. Chuang, S. Xie, A. Hu, W. Yan, X. Kong, X. Wu and H. Ji, et al. , J. Am. Chem. Soc., 2019, 141, 3977–3985.
26. Y. Li, J. Wu, B. Zhang, W. Wang, G. Zhang, Z. W. Seh, N. Zhang, J. Sun, L. Huang and J. Jiang, et al. , Energy Storage Mater., 2020, 30, 250–259.
27. Z. Zeng, W. Nong, Y. Li and C. Wang, Adv. Sci., 2021, 8, 2102809.
28. T. Duan, L. Wang, Z. Ma and Y. Pei, Small, 2023, 19, 2303760.
29. I. Choudhuri, P. Bhauriyal and B. Pathak, Chem. Mater., 2019, 31, 8260–8285.
30. Z. Chen, J. Zhao, C. R. Cabrera and Z. Chen, Small Methods, 2019, 3, 1800368.
31. D. Zeng, W. Xu, W.-J. Ong, J. Xu, H. Ren, Y. Chen, H. Zheng and D.-L. Peng, Appl. Catal., B, 2018, 221, 47–55.
32. W. Sun, Z. Song, Z. Feng, Y. Huang, Z. J. Xu, Y.-C. Lu and Q. Zou, Nano–Micro Lett., 2022, 14, 222.
33. M. Jyothirmai, D. Roshini, B. M. Abraham and J. K. Singh, ACS Appl. Energy Mater., 2023, 6, 5598–5606.
34. H. Niu, X. Wan, X. Wang, C. Shao, J. Robertson, Z. Zhang and Y. Guo, ACS Sustainable Chem. Eng., 2021, 9, 3590–3599.
35. Y. Lu, H. Wang, P. Yu, Y. Yuan, R. Shahbazian-Yassar, Y. Sheng, S. Wu, W. Tu, G. Liu and M. Kraft, et al. , Nano Energy, 2020, 77, 105158.
36. S. He, J. Yang, S. Liu, X. Wang, X. Che, M. Wang and J. Qiu, Chem. Eng. J., 2023, 454, 140202.
37. W.-W. Liu, S.-T. Niu, Z.-Q. Xu, R. Zou, C.-Y. Cui, Y.-X. Lei, X.-B. Zhang and F. Ran, Appl. Surf. Sci., 2023, 609, 155327.
38. P. Zhou, F. Lv, N. Li, Y. Zhang, Z. Mu, Y. Tang, J. Lai, Y. Chao, M. Luo and F. Lin, et al. , Nano Energy, 2019, 56, 127–137.
39. X. Chen, X. Zhao, Z. Kong, W.-J. Ong and N. Li, J. Mater. Chem. A, 2018, 6, 21941–21948.
40. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
41. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
42. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
43. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953.
44. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
45. N. Yamsang, J. Sittiwong, P. Srifa, B. Boekfa, M. Sawangphruk, T. Maihom and J. Limtrakul, Appl. Surf. Sci., 2021, 565, 150378.
46. Y. Cheng, Y. Dou, D. Kan, Y. Wang and Y. Wei, Appl. Surf. Sci., 2023, 610, 155481.
47. G. D. Fao and J.-C. Jiang, Mol. Catal., 2022, 526, 112402.
48. G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904.
49. G. Henkelman and H. Jónsson, J. Chem. Phys., 2000, 113, 9978–9985.
50. W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21, 084204.
51. A. Togo, F. Oba and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 134106.
52. A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5.
53. S. Maintz, V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Comput. Chem., 2016, 37, 1030–1035.
54. V. Wang, N. Xu, J.-C. Liu, G. Tang and W.-T. Geng, Comput. Phys. Commun., 2021, 267, 108033.
55. K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276.
56. Y. Zhao and J. Zhao, Appl. Surf. Sci., 2017, 412, 591–598.
57. L. Song, M. Zhang and J. Guo, Chem. Phys. Lett., 2021, 777, 138711.
58. M. Jakhar, Y. Ding, B. D. Fahlman and V. Barone, Nano Express, 2024, 5, 015028.
59. S. S. Batsanov, Inorg. Mater., 2001, 37, 871–885.
60. X. Song, D. Tian, Y. Qiu, X. Sun, B. Jiang, C. Zhao, Y. Zhang, L. Fan and N. Zhang, Energy Storage Mater., 2021, 41, 248–254.
61. C. Wei, M. Ge, T. Fang, X. Tang and X. Liu, Phys. Chem. Chem. Phys., 2023, 25, 24948–24959.
62. N. Li, Y. Zhan, H. Wu, J. Fan and J. Jia, Nanoscale, 2022, 14, 17027–17035.
63. M. Sajjad, T. Hussain, N. Singh and J. A. Larsson, Langmuir, 2020, 36, 13104–13111.
64. R. Jayan and M. M. Islam, J. Phys. Chem. C, 2021, 125, 4458–4467.
65. N. Li, Y. Zhan, H. Wu, J. Fan and J. Jia, Nanoscale, 2023, 15, 2747–2755.
66. R. Jayan and M. M. Islam, ACS Appl. Mater. Interfaces, 2021, 13, 35848–35855.
67. T. Kaewmaraya, T. Hussain, R. Umer, Z. Hu and X. Zhao, Phys. Chem. Chem. Phys., 2020, 22, 27300–27307.
68. S. Mukherjee, L. Kavalsky, K. Chattopadhyay and C. V. Singh, Nanoscale, 2018, 10, 21335–21352.
69. Y. Liu, Y. Elias, J. Meng, D. Aurbach, R. Zou, D. Xia and Q. Pang, Joule, 2021, 5, 2323–2364.
70. H. Liu, W.-H. Lai, Q. Yang, Y. Lei, C. Wu, N. Wang, Y.-X. Wang, S.-L. Chou, H. K. Liu and S. X. Dou, Nano–Micro Lett., 2021, 13, 121.
71. G. Zhou, S. Zhao, T. Wang, S.-Z. Yang, B. Johannessen, H. Chen, C. Liu, Y. Ye, Y. Wu and Y. Peng, et al. , Nano Lett., 2019, 20, 1252–1261.
72. M. S. Nahian, R. Jayan, T. Kaewmaraya, T. Hussain and M. M. Islam, ACS Appl. Mater. Interfaces, 2022, 14, 10298–10307.
73. Z. Yi, F. Su, L. Huo, G. Cui, C. Zhang, P. Han, N. Dong and C. Chen, Appl. Surf. Sci., 2020, 503, 144446.
74. V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Phys. Chem. A, 2011, 115, 5461–5466.
75. M. Tachibana, K. Yoshizawa, A. Ogawa, H. Fujimoto and R. Hoffmann, J. Phys. Chem. B, 2002, 106, 12727–12736.
76. S. Bhattacharjee, U. V. Waghmare and S.-C. Lee, Sci. Rep., 2016, 6, 35916.

---

Footnote

† Electronic supplementary information (ESI) available: Phonon spectrum curves for SA@rg-C₃N₄; charge transfer and AIMD plot for the X₈ (X = S, Se) molecules; the optimized geometric configurations of Na–pXs (X = S, Se); geometric configurations of electrolyte solvent (DOL and DME); Gibbs free energy profile for sulfur/selenium reduction reactions (S/SeRRs); partial density of states (PDOS) of Na₂X–SA. See DOI: https://doi.org/10.1039/d4nr01134a

---