Ultrafast dynamics of fluorene initiated by highly intense laser fields†
Diksha
Garg
ab,
Pragya
Chopra
ac,
Jason W. L.
Lee
 ad,
Denis S.
Tikhonov
ad,
Denis S.
Tikhonov
 a,
Sonu
Kumar
a,
Sonu
Kumar
 ab,
Oender
Akcaalan
a,
Felix
Allum‡§
ab,
Oender
Akcaalan
a,
Felix
Allum‡§
 d,
Rebecca
Boll
d,
Rebecca
Boll
 e,
Alexander A.
Butler
d,
Benjamin
Erk
e,
Alexander A.
Butler
d,
Benjamin
Erk
 a,
Eva
Gougoula
a,
Eva
Gougoula
 a,
Sébastien P.
Gruet
a,
Lanhai
He
a,
Sébastien P.
Gruet
a,
Lanhai
He
 f,
David
Heathcote
f,
David
Heathcote
 d,
Ellen
Jones
d,
Mehdi M.
Kazemi
a,
Jan
Lahl
g,
Alexander K.
Lemmens
d,
Ellen
Jones
d,
Mehdi M.
Kazemi
a,
Jan
Lahl
g,
Alexander K.
Lemmens
 hi,
Zhihao
Liu
d,
Donatella
Loru
hi,
Zhihao
Liu
d,
Donatella
Loru
 a,
Sylvain
Maclot
a,
Sylvain
Maclot
 j,
Robert
Mason
d,
James
Merrick
d,
Erland
Müller
a,
Terry
Mullins
fe,
Christina C.
Papadopoulou
a,
Christopher
Passow
a,
Jasper
Peschel
g,
Marius
Plach
j,
Robert
Mason
d,
James
Merrick
d,
Erland
Müller
a,
Terry
Mullins
fe,
Christina C.
Papadopoulou
a,
Christopher
Passow
a,
Jasper
Peschel
g,
Marius
Plach
 g,
Daniel
Ramm
a,
Patrick
Robertson¶
g,
Daniel
Ramm
a,
Patrick
Robertson¶
 d,
Dimitrios
Rompotis
d,
Dimitrios
Rompotis
 ae,
Alcides
Simao||
ae,
Alcides
Simao||
 a,
Amanda L.
Steber**
a,
Amanda L.
Steber**
 a,
Ayhan
Tajalli
a,
Ayhan
Tajalli
 a,
Atia
Tul-Noor
a,
Atia
Tul-Noor
 a,
Nidin
Vadassery
fk,
Ivo S.
Vinklárek
f,
Simone
Techert
a,
Jochen
Küpper
a,
Nidin
Vadassery
fk,
Ivo S.
Vinklárek
f,
Simone
Techert
a,
Jochen
Küpper
 fblk,
Anouk M.
Rijs
fblk,
Anouk M.
Rijs
 m,
Daniel
Rolles
m,
Daniel
Rolles
 n,
Mark
Brouard
n,
Mark
Brouard
 d,
Sadia
Bari
d,
Sadia
Bari
 ao,
Per
Eng-Johnsson
ao,
Per
Eng-Johnsson
 g,
Claire
Vallance
g,
Claire
Vallance
 d,
Michael
Burt
d,
Michael
Burt
 d,
Bastian
Manschwetus††
d,
Bastian
Manschwetus††
 a and
Melanie
Schnell
a and
Melanie
Schnell
 *ac
*ac
aDeutsches Elektronen-Synchrotron DESY, Hamburg, Germany. E-mail: melanie.schnell@desy.de
bDepartment of Physics, Universität Hamburg, Hamburg, Germany
cInstitute of Physical Chemistry, Christian-Albrechts-Universität zu Kiel, Kiel, Germany
dChemistry Research Laboratory, Department of Chemistry, University of Oxford, Oxford, UK
eEuropean XFEL, Schenefeld, Germany
fCenter for Free-Electron Laser Science CFEL, Deutsches Elektronen-Synchrotron DESY, Germany
gDepartment of Physics, Lund University, Lund, Sweden
hVan’t Hoff Institute for Molecular Sciences, University of Amsterdam, Amsterdam, The Netherlands
iFELIX Laboratory, Radboud University, Nijmegen, The Netherlands
jUniversité Claude Bernard Lyon 1, Villeurbanne, France
kDepartment of Chemistry, Universität Hamburg, Hamburg, Germany
lCenter for Ultrafast Imaging, Universität Hamburg, Hamburg, Germany
mDivision of BioAnalytical Chemistry, Vrije Universiteit Amsterdam, Amsterdam, The Netherlands
nJ. R. Macdonald Laboratory, Department of Physics, Kansas State University, Manhattan, KS, USA
oZernike Institute for Advanced Materials, University of Groningen, Groningen, The Netherlands
First published on 20th June 2024
Abstract
We present an investigation of the ultrafast dynamics of the polycyclic aromatic hydrocarbon fluorene initiated by an intense femtosecond near-infrared laser pulse (810 nm) and probed by a weak visible pulse (405 nm). Using a multichannel detection scheme (mass spectra, electron and ion velocity-map imaging), we provide a full disentanglement of the complex dynamics of the vibronically excited parent molecule, its excited ionic states, and fragments. We observed various channels resulting from the strong-field ionization regime. In particular, we observed the formation of the unstable tetracation of fluorene, above-threshold ionization features in the photoelectron spectra, and evidence of ubiquitous secondary fragmentation. We produced a global fit of all observed time-dependent photoelectron and photoion channels. This global fit includes four parent ions extracted from the mass spectra, 15 kinetic-energy-resolved ionic fragments extracted from ion velocity map imaging, and five photoelectron channels obtained from electron velocity map imaging. The fit allowed for the extraction of 60 lifetimes of various metastable photoinduced intermediates.
1 Introduction
Polycyclic aromatic hydrocarbons (PAHs) are a large class of molecules that consist of carbon and hydrogen atoms. Each PAH contains at least two rings, of which at least one is aromatic. These molecules play an important role in astrochemistry since they are estimated to account for about 10% of all galactic carbon.1,2 PAHs can also form in combustion reactions of fossil fuels, which lead to the presence of PAHs in the Earth's atmosphere. Here, they act as environmental pollutants, and they impact the health of the population.3,4 In the interstellar medium (ISM) and planetary atmospheres, PAHs are subjected to high-energy particles.5–8 Therefore, investigating PAHs' radiation and photoinduced chemistry is a compelling study with broad implications. Upon passing near the molecule, fast-charged particles, such as electrons or alpha particles, will create a short, strong electric field comparable to the atomic scales. To mimic such strong-field excitation of molecules, we can apply strong-field laser pulses in the laboratory environment.Previously, strong-field-induced ionization and fragmentation of PAHs were studied with table-top laser setups.9–12 In particular, laser pulses with peak intensities of about ∼1014 W cm−2 interacting with PAHs have produced ionic species up to tetracations.9 Investigations of the ultrafast ionization and fragmentation of PAHs induced by highly energetic XUV photons have recently gained attention in the scientific community for tracing down mechanisms of photochemical reactions. The ultrafast pump–probe studies with ultrashort XUV pulses produced either by high-harmonic generation (HHG) sources13–16 or free-electron lasers (FELs)17–19 revealed rich dynamics of charge state evolutions up to PAH trications. Femtosecond strong-field laser pulses, produced by Ti:Sa lasers, were also used to induce dynamics in benzene and toluene.20,21 These studies found interesting dynamics, such as oscillations between vibrational states in toluene,21 or conical intersection relaxation20 in Jahn–Teller benzene cations.22,23
In this work, we present an investigation of the dynamics of a three-ring PAH fluorene (C13H10, FLU, see Fig. 1). This molecule can be thought of as a three-ring analog of indene, the first pure PAH identified in the ISM.24,25 The XUV-induced dynamics of FLU have recently been studied in detail.17,19 As a follow-up, here we chose to investigate how the observed dynamics change in a different excitation regime. We used ultrashort strong-field infrared (IR) laser pulses to excite FLU and subsequently probed it using a weaker visible (VIS) pulse. The pump pulse peak intensity was estimated to be 3.3 × 1013 W cm−2, which corresponds to a Keldysh parameter value of γ = 1.4,26 for the single ionization of FLU. Based on the calculated γ value and considering a non-uniform spatial distribution of intensities in the laser pulse, we expect to observe a mixed regime of strong-field ionization that could show features of both tunneling ionization (TI, γ ≪ 1) and multiphoton ionization (MPI, γ ≫ 1). The interaction of the strong-field laser with FLU results in the production of electrons and multiple ions, which were measured using a double-sided velocity map imaging (VMI) spectrometer. VMI enabled the disentangling of the various photodissociation fragmentation pathways on the basis of momentum. In addition, the time-of-flight (TOF) mass spectra (MS) of the ions were measured. This multi-channel data accumulation allowed for a detailed and comprehensive decomposition of the strong-field-induced dynamics of FLU. In this manuscript, we describe the experimental details, data analysis, and theoretical calculations. This is followed by pump–probe independent results, dynamical observations, and conclusions.
2 Methods
2.1 Experimental details
The IR (810 nm)–VIS (405 nm) pump–probe experiments were carried out at the permanent CAMP end-station27 at beamline BL1 at the free-electron laser in Hamburg (FLASH)28 facility. A Ti:Sa laser system29 produced pulses at 810 nm. The pulses were then split into two components with a beamsplitter in a ratio of 75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25.30 Most of each pulse was used as an IR pump, and a part of each pulse went to the second harmonic generation (SHG) to produce a weaker VIS probe pulse of 405 nm. The duration (full width at half maximum, FWHM) of the IR pulse was 60 fs, while the duration of the VIS pulse was estimated to be less than 150 fs. We measured the ion yield produced as a function of pump–probe delay time. The arrival time of the probe pulse was varied from −1 ps to +1 ps in 15 fs steps relative to the pump pulse using a mechanical delay stage.
25.30 Most of each pulse was used as an IR pump, and a part of each pulse went to the second harmonic generation (SHG) to produce a weaker VIS probe pulse of 405 nm. The duration (full width at half maximum, FWHM) of the IR pulse was 60 fs, while the duration of the VIS pulse was estimated to be less than 150 fs. We measured the ion yield produced as a function of pump–probe delay time. The arrival time of the probe pulse was varied from −1 ps to +1 ps in 15 fs steps relative to the pump pulse using a mechanical delay stage.
The CAMP end-station houses a double-sided ion and electron VMI spectrometer,31,32 enabling the measurement of ion and electron kinetic energies simultaneously. An open port in the vacuum chamber at the CAMP end-station allowed for the installation of a source chamber equipped with a high-temperature Even-Lavie valve (ELV),33 two subsequent skimmers and a differential pumping step for sample introduction into the experiment.
The sample of FLU was purchased from Sigma-Aldrich and Thermo Fisher with 98% purity and used without further purification in two different beamtimes performed in 2018 (F-20170540) and 2023 (F-20211752), respectively. In the experiment, fluorene powder was heated to 200 °C in an in-vacuum reservoir, implemented in the ELV, in order to obtain sufficient vapor pressure. The gas-phase molecules were then introduced into the vacuum chamber by means of a helium carrier gas with a backing pressure of 1 bar. A pulsed molecular jet was doubly skimmed on the way to the interaction region to obtain a well-collimated molecular beam.
Three types of data obtained from the experiments have been used for the analysis, namely, the TOF-MS, the electron VMI, and the ion VMI. Each ion and electron dataset were acquired using a combination of microchannel plate (MCP) in chevron configuration and phosphor screens, P47 and P20, respectively. The TOF-MS were obtained directly from the MCP readout with the help of a 2 GHz analog-to-digital-converter (ADQ412AC-4G-MTCA). The velocity map images of all individual ionic species simultaneously, together with lower-resolution TOF-MS, were obtained using a Pixel Imaging Mass Spectrometry (PImMS2) sensor.34,35 Lastly, the electron data was obtained directly from a charge-coupled device (CCD, in 2018) or complementary metal–oxide–semiconductor (CMOS, in 2023) camera readout.
2.2 Data analysis
Data extraction and analysis were performed using home-written scripts. To retrieve and analyze the data from the TOF-MS and electron VMI data, a combination of the BeamtimeDAQAccess36 and CAMPFancyAnalysis37 Python libraries was used. For the analysis of the PImMS data, a home-written set of LabView scripts and the CAMPFancyAnalysis library were employed. The inverse Abel transformation for the ion images was performed using the onion peeling method,38 processing of the photoelectron angularly-integrated images was done using direct Abel transformation. Both routines were used as implemented in the PyAbel package.39,40A detailed description of the recoil-frame covariance analysis for the ion VMI data can be found elsewhere.17,41–45 The photoelectron–photoion covariance analysis (PEPICOV) was performed in the following way:46,47 first, each single-shot electron image was converted into the radial distribution function (RDF), and each single-shot TOF-MS was converted into the mass-over-charge (m/z) MS. The centers of the images and the momentum calibration were determined based on the helium II photoelectron data, which was obtained in pre- and post-measurements for the same molecular beam with 41 eV XUV radiation from FLASH, published in ref. 17,19. Then, the covariance map was obtained as
| cov(IY, PEY) = 〈IY·PEY〉 − 〈IY〉·〈PEY〉, |
The observed dependencies of the ion and electron yields as a function of pump–probe delay time were fit as linear combinations of basis functions, describing pump–probe dynamical response17,49,50 using the MC3Fitting software.51 First, a global fitting was done, followed by the Monte-Carlo sampling of the parameters’ uncertainties, as described in detail in ref. 50. A simultaneous fitting was performed for the multiple channel data for the parent ions (from the high-resolution TOF-MS), momentum-disentangled fragment ion yields (from the ion VMI), and photoelectron yields (from the electron VMI). Fitting was done for 40 datasets of ion yield versus pump–probe delay time, which comprise momentum-resolved fragment ion yields of ions having 5 to 12 carbon atoms, the parent monocation, dication, and trication, dehydrogenated parent monocation, momentum-resolved dications of fragment ions having 5, 7, and 11 carbon atoms, and electron yields corresponding to five photoelectron bands. Fitting multiple datasets together enabled an estimation of the overlapping time of the pump and probe pulses (t0). Using this t0, four momentum-resolved fragment ions (1 to 4 carbon atoms) with more than one transient feature were also fitted, giving out 12 datasets.
The detailed results of the data analysis are given in the ESI.†
2.3 Computational details
To calculate the MS of FLU, augmented Born–Oppenheimer molecular dynamics (aBOMD) simulations of the fragmentation of FLU were done using the DissMD script from the PyRAMD software.52 The algorithm was based on the QCEIMS idea,53,54 and the modifications are described in detail in ref. 18,55. The forces for aBOMD were computed with the xTB software56 at the semi-empirical GFN2-xTB level of theory57 that was shown to be suitable for the fragmentation pattern predictions.58 To emulate the high-energy excitation regime, the excitation energy was represented as n × hν, where n is the number of photons, and hν is the photon energy, which was taken to be 1.5 eV (corresponding to a wavelength of 810 nm). The parameter n was sampled from the Poisson distribution with a mean number of photons 〈n〉 = 40, and the result was adjusted to fit in the interval of 6 ≤ n ≤ 100 by setting the outlier n value to the closest value of n = 6 or n = 100.The energetics of the reaction C22+ → 2C+, discussed later in Section 3.2.5, were computed at CCSD(T)/aug-cc-pVTZ59–61 using the ORCA 5 software.62 The geometries of C22+ were optimized for the singlet, triplet, and quintet multiplicities, with the triplet being the lowest energy state. For the carbon monocation, doublet and quadruplet states were computed, with the doublet found to be the lowest in energy. All the geometries and energies are given in the ESI.†
3 Results and discussion
3.1 Roadmap of the analysis
In the following two sections, we will present the analysis of the strong-field-induced reaction dynamics of FLU. First, we will discuss the main time-independent features observed in the photoion and photoelectron signals without consideration of the pump–probe effects. There, we will focus on the individual spectra of the species and on the covariance techniques that allow us to find relations between the different observables. Afterward, we will look into the pump–probe dependencies of the discussed signal, extracting the information on the ultrafast photochemical processes in FLU.3.2 Time-independent observations
In the first set of experiments, in which FLU was subjected to IR pulses of variable intensity, we also observed this ubiquitous behavior, which can be seen in Fig. 2. We see the production of the highly-charged parent species up to the trication (FLU3+), as well as a subsequent rise in the production of the fragment ions upon increasing the IR pulse peak power. The production of various fragments varies depending on the species. For instance, the parent monocationic species (FLU+), such as C13H10+ and C13H102+, monotonously increase with the rise of the IR pulse peak power. However, the highly-charged species, such as the parent trication (FLU3+), appear only as a threshold power of about 4 × 1013 W cm−2 is reached (see ESI† for details). This suggests that there might be an interplay of MPI and TI strong-field ionization regimes, as discussed in the literature.64–67
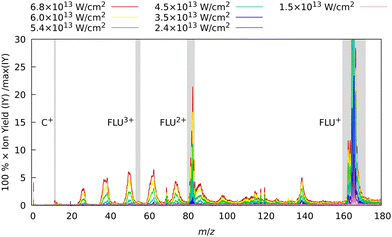 | ||
| Fig. 2 Experimental MS of FLU obtained with only the IR laser pulse for different intensities. The spectra were background-subtracted and normalized to the maximum intensity peak of the FLU monocation (C13H10+, m/z = 166) observed with the unattenuated data corresponding to a laser peak intensity of 6.8 × 1013 W cm−2. Gray-shaded areas highlight the four peaks of interest: C+ (m/z = 12), FLU3+ (m/z = 55.3), FLU2+ (m/z = 83), and FLU+ (m/z = 166). The full-range spectrum in the logarithmic scale and signal dependencies of the intensities of these peaks as a function of laser intensities are given in the ESI.† | ||
| Ek = (nmin + k)hν − IP − Up, | (1) |
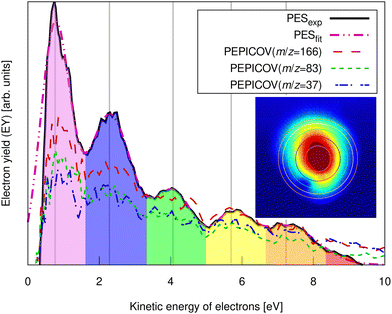 | ||
| Fig. 3 Experimental pump–probe delay averaged photoelectron spectrum of FLU (solid line) and PEPICOV-disentangled spectra for the parent FLU+ (m/z = 166), FLU2+ (m/z = 83), and the fragment ion at m/z = 37. The different colored areas underneath the spectrum and the vertical lines highlight different ATI peak orders. The inset shows the distorted raw electron VMI image. The vertical lines correspond to the circles in the inset image. The full PEPICOV map is available in the ESI.† | ||
The ATI features are clear signatures of MPI processes. The photoelectron–photoion covariance (PEPICOV) analysis revealed that the disentangled PES corresponding to all the ionic fragments look very similar and resemble the PES of the whole system, with the same set of ATI peaks (see dashed PEPICOV lines in Fig. 3). This indicates that the MPI regime dominates TI in producing low-charge parent ions and fragments. The similarity of the PEPICOV features for the FLU monocation (m/z = 166) and dication (m/z = 83) probably points to the photoionization proceeding sequentially, i.e., first, monocations are produced as FLU + IR → FLU+ + e1−, where e1− is the photoelectron appearing from the first ionization step. Then, the double ionization occurs according to a reaction FLU+ + IR → FLU2+ + e2−, where e2− is the second ejected electron, which should have a different ATI spectrum. The amount of the monocations in the MS is 4–5 times higher than of the dications, which means that mainly the covariance of FLU2+ with e1− will be visible, as the number of e1− will be exceedingly larger than of e2−. Additionally, the general mechanism of fragmentation implies obtaining first a highly excited mono- or dicationic state of the parent, which later decays into the charged fragments, thereby providing similar PES.
When we look at the covariance images obtained from the strong-field excitation (Fig. 4), we see a major difference from the results observed upon the ionization and fragmentation induced with the single-photon XUV.17,19 In the case of XUV excitation-ionization, the recoil features appeared on the diagonals, corresponding to C2Hx-fragment loss (shown as dashed boxes in Fig. 4). However, in the strong-field regime, we see distinct features off these diagonals, e.g., the C3Hx+ ion of interest recoiling against C7Hy+, or C4Hx+ against C6Hy+. Such off-diagonal signals indicate odd-carbon loss fragmentation channels, which were not observed in the XUV regime. The most probable reason for such a fragmentation pattern is that a larger variety of final states can be reached in the strong-field multiphoton regime compared to a single-photon excitation due to a change in selection rules.
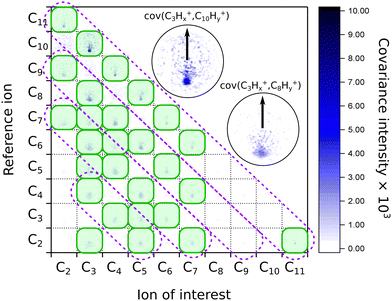 | ||
| Fig. 4 Matrix of the recoil-frame covariance images for different pairs of recoiling ions obtained from averaging all pump–probe delays of the IR-VIS pump–probe experiment. The diagonal violet dashed boxes indicate where the signal was present in the case of the XUV-UV experiment on FLU, from ref. 19. The green shaded boxes show the most intense recoil covariance signals in the current experiment. The two insets show zoomed images of the C3Hx+ ion of interest recoiling against the C10Hy+ and C8Hy+ reference ions, respectively. The arrows in both insets show the reference ion direction for all the recoil-frame covariance images. An enlarged version of this map without notations is available in the ESI.† | ||
We also see recoil relations between the smallest fragments: C3Hx+ ion of interest against C2Hy+. A significant broadening of the recoil feature (see enlarged insets in Fig. 4) may indicate that they are not produced in the same dissociation event but sequentially. In this case, the additional fragments would carry additional momentum, blurring out the recoil feature of the correlated ions.
A significant asymmetry in the intensities of the observed covariances was noted. On the one hand, in Fig. 4, we see clear signals for the small reference ions (C2+–C5+) of interest recoiling against larger monocations (C8+–C11+) in the pairwise dissociation of the parent and of the acetylene-loss fragment C11H82+. On the other hand, the inverted covariances, e.g., C10Hy+ ion of interest against C3Hx+, are significantly less intense (however, present). This asymmetry is also a signature of sequential fragmentation, in which the fraction of events producing stable large fragments is much lower than the fraction of metastable large fragments that undergo further fragmentation, producing smaller ions without larger counterparts.
| C13H10(n+m)+→C7Hxn+ + C6Hym+ | (2) |
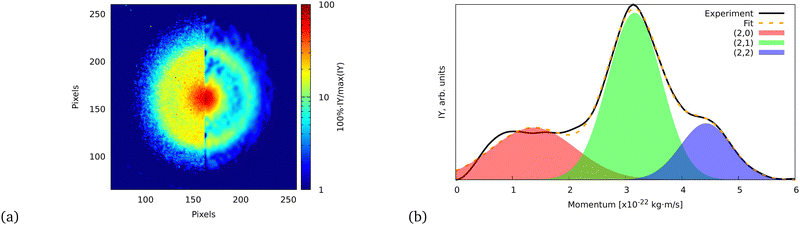 | ||
| Fig. 5 (a) Ion VMI of the C7Hx2+ fragment from FLU. The left side of the image is the raw experimental data, while the right part is the result of filtering and Abel inversion with the BASEX method. (b) Angularly integrated momentum distribution function of the C7Hx2+ ion with a three-Gaussian profile fit. The fit was performed similarly to the ATI PES, for which details are given in the ESI.† The shaded areas indicate the individual fit components that represent (2,0), (2,1), and (2,2) channels. | ||
The momentum value of C7Hx2+ formed via dissociation of FLU4+ into the (2,2) channel is calculated to be ∼4.6 × 10−22 kg m s−1 using the experimental KER value of FLU2+ dissociation for the (1,1) channel (2.46 ± 0.04 eV),18 which is in agreement with the observed momentum value of (4.43 ± 0.02) × 10−22 kg m s−1 (calculation is provided in the ESI†). This value is obtained by fitting the momentum profile of C7Hx2+ as shown in Fig. 5. The (2,2) channel is a direct indication of the FLU4+ production. However, FLU4+ itself is not observed in the MS, which indicates that it is unstable.
We do not observe any conclusive recoil-frame covariance features for this fragment. However, this might also be due to it displaying the strongest distortion of the ion VMI among all fragments, which makes the center determination for this ion complicated. The momentum distribution map for this ion has three dissociation channels that can be interpreted as (1,0), (1,1), and (1,2) or as (2,0), (2,1), and (2,2) (see eqn (2)), which does not favor either of the interpretations. However, the TOF-MS data is more in favor of the C+ interpretation of this peak: we see two peaks that are positioned at m/z = 12 and m/z = 13 (Fig. 6). This pattern suggests that this feature corresponds to C+ because, in case of the dication, we would expect m/z = 12 for C22+, m/z = 12.5 for C2H2+, and m/z = 13.0 for C2H22+. The isotope 13C in this case does not explain the observed pattern since, in the natural abundance, it is expected to be around 1% of the most intense peak, while the ratio of the peaks at m/z = 12 and m/z = 13 is about 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, respectively (Fig. 6).
1, respectively (Fig. 6).
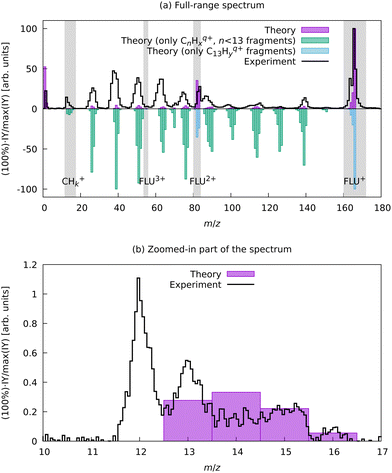
To support this assignment from the mass spectrum, we have calculated the equilibrium dissociation energy (De) for the reaction C22+ → 2C+ at the CCSD(T)/aug-cc-pVTZ level of theory. The obtained value of De = −5.3 eV shows that this reaction is strongly exothermic, which means that C+ is a more energetically favorable ion. The estimated lifetime of the metastable triplet C22+ into two C+ ions is 0.9 ns (see ESI† for details), which makes the detection of this species with MS impossible. Using aBOMD simulations of the fragmentation dynamics, we also observe peaks at the m/z region of interest (12 ≤ m/z ≤ 14), which all correspond to CHx+ species (Fig. 6). The further fragmentation of CHx+ up to C+ could not be traced with the semi-empirical method used for aBOMD due to electronic problem convergence issues. Nevertheless, from a combination of experimental data and simulations, we conclude that the fragments in the range 12 ≤ m/z ≤ 16 in the high laser power-induced MS of FLU correspond to C+.
3.3 Pump–probe-dependent results
Now, we present the analysis of the time-resolved pump–probe measurements for our system. The pump pulse was a strong-field IR (810 nm) laser pulse with an estimated peak power of 3 × 1013 W cm−2. This pulse initiated the ionization and fragmentation dynamics in FLU, which was described in the previous section. The probe pulse was a weaker VIS pulse (405 nm) produced from the same laser system. The comparison of the pump-only, probe-only, and pump–probe averaged MS is given in the ESI.† We monitor various observables (various ion and electron yields) as a function of the delay between pump and probe pulses (t). We chose the temporal overlap of both pulses (t0) to be at t = 0. The region in which the probe pulse comes before the pump pulse is t < 0, and the region in which the probe comes after the pump is t > 0.The time-dependent changes in the MS, PES, and a typical ion momentum distribution map of the C4Hx+ ion are shown in Fig. 7. The momentum map illustrates the evolution of the momentum of the ion extracted from the ion VMI (as in Fig. 5b) as a function of pump–probe delay t. In the pump–probe-dependent MS, we see similar trends for the fragmentation dynamics of PAHs as were observed with the XUV-pumped experiments.17,19 In the t < 0 region, we see more of the parent species than in the t > 0 region. For the fragments, this trend is inverse: for t < 0, we see fewer ions than for t > 0. Such behavior indicates that the pump pulse produces an excited state ensemble, and the probe pulse destroys it by pumping even more energy to overcome fragmentation thresholds. This is observed for the PAH in both XUV-excited regimes probed with IR and VIS pulses as well as for benzene and toluene excited by a strong-field laser.20,21
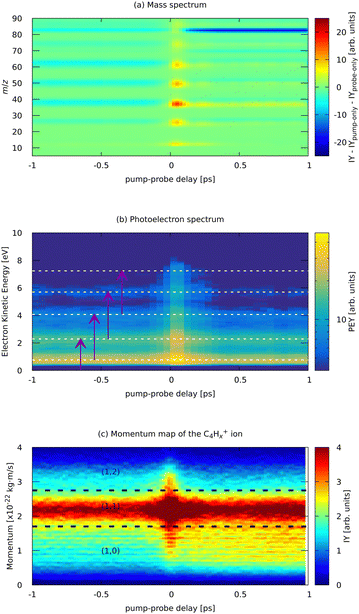 | ||
| Fig. 7 Experimental parts of the pump (810 nm) – probe (405 nm) dependent MS (a) and photoelectron spectrum (b) of FLU, and (c) ion momentum distribution map of the C4Hx+ fragment. Horizontal lines in (b) indicate the positions of the ATI peaks from Fig. 3. Purple arrows in (b) indicate the probe photon conversion of the ATI electrons. Horizontal lines in (c) show the approximate delimiters of the (1,0), (1,1), and (1,2) channels of the C4Hx+ ion. The ion yield (IY) in the MS corresponds to background-subtracted values, i.e., with corresponding values of pump-only and probe-only spectra subtracted. The full m/z-range version of (a) is available in the ESI.† | ||
Near the temporal overlap of the two laser pulses (t = 0), there is a strong increase in the ion production of all kinds of ions, as well as an increase in the yields of the ATI peaks. The PES (Fig. 7b) shows qualitatively the same ATI spectrum given by eqn (1) being present in the whole range of the pump–probe delays. The new photoelectron features, different from the ATI pattern, do not appear in the PES because the probe photons are just twice the energy of the IR pump photons. The transient increase in each ATI peak's intensity arises from transferring each k-th ATI peak into the (k + 2)-th peak by a probe VIS photon with 3 eV of energy (see eqn (1) and vertical arrows in Fig. 7(b) for details). The fitted lifetimes of the transients in the ATI bands seem to decrease with increasing order of the band, going from 102 ± 4 fs to 83 ± 3 fs (Table 1). However, they are all centered around 90 fs, which might indicate that the source of these ATI bands is the same set of excited states of the neutral FLU parent molecule.
| ATI band order k | Lifetime, fs | Parent species | Lifetime, fs |
|---|---|---|---|
| 1 | 102 ± 4 | C13H10+ | 62 ± 1 |
| 2 | 93 ± 3 | C13H9+ | 91 ± 1 |
| 3 | 87 ± 3 | C13H102+ | 79 ± 1 |
| 4 | 90 ± 5 | C13H103+ | 42 ± 6 |
| 5 | 83 ± 3 |
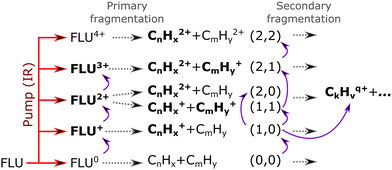
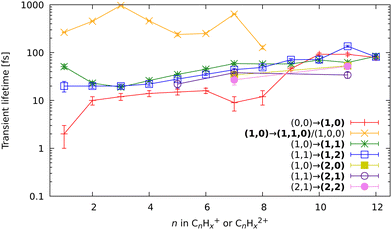
Based on the channels observed in XUV-pumped investigations13–19 and the time-independent results observed in the IR-only case from the previous section, the general scheme for the observed strong-field induced dynamics of FLU in the IR-VIS regime can be described as summarized in Fig. 8. Here, we will briefly describe it. Upon interaction with the IR pump pulse, FLU can produce multiple parent species, from the excited neutral molecules (FLU0) to tetracations (FLU4+). The probe VIS pulse can ionize the near-threshold species, providing the observed transient increase in the production of the higher-charge parent ions, which we directly detect from the MS. The excited parent species (FLU0, FLU+, FLU2+, FLU3+, and FLU4+) can fragment, producing the fragments in different momentum channels (n,m), i.e., (0,0), (1,0), (1,1), and so forth. The probe photon can increase the fragmentation charge state by one, switching from a (n,m) dissociation channel to a (n + 1,m) channel. The fragments can spontaneously fragment further into smaller species. However, the probe pulse can also enhance this fragmentation in the smaller fragments of the (1,0) channel, leading eventually to the C+ fragment, for which we see a transient increase in production. All the fitted lifetimes are shown in Fig. 9 and Table 1, and all the fitted pump–probe dependencies of the ion yield and numerical values are given in ESI.†
In general, the strong-field induced dynamics are in many aspects similar to the dynamics observed by the XUV pulses.13–19 This is direct evidence of general photochemical properties of the PAHs, dictated by their molecular and electronic structures, such as the closely connected carbon framework and a highly conjugated nature of π-bonds. However, there are some noticeable differences with the XUV regime, which are signs of the strong-field excitation character. Here, we will focus the discussion on the channels that were not observed with XUV excitation.
First, let us discuss the dynamics of the parent ions, given in Table 1. Unlike before, with the IR pump, we see short-lived transients in the monocations, corresponding to the lifetime of excited neutral FLU. We observed the transient peaks in both the intact parent FLU monocation (C13H10+) and in its monodehydrogenated version (C13H9+). The lifetime extracted from the C13H9+ ion yield is 30 fs longer than the lifetime from C13H10+, which is most likely a sign of the unresolved delay for the loss of hydrogen. The lifetime of the near-threshold FLU+ observed in the yield of the parent dication C13H102+ is longer than for the excited neutral. This could be due to a larger density of the excited states with the increase of the charge state. The fitted lifetimes of the near-ionization-threshold FLU dication FLU2+, observed through the pump–probe dependent IY of C13H103+, revealed a significantly shortened lifetime (42 ± 6 fs), compared to those obtained with the XUV pump (126 ± 16 fs in the XUV-IR experiment and 184 ± 44 fs in XUV-VIS).19 This drastic difference probably arises from a difference in the distribution of the population of the FLU2+ excited states obtained in the strong-field and single-XUV-photon ionization regimes.
In the kinetic-energy resolved IY of the monocationic fragments (Fig. 7c and “Peak 1” in Fig. 10), we see the same channels as in the XUV experiments,17,19 namely (1,0) → (1,1) and (1,1) → (2,1) (Fig. 8 and ESI†). However, because the low-energy IR pump photons do not necessarily ionize the molecule, a new channel was observed, namely (0,0) → (1,0), similar to that in the parent monocations (see Fig. 8). This channel has a much shorter lifetime on the order of a few fs to 10 fs than the analogous process in the parent ions (FLU0 → FLU+) with a lifetime of 62 ± 1 fs (see Table 1 and Fig. 9). Similar to the FLU0 → FLU+ and FLU+ → FLU2+ channels (Table 1), we see shorter lifetimes of metastable species in (0,0) → (1,0) channels compared to (1,0) → (1,1) channels (Fig. 9). This trend can be again explained by the decreased density of states in the neutral metastable species with respect to their monocationic analogs. The additional decrease in lifetimes of (0,0) → (1,0) compared to the parent species (FLU0 → FLU+ channel) can be explained in the same fashion: the smaller the molecular species, the smaller the near-ionization threshold density of states.
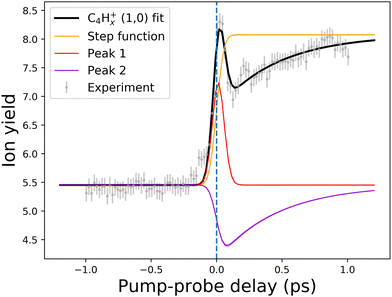 | ||
| Fig. 10 An example of the pump–probe fit for the (1,0) channel of the C4Hx+ fragment. Points with error bars present experimental points retrieved from the PImMS camera, while the solid lines demonstrate the fitted curve (black line) and fit components (colored lines). The step function (yellow line) represents the static change in given ionic species production in the pump before probe and probe before pump regimes. Peak 1 (red line) corresponds to the (0,0) → (1,0) channel, while Peak 2 (violet line) corresponds to the (1,0) → (1,1,0)/(1,0,0) channel (see Fig. 8 and 9). The vertical dashed line shows the temporal overlap of pump and probe pulses. All the fits are available in the ESI.† | ||
Another previously unseen channel corresponds to slow dynamics with lifetimes of 0.1–1 ps observed in the (1,0) channels of small ions (CHx+ to C8Hx+). An example of such a channel can be seen in Fig. 10, denoted as “Peak 2”. This dynamic feature is a transient decrease for the fragments from C2Hx+ to C8Hx+, but for the CHx+, it is a transient increase. Therefore, we attribute this channel to the secondary dissociation of the larger ions, eventually ending up with the smallest CHx+ fragment. We can denote this channel as (1,0) → (1,1,0)/(1,0,0) (Fig. 9), meaning that after probing, three fragments are produced, either two monocations and one neutral, or one monocation and two neutrals. The slow transient lifetimes could be attributed to the relaxation lifetimes of the vibrationally and vibronically excited fragment ions that eventually fragment further upon the interaction with the probe pulse, leading to transient decay of its own ion yield and corresponding transient increase in the ion yield of the CHx+ species. Such fragmentation is consistent with observations from the static recoil-frame covariance analysis, which demonstrates secondary fragmentation patterns (see Section 3.2.3).
The last new set of channels that have not been observed before for FLU in the XUV-pump regime19 are the (2,1) and (2,2) channels of the dicationic fragments (C7Hx2+, and C11Hx2+), as shown in Fig. 5. These channels indicate the lifetimes of the excited FLU trication (FLU3+) and tetracation (FLU4+). The lifetimes of these channels have similar values and show similar trends, as those observed in monocationic fragments for the (1,0) → (1,1) and (1,1) → (1,2) channels (Fig. 9). This might indicate that all these fragments are formed through a set of similar excited states of the di- and trications.
4 Conclusions
We investigated the behavior of fluorene (C13H10), a three-ring polycyclic aromatic hydrocarbon, under the influence of strong-field laser pulses and provided a complete disentanglement and characterization of the photochemical dynamics of fluorene in these photochemical conditions. Excitation by intense IR pulses tends to induce more secondary fragmentation and double and triple ionization than single-photon XUV ionization, which is seen from the recoil-frame covariance analysis and pump–probe dynamics. The strong-field excitation also opens new channels that were not observed in the XUV ionization. First of all, this is the dynamics of the near-threshold neutral molecule, which produces previously unobserved features appearing from the presence of the excited neutral molecule. The second new observation is the tetracation formation, which was observed via the (2,2) channel of the dicationic fragments C7Hx2+ and C11Hx2+.All the observed time-dependent channels in photoion and photoelectron spectra were included in a global fit. This fitting dataset consisted of four parent ions extracted from the mass spectra, 15 kinetic-energy resolved ionic fragments extracted from ion-velocity-map imaging, and five photoelectron channels obtained from electron-velocity-map imaging. From this analysis, we extracted 60 transient lifetimes corresponding to different photoinduced intermediates. This extensive dataset of the transient species' lifetimes of a prototypical polycyclic aromatic hydrocarbon provides new insights into the rich photochemistry of PAHs under the influence of intense electric fields.
Author contributions
BM, JWLL, and MS conceived and designed the experiments. DG, PC, JWLL, SK, OA, FA, RB, AAB, BE, EG, SPG, LH, DH, EJ, MMK, JL, AKL, ZL, DL, SM, RM, JM, EM, TM, CCP, CP, JP, MP, DRa, PR, DRom, AS, ALS, AT, SHT, ATN, NV, ISV, ST, JK, AMR, DRo, MBr, SB, PEJ, CV, MBu, BM, and MS performed the experiments. DG, JWLL, PC, SK, and DST analyzed the data. DST and PC performed theoretical simulations. DG, JWLL, DT, PC, BE, and MS performed detailed discussions of the results. DG, PC, DST, and MS wrote the manuscript with input from all authors.Data availability
ESI† consists of (1) a PDF file with the fitting results and detailed complementary pictures to those presented in the manuscript, (2) a ZIP archive with the pre-processed experimental and theoretical data (including data analysis and plotting scripts) that can be used to reproduce the results and figures in the paper. All additional data is available by request from the corresponding author.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the ERC Starting Grant ASTROROT, grant number 638027, and the project CALIPSOplus under grant agreement 730872 from the EU Framework Programme for Research and Innovation HORIZON 2020. We acknowledge DESY (Hamburg, Germany), a member of the Helmholtz Association HGF, for providing experimental facilities. Parts of this research were carried out at FLASH. Beamtime was allocated for proposals F-20170540 and F-20211752. This research was also supported through the Maxwell computational resources operated at Deutsches Elektronen-Synchrotron DESY, Hamburg, Germany. We acknowledge the Max Planck Society for funding the development and the initial operation of the CAMP end-station within the Max Planck Advanced Study Group at CFEL and for providing this equipment for CAMP@FLASH. The installation of CAMP@FLASH was partially funded by the BMBF grants 05K10KT2, 05K13KT2, 05K16KT3, and 05K10KTB from FSP-302. M. Br. and C. V. gratefully acknowledge support from the UK EPSRC EP/T021675/1, EP/V026690/1. M. Bu., E. J., Z. L., and J. M. gratefully acknowledge support from the UK EPSRC (EP/S028617/1). E. J., Z. L., and J. M. additionally thank Lincoln College, Oriel College, and University College, Oxford, for their respective travel funding. The research was further supported by the federal cluster of excellence “Advanced Imaging of Matter” (AIM, EXC 2056, ID 390715994) of the Deutsche Forschungsgemeinschaft (DFG). L. H. acknowledges a fellowship within the framework of the Helmholtz-OCPC postdoctoral exchange program. P. E.-J., J. P., J. L., and M. P. acknowledge the support of the Swedish Research Council (2017-04106) and the Knut and Alice Wallenberg Foundation (2020-0111). S. B. acknowledges funding by the Helmholtz Initiative and Networking Fund. D. Rol. acknowledges the National Science Foundation grant PHYS-1753324. A. S. acknowledges the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany's Excellence Strategy (EXC-2033, project no. 390677874).References
- C. Joblin and A. Tielens, EAS Publ. Ser., 2011, 46, 3–10 CrossRef.
- G. Lagache, H. Dole, J.-L. Puget, P. Pérez-González, E. Le Floch, G. H. Rieke, C. Papovich, E. Egami, A. Alonso-Herrero and C. Engelbracht, et al. , Astrophys. J., Suppl. Ser., 2004, 154, 112 CrossRef CAS.
- K. Srogi, Environ. Chem. Lett., 2007, 5, 169–195 CrossRef CAS PubMed.
- M. Låg, J. Øvrevik, M. Refsnes and J. A. Holme, Respir. Res., 2020, 21, 299 CrossRef PubMed.
- H. Kaneda, T. Onaka, I. Sakon, D. Ishihara, A. Mouri, M. Yamagishi and A. Yasuda, PAH Evolution in the Harsh Environment of the ISMSciences, Les Ulis, 2011, pp. 157–168.
- V. M. Bierbaum, V. L. Page and T. P. Snow, PAHs and the Chemistry of the ISM, EDP Sciences, Les Ulis, 2011, 427–440.
- E. R. Micelotta, A. P. Jones and A. G. G. M. Tielens, Astron. Astrophys., 2011, 526, A52 CrossRef.
- E. C. Sittler, J. F. Cooper, S. J. Sturner and A. Ali, Icarus, 2020, 344, 113246 CrossRef CAS.
- T. Yatsuhashi and N. Nakashima, J. Phys. Chem. A, 2010, 114, 7445–7452 CrossRef CAS PubMed.
- T. Yatsuhashi and N. Nakashima, J. Phys. Chem. A, 2005, 109, 9414–9418 CrossRef CAS PubMed.
- L. Robson, K. Ledingham, A. Tasker, P. McKenna, T. McCanny, C. Kosmidis, D. Jaroszynski, D. Jones, R. Issac and S. Jamieson, Chem. Phys. Lett., 2002, 360, 382–389 CrossRef CAS.
- L. Robson, A. Tasker, K. Ledingham, P. McKenna, T. McCanny, C. Kosmidis, P. Tzallas, D. Jaroszynski and D. Jones, Int. J. Mass Spectrom., 2002, 220, 69–85 CrossRef CAS.
- A. Marciniak, V. Despré, T. Barillot, A. Rouzée, M. C. E. Galbraith, J. Klei, C.-H. Yang, C. T. L. Smeenk, V. Loriot, S. N. Reddy, A. G. G. M. Tielens, S. Mahapatra, A. I. Kuleff, M. J. J. Vrakking and F. Lépine, Nat. Commun., 2015, 6, 7909 CrossRef CAS PubMed.
- A. Marciniak, V. Despré, V. Loriot, G. Karras, M. Hervé, L. Quintard, F. Catoire, C. Joblin, E. Constant, A. I. Kuleff and F. Lépine, Nat. Commun., 2019, 10, 337 CrossRef CAS PubMed.
- M. Hervé, V. Despré, P. Castellanos Nash, V. Loriot, A. Boyer, A. Scognamiglio, G. Karras, R. Brédy, E. Constant, A. G. G. M. Tielens, A. I. Kuleff and F. Lépine, Nat. Phys., 2021, 17, 327–331 Search PubMed.
- A. Boyer, M. Hervé, V. Despré, P. Castellanos Nash, V. Loriot, A. Marciniak, A. G. G. M. Tielens, A. I. Kuleff and F. Lépine, Phys. Rev. X, 2021, 11, 041012 Search PubMed.
- J. W. L. Lee, D. S. Tikhonov, P. Chopra, S. Maclot, A. L. Steber, S. Gruet, F. Allum, R. Boll, X. Cheng, S. Düsterer, B. Erk, D. Garg, L. He, D. Heathcote, M. Johny, M. M. Kazemi, H. Köckert, J. Lahl, A. K. Lemmens, D. Loru, R. Mason, E. Müller, T. Mullins, P. Olshin, C. Passow, J. Peschel, D. Ramm, D. Rompotis, N. Schirmel, S. Trippel, J. Wiese, F. Ziaee, S. Bari, M. Burt, J. Küpper, A. M. Rijs, D. Rolles, S. Techert, P. Eng-Johnsson, M. Brouard, C. Vallance, B. Manschwetus and M. Schnell, Nat. Commun., 2021, 12, 6107 Search PubMed.
- J. W. L. Lee, D. S. Tikhonov, F. Allum, R. Boll, P. Chopra, B. Erk, S. Gruet, L. He, D. Heathcote, M. M. Kazemi, J. Lahl, A. K. Lemmens, D. Loru, S. Maclot, R. Mason, E. Müller, T. Mullins, C. Passow, J. Peschel, D. Ramm, A. L. Steber, S. Bari, M. Brouard, M. Burt, J. Küpper, P. Eng-Johnsson, A. M. Rijs, D. Rolles, C. Vallance, B. Manschwetus and M. Schnell, Phys. Chem. Chem. Phys., 2022, 24, 23096–23105 RSC.
- D. Garg, J. W. L. Lee, D. S. Tikhonov, P. Chopra, A. L. Steber, A. K. Lemmens, B. Erk, F. Allum, R. Boll, X. Cheng, S. Düsterer, S. Gruet, L. He, D. Heathcote, M. Johny, M. M. Kazemi, H. Köckert, J. Lahl, D. Loru, S. Maclot, R. Mason, E. Müller, T. Mullins, P. Olshin, C. Passow, J. Peschel, D. Ramm, D. Rompotis, S. Trippel, J. Wiese, F. Ziaee, S. Bari, M. Burt, J. Küpper, A. M. Rijs, D. Rolles, S. Techert, P. Eng-Johnsson, M. Brouard, C. Vallance, B. Manschwetus and M. Schnell, Front. Phys., 2022, 10, 880793 CrossRef.
- L. Zhou, Y. Liu, T. Sun, S. Feng, H. Lv and H. Xu, J. Phys. Chem. A, 2019, 123, 8365–8369 CrossRef CAS PubMed.
- L. Zhou, Y. Liu, T. Sun, H. Yin, Y. Zhao, H. Lv and H. Xu, J. Phys. Chem. A, 2021, 125, 2095–2100 CrossRef CAS PubMed.
- M. L. Vidal, M. Epshtein, V. Scutelnic, Z. Yang, T. Xue, S. R. Leone, A. I. Krylov and S. Coriani, J. Phys. Chem. A, 2020, 124, 9532–9541 CrossRef CAS PubMed.
- M. Epshtein, V. Scutelnic, Z. Yang, T. Xue, M. L. Vidal, A. I. Krylov, S. Coriani and S. R. Leone, J. Phys. Chem. A, 2020, 124, 9524–9531 CrossRef CAS PubMed.
- A. M. Burkhardt, K. L. K. Lee, P. B. Changala, C. N. Shingledecker, I. R. Cooke, R. A. Loomis, H. Wei, S. B. Charnley, E. Herbst, M. C. McCarthy and B. A. McGuire, Astrophys. J. Lett., 2021, 913, L18 CrossRef CAS.
- J. Cernicharo, M. Agúndez, C. Cabezas, B. Tercero, N. Marcelino, J. R. Pardo and P. de Vicente, Astron. Astrophys., 2021, 649, L15 CrossRef CAS PubMed.
- L. Keldysh, J. Exp. Theor. Phys., 1965, 20, 1307–1314 Search PubMed.
- B. Erk, J. P. Müller, C. Bomme, R. Boll, G. Brenner, H. N. Chapman, J. Correa, S. Düsterer, S. Dziarzhytski, S. Eisebitt, H. Graafsma, S. Grunewald, L. Gumprecht, R. Hartmann, G. Hauser, B. Keitel, C. von Korff Schmising, M. Kuhlmann, B. Manschwetus, L. Mercadier, E. Müller, C. Passow, E. Plönjes, D. Ramm, D. Rompotis, A. Rudenko, D. Rupp, M. Sauppe, F. Siewert, D. Schlosser, L. Strüder, A. Swiderski, S. Techert, K. Tiedtke, T. Tilp, R. Treusch, I. Schlichting, J. Ullrich, R. Moshammer, T. Möller and D. Rolles, J. Synchrotron Radiat., 2018, 25, 1529–1540 CrossRef CAS PubMed.
- J. Feldhaus, J. Phys. B: At., Mol. Opt. Phys., 2010, 43, 194002 CrossRef.
- H. Redlin, A. Al-Shemmary, A. Azima, N. Stojanovic, F. Tavella, I. Will and S. Düsterer, Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, 2011, 635, S88–S93 Search PubMed.
- P. Chopra, PhD thesis, Christian-Albrechts-Universität zu Kiel, Germany, 2022.
- A. T. Eppink and D. H. Parker, Rev. Sci. Instrum., 1997, 68, 3477–3484 CrossRef CAS.
- D. H. Parker and A. T. Eppink, J. Chem. Phys., 1997, 107, 2357–2362 CrossRef CAS.
- U. Even, EPJ Tech. Instrum., 2015, 2, 17 CrossRef.
- A. T. Clark, J. P. Crooks, I. Sedgwick, R. Turchetta, J. W. L. Lee, J. J. John, E. S. Wilman, L. Hill, E. Halford, C. S. Slater, B. Winter, W. H. Yuen, S. H. Gardiner, M. L. Lipciuc, M. Brouard, A. Nomerotski and C. Vallance, J. Phys. Chem. A, 2012, 116, 10897–10903 CrossRef CAS PubMed.
- K. Amini, S. Blake, M. Brouard, M. B. Burt, E. Halford, A. Lauer, C. S. Slater, J. W. L. Lee and C. Vallance, Rev. Sci. Instrum., 2015, 86, 103113 CrossRef CAS PubMed.
- A. L. Steber and E. Müller, Beamtime DAQ Access, 2021, https://stash.desy.de/projects/CS/repos/pah/browse Search PubMed.
- D. S. Tikhonov, D. Garg and P. Chopra, CAMPFancyAnalysis, 2023, https://gitlab.desy.de/denis.tikhonov/campfancyanalysis.
- C. Bordas, F. Paulig, H. Helm and D. L. Huestis, Rev. Sci. Instrum., 1996, 67, 2257–2268 CrossRef CAS.
- S. Gibson, D. D. Hickstein, R. Yurchak, M. Ryazanov, D. Das and G. Shih, PyAbel/PyAbel: v0.9.0, 2022 DOI:10.5281/zenodo.7438595.
- D. D. Hickstein, S. T. Gibson, R. Yurchak, D. D. Das and M. Ryazanov, Rev. Sci. Instrum., 2019, 90, 065115 CrossRef PubMed.
- L. Minion, J. W. L. Lee and M. Burt, Phys. Chem. Chem. Phys., 2022, 24, 11636–11645 RSC.
- C. S. Slater, S. Blake, M. Brouard, A. Lauer, C. Vallance, J. J. John, R. Turchetta, A. Nomerotski, L. Christensen and J. H. Nielsen, et al. , Phys. Rev. A, 2014, 89, 011401 CrossRef.
- C. S. Slater, S. Blake, M. Brouard, A. Lauer, C. Vallance, C. S. Bohun, L. Christensen, J. H. Nielsen, M. P. Johansson and H. Stapelfeldt, Phys. Rev. A, 2015, 91, 053424 CrossRef.
- F. Allum, M. Burt, K. Amini, R. Boll, H. Köckert, P. K. Olshin, S. Bari, C. Bomme, F. Brauße and B. Cunha de Miranda, et al. , J. Chem. Phys., 2018, 149, 204313 CrossRef PubMed.
- K. Amini, R. Boll, A. Lauer, M. Burt, J. W. Lee, L. Christensen, F. Brauβe, T. Mullins, E. Savelyev and U. Ablikim, et al. , J. Chem. Phys., 2017, 147, 013933 CrossRef PubMed.
- J. Mikosch and S. Patchkovskii, J. Mod. Opt., 2013, 60, 1426–1438 CrossRef CAS.
- F. Allum, V. Music, L. Inhester, R. Boll, B. Erk, P. Schmidt, T. M. Baumann, G. Brenner, M. Burt, P. V. Demekhin, S. Dörner, A. Ehresmann, A. Galler, P. Grychtol, D. Heathcote, D. Kargin, M. Larsson, J. W. L. Lee, Z. Li, B. Manschwetus, L. Marder, R. Mason, M. Meyer, H. Otto, C. Passow, R. Pietschnig, D. Ramm, K. Schubert, L. Schwob, R. D. Thomas, C. Vallance, I. Vidanović, C. von Korff Schmising, R. Wagner, P. Walter, V. Zhaunerchyk, D. Rolles, S. Bari, M. Brouard and M. Ilchen, Commun. Chem., 2022, 5, 42 CrossRef CAS PubMed.
- L. J. Frasinski, J. Phys. B: At., Mol. Opt. Phys., 2016, 49, 152004 CrossRef.
- S. Pedersen and A. Zewail, Mol. Phys., 1996, 89, 1455–1502 CrossRef CAS.
- D. S. Tikhonov, D. Garg and M. Schnell, Photochemistry, 2024, 4, 57–110 CAS.
- D. S. Tikhonov, MC3 Fitting, 2021, https://gitlab.desy.de/denis.tikhonov/mcmcmcfitting.
- D. S. Tikhonov, PyRAMD, 2023, https://gitlab.desy.de/denis.tikhonov/pyramd.
- S. Grimme, Angew. Chem., Int. Ed., 2013, 52, 6306–6312 CrossRef CAS PubMed.
- C. A. Bauer and S. Grimme, J. Phys. Chem. A, 2016, 120, 3755–3766 CrossRef CAS PubMed.
- D. S. Tikhonov, A. Datta, P. Chopra, A. L. Steber, B. Manschwetus and M. Schnell, Z. Phys. Chem., 2020, 234, 1507–1531 CrossRef CAS.
- C. Bannwarth, E. Caldeweyher, S. Ehlert, A. Hansen, P. Pracht, J. Seibert, S. Spicher and S. Grimme, WIREs Comput. Mol. Sci., 2021, 11, e1493 CrossRef CAS.
- C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652–1671 CrossRef CAS PubMed.
- J. Koopman and S. Grimme, ACS Omega, 2019, 4, 15120–15133 CrossRef CAS PubMed.
- J. Cížek, J. Chem. Phys., 1966, 45, 4256–4266 CrossRef.
- T. H. Dunning, J. Chemical Phys., 1989, 90, 1007–1023 CrossRef CAS.
- R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108 CrossRef CAS PubMed.
- J.-F. Zhang, H. Lü, W.-L. Zuo, H.-F. Xu, M.-X. Jin and D.-J. Ding, Chin. Phys. B, 2015, 24, 113301 CrossRef.
- A. Kitashoji, A. Fujihara, T. Yoshikawa and T. Yatsuhashi, Chem. Lett., 2019, 48, 1472–1475 CrossRef CAS.
- T. Kawaguchi, K. Kitagawa, K. Toyota, M. Kozaki, K. Okada, N. Nakashima and T. Yatsuhashi, J. Phys. Chem. A, 2021, 125, 8014–8024 CrossRef CAS PubMed.
- W. A. Bryan, S. L. Stebbings, J. McKenna, E. M. L. English, M. Suresh, J. Wood, B. Srigengan, I. C. E. Turcu, J. M. Smith, E. J. Divall, C. J. Hooker, A. J. Langley, J. L. Collier, I. D. Williams and W. R. Newell, Nat. Phys., 2006, 2, 379–383 Search PubMed.
- M. G. Pullen, B. Wolter, X. Wang, X.-M. Tong, M. Sclafani, M. Baudisch, H. Pires, C. D. Schröter, J. Ullrich, T. Pfeifer, R. Moshammer, J. H. Eberly and J. Biegert, Phys. Rev. A, 2017, 96, 033401 CrossRef.
- J. H. Eberly and J. Javanainen, Eur. J. Phys., 1988, 9, 265 CrossRef CAS.
- R. R. Freeman, P. H. Bucksbaum, H. Milchberg, S. Darack, D. Schumacher and M. E. Geusic, Phys. Rev. Lett., 1987, 59, 1092–1095 CrossRef CAS PubMed.
- K. Lin, S. Eckart, A. Hartung, D. Trabert, K. Fehre, J. Rist, L. P. H. Schmidt, M. S. Schöffler, T. Jahnke, M. Kunitski and R. Dörner, Sci. Adv., 2022, 8, eabn7386 CrossRef CAS PubMed.
- R. Wang, Q. Zhang, D. Li, S. Xu, P. Cao, Y. Zhou, W. Cao and P. Lu, Opt. Express, 2019, 27, 6471–6482 CrossRef CAS PubMed.
- M. Frenklach and H. Wang, Symp. (Int.) Combust., 1991, 23, 1559–1566 CrossRef.
- V. V. Kislov, N. I. Islamova, A. M. Kolker, S. H. Lin and A. M. Mebel, J. Chem. Theory Comput., 2005, 1, 908–924 CrossRef CAS PubMed.
- D. S. N. Parker, R. I. Kaiser, T. P. Troy and M. Ahmed, Angew. Chem., Int. Ed., 2014, 53, 7740–7744 CrossRef CAS PubMed.
- K. Miyamoto, S. Narita, Y. Masumoto, T. Hashishin, T. Osawa, M. Kimura, M. Ochiai and M. Uchiyama, Nat. Commun., 2020, 11, 2134 CrossRef CAS PubMed.
- H. W. Lin, C.-H. Lee, D. W. Gerdes, F. C. Adams, J. Becker, K. Napier and L. Markwardt, Astrophysical J. Lett., 2020, 889, L30 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: The PDF file contains fitting results for the ultrafast dynamics, fitting of the electron spectrum and details of quantum-chemical calculations. The ZIP archive contains all the raw data and scripts needed for reproducing the figures and tables of the manuscript. See DOI: https://doi.org/10.1039/d3cp05063g |
| ‡ Present address: Stanford PULSE Institute, SLAC National Accelerator Laboratory, Menlo Park, California, USA. |
| § Present address: Linac Coherent Light Source, SLAC National Accelerator Laboratory, Menlo Park, California, USA. |
| ¶ Present address: School of Chemistry, University of Nottingham, Nottingham, UK. |
| || Present address: Ruhr-Universität Bochum, Bochum, Germany. |
| ** Present address: Universidad de Valladolid, Valladolid, Spain. |
| †† Present address: Class 5 Photonics, Hamburg, Germany. |
| This journal is © the Owner Societies 2024 |