Open Access Article
Open Access ArticleParticle alignment effects on mechanical properties of cellulose nanocrystal thin films†
Hyeyoung
Son
a,
Dawson Michael
Smith
a,
Zhaofan
Li
 b,
Taehoo
Chang
a,
Wenjie
Xia
b,
Taehoo
Chang
a,
Wenjie
Xia
 b and
Chelsea Simone
Davis
b and
Chelsea Simone
Davis
 *a
*a
aSchool of Materials Engineering, Purdue University, West Lafayette, Indiana, 47906, USA. E-mail: chelsea@purdue.edu
bDepartment of Civil, Construction and Environmental Engineering, North Dakota State University, Fargo, North Dakota 58108, USA
First published on 26th January 2023
Abstract
Cellulose nanocrystal (CNC) thin films are of increasing interest as sustainable materials due to their anisotropic mechanical properties. Previous computational work has shown that the fracture mechanisms of CNC films vary as a function of particle alignment with respect to the loading direction. However, it is challenging to experimentally measure the mechanical anisotropy of extremely thin CNC films due to their brittleness. Here, a new experimental approach was developed to identify the effect of CNC alignment on modulus while simultaneously observing the fracture mechanisms. In this method, uniaxial tensile strain is applied to a CNC film laminated on a silicone substrate with a mechanical stage mounted over a microscope. The modulus calculated by measuring the wavelength of wrinkles that formed perpendicular to the tensile strain direction at low strains during mechanical testing. The elastic modulus of CNC films decayed exponentially as the misalignment of particles to the loading direction increased. By carrying out coarse-grained modeling and comparing the misalignment angle with the crack opening direction beyond the fracture strains, fracture mechanism dependence on misalignment was observed.
Introduction
Recently, cellulose-based materials have gained attention as sustainable materials for packaging and textile applications due to their abundance, biodegradability, and renewability.1–4 Cellulose nanocrystals (CNCs) are cellulosic nanoparticles chemically extracted from various cellulose sources such as trees, bacteria, and plants through sulphuric acid hydrolysis.1,5–7 Individual CNCs are rod-like particles with a high aspect ratio and anisotropic mechanical properties,1,8,9 exhibiting a greater mechanical strength in the axial direction than in the transverse direction. Neat CNC materials, composed of only CNCs with no polymer matrix, also exhibit an anisotropic mechanical behavior when CNCs are aligned.10 For CNC films, the mechanical properties are strongly dependent on factors such as individual CNC strength, particle assembly,11–13 and the distribution of CNC orientations. Previous work has investigated the dependence of CNC film modulus and fracture strength on the order parameter of CNC alignments and casting methods.10,14,15 Alexander et al.10 developed a shear casting method and measured mechanical properties of CNC films with respect to the degree of particle alignment as well as the casting direction. Their work showed that when the ordering of CNCs in the film is increased, the elastic modulus increases in the axial direction and decreases in the transverse direction.10 To identify the fracture mechanisms of CNC films with respect to the angle of alignment, Shishehbor et al.16 investigated the effect of CNC alignment on mechanical properties by developing a coarse-grained (CG) molecular model. In that work, three different fracture mechanisms were predicted through both simulations and analytical solutions. The fracture mechanisms varied with degree of misalignment (defined here and throughout as the angle between the principal orientation direction of the CNCs and the applied tensile loading direction, θ). It was shown that a sliding mode occurs from 0° < θ ≤ 8°, a mixed mode from 8° < θ ≤ 70°, and a normal mode from 70° < θ ≤ 90°. These three fracture mechanisms were verified experimentally by measuring the elastic modulus via tensile testing and visualizing the subsequent fracture morphology. Although the trend of measured modulus with alignment angle corresponded well with the simulation results in that study, the measured modulus values were much smaller than the simulations moduli due to experimental limitations such as uncertain CNC film thickness and cracks in the film before testing. Thus, in this study we suggest a new experimental approach to identify the effects of misalignment on the mechanical properties and the fracture mechanisms of CNC films.To quantify the anisotropic moduli of aligned CNC films, observations of surface buckles were utilized. Surface buckling instabilities such as wrinkling have been used as a measurement tool to quantify the elastic modulus of a thin, rigid film adhered to a compliant substrate.17–23 When a uniaxial in-plane strain is applied to the bilayer, a sinusoidal surface buckling instability (wrinkling) is formed on the film due to the modulus mismatch between film and substrate. In the past few decades, this surface buckling phenomenon has been well demonstrated both theoretically and experimentally.24–27 The wrinkling wavelength depends on the film thickness and the plane strain moduli of the film and the substrate. Stafford et al. incorporated this well-defined relationship given in eqn (1) into a new technique that measures a thin film's modulus, called SIEBIMM (strain-induced elastic buckling instability for mechanical measurements).19
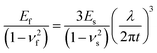 | (1) |
In the present study, a new experimental approach was developed to identify the effects of the CNC alignment direction on the mechanical properties by in situ observation of the onset of these surface buckling instabilities and the subsequent fracture behavior. By applying a uniaxial tensile strain in varying directions relative to the CNC alignment direction, the fracture behavior of CNC films was observed. The moduli were obtained through eqn (1) by measuring the wavelength of wrinkles that formed perpendicular to the tensile loading direction due to Poisson effects. By analyzing how crack angles and the modulus changed with respect to the CNC particle alignment relative to the applied loading direction, the effects of particle orientation on mechanical properties of CNC films were determined.
Materials and methods
CNC film preparation
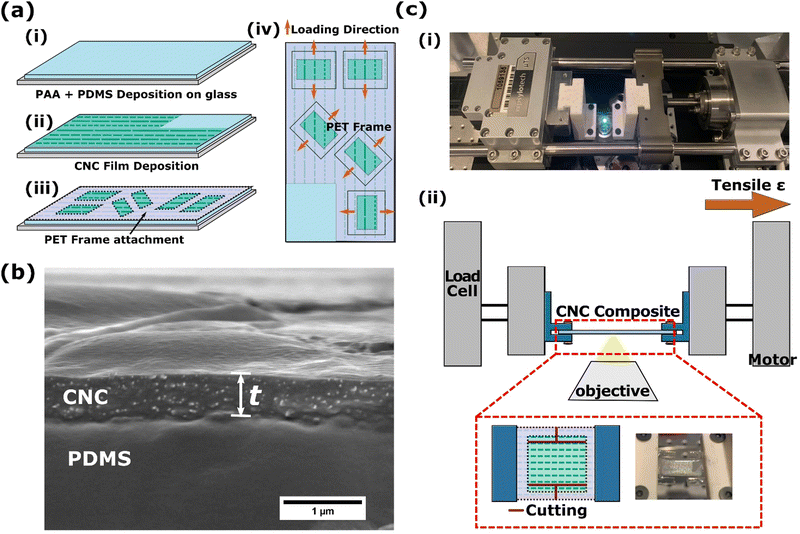
In this study, CNC films were supported on silicone substrates to enable observation of the film fracture mechanisms while tensile testing. Fig. 1(a) shows the sample fabrication of the CNC/silicone bilayer. The silicone substrate was poly(dimethylsiloxane) (PDMS, Dow Corning Sylgard 184). Oligomer (base) and cross-linker (curing agent) were mixed in a 10 to 1 ratio by weight. A glass slide was coated with poly(acrylic acid) (PAA, MW = 1.8 kg mol−1, Sigma Aldrich) spin cast from solution (2 wt% in isopropyl alcohol). Then, PDMS was spin cast as shown in Fig. 1(a(i)). The bilayer was cured at 70 °C for 4 h. Here, the PAA was used as a sacrificial layer to facilitate removal of the CNC/silicone bilayer from the glass slide for testing. The cured PDMS substrate was treated with oxygen plasma (GLOW Research GLOW Plasma System) for 300 s. Selective oxidation of targeted areas of the PDMS was achieved with a silicone mask placed on top of the PDMS. Unoxidized areas were used to measure the thickness and modulus of the PDMS substrate. An aqueous CNC suspension (University of Maine Forest Product Labs, 11.9 wt% CNC, 0.99 wt% sulfur) was diluted with ethanol to form an 8 wt% CNC suspension. The suspensions were shear cast onto the oxidized PDMS surface as shown in Fig. 1(a(ii)) with a flexible doctor blade on a motorized stage using a previously reported protocol.31,32 Dilution of the aqueous suspensions with ethanol enabled control of the vapor pressure of the suspensions to optimize the solvent evaporation rate. The resulting films were dried for 48 h in a custom-built humidity chamber (25 °C, 80%RH). Thermoplastic (poly(ethylene terephthalate), PET, 3M) frames were laser cut to control the CNC alignment with respect to the loading direction. Orientation of the major axis of the rectangular windows within the frame ranged from 0° to 90° in increments of 15°. The frames also prevented bending of the film while detaching the film from the glass slide before tensile testing. The frame was attached to the CNC/PDMS composite using the same 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) to
to![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 base
1 base![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) to
to![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) curing agent weight ratio PDMS, then cured at 70 °C for 2 h (Fig. 1(a(iii))). Fig. 1(a(iv)) shows the location of a few windows within a frame, which allows multiple alignment angles and a blank PDMS region without CNC on the same glass slide. This uncoated PDMS section was utilized for thickness and modulus measurements. The CNC/PDMS bilayer specimens were cut out with a small portion of the frame as shown in Fig. 1(a(iv)) to mechanically stabilize the composite and reduce premature cracking due to handling. Sections were detached from the glass slide by dissolving the PAA layer with water.
curing agent weight ratio PDMS, then cured at 70 °C for 2 h (Fig. 1(a(iii))). Fig. 1(a(iv)) shows the location of a few windows within a frame, which allows multiple alignment angles and a blank PDMS region without CNC on the same glass slide. This uncoated PDMS section was utilized for thickness and modulus measurements. The CNC/PDMS bilayer specimens were cut out with a small portion of the frame as shown in Fig. 1(a(iv)) to mechanically stabilize the composite and reduce premature cracking due to handling. Sections were detached from the glass slide by dissolving the PAA layer with water.
Film characterization
The thickness of the PDMS layer was measured with an optical microscope (DMi8, Leica) by observing the PDMS cross section. The PDMS thickness ranged from 150 μm to 200 μm. The thickness of the CNC layer was measured in cross section on a field emission scanning electron microscope (FE-SEM S-4800, Hitachi). Fig. 1(b) shows a representative cross section of the CNC/PDMS bilayer with the thickness indicated by white arrows. The measured thickness of the CNC film layer was 0.49 ± 0.09 μm over 10 measurements.Measurement of CNC modulus and observation of CNC fracture surface
Mechanical testing of CNC/PDMS bilayer samples was performed with a miniature uniaxial tensile tester (μTS, Psylotech) as shown in Fig. 1(c). After removing a CNC/PDMS sample from the glass slide, handling it only by the PET frame, it was carefully clamped within the mechanical stage (Fig. 1(c(i))). Once secured in the tensile tester, the sides of the frame were cut to separate the frame from the bilayer sample (Fig. 1(c(ii))). The dark lines in Fig. 1(c(ii)) indicate where the cuts were made. The mechanical stage was placed over the objective of an inverted optical microscope (DMi8, Leica Microsystems) to observe the deformation of the CNC films supported on the PDMS substrate. A uniaxial tensile strain was applied at a rate of 0.001 s−1. Images were acquired every 250 ms.Coarse-grained modelling of CNC films
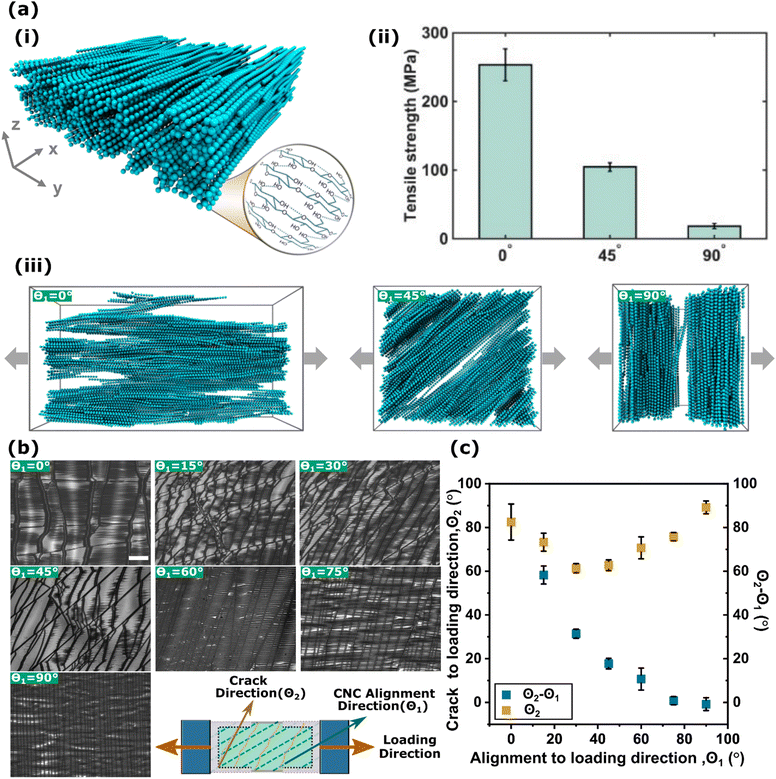
Coarse-grained molecular dynamic (CG-MD) simulations were carried out to systematically investigate the mechanical response of CNC films. In the mesoscopic ‘bead-spring’ CG model of CNC informed from an atomistic counterpart, each CG bead with a radius of 17 Å represents three repeat units of a 36-chain structured (110) cross-section of Iβ crystalline CNCs. The CG force field components were defined based on the contributions of bonds and angular bending along the fiber axial direction, which were captured via harmonic spring potentials and pairwise nonbonded interactions represented by the Morse potential. More detailed information on the CG model development and application can be found in previous studies.33–35To generate a representative thin film system with ordered CNCs, aligned CNCs were assembled into a fixed simulation cell with the size of 150 nm by 150 nm by 45 nm, forming an anisotropic system comprised of 435 CNCs with 32 CG beads per CNC (length approximately 100 nm) as illustrated in Fig. 5(a(i)). To mimic the thin film systems, periodic boundary conditions (PBCs) were applied in the xy-plane while non-PBCs was applied in the z-direction (i.e., the thickness direction); two completely smooth implicit repulsive walls using a 9-3 Lennard-Jones (LJ) potential were implemented below and above the film for better control of density and geometry of films. During the equilibrium process, the total potential energy was first minimized by the iterative conjugate gradient algorithm.36 The simulated CNC film was then equilibrated by two annealing cycles for 20 ns under a canonical ensemble (NVT), where the temperature was elevated from 300 K to 1000 K and then cooled down to 300 K. An integration timestep, Δt = 5 fs, was adopted for all CG-MD simulations. Prior to mechanical response, equilibration and structural stability were confirmed by ensuring the total potential energy convergence was achieved. To characterize the mechanical response, the strain-controlled uniaxial tensile deformation was performed with a constant strain rate of 0.05 ns−1, which is consistent with previous simulation studies.35,37 Three independent initial configurations were used to obtain the average value of tensile strength and corresponding standard deviation. All CG-MD simulations were carried out using the Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS)38 and the visualization of simulation snapshots was performed by Visual Molecular Dynamics (VMD).39
Results and discussion
Degree of CNC alignment
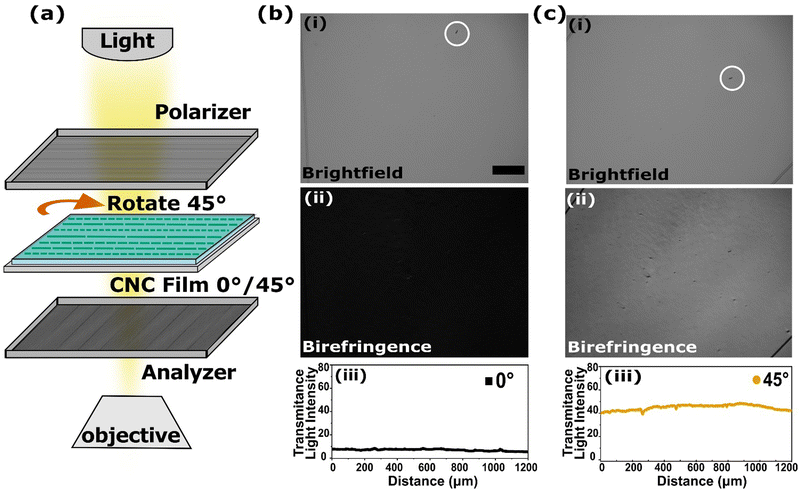
The extent of ordering of each CNC film supported on PDMS was measured using birefringence (DMi8, Leica Microsystems) based on a previously reported technique.5,40 In this method, images are obtained twice of each sample placed between crossed polarizers. First, the principal alignment direction of the CNC film was oriented at 0° and then rotated to 45° with respect to the polarizer. Fig. 2(a) shows the birefringence measurement configuration. Image pairs were obtained in the same location on each sample. Fig. 2(b(i) and c(i)) show bright field images of a sample at 0° and 45° to the polarizer, respectively, where no real difference in contrast is observed. Fig. 2(b(ii) and c(ii)) are the birefringence images for the same locations at 0° and 45°. Here, a horizontal line scan across the midplane of each birefringence image, shown in Fig. 2(b(iii) and c(iii)), indicates the change in transmitted light. The ratio of these two intensities is used to calculate the extent of ordering (Herman's order parameter).Using the transmitted light intensity from the birefringence images, Herman's order parameter (S) was calculated with eqn (2).5,40
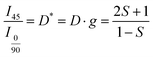 | (2) |
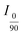 , I45, D, and g represent the transmitted light intensity of 0/90° and 45° configurations, dichroic ratio, and correction factor, respectively. Herman's order parameter is defined such that CNCs are randomly distributed when S = 0, and perfectly aligned when S = 1. The S value of the films in this study was calculated to be 0.5 ± 0.1.
, I45, D, and g represent the transmitted light intensity of 0/90° and 45° configurations, dichroic ratio, and correction factor, respectively. Herman's order parameter is defined such that CNCs are randomly distributed when S = 0, and perfectly aligned when S = 1. The S value of the films in this study was calculated to be 0.5 ± 0.1.
Observation of CNC film fracture surface
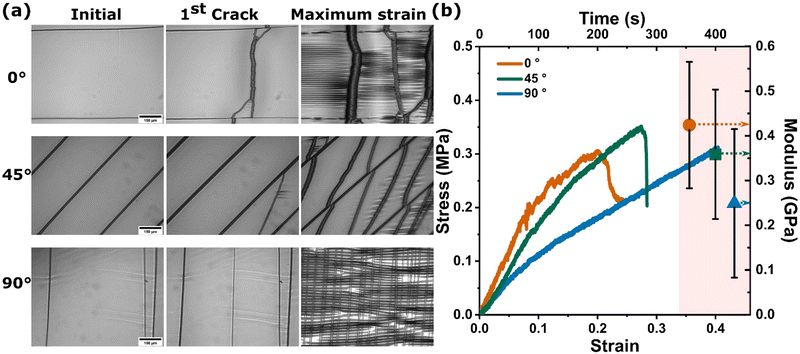
Deformation of each CNC film was observed microscopically while a uniaxial tensile strain was applied at a strain rate of 0.001 s−1. Fig. 3(a) shows a representative CNC film prior to the start of the test, at the onset of fracture (appearance of the first crack), and maximum strain prior to catastrophic failure of the CNC/PDMS bilayer sample for 0°, 45°, and 90° CNC misalignment to the loading direction. The images in the left column of Fig. 3 show undeformed CNC films. The CNC suspension contracts as the solvent evaporates during the drying process. This shrinkage causes residual in-plane tensile stresses in the CNC films that lead to cracking. The cracks propagate in the CNC alignment direction because the interparticle bonds between adjacent CNCs are much weaker than the covalent bonds within each particle.10,16 In the images of the undeformed specimens, a few pre-existing cracks that result from the CNC deposition and subsequent drying process are observed. The alignment of the particles is evident in the orientation of the pre-cracking on each sample.The images in the second column of Fig. 3(a) show the onset of CNC fracture resulting from tensile loading. For CNC films with the CNCs aligned in the same direction as the tensile loading direction (0°), cracks formed in the CNC films perpendicular to the loading direction. These cracks were fairly wide with diffuse edges. For the films with CNCs aligned at 45° relative to the loading direction, the cracks propagated at a slightly higher angle than the alignment direction, bridging pre-existing cracks that formed in the films during the drying process. For the films aligned at 90° relative to the loading direction, the film also fractured perpendicular to the loading direction. However, these cracks were much narrower, with smoother edges. The crack width at the onset of fracture varied as a function of the CNC misalignment angle. A wide, rough crack was generated for the 0° samples, while thin and linear fracture lines were observed for the 90° specimens.
At the maximum strain prior to substrate fracture, the fracture morphology of each oriented CNC film is given in the right column of Fig. 3(a). The fracture morphology of each testing orientation is in good agreement with previous computational work that predicted the fracture mechanisms and failure modes of CNC films with respect to the CNC misalignment with the loading direction.16 The CNC films failed in a “sliding mode” with shear dominated fracture, when the CNC alignment was parallel to the loading direction (difference of 0°). On the other hand, the 90° oriented CNC film failed in the “normal mode”, dominated by particle separation. The 45° aligned CNC film failed in a “mixed mode”, consisting of combined sliding and normal modes. Fig. 3(b) shows representative stress–strain responses of the CNC/PDMS composites for film alignments of 0°, 45° and 90° to the loading direction during uniaxial tensile experiments. The modulus of PDMS was the same, approximately 1 MPa, while the apparent stiffness of the CNC/PDMS composite varied significantly with respect to the orientation of the CNC films. As the angle between CNC misalignment and the loading direction increased, the modulus of the CNC/PDMS composite decreased. Since the film contained cracks before the tensile test, it is difficult to quantitatively determine the modulus and strength of CNC films from these results. Videos of the deformation of representative bilayers during tensile testing are provided in the ESI.†
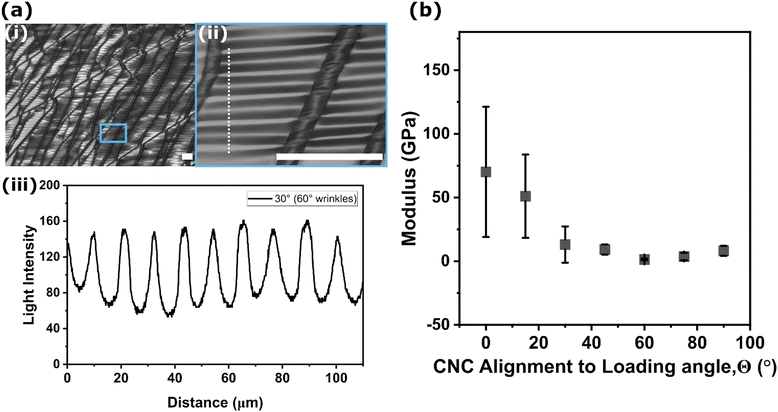
The SIEBIMM technique was used to determine the elastic modulus of the CNC films with regard to the angle between CNC alignment and loading direction.19 During the mechanical test, a compressive strain was generated perpendicular to the tensile direction due to Poisson effects in the incompressible PDMS substrate (υ ≈ 0.5). Periodic buckling instabilities (wrinkles) appear due to the combined Poisson effects and the modulus mismatch between the rigid CNC film and the softer PDMS substrate. Fig. 4(a(i and ii)) show the CNC film surface of 30° misaligned CNC at the maximum strain. Regardless of the crack direction and density, the wrinkles are distributed evenly in the undamaged regions of the film as shown in Fig. 4(a(ii)). Fig. 4(a(iii)) shows the wrinkling profile obtained from the image in Fig. 4(a(ii)). When the CNC alignment was 30° relative to the tensile loading direction, the compressive stress generated is perpendicular at 60° to the loading direction, and thus the modulus calculated is for a CNC misalignment of 60°. Fig. 4(a(iii)) shows the wrinkling profiles obtained along with the vertical dashed line in Fig. 4(a(ii)). A line scan of a brightfield microscopy image of wrinkles, like the one taken at the dashed line in the figure, can be used to determine the wavelength of wrinkles. The peak-to-peak distance is used to calculate the wavelength over an average of 10 peaks. Fig. 4(b) shows the calculated modulus with respect to the CNC misalignment from 0° to 90° in 15° increments based on eqn (1). The film thickness (t) was measured to be 0.5 μm, and the modulus of PDMS without CNC as shown in Fig. 1(a(iv)) was measured with the same strain rate as the composites.
The Poisson's ratio of the CNC film is taken to be 0.3 based on previously reported literature values.41 The moduli of CNC films decreased exponentially as a result of increasing the misalignment between the loading direction and the tensile direction from 0° to 30°, then the modulus slightly increased from 60° to 90° because of the constrained lateral deformation by stiff CNCs. The modulus trend was in good agreement with the simulation results of Shishehbor et al.,16 in which the moduli of the CNC films decreased exponentially as the misalignment increased until 45°, then the moduli of CNC films slightly increased to a misalignment of 90°. Though the measured moduli agreed in trend, the recorded modulus values were slightly lower than those reported in the simulated work since in simulations, both the degree of alignment and CNC width and length distribution could be controlled.
We further carried out CG modeling of CNC films Fig. 5(a) to gain deeper insights into the morphology of the films upon fracturing at the nanoscale. Specifically, a tensile loading was applied at 0°, 45°, and 90° of CNC alignment relative to the loading direction. From the simulations, the results displayed a sudden drop in tensile strength from approximately 250 MPa at 0° to around 100 MPa at 45°, and then the strength decreased further to 20 MPa at 90° as shown in Fig. 5(a(ii)). This monotonic decrease in strength verifies the direct influence of the local directionality of CNC orientation on the mechanical response of CNC films. Fig. 5(a(iii)) shows a comparison of different failure morphologies of CNC films with respect to the orientation angles (i.e., 0°, 45°, and 90°). It is observed that when CNCs are aligned in the same direction as the loading direction (0°), the fracture happens with wide and rough cracks having diffuse edges due to the sliding of CNC fibers. However, for the 90° case where CNC separation dominates, the film fractured perpendicular to the tensile direction with a congregate crack having a relatively smooth edge. Moreover, for the film with CNCs aligned at 45° relative to the loading direction, fractures formed when CNC fibers slide and separate at the same time, resulting in the crack propagation at a higher angle. This observation provides direct visual evidence for different fracture morphology, yielding a reasonable agreement with the experimental results shown in Fig. 5(b). Additionally, the maximum strain prior to CNC film rupture at 0° was greater than that at 45°, which was slightly larger than that at 90°, corroborating the finding that the mechanical response varies significantly with respect to directionality of CNCs in thin film systems.
To identify the relationship between fracture behavior and modulus of CNC films, the crack angle was measured with respect to the CNC alignment direction. Fig. 5(b) shows the fracture morphology, obtained at the maximum strain, with the corresponding CNC misalignment to the loading direction (θ1) labeled in each image. The schematic image (bottom right) in Fig. 5(b) explains the directions of the crack, CNC alignment, and loading. All cracks displayed a relationship with and were affected by the CNC alignment. Fig. 5(c) shows the difference in angle between the cracking and the loading directions (θ2), which were measured from the optical micrographs of the CNC/PDMS composites at maximum strain. The difference in angle between the crack propagation direction and the CNC misalignment direction is θ2 − θ1. The crack angle decreased from 90° to 60° as the angle between CNC alignment and loading direction increased from 0° to 30°. Then the crack angle increased from 60° to 90° again as the CNC misalignment increased from 45° to 90°. The difference between the crack angle and CNC alignment exponentially decreased as the CNC misalignment increased. The difference in angles (θ2 − θ1) between the crack and CNC alignment corresponded with the observed moduli in Fig. 4(b). It is hypothesized that the angle difference represents the degree of shearing between CNC particles when films failed. The shearing between CNC particles is a dominant factor in the fracture behavior of 0° misalignments.16 For angles between 15° and 70°, the film failed with a mixed mode, which combines shear and fiber separation. For example, as the crack angle approaches the alignment angle, the normal fracture mode increasingly dominates, while the shearing of CNC particles dominates as the difference in crack angle and CNC alignment angle approaches 90°.
Conclusions
The mechanics of anisotropic CNC thin films were explored in this study. The impact of this anisotropy has been studied computationally in prior work but was measured experimentally here. It is challenging to experimentally measure the modulus, fracture toughness, and fracture mechanisms with respect to the CNC alignment direction in a single experiment due to the brittleness of neat thin films. In this work, a new approach was developed by observing in situ deformation to measure the modulus of CNC films and determine the fracture mechanisms with respect to the CNC misalignment. To observe the fracture morphology and the mechanical properties, CNC/PDMS bilayers were fabricated. To vary the angle mismatch between CNC alignment and loading direction, a laser-cut PET frame was fabricated. The surface deformation was observed by applying a tensile strain with the mechanical stage positioned over an inverted optical microscope. By analyzing the wavelength of wrinkles generated under tension which appeared parallel to the applied loading direction, the anisotropy of the modulus of aligned CNC films was determined. The modulus of CNC films exponentially decreased as the angle between CNC alignment and loading direction increased. Fracture mechanisms were observed which change with respect to misalignment angle, in good agreement with computational work. The relationship between the modulus and the dominant factors causing film fracture was determined by analyzing the crack orientation and morphology with respect to the CNC alignment. Shearing or sliding between CNC particles dominated as the mismatch in the crack and CNC alignment angle approached 90°, while clean interparticle separation between CNCs dominated as the angular mismatch approached 0°. Utilizing this new measurement approach, the modulus of brittle and thin CNC films can be measured while simultaneously investigating their fracture mechanisms.Author contributions
All authors contributed to this work and have approved of the final manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to thank J. Youngblood for providing the CNC materials for this project. Financial support was provided by Purdue University. ZL and WX acknowledge the support from National Science Foundation (NSF) under NSF CMMI Award No. 2113558. Publication of this article was funded in part by Purdue University Libraries Open Access Publishing Fund.Notes and references
- R. J. Moon, A. Martini, J. Nairn, J. Simonsen and J. P. Youngblood, Chem. Soc. Rev., 2011, 40, 3941–3994 RSC.
- D. Klemm, B. Heublein, H. P. Fink and A. Bohn, Angew. Chem., Int. Ed., 2005, 44, 3358–3393 CrossRef CAS PubMed.
- J. Luo, H. Chang, A. A. Bakhtiary Davijani, H. C. Liu, P. H. Wang, R. J. Moon and S. Kumar, Cellulose, 2017, 24, 1745–1758 CrossRef CAS.
- D. Bondeson, A. Mathew and K. Oksman, Cellulose, 2006, 13, 171–180 CrossRef CAS.
- R. A. Chowdhury, M. Nuruddin, C. Clarkson, F. Montes, J. Howarter and J. P. Youngblood, ACS Appl. Mater. Interfaces, 2019, 11, 1376–1383 CrossRef CAS PubMed.
- Y. Habibi, L. A. Lucia and O. J. Rojas, Chem. Rev., 2010, 110, 3479–3500 CrossRef CAS PubMed.
- M. A. Hubbe, O. J. Rojas, L. A. Lucia and M. Sain, Int. J. Interact. Mob. Technol., 2018, 12, 929–980 Search PubMed.
- M. Chen, J. Parot, V. A. Hackley, S. Zou and L. J. Johnston, Cellulose, 2021, 28, 1933–1946 CrossRef CAS.
- A. Ishikawa, T. Okano and J. Sugiyama, Polymer, 1997, 38, 463–468 CrossRef CAS.
- A. B. Reising, R. J. Moon and J. P. Youngblood, J. Sci. Technol. For. Prod. Processes, 2012, 2, 32–41 Search PubMed.
- B. Natarajan and J. W. Gilman, Philos. Trans. R. Soc., A, 2018, 376, 20170050 CrossRef PubMed.
- B. Natarajan, A. Krishnamurthy, X. Qin, C. D. Emiroglu, A. Förster, E. J. Foster, C. Weder, D. M. Fox, S. Keten, J. Obrzut and J. W. Gilman, Adv. Funct. Mater., 2018, 28, 1800032 CrossRef.
- A. Tran, W. Y. Hamad and M. J. MacLachlan, Langmuir, 2018, 34, 646–652 CrossRef CAS PubMed.
- W. Gindl and J. Keckes, J. Appl. Polym. Sci., 2007, 103, 2703–2708 CrossRef CAS.
- A. Bohn, H. P. Fink, J. Ganster and M. Pinnow, Macromol. Chem. Phys., 2000, 201, 1913–1921 CrossRef.
- M. Shishehbor, H. Son, M. Nuruddin, J. P. Youngblood, C. Davis and P. D. Zavattieri, J. Mech. Behav. Biomed. Mater., 2021, 118, 104399 CrossRef CAS PubMed.
- J. Y. Chung, A. J. Nolte and C. M. Stafford, Adv. Mater., 2011, 23, 349–368 CrossRef CAS PubMed.
- J. A. Howarter and C. M. Stafford, Soft Matter, 2010, 6, 5661–5666 RSC.
- C. M. Stafford, C. Harrison, K. L. Beers, A. Karim, E. J. Amis, M. R. VanLandingham, H. C. Kim, W. Volksen, R. D. Miller and E. E. Simonyi, Nat. Mater., 2004, 3, 545–550 CrossRef CAS PubMed.
- H. Son, A. L. Chau and C. S. Davis, Soft Matter, 2019, 15, 6375–6382 RSC.
- C. M. Stafford, B. D. Vogt, C. Harrison, D. Julthongpiput, R. Huang, R. V. April, V. Re, M. Recei and V. June, Macromolecules, 2006, 39, 5095–5099 CrossRef CAS.
- J. Y. Chung, T. Q. Chastek, M. J. Fasolka, H. W. Ro and C. M. Stafford, ACS Nano, 2009, 3, 844–852 CrossRef CAS PubMed.
- E. A. Wilder, S. Guo, S. Lin-Gibson, M. J. Fasolka and C. M. Stafford, Macromolecules, 2006, 39, 4138–4143 CrossRef CAS.
- S. Cai, D. Breid, A. J. Crosby, Z. Suo and J. W. Hutchinson, J. Mech. Phys. Solids, 2011, 59, 1094–1114 CrossRef.
- C. S. Davis and A. J. Crosby, J. Polym. Sci., Part B: Polym. Phys., 2012, 50, 1225–1232 CrossRef CAS.
- Y. C. Chen and A. J. Crosby, Adv. Mater., 2014, 26, 5626–5631 CrossRef CAS PubMed.
- Y. Ebata, A. B. Croll and A. J. Crosby, Soft Matter, 2012, 8, 9086–9091 RSC.
- J. Zou, S. Wu, J. Chen, X. Lei, Q. Li, H. Yu, S. Tang and D. Ye, Adv. Mater., 2019, 31, 1–8 Search PubMed.
- E. Niinivaara, J. Desmaisons, A. Dufresne, J. Bras and E. D. Cranston, J. Colloid Interface Sci., 2021, 582, 227–235 CrossRef CAS.
- M. Trejo, C. Douarche, V. Bailleux, C. Poulard, S. Mariot, C. Regeard and E. Raspaud, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 2011–2016 CrossRef CAS.
- D. Y. Lee, J. T. Pham, J. Lawrence, C. H. Lee, C. Parkos, T. Emrick and A. J. Crosby, Adv. Mater., 2013, 25, 1248–1253 CrossRef CAS PubMed.
- H. S. Kim, C. H. Lee, P. K. Sudeep, T. Emrick and A. J. Crosby, Adv. Mater., 2010, 22, 4600–4604 CrossRef CAS PubMed.
- X. Qin, S. Feng, Z. Meng and S. Keten, Cellulose, 2017, 24, 3289–3299 CrossRef CAS.
- Z. Li and W. Xia, Extrem. Mech. Lett., 2020, 40, 100942 CrossRef.
- Z. Li, Y. Liao, Y. Zhang, Y. Zhang and W. Xia, Extrem. Mech. Lett., 2022, 50, 101519 CrossRef.
- C. Payne, M. Teeter, D. Allan, T. Arias and J. Joannopoulos, Rev. Mod. Phys., 1992, 64, 1045–1097 CrossRef.
- N. A. Miller, Z. Li, W. Xia and C. S. Davis, ACS Appl. Polym. Mater., 2022, 4, 3045–3053 CrossRef CAS.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- M. Nuruddin, R. A. Chowdhury, N. Lopez-Perez, F. J. Montes, J. P. Youngblood and J. A. Howarter, ACS Appl. Mater. Interfaces, 2020, 12, 24380–24389 CrossRef CAS PubMed.
- E. Chanliaud, K. M. Burrows, G. Jeronimidis and M. J. Gidley, Planta, 2002, 215, 989–996 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Videos of variously oriented CNC films upon deformation, 3 Videos. See DOI: https://doi.org/10.1039/d2ma00870j |
| This journal is © The Royal Society of Chemistry 2023 |