Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Direct measurement of the genuine efficiency of thermogalvanic heat-to-electricity conversion in thermocells†
Maria A.
Trosheva
,
Mark A.
Buckingham‡
 and
Leigh
Aldous
and
Leigh
Aldous
 *
*
Department of Chemistry, King's College London, Britannia House, London, SE1 1DB, UK. E-mail: leigh.aldous@kcl.ac.uk
First published on 5th April 2022
Abstract
Harvesting wasted thermal energy could make important contributions to global energy sustainability. Thermogalvanic devices are simple, chemistry-based devices which can convert heat to electricity, through facile redox chemistry. The efficiency of this process is the ratio of electrical energy generated by the cell (in Watts) to the quantity of thermal energy that passes through the cell (also in Watts). Prior work estimated the quantity of thermal energy passed through a thermocell by applying a conductive heat transfer model to the electrolyte. Here, we employ a heat flux sensor to unambiguously quantify both heat flux and electrical power. By evaluating the effect of electrode separation, temperature difference and gelation of the electrolyte, we found significant discrepancy between the estimated model and the quantified reality. For electrode separation, the trend between estimated and measured efficiency went in opposite directions; as a function of temperature difference, they demonstrated the same trend, but estimated values were significantly higher. This was due to significant additional convection and radiation contributions to the heat flux. Conversely, gelled electrolytes were able to suppress heat flux mechanisms and achieve experimentally determined efficiency values in excess of the estimated values (at small electrode separations), with partially gelled systems being particularly effective. This study provides the ability to unambiguously benchmark and assess the absolute efficiency and Carnot efficiency of thermogalvanic electrolytes and even the whole thermocell device, allowing ‘total device efficiency’ to be quantified. The deviation between the routinely applied estimation methodology and actual measurement will support the rational development of novel thermal energy harvesting chemistries, materials and devices.
Introduction
Thermoelectrochemistry – or electrochemistry where temperature is applied as an active variable – has many implications and applications, given the significant impact of temperature upon both thermodynamic and kinetic parameters.1 A key thermodynamic parameter is the temperature effect upon the standard electrode potential.2,3 A growing application of this is thermogalvanic cells; these are devices that typically comprise of two electrodes at different temperatures in contact with a solution or gel that contains both oxidation states of the same redox couple (i.e. both [Fe(CN)6]3− and [Fe(CN)6]4− or Fe2+ and Fe3+).4 The presence of a temperature difference (ΔT) across the two electrodes results in a thermodynamically-driven induced potential difference (ΔV) between the electrodes, which drives redox processes that results in a flow of electrical current. This, coupled with diffusion of the redox couple between the two electrodes – results in an elegant, purely chemical route for the conversion of a temperature gradient into electricity.5 Given that ca. two-thirds of the energy from human industry (even down to the human metabolism) is dissipated as low grade waste heat,6 widespread application could result in major efficiency gains, e.g. such as on industrial piping7 or skin.8–10Thermogalvanic electricity production is an entropically-driven process, and the magnitude of the driving force is normally expressed as the ‘thermogalvanic Seebeck coefficient’, or Se;
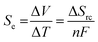 | (1) |
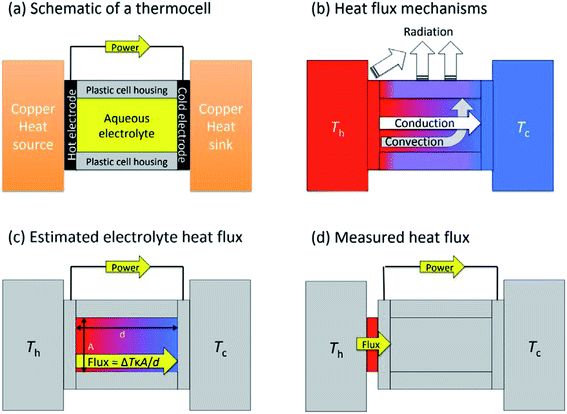
Fig. 1(a) shows a general layout for measuring a thermogalvanic cell, where a temperature difference can be easily applied across the two electrodes. The electrical power produced by the two electrodes can then be easily quantified via a variety of routes.15 Once the cell comes to equilibrium and steady state power output is achieved, the power is often limited by one dominant resistance, which is typically either kinetics (e.g. rate of electron transfer) or the rate of mass-transport between the two electrodes.5,15 This one major resistance factor, R, means the thermogalvanic cell displays a linear but inverse relationship between the voltage and the current produced, in line with Ohm's Law, so V = IR. The maximum voltage from the cell is characterised as the open circuit potential (Vocp, in V), and the maximum current as the short-circuit current density (jsc, in A m−2). Power generated follows Watt's Law, so P = IV. The inverse relationship between Vocp and jsc means that thermogalvanic cells typically generate a parabolic power curve,15 where the maximum power density generated by the cell (Pmax, W m−2) occurs at half the maximum current and half the maximum voltage, such that;
| Pmax = 0.25Vocpjsc | (2) |
Thermogalvanic conversion of thermal energy to electrical energy is not a perfect process and is limited by both Carnot efficiency and non-ideal processes. Fig. 1(b) highlights the scenario if the hot electrode temperature is far above ambient temperature while the cold electrode is close to ambient; conduction of heat will occur through the cell and electrolyte, temperature-difference induced convection in the electrolyte will exacerbate this, and radiative heat loss into the surroundings will also occur. The thermoelectric-inspired ‘dimensionless ZT figure of merit’ is sometimes referred to in thermogalvanic literature in an effort to consider the competing thermogalvanic current and heat flux processes;
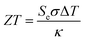 | (3) |
The absolute efficiency, η, is another key (and in theory unambiguous) means of benchmarking thermogalvanic device performance. The absolute efficiency is quantified by the proportion of thermogalvanic electrical power generated by the cell (pmax in W) from the corresponding heat flux passing into the cell (q, also in W), as shown in eqn (4). This can then be expressed as the fraction of the theoretically limiting Carnot cycle efficiency, ηr, based upon the applied hot and cold electrode temperatures (Th and Tc, respectively), as shown in eqn (5);
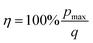 | (4) |
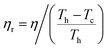 | (5) |
Arguably the magnitude of the efficiency doesn't necessarily matter; if thermal energy that would otherwise be wasted is instead valorised then that can be a net benefit. It's been stated that thermogalvanic devices with Carnot-relative efficiencies in the range of 2 to 5% could be commercially competitive,11 although a full technoeconomic comparison is still required to confirm if these values should be higher or lower. Nevertheless, the more efficient this process is at valorising waste, the more ‘green’ it is (alongside a series of other considerations).17,18 Additionally the more green and cost-effective it is, the more ‘sustainable’ the process is.19
In an effort to benchmark efficiencies, an ‘electrolyte-only’ heat flux estimation is commonly employed for thermogalvanic cells. This is exemplified in Fig. 1(c). Typically, the heat flux through the cell housing itself is disregarded, since most early cell constructions were not representative of application-appropriate cells. Instead, only the body of the electrolyte is considered, and is treated as a 1D heat flux through a 2D solid material using Fourier's Law;
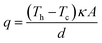 | (6) |
Early adoption of this estimation was mathematically justified, since it was suggested convective heat flux was negligible under their particular circumstances.11 However, cell design has since diversified, and several studies have highlighted the very significant role convection can play in certain thermogalvanic cells.20–22 The use of IR cameras in electrolyte measurements explicitly relies upon radiation out of the cell,20,23 which is also not considered by eqn (6). Numerous application-appropriate cell designs have also been reported, such as integrated into clothing,8 wearable on skin,9,10 installed onto hot water pipes,7etc., yet heat flux quantification has not advanced in step with this progress. While flawed, this estimated heat flux has nevertheless been the most valid approach available for benchmarking the efficiencies of new systems, with several solution-based, nano-structured electrode systems having Carnot-relative efficiencies predicted in excess of 0.5%,7,23–33 and even >2%.23,34–36
Two recent studies have gone beyond directly measuring thermogalvanic power and estimating the heat flux. Wu et al. investigated gelled vs. non-gelled electrolytes, and calculated the efficiency via the estimated heat flux; no significant difference was observed between the two types of electrolytes.22 However, the cold electrode temperature was maintained using a peltier device, and the power required to keep that electrode isothermal was two-fold higher in the ungelled electrolyte than the gelled electrolyte, demonstrating there was a significant difference in the genuine bulk heat flux through the cell that was not detected by the thermogalvanic measurements; likely because the thermal apparatus actively compensated for this difference by providing more cooling power.22 Yu et al. reported the efficiency of a thermogalvanic cell using the estimated heat flux equation, but rather than apply the conduction-only thermal conductivity, κ, they used IR imaging to estimate the effective thermal conductivity, κeff.23 This indirect measurement (via heat radiated from a cell wall) suggested that at an applied temperature difference of 50 K, the κeff reached 1.64 W m−1 K−1;23 far above the κ = 0.55 W m−1 K−1 measured in other studies.34,37 Interestingly, the addition of guanidinium resulted in crystallisation of the [Fe(CN)6]4−, and the presence of this solid material in the cell reduced κeff to ca. 0.4 W m−1 K−1. This value of κeff, combined with a significantly boosted Se value due to the crystallisation process, resulted in a very significant electrolyte-only Carnot efficiency value of 11.1% being stated (at ΔT = 40 K).23
The purpose of this study was to prepare a thermoelectrochemical cell that could unambiguously measure both the heat flux and the thermogalvanic power; the ratio of these two quantified values will then yield the absolute efficiency for an entire thermogalvanic device, for the first time. Fig. 1(d) describes this concept, whereby a heat flux sensor is introduced as a thermal bottleneck through which all thermal energy from the hot electrode must pass, thus allowing total quantification of the heat flux (qtotal, which subsequently passes through and out of the cell, via conduction, convection and/or radiation). If the heat flux through the empty cell, qempty, is subtracted it can yield a directly measured and quantified electrolyte-only heat flux, qm. That was performed in this study, and the trends in efficiency compared between those obtained using direct measurements vs. those predicted using the estimated heat flux given viaeqn (6). This study was used to achieve unambiguous quantification, then explore the effect of the parameters ΔT, d and gelled vs. un-gelled electrolytes upon efficiency.
Experimental
Electrode material comparison using conventional thermogalvanic assembly
Initial experiments used a setup that has been previously reported in detail elsewhere;4 namely a 6.7 mm diameter cylinder was machined from a block of PMMA (8.4 mm deep). At either end larger, shallow cylinders (10 mm diameter, 0.5 mm deep) were machined to form lips around the main cylinder, into which were inserted solid platinum electrodes (10 mm diameter, 1 mm thick disc, from SurePure Chemetals, USA). This gave a geometric electrode surface area of 35 mm2 and an inter-electrode spacing of 7.4 mm. Different types of carbon electrode materials were then cut into ca. 10 mm circles by hand, and inserted between the platinum electrode and the cylinder, into which the electrolyte was injected. The carbon electrodes were Pyrolytic Graphite Thermal Interface Material (0.017 mm thick, 1750 W m−1 thermal conductivity, RS Components, UK) or two thicknesses of flexible graphite ‘graphoil’ gasket sheets (0.3 mm thick or 1 mm thick, both from Xiaochengshop, China).The platinum electrodes were temperature controlled by contacting with RS-TX150 thermostatic circulator baths (Grant Instruments Ltd, UK) via copper heat exchangers, as previously described.4
Thermogalvanic characterisation methodology
All thermogalvanic measurements were allowed to reach steady state (unless otherwise specified in the manuscript), and characterisation was performed using the ‘sequence of constant voltages’ method previously reported, using either 2-point or 5-point power curve measurements.15 Specifically, these measurements yielded the voltage and current density (Vocp and jsc) as well as maximum power density (Pmax, in W m−2). This was converted into the absolute maximum power generated by the cell (pmax, in W) by dividing by the exposed electrode surface area (0.000094 m2 for the filled electrolyte cells; surface area for the three-sided gel cells are specified later). A Keysight B2901A Source Measure Unit and Quick IV software (Keysight, UK) were used throughout. For ungelled systems, current and voltage were measured for 300 s, and the average of the data from 151–300 s reported; for the gel systems, this expanded to 600 s with the average taken from 301–600 s.Thermogalvanic assemblies incorporating the heat flux sensor
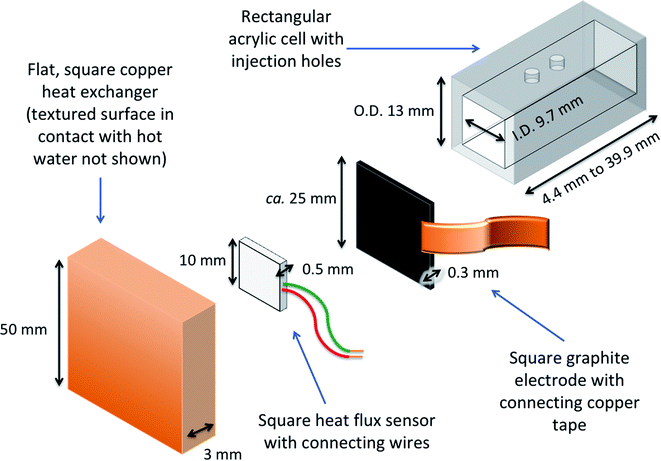
A dedicated thermogalvanic cell was developed to interface reproducibly with a commercial heat flux sensor (gSKIN-XP26 9C calibrated, greenTEC, Switzerland), which was a 10 mm by 10 mm square. The resulting assembly is described visually in Fig. 2 (a photograph is also shown later, in Fig. 4). The thermostatic water baths, copper heat exchangers and measurement techniques were unchanged from above, but the main cell was a hollow rectangular tube (extruded, clear acrylic hollow square tubing, 13 mm diameter and 9.7 mm bore, eBay Co. UK), which was cut to shape to vary the electrode separation distance, and had two injection holes drilled in the top. Squares of the 0.3 mm thick graphite were cut out and held in place at both ends of the cell by compressing it between the cell and the heat exchangers; the heat flux sensor was also compressed between the graphite electrode and hot copper heat exchanger. The electrodes and heat exchanger were both larger than the heat flux sensor, ensuring that all conductive thermal energy passing from the hot side into the thermogalvanic cell had to pass through the heat flux sensor (an irradiation effect could occur through the air gaps, but this has been modelled elsewhere22 and is expected to be negligible). Repeated use of the graphite resulted in increasing deformation and therefore worsening thermal contact, hence the electrodes could not be glued and each electrode was only used for one experiment before being disposed of. This arrangement gave an electrolyte-exposed square electrode surface area, A, of 94 mm2.Photographs and IR images were obtained using an iPhone 11 Pro Max (Apple Inc., USA) and a Seek Thermal CompactXR with iPhone connector (Seek Thermal Inc., USA), respectively.
Gelled electrolyte preparation and cell
Electrolytes were partially or fully gelled by the addition of 1.5 wt% or 3 wt% equivalents of sodium polyacrylate powder (SnoWonder Instant Snow Mix, SnoWonder, USA), which achieved the majority of its swelling within ca. 1 minute. Physically moving the gelled electrolyte into the thermogalvanic cell was found to result in significant reproducibility issues, due to different packing, trapped air, etc. Reproducible measurement was only achieved by physically removing one side of the rectangular cell housing, changing it from an enclosed square into a U-shape. All measurements reported here were recorded in three cells with electrode separation of 13.6, 20.9 or 29.2 mm; these cells were set up and the heat flux through the empty three-sided cell was measured. Then 0.4 M K3/K4[Fe(CN)6] electrolyte was added to fill the cell by ca. 80%; for 13.6, 20.9 or 29.2 mm this was 1, 1.57 and 2.15 mL, respectively, affording electrode–electrolyte surface areas of ca. 71, 71 and 73 mm2, respectively. The electrolyte was allowed to thermally equilibrate, measured, and then either 1.5 wt% or 3 wt% equivalents of sodium polyacrylate powder was added through the open side of the cell. This resulted in a homogenous dispersion of the powder and reproducibly formed a fully packed, air bubble-free gel. The system was measured using the thermogalvanic characterisation methodology described above, when the output from the heat flux sensor reached steady state (ca. 5 min).Conversion of the heat flux sensor output into heat flux
The potential difference generated across the commercial heat flux sensor (gSKIN-XP26 9C calibrated, greenTEC, Switzerland) was recorded every 0.25 s using chronopotentiometric measurements via a potentiostat (PGSTAT204 potentiostat with NOVA 2 software, Metrohm, UK). It was found that disabling the auto-ranging on the current and selecting the smallest current option (i.e. highest impedance) improved the reliability of the measurements as it suppressed any parasitic thermoelectric processes. Raw output data is presented later in Fig. 3 and 6.The heat flux sensor is a thermoelectric module designed for ultra-high resolution of conductive heat flux, and the potential difference generated across the sensor (ΔVs) was converted into heat flux using the manufacturer-supplied sensitivity factor of 15.09 μV per W m−2 of heat flux (at 295.65 K).38 The temperature-corrected sensitivity factor for this particular sensor was determined using the supplied 15.09 + 0.0189 (Ts − 295.65) relationship, where Ts is the temperature of the sensor in K. This value for Ts can be approximated using the temperature of the hot heat exchanger, Th, except the heat flux sensor acted as an additional thermal resistance in-series between the heat exchanger and graphite electrode meaning it was not as hot as the copper. Therefore, Ts was instead calculated for each experiment by first calculating the experienced temperature difference across the cell using:
| ΔTexp = Vocp/Se | (7) |
| Ts = Th − (ΔTapp − ΔTexp) | (8) |
Most experiments used Th = 313.15 K. While the Ts varied as a function of cell and experiment, it fell within the narrow range of 308.45 to 309.85 K; the values for ΔTexp are included in Table S2.† Arguably an even more accurate value would have been the value halfway between Th and Ts (i.e. 0.5(Th + Ts)) given that these values represent the temperature gradient across the sensor, but this additional correction factor was found to have only a very minor effect upon the heat flux values.
As such, the measured total heat flux (qtotal, in W) through the cell is given by:
| qtotal = As(15.09ΔVs + 0.0189)((Th − (ΔTapp − Vocp/Se)) − 295.65) | (9) |
This procedure was performed first using the cell assembly without electrolyte, and then the cell was filled in situ and the measurement repeated. The heat flux for the empty cell, qempty, was subtracted from the filled cell value, qtotal, to afford the electrolyte-only, measured heat flux value, qm.
Calculation of the estimated heat flux
The estimated heat flux was calculated using the often-reported adaption of Fourier's Law (eqn (6)) except the estimated absolute heat flux (qe, in W) was explicitly calculated from experimental data using: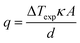 | (10) |
Calculation of the efficiency values
The absolute maximum power of the thermogalvanic cell (pmax) was measured; the absolute efficiency of the electrolyte's thermogalvanic performance, η, was then determined using both the experimentally measured heat flux (qm) and the heat flux estimated using Fourier's Law (qe). The absolute efficiency of conversion was given by the ratio of pmax to q (cf.eqn (4)).Efficiency relative to the theoretical Carnot cycle maximum, ηr, was determined using the fractional relationship in the Introduction (cf.eqn (5)) except instead of using the applied Th value, the temperature of the heat flux sensor, Ts, was used. The Ts was determined based upon the measured Vocp, as described by eqn (7) and (8).
Empty cell heat flux and the total device efficiency
As noted above, the measured total heat flux, qtotal, was corrected to measure the electrolyte-only value, qm, by subtracting the heat flux of the empty cell, qempty; these measured values of qempty are tabulated in the ESI.† It is also possible to predict the heat flux through the acrylic cell using the eqn (10), using the κ value for this plastic (ca. 0.20 W m−1 K−1) and the surface area of the plastic (0.000075 m2) that made up the face of the hollow square. Typically this predicted value was ca. 40% of the total measured empty cell heat flux, as shown later in this paper. As for the remaining measured heat flux for the empty cell, it is estimated that the majority of this was lost via conduction through the graphite electrode and into the metallic crocodile clip and wiring at the hot electrode side. The remainder would have been lost to the surroundings and air via radiation and air convection, respectively (from the plastic cell body, graphite electrode, metallic clip and wiring).As these factors were neither systematically investigated nor optimised, the majority of this paper focuses upon electrolyte-only efficiency parameters. However, the measured total device efficiency parameters can be derived by eqn (4) and (5), but using qtotal instead of qm; all measured values are tabulated in Tables S2 and S3.†
Results and discussion
Initial selection of the electrode material
As summarised in the Introduction, to the best of our knowledge the direct heat flux through thermogalvanic cells has not been quantified. This was achieved here by putting a heat flux sensor thermally in-series with the cell at the ‘hot’ electrode, as shown in Fig. 1(d). This, in conjunction to the quantification of the absolute thermogalvanic power, allowed unambiguous comparison of the ratio of the two.A detailed explanation of this set-up is included in the Experimental section. However, a flexible electrode material was required to work reproducibly in this set-up, and therefore a range of electrode materials were screened using a conventional thermogalvanic cell setup. This was achieved using a previously-reported4 thermocell setup, using solid platinum electrodes, filled with 0.2 M K3[FeCN6] and 0.2 M K4[FeCN6] (or 0.4 M K3/K4[Fe(CN)6]), exposed to a temperature gradient of 20 K, and measured using the formalised sequence of potentials.15 Three different types of graphite materials were then evaluated by placing them between the platinum and the electrolyte.
The resulting thermogalvanic steady-state outputs are summarised in Table 1; clearly platinum possessed the optimum performance due to the high output current density expected of such a highly electrocatalytic electrode towards [Fe(CN)6]3−/4− electron transfer kinetics,4 but this electrode material was too firm to reproducibly interface with the heat flux sensor and could not be utilised further. Pyrolytic crystalline graphite was bought as a thermal interface material, and it displayed excellent thermal properties (actually increasing the Vocp when placed on top of the Pt), but also demonstrated very poor electrocatalytic properties with the current decreasing ca. 60-fold. Two thicknesses of amorphous gasket (graphoil) graphite were also evaluated; as the thickness increased the thermal resistance also increased, resulting in a drop in Vocp. However, the current was far higher than that recorded at the crystalline graphite and increased as the thickness increased; this is likely due to partial porosity of the graphoil material increasing the electrochemically active surface area, and exposed electrocatalytic edge sites39 that comes with its expansion and compression during manufacturing.4 The 0.3 mm thick graphite was chosen as it was suitably thin and deformable while maintaining reasonable electrocatalytic ability, although it's important to note it generates only ca. 35% of the power of pure platinum (40 mW m−2vs. 114 mW m−2).
| Electrode material | Electrode thickness/mm | −Vocp/mV | −jsc/A m−2 | P max/mW m−2 |
|---|---|---|---|---|
| Platinum | N/A | 24.6 | 18.5 | 114 |
| Pyrolytic graphite | 0.017 | 24.8 | 0.3 | 2 |
| Amorphous graphite | 0.3 | 24.3 | 6.6 | 40 |
| Amorphous graphite | 1.0 | 23.5 | 11.9 | 70 |
Introduction of the heat flux sensor thermally in-series
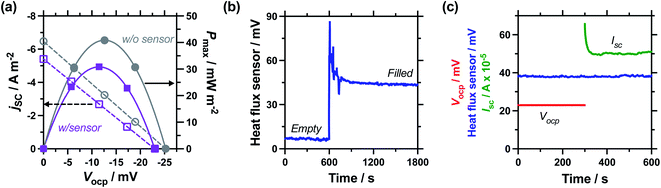
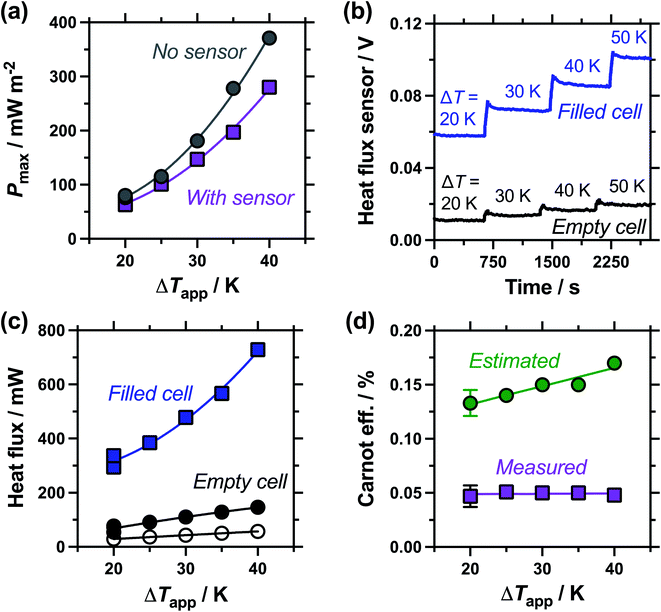
Next, the effect of introducing the heat flux sensor was explored, using the novel rectangular cell design described in detail in the Experimental section. Firstly, the thermogalvanic power was measured. Fig. 3(a) displays overlaid power curves for a rectangular cell with an electrode separation of 29.3 mm, filled with 0.4 M K3/K4[FeCN6] electrolyte, and equilibrated at an applied ΔT = 20.0 K (Tc = 20.0 °C, Th = 40.0 °C). Power curves were recorded for the same cell with (grey circles) and without (purple squares) the heat flux sensor thermally in-series. The heat flux sensor clearly added additional thermal resistance, reducing the Vocp and therefore the current and the power; despite this, an ideal power curve was still obtained for the thermogalvanic cell power output. Using a thermogalvanic Se value of −1.4 mV K−1,4,5,11,40,41 for the electrolyte, it implies an applied ΔTapp = 20.0 K translated into the graphite electrodes experiencing ΔTexp = 16.4 K with the heat flux sensor in-series.Next, the output from the heat flux sensor was quantified. Fig. 3(b) displays the voltage output from the heat flux sensor when connected thermally in-series with an empty cell (same cell and conditions as above). A constant output of ca. 7 mV was recorded, corresponding to a heat flux of ca. 45 mW (or heat flux density of 450 W m−2) through the sensor. After 10 min the 0.4 M K3/K4[FeCN6] electrolyte was injected to fill the cell, and a sharp spike in voltage (indicating increased heat flux) was observed; this dropped over ca. 5 min as the solution came to temperature, with further spikes and dips in this period due to injecting and extracting liquid from the cell in order to remove all the trapped bubbles. This equilibrated to give a constant value of ca. 44 mV, or a total measured heat flux of qtotal = 295 mW; this was how the heat flux for a filled cell and the corresponding empty cell were measured, and unless specified otherwise the empty cell-corrected electrolyte heat flux values were used, e.g. qm = 295 mW − 45 mW = 250 mW.
Power was characterised for all subsequent cells using 2-point measurements, e.g. measuring just Vocp and jsc, and determining the power density using Pmax = 0.25Vocpjsc.15Fig. 3(c) displays a 10 min characterisation measurement after the cell has come to thermal equilibrium; the Vocp for the first 300 s is shown and was very stable, followed by Isc measurement (then converted from Isc to jsc by dividing by the electrode surface area). An initial drop in current is observed as concentration gradients are established at the two electrodes, but it rapidly comes to equilibrium as the rate of consumption and mass transport equilibrate, resulting in genuine steady state power generation.15 The average from 151–300 s was used to quantify both Vocp and jsc. The simultaneous measurement of heat flux through the sensor was also measured (as overlaid in Fig. 3(c)), and this didn't display any significant changes, even when current was allowed to flow through the thermogalvanic cell.
The cell was found to generate ca. 31 ± 3 μW thermogalvanic power at steady state (from triplicate measurements), whereas the cell-corrected electrolyte heat flux value was ca. 236 ± 17 mW; this equates to an absolute efficiency of 0.013 ± 0.002%, or 0.024 ± 0.003% vs. Carnot efficiency. Conversely, the estimated heat flux using the typical model employed for thermogalvanic cells of 1D transport through a solid (eqn (6)) predicted nearly an order of magnitude less heat flux at 30 ± 1 mW. This results in an estimated Carnot efficiency of 0.19 ± 0.02%, i.e. the estimated efficiency was nearly 8-fold higher than the directly measured efficiency of conversion. This value increases to 9-fold if the total heat flux (qtotal) of the entire device is used, rather than the empty cell-corrected electrolyte heat flux value (qm).
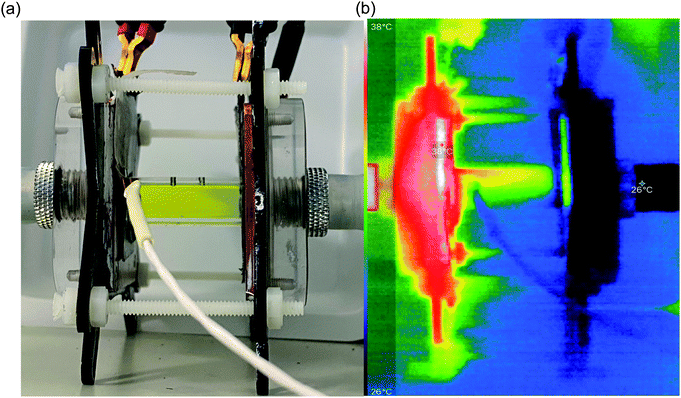
In order to identify the source of this additional heat flux, IR imaging was employed. Fig. 4 compares photos vs. IR images of the setup, and the latter clearly indicates how the top of the cell was significantly hotter than the bottom, indicating a significant amount of convection is occurring; this in turn results in significant radiation heat loss from the top of the cell. Neither convective nor radiation heat-transfer mechanisms are considered by the 1D Fourier's Law prediction (eqn (6)), thus accounting for the very significant difference observed here between actual measurement of the heat flux vs. the routinely employed estimated heat flux.
The implications of this order-of-magnitude difference, and a comparison against other published values are both discussed in detail at the end of this paper. Given the observed key role of the cells external surface, different electrode separations were evaluated next.
Effect of the inter-electrode separation distance
It has been previously reported that the power density of a thermogalvanic cell drops significantly with increasing inter-electrode separation, but power conversion efficiency will increase.27,40,42 Given this expected relationship, we set out to measure efficiency over 5 different electrode separations, all at an applied ΔT = 20 K. The results are summarised in Table 2 (full experimental results for cells without the heat flux sensor are in Table S1,† and with the heat flux sensor in Table S2†); key results are visualised in Fig. 5.| Experimental conditions | Measurement results | Measured efficiencies | Estimated heat flux and estimated efficiencies | ||||||
|---|---|---|---|---|---|---|---|---|---|
| d/mm | T h/°C | T c/°C | p max /μW | q m/mW | η m/10−3 % | η r,m/% | q e/mW | η e/10−3 % | η r,e/% |
| 4.4 | 40 | 20 | 7.1 | 239 | 3.0 | 0.060 | 180 | 4.0 | 0.08 |
| 9.5 | 40 | 20 | 6.1 (±0.1) | 248 (±24) | 2.4 (±0.2) | 0.047 (±0.005) | 87.5 (±3.6) | 6.9 (±0.3) | 0.13 (±0.01) |
| 18.9 | 40 | 20 | 3.9 | 268 | 1.4 | 0.027 | 44.8 | 8.7 | 0.16 |
| 29.3 | 40 | 20 | 3.1 (±0.3) | 236 (±17) | 1.3 (±0.2) | 0.024 (±0.003) | 29.6 (±1.2) | 10.4 (±0.1) | 0.19 (±0.02) |
| 39.9 | 40 | 20 | 2.3 | 259 | 0.9 | 0.017 | 20.7 | 11.0 | 0.21 |
| 9.5 | 40 | 20 | 6.1 | 248 | 2.4 | 0.047 | 87.5 | 6.9 | 0.13 |
| 9.5 | 45 | 20 | 9.5 | 295 | 3.2 | 0.051 | 107 | 8.9 | 0.14 |
| 9.5 | 50 | 20 | 13.8 | 368 | 3.7 | 0.050 | 128 | 10.8 | 0.15 |
| 9.5 | 55 | 20 | 18.6 | 439 | 4.2 | 0.050 | 149 | 12.5 | 0.15 |
| 9.5 | 60 | 20 | 26.4 | 584 | 4.5 | 0.048 | 164 | 16.1 | 0.17 |
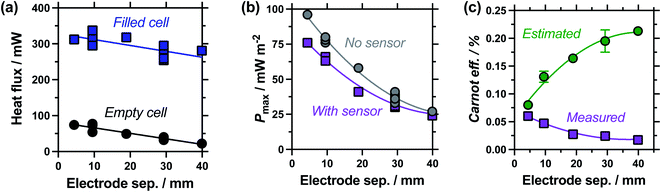
Measuring the heat flux through the empty and filled cells (Fig. 5(a)), the heat flux decreased in a linear manner as the electrode separation of the empty cells increases, in line with expectations for frustrated conduction through the longer plastic. A similar trend was observed in the electrolyte-filled cells, meaning that the corrected heat flux was essentially constant for all the cells, regardless of the electrode separation. This trend of largely constant heat flux vs. electrode separation deviates from the calculated heat flux, which considers conduction only and predicts the overall heat flux should decrease with increasing separation. It is likely that as the cell becomes longer, conduction decreases whereas convection and radiation increases, with these two effects thus cancelling each other out. As the electrode separation increases power also decreases exponentially (plotted in Fig. 5(b)), in line with expectations for a mass-transport limited thermogalvanic cell and prior studies.27,40 This trend was observed both with and without the heat flux sensor in series.
Fig. 5(c) compares the Carnot efficiency for the cells as a function of electrode separation, using either the genuinely measured heat flux or estimated heat flux; the absolute efficiency values followed the same trend (Fig. S1(a)†). Interestingly, the smallest cell shows fair correlation between measured and estimated efficiencies, consistent with the smallest cell being a conduction-dominated system. Our estimated heat flux model predicts increasing efficiency with increasing electrode separation, but with increasingly diminishing returns; this is in excellent agreement with earlier fundamental work.27 However, the genuinely measured heat flux results indicate decreasing efficiency, due to frustrated ion transport yet convection-boosted heat loss. This complete divergence of prior predictions vs. genuine measurements is of significance for future cell design and optimisation.
Effect of the applied temperature difference
Following the investigation into inter-electrode separation, the effect of temperature difference was explored, using a fixed, 9.5 mm electrode separation. Here the temperature difference was increased from ΔTapp = 20 K to ΔTapp = 40 K, by increasing the temperature of the hot electrode. As shown in Fig. 6(a), the power increased as the ΔTapp increased, in line with expectations.5,15 While the trends in Pmax with and without the heat flux sensor in-series deviated vs. ΔTapp, the two trends were comparable if plotted vs. ΔTexp (as shown in Fig. S1(b)),† as this corrects for the additional thermal resistance introduced by the sensor.Fig. 6(b) displays the raw data output by the heat flux sensor in-series with both the empty cell and the electrolyte-filled cells, whereas Fig. 6(c) plots the actual heat flux as a function of ΔTapp (the same trend exists vs. ΔTexp). The heat flux measured for the empty cell increased in a linear manner in line with Fourier's Law, whereas the electrolyte-filled cell increased in a non-linear manner, consistent with enhanced convection at greater values of ΔT. Also overlaid in Fig. 6(c) is the predicted heat flux calculated solely for conduction through the perspex cell using Fourier's Law (hollow circles), which is only ca. 40% of the heat flux measured for the whole device. Therefore some additional thermal energy is presumably lost to radiation and air-convection, with the majority lost to conduction through the electrode and into the wiring; this parasitic thermal lost is well recognised,43 and device-design requires two dissimilar thermogalvanic cell chemistries to be employed to help combat this thermal short-circuit.18,43 This effect is also clearly seen in Fig. 4(b), with the image achieved via IR radiation heat loss, and the clip at the hot electrode also being visually warmer than the background.
Both Pmax and heat flux increased with increasing ΔT, but Pmax increased by a greater magnitude and thus the overall absolute (electrolyte-only) efficiency increased with increasing ΔT (shown in Fig. S1(c)†). However, this overall efficiency gain was equivalent to expected gains from a Carnot engine at the increased ΔT, meaning the overall Carnot relative efficiency was independent of ΔT (Fig. 6(d)). Once again, the estimated heat flux lacked this nuance, with both the estimated absolute efficiency and estimated Carnot efficiency values increasing with ΔT. The divergence in these trends, combined with the smaller estimated heat flux, resulted in the estimated vs. measured efficiency values differing by a factor of 4.5 by ΔTapp = 40 K, in this 9.5 mm separation cell.
Effect of gelling the electrolyte
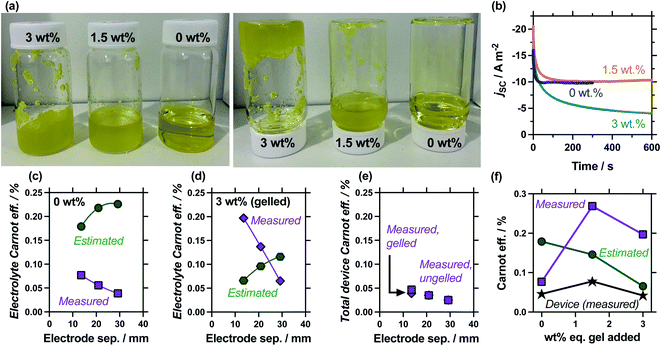
Gelled or ‘quasi-solid’ electrolytes have appeared numerous times, e.g.9,10,12–14,44–48 in thermogalvanic cells as a method of producing an electrolyte which is not susceptible to leaking and so supported the development of wearable devices;9,10 theoretically it also reduces the thermal conductivity through the thermocell. We therefore investigated the effect of gelling the electrolyte, especially since gelation was expected to ‘switch off’ the convection found to be so influential earlier in this study. This was performed by adding either 1.5 wt% or 3.0 wt%-equivalent of sodium polyacrylate powder; this is a textured, superabsorbent material that can rapidly swell and even gel highly concentrated electrolytes, within seconds.22Fig. 7(a) shows photographs of these systems being exposed to the inversion test, which demonstrates that 0.4 M K3/K4[FeCN6] electrolyte containing 1.5 wt% eq. sodium polyacrylate powder forms a heterogeneous, free-flowing slurry, whereas 3.0 wt% eq. results in a genuinely gelled electrolyte. Table S3† summarises all relevant values, while Fig. 7(b) plots the measurement of the jscversus time; addition of 1.5 wt% equivalent gelling agent resulted in a slightly slower equilibration time before steady state current was achieved, but otherwise didn't change the jsc, whereas the gelled 3.0 wt% equivalent system failed to reach equilibrium. The latter observation is common with fully-gelled electrolytes, which frustrate the transport of ions to such an extent that concentration imbalances accumulate and persist at the electrode surfaces.14
The comparison of gelled vs. ungelled electrolytes was also explored as a function of electrode separation. Fig. S2† plots the measured thermogalvanic powers, both with and without the heat flux sensor in-series, while Fig. 7(c) and (d) summarise the electrolyte-only Carnot efficiency values. The ungelled system (0 wt%, Fig. 7(c)) displayed the expected deviation between estimated and measured values (cf.Fig. 5(c)), but significant differences were observed in the gelled system (3 wt%, Fig. 7(d)). In the gelled system, measured efficiency still decreased with electrode separation while estimated efficiency increased. However, the estimated efficiency values were significantly lower, because the power generated by the gelled systems was lower but the predicted heat flux remained unchanged (as κ = 0.55 W m−1 K−1 was assumed throughout). Conversely, the measured actual heat flux was significantly reduced upon gelation; because heat flux was reduced even more than the current was reduced, the measured efficiency actually increased significantly. This difference means at relatively small electrode separations (<20 mm), the measured gelled electrolyte efficiency actually exceed estimated efficiency.
These results highlight how the assumption of κ = 0.55 W m−1 K−1 is flawed for both convective (e.g. liquid) and convection-supressed (e.g. gelled) systems. This mirrors the observations of Yu et al. who estimated the effective thermal conductivity, κeff, of their [Fe(CN)6]3−/4− electrolyte using IR imaging; while the conduction-only thermal conductivity should have been ca. 0.55 W m−1 K−1,34,37 at an applied ΔT = 50 K the effective thermal conductivity was 1.64 W m−1 K−1; after guanidinium-induced crystallisation this dropped down to ca. 0.4 W m−1 K−1,23 with the crystals presumably physically causing a reduction in heat flux. Additionally, Pu et al. reported κ values in the range of 0.31 to 0.38 W m−1 K−1 for a crosslinked polyacrylamide hydrogel monolith saturated with a 0.1 M K3/K4[Fe(CN)6] + 5.4 M LiBr electrolyte.48 Different κeff values were applied to our model such that the estimated electrolyte-only heat flux matched the measured heat flux; this gave κeff = 1.28 W m−1 K−1 for the 0 wt% system in the 13.6 mm cell, and κeff = 0.18 W m−1 K−1 for the 3 wt% system. However, κeff is also a cell-dependant value, and increased in the 20.9 mm cell to 2.14 W m−1 K−1 and 0.39 W m−1 K−1 for the gelled and ungelled systems, respectively, likely due to increased convective and radiative losses as the cell gets larger.
An additional concept that has apparently never been examined before is total device efficiency. Throughout, the electrolyte-only heat flux has been employed, but total heat flux was quantified. The measured Carnot efficiency was recalculated using the total heat flux, and these values are plotted in Fig. 7(e). It demonstrates that device-efficiency was essentially indistinguishable for gelled and ungelled electrolytes. This was because even though heat flux was suppressed more than current flow upon gelation, the additional heat flux through the cell assembly itself became a much more significant fraction of total heat flux, and reduced the overall total device efficiency. More thermally resistive electrolytes therefore require more thermally resistive cell housings in order to achieve boosts in efficiency in genuine ‘real world’ whole device applications.
Finally, the 1.5 wt% eq. gelling agent yielded a heterogeneous suspension; the ionic, solid particles appear to frustrate bulk thermal transfer (such as convection, and even to a degree conduction) but remains a highly ionically conductive system, boosting the (genuine) efficiency relative to the electrolyte alone. The measured and estimated Carnot relative efficiency is plotted in Fig. 7(f) for 0 wt%, 1.5 wt% and 3 wt% eq. sodium polyacrylate in the 13.6 mm cell. These values demonstrate the heterogeneous suspension caused by 1.5 wt% eq. possesses optimal conditions and displays the highest efficiency; this was reflected in an additionally boosted total device efficiency. Broadly, these precise measurements prove an often stated but only previously tentatively proven22 concept; that gelled and pseudo-gelled electrolytes can result in genuinely more efficient conversion in thermogalvanic cells, provided they selectively frustrate heat flux more than current generation.
A comparison of the factors and values vs. previous reports
Table 3 summarises a number of published papers that quote estimated Carnot efficiency values (using directly measured thermogalvanic power and estimated heat flux for the electrolyte only). The table is not an exhaustive summary of the literature, and is restricted to studies using aqueous [Fe(CN)6]3−/4−; it primarily summarises fundamental studies employing planar platinum electrodes (by Quickenden et al.24,25,27 or Lee et al.37) who performed limited temperature, orientation and concentration studies, as well as three high surface area carbon electrode studies as exemplars,23,34,40 and stainless steel as a comparison.22 A number of other studies that use nanostructured electrodes have been excluded, because that is an additional factor not studied here; others have reported seemingly promising systems, e.g. [Fe(CN)6]3−/4−/KCl gelatine hydrogels with a Se up to 17 mV K−1,12 but didn't report sufficient thermogalvanic characterisation parameters such that their performance can be compared with others.| Aqueous electrolyte composition | ΔT/K | Electrode | Electrode sep./mm (orientation) | Estimated Carnot efficiency/% | Measured Carnot efficiency/% | Ref. |
|---|---|---|---|---|---|---|
| a For orientation c-o-h and h-o-c represents cold-over-hot and hot-over-cold electrode arrangements, respectively. The symbol ∼ indicates the authors had to extract estimated values directly from graphs. b Unclear if stated concentration is [FeCN6]3− + [FeCN6]4− = concentration, or [FeCN6]3− = [FeCN6]4− = concentration. c A forest of CNT was drawn onto a 0.3 mm tungsten wire, and wrapped around to form a ca. 3 to 3.5 mm diameter scroll. Results are reported for (i) CNT scroll as prepared, (ii) scroll thermally oxidised, (iii) scroll platinised, and (iv) scroll platinised and compressed. d The heat flux was estimated using the same equation as the other studies, except an effective thermal conductivity was calculated via IR imaging and used, rather than a conduction-only thermal conductivity. | ||||||
| 0.1 M K3[Fe(CN)6] + 0.1 M K4[Fe(CN)6] | 20 | Stainless steel | ca. 2 | 0.0002 | 22 | |
| 0.1 M K3/K4[Fe(CN)6]b | 20 | SWCNT sheet electrode | 10 | 0.0010 | — | 40 |
| 40 (parallel) | 0.0028 | |||||
| 0.4 M K3/K4[Fe(CN)6]b | 51 | CNT scrollc | 25 (parallel) | — | 34 | |
| (i) | ∼1.2 | |||||
| (ii) | ∼2.2 | |||||
| (iii) | ∼3.6 | |||||
| (iv) | 3.95 | |||||
| 0.4 M K3[Fe(CN)6] + 0.4 M K4[Fe(CN)6] | 10 | Porous carbon fabric paper on graphite | 15 (c-o-h) | ∼0.68d | 23 | |
| 50 | ∼0.48d | |||||
| 0.26 M K3[Fe(CN)6] + 0.26 M K4[Fe(CN)6] + 0.8 M KCl | 20 | Pre-treated Pt foil | 30 (h-o-c) | 0.44 (t = 16 s) | — | 25 |
| 0.11 (t = 600 s) | ||||||
| 0.26 M K3[Fe(CN)6] + 0.26 M K4[Fe(CN)6] + 0.8 M KCl | 20 | Pre-treated Pt foil | 100 (parallel) | 0.50 | — | 24 |
| (c-o-h) | 0.50 | |||||
| (h-o-c) | 0.17 | |||||
| 0.26 M K3[Fe(CN)6] + 0.26 M K4[Fe(CN)6] + 0.8 M KCl | 30 | Pre-treated Pt foil | 3 | 0.08 | — | 27 |
| 1500 (c-o-h) | 0.60 | |||||
| 0.4 M K3/K4[Fe(CN)6]b | 15 | Pt foil | 8 (parallel) | 0.288 | — | 37 |
| 0.9 M K3/(NH4)4[Fe(CN)6]b | 25 | 0.276 | ||||
| 35 | 0.271 | |||||
| 15 | 0.392 | |||||
| 25 | 0.417 | |||||
| 35 | 0.399 | |||||
| All 0.2 M K3[Fe(CN)6] + 0.2 M K4[Fe(CN)6] | 20 | 0.3 mm thick amorphous graphite | 9.5 | 0.133 | 0.047 | This work |
| +0 wt% eq. | 40 | 9.5 | 0.172 | 0.048 | ||
| +1.5 wt% eq. | 20 | 4.4 | 0.080 | 0.060 | ||
| +3.0 wt% eq. | 20 | 39.9 | 0.213 | 0.017 | ||
| +3.0 wt% eq. sodium polyacrylate | 20 | 13.6 | 0.179 | 0.077 | ||
| 20 | 13.6 | 0.146 | 0.269 | |||
| 20 | 13.6 | 0.066 | 0.197 | |||
| 20 | 29.2 (parallel) | 0.116 | 0.065 | |||
Also listed in Table 3 are some estimated and genuinely measured efficiencies from this work. Recalling that all measurements were made at amorphous graphite that generates ca. one-third of the power of platinum electrodes, the efficiency values can in theory be converted to approximate planar platinum values by multiplying by 3 (which assumes thermal conduction routes would be unaffected by this substitution, but current roughly tripled). Doing this, the range of estimated Carnot efficiency values recorded in this study at graphite (0.066–0.213%) converted to platinum-equivalent values (ca. 0.2–0.6%) then sit well within the range of values reported by Lee et al.37 and Quickenden et al.24,25,27 for similar electrolytes at planar platinum electrodes (0.08–0.6%).
What stands out from the tabulated results is the general assertion of previous reports that (estimated) efficiency will increase with increasing electrode separation,27,40 which this study mirrors. However, the directly measured efficiency displays the completely opposite trend, which is significant for future device design.
In this study, the absolute efficiency (both estimated and measured) increased with increasing ΔT, as did the estimated Carnot efficiency, while the measured Carnot efficiency showed a minor decease with increasing ΔT. Interestingly, Lee et al. reported estimated Carnot efficiency values were also largely independent of ΔT,37 while Zhou et al. used indirect IR imaging to more accurately estimate the Carnot efficiency and reported a slight decrease with increasing ΔT.23 The reason for these slight differences is not currently known, but it's likely the Carnot efficiency can be taken as approximately independent of the applied ΔT (for conventional [Fe(CN)6]3−/4−-based cells). Regardless, the overall absolute efficiency does genuinely increase quite significantly with increasing ΔT, albeit it to a lesser degree than that predicted by the estimated heat flux methodology.
Aspects that are missing from this study are the affect upon the directly measured efficiency of (i) the electrolyte concentration, (ii) high(er) surface area electrode materials, (iii) orientation with respect to gravity, and (iv) when cells are incorporated in multi-cell devices. With regards to concentration, earlier results have already indicated that increasing the concentration of the redox active species increases the current and thus will also increase the efficiency. For example Quickenden and Vernon stated that increasing the concentration by an order of magnitude from 0.007 M each of [Fe(CN)6]3− and [Fe(CN)6]4− to 0.07 M of each (both containing 3 M KCl) increased the estimated Carnot efficiency by roughly an order of magnitude.25 Additionally, Lee et al. demonstrated that moving from 0.4 M [Fe(CN)6]3−/4− (as K+ salts) to 0.9 M [Fe(CN)6]3−/4− (as K3[Fe(CN)6] and (NH4)4[Fe(CN)6]) resulted in a ca. 50% increase in the estimated Carnot efficiency.37 However, increasing concentration can also have diminishing returns and in fact reduce the current in both super-concentrated41 and ion-pairing prone systems.37 While we believe the measured efficiency will change in proportion to concentration (at reasonably low electrolyte concentrations), this area nevertheless requires further study for genuine confirmation, especially given the potential impact of concentration upon heat flux through the entire cell due to density and viscosity changes.
The majority of papers quoting estimated Carnot efficiency values are those reporting nano-structured electrode studies. Nano-structuring is frequently employed to boost the estimated efficiency, since it is capable of enhancing electrocatalysis and/or dramatically increasing the electroactive surface area; the latter is particularly significant since nanostructing results in 3D areas where electron transfer can occur, but heat flux is predicted to remain a 1D process (via the estimated heat flux equation). The three nano-carbon entries in the table demonstrates how SWCNT resulted in poorly electrocatalytic electrodes (likely equivalent to the poor results observed in this study at the pyrolytic graphite electrodes), but the estimated efficiency could be boosted ca. 4000-fold upon moving to an exquisitely crafted platinum/carbon nanocomposite.34 Significantly, the high estimated Carnot efficiency value of 3.95% in the latter likely has a significantly lower genuine efficiency, given that the utilised cell was a long, thin glass tube that would lose significant heat via convection then radiation (cf.Fig. 4). The methodology described here can now be employed to accurately quantify the efficiency, and will not only aid cell design but also be able to answer the question of whether nanostructured electrodes affect heat flux through the device; this affect could be acting as thermal baffles to reduce total heat flux, or they could act as heat-exchange catalysts and boost total heat flux. Both observations are likely possibilities, given the diverse range of different electrode materials currently being reported.
With regards to the cell orientation, all measurements were performed in this study in a thermally side-by-side or parallel arrangement (as visualised in Fig. 4). Employing one electrode physically higher than the other (hot-over-cold and cold-over-hot arrangements) can have a very significant impact due to gravity effects upon convection, and this has been reported previously for thermogalvanic cells,20,21,24,42,49–51 with the former arrangement resulting in stagnation and a suppression of thermogalvanic current, while the latter can result in significant gravity-driven convective transfer of thermal energy.21,24 The effect of this upon the estimated efficiency can be seen in Table 3. Unfortunately, when orientation experiments were attempted in our thermocell setup, persistent leakage and bubble-formation issues at the graphite prohibited accurate measurement, with even small bubbles strongly impacting both current and heat flux through the cell. As such, a more robust cell design is required before orientation studies can be performed to measure the genuine efficiency.
Finally, convection-induced radiation heat loss was significant in this study, and this could be ‘fixed’ by employing a heavily insulated cell. However, multiple thermogalvanic cells are typically combined into a single device, with cells of similar chemistry being electrically connected to boost current, while dissimilar cell chemistry is used to boost voltage.43 This could be via two different cells electrically connected,43 or be a single monolithic block into which several cells have been machined.18,41 A high power density device cannot be achieved with thick, insulated walls installed between dozens of individual cells, and instead the wall thickness is (ideally) relatively thin. For thin walls, the significant convective heat loss visualised through the upper surface of the cell in this work takes on a different aspect; it could be absent in the centre of the device, or could result in a thermally parasitic transfer process that significantly unbalances the temperature difference and heat flux across the device. Those cells around the edge of the device will demonstrate this heat-loss mechanism (subject to orientation with respect to gravity); it could act as a thermal short-circuit holding back the efficiency of the entire device, or compromise the ΔT in these cells thus negatively impacting the overall power produced by the device, or could even have no effect at all (beyond external cells having a lower genuine efficiency relative to cells deep inside the device). The methodology presented in this study now enables such complex questions to be interrogated, though the use of multiple heat flux sensors.
All discussions above have focussed upon electrolyte-only values. Significantly, this study has also enabled the quantification of the ‘total device efficiency’ (via the methodology described in the Experimental section), but the parasitic cell contributions to heat flux were routinely subtracted throughout this work. This is largely because device contributions are so variable across groups, and were never deliberately adjusted or optimised in this study. For examples like the 9.5 mm cell (cf.Fig. 6), the device-only heat flux was a minor part of the total heat flux; some of which was conduction through the plastic cell, and the rest primarily lost to conduction into the wiring and radiation into the surroundings. Heat loss into the wiring has been recognised before,43 and is relatively easily addressed; for example connecting 100 electrolyte pairs thermally in-parallel but electrically in-series43 will likely reduce this parasitic effect of the external wiring by 100-fold per cell. Thinner wires will also reduce this. Substituting the acrylic cell used here for thinner, more insulating material and insulating the entire device will also reduce this parasitic heat transfer. While the parasitic device heat flux was a minor factor for electrolyte-containing cells, it is more significant for cells containing gelled electrolyte, as discussed above and shown in Fig. 7.
Significantly, while genuine efficiency was consistently lower than estimated efficiency through this work, gelled and partially-gelled electrolytes with small electrode separation values deviated from this trend and offer clear promise for more efficient thermogalvanic devices, particularly when coupled with good cell, device and electrode design. These synergies can now be unambiguously quantified, especially via the quantification of total heat flux (as opposed to electrolyte-only heat flux) and this is expected to facilitate total-device optimisation studies.
Conclusions
This study has demonstrated methodology by which the efficiency of thermogalvanic conversion (of a heat flux through a temperature gradient into electricity) can be unambiguously quantified. This was demonstrated for just the electrolyte, and for the entire assembly; the latter allows ‘total device efficiency’ to be quantified. By comparing the measured efficiency vs. the standard route of estimating efficiency, this study shows that they are only comparable for cells with negligible temperature gradients and very small inter-electrode separations. As the temperature gradient increases, the estimated efficiency will overestimate the actual performance by a significant degree; this difference is even more significant with increasing electrode separation, with a complete divergence between estimated and measured efficiency values. Conversely, the measured genuine efficiency of fully-gelled electrolytes can actually exceed the estimated efficiency, but only with small inter-electrode separations, and only if parasitic heat flux through the device apparatus is also discounted. Partially-gelled electrolytes were also identified as the optimum system for efficient thermogalvanic heat-to-electricity conversion, both as an electrolyte and as part of a whole device.The distinction between absolute efficiency and Carnot efficiency is also important; as the applied temperature difference increases the Carnot efficiency of the thermogalvanic cell decreases slightly, but this is slightly misleading as the absolute overall efficiency actually increases significantly. These observations, combined with this new methodology, will support the rational design of complete thermogalvanic devices, and thus support increasingly efficient waste heat valorisation.
Data availability
The datasets supporting this article have been uploaded as part of the ESI.†Author contributions
Conceptualisation, LA; funding acquisition, LA; investigation, M. A. T., M. A. B. and L. A.; methodology, M. A. T., M. A. B. and L. A.; project administration, LA; supervision, M. A. B. and L. A.; visualisation, L. A.; writing, M. A. T., M. A. B. and L. A.Conflicts of interest
There are no conflicts to declare.Acknowledgements
M. A. B. acknowledges the EPSRC for funding (Standard Research Studentship (DTP), EP/N509498/1). M. A. T. acknowledges King's College London for a King's Undergraduate Research Fellowship (KURF).References
- P. Gründler, A. Kirbs and L. Dunsch, ChemPhysChem, 2009, 10, 1722–1746 CrossRef PubMed.
- A. J. deBethune, T. S. Licht and N. Swendeman, J. Electrochem. Soc., 1959, 106, 626–627 CrossRef.
- G. R. Salvi and A. J. DeBethune, J. Electrochem. Soc., 1961, 108, 672 CrossRef CAS.
- M. A. Buckingham, S. Hammoud, H. Li, C. J. Beale, J. T. Sengel and L. Aldous, Sustainable Energy Fuels, 2020, 4, 3388–3399 RSC.
- B. Burrows, J. Electrochem. Soc., 1976, 123, 154–159 CrossRef CAS.
- M. Papapetrou, G. Kosmadakis, A. Cipollina, U. La Commare and G. Micale, Appl. Therm. Eng., 2018, 138, 207–216 CrossRef.
- R. Hu, B. A. Cola, N. Haram, J. N. Barisci, S. Lee, S. Stoughton, G. Wallace, C. Too, M. Thomas, A. Gestos, M. E. Dela Cruz, J. P. Ferraris, A. A. Zakhidov and R. H. Baughman, Nano Lett., 2010, 10, 838–846 CrossRef CAS PubMed.
- H. Im, H. G. Moon, J. S. Lee, I. Y. Chung, T. J. Kang and Y. H. Kim, Nano Res., 2014, 7, 443–452 CrossRef CAS.
- P. Yang, K. Liu, Q. Chen, X. Mo, Y. Zhou, S. Li, G. Feng and J. Zhou, Angew. Chem., Int. Ed., 2016, 55, 12050–12053 CrossRef CAS PubMed.
- Y. Liu, S. Zhang, Y. Zhou, M. A. Buckingham, L. Aldous, P. C. Sherrell, G. G. Wallace, G. Ryder, S. Faisal, D. L. Officer, S. Beirne and J. Chen, Adv. Energy Mater., 2020, 10, 2002539 CrossRef CAS.
- T. I. Quickenden and Y. Mua, J. Electrochem. Soc., 1995, 142, 3985–3994 CrossRef CAS.
- C. Han, X. Qian, Q. Li, B. Deng, Y. Zhu, Z. Han, W. Zhang, W. Wang, S. Feng, G. Chen and W. Liu, Science, 2020, 368, 1091–1098 CrossRef CAS.
- M. A. Buckingham, F. Stoffel, S. Zhang, Y. Liu, F. Marken, J. Chen and L. Aldous, ACS Appl. Nano Mater., 2022, 5, 438–445 CrossRef CAS.
- M. A. Buckingham, S. Zhang, Y. Liu, J. Chen, F. Marken and L. Aldous, ACS Appl. Energy Mater., 2021, 4, 11204 CrossRef CAS.
- M. A. Buckingham and L. Aldous, J. Electroanal. Chem., 2020, 872, 114280 CrossRef CAS.
- T. J. Abraham, D. R. Macfarlane, R. H. Baughman, L. Jin, N. Li and J. M. Pringle, Electrochim. Acta, 2013, 113, 87–93 CrossRef CAS.
- M. A. Buckingham, K. Laws, E. Cross, A. J. Surman and L. Aldous, Green Chem., 2021, 23, 8901–8915 RSC.
- M. A. Buckingham, K. Laws, J. T. Sengel and L. Aldous, Green Chem., 2020, 22, 6062–6074 RSC.
- M. Philippe, B. Didillon and L. Gilbert, Green Chem., 2012, 14, 952–956 RSC.
- S. W. Hasan, S. M. Said, M. F. M. Sabri, A. S. A. Bakar, N. A. Hashim, M. M. I. M. Hasnan, J. M. Pringle and D. R. Macfarlane, Sci. Rep., 2016, 6, 29328–29339 CrossRef CAS.
- A. Gunawan, H. Li, C. H. Lin, D. A. Buttry, V. Mujica, R. A. Taylor, R. S. Prasher and P. E. Phelan, Int. J. Heat Mass Transfer, 2014, 78, 423–434 CrossRef CAS.
- J. Wu, J. J. Black and L. Aldous, Electrochim. Acta, 2017, 225, 482–492 CrossRef CAS.
- B. Yu, J. Duan, H. Cong, W. Xie, R. Liu, X. Zhuang, H. Wang, B. Qi, M. Xu, Z. L. Wang and J. Zhou, Science, 2020, 370, 342–346 CrossRef CAS.
- T. I. Quickenden and Y. Mua, J. Electrochem. Soc., 1995, 142, 3652–3659 CrossRef CAS.
- T. I. Quickenden and C. F. Vernon, Sol. Energy, 1986, 36, 63–72 CrossRef CAS.
- W. Qian, M. Li, L. Chen, J. Zhang and C. Dong, RSC Adv., 2015, 5, 97982–97987 RSC.
- Y. Mua and T. I. Quickenden, J. Electrochem. Soc., 1996, 143, 2558–2564 CrossRef CAS.
- G. Li, D. Dong, G. Hong, L. Yan, X. Zhang and W. Song, Adv. Mater., 2019, 31, 1901403 CrossRef PubMed.
- W. Huang, J. Xu, K. He, Z. Li, W. Qian and C. Dong, in IOP Conference Series: Earth and Environmental Science, 2018, vol. 121 Search PubMed.
- W. Qian, M. Cao, F. Xie and C. Dong, Nano-Micro Lett., 2016, 8, 240–246 CrossRef CAS PubMed.
- F. Zhao, W. Qian, M. Li, W. Li, L. Chen, F. Zhong, W. Huang and C. Dong, RSC Adv., 2017, 7, 23890–23895 RSC.
- Y. Zhou, W. Qian, W. Huang, B. Liu, H. Lin and C. Dong, Nanomaterials, 2019, 9, 1450 CrossRef CAS PubMed.
- D. Dong, H. Guo, G. Li, L. Yan, X. Zhang and W. Song, Nano Energy, 2017, 39, 470–477 CrossRef CAS.
- H. Im, T. Kim, H. Song, J. Choi, J. S. Park, R. Ovalle-Robles, H. D. Yang, K. D. Kihm, R. H. Baughman, H. H. Lee, T. J. Kang and Y. H. Kim, Nat. Commun., 2016, 7, 10600 CrossRef CAS PubMed.
- M. S. Romano, N. Li, D. Antiohos, J. M. Razal, A. Nattestad, S. Beirne, S. Fang, Y. Chen, R. Jalili, G. G. Wallace, R. Baughman and J. Chen, Adv. Mater., 2013, 25, 6602–6606 CrossRef CAS PubMed.
- S. Gupta and R. Meek, Appl. Phys. A, 2020, 126, 704 CrossRef CAS.
- K. Kim, S. Hwang and H. Lee, Electrochim. Acta, 2020, 335, 135651 CrossRef CAS.
- E. S. Schwyter, T. Helbling, W. Glatz and C. Hierold, Rev. Sci. Instrum., 2012, 83, 74904 CrossRef CAS PubMed.
- C. E. Banks, M. R. Moore, T. J. Davies and R. G. Compton, Chem. Commun., 2004, 10, 1804–1805 RSC.
- T. J. Kang, S. Fang, M. E. Kozlov, C. S. Haines, N. Li, Y. H. Kim, Y. Chen and R. H. Baughman, Adv. Funct. Mater., 2012, 22, 477–489 CrossRef CAS.
- M. A. Buckingham, K. Laws, H. Li, Y. Kuang and L. Aldous, Cell Rep. Phys. Sci., 2021, 2, 100510 CrossRef CAS.
- G. Qian, Y. Lu, Y. Huang, Z. Li, X. Yu and A. P. Roskilly, Energy Procedia, 2017, 142, 374–380 CrossRef CAS.
- M. Al Maimani, J. J. Black and L. Aldous, Electrochem. Commun., 2016, 72, 181–185 CrossRef CAS.
- H. A. H. Alzahrani, M. A. Buckingham, F. Marken and L. Aldous, Electrochem. Commun., 2019, 102, 41–45 CrossRef CAS.
- Y. Zhou, Y. Liu, M. A. Buckingham, S. Zhang, L. Aldous, S. Beirne, G. Wallace and J. Chen, Electrochem. Commun., 2021, 124, 106938 CrossRef CAS.
- L. Jin, G. W. Greene, D. R. MacFarlane and J. M. Pringle, ACS Energy Lett., 2016, 1, 654–658 CrossRef CAS.
- Z. Lei, W. Gao and P. Wu, Joule, 2021, 5, 2211–2222 CrossRef.
- S. Pu, Y. Liao, K. Chen, J. Fu, S. Zhang, L. Ge, G. Conta, S. Bouzarif, T. Cheng, X. Hu, K. Liu and J. Chen, Nano Lett., 2020, 20, 3791–3797 CrossRef CAS PubMed.
- P. F. Salazar, S. Kumar and B. A. Cola, J. Appl. Electrochem., 2014, 44, 325–336 CrossRef CAS.
- T. Ikeshoji, Bull. Chem. Soc. Jpn., 1987, 60, 1505–1514 CrossRef CAS.
- A. C. U. Cu, A. Thermogalvanic, C. Lin, A. Gunawan, P. E. Phelan, D. A. Buttry and R. A. Taylor, Proc. ASME 2012 Int. Mech. Eng. Congr. Expo., IMECE2012, 2012, pp. 1–7 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d1sc06340e |
| ‡ Present address: Department of Materials, The University of Manchester, Oxford Road, Manchester, M13 9PL, UK |
| This journal is © The Royal Society of Chemistry 2022 |