Open Access Article
Open Access ArticlePersistent nucleation and size dependent attachment kinetics produce monodisperse PbS nanocrystals†
Benjamin
Abécassis‡
 *c,
Matthew W.
Greenberg‡
a,
Vivekananda
Bal
b,
Brandon M.
McMurtry
*c,
Matthew W.
Greenberg‡
a,
Vivekananda
Bal
b,
Brandon M.
McMurtry
 a,
Michael P.
Campos
a,
Lilian
Guillemeney
c,
Benoit
Mahler
a,
Michael P.
Campos
a,
Lilian
Guillemeney
c,
Benoit
Mahler
 e,
Sylvain
Prevost
e,
Sylvain
Prevost
 f,
Lewis
Sharpnack
g,
Mark P.
Hendricks
f,
Lewis
Sharpnack
g,
Mark P.
Hendricks
 ad,
Daniel
DeRosha
a,
Ellie
Bennett
ad,
Daniel
DeRosha
a,
Ellie
Bennett
 a,
Natalie
Saenz
a,
Baron
Peters
*b and
Jonathan S.
Owen
a,
Natalie
Saenz
a,
Baron
Peters
*b and
Jonathan S.
Owen
 *a
*a
aDepartment of Chemistry, Columbia University, New York, New York 10027, USA. E-mail: jso2115@columbia.edu
bDepartment of Chemical Engineering, University of Illinois, Urbana-Champaign, Illinois 10027, USA
cLaboratoire de Chimie, ENS de Lyon, CNRS, Université Claude Bernard Lyon 1, F69342, Lyon, France
dDepartment of Chemistry, Whitman College, Walla Walla, WA 99362, USA
eUniv Lyon, Université Claude Bernard Lyon 1, CNRS, Institut Lumière Matière, F-69622, Villeurbanne, France
fInstitut Laue-Langevin, 71 Avenue des Martyrs, 38042 Grenoble, France
gDepartment of Earth Science, University of California, Santa Barbara, CA 93106, USA
First published on 30th March 2022
Abstract
Modern syntheses of colloidal nanocrystals yield extraordinarily narrow size distributions that are believed to result from a rapid “burst of nucleation” (La Mer, JACS, 1950, 72(11), 4847–4854) followed by diffusion limited growth and size distribution focusing (Reiss, J. Chem. Phys., 1951, 19, 482). Using a combination of in situ X-ray scattering, optical absorption, and 13C nuclear magnetic resonance (NMR) spectroscopy, we monitor the kinetics of PbS solute generation, nucleation, and crystal growth from three thiourea precursors whose conversion reactivity spans a 2-fold range. In all three cases, nucleation is found to be slow and continues during >50% of the precipitation. A population balance model based on a size dependent growth law (1/r) fits the data with a single growth rate constant (kG) across all three precursors. However, the magnitude of the kG and the lack of solvent viscosity dependence indicates that the rate limiting step is not diffusion from solution to the nanoparticle surface. Several surface reaction limited mechanisms and a ligand penetration model that fits data our experiments using a single fit parameter are proposed to explain the results.
Introduction
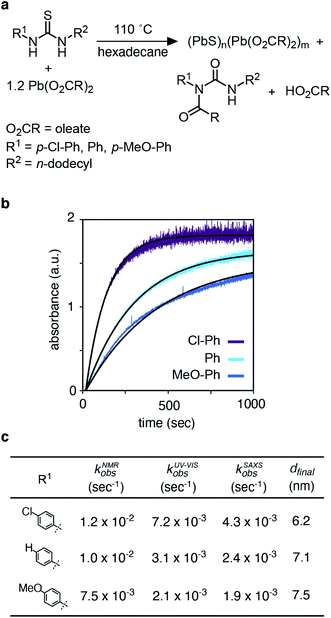
Nanometer scale colloidal crystals of metal, metal oxide, metal chalcogenide, and metal pnictide materials can be synthesized with extraordinary size and shape uniformity. It is widely assumed that monodisperse particle size distributions result from a short burst of nucleation followed by diffusion controlled growth.1–3 However, even in the case of colloidal quantum dots (QDs) where the nanocrystal size, size distribution, and nanocrystal concentration are readily monitored with optical spectroscopy, direct measurements of the nucleation kinetics are challenging. Few experimental studies simultaneously achieve the necessary time resolution and precision to monitor the nanocrystal concentration and size during the nucleation phase.4–9 It is therefore uncertain whether the duration of the nucleation period explains the monodispersity.In typical QD syntheses molecular precursors are injected into hot surfactant solution at a temperature that converts them to solutes.10 These solutes supersaturate leading to crystal nucleation and growth. When the conversion reaction is very rapid, nucleation can occur in a transient region of solution with non-uniform temperature and concentration that is impractical for mechanistic study. Slow and controlled precursor conversion reactivity, on the other hand, allows nucleation and growth to occur after mixing has eliminated concentration or temperature gradients. In these syntheses, the precursor conversion reaction is rate limiting and governs the kinetics of solute supersaturation and nucleation.10,11
Among QD materials, lead sulfide produced from chalcogenourea precursors and lead oleate form with extraordinarily narrow size distributions.12 By modifying the chalcogenourea substitution pattern, the kinetics of solute generation can be precisely controlled over a wide range of temperatures.12–14 These reagents have recently been used to study the temperature dependence of the crystal nucleation and growth steps, where in situ X-ray pair distribution function analysis demonstrated the formation of molecular solute intermediates.14 Moreover, the precisely controlled solute supply is orthogonal to the crystal growth reaction and therefore ideally suited to explore the connection between the solute concentration and the kinetics of lead sulfide nucleation and growth.
High supersaturation and diffusion limited growth kinetics are widely believed to cause size distribution focusing.15,16 While numerous studies argue for focusing on the basis of diffusion limited growth kinetics, we are unaware of any direct evidence for diffusion limited growth in colloidal QD formation, nor any measurements of the solute concentration during growth. Moreover, claims that size distribution focusing occurs during the formation of colloidal QDs typically rely on the temporal evolution of the absorption spectral linewidth.2 That analysis, however, does not properly account for the intrinsic width of a single QD absorber nor its size dependence.13,17,18 In addition, arguments based on changes to the percent standard deviation rather than changes to the absolute polydispersity are obscured by the evolving nanocrystal size. Thus, the mechanistic origins of size distribution focusing are unclear.
To probe the origins of monodispersity, we performed a direct measurement of QD nucleation and growth kinetics using in situ X-ray scattering. Coupled with measurements of the solute supply kinetics using NMR spectroscopy and 13C-labeled thiourea precursors, we deduce the solute concentration throughout the reaction. These experiments reveal a slow steady increase in the number of nanocrystals that continues throughout a large fraction of the synthesis. Population balance modeling and a weak dependence on the solvent viscosity demonstrate that the canonical diffusion limited growth mechanism cannot explain the size focusing.
Results and discussion
The kinetics of PbS nanocrystal formation were monitored in situ using optical absorption and time resolved small angle and wide angle X-ray scattering (SAXS and WAXS) on the ID02 beamline of the European Synchrotron Radiation Facility (ESRF).19 Several disubstituted thiourea (Fig. 1) derivatives were selected whose conversion to PbS QDs (d = 3.1–7.5 nm) reaches completion in 1–30 minutes at 110 °C. Following injection of the thiourea (t = 0 s), the reaction solution is pumped through a thin X-ray capillary and SAXS and WAXS patterns are recorded every second (Fig. S1†). In parallel, an optical probe records the absorbance of the solution at λ = 400 nm. Fig. 1B shows the evolution of the absorbance at 400 nm, where an induction delay is observed (21–56 seconds), following which the absorbance increases with kinetics that are well described by a single exponential (kUV-Visobs = 2.1–7.2 × 10−3 s−1).Fig. 2 shows the evolution of the SAXS and WAXS signal during a synthesis. The increasing SAXS intensity at small wave-vectors (q) and the appearance of oscillations at high q are characteristic of an ensemble of monodisperse nanoparticles that grow in size.20–22 The SAXS patterns were fitted using a quantitative model consisting of the sum of two terms, each one having the form of a polydisperse distribution of spheres (see ESI† for details). The first term captures the concentration, mean radius and polydispersity of PbS nanoparticles. The second term captures the concentration of lead oleate and is based on the signal of a lead oleate solution measured separately that is well fit to a spherical scatterer with radius of 0.13 nm. The lead oleate precursor was further probed using small angle neutron scattering (SANS) in tetradecane-d30 solution. The strong scattering contrast between the hydrogenated surfactant alkyl chains and the solvent produces a SANS signal that can be fit to a spherical scatterer with radius of 1.74 nm and polydispersity of 20%. Both measurements are consistent with a small molecular complex composed of one or two lead oleate units (Fig. S7†).
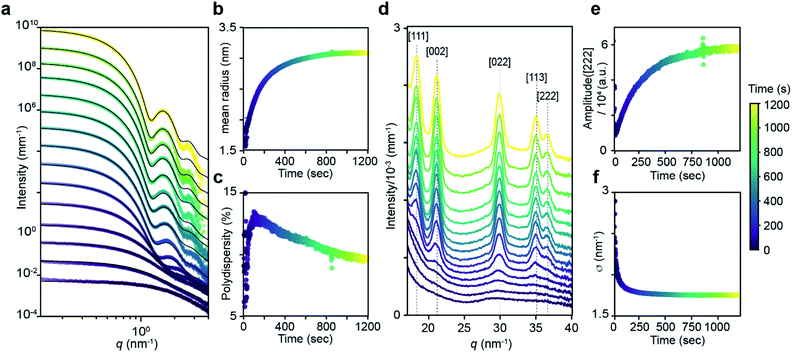 | ||
| Fig. 2 (a) Evolution of the SAXS pattern during the course of the reaction: N-4-chloro-phenyl-N′-dodecylthiourea at 110 °C, 10.8 mM in lead oleate, 9 mM in thiourea. Black lines correspond to fits to the data with a model of polydisperse spheres as described in the main text and ESI.†t = 1, 20, 30, 50, 100, 200, 300, 400, 500, 600, 700, 800, 900, 1000, 1198. (b) Mean radius and (c) polydispersity evolution during the course of the reaction determined by the fit of the SAXS patterns. (d) WAXS pattern showing the evolution of the [111], [002], [022], [113] and [222] reflections of the PbS rock-salt structure at q = 18.33, 21.17, 29.94, 35.11 and 36.67 nm−1 respectively. t = 1, 20, 30, 50, 100, 200, 300, 400, 500, 600, 700, 800, 900, 1000, 1198. (e) Amplitude and (f) sigma parameter determined by the [022] peak shape fitting by a Gaussian. The amplitude is proportional to the crystal volume fraction and the crystallite size is inversely proportional to the FWHM through the Scherrer formula (see ESI† for details). | ||
As the reaction proceeds the scattering from lead oleate decreases while the scattering from the nanocrystals increases (Fig. S20†). Fits of the nanocrystal component provide the mean radius of the size distribution, its polydispersity and the nanocrystal concentration at each time point. The signal to noise ratio of the data at very early times prevents precise measurement of the polydispersity and concentration (see ESI† discussion on this point) but following this period, oscillations in the SAXS pattern appear at high q and allow a reliable fit. The absolute value of PbS units within nanocrystals can be retrieved from the size distribution and the overall concentration in nanocrystals. A single exponential fit of PbS concentration provides rate constants for PbS precipitation of kSAXSobs = 2.4–4.3 × 10−3 s−1 depending on the precursor used (Fig. S21 and S22†).
WAXS patterns display five peaks characteristic of the PbS rock salt crystal structure. By fitting the [022] peak to a Gaussian model with a linear background we independently determine the concentration of scattering material and the size of crystallites. The decreasing full width at half maximum (FWHM) is indicative of an increasing mean nanoparticle size that can be extracted using the Debye–Scherrer relation. This estimate of the crystallite size is systematically slightly smaller than the one estimated from SAXS measurements. A single exponential fit of the WAXS [002] peak area versus time provides a rate constant for the precipitation of PbS which is equal to the one found by SAXS (Fig. S22†). After 50 s, good agreement between SAXS and WAXS signals indicate that the PbS is crystalline rather than amorphous throughout the reaction.
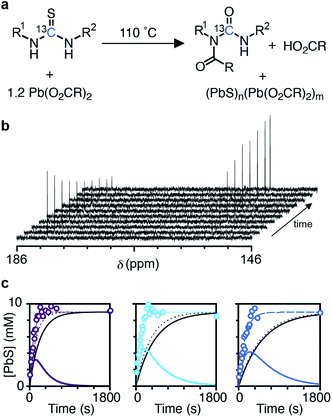
The kinetics of nanocrystal formation were compared to the kinetics of the precursor conversion reaction using 1H and 13C nuclear magnetic resonance (NMR) spectroscopy. The disappearance of N-(p-X-phenyl)-N′-dodecylthiourea-13C (X = Cl, H, OMe) and the formation of the N-oleoyl-N(p-X-phenyl)-N′-dodecylurea-13C coproduct could be monitored by tracking the integral of the thiocarbonyl and urea carbonyl carbons as shown in Fig. 3. Both measures provide similar rate constants for the conversion of each thiourea respectively (kNMRobs = 8.8–13.3 × 10−3 s−1) (see ESI† and Fig. 3). The kinetics measured by NMR are faster than those measured using UV-Vis absorption spectroscopy, which are both faster than those measured using SAXS and WAXS. The differences between each measurement technique can be explained by the formation of PbS solutes that do not contribute significant intensity to the SAXS or WAXS signal, but do influence the absorbance at λ = 400 nm. Spectroscopic and X-ray scattering characterization of these solutes suggests a molecular complex with formula [(PbS)(Pb(oleate)2)]2.14 Collectively, the NMR, UV-vis, and X-ray scattering kinetics data support a stepwise process where the lead oleate and thiourea are converted to solutes that accumulate and are then consumed by nanocrystal growth.
The concentration of solute (Csolute) can be determined from the amount of precursor converted and the amount of PbS in nanocrystals (Csolute = Cconv − Csolid) where Cconv = [thiourea]0(1 − exp[−kNMRobst]) and Csolid = [thiourea]0(exp[−kSAXSobst]). As can be seen in Fig. 3c, the Csolute for each thiourea peaks following ∼50% conversion of the precursors with a maximum solute concentration of ∼4 mM or ∼45% of the total sulfur. Both nucleation and growth to a larger average size occurs in parallel with the rise in Csolute.
The concentration of nanocrystals measured with SAXS steadily increases to 0.9–4.4 μM over ∼200 seconds and then plateaus as the nanocrystals grow to their final size (Fig. 4 and S23†). The production of such a large concentration of crystallites is in itself evidence of a homogeneous nucleation process. No further evolution of the nanocrystal concentration or size is observed after the plateau. We conclude that the nanocrystals do not agglomerate or ripen following precursor conversion as was previously reported.12,13 The increasing number of nanocrystals can be used as a measure of the nucleation kinetics without considering the nucleus size or structure. The instantaneous nucleation rate is extracted from a polynomial fit to the nanocrystal concentration as described in the ESI† and shown in Fig. 4b. These curves illustrate how the nucleation phase continues across ∼2 minutes, long after the induction delay observed using optical spectroscopy and spanning more than ∼10% of total reaction time (>50% of the precipitation). Reactions performed at lower temperatures display even longer nucleation times.14
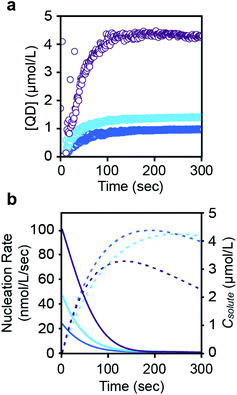 | ||
| Fig. 4 (a) Evolution of the concentration in PbS nanocrystals during their formation for each of three thiourea precursors (N-4-chloro-phenyl-N′-dodecylthiourea (purple), N-phenyl-N′-dodecylthiourea (light blue), and N-4-methoxy-N′-phenyl-dodecylthiourea (dark blue)) (see also ESI†). A polynomial fit of the evolving nanocrystal concentration is used as an input for the population balance modeling. An induction delay at early times prior to the appearance of nanocrystals is more clearly displayed in the ESI.† (b) The rate of nucleation (colored, solid line), taken from the derivative of the polynomial fit shown in a, is compared to the solute concentration (colored, dashed line). Note that the nanocrystal concentration during the induction delay is zero. Data points during this period were not used when fitting the nucleation rate shown in (b). | ||
Interestingly, the nucleation rate decays as the solute concentration climbs to its maximum value. The inverse correlation between nucleation rate and solute concentration is counterintuitive, however, a variety of factors may directly or indirectly influence the nucleation rate. For example, conversion of the thiourea precursor consumes lead oleate, which may impact the nucleation or growth rates. High lead oleate and lead chloride precursor concentrations are known to increase the extent of PbS nucleation and narrow the size distribution.23,24 Nanocrystal coalescence could also cause an apparent reduction in the nucleation rate, but we do not observe ripening or reduction of the nanoparticle concentration over long periods of time at the reaction temperature.
While it is not yet clear why a decrease in the nucleation rate accompanies the increase in solute concentration, this behavior may be related to the prolonged nucleation period observed. On the other hand, the burst of nucleation postulated by LaMer occurs when the nucleation rate is a stronger function of solute concentration than the growth rate,25 a condition that is not met in our experiments. Thus, the prolonged nucleation period and the inverse relation between nucleation and solute concentration are perplexing but possibly related observations that warrant further study.
The size distributions obtained here cannot be explained by a short nucleation phase that is separate from growth. Instead, a size focusing mechanism is needed to achieve the characteristically narrow size distribution. We use population balance modeling to probe the size dependence of the crystal growth rate and determine the magnitude of the size focusing effect. The particle size distribution n(r, t) during nucleation and growth evolves according to the population balance equation (PBE, eqn (1)).
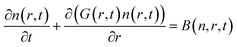 | (1) |
PBEs with growth models where α = 0–4 were fit to the radius evolution with time by optimizing the corresponding kG, the only adjustable parameter for each growth model (Fig. S15†). An example particle size and size distribution predicted by the PBE is shown in Fig. 5. Specific values of correspond to different limiting resistances in the attachment of PbS. A model with size independent growth kinetics (α = 0) was unable to fit the observed evolution in average radius for any value of kG (Fig. S13†). Moreover, the standard deviation in diameter obtained from the SAXS data is much smaller than that predicted from the length of the nucleation phase followed by a linear growth rate. Thus, our results cannot be explained by a size independent growth rate, nor by a brief “burst” of nucleation followed by growth.
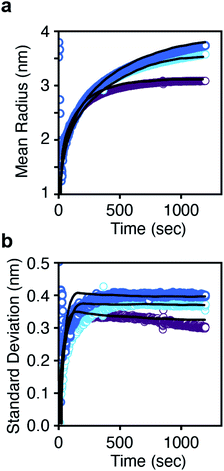 | ||
| Fig. 5 (a) Mean radius and (b) standard deviation in radius versus time for each thiourea. The solid lines are the prediction from the population balance model using eqn (2). A single growth rate constant is found that is consistent across all three thioureas. | ||
Models with α = 1–1.5 are sufficient to describe the mean particle size and polydispersity as a function of time (Fig. S15†) and the total amount of solid PbS (Fig. S16†) across all precursors using a narrow range of kG. An inverse dependence of G on radius (α = 1) is consistent with a diffusion controlled growth process in which kG = D so that G = vmDCsolute(t)/r. However, the fitted value of kG corresponds to a solute diffusion constant (D = 3.46 × 10−11 m2 s−1) on the same order as the diffusivity of a 10 nm nanocrystal. 1H nuclear magnetic resonance diffusion order spectroscopy (DOSY NMR) of lead oleate in hexadecane at 110 °C gives a diffusivity of 3.6 × 10−10 m2 s−1, an order of magnitude faster than the diffusivity from the G = vmDCsolute(t)/r model fit. Thus the fitted value of D is too slow to be explained by diffusion of surfactant stabilized monomers through the solvent.
To further test whether diffusion through the bulk solution limits the growth kinetics, PbS syntheses were performed in several n-alkane solvents (C8 to C20), whose viscosity varies from 0.24 to 1.41 N m s−2 at 100 °C.29 The viscosity increase causes a small reduction (∼25%) in kUV-Visobs and slightly reduces the final nanocrystal size (Fig. S19†). If the growth is limited by diffusion under these conditions, the seven-fold increase in viscosity should cause an approximately seven-fold decrease in the diffusion coefficient and a corresponding increase in the nanocrystal volume. As seen in Fig. S19,† the increase in solvent viscosity slightly decreases the final size, contrary to this prediction. Instead, the increased viscosity correlates with a slight increase in the growth rate. These observations are inconsistent with a growth process that is limited by diffusion through bulk solution. Thus, another mechanism is required to explain the size dependence of the growth rate.
Each of the microscopic steps during the surface reaction may depend on the nanoparticle size, including ligand penetration, surface binding, migration, and facet nucleation. Any or all of these steps could be influenced by size dependent structures, such as: (1) strain,30,31 ligand coverage and binding strength,32,33 and the ratio of atoms on corners, edges, and facets, (2) transitions between magic sizes with kinetics that are governed by 2D facet nucleation,34 and (3) attachment kinetics that are limited by penetration of a surfactant ligand layer, among others.
Mechanisms (2) and (3) are amenable to simple phenomenological models based on the nanoparticle size and geometry. The central idea in mechanism (2), for example, is that nanocrystal shapes with completed facets constitute highly stable magic clusters.34 Each facet represents a confined region where 2D-nucleation and growth must occur to make the transition to the next size. Models suggest that the transitions from one magic cluster size to the next become more difficult as the nanoparticle grows larger.35 It is not yet clear whether the magic cluster mechanisms are important for quasi-spherical metal chalcogenide nanocrystals.
Here we elaborate on model (3), i.e. attachment limited by penetration of the surfactant ligand shell. We construct a model based on three key assumptions: (i) that PbS units in the bulk solution diffuse to the outer edge of the ligand shell with negligible resistance, (ii) that the ligand shell has approximately uniform thickness around the nanoparticle, and (iii) those PbS units that penetrate to the inner edge of the shell are immediately incorporated into the PbS nanoparticle. According to this mechanism, the key parameters that control the attachment rate are the thickness of the oleate ligand shell, the partition coefficient of PbS to the oleate ligand shell from the bulk solution, and the effective diffusivity of PbS through the ligand layer. The predicted growth rate is
| G = vmCsolute(t)DshellK(r + l)/(rl) | (2) |
For large radii (where r ≫ l), the growth rate becomes proportional to the ligand shell permeability (G = vmCsolute(t)DshellK/l). At small sizes (l > r) the growth rate approaches vmDshellKCsolute(t)/r. Note that the oleate ligand shell thickness is about 2 nm, which is similar to the diameter of nanocrystals produced during the nucleation period shown in Fig. 3 and 4. In our calculations, v and l are known quantities, and Csolute(t) was experimentally determined as described above. Only the distribution of radii (r) is being predicted and DshellK is a fitting parameter. Fig. 5 shows that the model based on eqn (2) accurately predicts the experimental mean radius and polydispersity data across all three precursors using a narrow range of the lumped adjustable parameter DshellK. The ability to fit our results using a single parameter across a factor of two in solute supply kinetics highlights the reproducibility of our reaction conditions and the reliability of our model.
The binding strength and coverage of ligands was recently proposed to cause size dependent growth kinetics and size distribution focusing of Pd nanocrystals.33 Population balance modelling and density functional theory calculations demonstrated that phosphine ligands bind small Pd nanocrystals with lower affinity and can thereby induce size dependent growth kinetics and size distribution focusing. Another computational study on the growth mechanism of indium phosphide nanocrystals32 demonstrated size dependent surface reactivity including tighter binding of carboxylates and less favorable attachment of phosphide to large crystallites. These findings were proposed to explain the well-known reluctance of InP nanocrystals to grow beyond a few nanometers in size.36 Similarly, the binding of lead oleate to PbS is known to be weaker for small crystallites.37 Moreover, increasing the concentration of lead oleate and lead chloride during the synthesis of PbS nanocrystals,23,24 or phosphines in the synthesis of Pd nanocrystals33 decreases the final size and size distribution. These effects are consistent with slower, more size dependent growth kinetics at higher ligand coverages. Finally, it has been demonstrated that increasing the chain length of carboxylate surfactants decreases the size and size distribution of colloidal CdSe nanocrystals.38 These results clearly illustrate how ligand binding, coverage, and structure can induce size dependent growth kinetics. Together they point to a new picture of size distribution focusing that can be addressed using surface coordination chemistry.
The slow nucleation observed here clearly demonstrates that the burst of nucleation inherent in LaMer's proposal39 is not applicable to this canonical colloidal crystalline material. Neither is the diffusion limited size focusing mechanism described by Reiss.15 Several recent studies on platinum,40 cadmium selenide,41 indium phosphide,36 and palladium33 nanocrystals reach a similar conclusion. These results require a reinvention of the core principles used to explain the size distributions of colloidal crystals. More detailed investigations of the rate limiting attachment process and its structural origins are important opportunities to advance the rational design of crystalline materials.
Data availability
Experimental data is available in the ESI online.†Author contributions
The manuscript was written through contributions of all authors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Science Foundation under award number NSF CHE-2004008. The SAXS/WAXS experiments were performed on beamline ID02 at the European Synchrotron Radiation Facility (ESRF), Grenoble, France. The SANS experiments were performed on beamline D33 at the Institut Laue Langevin (ILL). Work at the Molecular Foundry was supported by the Office of Science, Office of Basic Energy Sciences, of the U.S. Department of Energy under Contract no. DE-AC02-05CH11231. V. B. and B. P. acknowledge support from the W. H. and J. G. Lycan Professorship at the University of Illinois. We thank Ivan Infante for sending us the atomic models of PbS nanocrystals. We thank Vincent Klein and the “ELINSTRU” team of the Laboratoire de Physique des Solides for the conception and building of the remotely controlled injector.Notes and references
- C. B. Murray, C. R. Kagan and M. G. Bawendi, Annu. Rev. Mater. Sci., 2000, 30, 545–610 CrossRef CAS.
- X. G. Peng, J. Wickham and A. P. Alivisatos, J. Am. Chem. Soc., 1998, 120, 5343–5344 CrossRef CAS.
- Y. Yin and A. P. Alivisatos, Nature, 2005, 437, 664–670 CrossRef CAS PubMed.
- C. B. Whitehead, S. Ozkar and R. G. Finke, Mater. Adv., 2021, 2, 186–235 RSC.
- C. B. Whitehead, S. Ozkar and R. G. Finke, Chem. Mater., 2019, 31, 7116–7132 CrossRef CAS.
- B. Abécassis, C. Bouet, C. Garnero, D. Constantin, N. Lequeux, S. Ithurria, B. Dubertret, B. R. Pauw and D. Pontoni, Nano Lett., 2015, 15, 2620–2626 CrossRef PubMed.
- B. Abécassis, F. Testard, O. Spalla and P. Barboux, Nano Lett., 2007, 7, 1723–1727 CrossRef PubMed.
- J. Polte, R. Erler, A. F. Thünemann, S. Sokolov, T. T. Ahner, K. Rademann, F. Emmerling and R. Kraehnert, ACS Nano, 2010, 4, 1076–1082 CrossRef CAS PubMed.
- D. Pontoni, T. Narayanan and A. R. Rennie, Langmuir, 2002, 18, 56–59 CrossRef CAS.
- R. Garcia-Rodriguez, M. P. Hendricks, B. M. Cossairt, H. T. Liu and J. S. Owen, Chem. Mater., 2013, 25, 1233–1249 CrossRef CAS.
- H. T. Liu, J. S. Owen and A. P. Alivisatos, J. Am. Chem. Soc., 2007, 129, 305–312 CrossRef CAS PubMed.
- M. P. Hendricks, M. P. Campos, G. T. Cleveland, I. Jen-La Plante and J. S. Owen, Science, 2015, 348, 1226–1230 CrossRef CAS PubMed.
- M. P. Campos, M. P. Hendricks, A. N. Beecher, W. Walravens, R. A. Swain, G. T. Cleyeland, Z. Hens, M. Y. Sfeir and J. S. Owen, J. Am. Chem. Soc., 2017, 139, 2296–2305 CrossRef CAS PubMed.
- M. P. Campos, J. d. Roo, M. W. Greenberg, B. McMurtry, M. P. Hendricks, E. Bennett, N. Saenz, M. Y. Sfeir, B. Abécassis, S. K. Ghose and J. S. Owen, Chem. Sci., 2022 10.1039/d1sc06098h.
- H. Reiss, J. Chem. Phys., 1951, 19, 482–487 CrossRef CAS.
- M. D. Clark, S. K. Kumar, J. S. Owen and E. M. Chan, Nano Lett., 2011, 11, 1976–1980 CrossRef CAS PubMed.
- J. Cui, A. P. Beyler, I. Coropceanu, L. Cleary, T. R. Avila, Y. Chen, J. M. Cordero, S. L. Heathcote, D. K. Harris, O. Chen, J. S. Cao and M. G. Bawendi, Nano Lett., 2016, 16, 289–296 CrossRef CAS PubMed.
- S. D. Park, D. Baranov, J. Ryu, B. Cho, A. Halder, S. Seifert, S. Vajda and D. M. Jonas, Nano Lett., 2017, 17, 762–771 CrossRef CAS PubMed.
- T. Narayanan, M. Sztucki, P. Van Vaerenbergh, J. Leonardon, J. Gorini, L. Claustre, F. Sever, J. Morse and P. Boesecke, J. Appl. Crystallogr., 2018, 51, 1511–1524 CrossRef CAS PubMed.
- J. Als-Nielsen and D. McMorrow, Elements of modern X-ray physics, Wiley, New York, 2001 Search PubMed.
- A. Guinier and G. r. Fournet, Small-angle scattering of X-rays, Wiley, New York, 1955 Search PubMed.
- T. Li, A. J. Senesi and B. Lee, Chem. Rev., 2016, 116, 11128–11180 CrossRef CAS PubMed.
- O. Voznyy, L. Levina, J. Z. Fan, M. Askerka, A. Jain, M. J. Choi, O. Ouellette, P. Todorovic, L. K. Sagar and E. H. Sargent, ACS Nano, 2019, 13, 11122–11128 CrossRef CAS PubMed.
- M. C. Weidman, M. E. Beck, R. S. Hoffman, F. Prins and W. A. Tisdale, ACS Nano, 2014, 8, 6363–6371 CrossRef CAS PubMed.
- D. B. K. Chu, J. S. Owen and B. Peters, J. Phys. Chem. A, 2017, 121, 7511–7517 CrossRef CAS PubMed.
- D. Ramkrishna and M. R. Singh, Annu. Rev. Chem. Biomol. Eng., 2014, 5, 123–146 CrossRef CAS PubMed.
- A. D. Randolph and M. A. Larson, Theory of Particulate Processes: Analysis and Techniques of Continuous Crystallization, Academic Press, New York, 1971 Search PubMed.
- T. Vetter, M. Iggland, D. R. Ochsenbein, F. S. Hanseler and M. Mazzotti, Cryst. Growth Des., 2013, 13, 4890–4905 CrossRef CAS.
- D. S. Viswanath, Viscosity of liquids: theory, estimation, experiment, and data, Springer, Dordrecht, 2007 Search PubMed.
- B. Gilbert, F. Huang, H. Z. Zhang, G. A. Waychunas and J. F. Banfield, Science, 2004, 305, 651–654 CrossRef CAS PubMed.
- A. S. Masadeh, E. S. Bozin, C. L. Farrow, G. Paglia, P. Juhas, S. J. L. Billinge, A. Karkamkar and M. G. Kanatzidis, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 115413 CrossRef.
- Q. Zhao and H. J. Kulik, Chem. Mater., 2018, 30, 7154–7165 CrossRef CAS.
- S. Mozaffari, W. Li, M. Dixit, S. Seifert, B. Lee, L. Kovarik, G. Mpourmpakis and A. M. Karim, Nanoscale Adv., 2019, 1, 4052–4066 RSC.
- D. Kashchiev, J. Chem. Phys., 2008, 129, 164701 CrossRef PubMed.
- A. S. Mule, S. Mazzotti, A. A. Rossinelli, M. Aellen, P. T. Prins, J. C. van der Bok, S. F. Solari, Y. M. Glauser, P. V. Kumar, A. Riedinger and D. J. Norris, J. Am. Chem. Soc., 2021, 143, 2037–2048 CrossRef CAS PubMed.
- B. M. McMurtry, K. Qan, J. K. Teglasi, A. K. Swarnakar, J. De Roo and J. S. Owen, Chem. Mater., 2020, 32, 4358–4368 CrossRef CAS.
- M. L. Kessler and J. L. Dempsey, Chem. Mater., 2020, 32, 2561–2571 CrossRef CAS.
- K. De Nolf, R. K. Capek, S. Abe, M. Sluydts, Y. J. Jang, J. C. Martins, S. Cottenier, E. Lifshitz and Z. Hens, J. Am. Chem. Soc., 2015, 137, 2495–2505 CrossRef CAS PubMed.
- V. K. Lamer and R. H. Dinegar, J. Am. Chem. Soc., 1950, 72, 4847–4854 CrossRef CAS.
- D. R. Handwerk, P. D. Shipman, C. B. Whitehead, S. Ozkar and R. G. Finke, J. Am. Chem. Soc., 2019, 141, 15827–15839 CrossRef CAS PubMed.
- P. T. Prins, F. Montanarella, K. Dumbgen, Y. Justo, J. C. van der Bok, S. O. M. Hinterding, J. J. Geuchies, J. Maes, K. De Nolf, S. Deelen, H. Meijer, T. Zinn, A. V. Petukhov, F. T. Rabouw, C. D. Donega, D. Vanmaekelbergh and Z. Hens, Nano Lett., 2021, 21, 2487–2496 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Detailed experimental methods, X-ray scattering analysis, modeling methods, and derivation of ligand penetration model. See DOI: 10.1039/d1sc06134h |
| ‡ These authors contributed equally to this manuscript. |
| This journal is © The Royal Society of Chemistry 2022 |