Rethinking nuclear shaping: insights from the nuclear drop model

Abstract

Changes in the nuclear shape caused by cellular shape changes are generally assumed to reflect an elastic deformation from a spherical nuclear shape. Recent evidence, however, suggests that the nuclear lamina, which forms the outer nuclear surface together with the nuclear envelope, possesses more area than that of a sphere of the same volume. This excess area manifests as folds/wrinkles in the nuclear surface in rounded cells and allows facile nuclear flattening during cell spreading without any changes in nuclear volume or surface area. When the lamina becomes smooth and taut, it is inextensible, and supports a surface tension. At this point, it is possible to mathematically calculate the limiting nuclear shape purely based on geometric considerations. In this paper, we provide a commentary on the “nuclear drop model” which seeks to integrate the above features. We outline its testable physical properties and explore its biological implications.

---

Introduction

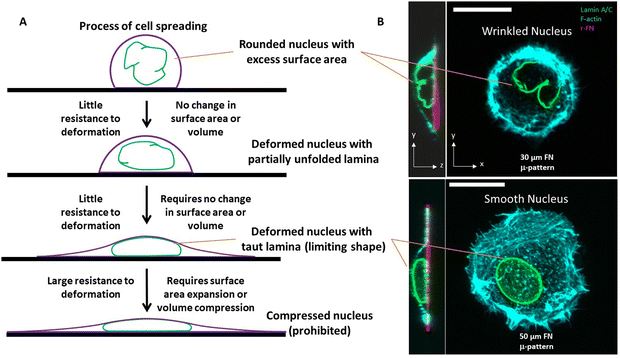
Nuclei in fully spread cultured cells typically appear circular and smooth when seen in microscopic images in the x–y plane (i.e. from above or below). Perhaps for this reason, nuclei have historically been assumed to be spherical organelles, both in textbook presentations and in biomechanical models. Nuclei in spread cells are not spherical, but instead are highly flattened with small height/width aspect ratios and are non-spherical with diverse shapes in vivo. In general, nuclear shape is coordinated with cell shape, with elongated cells featuring elongated cells and rounded cells featuring rounded nuclei.^1,2

Our understanding of how the shape of the nucleus is established in cells is rapidly evolving. It is known that dynamic cytoskeletal forces that impinge on the nuclear surface cause deformations in the nucleus.³ Nuclear shape adjusts to the changing force distribution on their surface in motile cells. The mechanical response of the nucleus to the changing force distribution is determined by the nuclear lamina and chromatin.^4,5 The nuclear lamina, a 15 nm thick shell-like structure composed of nuclear lamin A/C and B-type lamins⁶ which underlies the nuclear envelope, is particularly important in nuclear shaping. Perturbation of the thin lamina through depletion of lamin A/C softens the entire nucleus which is many microns in size through mechanisms that are poorly understood.

A natural starting point for modeling of nuclear shaping is to consider the nucleus as a viscoelastic object. There is a significant body of experimental papers that have probed the nucleus with various external mechanical force applying techniques, whether with atomic force microscopy (AFM), or micropipette aspiration or nuclear compression.^7–20 The nuclear lamina was reported to resist extensional strain in micropipette aspiration experiments, and it was proposed that this resistance largely determines nuclear deformation under applied force.²¹ Indeed, the nucleus deforms substantially more under force in cells lacking lamin A/C or with low levels of lamin A/C.^{10,15,16,22–25} More recent work has additionally implicated chromatin in elastically resisting deformation at smaller nuclear deformations.²⁶ Imaging of chromatin motion in nuclei of living cells has shown that chromatin behaves like a viscoelastic material,^27,28 with perhaps a short-lived elastic component²⁹ or a weak gel-like structure with short-lived crosslinks.²⁸ Also, rapid elastic shape fluctuations in the nuclear lamina have been reported.³⁰ The viscoelastic behavior of chromatin may potentially reflect persistent solid-like chromatin subdomains interspersed within a liquid-like structure.³¹

That the nucleus clearly has viscoelastic properties has inspired models in which the shape of the nucleus is established by deformation from a spherical, smooth resting shape by cellular forces.^32–36 Geometrically, deformation of a sphere requires either an expansion of its surface area, compression of its volume, or both. Indeed, elastic models of nuclear deformation consider an expansion in the nuclear laminar area and/or compression in volume for predicting nuclear shape.^1,33,37 However, we and others have found that nuclei can undergo deformations without changes to surface area or volume.^3,38,39 This is possible, because rounded nuclei have folds and wrinkles in the nuclear lamina.^3,40–43 These folds/wrinkles permit a wide range of shape changes of the nucleus without requiring the mechanical work to stretch the lamina or compress the nuclear volume. For this reason, we have concluded that the amount of excess surface area of the nuclear lamina is critical in determining the mechanical resistance of the nucleus to deformation, and nuclear shape.⁴⁴ Models based on elastic deformation of the nuclear lamina or chromatin from a spherical resting state ignore the critical role of excess surface area in determining nuclear shape and mechanics.^33,37

Here, we provide a commentary on our recently proposed nuclear drop model,^45,46 which seeks to integrate the above considerations into an alternative model of nuclear shaping in cells.

A new model for nuclear shaping

In the nuclear drop model, laminar tension is considered to emerge when the wrinkled lamina becomes smooth and taut whereupon it resists expansion of its surface area (Fig. 1A). Analogous to how the surface tension balances pressure across a curved interface of a liquid drop, the surface tension of the curved, smooth lamina balances the pressure difference between the nuclear interior and the cytoplasm. At mechanical equilibrium, the pressure difference ΔP between the nucleoplasm and the cytoplasm will be related to the mean curvature, H, and surface tension τ by the law of Laplace

ΔP = 2τH

Fig. 1 A. The resistance of the liquid drop-like nucleus to deformation is highly dependent on the state of the excess surface area of the nuclear lamina. Excess surface area allows a rounded nucleus to easily change shape with little resistance, without stretching the lamina area or compressing the nuclear volume. Only under larger deformations does the lamina becomes taut (with surface tension). At this point, the nucleus strongly resists any further deformation that would require stretching of the surface area of the lamina or compression of the nuclear volume. B. High resolution confocal fluorescence images of HT-1080 cells expressing GFP-LMNA (green) and stained for F-actin (cyan) cultured on rhodamine-fibronectin micropatterned circular islands with 30 or 50 μm diameter. The scale bar is 20 μm.

Assuming ΔP and τ are nearly uniform across the nucleus–cytoplasm interface, this relation explains why the taut nuclear lamina in spread cells typically appears as a surface of constant mean curvature.⁴⁴

However, the nucleus is not like a liquid drop in other respects. The source of nuclear surface tension is the resistance of the taut lamina to areal expansion; further, this surface tension emerges abruptly and only when the lamina becomes taut.

Overall, when the lamina is highly wrinkled, the nucleus is predicted to be highly compliant to cellular forces. When nuclei flatten or elongate such that the lamina eventually becomes smooth and taut, the resistance to laminar stretching or volume compression are predicted to be too high for cellular forces, resulting in a steady state nuclear shape (an example of a wrinkled nucleus in rounded cells and taut nucleus in spread cells is in Fig. 1B). That the taut lamina is likely to be essentially inextensible in cells can be seen from an estimate of the upper bound on lamina area strain. For a typical estimate of the nuclear bulk modulus of ∼5 kPa (or 5 nN μm⁻²),⁴⁷ a reasonable upper bound on nuclear pressure (relative to cytoplasm) is < 0.5 nN μm⁻² (assuming <10% volume compression). From observed limiting nuclear shapes of flattened nuclei, the upper bound on highest mean curvature at the sides of the nucleus is < 0.4 μm⁻¹. As such, the laminar surface tension is unlikely to exceed 0.6 nN μm⁻¹ based on the law of Laplace. Thus, upon applying the measured dilational modulus of the lamina of 390 nN μm⁻¹,²¹ we conservatively estimate an upper bound on laminar areal strain to be <0.2%, which is very small.

Excess surface area of the nuclear lamina determines nuclear shape

One insight of the model in Fig. 1, in which the nucleus deforms at constant area and volume and a limiting, final nuclear shape is reached when the lamina is fully unfolded (at which point it is inextensible), is that the three-dimensional limiting nuclear shapes in cells are geometrically determined. Thus, the model predicts that the limiting nuclear shape is not determined by cellular forces⁴⁴ as is typically assumed. Rather it is the amount of excess area in the nuclear lamina that impacts the final shape of the nucleus.

Fig. 2A shows cell and nuclear shapes which were calculated entirely from geometric considerations, by solving for the surfaces of constant mean curvature under the constraints of fixed area of the nuclear lamina, cell volume, and nuclear volume. Details of the mathematical derivation can be found in ref. 44. The calculation shows three cell and nuclear surfaces with distinct curvatures observable in x–z cross-sections of fully spread cells (see x–z cell shape in bottom panel of Fig. 1B, and calculation of nuclear shape in Fig. 2B). The model predicts progressively more flattened nuclear shapes for higher excess areas (Fig. 2C). This calculation quantitatively confirms the principle that the flattened shapes of nuclei, and corresponding levels of cell flattening, are determined geometrically by the excess area of the lamina.

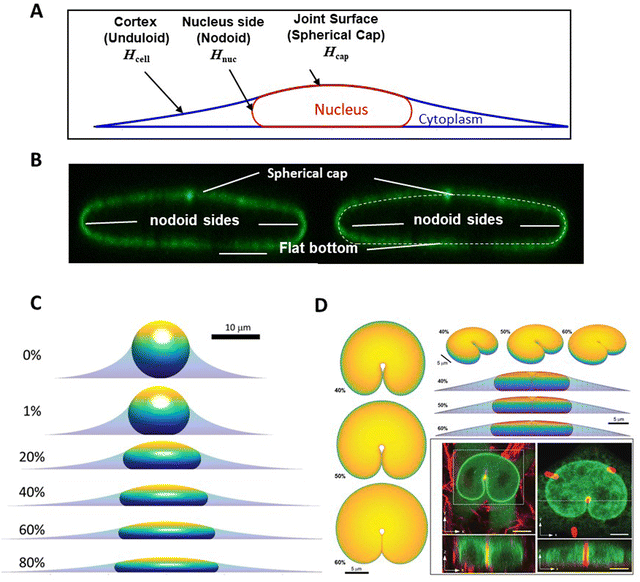Fig. 2 Calculation of nuclear shapes based on the nuclear drop model (sub-parts of the figure adapted from Dickinson and Lele, Front. Cell Develop. Biol. 2023⁴⁴). (A) Calculations of x–z profile of cell and nuclear surfaces. Shown are the calculated cell cortical-extracellular medium interface (an unduloid surface of curvature H_cell), the nuclear–cytoplasmic interface (a nodoid surface of curvature H_nuc), and the nuclear-cortical interface with the extracellular medium (a spherical cap of curvature H_cap). (B) Calculated cell and nuclear shapes at different values of excess surface area. Higher excess lamina area corresponds to flatter nuclei for the same nuclear and cell volume. (C) Predicted nuclear shape (white-dotted line) overlaid with an x–z cross-section of an image of the nuclear lamina, showing close agreement for the distinct labeled surfaces. (D) Comparison of predicted 3D shapes of nuclei indented by a 1-μm diameter micropost compared to shapes of GFP-lamin expressing nuclei (green) deformed against a collagen fiber (left) or a micropost (right) reported in Katiyar et al. Adv. Sci. 2022.⁴⁶ Calculated shapes are showing from different viewing angles and for varying excess area. Scale bar is 5 microns.

The geometric model successfully explains the indented nuclear shapes developed when the nucleus deforms against slender microposts during cell migration⁴⁶ (Fig. 2D). The experimentally observed nuclear shapes look similar to the indented shapes of an oil drop in liquid by a metal wire,⁴⁶ suggestive of drop-like nuclear deformation. Model calculations predict similar nuclear shapes (Fig. 2D); the predicted shapes are again sensitive to the amount of excess area (Fig. 2D).

Consistent with the notion that there is little resistance to deformation when the nuclear lamina has folds/wrinkles in it, the nucleus can flatten to limiting shapes even after pharmacological inhibition of actomyosin forces.³ That myosin II inhibition impacts nuclear height in spread cells has been broadly reported.^32,48,49 We reported similar results previously,³ however, we noted that so long as there is no change in cell shape owing to actomyosin inhibition, nuclei will stay flattened in spread cells even after myosin inhibition. If myosin inhibition causes cell rounding, then the nucleus will undergo a rounding – thus interpretations of how inhibiting specific force generating elements in the cell impact nuclear shape must critically account for concomitant changes in cell shape.

Given the success of the drop model in predicting nuclear shapes while accounting for excess area, we propose that the viscoelastic properties of the nucleus, while governing the dynamic response of the nucleus to cellular force, do not actually determine nuclear shape in cells. However, the constant volume and constant area constraint on the nucleus is obviously due to the specific values of the extensional and bulk moduli of the nucleus. Modifications to the laminar modulus or the bulk modulus will in turn impact these properties of the nuclear drop. For example, a decrease in lamin A/C levels, as occurs in human diseases like cancer, will relax the areal constraint. Alterations to chromatin conformation or osmotic coupling with the cytoplasm,^50–52 which determine the bulk modulus, could modify the nuclear pressure, altering nuclear shape.

The drop model has the following testable properties, which are supported by or are consistent with evidence in the corresponding cited papers:

(1) Presence of wrinkles in the nuclear lamina in a rounded nucleus⁵³ and a dynamic folding/unfolding of the lamina during nuclear shape changes.⁵⁴

(2) The steady state shape of a compressed nucleus features a taut lamina resulting in a surface tension.⁵⁵

(3) Little resistance to nuclear deformation when the lamina is wrinkled, detectable as an abrupt stiffening when a steadily deforming nucleus reaches a shape with a smooth, taut lamina.^3,26,56,57

(4) Small resistance to deformation at the typical slow times of nuclear shape changes in cells.⁴⁶

(5) When the lamin A/C containing nuclear lamina is fully taut, free surfaces of the nuclei have constant mean curvatures^44,46 consistent with the law of Laplace.

(6) The interior of the nucleus is pressurized when the lamina is taut, detectable in confinement through blebbing or rupture.^49,58

(7) Knockdown of lamin A/C causes irregular nuclear shapes, indicative of a lack of resistance to changes in surface area^46,59 (i.e. a reduction in surface tension).

(8) Force insensitivity of limiting nuclear shapes allowing calculation of nuclear shapes purely based on geometric analysis.^3,44

(9) Resistance of nuclear contents to volume changes due to osmotic pressure of nuclear contents.⁶⁰

(10) A lack of stored elastic energy in the nuclear shape on physiologically relevant time scales.⁶¹

Future directions: exploring biological implications of the nuclear drop model

The nuclear drop model may require a rethink of how alterations to nuclear lamins and chromatin contribute to nuclear defects such as shape anomalies or nuclear rupturing in human diseases and how nuclear deformations mediate cell functions such as cell migration in confinement or cellular sensing of mechanical cues such as matrix stiffness.

A model of a nucleus in which its shape when the lamina is taut/smooth is determined purely by geometric considerations offers alternative explanations for the diverse types of nuclear deformations with biological functions that have been reported.⁶² When the nuclear lamina reaches a smooth, taut state, the nucleus should deform into shapes such that free, smooth laminar surfaces have constant curvatures like a drop; this is indeed what is observed. Second, the effect of perturbing the nuclear lamins on nuclear shape can be explained by analogy with treatment of oil drop emulsions in water with surfactant, which reduces the surface tension and the pressure difference across the interface. A drop without surface tension can deform without limit on its surface area. Nuclei lacking lamin A/C deform around slender obstacles without a limit on surface area resulting in highly abnormal nuclear shapes.⁴⁶ Thus, the ability of the nuclear lamina to support a surface tension is strongly dependent on the presence of lamin A/C. This principle may underlie abnormal nuclear shapes observed in human diseases such as cancer where lamin levels can be altered⁶³ or in diseases associated with lamin mutations such as progeria.^64–66 Likewise, the drop model can explain the polymorphonuclear shapes in granulocytes because they have low levels of lamin A/C.⁶⁷

Nuclei are observed to bleb upon confinement and eventually rupture.^68–70 Nuclear blebbing in confinement and subsequent rupture can be explained as caused by an increased pressure inside the nuclear drop, that is balanced by eventual, unsustainable levels of tension in the lamina resulting in local tearing, pressurized membrane blebs and subsequent rupture.^49,68,71 Similarly, blebbing and rupture of the nuclear envelope upon chromatin decondensation⁷² may be explained by an increase in the pressure differential across the nuclear envelope resulting in a breach in the lamina. Rupture of the lamina and bleb formation breaks the constraint of an inextensible lamina surface area enclosing the nuclear volume, thereby releasing nuclear pressure and allowing the nucleus to take on more extreme deformations.

Beyond balancing nuclear pressure and establishing nuclear shape, the biological functions of the tension in the taut nuclear lamina are worth investigating. Tethering between the nuclear lamina and the nuclear envelope could transmit laminar tension to the nuclear envelope. As tension in the nuclear membrane can dilate nuclear pores,^73,74 or open mechanosensitive channels,⁷⁵ tension in the nuclear lamina may exert indirect control on nuclear pore transport and cell signaling. Likewise, how the drop-like properties of the nucleus, particularly surface tension conferred by lamin A/C, allow it to limit migration through confinement,^59,71,76 remains to be investigated.

Summary

The nucleus is considered to be far stiffer than the cytoskeleton because of its high resistance to deformation apparent in AFM or micropipette aspiration experiments that rapidly deform the nucleus on time scales of a few seconds. But on the slow time scales of deformation typical in cells (tens of seconds to minutes), the nucleus is not stiff to deformation. When the nucleus is rounded, its nuclear lamina is wrinkled owing to the presence of an excess area over a sphere of the same volume. The resistance to changing the shape of such a rounded nucleus is minimal as the apparent surface area of such a shape can increase without making the lamina taut owing to the excess surface area. When the lamina eventually becomes taut, it resists an increase in area. A surface tension develops in the nuclear lamina at this point that is balanced by nuclear pressure. Then, the nucleus becomes ‘stiff’ to deformation, but even after this point, the nucleus can easily change shape so long as it maintains constant area and volume. This is possible as the nuclear contents behave as a viscous fluid on slow time scales of deformation. As such, nuclei do not appear stiff to cells, except with respect to extreme deformations that would require a stretching of the area of the lamina or compression of the volume. The nuclear drop model explains these key features of nuclear deformation, and quantitatively explains limiting nuclear shapes as a simple consequence of excess area in the nuclear lamina. The full biological implications of drop-like behavior of the nucleus await further investigation.

Data availability

Data in Fig. 2 is reproduced from papers cited in the corresponding figure legend. All other data is available within the article.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

T. P. L., CPRIT Scholar in Cancer Research, acknowledges support from NIH U01 CA225566, CPRIT Established Investigator Award RR200043 and NSF award 2226157. R. B. D. acknowledges support from NIH U01 CA225566 and NSF award 2226156.

References

1. M. Versaevel, T. Grevesse and S. Gabriele, Spatial coordination between cell and nuclear shape within micropatterned endothelial cells, Nat. Commun., 2012, 3, 671.
2. R. Vishavkarma, S. Raghavan, C. Kuyyamudi, A. Majumder, J. Dhawan and P. A. Pullarkat, Role of actin filaments in correlating nuclear shape and cell spreading, PLoS One, 2014, 9(9), e107895.
3. Y. Li, D. Lovett, Q. Zhang, S. Neelam, R. A. Kuchibhotla, R. Zhu, G. G. Gundersen, T. P. Lele and R. B. Dickinson, Moving cell boundaries drive nuclear shaping during cell spreading, Biophys. J., 2015, 109(4), 670–686.
4. T. P. Lele, R. B. Dickinson and G. G. Gundersen, Mechanical principles of nuclear shaping and positioning, J. Cell Biol., 2018, 217(10), 3330–3342.
5. P. M. Davidson and J. Lammerding, Broken nuclei--lamins, nuclear mechanics, and disease, Trends Cell Biol., 2014, 24(4), 247–256.
6. Y. Turgay, M. Eibauer, A. E. Goldman, T. Shimi, M. Khayat, K. Ben-Harush, A. Dubrovsky-Gaupp, K. T. Sapra, R. D. Goldman and O. Medalia, The molecular architecture of lamins in somatic cells, Nature, 2017, 543(7644), 261–264.
7. F. Guilak, J. R. Tedrow and R. Burgkart, Viscoelastic properties of the cell nucleus, Biochem. Biophys. Res. Commun., 2000, 269(3), 781–786.
8. K. N. Dahl, A. J. Engler, J. D. Pajerowski and D. E. Discher, Power-law rheology of isolated nuclei with deformation mapping of nuclear substructures, Biophys. J., 2005, 89(4), 2855–2864.
9. I. Ivanovska, J. Swift, T. Harada, J. D. Pajerowski and D. E. Discher, Physical plasticity of the nucleus and its manipulation, Methods Cell Biol., 2010, 98, 207–220.
10. J. Swift, I. L. Ivanovska, A. Buxboim, T. Harada, P. C. Dingal, J. Pinter, J. D. Pajerowski, K. R. Spinler, J. W. Shin, M. Tewari, F. Rehfeldt, D. W. Speicher and D. E. Discher, Nuclear lamin-A scales with tissue stiffness and enhances matrix-directed differentiation, Science, 2013, 341(6149), 1240104.
11. J. W. Shin, K. R. Spinler, J. Swift, J. A. Chasis, N. Mohandas and D. E. Discher, Lamins regulate cell trafficking and lineage maturation of adult human hematopoietic cells, Proc. Natl. Acad. Sci. U. S. A., 2013, 110(47), 18892–18897.
12. T. Harada, J. Swift, J. Irianto, J. W. Shin, K. R. Spinler, A. Athirasala, R. Diegmiller, P. C. Dingal, I. L. Ivanovska and D. E. Discher, Nuclear lamin stiffness is a barrier to 3D migration, but softness can limit survival, J. Cell Biol., 2014, 204(5), 669–682.
13. O. Wintner, N. Hirsch-Attas, M. Schlossberg, F. Brofman, R. Friedman, M. Kupervaser, D. Kitsberg and A. Buxboim, A Unified Linear Viscoelastic Model of the Cell Nucleus Defines the Mechanical Contributions of Lamins and Chromatin, Adv. Sci., 2020, 7(8), 1901222.
14. N. Zuela-Sopilniak, D. Bar-Sela, C. Charar, O. Wintner, Y. Gruenbaum and A. Buxboim, Measuring nucleus mechanics within a living multicellular organism: Physical decoupling and attenuated recovery rate are physiological protective mechanisms of the cell nucleus under high mechanical load, Mol. Biol. Cell, 2020, 31(17), 1943–1950.
15. J. D. Pajerowski, K. N. Dahl, F. L. Zhong, P. J. Sammak and D. E. Discher, Physical plasticity of the nucleus in stem cell differentiation, Proc. Natl. Acad. Sci. U. S. A., 2007, 104(40), 15619–15624.
16. S. Neelam, T. J. Chancellor, Y. Li, J. A. Nickerson, K. J. Roux, R. B. Dickinson and T. P. Lele, Direct force probe reveals the mechanics of nuclear homeostasis in the mammalian cell, Proc. Natl. Acad. Sci. U. S. A., 2015, 112(18), 5720–5725.
17. Q. Zhang, A. C. Tamashunas, A. Agrawal, M. Torbati, A. Katiyar, R. B. Dickinson, J. Lammerding and T. P. Lele, Local, transient tensile stress on the nuclear membrane causes membrane rupture, Mol. Biol. Cell, 2019, 30(7), 899–906.
18. A. Vaziri and M. R. Mofrad, Mechanics and deformation of the nucleus in micropipette aspiration experiment, J. Biomech., 2007, 40(9), 2053–2062.
19. A. E. Patteson, A. Vahabikashi, K. Pogoda, S. A. Adam, K. Mandal, M. Kittisopikul, S. Sivagurunathan, A. Goldman, R. D. Goldman and P. A. Janmey, Vimentin protects cells against nuclear rupture and DNA damage during migration, J. Cell Biol., 2019, 218(12), 4079–4092.
20. F. Guilak, J. R. Tedrow and R. Burgkart, Viscoelastic properties of the cell nucleus, Biochem. Biophys. Res. Commun., 2000, 269(3), 781–786.
21. K. N. Dahl, S. M. Kahn, K. L. Wilson and D. E. Discher, The nuclear envelope lamina network has elasticity and a compressibility limit suggestive of a molecular shock absorber, J. Cell Sci., 2004, 117(Pt 20), 4779–4786.
22. P. M. Davidson, C. Denais, M. C. Bakshi and J. Lammerding, Nuclear deformability constitutes a rate-limiting step during cell migration in 3-D environments, Cell. Mol. Bioeng., 2014, 7(3), 293–306.
23. J. Lammerding, P. C. Schulze, T. Takahashi, S. Kozlov, T. Sullivan, R. D. Kamm, C. L. Stewart and R. T. Lee, Lamin A/C deficiency causes defective nuclear mechanics and mechanotransduction, J. Clin. Invest., 2004, 113(3), 370–378.
24. J. Schäpe, S. Prausse, M. Radmacher and R. Stick, Influence of lamin A on the mechanical properties of amphibian oocyte nuclei measured by atomic force microscopy, Biophys. J., 2009, 96(10), 4319–4325.
25. J. L. Broers, E. A. Peeters, H. J. Kuijpers, J. Endert, C. V. Bouten, C. W. Oomens, F. P. Baaijens and F. C. Ramaekers, Decreased mechanical stiffness in LMNA-/- cells is caused by defective nucleo-cytoskeletal integrity: implications for the development of laminopathies, Hum. Mol. Genet., 2004, 13(21), 2567–2580.
26. A. D. Stephens, E. J. Banigan, S. A. Adam, R. D. Goldman and J. F. Marko, Chromatin and lamin A determine two different mechanical response regimes of the cell nucleus, Mol. Biol. Cell, 2017, 28(14), 1984–1996.
27. S. Sanulli, M. J. Trnka, V. Dharmarajan, R. W. Tibble, B. D. Pascal, A. L. Burlingame, P. R. Griffin, J. D. Gross and G. J. Narlikar, HP1 reshapes nucleosome core to promote phase separation of heterochromatin, Nature, 2019, 575(7782), 390–394.
28. V. I. P. Keizer, S. Grosse-Holz, M. Woringer, L. Zambon, K. Aizel, M. Bongaerts, F. Delille, L. Kolar-Znika, V. F. Scolari, S. Hoffmann, E. J. Banigan, L. A. Mirny, M. Dahan, D. Fachinetti and A. Coulon, Live-cell micromanipulation of a genomic locus reveals interphase chromatin mechanics, Science, 2022, 377(6605), 489–495.
29. N. Khanna, Y. Zhang, J. S. Lucas, O. K. Dudko and C. Murre, Chromosome dynamics near the sol-gel phase transition dictate the timing of remote genomic interactions, Nat. Commun., 2019, 10(1), 2771.
30. F. Y. Chu, S. C. Haley and A. Zidovska, On the origin of shape fluctuations of the cell nucleus, Proc. Natl. Acad. Sci. U. S. A., 2017, 114(39), 10338–10343.
31. H. Strickfaden, T. O. Tolsma, A. Sharma, D. A. Underhill, J. C. Hansen and M. J. Hendzel, Condensed Chromatin Behaves like a Solid on the Mesoscale In Vitro and in Living Cells, Cell, 2020, 183(7), 1772–1784.
32. S. B. Khatau, C. M. Hale, P. J. Stewart-Hutchinson, M. S. Patel, C. L. Stewart, P. C. Searson, D. Hodzic and D. Wirtz, A perinuclear actin cap regulates nuclear shape, Proc. Natl. Acad. Sci. U. S. A., 2009, 106(45), 19017–19022.
33. F. Alisafaei, D. S. Jokhun, G. V. Shivashankar and V. B. Shenoy, Regulation of nuclear architecture, mechanics, and nucleocytoplasmic shuttling of epigenetic factors by cell geometric constraints, Proc. Natl. Acad. Sci. U. S. A., 2019, 116(27), 13200–13209.
34. A. Mukherjee, A. Barai, R. K. Singh, W. Yan and S. Sen, Nuclear plasticity increases susceptibility to damage during confined migration, PLoS Comput. Biol., 2020, 16(10), e1008300.
35. Q. Li, A. Kumar, E. Makhija and G. V. Shivashankar, The regulation of dynamic mechanical coupling between actin cytoskeleton and nucleus by matrix geometry, Biomaterials, 2014, 35(3), 961–969.
36. A. Vaziri, A. Gopinath and V. Deshpande, Continuum-based computational models for cell and nuclear mechanics, J. Mech. Mater. Struct., 2007, 2(6), 1169–1191.
37. X. Cao, E. Moeendarbary, P. Isermann, P. M. Davidson, X. Wang, M. B. Chen, A. K. Burkart, J. Lammerding, R. D. Kamm and V. B. Shenoy, A Chemomechanical Model for Nuclear Morphology and Stresses during Cell Transendothelial Migration, Biophys. J., 2016, 111(7), 1541–1552.
38. I. F. Sbalzarini and P. Koumoutsakos, Feature point tracking and trajectory analysis for video imaging in cell biology, J. Struct. Biol., 2005, 151(2), 182–195.
39. M. Guo, A. F. Pegoraro, A. Mao, E. H. Zhou, P. R. Arany, Y. Han, D. T. Burnette, M. H. Jensen, K. E. Kasza, J. R. Moore, F. C. Mackintosh, J. J. Fredberg, D. J. Mooney, J. Lippincott-Schwartz and D. A. Weitz, Cell volume change through water efflux impacts cell stiffness and stem cell fate, Proc. Natl. Acad. Sci. U. S. A., 2017, 114(41), E8618–E8627.
40. R. B. Dickinson, A. Katiyar, C. R. Dubell and T. P. Lele, Viscous shaping of the compliant cell nucleus, APL Bioeng., 2022, 6(1), 010901.
41. B. D. Cosgrove, C. Loebel, T. P. Driscoll, T. K. Tsinman, E. N. Dai, S. J. Heo, N. A. Dyment, J. A. Burdick and R. L. Mauck, Nuclear envelope wrinkling predicts mesenchymal progenitor cell mechano-response in 2D and 3D microenvironments, Biomaterials, 2021, 270, 120662.
42. J. Swift and D. E. Discher, The nuclear lamina is mechano-responsive to ECM elasticity in mature tissue, J. Cell Sci., 2014, 127(Pt 14), 3005–3015.
43. S. Neelam, P. Hayes, Q. Zhang, R. Dickinson and T. Lele, Vertical uniformity of cells and nuclei in epithelial monolayers, Sci. Rep., 2016, 6, 19689.
44. R. B. Dickinson and T. P. Lele, Nuclear shapes are geometrically determined by the excess surface area of the nuclear lamina, Front. Cell Develop. Biol., 2023, 11, 1058727.
45. R. B. Dickinson and T. P. Lele, A new function for nuclear lamins: Providing surface tension to the nuclear drop, Curr. Opin. Biomed. Eng., 2023, 28, 100483.
46. A. Katiyar, J. Zhang, J. D. Antani, Y. Yu, K. L. Scott, P. P. Lele, C. A. Reinhart-King, N. J. Sniadecki, K. J. Roux, R. B. Dickinson and T. P. Lele, The Nucleus Bypasses Obstacles by Deforming Like a Drop with Surface Tension Mediated by Lamin A/C, Adv. Sci., 2022, 9(23), e2201248.
47. N. Caille, O. Thoumine, Y. Tardy and J. J. Meister, Contribution of the nucleus to the mechanical properties of endothelial cells, J. Biomech., 2002, 35(2), 177–187.
48. J. Aureille, V. Buffiere-Ribot, B. E. Harvey, C. Boyault, L. Pernet, T. Andersen, G. Bacola, M. Balland, S. Fraboulet, L. Van Landeghem and C. Guilluy, Nuclear envelope deformation controls cell cycle progression in response to mechanical force, EMBO Rep., 2019, 20(9), e48084.
49. E. M. Hatch and M. W. Hetzer, Nuclear envelope rupture is induced by actin-based nucleus confinement, J. Cell Biol., 2016, 215(1), 27–36.
50. J. D. Finan, H. A. Leddy and F. Guilak, Osmotic stress alters chromatin condensation and nucleocytoplasmic transport, Biochem. Biophys. Res. Commun., 2011, 408(2), 230–235.
51. J. D. Finan and F. Guilak, The effects of osmotic stress on the structure and function of the cell nucleus, J. Cell. Biochem., 2010, 109(3), 460–467.
52. J. D. Finan, K. J. Chalut, A. Wax and F. Guilak, Nonlinear osmotic properties of the cell nucleus, Ann. Biomed. Eng., 2009, 37(3), 477–491.
53. J. A. Jackson, N. Romeo, A. Mietke, K. J. Burns, J. F. Totz, A. C. Martin, J. Dunkel and J. Imran Alsous, Scaling behaviour and control of nuclear wrinkling, Nat. Phys., 2023, 19(12), 1927–1935.
54. A. Katiyar, V. J. Tocco, Y. Li, V. Aggarwal, A. C. Tamashunas, R. B. Dickinson and T. P. Lele, Nuclear size changes caused by local motion of cell boundaries unfold the nuclear lamina and dilate chromatin and intranuclear bodies, Soft Matter, 2019, 15(45), 9310–9317.
55. B. E. Danielsson, B. George Abraham, E. Mantyla, J. I. Cabe, C. R. Mayer, A. Rekonen, F. Ek, D. E. Conway and T. O. Ihalainen, Nuclear lamina strain states revealed by intermolecular force biosensor, Nat. Commun., 2023, 14(1), 3867.
56. W. Tang, X. Chen, X. Wang, M. Zhu, G. Shan, T. Wang, W. Dou, J. Wang, J. Law, Z. Gong, S. Hopyan, X. Huang and Y. Sun, Indentation induces instantaneous nuclear stiffening and unfolding of nuclear envelope wrinkles, Proc. Natl. Acad. Sci. U. S. A., 2023, 120(36), e2307356120.
57. E. J. Banigan, A. D. Stephens and J. F. Marko, Mechanics and Buckling of Biopolymeric Shells and Cell Nuclei, Biophys. J., 2017, 113(8), 1654–1663.
58. P. Mistriotis, E. O. Wisniewski, K. Bera, J. Keys, Y. Li, S. Tuntithavornwat, R. A. Law, N. A. Perez-Gonzalez, E. Erdogmus, Y. Zhang, R. Zhao, S. X. Sun, P. Kalab, J. Lammerding and K. Konstantopoulos, Confinement hinders motility by inducing RhoA-mediated nuclear influx, volume expansion, and blebbing, J. Cell Biol., 2019, 218(12), 4093–4111.
59. E. S. Bell, P. Shah, N. Zuela-Sopilniak, D. Kim, A. A. Varlet, J. L. P. Morival, A. L. McGregor, P. Isermann, P. M. Davidson, J. J. Elacqua, J. N. Lakins, L. Vahdat, V. M. Weaver, M. B. Smolka, P. N. Span and J. Lammerding, Low lamin A levels enhance confined cell migration and metastatic capacity in breast cancer, Oncogene, 2022, 41(36), 4211–4230.
60. D. Deviri and S. A. Safran, Balance of osmotic pressures determines the nuclear-to-cytoplasmic volume ratio of the cell, Proc. Natl. Acad. Sci. U. S. A., 2022, 119(21), e2118301119.
61. V. J. Tocco, Y. Li, K. G. Christopher, J. H. Matthews, V. Aggarwal, L. Paschall, H. Luesch, J. D. Licht, R. B. Dickinson and T. P. Lele, The nucleus is irreversibly shaped by motion of cell boundaries in cancer and non-cancer cells, J. Cell. Physiol., 2018, 233(2), 1446–1454.
62. Y. Kalukula, A. D. Stephens, J. Lammerding and S. Gabriele, Mechanics and functional consequences of nuclear deformations, Nat. Rev. Mol. Cell Biol., 2022, 23, 583–602.
63. I. Singh and T. P. Lele, Nuclear Morphological Abnormalities in Cancer: A Search for Unifying Mechanisms, Results Probl. Cell Differ., 2022, 70, 443–467.
64. R. D. Goldman, D. K. Shumaker, M. R. Erdos, M. Eriksson, A. E. Goldman, L. B. Gordon, Y. Gruenbaum, S. Khuon, M. Mendez, R. Varga and F. S. Collins, Accumulation of mutant lamin A causes progressive changes in nuclear architecture in Hutchinson-Gilford progeria syndrome, Proc. Natl. Acad. Sci. U. S. A., 2004, 101(24), 8963–8968.
65. J. Y. Shin and H. J. Worman, Molecular Pathology of Laminopathies, Annu. Rev. Pathol., 2022, 17, 159–180.
66. J. Hasper, K. Welle, K. Swovick, J. Hryhorenko, S. Ghaemmaghami and A. Buchwalter, Long lifetime and tissue-specific accumulation of lamin A/C in Hutchinson-Gilford progeria syndrome, J. Cell Biol., 2024, 223(1), e202307049.
67. A. L. Olins, M. Zwerger, H. Herrmann, H. Zentgraf, A. J. Simon, M. Monestier and D. E. Olins, The human granulocyte nucleus: Unusual nuclear envelope and heterochromatin composition, Eur. J. Cell Biol., 2008, 87(5), 279–290.
68. C. M. Denais, R. M. Gilbert, P. Isermann, A. L. McGregor, M. te Lindert, B. Weigelin, P. M. Davidson, P. Friedl, K. Wolf and J. Lammerding, Nuclear envelope rupture and repair during cancer cell migration, Science, 2016, 352(6283), 353–358.
69. M. Raab, M. Gentili, H. de Belly, H. R. Thiam, P. Vargas, A. J. Jimenez, F. Lautenschlaeger, R. Voituriez, A. M. Lennon-Duménil, N. Manel and M. Piel, ESCRT III repairs nuclear envelope ruptures during cell migration to limit DNA damage and cell death, Science, 2016, 352(6283), 359–362.
70. C. T. Halfmann, R. M. Sears, A. Katiyar, B. W. Busselman, L. K. Aman, Q. Zhang, C. S. O'Bryan, T. E. Angelini, T. P. Lele and K. J. Roux, Repair of nuclear ruptures requires barrier-to-autointegration factor, J. Cell Biol., 2019, 218(7), 2136–2149.
71. H. R. Thiam, P. Vargas, N. Carpi, C. L. Crespo, M. Raab, E. Terriac, M. C. King, J. Jacobelli, A. S. Alberts, T. Stradal, A. M. Lennon-Dumenil and M. Piel, Perinuclear Arp2/3-driven actin polymerization enables nuclear deformation to facilitate cell migration through complex environments, Nat. Commun., 2016, 7, 10997.
72. A. D. Stephens, P. Z. Liu, E. J. Banigan, L. M. Almassalha, V. Backman, S. A. Adam, R. D. Goldman and J. F. Marko, Chromatin histone modifications and rigidity affect nuclear morphology independent of lamins, Mol. Biol. Cell, 2018, 29(2), 220–233.
73. C. E. Zimmerli, M. Allegretti, V. Rantos, S. K. Goetz, A. Obarska-Kosinska, I. Zagoriy, A. Halavatyi, G. Hummer, J. Mahamid, J. Kosinski and M. Beck, Nuclear pores dilate and constrict in cellulo, Science, 2021, 374(6573), eabd9776.
74. I. Andreu, I. Granero-Moya, N. R. Chahare, K. Clein, M. Molina-Jordan, A. E. M. Beedle, A. Elosegui-Artola, J. F. Abenza, L. Rossetti, X. Trepat, B. Raveh and P. Roca-Cusachs, Mechanical force application to the nucleus regulates nucleocytoplasmic transport, Nat. Cell Biol., 2022, 24(6), 896–905.
75. A. J. Lomakin, C. J. Cattin, D. Cuvelier, Z. Alraies, M. Molina, G. P. F. Nader, N. Srivastava, P. J. Saez, J. M. Garcia-Arcos, I. Y. Zhitnyak, A. Bhargava, M. K. Driscoll, E. S. Welf, R. Fiolka, R. J. Petrie, N. S. De Silva, J. M. Gonzalez-Granado, N. Manel, A. M. Lennon-Dumenil, D. J. Muller and M. Piel, The nucleus acts as a ruler tailoring cell responses to spatial constraints, Science, 2020, 370(6514), eaba2894.
76. K. Wolf, M. Te Lindert, M. Krause, S. Alexander, J. Te Riet, A. L. Willis, R. M. Hoffman, C. G. Figdor, S. J. Weiss and P. Friedl, Physical limits of cell migration: control by ECM space and nuclear deformation and tuning by proteolysis and traction force, J. Cell Biol., 2013, 201(7), 1069–1084.

---