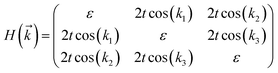Tunable Dirac cones in two-dimensional covalent organic materials: C₂N₆S₃ and its analogs

Abstract

Two-dimensional covalent organic frameworks (2D-COFs) are drawing increasing interest due to the unique configurations and exotic properties. Here, using density-functional theory calculations, we prove the stability of C₂N₆S₃ monolayer by an imagery-frequency-free phonon spectrum, and demonstrate a new ternary 2D-COF: C₂N₆O₃, C₂N₆Se₃ and C₂N₆Te₃ monolayers. The sawtooth-like linkages make the C₂N₆S₃ is soft, and sustain a biaxial tensile strain up to 24% which is as much as graphene. The electronic band structure exhibits linear dispersion near the Fermi level with a flat band right above the Dirac bands, which is unlike the other hexagonal organic monolayers with Dirac cone. The Fermi velocity is comparable to that in graphene and can be tuned by applying biaxial tensile strain. Similar results are also found in its analogs, such as C₂N₆O₃, C₂N₆Se₃ and C₂N₆Te₃ monolayers. This opens an avenue for the design of 2D Dirac materials.

---

1 Introduction

Dirac materials represent a family of materials which have linear energy–momentum dispersion relationships (namely Dirac cones) near the Fermi level. In this kind of electronic band structure, the valence and conduction bands meet at a single point (Dirac point). The low-energy excitation near the Dirac point behaves as massless Dirac fermions, and thus can be employed to mimic the properties of Dirac fermions in high-energy physics. The most representative two-dimensional (2D) Dirac material is graphene where the sp²-hybridized carbon atoms are arranged in a honeycomb lattice with superior mechanical properties arising from the strong covalent bonds.^1–3 The Dirac cones originate from the p_z orbitals which constitute a conjugated π orbital throughout the graphene. The carriers near the Dirac cones have ultrafast velocity (1/300 of velocity of light) which are quite promising for building high-speed nanoscaled electronic devices. Motivated by the great successes of graphene, considerable efforts have been devoted to search for new 2D Dirac materials. So far, a number of 2D materials have been predicted to possess Dirac cones in their electronic band structures without the spin–orbit coupling (SOC), such as graphene allotropes,^4–8 single-walled graphene hexagonal antidot lattice,⁹ silicene,¹⁰ germanene,¹¹ silicon carbide,^12,13 silicongermanide,¹⁴ conjugated polymer networks,^15–17 organometallic lattices,¹⁸ and etc.^19,20 These theoretical works enrich the database of 2D materials and promote the relevant experimental exploration.

Beside the honeycomb lattice like graphene, kagome lattice has also been predicted to have Dirac cones.²¹ In addition to the two Dirac bands, kagome lattices also have a topological flat band touching with the two Dirac bands at a single point.^18,22,23 Such a unique band alignment can host quantum spin Hall effects and fractional quantum Hall effects as the spin–orbit coupling (SOC) is taking into account. SOC opens band gaps at the Dirac point and between the flat band and the Dirac bands, both of which are topologically nontrivial characterized by nonzero topological invariants.^5,24 Moreover, the unique geometric frustration of kagome lattice may lead to spin-glass states.²⁵ Considerable efforts have been devoted to search for the 2D materials with this type of band alignments and lots of candidate materials have been proposed based on first-principles calculations.^26,27

Based on the early work of Whangbo et al. on the carbazidyl sesquisulphide,¹⁵ Adjizian et al. proposed a 2D framework of C₂N₆S₃ and demonstrated that it is a Dirac material.²⁸ Here we showed that this 2D covalent organic framework (COF) represents a new family of kagome materials with tunable electronic band structures. These 2D COFs have distorted kagome lattices containing sp²-hybridized carbon atoms connected by sulfur nitride (or N–O–N, N–Se–N, N–Te–N) linkages, as shown in Fig. 1. The sawtooth-like N–S–N linkages make the C₂N₆S₃ sustain a biaxial tensile strain up to 24%, which is much larger than graphene. Dirac cones appear at the corners of Brillouin zone with a flat band right above the Dirac bands, which obey the kagome tight-binding (TB) model. Fermi level is right at the Dirac point. The Dirac cones are robust against the biaxial tensile strain. The Fermi velocity is comparable to that in graphene and can be tuned by applying biaxial strain. Similar results are also found in its analogs: C₂N₆O₃, C₂N₆Se₃ and C₂N₆Te₃ monolayers. This work not only enriches the family the kagome materials, but also opens an avenue for the design of 2D materials with exotic properties.

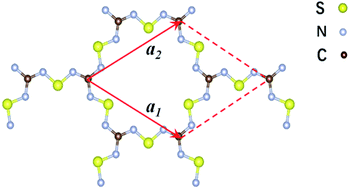Fig. 1 Schematic representation of the structure of the two-dimensional C₂S₃N₆ monolayer. The unit cell is indicated by the read lines with a₁ and a₂ being the lattice vectors.

2 Methods and computational details

We performed first-principles calculations in the framework of density-functional theory (DFT) using the Vienna ab initio simulation package known as VASP,^29–31 The electron–electron interactions were treated within a generalized gradient approximation (GGA) in the form of Perdew–Burke–Ernzerhof (PBE) for the exchange–correlation functional.³² The electron wave-functions were expanded by plane-waves with an energy cut-off of 530 eV. The electron–ion interaction was described by projector-augmented wave (PAW) potentials.^33,34 The supercells were repeated periodically on the x–y plane while a vacuum region of about 15 Å was applied to the z-direction to exclude the interaction between adjacent images. The Brillouin zone (BZ) integration was sampled on a gamma-centred Monkhorst–Pack (MP) using a 15 × 15 × 1 k-points. Structural optimizations were carried out using a conjugate gradient (CG) method until the remaining force on each atom is less than 0.01 eV Å⁻¹.

To evaluate the dynamical stability of C₂N₆S₃ monolayer structure, phonon dispersions were calculated based on the force-constant theory as embedded in phonopy program combined with the VASP code.^35–37 The stability of C₂N₆S₃ monolayer was also checked by annealing it at 300 K using the molecular dynamics simulations (MDS). A 4 × 4 supercell was adopted in the simulations. The MDS in NVT ensemble lasted for 2.5 ps with a time step of 0.5 fs. The temperature was controlled by using the Nose–Hoover method.³⁸

3 Results and discussion

The 2D C₂N₆S₃ considered in this work is composed of sp²-hybridized carbon atoms connected by sawtooth-like sulphur–nitride linkages, forming a planar configuration with a space group of P6̄2m. The optimized lattice constant is about 8.66 Å. The lengths of the C–N and N–S bonds are 1.36 Å and 1.59 Å respectively. The angle of the N–C–N is 120°, which is the standard value of sp²-hybridization, while the values of the C–N–S and N–S–N are respectively 119° and 102°. Noting that each unit cell has fourteen π-electrons totally, the conjugated flatten 2D framework thus has stable aromatic resonance according to the Hückel 4n + 2 π-electron count rule.³⁹ In addition, polysulfurnitride materials have been investigated and the plausibility has been confirmed,^40–44 suggesting the plausibility of the C₂N₆S₃ framework.

To evaluate the energetic stability of the C₂N₆S₃ monolayer, we calculated the formation energy (E_form) according to the hypothetic reaction:

4C (graphene) + 3S₄N₄ (crystal) → 2C₂N₆S₃ + 6S (crystal)

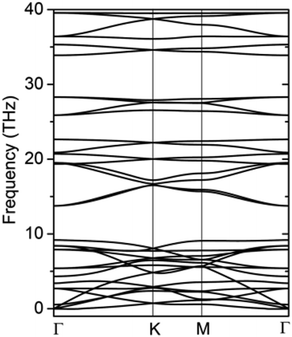
The formation energy calculated from the total energy difference between products and reactants is −13.54 kJ mol⁻¹, suggesting that the reaction is exothermic. This implies the energy favourability of the C₂N₆S₃ monolayer. The dynamic stability of the C₂N₆S₃ monolayer was also confirmed by the phonon spectrum calculated from the force-constant theory combined with the VASP code. The phonon dispersion relationships along highly-symmetric directions in BZ are plotted in Fig. 2. Clearly the phonon spectrum is free from imaginary frequencies, confirming the dynamic stability. Finally, we preformed MDS using a large supercell (4 × 4) at room temperature (300 K) to examine its thermal stability. It was found that the total energy of the system converged to a value within 2.5 ps without any structure decomposition. All these results indicate the stability and the synthetic possibility of the C₂N₆S₃ monolayer.

Fig. 2 The phonon spectrum of the C₂S₃N₆ monolayer along the highly-symmetric directions in the BZ.

The π-conjugated 2D materials like graphene were demonstrated to have unusual mechanical properties, e.g. high in-plane strength and transversal flexibility.⁴⁵ We therefore investigated the mechanical properties of C₂N₆S₃ monolayer using a rectangular supercell. A series of biaxial tensile stains varying from −1.5% to 1.5% were applied along the x- and y-directions. The profile of the strain energy (E_s) with respect to the x- and y-strains (ε_x and ε_y) is plotted in Fig. 3(a), which can be fitted using a quadratic polynomial expressed as: E_s = a₁ε_x² + a₂ε_y² + a₁ε_x²ε_y². The Poisson's ratio (v) and the in-plane stiffness (C) can then be evaluated using the formulae: υ_x = a₃/(2a₁), υ_y = a₃/(2a₂), C_x = [2a₁ − a₃²/(2a₁)]/A₀ and C_y = [2a₂ − a₃²/(2a₂)]/A₀, respectively. A₀ represents the area of the system at the equilibrium state. Our calculations showed that the difference between a₁ and a₂ is smaller than 0.02. Therefore, the Possion's ratio and in-plane stiffness along the x- and y-direction are almost identical, which are 0.68 and 23.85 J m⁻². The Possion's ratio is much larger than that (0.16) of graphene, but the in-plane stiffness of the 2D MOF is smaller than that of graphene (335 J m⁻²) by more than one order. Moreover, thanks to the sawtooth-like N–S–N linkages, the C₂N₆S₃ can sustain a biaxial tensile strain up to 24%, as shown in Fig. 3(b), which is larger than graphene.^46–48 With the increase of the tensile strain, both the bond length and bond angles increase. At a tensile strain of 24%, the lengths of the C–N and N–S bonds increase to 1.382 Å and 1.719 Å, while the bond angles of C–N–S and N–S–N attain 179° and 178°, respectively. The changes of bond angles in response to tensile strain is more significant than those of bond lengths.

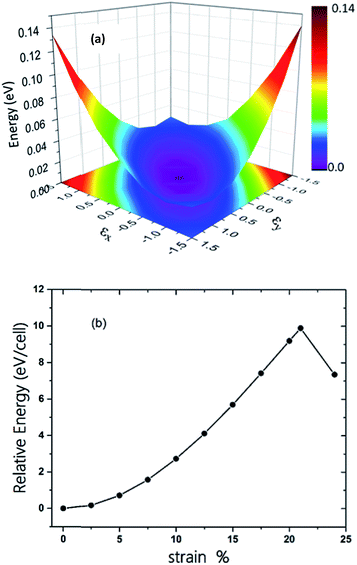Fig. 3 (a) The three-dimensional surface plots of strain energy versus uniaxial strain. (b) Energy of C₂S₃N₆ monolayer as a function of uniform biaxial strain.

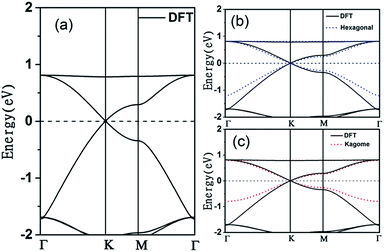
The electronic band structure of the C₂N₆S₃ monolayer is plotted in Fig. 4(a). There are obvious linear energy–momentum relations (Dirac cone) near the Fermi level, similar to the case of graphene. The Dirac cones locate at the six corners of the BZ with the Fermi level passing through the Dirac points, exhibiting the features of zero-band-gap semiconductors. The Fermi velocity near the Dirac point calculated from the slop of the band lines is about 5.29 × 10⁵ m s⁻¹, which is comparable to that of graphene (9.67 × 10⁵ m s⁻¹), implying high carrier mobility in the C₂N₆S₃ monolayer. Beside the Dirac cones, it is interesting to see the flat band right above the two Dirac bands. The width of the flat band is smaller than 0.028 eV. At the center of the BZ (Γ point), the flat band touches with the Dirac band at a single point. Such a band alignment is the signature of the kagome model.²¹

Fig. 4 (a) Electronic band structures of the C₂S₃N₆ monolayer obtained from DFT calculations (b) tight binding Hamiltonian in hexagonal model (hexagonal model is blue dotted lines), (c) tight binding in kagome (kagome model red dotted lines). The energy at the Fermi level was set to zero.

The tight-binding (TB) Hamiltonian of the standard kagome model in the momentum space can be written as:²²

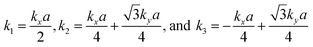with . The parameters ε and t represent the onsite energy and hopping energy of electron between adjacent sites. Both the flat band and two Dirac bands can be fitted by using the Hamiltonian with ε = t = 0.35 eV, as indicated by the dotted lines in Fig. 4(c), confirming the kagome nature of the lattice. The relatively large deviation of the TB bands to the DFT bands in the low energy region can be attributed to the atomic arrangement in the unit cell of the C₂S₂N₆ monolayer. For the standard kagome model, there are only three atoms in one unit cell.²⁴ The C₂N₆S₃ monolayer and its anologs, however, have eleven atoms in one unit cell. Some of the hoping were not taken into account in the TB Hamiltonian. The TB bands can be further improved by taking more atomic orbitals into account. We considered eleven p_z orbitals in one unit cell with different onsite energies and hopping energies between them. These atomic orbitals are arranged in the manner similar to the α-graphyne.⁴⁹ The obtained TB bands of this hexagonal lattice with the electron filling factor of 7/11 agree well with the DFT results, as shown in Fig. 4(b)

To reveal the origins of the Dirac bands and the flat band, we plotted the electron density of states (PDOS) projected onto the atomic orbitals of C, N and S atoms, as shown in Fig. 5. From this figure, we can clearly see that the electronic states in the proximate of the Fermi level arise mainly from the p_z orbitals of C, N and S atoms, while the contributions of other atomic orbital are neglectable. This is also consistent with the profile the electron wavefuctions of the three bands which exhibit clearly features of p_z atomic orbitals. The p_z orbitals in this framework form a π-conjugated system with a unique electronic band structure characterized by Dirac cones and a topological flat band.

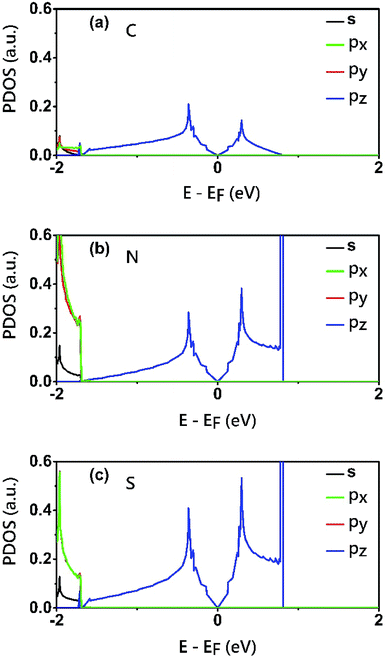Fig. 5 Electron density of states (PDOS) projected onto the atomic orbitals (s, p_x, p_y and p_z) of (a) C (b) N and (c) S atoms of the C₂S₃N₆ monolayer. The energy at the Fermi level was set to zero.

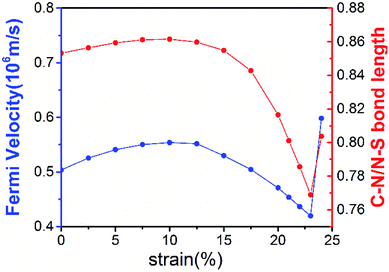
The robustness and tunability of the Dirac cones in response to strain were investigated. We applied uniform biaxial strain to the C₂N₆S₃ monolayer while keeping the hexagonal symmetry of the system. It was found that the both the Dirac cones and the flat band are robust again strain. However, the Fermi velocity can be tuned by strain, as shown in Fig. 6. With the increase of tensile strain, the Fermi velocity first increases to a maximum value of 5.92 × 10⁵ m s⁻¹ and then decreasing, which shows the same trend as the ratio of C–N/N–S bonds lengths. Such non-monotonous variation of Fermi velocity in response to external strain opens an avenue for tuning carrier mobility in 2D materials which is quite crucial for mechanical-electronic device applications.

Fig. 6 The Fermi velocities of the C₂X₃N₆ monolayer and the ratio of C–N bonds vs. N–S bonds under uniform biaxial strains. Fermi velocities is blue solid lines and ration of bonds is red solid lines.

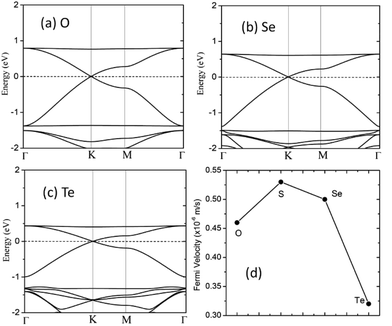
We also considered the analogs of the C₂N₆S₃ monolayer, C₂N₆X₃ with X = O, Se and Te. First-principles calculations showed that these C₂N₆X₃ have similar configurations as C₂N₆S₃ monolayer, except the slight difference in bond lengths and bond angles, as listed in Table 1. C₂N₆O₃, C₂N₆Se₃ and C₂N₆Te₃ monolayer has a planar configuration as C₂N₆S₃, these C₂N₆X₃ were found to have similar electronic band structures, as shown in Fig. 7. Both Dirac cones and a flat are well preserved, suggesting that they are the intrinsic properties of the lattices. The velocities of C₂N₆X₃ are slightly lower than that of C₂N₆S₃ monolayer but still comparable to that of graphene.

Table 1 Structure parameters and Fermi velocities (υ_F) of C₂X₃N₆ (with X = O, S, Se and Te) monolayer. d_C–N and d_N–X are the lengths of the C–N and N–X bonds. C–N–X and N–X–N are the bond angles, a is the length of the base vector, h is the buckling height. All the lengths are in angstroms and angles are in degrees

	dC–N	dN–X	C–N–X	N–X–N	a	h	υF (×10^6 m s^−1)
C2O3N6	1.366	1.370	110.1	111.0	7.951	0	0.46
C2S3N6	1.360	1.595	119.0	102.0	8.646	0	0.53
C2Se3N6	1.360	1.781	112.9	96.2	8.827	0	0.50
C2Te3N6	1.362	1.974	113.0	93.0	9.281	0	0.32

---

Fig. 7 (a–c) Electronic band structures of the C₂X₃N₆ monolayer with X = O, Se and Te. The energy at the Fermi level was set to zero. (d) The Fermi velocities of C₂S₃N₆ monolayer and its analogs at the equilibrium states.

4 Conclusions

Using first-principles calculations, we prove the stability of C₂N₆S₃ monolayer and propose its analogs. The sawtooth-like N–S–N linkages in the C₂N₆S₃ monolayer lead to exotic mechanical and electronic properties. C₂N₆S₃ is soft, which can sustain a biaxial tensile strain up to 24% as much as graphene. The electronic band structure in the proximate of Fermi level possesses the features of kagome model, i.e., Dirac cones at the cones of Brillouin zone with a flat band right above the Dirac bands. The Dirac cones are robust again the biaxial strain. The Fermi velocity is comparable to that in graphene and can be tuned by applying biaxial strain. Similar results are also found in its analogs: C₂N₆O₃, C₂N₆Se₃ and C₂N₆Te₃ monolayers. This work not only enriches the family the kagome materials, but also opens an avenue for the design of 2D materials with exotic properties.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work is supported by the National Natural Science Foundation of China (No. 21433006 and 11774201), the 111 project (No. B13029), the National Key Research and Development Program of China grant 2016YFA0301200, and the National Super Computing Centre in Jinan.

Notes and references

1. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669.
2. S. Z. Butler, S. M. Hollen, L. Cao, Y. Cui, J. A. Gupta, H. R. Gutierrez, T. F. Heinz, S. S. Hong, J. Huang, A. F. Ismach, E. Johnston-Halperin, M. Kuno, V. V. Plashnitsa, R. D. Robinson, R. S. Ruoff, S. Salahuddin, J. Shan, L. Shi, M. G. Spencer, M. Terrones, W. Windl and J. E. Goldberger, ACS Nano, 2013, 7, 2898–2926.
3. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, M. I. Katsnelson, I. V. Grigorieva, S. V. Dubonos and A. A. Firsov, Nature, 2005, 438, 197–200.
4. J. Chen, J. Xi, D. Wang and Z. Shuai, J. Phys. Chem. Lett., 2013, 4, 1443–1448.
5. M. Zhao, W. Dong and A. Wang, Sci. Rep., 2013, 3, 3532.
6. C. Gu, N. Huang, Y. Chen, L. Qin, H. Xu, S. Zhang, F. Li, Y. Ma and D. Jiang, Angew. Chem., Int. Ed., 2015, 54, 13594–13598.
7. L. C. Xu, R. Z. Wang, M. S. Miao, X. L. Wei, Y. P. Chen, H. Yan, W. M. Lau, L. M. Liu and Y. M. Ma, Nanoscale, 2014, 6, 1113–1118.
8. Z. Wang, X. F. Zhou, X. Zhang, Q. Zhu, H. Dong, M. Zhao and A. R. Oganov, Nano Lett., 2015, 15, 6182–6186.
9. F. Ouyang, S. Peng, Z. Liu and Z. Liu, ACS Nano, 2011, 5, 4023–4030.
10. D. Jose and A. Datta, J. Phys. Chem. C, 2012, 116, 24639–24648.
11. S. Cahangirov, M. Topsakal, E. Akturk, H. Sahin and S. Ciraci, Phys. Rev. Lett., 2009, 102, 236804.
12. M. Zhao, A. Wang and X. Zhang, Nanoscale, 2013, 5, 10404–10408.
13. X. Qin, Y. Liu, X. Li, J. Xu, B. Chi, D. Zhai and X. Zhao, J. Phys. Chem. Lett., 2015, 6, 1333–1339.
14. H. C. Zhou, M. W. Zhao, X. M. Zhang, W. Z. Dong, X. P. Wang, H. X. Bu and A. Z. Wang, J. Phys.: Condens. Matter, 2013, 25, 395501.
15. M. H. Whangbo, R. Hoffmann and R. B. Woodward, Proc. R. Soc. A, 1979, 366, 23–46.
16. M. Wu, Z. Wang, J. Liu, W. Li, H. Fu, L. Sun, X. Liu, M. Pan, H. Weng, M. Dincă, L. Fu and J. Li, 2D Mater., 2016, 4, 015015.
17. Y. Ma, Y. Dai, X. Li, Q. Sun and B. Huang, Carbon, 2014, 73, 382–388.
18. Z. F. Wang, Z. Liu and F. Liu, Nat. Commun., 2013, 4, 1471.
19. B. Wang, S. Yuan, Y. Li, L. Shi and J. Wang, Nanoscale, 2017, 9, 5577–5582.
20. F. Ma, Y. Jiao, G. Gao, Y. Gu, A. Bilic, Z. Chen and A. Du, Nano Lett., 2016, 16, 3022–3028.
21. H. M. Guo and M. Franz, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 113102.
22. X. Zhang, Z. Wang, M. Zhao and F. Liu, Phys. Rev. B, 2016, 93, 165401.
23. Z. F. Wang, N. Su and F. Liu, Nano Lett., 2013, 13, 2842–2845.
24. A. Wang, X. Zhang and M. Zhao, Nanoscale, 2014, 6, 11157–11162.
25. X. Liu, J. Tan, A. Wang, X. Zhang and M. Zhao, Phys. Chem. Chem. Phys., 2014, 16, 23286–23291.
26. M. Zhou, Z. Liu, W. Ming, Z. Wang and F. Liu, Phys. Rev. Lett., 2014, 113, 236802.
27. J.-L. Lu, W. Luo, X.-Y. Li, S.-Q. Yang, J.-X. Cao, X.-G. Gong and H.-J. Xiang, Chin. Phys. Lett., 2017, 34, 057302.
28. J. J. Adjizian, P. Briddon, B. Humbert, J. L. Duvail, P. Wagner, C. Adda and C. Ewels, Nat. Commun., 2014, 5, 5842.
29. J. P. Perdew and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 5048–5079.
30. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
31. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
32. C. L. Kane and E. J. Mele, Phys. Rev. Lett., 2005, 95, 226801.
33. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
34. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
35. A. Togo, F. Oba and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 134106.
36. J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2006, 124, 219906.
37. P. E. Trevisanutto, C. Giorgetti, L. Reining, M. Ladisa and V. Olevano, Phys. Rev. Lett., 2008, 101, 226405.
38. G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
39. A. P. Cote, A. I. Benin, N. W. Ockwig, M. O'Keeffe, A. J. Matzger and O. M. Yaghi, Science, 2005, 310, 1166–1170.
40. G. H. Zhang, Y. F. Zhao, J. I. Wu and P. V. R. Schleyer, Inorg. Chem., 2012, 51, 13321–13327.
41. D. Li, F. Tian, Y. Lv, S. Wei, D. Duan, B. Liu and T. Cui, J. Phys. Chem. C, 2017, 121, 1515–1520.
42. M. Taki, K. Akaoka, S. Iyoshi and Y. Yamamoto, Inorg. Chem., 2012, 51, 13075–13077.
43. J. E. Padilha, A. Fazzio and A. J. R. da Silva, J. Phys. Chem. C, 2014, 118, 18793–18798.
44. A. Hamza and H. W. Roesky, Angew. Chem., Int. Ed., 1976, 15, 226.
45. H. Şahin, S. Cahangirov, M. Topsakal, E. Bekaroglu, E. Akturk, R. T. Senger and S. Ciraci, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 155453.
46. V. M. Pereira, A. H. Castro Neto and N. M. R. Peres, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 045401.
47. S.-M. Choi, S.-H. Jhi and Y.-W. Son, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 081407.
48. Y. Zhang and F. Liu, Appl. Phys. Lett., 2011, 99, 241908.
49. X. Qin, Y. Liu, B. Chi, X. Zhao and X. Li, Nanoscale, 2016, 8, 15223–15232.

---