Rational design of a series of non-centrosymmetric antiperovskite and double antiperovskite borate fluorides

Abstract

Non-centrosymmetric (NCS) compounds can exhibit many symmetry-dependent functional properties, yet their rational structure design remains a great challenge. Herein, a strategy to introduce F-centered octahedra to construct a perovskite-type framework filled by π-conjugated [B₂O₅]⁴⁻ dimers is proposed to obtain NCS compounds. The first examples of antiperovskite or double antiperovskite borate fluorides, [(M/Ba)₂Ca]F[B₂O₅] (M = K, Rb) and [CsBaCa]F[B₂O₅], have been successfully designed and synthesized. All three compounds exhibit a novel three-dimensional framework constructed from [F(M/Ba)₄Ca₂] (M = K, Rb), [FCs₄Ca₂] and [FBa₄Ca₂] octahedra, which are further filled by [B₂O₅]⁴⁻ dimers to form antiperovskite-type structures. They all crystallize in the NCS space group P4̄2₁m, and can exhibit moderate second harmonic generation (SHG) responses (∼0.5 × KDP@1064 nm) and short UV cut-off edges (∼190 nm), as well as suitable birefringence (Δn = 0.0405–0.0548@532 nm). This suggests their potential as UV nonlinear optical crystals.

---

Introduction

Non-centrosymmetric (NCS) structures capable of exhibiting many symmetry-dependent properties, such as piezoelectric, ferroelectric, and second-order nonlinear optical (NLO) properties, are of the current academic and technological interest.¹ In particular, NCS borates have been widely applied as ultraviolet (UV) or even deep-UV NLO crystals.^2–6 However, the rational synthesis of new NCS structures remains an important ongoing challenge for chemists and experimentalists due to the weak predictability of the structure of inorganic materials. During past decades, some widely-used strategies for increasing the odds of generating NCS structures through introducing special cations with inherent asymmetric coordination environments or asymmetric anionic groups have been put forward, such as (i) the use of cations susceptible to second-order Jahn–Teller (SOJT) distortions, i.e., high-valent d⁰ transition metal cations in an octahedral coordination environment (Ti⁴⁺, V⁵⁺, Nb⁵⁺, Mo⁶⁺, W⁶⁺, etc.) and cations possessing stereochemically active lone pairs (Pb²⁺, Sb³⁺, Bi³⁺, Se⁴⁺, Te⁴⁺, I⁵⁺, etc.);^7,8 (ii) the use of d¹⁰ transition metal cations revealing highly polar displacement in the center of the coordination environment (Zn²⁺, Cd²⁺, etc.);⁹ and (iii) the use of anions with trigonal-planar geometry exhibiting asymmetric π-conjugated molecular orbitals ([NO₃]⁻, [CO₃]²⁻, [BO₃]³⁻, etc.).^10–14 In addition, it is impressive that a series of polar small molecule compounds with excellent NLO response have been successfully designed through introducing a chiral backbone to a dipolar molecule.¹⁵ However, the majority of solid-state materials still crystallize in centrosymmetric (CS) structures because the locally asymmetric basic building units (BBUs) are more likely packed in structures in an antiparallel manner that can increase the local electroneutrality and is more energetically favorable according to Pauling's second rule.¹⁶ Therefore, exploring new strategies for controlling the orientation of acentric BBUs in structures will be essential for the design of new NCS compounds.

The perovskite template is considered the most important and typical inorganic structural template. Its structural stability can be well predicted by the tolerance factor t (t = (r_A + r_X)/2(r_B + r_X)).¹⁷ With perovskite as the template, over 100 000 perovskite-type structures have been designed and synthesized in many different fields, such as catalysis, photovoltaics, luminescence, etc.^18,19 Beyond the perovskite template, we have noticed that antiperovskites are also a new interesting materials class, especially for the design of NCS structures. First, structurally, antiperovskite structures are isomorphic to perovskite ones. Therefore their structural stability can also be predicted by the tolerance factor t. Next, the structural frameworks of antiperovskites are generally constructed from modifiable ionic octahedra, and the rigid anion groups are filled in the voids of octahedral ionic frameworks.²⁰ Thus, the orientation and distortion of the anion groups are easier to control or modulate in antiperovskite structures. Based on this, a series of NCS antiperovskite structures have been designed and synthesized in recent research, including M₃X[B₆O₁₀] (M = K, Na/Rb; X = Cl, Br),²¹ Sr₃[CO₃][SnOSe₃],²² Ae₃Q[GeOQ₃] (Ae = Ba, Sr; Q = S, Se),²³etc. Clearly, these compounds all exhibit intriguing symmetry-dependent NLO properties. In particular, K₃Cl[B₆O₁₀] and K₃Br[B₆O₁₀] have been widely studied as promising UV NLO crystals.

In this research, we are also interested in the NCS antiperovskite borates because of their potential applications as UV or even deep-UV NLO crystals. As NLO crystals, a basic structural requirement, besides those of NCS structures, is that materials must be optically anisotropic to achieve phase-matching,²⁴i.e. materials must crystallize in a non-cubic system. Therefore, mixed-cation-coordinated octahedra will be the best choices. Meanwhile, we have realized that borate-fluorides have more advantages than borate-chlorides/bromides for NLO crystals.²⁵ However, to date there have been few perovskite or antiperovskite borate-fluorides reported. Therefore, we chose the F⁻ anion as the center of octahedra of antiperovskite structures. With this in mind, we introduced F-centered [F(M/Ba)₄Ca₂] (M = K, Rb, Cs) octahedra to construct the antiperovskite structural framework. Then, in order to further increase the anisotropy of the structures, we filled the voids of the octahedral framework with π-conjugated [B₂O₅]⁴⁻ groups. By doing this, two new NCS antiperovskite borate-fluorides, [(M/Ba)₂Ca]F[B₂O₅] (M = K, Rb), and one double antiperovskite borate-fluoride, [CsBaCa]F[B₂O₅], were successfully designed and synthesized for the first time. Unexpectedly, the structural change from antiperovskite to double antiperovskite is caused by simple cation substitution, which is certainly exciting and worth studying. Therefore, in this communication, we will focus on finding the reasons for the structural transformation, hoping to provide ideas for the design of new antiperovskite structures. We will also report their syntheses, structures, and functional properties as well as first-principles calculation.

Results and discussion

Polycrystalline samples of [(M/Ba)₂Ca]F[B₂O₅] (M = K, Rb) and [CsBaCa]F[B₂O₅] were all synthesized via conventional solid-state reactions. Stoichiometric MF (M = K, Rb, Cs), BaCO₃, CaCO₃ and H₃BO₃ were thoroughly mixed and preheated at 300 °C for 24 h to decompose carbonates and boric acid. Then, the temperature was gradually increased to 700 °C and held for 72 h with several intermediate grindings and mixings. By doing this, the pure polycrystalline samples of [(M/Ba)₂Ca]F[B₂O₅] (M = K, Rb) and [CsBaCa]F[B₂O₅] can be obtained, and their purity can be confirmed by powder X-ray diffraction (PXRD) (Fig. S1†). For these polycrystalline samples, the thermal behaviors were studied by thermogravimetric (TG) and differential scanning calorimetry (DSC) measurements (Fig. S2a–c†). Clearly, for the three compounds, the heating DSC curves show sharp endothermic peaks at 1000 °C, 988 °C and 904 °C, accompanied by obvious weight loss in the TG curves. This suggests [(M/Ba)₂Ca]F[B₂O₅] (M = K, Rb) and [CsBaCa]F[B₂O₅] melt incongruently. Furthermore, the PXRD measurements show the residue after TG/DSC is mainly Ba₂Ca(BO₃)₂ (PDF #01-085-2268) and Ca₃(BO₃)₂ (PDF #01-070-0868) (Fig. S2d–f†). This indicates [(M/Ba)₂Ca]F[B₂O₅] (M = K, Rb) and [CsBaCa]F[B₂O₅] decomposed before melting. Therefore, a suitable flux is necessary for their single-crystal growth. With 2B₂O₃:0.65M₂O (M = K, Rb, Cs) as the self-flux, single crystals (yields, about 80%, 85% and 90% based on Ba for [(K/Ba)₂Ca]F[B₂O₅], [(Rb/Ba)₂Ca]F[B₂O₅] and [CsBaCa]F[B₂O₅], respectively) were also obtained in the open air around 780 °C, 750 °C and 720 °C for K-, Rb- and Cs-based compounds, respectively. The crystallographic data are listed in Table 1. The related crystal data, including selected bond lengths and atomic coordinate equivalent isotropic displacement parameters, are listed in Tables S2–S6 in the ESI.†

Table 1 Single crystal data and structure refinement for [(M/Ba)₂Ca]F[B₂O₅] (M = K, Rb) and [CsBaCa]F[B₂O₅]

Empirical formula	[(K/Ba)2Ca]F[B2O5]	[(Rb/Ba)2Ca]F[B2O5]	[CsBaCa]F[B2O5]
a R 1 = ∑‖Fo| – |Fc‖/∑|Fo| and wR2 = [∑w(Fo^2 − Fc^2)^2/∑wFo^4]^1/2 for Fo^2 > 2σ(Fo^2).
Formula weight	337.14	383.51	430.95
Crystal system	Tetragonal	Tetragonal	Tetragonal
Space group	P4̄21m (113)	P4̄21m (113)	P4̄21m (113)
a (Å)	8.7276(1)	8.7713(3)	8.8668(4)
c (Å)	4.2840(9)	4.3173(3)	8.7669(4)
Z	2	2	4
Volume (Å^3)	326.32(1)	332.15(3)	689.26(7)
F (000)	308	344	760
Completeness (%)	100.0%	100.0%	98.8%
Absolute structure parameter	0.18(1)	0.17(5)	0.31(8)
Goodness-of-fit on F^2	1.076	1.088	1.085
Final R indices [(I > 2σ(I)]^a	R 1 = 0.0401 wR2 = 0.1018	R 1 = 0.0375 wR2 = 0.1016	R 1 = 0.0455 wR2 = 0.1382
R indices (all data)^a	R 1 = 0.0506 wR2 = 0.1105	R 1 = 0.0434 wR2 = 0.1082	R 1 = 0.0504 wR2 = 0.1491

---

The single-crystal XRD shows [(M/Ba)₂Ca]F[B₂O₅] (M = K, Rb) and [CsBaCa]F[B₂O₅] all crystallize in the NCS space group P4̄2₁m. Remarkably, [(Rb/Ba)₂Ca]F[B₂O₅] and [(K/Ba)₂Ca]F[B₂O₅] are iso-structural, but they are not iso-structural with [CsBaCa]F[B₂O₅]. Therefore, only the structures of [(Rb/Ba)₂Ca]F[B₂O₅] and [CsBaCa]F[B₂O₅] will be described in detail.

For [(Rb/Ba)₂Ca]F[B₂O₅], the asymmetric unit contains one unique Rb/Ba (the Rb⁺ cations and the Ba²⁺ cations are disordered and occupy the same 4e Wyckoff position with 50% and 50% occupation, respectively), one Ca (Wyckoff position 2b), one B (Wyckoff position 4e), one F (Wyckoff position 2a) and two O (Wyckoff position 2c and 2f) atom(s). Each B atom is coordinated with three O atoms forming BO₃ triangles, and two BO₃ triangles further condensed into [B₂O₅]⁴⁻ dimers (Fig. 1b) with B–O distances in the range of 1.352(17)–1.378(14) Å. The F⁻ anion is surrounded by four Rb/Ba and two Ca cations to form the [F(K/Ba)₄Ca₂] octahedron (Fig. 1a) with Rb⁺/Ba²⁺ cations occupying four equator positions and Ca²⁺ cations occupying the apical position. The Rb/Ba–F and Ca–F distances are 3.1745(2) Å and 2.15865(15) Å, respectively. In the structure, the [F(Rb/Ba)₄Ca₂] octahedra connect with each other through corner-sharing to form the [F(Rb/Ba)₂Ca]_∞ octahedral framework (Fig. 1c). The [B₂O₅]⁴⁻ dimers are fixed into the spaces of the [F(Rb/Ba)₂Ca]_∞ octahedral framework (Fig. 1d) by the Rb/Ba–O bonds with distances ranging from 2.899(14) to 3.329(11) Å and all Ca–O distances are identical at 2.311(10) Å. Clearly, [(Rb/Ba)₂Ca]F[B₂O₅] exhibits an antiperovskite structure with the [B₂O₅]⁴⁻ and F⁻ anions, and Rb⁺/Ba²⁺ and Ca²⁺ cations occupying A-, B- and X-sites of the perovskite, respectively. Its crystal structure is also analogous with the antiperovskite aluminate fluoride, Sr₃F[AlO₄].²⁶ As shown in Fig. 1e and f, the positions of [AlO₄]⁵⁻ anions are occupied by the isolated [B₂O₅]⁴⁻ groups and the positions of Sr²⁺ cations are occupied by Rb⁺/Ba²⁺ and Ca²⁺ cations. Furthermore, the calculations of bond valence indicate that the coordination numbers of the corresponding atoms are reasonable (Tables S1 and S2†).

Fig. 1 (a) The [F(Rb/Ba)₄Ca₂] F-centered octahedra; (b) the B–O skeleton in [(Rb/Ba)₂Ca]F[B₂O₅]; (c) the three-dimensional [F(Rb/Ba)₂Ca]_∞ octahedral framework; (d) the view of [(Rb/Ba)₂Ca]F[B₂O₅] along the c-axis; (e and f) the analogy between the antiperovskite-type structure of [(Rb/Ba)₂Ca]F[B₂O₅] and the antiperovskite structure of Sr₃F[AlO₄].

For [CsBaCa]F[B₂O₅], the asymmetric unit contains one crystallographically independent Cs (Wyckoff position 4e), one Ba (Wyckoff position 4e), one Ca (Wyckoff position 4d), two B (Wyckoff position 4e), two F (Wyckoff position 2a and 2b) and four O (Wyckoff position 2c and 8f) atom(s). All the B atoms are condensed into [B₂O₅]⁴⁻ dimers (Fig. 2b) with B–O distances in the range of 1.317(11)–1.490(19) Å. The F(1)⁻ and F(2)⁻ anions are surrounded by four Ba²⁺ or Cs⁺ and two Ca²⁺ cations to form [F(1)Ba₄Ca₂] and [F(2)Cs₄Ca₂] octahedra, respectively (Fig. 2a). The Cs–F and Ca–F distances are in the range of 3.2012(2) to 3.1999(2) Å, and 2.1521(18) to 2.2313(18) Å, respectively. The Ba–F distances are identical, at 3.1999(6) Å. In the structure, the [FBa₄Ca₂] and [FCs₄Ca₂] octahedra connect with each other through corner-sharing to form the [FCsBaCa]_∞ octahedral framework (Fig. 2c) filled by the [B(1)₂O₅]⁴⁻ and [B(2)₂O₅]⁴⁻ dimers to form the antiperovskite structure (Fig. 2d). Clearly, this structure has two different anionic groups at the A site, which is similar to the double antiperovskite Li₆NBrBr₂ (Fig. 2f) with two different anions (N and Br) at the B-site. Hence, the structure can also be written as the double antiperovskite formula [CsBaCa]₂F₂[B(1)₂O₅][B(2)₂O₅]. [CsBaCa]F[B₂O₅] is also the first reported double antiperovskite borate-fluoride. Furthermore, for the Cs–O, Ba–O and Ca–O bonds, the bond distances range from 3.029(11) to 3.444(10) Å, 2.765(8) to 2.972(9) Å and 2.320(9) to 2.345(9) Å, respectively. These bond distances are consistent with those reported in other compounds.^11a,27 Bond valence sum (BVS) calculations are shown in Table S3.† The BVS indicates that the coordination numbers of corresponding atoms are reasonable.

Fig. 2 (a) The [FBa₄Ca₂] and [FCs₄Ca₂] F-centered octahedra; (b) the B–O skeleton in [CsBaCa]F[B₂O₅]; (c) the three-dimensional [FCsBaCa]_∞ octahedral framework; (d) the view of [CsBaCa]F[B₂O₅] along the c-axis; (e and f) the analogy between the double antiperovskite-type structure of [CsBaCa]F[B₂O₅] and the double antiperovskite structure of Li₆NBrBr₂.

From the chemical formulae, it can be seen that on going from [(Rb/Ba)₂Ca]F[B₂O₅] to [CsBaCa]F[B₂O₅], the substitution of Rb⁺ by Cs⁺ cations results in a different configuration of F-based octahedra and the structure transforms from the antiperovskite to the double antiperovskite structure. For their lattice parameters, the length the of crystallographic c-axis of [CsBaCa]F[B₂O₅] is almost twice that of [(Rb/Ba)₂Ca]F[B₂O₅], and the remaining lengths are nearly equal in the two structures (Table 1). This difference may be considered an effect of the cation sizes. As the cation radius on the X sites (equator positions) changes from Rb⁺ (1.69 Å) to Cs⁺ (1.85 Å),²⁸ it will inevitably lead to an increase in the volume of the [F(M/Ba)Ca]_∞ framework, which is equivalent to an increase in the effective radius of the anion F⁻ at the B site. According to the Goldschmidt tolerance factor t = (r_A + r_X)/2(r_B + r_X), where r_A, r_B and r_X are the effective radii of ions/groups at the A, B and X sites, in order to maintain the stability of the structure, the effective radius of the anionic group [B₂O₅]⁴⁻ located at the A site also needs to be increased. That is to say, the [B₂O₅]⁴⁻ dimers will be stretched. That results in an increase of the bond distances between the B atoms and the bridging O atom. As shown in Fig. 3a, the distances between the B atoms and the bridging O atom in [CsBaCa]F[B₂O₅] clearly increased to 1.45(2) and 1.49(19) Å (Table S7†). This means that the bridging O obtains less electrovalence from the B atoms, that is, the O atom needs to obtain more electrovalence from the cation at the X sites to ensure that its valence state is within the normal range. Therefore, the bridging O atoms need to bond with Cs⁺ cations with short Cs–O distances (3.029(11) Å) or directly coordinate with higher valence Ba²⁺ cations to increase the BVS (Fig. 3b). Thanks to the different coordination manners of bridging O atoms, the Cs⁺ and Ba²⁺ cations on the X sites no longer occupy the 4e Wyckoff position in the disordered manner of Rb⁺/Ba²⁺ in [(Rb/Ba)₂Ca]F[B₂O₅], but instead occupy the 4e Wyckoff position separately. This coordination mode results in the formation of different F-based octahedra in the c-axis direction, further resulting in different cavities filled by two kinds of [B₂O₅]⁴⁻ dimers (Fig. 3c). We also noticed that with the substitution of Cs⁺ for Rb⁺, the dihedral angle of the [B₂O₅]⁴⁻ (the angle between two BO₃ groups) decreased from 52.176° to 47.878° and 39.667° due to the stretching of the [B₂O₅]⁴⁻ dimers.

Fig. 3 The evolution from the antiperovskite structure [(Rb/Ba)₂Ca]F[B₂O₅] to the double antiperovskite [CsBaCa]F[B₂O₅]. (a) The stretching of the [B₂O₅]⁴⁻ dimer leads to an increase in the distances between the bridging O atom and B atoms; (b) the bridging O atoms coordinate with Cs and Ba, instead of coordinating with disordered Rb/Ba in the [(Rb/Ba)₂Ca]F[B₂O₅] structure; (c) the A site of the [(Rb/Ba)₂Ca]F[B₂O₅] and [CsBaCa]F[B₂O₅] structures is occupied by one and two different sized [B₂O₅]⁴⁻ dimers, respectively; (d) the dihedral angle of the [B₂O₅]⁴⁻ (the angle between two BO₃ units) decreased from 52.176° to 47.878° and 39.667°.

In addition, it is clear that the octahedral frameworks for [(Rb/Ba)₂Ca]F[B₂O₅] to [CsBaCa]F[B₂O₅] are distorted as can be seen from the F-M/Ba–F (M = Rb, Cs) bond angles (Table 2), which are much lower than 180°.²⁹ According to Glazer's notation,³⁰ their tilt systems can all be written as a⁰a⁰c⁺. Additionally, their octahedral rotation angles φ along the c-axis are 12.34° (for [(Rb/Ba)₂Ca]F[B₂O₅]) (Fig. S3a†), and 11.57° (for [CsBaCa]F[B₂O₅]) (Fig. S3b†). Clearly, when going from antiperovskite [(Rb/Ba)₂Ca]F[B₂O₅] to double antiperovskite [CsBaCa]F[B₂O₅], the octahedral rotation angles are slightly reduced. These indicate that on going from antiperovskite [(Rb/Ba)₂Ca]F[B₂O₅] to double antiperovskite [CsBaCa]F[B₂O₅], the strain can be further alleviated. To further evaluate the stability of [(M/Ba)₂Ca]F[B₂O₅] (M = K,Rb) and [CsBaCa]F[B₂O₅], the bond strain index (BSI) and global instability index (GII) were also calculated (Table 2).³¹ Generally, BSI and GII values imply the strain caused by electronic-induced and lattice-induced strains, respectively. The BSI values of the three title compounds are larger than 0.05 vu, indicating that they are all strained. In addition, the GII values are 0.223 vu, 0.260 vu, and 0.116 vu for K-, Rb-, and Cs-based compounds, respectively. According to Salinas-Sanchez's report,^31b GII values of around 0.2 are considered highly strained and unstable and 0.1 is considered stable, which indicates that when the structure transforms from the antiperovskite to the double antiperovskite, the electronic-induced and lattice-induced strains can be released with a decrease in the BSI and GII values. As a result, the structure changes from antiperovskite [(Rb/Ba)₂Ca]F[B₂O₅] to double antiperovskite [CsBaCa]F[B₂O₅] with the substitution of Rb⁺ by Cs⁺ cations.

Table 2 Bond valence sum (BVS), bond strain index (BSI), global instability index (GII), and angle of F–M/Ba–F (M = K, Rb, Cs) for [(M/Ba)₂Ca]F[B₂O₅] (M = K, Rb) and [CsBaCa]F[B₂O₅]

Compound	BVS			BSI (vu)	GII (vu)	Angle of F–M/Ba–F (°)
	M0.5Ba0.5	Cs and Ba	B
[(K/Ba)2Ca]F[B2O5]	1.32		3.25	0.102	0.223	154.20
(Rb/Ba)2Ca]F[B2O5]	1.26		3.01	0.111	0.260	155.32
[CsBaCa]F[B2O5]		0.98 and 1.87	2.97–3.03	0.084	0.116	156.64

---

Furthermore, the existence of the [B₂O₅]⁴⁻ groups was also confirmed by infrared spectra. As shown in Fig. 4a, the peaks in the range of 1348 cm⁻¹ to 1207 cm⁻¹ for the three compounds can be assigned to the asymmetric stretching of [BO₃]³⁻ units. The peaks around 1054–1106 cm⁻¹ may be associated with the stretching vibration of B–O–B in [B₂O₅]⁴⁻ groups. The weak absorption bands are assigned to the asymmetric stretching of [BO₃]³⁻ units. The peaks around 1054–1106 cm⁻¹ may be associated with the stretching vibration of B–O–B in [B₂O₅]⁴⁻ groups. The weak absorption bands at 1010–808 cm⁻¹ can be attributed to the [BO₃]³⁻ symmetric stretching vibrations. In addition, the absorption bands around 748–596 cm⁻¹ may be caused by the out-of-plane bending of the [BO₃]³⁻ groups. All of these are consistent with other reported borates.^27,32

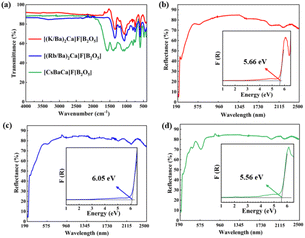Fig. 4 (a) The infrared spectra of the title compounds; the UV-Vis diffuse reflectance spectra and optical band gaps of [(K/Ba)₂Ca]F[B₂O₅] (b), [(Rb/Ba)₂Ca]F[B₂O₅] (c), and [CsBaCa]F[B₂O₅] (d).

The UV-vis-NIR diffuse reflectance spectra of [(M/Ba)₂Ca]F[B₂O₅] (M = K, Rb) and [CsBaCa]F[B₂O₅] are shown in Fig. 4b–d. It is clear that the three compounds exhibit wide UV transparent regions with UV cut-off edges around 190 nm. Based on the Kubelka–Munk function,^33a the reflectance was converted into absorption. Extrapolating the linear part of the rising curve of absorption to zero, band-gaps of 5.68, 6.05, and 5.56 eV were obtained for [(M/Ba)₂Ca]F[B₂O₅] (M = K, Rb) and [CsBaCa]F[B₂O₅], respectively.

Since [(M/Ba)₂Ca]F[B₂O₅] (M = K, Rb) and [CsBaCa]F[B₂O₅] all crystallize in NCS structures, their SHG responses were also measured by the Kurtz and Perry technique.^33b Plots of the SHG intensity versus particle sizes for ground polycrystalline samples of [(M/Ba)₂Ca]F[B₂O₅] (M = K, Rb) and [CsBaCa]F[B₂O₅] are shown in Fig. 5a. Detailed features of those curves indicate that all three crystals are phase-matchable (PM). The comparison of the SHG signal produced by the [(M/Ba)₂Ca]F[B₂O₅] (M = K, Rb) and [CsBaCa]F[B₂O₅] polycrystalline samples and the KDP samples in the same particle sizes (180–200 μm) reveals that they exhibit moderate SHG responses, ∼0.50, 0.44, and 0.39 × KDP, respectively (Fig. 5b). Clearly, these SHG responses are smaller than expected. According to the anionic group theory,^33c the relatively small SHG responses should be mainly attributed to the non-aligned arrangement of the [B₂O₅]⁴⁻ groups. In order to better understand the effect of orientation of [B₂O₅]⁴⁻ groups on SHG responses, we calculated their dipole moments in the unit cell with a simple bond-valence approach.^33d As shown in Table S8,† the dipole moments generated by the [B₂O₅]⁴⁻ groups are largely cancelled in the unit cell. In addition, it should be noted that from Cs-, to Rb- to K-homologues, the SHG responses gradually increase. In order to better understand these, the number density of [B₂O₅]⁴⁻ and the empirical ‘flexibility index’ F were also calculated (Table S9†).^33e The calculation results indicate that the number density and F of [B₂O₅]⁴⁻ groups in [(K/Ba)₂Ca]F[B₂O₅] are the highest, followed by [(Rb/Ba)₂Ca]F[B₂O₅] and [CsBaCa]F[B₂O₅], which is consistent with the experimental results of SHG responses.

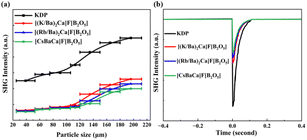Fig. 5 (a) The particle size dependence of SHG intensities for the title compounds and KDP as a reference; (b) the SHG signals for the three title compounds and KDP for exact particle sizes.

The birefringence is also important for materials to achieve PM in a wide spectral region, so the birefringence of [(M/Ba)₂Ca]F[B₂O₅] (M = K, Rb) and [CsBaCa]F[B₂O₅] was also measured through cross polarization microscopy based on the formula R = Δn × d, where R, Δn, and d represent the optical path difference, birefringence, and thickness, respectively.^33f Fig. S4† shows the original interference colour and the thickness measured on a Bruker single crystal diffractometer. The observed interference colours in cross-polarized light were second-order green for the title compounds, and matching with the Michal–Levy chart, the retardations (R values) were found to be 800 nm. The crystal thicknesses were found to be 17.1, 17.0, and 19.2 μm for [(M/Ba)₂Ca]F[B₂O₅] (M = K, Rb) and [CsBaCa]F[B₂O₅], respectively. Therefore, the birefringence values were determined to be 0.046, 0.052 and 0.041, respectively. Clearly, the birefringence is consistent with the calculated values based on first principles calculations (Fig. 6), and is comparable with other UV borate NLO crystals, such as LiB₃O₅ (0.0427@532 nm),^2c CsLiB₆O₁₀ (0.050@532 nm)^3c and Ba₃Mg₃(BO₃)₃F₃ (0.045@532 nm),³⁴ indicating the potential as UV NLO crystals.

Fig. 6 Calculated birefringence for [(M/Ba)₂Ca]F[B₂O₅] (M = K, Rb) and [CsBaCa]F[B₂O₅].

In order to further understand the origin of the optical and NLO properties of the title compounds, their electronic structures were analysed by first principles calculations based on density functional theory (DFT).³⁵ The results show that [(M/Ba)₂Ca]F[B₂O₅] (M = K, Rb) and [CsBaCa]F[B₂O₅] are all indirect band-gap compounds with calculated band gaps of 3.86, 5.55, and 3.95 eV, respectively (Fig. S5a–c†). The smaller calculated band-gaps than experimental ones can be attributed to the underestimation of the DFT method.³⁶ The partial densities of states (PDOS) projected on the constituent atoms of [(M/Ba)₂Ca]F[B₂O₅] (M = K, Rb) and [CsBaCa]F[B₂O₅] are given in Fig. S5d–f.† Clearly, for [(M/Ba)₂Ca]F[B₂O₅] (M = K, Rb), the top of the valence band (VB) in the region of −8 eV to the Fermi level is dominated by O 2p, B 2p, and F 2p orbitals with partial contributions of B 2s, and the upper two peaks of the VB between 0 and −2 eV mainly consist of O 2p and B 2p orbitals. The conduction band (CB) above the Fermi level is dominated by O 2p and B 2p orbitals with partial contributions of Ba 5d and Ca 3d orbitals, and the bottom of the CB mostly consists of O 2p and B 2p orbitals. For [CsBaCa]F[B₂O₅], the valence band maximum (VBM) is also mostly from the O 2p, B 2p and F 2p orbitals, with a small amount of O 2s and B 2s orbitals. The conduction band minimum (CBM) is mainly dominated by the O 2p and B 2p orbitals, with a small amount of Ca 3d and Ba 5d orbitals. It is obvious that the electronic states of the B atom are fully overlapped with the O atom in the energy region near the Fermi level, showing the strong interactions of B–O in the three compounds. These results indicate that the [B₂O₅]⁴⁻ group makes the main contribution to the optical properties of [(M/Ba)₂Ca]F[B₂O₅] (M = K, Rb) and [CsBaCa]F[B₂O₅].

Based on the electronic structures, the SHG coefficients were also calculated. Since [(M/Ba)₂Ca]F[B₂O₅] (M = K, Rb) and [CsBaCa]F[B₂O₅] crystallize in the space group P4̄2₁m, belonging to the point group 4̄2m, they all have the only independent non-zero SHG coefficient, d₃₆, which can be calculated as 0.192, 0.185, and 0.181 pm V⁻¹ for [(M/Ba)₂Ca]F[B₂O₅] (M = K, Rb) and [CsBaCa]F[B₂O₅], respectively. This is basically consistent with the experimental values. Remarkably, as [(M/Ba)₂Ca]F[B₂O₅] (M = K, Rb) and [CsBaCa]F[B₂O₅] crystallize in the tetragonal system, the calculation equation of effective NLO coefficients (d_eff) for type-I PM for them will be ‘d_eff = d₁₄sin²θcos2ψ’, where θ and ψ are the angle between the wave vector of fundamental frequency light and the optical axis and the projection of the phase matching direction on the a–b plane, respectively. This means [(M/Ba)₂Ca]F[B₂O₅] (M = K, Rb) and [CsBaCa]F[B₂O₅] would have larger effective NLO coefficients when they are used in the UV spectral regions, especially when the wavelengths are close to their PM limit where θ is approaching 90°. Therefore, [(M/Ba)₂Ca]F[B₂O₅] (M = K, Rb) and [CsBaCa]F[B₂O₅] can exhibit larger SHG responses in the UV regions.

Conclusions

In summary, through rationally choosing an antiperovskite structure as a template, two new antiperovskite borate fluorides, [(M/Ba)₂Ca]F[B₂O₅] (M = K, Rb), and the first double antiperovskite borate fluoride, [CsBaCa]F[B₂O₅], have been successfully designed and synthesized. Interestingly, with the change of cation size, the structure undergoes an evolution from an antiperovskite structure to a double antiperovskite structure. Moreover, all the structures crystallize in the NCS space group P4̄2₁m. The physiochemical property measurements show they all exhibit wide UV transparent regions with short UV cut-off edges (∼190 nm) and suitable birefringence (0.0405, 0.0548, and 0.0414@532 nm for Cs-, Rb- and K-based compounds), as well as moderate SHG responses (∼0.5 × KDP@1064 nm). In particular, they crystallize in the tetragonal point group 4̄2m, so they can exhibit larger SHG responses in the UV region, close to their PM limit. This suggests their potential as UV NLO crystals, and indicates that using an antiperovskite structural template is an effective way to design new inorganic NCS solids.

Data availability

The data supporting this article have been included as part of the ESI.† Crystallographic data for 2379650–2379652 has been deposited at the CCDC.

Author contributions

F. Q. C. performed the experiments, data analysis, theoretical calculations, and paper writing. H. W. Y. designed and supervised the experiments. H. P. W. provided major revisions of the manuscript. Z. G. H. supervised the optical experiments. J. Y. W. and Y. C. W. helped the analyses of the crystallization process and the data. All the authors discussed the results and commented on the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work is supported by the National Natural Science Foundation of China (Grant No. 22071179, 52322202, 52172006) and Tianjin Municipal Science and Technology Bureau (Grant No. 21JCJQJC00090 and 20JCJQJC00060).

Notes and references

1. (a) P. S. Halasyamani and K. R. Poeppelmeier, Chem. Mater., 1998, 10, 2753–2769; (b) K. M. Ok, E. O. Chi and P. S. Halasyamani, Chem. Soc. Rev., 2006, 35, 710–717.
2. (a) C. T. Chen, B. C. Wu, A. D. Jiang and G. M. You, Sci. Sin., Ser. B, 1985, 28, 235; (b) C. T. Chen and G. Z. Liu, Annu. Rev. Mater. Sci., 1986, 16, 136; (c) C. T. Chen, Y. C. Wu, A. D. Jiang, B. C. Wu, G. M. You, R. K. Li and S. J. Lin, J. Opt. Soc. Am. B, 1989, 6, 616.
3. (a) Y. Wu, T. Sasaki, S. Nakai, A. Yokotani, H. Tang and C. Chen, Appl. Phys. Lett., 1993, 62, 2614; (b) D. A. Keszler, A. Akella, K. I. Schaoers and T. Alekel III, Mater. Res. Soc. Symp. Proc., 1994, 329, 15; (c) Y. Mori, I. Kuroda, S. Nakajima, T. Sasaki and S. Nakai, Appl. Phys. Lett., 1995, 67, 1818.
4. (a) P. Becker, Adv. Mater., 1998, 10, 979; (b) N. Ye, W. R. Zeng, J. Jiang, B. C. Wu, C. T. Chen, B. H. Feng and X. L. Zhang, J. Opt. Soc. Am. B, 2000, 17, 764; (c) H. W. Huang, J. Y. Yao, Z. S. Lin, X. Y. Wang, R. He, W. J Yao, N. X. Zhai and C. T. Chen, Angew. Chem., Int. Ed., 2011, 50, 9141.
5. (a) S. C. Wang, N. Ye, W. Li and D. Zhao, J. Am. Chem. Soc., 2010, 132, 8779; (b) S. C. Wang and N. Ye, J. Am. Chem. Soc., 2011, 133, 11458; (c) H. W. Yu, S. L. Pan, H. P. Wu, W. W. Zhao, F. F. Zhang, H. Y. Li and Z. H. Yang, J. Mater. Chem., 2012, 22, 2105; (d) H. W. Huang, J. Y. Yao, Z. S. Lin, X. Y. Wang, R. He, W. J. Yao, N. X. Zhai and C. Y. Chen, Chem. Mater., 2011, 23, 5457.
6. (a) Y. Z. Huang, L. M. Wu, X. T. Wu, L. H. Li, L. Chen and Y. F. Zhang, J. Am. Chem. Soc., 2010, 132, 12788; (b) H. Yang, C. L. Hu, J. L. Song and J. G. Mao, RSC Adv., 2014, 4, 45258; (c) M. R. D. Mutailipu, K. R. Poeppelmeier and S. L. Pan, Chem. Rev., 2021, 121, 1130–1202.
7. (a) U. Opik and M. H. L. Pryce, Proc. R. Soc. London, Ser. A, 1957, 238, 425–447; (b) R. F. W. Bader, Can. J. Chem., 1962, 40, 1164–1175; (c) R. G. Pearson, J. Am. Chem. Soc., 1969, 91, 4947–4955.
8. (a) R. G. Pearson, J. Mol. Struct.:THEOCHEM, 1983, 103, 25–34; (b) R. A. Wheeler, M. H. Whangbo, T. Hughbanks, R. Hoffmann, J. K. Burdett and T. A. Albright, J. Am. Chem. Soc., 1986, 108, 2222–2236; (c) S. E. Bang, Z. Pan, Y. H. Kim, D. W. Lee and K. M. Ok, J. Solid State Chem., 2013, 208, 65–70.
9. (a) H. L. Jiang, S. P. Huang, Y. Fan, J. G. Mao and W. D. Cheng, Chem.–Eur., J., 2008, 14, 1972–1981; (b) H. L. Jiang, F. Kong, Y. Fan and J. G. Mao, Inorg. Chem., 2008, 47, 7430–7437; (c) Y. C. Hao, X. Xu, F. Kong, J. L. Song and J. G. Mao, CrystEngComm, 2014, 16, 7689–7695; (d) H. W. Yu, H. P. Wu, S. L. Pan, Z. H. Yang, X. L. Hou, X. Su, Q. Jing, K. R. Poeppelmeier and J. M. Rondinelli, J. Am. Chem. Soc., 2014, 136, 1264–1267.
10. (a) R. H. Cong, T. Yang, F. H. Liao, Y. X. Wang, Z. S. Lin and J. H. Lin, Mater. Res. Bull., 2012, 47, 2573–2578; (b) J. L. Song, C. L. Hu, X. Xu, F. Kong and J. G. Mao, Angew. Chem., Int. Ed., 2015, 54, 3679–3682; (c) S. G. Zhao, Y. Yang, Y. G. Shen, B. Q. Zhao, L. N. Li, C. M. Ji, Z. Y. Wu, D. Q. Yuan, Z. S. Lin, M. C. Hong and J. H. Luo, Angew. Chem., Int. Ed., 2017, 129, 555–559; (d) Y. X. Song, M. Luo, C. S. Lin and N. Ye, Chem. Mater., 2017, 29, 896–903; (e) C. Wu, X. X. Jiang, Z. J. Wang, L. Lin, Z. S. Lin, Z. P. Huang, X. F. Long, M. G. Humphrey and C. Zhang, Angew. Chem., Int. Ed., 2021, 60, 3464–3468.
11. (a) G. H. Zou, N. Ye, L. Huang and X. S. Lin, J. Am. Chem. Soc., 2011, 133, 20001–20007; (b) L. Kang, S. Y. Luo, H. W. Huang, N. Ye, Z. S. Lin, J. G. Qin and C. T. Chen, J. Phys. Chem. C, 2013, 117, 25684–25692; (c) T. T. Tran, J. H. He, J. M. Rondinelli and P. S. Halasyamani, J. Am. Chem. Soc., 2015, 137, 10504–10507; (d) G. Peng, C. S. Lin and N. Ye, J. Am. Chem. Soc., 2020, 142, 20542–20546; (e) X. M. Liu, L. Kang, P. F. Gong and Z. S. Lin, Angew. Chem., Int. Ed., 2021, 60, 13574–13578; (f) L. Xiong, L. M. Wu and L. Chen, Angew. Chem., Int. Ed., 2021, 60, 25063–25067.
12. (a) B. C. Wu, D. Y. Tang, N. Ye and C. T. Chen, Opt. Mater., 1996, 5, 105; (b) S. G. Zhao, P. F. Gong, L. Bai, X. Xu, S. Q. Zhang, Z. H. Sun, Z. S. Lin, M. C. Hong, C. T. Chen and J. H. Luo, Nat. Commun., 2014, 5, 4019; (c) S. G. Zhao, P. F. Gong, S. Y. Luo, S. J. Liu, L. Li, M. Adnan, T. Khan, M. C. Hong, Z. S. Lin and J. H. Luo, J. Am. Chem. Soc., 2015, 137, 2207–2210; (d) G. H. Zou, C. S. Lin, H. Jo, G. Nam, T. S. You and K. M. Ok, Angew. Chem., Int. Ed., 2016, 55, 12078–12082; (e) H. W. Yu, N. Z. Koocher, J. M. Rondinelli and P. S. Halasyamani, Angew. Chem., Int. Ed., 2018, 57, 6100–6103.
13. (a) X. F. Wang, Y. Wang, B. B. Zhang, F. F. Zhang, Z. H. Yang and S. L. Pan, Angew. Chem., Int. Ed., 2017, 56, 14119–14123; (b) G. Q. Shi, Y. Wang, F. F. Zhang, B. B. Zhang, Z. H. Yang, X. L. Hou, S. L. Pan and K. R. Poeppelmeier, J. Am. Chem. Soc., 2017, 139, 10645–10648; (c) Y. Wang, B. B. Zhang, Z. H. Yang and S. L. Pan, Angew. Chem., Int. Ed., 2018, 57, 2150–2154; (d) C. Wu, X. X. Jiang, L. Lin, W. Y. Dan, Z. S. Lin, Z. P. Huang, M. G. Humphrey and C. Zhang, Angew. Chem., Int. Ed., 2021, 60, 27151–27157; (e) H. T. Qiu, F. M. Li, Z. Li, Z. H. Yang, S. L. Pan and M. R. D. Mutailipu, J. Am. Chem. Soc., 2023, 145, 24401–24407; (f) S. Liu, X. X. Jiang, L. Qi, Y. L. Hu, K. N. Duanmu, C. Wu, Z. S. Lin, Z. P. Huang, M. G. Humphrey and C. Zhang, Angew. Chem., Int. Ed., 2024, 63, e202318107.
14. (a) R. Q. Liu, H. P. Wu, H. W. Yu, Z. G. Hu, J. Y. Wang and Y. C. Wu, Chem. Mater., 2021, 33, 4240–4246; (b) J. J. Zhou, Y. Y. Liu, H. P. Wu, H. W. Yu, Z. S. Lin, Z. G. Hu, J. Y. Wang and Y. C. Wu, Angew. Chem., Int. Ed., 2020, 59, 19006–19010; (c) H. P. Wu, Z. J. Wei, Z. G. Hu, J. Y. Wang, Y. C. Wu and H. W. Yu, Angew. Chem., Int. Ed., 2024, 63, e202406318.
15. (a) S. De, D. Asthana, C. Thirmal, S. K. Keshri, R. K. Ghosh, G. Hundal, R. Kumar, S. Singh, R. Chatterjeec and P. Mukhopadhyay, Chem. Sci., 2023, 14, 2547–2552; (b) S. Bhunia, S. Chandel, S. K. Karan, S. Dey, A. Tiwari, S. Das, N. Kumar, R. Chowdhury, S. Mondal, I. Ghosh, A. Mondal, B. B. Khatua, N. Ghosh and C. Malla Reddy, Science, 2021, 373, 321.
16. L. Pauling, J. Am. Chem. Soc., 1929, 51, 1010–1026.
17. M. R. Filip and F. Giustino, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 5397–5402.
18. (a) M. A. Pena and J. L. G. Fierro, Chem. Rev., 2001, 101, 1981; (b) C. C. Stoumpos and M. G. Kanatzidis, Adv. Mater., 2016, 28, 5778; (c) P. Gao, M. Graetzel and M. K. Nazeeruddin, Energy Environ. Sci., 2014, 7, 2448; (d) M. A. Green, A. Ho-Baillie and H. J. Snaith, Nat. Photonics, 2014, 8, 506; (e) B. V. Lotsch, Angew. Chem., Int. Ed., 2014, 53, 635.
19. (a) X. T. Li, M. Kepenekian, L. D. Li, H. Dong, C. C. Stoumpos, R. Seshadri, C. Katan, P. J. Guo, J. Even and M. G. Kanatzidis, J. Am. Chem. Soc., 2022, 144, 3902; (b) L. M. Kong, Y. Q. Sun, B. Zhao, K. Y. Ji, J. Feng, J. C. Dong, Y. Z. Wang, Z. R. Liu, S. B. Maqbool, Y. G. Li, Y. G. Yang, L. J. Dai, W. Lee, C. Cho, S. D. Stranks, R. H. Friend, N. Wang, N. C. Greenham and X. Y. Yang, Nature, 2024, 631, 73–79; (c) H. N. Liu, H. P. Wu, Z. G. Hu, J. Y. Wang, Y. C. Wu, P. S. Halasyamani and H. W. Yu, ACS Mater. Lett., 2023, 5, 155–161.
20. Y. G. Wang, H. Zhang, J. L. Zhu, X. J. LU, S. Li, R. Q. Zou and Y. S. Zhao, Adv. Mater., 2020, 32, e1905007.
21. (a) H. P. Wu, S. L. Pan, K. R. Poeppelmeier, H. Y. Li, D. Z. Jia, Z. H. Chen, X. Y. Fan, Y. Yang, J. M. Rondinelli and H. S. Luo, J. Am. Chem. Soc., 2011, 133, 7786–7790; (b) M. Zhang, X. Su, S. L. Pan, Z. Wang, H. Zhang, Z. H. Yang, B. B. Zhang, L. Y. Dong, Y. Wang, F. F. Zhang and Y. Yang, J. Phys. Chem. C, 2014, 118, 11849–11856; (c) Z. H. Chen, S. L. Pan, X. Y. Dong, Z. H. Yang, M. Zhang and X. Su, Inorg. Chim. Acta, 2013, 406, 205–210; (d) C. Y. Bai, H. W. Yu, S. J. Han, S. L. Pan, B. B. Zhang, Y. Wang, H. P. Wu and Z. H. Yang, Inorg. Chem., 2014, 53, 11213–11220.
22. J. K. Wang, Y. S. Cheng, H. P. Wu, Z. G. Hu, J. Y. Wang, Y. C. Wu and H. W. Yu, Angew. Chem., Int. Ed., 2022, 61, e202201616.
23. S. X. Cui, H. P. Wu, Z. G. Hu, J. Y. Wang, Y. C. Wu and H. W. Yu, Adv. Sci., 2023, 10, e2204755.
24. P. S. Halasyamani and J. M Rondinelli, Nat. Commun., 2018, 9, 2972.
25. J. K. Harada, N. Charles, K. R. Poeppelmeier and J. M. Rondinelli, Adv. Mater., 2019, 31, 1805295.
26. R. Green, M. Avdeev and T. Vogt, J. Solid State Chem., 2015, 228, 1–8.
27. S. S. Li, X. M. Liu, H. P. Wu, Z. F. Song, H. W. Yu, Z. S. Lin, Z. G. Hu, J. Y. Wang and Y. C. Wu, Chem. Sci., 2021, 12, 13897–13901.
28. R. D. Shannon, Acta Cryst., 1976, A32, 751–767.
29. T. K. Mandal, A. M. Abakumov, M. V. Lobanov, M. Croft, V. V. Poltavets and M. Greenblatt, Chem. Mater., 2008, 20, 4653–4660.
30. A. M. Glazer, Acta Crystallogr., Sect. B:Struct. Sci., Cryst. Eng. Mater. , 1972, 28, 3384.
31. (a) C. Preiser, J. Lösel, I. D. Brown, M. Kunz and A. Skowron, Acta Crystallogr., Sect. B:Struct. Sci., Cryst. Eng. Mater. , 1999, 55, 698; (b) A. Salinas-Sanchez, J. L. Garcia-Muñoz, J. Rodriguez-Carvajal, R. Saez-Puche and J. L. Martinez, J. Solid State Chem., 1992, 100, 201–211.
32. (a) M. E. Gao, H. P. Wu, H. W. Yu, Z. G. Hu, J. Y. Wang and Y. C. Wu, Sci. China: Chem., 2021, 64, 1184–1191; (b) M. M. Ding, J. J. Xu, H. P. Wu, H. W. Yu, Z. G. Hu, J. Y. Wang and Y. C. Wu, Dalton Trans., 2020, 49, 12184–12188; (c) X. Meng, M. Xia and R. Li, New J. Chem., 2019, 43, 11469–11472.
33. (a) J. Tauc, Mater. Res. Bull., 1970, 5, 721–729; (b) S. K. Kurtz and T. T. Perry, J. Appl. Phys., 1968, 39, 3798–3813; (c) C. T. Chen, Y. C. Wu and R. K. Li, Int. Rev. Phys. Chem., 1989, 8, 65–91; (d) P. A. Maggard, T. S. Nault, C. L. Stern and K. R. Poeppelmeier, J. Solid State Chem., 2003, 175, 27–33; (e) X. X. Jiang, S. G. Zhao, Z. S. Lin, J. H. Luo, P. D. Bristowe, X. G. Guand and C. T. Chen, J. Mater. Chem. C, 2014, 2, 530; (f) B. E. Sørensen, Eur. J. Mineral., 2013, 25, 5–10.
34. M. R. D. Mutailipu, M. Zhang, H. P. Wu, Z. H. Yang, Y. H. Shen, J. L. Sun and S. L. Pan, Nat. Commun., 2018, 9, 3089.
35. L. Kang, F. Liang, X. X. Jiang, Z. S. Lin and C. T. Chen, Acc. Chem. Res., 2020, 53, 209–217.
36. R. W. Godby, M. Schlüter and L. J. Sham, Phys. Rev. Lett., 1986, 56, 2415–2418.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 2379650, 2379651 and 2379652 for [CsBaCa]F[B₂O₅], [(Rb/Ba)₂Ca]F[B₂O₅] and [(K/Ba)₂Ca]F[B₂O₅], respectively. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4sc05747c

---