Open Access Article
Open Access ArticleA comprehensive approach for elucidating the interplay between 4fn+1 and 4fn5d1 configurations in Ln2+ complexes†
Maria J.
Beltran-Leiva
 a,
William N. G.
Moore
a,
William N. G.
Moore
 b,
Tener F.
Jenkins
b,
William J.
Evans
b,
Tener F.
Jenkins
b,
William J.
Evans
 *b,
Thomas E.
Albrecht
*d and
Cristian
Celis-Barros
*b,
Thomas E.
Albrecht
*d and
Cristian
Celis-Barros
 *c
*c
aTheoretical Division, Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA
bDepartment of Chemistry, University of California, Irvine, California 92697-2025, USA
cRadioisotope Science and Technology Division, Oak Ridge National Laboratory, Oak Ridge, TN 37830, USA. E-mail: celisbarroca@ornl.gov
dDepartment of Chemistry, Nuclear Science & Engineering Center, Colorado School of Mines, Golden, Colorado 80401, USA
First published on 3rd January 2025
Abstract
Lanthanides (Ln) are typically found in the +3 oxidation state. However, in recent decades, their chemistry has been expanded to include the less stable +2 oxidation state across the entire series except promethium (Pm), facilitated by the coordination of ligands such as trimethylsilylcyclopentadienyl, C5H4SiMe3 (Cp′). The  complexes have been the workhorse for the synthesis and theoretical study of the fundamental aspects of divalent lanthanide chemistry, where experimental and computational evidence have suggested the existence of different ground state (GS) configurations, 4fn+1 or 4fn5d1, depending on the specific metal. Standard reduction potentials and 4fn+1 to 4fn5d1 promotion energies have been two factors usually considered to rationalize the occurrence of these variable GS configurations, however the driving force behind this phenomenon is still not clear. In this work we present a comprehensive theoretical approach to shed light on this matter using the [LnCp3]− model systems. We begin by calculating 4fn+1 to 4fn5d1 promotion energies and successfully correlate them with existing experimental data. Furthermore, we analyze how changes in the GS charge distribution between the Ln ions, LnCp3 and the reduced [LnCp3]− complexes (Ln = La, Ce, Pr, Nd, Sm, Eu, Gd, Tb, Dy, Ho, Er, Tm, Yb, Lu) correlate with experimental trends in redox potentials and the calculated promotion energies. For this purpose, a comprehensive theoretical work that includes relativistic ligand field density functional theory (LFDFT) and relativistic ab initio wavefunction methods was performed. This study will help the rational design of suitable environments to tune the different GS configurations as well as modulating the spectroscopic properties of new Ln2+ complexes.
complexes have been the workhorse for the synthesis and theoretical study of the fundamental aspects of divalent lanthanide chemistry, where experimental and computational evidence have suggested the existence of different ground state (GS) configurations, 4fn+1 or 4fn5d1, depending on the specific metal. Standard reduction potentials and 4fn+1 to 4fn5d1 promotion energies have been two factors usually considered to rationalize the occurrence of these variable GS configurations, however the driving force behind this phenomenon is still not clear. In this work we present a comprehensive theoretical approach to shed light on this matter using the [LnCp3]− model systems. We begin by calculating 4fn+1 to 4fn5d1 promotion energies and successfully correlate them with existing experimental data. Furthermore, we analyze how changes in the GS charge distribution between the Ln ions, LnCp3 and the reduced [LnCp3]− complexes (Ln = La, Ce, Pr, Nd, Sm, Eu, Gd, Tb, Dy, Ho, Er, Tm, Yb, Lu) correlate with experimental trends in redox potentials and the calculated promotion energies. For this purpose, a comprehensive theoretical work that includes relativistic ligand field density functional theory (LFDFT) and relativistic ab initio wavefunction methods was performed. This study will help the rational design of suitable environments to tune the different GS configurations as well as modulating the spectroscopic properties of new Ln2+ complexes.
1. Introduction
Lanthanide (Ln) chemistry is usually governed by the +3 oxidation state. Before the 1990s, just a small number of molecules containing metal ions in the +2 oxidation state were known for Sm, Eu, and Yb.1 In these elements, reduction results in stable electron configurations where the 4f orbitals are nearly half-filled (Sm, 4f6), half-filled (Eu, 4f7) and fully filled (Yb, 4f14). Consequently, they exhibit the most accessible Ln3+/Ln2+ reduction potentials of the lanthanide series.2 Over the last few decades, lanthanide (Ln) chemistry has been extended to the less stable +2 oxidation state in molecular compounds for the entire series by coordinating the metal center to ligands such as cryptates,3 cryptands,4 aryloxides,5,6 crown ethers,7–9 and cyclopentadienyl ([C5H5]−, Cp) derivatives.8,10–17 The unique electronic configurations and chemical properties displayed by these reduced systems have been explored from a fundamental perspective leading to promising applications in the field of quantum information science.18,19 However, further studies on divalent lanthanide complexes are essential to understand and optimize their electronic properties.Among the diversity of Ln2+ complexes that have been reported to date,  (Cp′ = trimethylsilylcyclopentadienyl, C5H4SiMe3) systems are the most widely explored primarily because of the well-established protocols that allow for their synthesis and characterization. Experimental and theoretical evidence has shown that these compounds exhibit variable ground state (GS) configurations across the lanthanides series, which results in different spectroscopic features and variable bond lengths.11–13 For example, a 4fn+1 GS configuration has been reported for Sm2+, Eu2+, Tm2+ and Yb2+ whereas the 4fn5d1 configuration has been seen for La2+, Ce2+, Pr2+, Gd2+, Tb2+, Ho2+, Er2+ and Lu2+.11,12 Interestingly, Nd2+ and Dy2+ can switch configurations depending on the coordination environment for which they are considered “crossover ions”.13,20 Density functional theory (DFT) has been used to rationalize the origin of these 4fn5d1 configurations, suggesting that the tris(cyclopentadienyl) ligand field, stabilizes the 5dz2 orbital relative to the 4f orbital shell making their population feasible.11–13 Nonetheless, the driving force that determines the GS configuration is still not clear. In general, two main factors have been considered to get a better understanding of this phenomenon: the standard reduction potentials and the 4fn+1 to 4fn5d1 promotion energies for the Ln2+ free ions.
(Cp′ = trimethylsilylcyclopentadienyl, C5H4SiMe3) systems are the most widely explored primarily because of the well-established protocols that allow for their synthesis and characterization. Experimental and theoretical evidence has shown that these compounds exhibit variable ground state (GS) configurations across the lanthanides series, which results in different spectroscopic features and variable bond lengths.11–13 For example, a 4fn+1 GS configuration has been reported for Sm2+, Eu2+, Tm2+ and Yb2+ whereas the 4fn5d1 configuration has been seen for La2+, Ce2+, Pr2+, Gd2+, Tb2+, Ho2+, Er2+ and Lu2+.11,12 Interestingly, Nd2+ and Dy2+ can switch configurations depending on the coordination environment for which they are considered “crossover ions”.13,20 Density functional theory (DFT) has been used to rationalize the origin of these 4fn5d1 configurations, suggesting that the tris(cyclopentadienyl) ligand field, stabilizes the 5dz2 orbital relative to the 4f orbital shell making their population feasible.11–13 Nonetheless, the driving force that determines the GS configuration is still not clear. In general, two main factors have been considered to get a better understanding of this phenomenon: the standard reduction potentials and the 4fn+1 to 4fn5d1 promotion energies for the Ln2+ free ions.
The standard reduction potentials for the Ln3+/Ln2+ couple have usually been the first approximation to rationalize the accessibility to the different Ln2+ ions.1,2,21 Accordingly, several reduction potentials have been reported in literature (Fig. S1†). Over five decades ago, Nugent et al. extrapolated the values of the unknown Ln2+ ions using the experimental redox potentials of Eu2+, Yb2+, and Sm2+. Their redox potentials were correlated through their effective nuclear charge, Racah crystal field, spin–orbit coupling parameters, and 4f–5d absorption energies.21–23 At the time, another set of reduction potentials derived from thermodynamic cycles were reported by Johnson in 1973.24 Nearly a decade later, potentials based on correlations obtained from molten salt chemistry were also reported by Mikheev, Kamenskaya, and coworkers.25–29 Despite the differences among these different redox potentials, they agree on the Eu2+, Yb2+, Sm2+, Tm2+, Dy2+, and Nd2+ values. This is not surprising because these divalent ions were characterized in the solid-state more than fifty years ago.
Some authors have looked for a correlation between the Ln3+/Ln2+ reduction potentials and 4fn+1 → 4fn5d1 promotion energies employing 4f–5d absorption energies for the Ln2+ ions.30 A pioneering study published in 1963 by McClure and Kiss paved the way for this pursuit.23 Firstly, they reported the absorption spectra for the Ln2+ series in cubic crystals of CaF2, which was a valuable source of information since all the data was obtained through a systematic procedure. Then, they used this spectroscopic data, along with some theoretical approximations to calculate the 4fn+1 → 4fn5d1 promotion energies as the difference between the Russell Saunders ground states of the 4fn+1 and 4fn−15d1 configurations. Since significant deviations were detected in some lanthanides such as La2+, Ce2+, Gd2+ and Tb2+, new adjustments were incorporated to get more reasonable values. However, a deficient correspondence with the standard reduction potential curves was observed.
Several 4fn+1 → 4fn5d1 promotion energy curves have been reported using a similar methodology as Kiss and McClure and have been employed for comparative purposes.10,29,31–33 If the energy values reported by Dorenbos et al. (Fig. S2†) are considered to analyze the energetics of the GS configurations in  systems, only La2+ and Gd2+ exhibit a 4fn5d1 GS which suggests that there is an energy gap of around 20
systems, only La2+ and Gd2+ exhibit a 4fn5d1 GS which suggests that there is an energy gap of around 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 that must be overcome in order to allow the 4fn5d1 GS configuration.30 As mentioned by Fieser et al., this presumably relates to the crystal field stabilization provided by the tris(cyclopentadienyl) ligand set.13 This scheme also shows that Ho2+ and Er2+ are closer to be considered crossover ions than Dy2+ and Nd2+. However, experimental, and theoretical evidence does not support this observation which suggests that more factors should be considered to solve this puzzle.
000 cm−1 that must be overcome in order to allow the 4fn5d1 GS configuration.30 As mentioned by Fieser et al., this presumably relates to the crystal field stabilization provided by the tris(cyclopentadienyl) ligand set.13 This scheme also shows that Ho2+ and Er2+ are closer to be considered crossover ions than Dy2+ and Nd2+. However, experimental, and theoretical evidence does not support this observation which suggests that more factors should be considered to solve this puzzle.
A third parameter yet to be explored is the GS charge distribution of the lanthanide ions. The charge distribution is determined by the composition of the wave function in terms of projections (MJ) of the total angular momentum J that can be associated to a prolate, oblate, or spherical shape, based on the quadrupole moment Q. Therefore, Q > 0 indicates a prolate shape whereas Q < 0 an oblate charge distribution.34 Under the assumption that the lanthanide ion is in its largest Mj state, equatorial ligand field environments such as those provided by Cp derivatives in LnCp3/[LnCp3]− systems should destabilize the fn+1-states for oblate-shaped ions such as cerium or terbium. This agrees with the rules provided by Long and Rinehart, where this type of charge distributions minimizes the MJ value of their GS which means that a prolate shape is favored.31 The opposite is expected for prolate-shaped densities because an equatorial coordination environment is energetically more favorable. From this perspective, it is reasonable to think that variations in the preferred Ln charge distribution shape can be an important piece to explain the intricate behavior of the electronic structure of Ln2+ complexes.
In this work, we propose a general approach to elucidate the variable nature of the GS in divalent lanthanide complexes. We start revisiting well-known concepts in the field of Ln2+ chemistry such as 4fn+1 → 4fn5d1 promotion energies and its correlation with some standard reduction potentials. Then we analyze the Ln charge distribution shapes in terms of the MJ projections of J to determine if this is the missing piece that allows to explain the interplay between the two configurations observed in  systems. For this purpose, an extensive theoretical work including the relativistic ligand field density functional theory (LFDFT) and relativistic ab initio methods was performed on Ln3+ free ions as well as in LnCp3 and [LnCp3]− model systems (Fig. 1). The impact of this study will enable the rational design of suitable environments to tune the different GS configurations as well as modulating the spectroscopic properties of new Ln2+ complexes.
systems. For this purpose, an extensive theoretical work including the relativistic ligand field density functional theory (LFDFT) and relativistic ab initio methods was performed on Ln3+ free ions as well as in LnCp3 and [LnCp3]− model systems (Fig. 1). The impact of this study will enable the rational design of suitable environments to tune the different GS configurations as well as modulating the spectroscopic properties of new Ln2+ complexes.
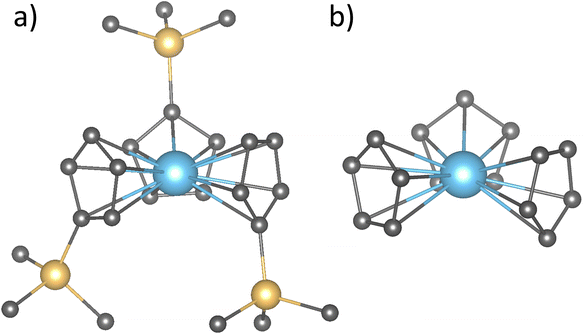 | ||
Fig. 1 (a) Structures of the  complex and (b) the truncated model where the SiMe3 groups were replaced with hydrogen atoms. See Table S3† for a comparison in the 4fn+1 to 4fn5d1 promotion energies when using both structures for Tm and Eu systems. complex and (b) the truncated model where the SiMe3 groups were replaced with hydrogen atoms. See Table S3† for a comparison in the 4fn+1 to 4fn5d1 promotion energies when using both structures for Tm and Eu systems. | ||
2. Results and discussion
2.1 Theoretical approach
There are several reports accounting for the 4fn+1 → 4fn5d1 promotion energies in Ln2+ systems and most of them were derived from lanthanide-doped inorganic matrices through experimental fittings and theoretical extrapolations.23,32,35,36 To the best of our knowledge, there are no reports of 4fn+1 → 4fn5d1 promotion energies for the Ln2+ series obtained through systematic procedures. From the theoretical and computational perspective, this is understandable since it is well known that the electronic structure of Ln2+ complexes is difficult to predict. Although single-reference DFT calculations have contributed to the general understanding of the spectroscopic properties of some divalent lanthanide complexes, they usually fail in the determination of their electronic structure due to their lack of static correlation. Methods that account for this type of correlation, such as LFDFT and CASSCF, become more appropriate to analyze these elements.37,38The LFDFT approximation is a promising tool in the field of Ln2+ chemistry. It has proven accurate and efficient from a computational perspective, and it has been employed successfully in previous studies.3,7,39,40 Nonetheless, due to the over delocalization of the molecular electron density intrinsic to DFT that significantly affects the description of the more polarizable and diffuse 5d shell in lanthanides, it requires significant fine tuning to obtain reliable results. On the other hand, the CASSCF method is a robust tool to analyze GS of multiconfigurational systems and it has proven valuable to analyze several Ln2+ complexes.3,7,41 However, a couple of issues have been identified regarding the calculation of excited states. Firstly, a double f shell is needed to account for the so-called “radial correlation” that is particularly relevant in divalent lanthanides within this CASSCF formalism.35 Additionally, the lack of dynamic correlation can introduce non-negligible errors in the prediction of the 4fn+1 → 4fn5d1 promotion energies. For this reason, second-order perturbation (PT2) methods are employed to solve this problem, but they are usually impractical to calculate molecular systems.42,43 An alternative method that overcome this issue at a lower computational cost is the multiconfigurational pair-density DFT method (MC-pDFT).44 This approximation combines the multiconfigurational approach with on-top density functionals to obtain electronic energies and has been successfully applied by Fleischauer et al. to predict the magnetic circular dichroism (MCD) spectra of some Ln2+ complexes.45
In the first part of this work, we use the LFDFT and CASSCF in combination with CASPT2/MC-pDFT approximations to calculate, in a systematic way, the 4fn+1 → 4fn5d1 promotion energies of both Ln2+ free ions and [LnCp3]− complexes (Ln = La, Ce, Pr, Nd, Sm, Eu, Gd, Tb, Dy, Ho, Er, Tm, Yb) to evaluate the correlation between the resulting curves and the aforementioned standard reduction potentials alongside previously reported 4fn+1 → 4fn5d1 promotion energies curves.
2.2 LFDFT and CASSCF/CASPT2/MC-pDFT 4fn+1 → 4fn5d1 promotion energies in Ln2+ free ions
LFDFT and CASSCF/CASPT2/MC-pDFT approximations show the same trend in the promotion energies through the lanthanide series which results in similar curves, as observed in Fig. 2a. As expected, Gd2+ is the only ion that possesses a 4f75d1 configuration, which is predicted to be around 2000–3000 cm−1 more stabilized than the 4f8 configuration. Lanthanum and lutetium are also expected to exhibit 4f05d1 and 4f145d1 GS configurations, respectively. In La3+ the 5d orbital occupation is favored since the 5d shell is more stabilized than the 4f shell at the beginning of the lanthanide series while in Lu3+, a full-filled 4f shell is the responsible. However, neither method was able to recover a reasonable difference of energy between both configurations. With respect to the promotion energies reported by Dorenbos and coworkers (Fig. S2†).30 resemblances are observed in the positions of Sm2+, Eu2+, Tm2+ and Yb2+. Nevertheless, significant differences are evidenced in Nd2+, Dy2+, Ho2+ and Er2+ which correspond to those ions close to the “crossover” region in the systems. According to these authors, the promotion energy decreases following the sequence Ho2+ > Er2+ > Dy2+ > Nd2+, contrary to our calculations where the promotion energy decreases following the sequence Dy2+ > Nd2+ > Ho2+ > Er2+. Interestingly, this order agrees with the curves of reduction potentials shown in Fig. 2a and S1,† where the best correspondence is with those values derived from thermodynamic data.
systems. According to these authors, the promotion energy decreases following the sequence Ho2+ > Er2+ > Dy2+ > Nd2+, contrary to our calculations where the promotion energy decreases following the sequence Dy2+ > Nd2+ > Ho2+ > Er2+. Interestingly, this order agrees with the curves of reduction potentials shown in Fig. 2a and S1,† where the best correspondence is with those values derived from thermodynamic data.
2.3 CASSCF/CASPT2/MC-pDFT 4fn+1 → 4fn5d1 promotion energies in [LnCp3]−
Once the ions are in the tris(cyclopentadienyl) coordination environment, the promotion energies are significantly lower. While the overall shape of the curve is retained, not all the Ln2+ ions are stabilized equally (Fig. 2b). In the case of the ions with a 4fn+1 GS, the stabilization is ca. 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1. Conversely, ions possessing a 4fn5d1 GS show are stabilized by ca. 30
500 cm−1. Conversely, ions possessing a 4fn5d1 GS show are stabilized by ca. 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 (vide infra). Below the black dashed-line that indicates the crossover between GS configurations, the promotion energy decreases following the same sequence as in the Ln2+ free ions: Dy2+ > Nd2+ > Ho2+ > Er2+. This result agrees with experimental evidence that classifies the Dy2+ and Nd2+ as crossover ions depending on the ligand environment surrounding the metal.
000 cm−1 (vide infra). Below the black dashed-line that indicates the crossover between GS configurations, the promotion energy decreases following the same sequence as in the Ln2+ free ions: Dy2+ > Nd2+ > Ho2+ > Er2+. This result agrees with experimental evidence that classifies the Dy2+ and Nd2+ as crossover ions depending on the ligand environment surrounding the metal.
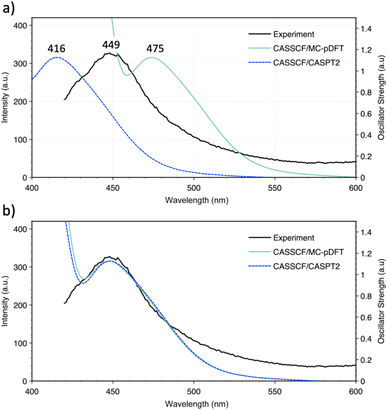
Since the experimental 4fn+1 → 4fn5d1 promotion energies have not been measured within this molecular framework, the Eu2+ ion was used as a reference. Given its 4f7 ground state, Eu2+ is the ideal candidate to experimentally measure the promotion energy between configurations since its value is equivalent to the lowest electronic transition, easily observable in an emission spectrum. This suggests that the  is the most suitable system to measure the position of this band and to validate our theoretical approach. In Fig. 3, a comparison between the experimental and simulated emission spectrum of [EuCp3]− is shown, where a prominent band centered at 449 nm (22
is the most suitable system to measure the position of this band and to validate our theoretical approach. In Fig. 3, a comparison between the experimental and simulated emission spectrum of [EuCp3]− is shown, where a prominent band centered at 449 nm (22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 271 cm−1) is observed and ascribed to a 4f65d1 → 4f7 transition. Overall, the agreement between this and the simulated spectra is good, with errors in the range of 26 nm (1257.7 cm−1) and 33 nm (1766.8 cm−1) for CASSCF/MC-pDFT and CASSCF/CASPT2, respectively. Once we validated our calculations against this system, the rest of the series was analyzed.
271 cm−1) is observed and ascribed to a 4f65d1 → 4f7 transition. Overall, the agreement between this and the simulated spectra is good, with errors in the range of 26 nm (1257.7 cm−1) and 33 nm (1766.8 cm−1) for CASSCF/MC-pDFT and CASSCF/CASPT2, respectively. Once we validated our calculations against this system, the rest of the series was analyzed.
It is noteworthy that historically Dy(II) and Nd(II) were thought to be 4fn+1 ions because they were the most stable in the +2 oxidation state along with Sm2+, Eu2+, Tm2+ and Yb2+. However, experimental evidence supporting a 4fn5d1 configuration for Nd2+ and Dy2+ has been available since 1976.46–49 These precedents were based on structural comparisons, where small metal–ligand bond length differences going from trivalent to divalent species were observed, which is usually attributed to the localization of the additional electron in a d orbital. In the case of the metals coordinated to Cp derivatives, both  and
and 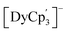 complexes display 4f35d1 and a 4f95d1 GS configurations, respectively. However, in 2018 Jenkins et al. reported the isolation of [LnCptet3]− (Ln = La, Ce, Pr, Nd, Sm, Gd, Tb, Dy; Cptet = C5Me4H) complexes across the lanthanide series, where all the systems excepting [SmCptet3]− and [DyCptet3]− exhibited a 4fn5d1 GS. This confers additional experimental validation to the curves shown in Fig. 2b as it shows that after the four well-known 4fn+1 ions, dysprosium is the next to display this GS configuration in a molecular environment. Furthermore, this suggests that the Cp′ can stabilize the 5dz2 orbital and/or destabilize the f-orbitals better than the Cptet ligand, thus making it more energetically available to accept the additional electron in Ln2+ ions closer to the crossover line. The reason behind this observation may be attributed to an increased energy of the 5dz2 orbital due to its potential interaction with occluding methyl groups of the Cptet with respect to the Cp′ ligands. This increases the electronic repulsion produced by the methyl groups of the Cptet rings, which results in a probable destabilization of the 5dz2 orbital thus making it less accessible and in consequence more difficult to populate.
complexes display 4f35d1 and a 4f95d1 GS configurations, respectively. However, in 2018 Jenkins et al. reported the isolation of [LnCptet3]− (Ln = La, Ce, Pr, Nd, Sm, Gd, Tb, Dy; Cptet = C5Me4H) complexes across the lanthanide series, where all the systems excepting [SmCptet3]− and [DyCptet3]− exhibited a 4fn5d1 GS. This confers additional experimental validation to the curves shown in Fig. 2b as it shows that after the four well-known 4fn+1 ions, dysprosium is the next to display this GS configuration in a molecular environment. Furthermore, this suggests that the Cp′ can stabilize the 5dz2 orbital and/or destabilize the f-orbitals better than the Cptet ligand, thus making it more energetically available to accept the additional electron in Ln2+ ions closer to the crossover line. The reason behind this observation may be attributed to an increased energy of the 5dz2 orbital due to its potential interaction with occluding methyl groups of the Cptet with respect to the Cp′ ligands. This increases the electronic repulsion produced by the methyl groups of the Cptet rings, which results in a probable destabilization of the 5dz2 orbital thus making it less accessible and in consequence more difficult to populate.
The theoretical calculations of 4fn+1 → 4fn5d1 promotion energies for both the Ln2+ free ions and the [LnCp3]− complexes provide a consistent source of information that supports several experimental observations. Interestingly, the differential stabilization of the promotion energies observed upon coordination of the Cp3 ligands correlates with the observed differences in the GS configurations in Ln2+ systems. However, it does not explain the fundamental reason on why lanthanides such as Dy and Nd are able to display both 4fn+1and 4fn5d1 configurations, depending on the coordinating ligands. To enhance our understanding of this phenomenon, we investigated how variations in charge distributions among [LnCp3]−, LnCp3, and free Ln ions correlate with the trends observed in their 4fn+1 → 4fn5d1 promotion energies.
2.4 Charge distributions of Ln single ions, [LnCp3]−, and LnCp3 model systems
The charge distribution of lanthanide GS is typically employed in magnetism to quantify the anisotropy of these ions and it is defined by prolate (axially elongated), oblate (equatorially expanded) or spherical shapes, based on its quadrupole moment. In 1981, Sievers reported the angular dependence of the charge distribution based on pure ± Mj states to visualize the asphericity of the 4f shells in their Russell Saunders ground states.50 Under these conditions, the Ln(III) ions of Ce, Pr, Nd, Tb, Dy and Ho exhibited oblate shapes while the Ln(III) ions of Sm, Er, Tm and Yb exhibited prolate shapes for their maximal Mj projections. Gd(III) and Lu(III) are the only ions displaying a spherical shape given their 4f7 and 4f14 GS configurations. Following this classification, Long and Rinehart31 proposed that a judicious choice of the crystal field that surrounds the metal center can be done to maximize the GS anisotropy and minimize the electron repulsion between the intrinsic metal electron density and the ligand field. In consequence, two general ligand architectures can be used. In the case of ions with oblate-shaped densities for their maximal Mj projections, the anisotropy can be maximized by using axial ligands (above and below the xy plane, assuming that z is axial in the frame of reference). Conversely, for ions with prolate-shaped densities, equatorial ligands should be preferred.This concept can be extended to further explore the complex interplay between GS configurations in divalent lanthanides systems. If we consider the simplest yet chemically intuitive model, it is reasonable to assume an ideal ground state where the anisotropy of the metal center is maximized (largest Mj value) in a favorable crystal field environment.51,52 Though this is not necessarily the case for every system, it helps to simplify the discussion. By using this ideal model, it is possible to analyze sequential differences in charge density changes between Ln3+, Ln2+, LnCp3 (model trivalent complex), and [LnCp3]− (model divalent complex). Interestingly, this sequence suggests that [LnCp3]− complexes displaying 4fn+1 GS configurations (Ln = Sm, Eu, Tm, Yb) retain a spherical (or nearly spherical) density. It is possible to infer that these Ln2+ ions show small variations with respect to the Ln3+ free-ion in their largest Mj state and the analogous 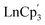 trivalent systems. Conversely, ions displaying more pronounced variations in the shape of the metal density are consistent with a 4fn5d1 GS (Ln = La, Ce, Pr, Nd, Gd, Tb, Dy, Ho, Er, Lu). Although, Nd2+ and Dy2+, which can display both GS configurations depending on the ligand environment, should be considered intermediate cases. The results are rationalized in terms of the composition of the wavefunction, occupation of the natural orbitals, and the Long–Rinehart model described above (the details of these calculations can be found in the Computational methods section and ESI†).
trivalent systems. Conversely, ions displaying more pronounced variations in the shape of the metal density are consistent with a 4fn5d1 GS (Ln = La, Ce, Pr, Nd, Gd, Tb, Dy, Ho, Er, Lu). Although, Nd2+ and Dy2+, which can display both GS configurations depending on the ligand environment, should be considered intermediate cases. The results are rationalized in terms of the composition of the wavefunction, occupation of the natural orbitals, and the Long–Rinehart model described above (the details of these calculations can be found in the Computational methods section and ESI†).
Although the spin-free analysis is consistent with the model proposed by Sievers,50 the effect of the spin–orbit (SO) coupling was also incorporated by state interactions between CASSCF wavefunctions to obtain the natural spin-orbitals (NSO). At this level, the mixing of spin-free natural orbitals driven by SO coupling can further deviate occupations from 0 or 1, as observed in Table 1 and Table S4.† This is shown by the Ce3+ ion where the electron in the largest Mj state now resides in an NSO that mixes both fy(3x2−y2) and fx(x2−3y2) spin-free orbitals featuring fractional occupations (0.43) with a maximum value of MJ = 5/2. Similarly, the rest of the series shows the same behavior of maximizing MJ in the absence of a ligand field (Table 1). Since the distribution of the electron density is defined by the nature of the occupied orbitals, its density can be determined and ascribed to oblate, prolate or spherical shapes. As observed in Fig. 4, Ln ions having an electron in the fy(3x2−y2) or fx(x2−3y2) orbitals (L = 3), such as Ce or Tb, display the most pronounced oblate shapes. Conversely, ions such as Sm or Tm have a more prolate shape due to the occupation of the f(yz2), f(xz2), and f(z3) orbitals, which are axially elongated. Finally, in case of Eu, Gd and Yb, the electron density is more spherical, consistent with their almost half-filled, and full filled 4f shells. Overall, these results support reports by Sievers on the Ln3+ series.
| Ln | J | Mj | f3− | f2− | f1− | f0 | f1+ | f2+ | f3+ | d0 |
|---|---|---|---|---|---|---|---|---|---|---|
| Ce3+ | 5/2 | 5/2 | 0.43 | 0.08 | 0 | 0 | 0 | 0.08 | 0.43 | 0 |
| CeCp3 | 5/2 | 1/2 | 0 | 0 | 0.33 | 0.34 | 0.33 | 0 | 0 | 0 |
| [CeCp3]− | 0 | 0 | 0.06 | 0 | 0.06 | 0 | 0.92 | 0.98 | ||
| Pr3+ | 4 | 4 | 0.49 | 0.41 | 0.09 | 0.01 | 0.09 | 0.41 | 0.49 | 0 |
| PrCp3 | 4 | 0 | 0.03 | 0.36 | 0.53 | 0.15 | 0.53 | 0.36 | 0.03 | 0 |
| [PrCp3]− | 7/2 | 5/2 | 0.25 | 0.07 | 0.35 | 0.3 | 0.35 | 0.07 | 0.62 | 1 |
| Nd3+ | 9/2 | 9/2 | 0.50 | 0.49 | 0.41 | 0.21 | 0.41 | 0.49 | 0.50 | 0 |
| NdCp3 | 9/2 | 5/2 | 0.15 | 0.31 | 0.56 | 0.36 | 0.56 | 0.31 | 0.77 | 0 |
| [NdCp3]− | 4 | 3 | 0.11 | 0.31 | 0.49 | 0.44 | 0.5 | 0.33 | 0.82 | 1 |
| Sm3+ | 5/2 | 5/2 | 0.54 | 0.69 | 0.83 | 0.88 | 0.83 | 0.69 | 0.54 | 0 |
| SmCp3 | 5/2 | 5/2 | 0.4 | 0.64 | 0.87 | 0.93 | 0.87 | 0.64 | 0.66 | 0 |
| [SmCp3]− | 0 | 0 | 0.62 | 0.88 | 0.94 | 0.94 | 0.94 | 0.88 | 0.8 | 0 |
| Eu3+ | 0 | 0 | 0.86 | 0.86 | 0.86 | 0.86 | 0.86 | 0.86 | 0.86 | 0 |
| EuCp3 | 0 | 0 | 0.61 | 0.88 | 0.95 | 0.94 | 0.95 | 0.88 | 0.79 | 0 |
| [EuCp3]− | — | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | |
| Gd3+ | — | — | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| GdCp3 | — | — | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| [GdCp3]− | — | — | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| Tb3+ | 6 | 6 | 1.49 | 1 | 1 | 1 | 1 | 1 | 1.49 | 0 |
| TbCp3 | 6 | 0 | 0.99 | 1.04 | 1.2 | 1.43 | 1.3 | 1.04 | 0.99 | 0 |
| [TbCp3]− | 13/2 | 13/2 | 1.45 | 1 | 1 | 1 | 1 | 1 | 1.55 | 1 |
| Dy3+ | 15/2 | 15/2 | 1.5 | 1.5 | 1.01 | 1 | 1.01 | 1.5 | 1.5 | 0 |
| DyCp3 | 15/2 | 1/2 | 1 | 1.36 | 1.48 | 1.2 | 1.48 | 1.3 | 1.13 | 0 |
| [DyCp3]− | 8 | 8 | 1.46 | 1.49 | 1.01 | 1 | 1.01 | 1.49 | 1.52 | 1 |
| Ho3+ | 8 | 8 | 1.5 | 1.5 | 1.5 | 1 | 1.5 | 1.5 | 1.5 | 0 |
| HoCp3 | 8 | 2 | 1.11 | 1.36 | 1.6 | 1.29 | 1.6 | 1.36 | 1.69 | 0 |
| [HoCp3]− | 17/2 | 17/2 | 1.39 | 1.5 | 1.5 | 1 | 1.5 | 1.5 | 1.61 | 1 |
| Er3+ | 15/2 | 15/2 | 1.5 | 1.50 | 1.5 | 2.00 | 1.5 | 1.50 | 1.50 | 0 |
| ErCp3 | 15/2 | 11/2 | 1.36 | 1.5 | 1.81 | 1.27 | 1.86 | 1.5 | 1.7 | 0 |
| [ErCp3]− | 8 | 3 | 1.27 | 1.61 | 1.48 | 1.52 | 1.81 | 1.4 | 1.91 | 1 |
| Tm3+ | 6 | 6 | 1.5 | 1.50 | 2 | 2 | 2 | 1.50 | 1.50 | 0 |
| TmCp3 | 6 | 6 | 1.46 | 1.5 | 2 | 2 | 2 | 1.5 | 1.54 | 0 |
| [TmCp3]− | 7/2 | 7/2 | 1.38 | 2 | 2 | 2 | 2 | 2 | 1.62 | 0 |
| Yb3+ | 7/2 | 7/2 | 1.54 | 1.96 | 2 | 2 | 2 | 1.96 | 1.54 | 0 |
| YbCp3 | 7/2 | 7/2 | 1.7 | 1.8 | 2 | 2 | 2 | 1.8 | 1.7 | 0 |
| [YbCp3]− | — | — | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 0 |
From a convenient standpoint, we compared differences in 4f asphericities between Ln3+ and Ln2+ in their maximal Mj states (Table S5†). Quadrupole moments (Q2) have shown useful to discuss differences in the shapes of the 4f electron densities. Q2 values have been previously reported for trivalent ions but not for divalent lanthanides possibly due to the interplay of the 4fn+1 and 4fn5d1 configurations.51,52 For comparisons, we have calculated Q2 values of the Ln2+ for their maximal Mj states assuming a 4fn+1 configuration. Fig. S5† shows how lanthanide single ion shapes vary as they move from a trivalent to divalent ion. Interestingly, ions displaying highly anisotropic 4f densities correlate with 4fn5d1 GS configurations such as Ce, Gd, and Tb (except Tm). As expected, ions with spherical densities match the 4fn+1 GS configuration leaving the ions with decreased or low anisotropies as intermediate or crossover cases. The exception of Tm is discussed below.
 complexes.
The perturbation of the electron distribution on the Ln3+ ions induced by the Cp3 coordination can be rationalized through the rules proposed by Long and Rinehart.31 Because the Cp ligands coordinate equatorially imposing a pseudo-trigonal symmetry around the metal center (Fig. 5), it forces Ln3+ ions become prolate to reduce the electronic repulsion in the equatorial region (Fig. S3,† and Table 1). However, since not all the Ln display the same intrinsic density distribution, the energy “cost” involved to become prolate varies according to the ion. For instance, ions such as Ce or Tb experience the most pronounced variations in terms of shape, going from oblate to prolate. Unlike the free ion analogs, where the fy(3x2−y2) or fx(x2−3y2) orbitals (L = 3) were preferentially occupied and the Mj was maximized (5/2 and 6 for Ce and Tb, respectively), in the CeCp3 and TbCp3 complexes, the electrons are mostly distributed across the fxz2 and fyz2 (L = 1), and fz3 (L = 0) orbitals thus minimizing the Mj value (1/2 and 0 for Ce and Tb, respectively) favoring a prolate shape (see Table S4†). This is not the case for ions such as Sm, Eu, Gd, Er, Tm and Yb which possess intrinsic prolate or spherical shapes. In these cases, the “cost” of coordinating the Cp3 ligand set is lower. Finally, for ions such as Pr, Nd, Dy, Ho, and Er the GS shapes fall outside the general classification as oblate or prolate owing to a more complex angular dependence. Thus, these Ln3+ ions can be interpreted as intermediate cases.
complexes.
The perturbation of the electron distribution on the Ln3+ ions induced by the Cp3 coordination can be rationalized through the rules proposed by Long and Rinehart.31 Because the Cp ligands coordinate equatorially imposing a pseudo-trigonal symmetry around the metal center (Fig. 5), it forces Ln3+ ions become prolate to reduce the electronic repulsion in the equatorial region (Fig. S3,† and Table 1). However, since not all the Ln display the same intrinsic density distribution, the energy “cost” involved to become prolate varies according to the ion. For instance, ions such as Ce or Tb experience the most pronounced variations in terms of shape, going from oblate to prolate. Unlike the free ion analogs, where the fy(3x2−y2) or fx(x2−3y2) orbitals (L = 3) were preferentially occupied and the Mj was maximized (5/2 and 6 for Ce and Tb, respectively), in the CeCp3 and TbCp3 complexes, the electrons are mostly distributed across the fxz2 and fyz2 (L = 1), and fz3 (L = 0) orbitals thus minimizing the Mj value (1/2 and 0 for Ce and Tb, respectively) favoring a prolate shape (see Table S4†). This is not the case for ions such as Sm, Eu, Gd, Er, Tm and Yb which possess intrinsic prolate or spherical shapes. In these cases, the “cost” of coordinating the Cp3 ligand set is lower. Finally, for ions such as Pr, Nd, Dy, Ho, and Er the GS shapes fall outside the general classification as oblate or prolate owing to a more complex angular dependence. Thus, these Ln3+ ions can be interpreted as intermediate cases.
2.4.3.1 Sm, Eu, Tm, Yb. In their trivalent oxidation state, these ions possess 4f5, 4f6, 4f12 and 4f13 GS configurations, respectively. Upon reduction, it would be reasonable to think that the additional electron can either occupy the low-lying 5dz2 orbital in cases like Sm and Yb or populate the 4f shell in the case of Eu or Yb. For example, and according to Fig. 2b, the promotion energies favoring the 4fn+1 configuration over the 4fn5d1 are ∼23
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 325 cm−1 and 20
325 cm−1 and 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 941 cm−1 in Eu and Yb, respectively. This case is probably the simplest to rationalize as achieving a half- and full-filled shell is more energetically favorable than populating the d orbital. Conversely, while Sm and Tm do not achieve a half-filled shell, their 4f density seems to be nearly spherical in the [LnCp3]− system (Table 1 and Fig. S4†). This suggests that ions able to acquire a spherical or nearly spherical density shapes upon reduction will display a 4fn+1 configuration.
941 cm−1 in Eu and Yb, respectively. This case is probably the simplest to rationalize as achieving a half- and full-filled shell is more energetically favorable than populating the d orbital. Conversely, while Sm and Tm do not achieve a half-filled shell, their 4f density seems to be nearly spherical in the [LnCp3]− system (Table 1 and Fig. S4†). This suggests that ions able to acquire a spherical or nearly spherical density shapes upon reduction will display a 4fn+1 configuration.
2.4.3.2 Ce, Tb, Gd. According to Fig. 2b, these ions possess the most stable 4fn5d1 GS configurations with promotion energies of ca. −15
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 524 cm−1, −10
524 cm−1, −10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 415 cm−1, and −22
415 cm−1, and −22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 250 cm−1 for Ce, Tb and Gd, respectively. In case of Ce and Tb, we observe that this correlates with the pronounced changes in the density distribution when going from the maximal Mj state (oblate) to
250 cm−1 for Ce, Tb and Gd, respectively. In case of Ce and Tb, we observe that this correlates with the pronounced changes in the density distribution when going from the maximal Mj state (oblate) to 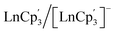 (prolate) complexes (Table 1, Fig. 4 and S4†). For Gd, the reason is rather simple as the energy penalty to break the half-filled 4f7 configuration is greater than the energy required to populate the 5dz2 orbital. This is also why Gd is the Ln with the most stable 4fn5d1 configuration in the series (Fig. 2).
(prolate) complexes (Table 1, Fig. 4 and S4†). For Gd, the reason is rather simple as the energy penalty to break the half-filled 4f7 configuration is greater than the energy required to populate the 5dz2 orbital. This is also why Gd is the Ln with the most stable 4fn5d1 configuration in the series (Fig. 2).
2.4.3.3 Pr, Nd, Dy, Ho, Er. In terms of 4fn+1 → 4fn5d1 promotion energies, these ions are close to the crossover line (Fig. 2b). Their 4fn5d1 GS configurations are found to be ∼2300–6300 cm−1 more stable than the 4fn+1, suggesting that their GS configurations can be altered by modulating the ligand field. This correlates with their density distribution because these ions do not fall under the oblate/prolate classification. If contrasted with the single ion anisotropies, we could infer that because the less anisotropic densities in their divalent oxidation state the electron repulsion is reduced in a the crystal field compared to other more anisotropic Ln ions. They can be considered intermediate cases lying in between the rest of the Ln series. Therefore, upon coordination and reduction they do not undergo pronounced variations in terms of density shape.
3. Conclusions
In conclusion, we have presented an extensive and systematic theoretical study to rationalize experimental observations regarding the complex interplay of GS configurations of Ln2+ ions in a tris(cyclopentadienyl) molecular framework. Using ab initio wavefunction methods, we have calculated the 4fn+1 → 4fn5d1 promotion energies across the entire series of Ln2+ free ions along with the [LnCp3]− model complexes. Our results show a good correlation with Ln3+/Ln2+ reduction potentials along with available structural and spectroscopic data that assigns 4fn+1 GS to Eu, Sm, Tm and Yb, and 4fn5d1 GS to La, Ce, Pr, Nd, Gd, Tb, Dy, Ho and Er. Interestingly, unlike previous studies of 4fn+1 → 4fn5d1 promotion energies based on semi-empirical approximations, our results find Nd and Dy ions next in line to display the 4fn+1 configuration, consistent with previous reports that describe these ions as “crossover” due to its ability to display both GS configurations depending on the coordinating ligands.We finally correlated the electronic structure of the Ln series with the spatial shape of the metal electron density in both Ln single ions as well as the LnCp3/[LnCp3]− complexes to provide further explanation on the intricate interplay between GS configurations, particularly for ions close to the crossover line. Building upon the work of Sievers and Long,31,50 we investigated changes in the shape of the density resulting from the coordination of the Cp ligands to the Ln3+ center (LnCp3) as well as changes induced by the reduction of these systems ([LnCp3]−). We demonstrate that Ln centers that retain near-spherical densities are more prompt to access 4fn+1 GS configurations, which is supported by a lower energy penalty in the 4f-intraelectron repulsion. Conversely, ions that display pronounced variation in their shapes, particularly going from oblate to prolate, prefer 4fn5d1 GS configurations. The case of Nd(II) and Dy(II) and other ions near the crossover line can be considered as intermediate, where the near-spherical density shape is not retained, but it remains accessible since they do not exhibit marked changes in their density. This leads us to think that Pr(II), Ho(II), and Er(II) could display 4fn+1 configurations if using a suitable crystal field that aligns with their shapes.
These calculations mark an initial step toward a deeper understanding of Ln2+ chemistry. To strengthen these findings, it is essential to extend the analysis to linear geometries and additional coordination frameworks, such as aryloxides or crown ethers, that can stabilize this oxidation state. Ultimately, this study will provide valuable insights into the rational design of environments to optimize various ground state configurations and modulate the spectroscopic properties of new Ln2+ complexes, thereby guiding and enhancing future experimental efforts.
4. Computational methods
Below a summary of the computational methods employed for these calculations is found. More details are given in the ESI.†4.1 Geometry optimizations
The experimental coordinates of and
and  (Ln = La, Ce, Pr, Nd, Sm, Eu, Gd, Tb, Dy, Ho, Er, Tm and Yb) complexes were obtained from the experimental structures13 and optimized in ADF version 2019,53 with no symmetry or geometry constraints at M06-2X/TZP level of theory.54 The relativistic effects were incorporated through the zeroth-order regular approximation (ZORA) of the Dirac equation.55 Finally, analytical frequency calculations were performed on the optimized structures to confirm them as true minima. Since these optimized structures are being subjected to expensive ab initio wavefunction calculations, the SiMe3 groups were replaced with hydrogen atoms as shown in Fig. 1.
(Ln = La, Ce, Pr, Nd, Sm, Eu, Gd, Tb, Dy, Ho, Er, Tm and Yb) complexes were obtained from the experimental structures13 and optimized in ADF version 2019,53 with no symmetry or geometry constraints at M06-2X/TZP level of theory.54 The relativistic effects were incorporated through the zeroth-order regular approximation (ZORA) of the Dirac equation.55 Finally, analytical frequency calculations were performed on the optimized structures to confirm them as true minima. Since these optimized structures are being subjected to expensive ab initio wavefunction calculations, the SiMe3 groups were replaced with hydrogen atoms as shown in Fig. 1.
4.2 Wavefunction calculations
Both LnCp3 and [LnCp3]− complexes along with the Ln2+ and Ln3+ free ions were subjected to ab initio wavefunction calculations using the OpenMolcas software.56 The choice of theoretical approximation and active space was made depending on the lanthanide oxidation state. For Ln3+ and LnCp3 systems, a minimum active space, nf-electrons in 7 orbitals, was calculated through the Complete Active Space Self-Consistent Field (CASSCF) method38 (see details of the multiplicities and roots in Table S1†). Conversely, for the Ln2+ an extended active space including n electrons in 19 orbitals (4f shell + 5f shell + 5d shell orbitals) was calculated through the Restricted Active Space Self-Consistent Field (RASSCF)57 to properly account for the radial correlation as defined by Seijo and Barandiarán (Table S02†).41 Finally in [LnCp3]− systems the active space consisted of n + 2 electrons in 17 orbitals (4f shell + 5f shell + 6s orbital + 5dz2 orbital). Dynamic correlation effects were calculated through MC-pDFT and CASPT2 approximations.43,44 In a final step, the spin–orbit coupling (SOC) was included via state interactions between the CASSCF/RASSCF wavefunctions through the restricted active space state interaction (RASSI) method.584.3 Ligand field DFT calculations
This approach was considered to obtain the 4fn+1 to 4fn5d1 promotion energies corresponding to the Ln3+ free ions. The calculations were performed using the ADF package version 2019.53 The level of theory consisted of the PBE functional with Grimme corrections in its D3 formulation to account for the dispersion forces along with TZP basis sets for all the elements.59 The relativistic effects were incorporated through the ZORA Hamiltonian. The multiplet manifolds of each Ln were calculated by diagonalizing the matrix elements of the LFDFT Hamiltonian.Data availability
The data supporting this article have been included as part of the ESI.†Author contributions
The study was conceived by M. J. B. L., C. C. B., T. E. A., and W. J. E. The theoretical calculations and analysis of the results was performed by M. J. B. L. and C. C. B., W. N. G. M., T. F. J., and W. J. E. contributed with the experimental portion. All the authors contributed to the writing and proofreading the manuscript.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work was supported by the U.S. Department of Energy, Office of Basic Energy Sciences, Chemical Sciences, Geosciences, Biosciences and Heavy Elements Chemistry Program, under award number DE-SC0023693 (T. E. A.) and the U.S. National Science Foundation under award CHE-2154255 (W. J. E). M. J. B.-L. acknowledge the postdoctoral support provided by the Glenn T. Seaborg Institute. The authors thank Professor Zoila Barandiaran for her valuable input on the theoretical treatment of these systems and Valentina Villegas for her help designing the TOC. This work was partially executed at Los Alamos National Laboratory. Los Alamos National Laboratory is operated by Triad National Security, LLC, for the National Nuclear Security Administration of the U.S. Department of Energy (contract no. 89233218CNA000001).References
- D. H. Woen and W. J. Evans, in Handbook on the Physics and Chemistry of Rare Earths, ed. J.-C. G. Bünzli and V. K. Pecharsky, Elsevier, 2016, vol. 50, pp. 337–394 Search PubMed.
- L. R. Morss, Chem. Rev., 1976, 76, 827–841 CrossRef CAS.
- T. N. Poe, M. J. Beltrán-Leiva, C. Celis-Barros, W. L. Nelson, J. M. Sperling, R. E. Baumbach, H. Ramanantoanina, M. Speldrich and T. E. Albrecht-Schönzart, Inorg. Chem., 2021, 60, 7815–7826 CrossRef CAS PubMed.
- S. S. Bokouende, D. N. Kulasekara, S. A. Worku, C. L. Ward, A. B. Kajjam, J. C. Lutter and M. J. Allen, Inorg. Chem., 2024, 63, 9434–9450 CrossRef CAS PubMed.
- L. M. Anderson-Sanchez, J. M. Yu, J. W. Ziller, F. Furche and W. J. Evans, Inorg. Chem., 2023, 62, 706–714 CrossRef CAS PubMed.
- S. A. Moehring, M. J. Beltrán-Leiva, D. Páez-Hernández, R. Arratia-Pérez, J. W. Ziller and W. J. Evans, Chem. – Eur. J., 2018, 24, 18059–18067 CrossRef CAS PubMed.
- T. N. Poe, S. Molinari, M. J. Beltran-Leiva, C. Celis-Barros, H. Ramanantoanina and T. E. Albrecht-Schönzart, Inorg. Chem., 2021, 60, 15196–15207 CrossRef CAS PubMed.
- D. N. Huh, J. W. Ziller and W. J. Evans, Dalton Trans., 2018, 47, 17285–17290 RSC.
- T. N. Poe, S. Molinari, S. Justiniano, G. M. McLeod and T. E. Albrecht-Schönzart, Cryst. Growth Des., 2022, 22, 842–852 CrossRef CAS.
- J. K. Peterson, M. R. MacDonald, J. W. Ziller and W. J. Evans, Organometallics, 2013, 32, 2625–2631 CrossRef CAS.
- M. R. MacDonald, J. E. Bates, J. W. Ziller, F. Furche and W. J. Evans, J. Am. Chem. Soc., 2013, 135, 9857–9868 CrossRef CAS PubMed.
- M. R. MacDonald, J. E. Bates, M. E. Fieser, J. W. Ziller, F. Furche and W. J. Evans, J. Am. Chem. Soc., 2012, 134, 8420–8423 CrossRef CAS PubMed.
- M. E. Fieser, M. R. MacDonald, B. T. Krull, J. E. Bates, J. W. Ziller, F. Furche and W. J. Evans, J. Am. Chem. Soc., 2015, 137, 369–382 CrossRef CAS PubMed.
- P. B. Hitchcock, M. F. Lappert, L. Maron and A. V. Protchenko, Angew. Chem., Int. Ed., 2008, 47, 1488–1491 CrossRef CAS PubMed.
- R. E. MacKenzie, T. Hajdu, J. A. Seed, G. F. S. Whitehead, R. W. Adams, N. F. Chilton, D. Collison, E. J. L. McInnes and C. A. P. Goodwin, Chem. Sci., 2024, 15, 15160–15169 RSC.
- K. R. McClain, C. A. Gould, D. A. Marchiori, H. Kwon, T. T. Nguyen, K. E. Rosenkoetter, D. Kuzmina, F. Tuna, R. D. Britt, J. R. Long and B. G. Harvey, J. Am. Chem. Soc., 2022, 144, 22193–22201 CrossRef CAS PubMed.
- P.-B. Jin, Q.-C. Luo, G. K. Gransbury, I. J. Vitorica-Yrezabal, T. Hajdu, I. Strashnov, E. J. L. McInnes, R. E. P. Winpenny, N. F. Chilton, D. P. Mills and Y.-Z. Zheng, J. Am. Chem. Soc., 2023, 145, 27993–28009 CrossRef CAS PubMed.
- K. Kundu, J. R. K. White, S. A. Moehring, J. M. Yu, J. W. Ziller, F. Furche, W. J. Evans and S. Hill, Nat. Chem., 2022, 14, 392–397 CrossRef CAS PubMed.
- P. W. Smith, J. Hrubý, W. J. Evans, S. Hill and S. G. Minasian, J. Am. Chem. Soc., 2024, 146, 5781–5785 CrossRef CAS PubMed.
- T. F. Jenkins, D. H. Woen, L. N. Mohanam, J. W. Ziller, F. Furche and W. J. Evans, Organometallics, 2018, 37, 3863–3873 CrossRef CAS.
- L. J. Nugent, R. D. Baybarz, J. L. Burnett and J. L. Ryan, J. Phys. Chem., 1973, 77, 1528–1539 CrossRef CAS.
- L. J. Nugent, in Lanthanides and Actinides, University Park Press, Baltimore, 2nd edn, 1975, vol. 7, pp. 195–219 Search PubMed.
- D. S. McClure and Z. Kiss, J. Chem. Phys., 1963, 39, 3251–3257 CrossRef CAS.
- D. A. Johnson, J. Chem. Soc., Dalton Trans., 1974, 1671–1675 RSC.
- A. N. Kamenskaya, Russ. J. Inorg. Chem., 1984, 29, 251–258 Search PubMed.
- N. B. Mikheev and A. N. Kamenskaya, Coord. Chem. Rev., 1991, 109, 1–59 CrossRef CAS.
- N. B. Mikheev, L. N. Auerman, I. A. Rumer, A. N. Kamenskaya and M. Z. Kazakevich, Russ. Chem. Rev., 1992, 76, 827–841 Search PubMed.
- N. B. Mikheev, Inorg. Chim. Acta, 1984, 94, 241–248 CrossRef CAS.
- N. B. Mikheev, Russ. J. Inorg. Chem., 1984, 29, 258–263 Search PubMed.
- P. Dorenbos, J. Phys.: Condens. Matter, 2003, 15, 575 CrossRef CAS.
- J. D. Rinehart and J. R. Long, Chem. Sci., 2011, 2, 2078–2085 RSC.
- L. Brewer, J. Opt. Soc. Am., 1971, 61, 1666–1682 CrossRef CAS.
- P. Dorenbos, J. Lumin., 2000, 91, 91–106 CrossRef CAS.
- J. Tang and P. Zhang, in Lanthanide Single Molecule Magnets, Springer HeidelbergNew York Dordrecht London, 2015, pp. 2–11 Search PubMed.
- E. Loh, Phys. Rev., 1968, 175, 533–536 CrossRef CAS.
- J. Rubio O., J. Phys. Chem. Solids, 1991, 52, 101–174 CrossRef CAS.
- H. Ramanantoanina, M. Sahnoun, A. Barbiero, M. Ferbinteanu and F. Cimpoesu, Phys. Chem. Chem. Phys., 2015, 17, 18547–18557 RSC.
- B. O. Roos, P. R. Taylor and P. E. M. Sigbahn, Chem. Phys., 1980, 48, 157–173 CrossRef CAS.
- A. García-Fuente, F. Cimpoesu, H. Ramanantoanina, B. Herden, C. Daul, M. Suta, C. Wickleder and W. Urland, Chem. Phys. Lett., 2015, 622, 120–123 CrossRef.
- H. Ramanantoanina, F. Cimpoesu, C. Göttel, M. Sahnoun, B. Herden, M. Suta, C. Wickleder, W. Urland and C. Daul, Inorg. Chem., 2015, 54, 8319–8326 CrossRef CAS PubMed.
- Z. Barandiarán and L. Seijo, J. Chem. Phys., 2013, 138, 074102 CrossRef PubMed.
- C. Angeli, R. Cimiraglia, S. Evangelisti, T. Leininger and J.-P. Malrieu, J. Chem. Phys., 2001, 114, 10252–10264 CrossRef CAS.
- J. Finley, P.-Å. Malmqvist, B. O. Roos and L. Serrano-Andrés, Chem. Phys. Lett., 1998, 288, 299–306 CrossRef CAS.
- L. Gagliardi, D. G. Truhlar, G. Li Manni, R. K. Carlson, C. E. Hoyer and J. L. Bao, Acc. Chem. Res., 2017, 50, 66–73 CrossRef CAS PubMed.
- V. E. Fleischauer, G. Ganguly, D. H. Woen, N. J. Wolford, W. J. Evans, J. Autschbach and M. L. Neidig, Organometallics, 2019, 38, 3124–3131 CrossRef CAS.
- H. P. Beck, Z. Naturforsch. B, 1976, 31, 1548–1549 CrossRef.
- F. Jaroschik, F. Nief, X.-F. Le Goff and L. Ricard, Organometallics, 2007, 26, 1123–1125 CrossRef CAS.
- F. Jaroschik, A. Momin, F. Nief, X.-F. Le Goff, G. B. Deacon and P. C. Junk, Angew. Chem., Int. Ed., 2009, 48, 1117–1121 CrossRef CAS PubMed.
- M. D. Walter, D. Bentz, F. Weber, O. Schmitt, G. Wolmershäuser and H. Sitzmann, New J. Chem., 2007, 31, 305–318 RSC.
- J. Sievers, Z. Phys. B: Condens. Matter, 1982, 45, 289–296 CrossRef CAS.
- J. Tang and P. Zhang, Lanthanide Single Molecule Magnets, Springer Berlin, Heidelberg, 1st edn, 2015 Search PubMed.
- R. Skomski and D. J. Sellmyer, J. Rare Earths, 2009, 27, 675–679 CrossRef.
- G. te Velde, F. M. Bickelhaupt, E. J. Baerend, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967 CrossRef CAS.
- E. Van Lenthe and E. J. Baerends, J. Comput. Chem., 2003, 24, 1142–1156 CrossRef CAS PubMed.
- E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1993, 99, 4597–4610 CrossRef CAS.
- G. Li Manni, I. F. Galván, A. Alavi, F. Aleotti, F. Aquilante, J. Autschbach, D. Avagliano, A. Baiardi, J. J. Bao, S. Battaglia, L. Birnoschi, A. Blanco-González, S. I. Bokarev, R. Broer, R. Cacciari, P. B. Calio, R. K. Carlson, R. Carvalho Couto, L. Cerdán, L. F. Chibotaru, N. F. Chilton, J. R. Church, I. Conti, S. Coriani, J. Cuéllar-Zuquin, R. E. Daoud, N. Dattani, P. Decleva, C. de Graaf, M. G. Delcey, L. De Vico, W. Dobrautz, S. S. Dong, R. Feng, N. Ferré, M. Filatov(Gulak), L. Gagliardi, M. Garavelli, L. González, Y. Guan, M. Guo, M. R. Hennefarth, M. R. Hermes, C. E. Hoyer, M. Huix-Rotllant, V. K. Jaiswal, A. Kaiser, D. S. Kaliakin, M. Khamesian, D. S. King, V. Kochetov, M. Krośnicki, A. A. Kumaar, E. D. Larsson, S. Lehtola, M.-B. Lepetit, H. Lischka, P. López Ríos, M. Lundberg, D. Ma, S. Mai, P. Marquetand, I. C. D. Merritt, F. Montorsi, M. Mörchen, A. Nenov, V. H. A. Nguyen, Y. Nishimoto, M. S. Oakley, M. Olivucci, M. Oppel, D. Padula, R. Pandharkar, Q. M. Phung, F. Plasser, G. Raggi, E. Rebolini, M. Reiher, I. Rivalta, D. Roca-Sanjuán, T. Romig, A. A. Safari, A. Sánchez-Mansilla, A. M. Sand, I. Schapiro, T. R. Scott, J. Segarra-Martí, F. Segatta, D.-C. Sergentu, P. Sharma, R. Shepard, Y. Shu, J. K. Staab, T. P. Straatsma, L. K. Sørensen, B. N. C. Tenorio, D. G. Truhlar, L. Ungur, M. Vacher, V. Veryazov, T. A. Voß, O. Weser, D. Wu, X. Yang, D. Yarkony, C. Zhou, J. P. Zobel and R. Lindh, J. Chem. Theory Comput., 2023, 19, 6933–6991 CrossRef CAS PubMed.
- P. A. Malmqvist, A. Rendell and B. O. Roos, J. Phys. Chem., 1990, 94, 5477–5482 CrossRef CAS.
- P. Å. Malmqvist, B. O. Roos and B. Schimmelpfennig, Chem. Phys. Lett., 2002, 357, 230–240 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sc05438e |
| This journal is © The Royal Society of Chemistry 2025 |