Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Carrier density and delocalization signatures in doped carbon nanotubes from quantitative magnetic resonance†
M. Alejandra
Hermosilla-Palacios
a,
Marissa
Martinez
a,
Evan A.
Doud
b,
Tobias
Hertel
 c,
Alexander M.
Spokoyny
c,
Alexander M.
Spokoyny
 b,
Sofie
Cambré
b,
Sofie
Cambré
 d,
Wim
Wenseleers
d,
Wim
Wenseleers
 d,
Yong-Hyun
Kim
d,
Yong-Hyun
Kim
 e,
Andrew J.
Ferguson
e,
Andrew J.
Ferguson
 a and
Jeffrey L.
Blackburn
a and
Jeffrey L.
Blackburn
 *a
*a
aNational Renewable Energy Laboratory, Golden, Colorado 80401, USA. E-mail: jeffrey.blackburn@nrel.gov
bDepartment of Chemistry and Biochemistry, University of California, Los Angeles, California 90095, USA
cInstitute of Physical and Theoretical Chemistry, Julius-Maximilian, University Würzburg, 97074, Würzburg, Germany
dDepartment of Physics, University of Antwerp, Antwerp 2610, Belgium
eDepartment of Physics, Korea Advanced Institute of Science and Technology, Daejeon 34141, Republic of Korea
First published on 22nd November 2023
Abstract
High-performance semiconductor materials and devices are needed to supply the growing energy and computing demand. Organic semiconductors (OSCs) are attractive options for opto-electronic devices, due to their low cost, extensive tunability, easy fabrication, and flexibility. Semiconducting single-walled carbon nanotubes (s-SWCNTs) have been extensively studied due to their high carrier mobility, stability and opto-electronic tunability. Although molecular charge transfer doping affords widely tunable carrier density and conductivity in s-SWCNTs (and OSCs in general), a pervasive challenge for such systems is reliable measurement of charge carrier density and mobility. In this work we demonstrate a direct quantification of charge carrier density, and by extension carrier mobility, in chemically doped s-SWCNTs by a nuclear magnetic resonance approach. The experimental results are verified by a phase-space filling doping model, and we suggest this approach should be broadly applicable for OSCs. Our results show that hole mobility in doped s-SWCNT networks increases with increasing charge carrier density, a finding that is contrary to that expected for mobility limited by ionized impurity scattering. We discuss the implications of this important finding for additional tunability and applicability of s-SWCNT and OSC devices.
New conceptsSemiconducting single-walled carbon nanotubes (s-SWCNTs) are an important class of π-conjugated organic semiconductors (OSCs) that can enable emerging opto-electronic applications. Understanding charge transport mechanisms in s-SWCNTs (and OSCs generally) is essential for material and device design. Applications like photovoltaics, sensors, light-emitting diodes, field-effect transistors, and thermoelectric devices require good electrical conductivity and carrier mobility. Common methods to measure conductivity in OSCs do not allow to independently measure charge carrier density or mobility, making it difficult to answer important fundamental and applied questions and hindering performance optimization. To address this knowledge gap, we develop a combined approach, using optical absorption and nuclear magnetic resonance spectroscopy, to directly measure charge carrier density in doped s-SWCNTs. We demonstrate that carrier density impacts charge delocalization, leading to a carrier density-dependent mobility that is contrary to that expected for mobility limited by ionized impurity scattering. Combining simulations with our experimental data produces a correlation curve that enables determination of carrier density in doped s-SWCNTs by rapid and readily available absorption spectroscopy measurements. The results provide a valuable roadmap to the OSC community for tuning, quantifying, and optimizing carrier density for a broad range of energy harvesting and optoelectronic applications. |
Introduction
Versatile semiconductors are needed to supply growing energy and computing demands.1,2 Organic semiconductors (OSCs) are attractive for many applications such as photovoltaic cells, field-effect transistors, thermoelectrics, sensors and light-emitting diodes because they are inexpensive, easy to fabricate, and flexible.3–6 Semiconducting single-walled carbon nanotubes (s-SWCNTs) – an important class of nanoscale OSCs with high carrier mobility, strong optical transitions, and chemical stability16–19 – can enable emerging applications in digital logic, energy harvesting, and quantum information science.20–24 Importantly, understanding operational mechanisms and optimizing the performance of s-SWCNTs and other OSCs in such applications relies on both tuning and quantifying charge carrier type (electron/hole), density, and conductivity.The most common way to tune carrier density and conductivity in OSCs is by doping with p- or n-type molecular dopants.7–11 Unfortunately, most common methods to measure OSC conductivity do not allow to separately extract charge carrier density and mobility. For example, Hall effect measurements that are commonly used to extract carrier density and mobility in crystalline inorganic semiconductors, are not well suited for amorphous OSCs.25 As such, most studies on OSC (and s-SWCNT) transport must make several assumptions to interpret carrier density-dependent mechanisms or performance trends.12–15
Nuclear magnetic resonance (NMR) has been used to indirectly estimate charge carrier density in inorganic semiconductors26,27 such as Cu2−xSe nanoparticles,28 based on the so-called Knight shift induced by free holes.29 The dependence of the spin–lattice relaxation rate on temperature and carrier density, based on the Korringa behavior,30 can be used to quantify free carriers. Inspired by these studies, we introduce a combined method, utilizing 19F NMR and absorption measurements on s-SWCNTs doped p-type with F-containing molecular dopants, to directly quantify free charge carriers and extract carrier mobility. Our measurements demonstrate that hole mobility increases substantially with increasing carrier density in doped s-SWCNT networks, reaching ca. 40 cm2 V−1 s−1 at high carrier density. Consistently, we observe a carrier density-dependent NMR chemical shift for dopant counterions, consistent with both the carrier density-dependent mobility of s-SWCNT holes and a Coulomb screening-induced modulation of the NMR ring current effect. This method can be broadly applied to a wide variety of π-conjugated semiconductors by utilizing dopants with suitable NMR-active nuclei as reporters.
Results and discussion
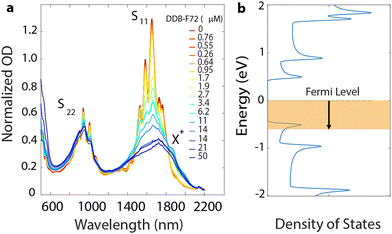
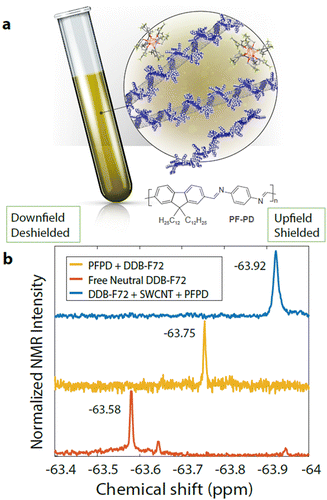
Bleaching of the first excitonic optical transition,31 S11, induced by the phase space filling effect, is commonly used as a proxy for the relative free charge carrier density in SWCNTs.12,32 The absorption spectra shown in Fig. 1a show this bleaching upon doping SWCNTs p-type with non-covalently adsorbed dodecaborane clusters (DDB-F72).33–35 Doping also produces a new envelope of overlapping, red-shifted absorption peaks, attributed to the absorption of positively charged excitons (trions, X+). Plasma torch (PT) SWCNTs used in this work yield several chiralities resulting in the aforementioned envelope (i.e. sum of all excitonic transitions, S11, corresponding to each chirality). Fig. 1b schematically depicts the shift in Fermi level induced by DDB-F72 doping, that produces the exciton bleach and progressively increases conductivity.36 We attribute incomplete bleaching at high doping concentrations to steric constraints imposed by the large DDB-F72 molecules, given that the redox potential of the dopant has been measured previously34,35 (Fig. 1 and Fig. S1, ESI†) and it is expected to efficiently remove an electron from the s-SWCNTs. While the exciton bleach extent offers valuable insights, it cannot independently quantify carrier density. Complementary quantitative methods are thus essential for a more comprehensive understanding and validation of molecular doping mechanisms.37,38In this work, we quantified free charge carriers using solution-phase 19F NMR (Fig. 2a) since DDB-F72 contains 72 fluorine atoms and the bound dopant counter anion has a unique 19F NMR chemical shift (vide infra). Fig. 2b shows 19F NMR spectra for control samples of neutral DDB-F72 in deuterated (d8)-toluene, as well as DDB-F72 mixed with the polymer39 used to disperse the s-SWCNTs. The 19F chemical shift of DDB-F72 doped s-SWCNTs is shifted substantially up-field (higher ppm) from both control samples. The chemical shifts for each sample arise from the unique environments of atoms. The large up-field shift of the s-SWCNT sample, relative to the neutral molecule, is consistent with the electronegativity and π-donating ability introduced by the SWCNT, which serve to shield the magnetic field.40
Additionally, the linewidth of the signal reports on the nature of the interaction of the dopant with other species in solution. Freely tumbling unbound molecules typically display narrow linewidths, while rotationally hindered bound molecules display broadened linewidths.41 From the chemical shifts and linewidths in Fig. 2b we can conclude that the signal for the s-SWCNT sample is dominated by bound dopant anions that have removed an electron from the occupied density of states of the s-SWCNTs. Control polymer doping experiments where the excitonic transition of the wrapping polymer was monitored and compared to the s-SWCNTs transition, Fig. S2a (ESI†), also support the claim that only dopant injecting charge onto the SWCNTs is quantified. The polymer excitonic transition shows no measurable bleaching, even when the S11 has been fully bleached (Fig. S2b, ESI†).
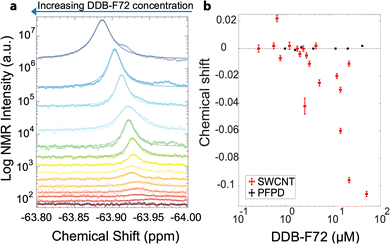
Fig. 3a displays 19F NMR spectra for the s-SWCNT doping series shown in Fig. 1. With increasing dopant concentration, the [DDB-F72]−1 peak intensity increases, and the area under each curve provides the total number of fluorine atoms. Interestingly, increasing dopant concentration also induces a downfield chemical shift (Fig. 3b) that we assign to charge delocalization of the hole distribution in the s-SWCNTs. For higher doping concentrations, the hole distributions in s-SWCNTs for individual dopants start to merge and delocalize.32,34 This carrier density-dependent delocalization should reduce the coulomb attraction between hole and [DDB-F72]−1 counterion, resulting in a larger distance between the SWCNT holes and their counterions, [DDB-F72]−1, as the dopant concentration increases (Fig. 3a). Additional interactions between dopants are also expected at very high dopant concentrations (above 40 μM) due to aggregation. Aggregation shows as additional NMR signal as seen for the polymer control NMR experiment (Fig. S6, ESI†) and as seen in the top two NMR spectra in Fig. 3a. The aggregation contribution is avoided by only integrating under the curve of the main peak.
A known NMR effect for π-conjugated systems is the ring current effect,42–44 where nuclei in proximity to (above or below) the plane of benzene ring(s) are shielded from the magnetic field and move up-field in chemical shift. This is an effect only measurable at adsorption distances, i.e., bound dopants. The shielding is inversely proportional to the distance between the probing nucleus and benzene rings.45 As the distance increases between these two species, the ring current-induced shielding decreases and the chemical shift moves downfield. Thus, the observation of a strong concentration-dependent ring current effect confirms the conclusion from our prior solid-state doping study that the s-SWCNT hole delocalization increases with increasing carrier density.34 In contrast, the polymer doping series does not shift downfield with increased DDB-F72 concentration (Fig. 3b), suggesting weak physical interaction and ineffective doping, consistent with the expected band alignment34 and absence of DDB-induced bleach of the polymer's exciton transition (Fig. S2, ESI†).
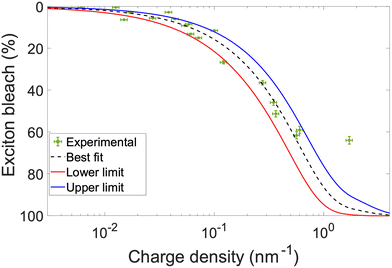
To calculate charge density, the area under each 19F NMR spectrum is integrated, with a known concentration standard serving as reference. The area under the curve is equal to the number of F atoms in the solution. Each DDB-F72 molecule contains 72 F atoms, thus the number of DDB-F72 molecules is the integrated area divided by 72. For the s-SWCNT samples, we do not observe other peaks that correspond to unbound DDB-F72 molecules (refer to Fig. S7, ESI†), i.e., the calculated DDB-F72 number of molecules correspond only to bound dopants. Since each dopant contributes one hole, the number of holes (charges on the SWCNTs) is equal to the number of DDB-F72 anions calculated from NMR. The correlation between NMR-extracted hole density and exciton bleach is presented in Fig. 4, together with a fit modelled on the phase-space filling model introduced by Eckstein et al.32 Complete derivation and fitting is shown in the ESI.† The model uses the density of states from (10,8) SWCNTs as a representative s-SWCNT species found in high abundance from a detailed analysis of photoluminescence excitation (PLE) maps (Fig. S4, ESI†).
The best fit was obtained for an exciton size of 3 nm and hole effective mass of 0.06 me, see Fig. S10 and S11 (ESI†). Good agreement is found between the experimental data and the model. DDB-F72 doping does not achieve 100% exciton bleaching due to steric hindrance of the bulky counterion, producing minor deviation at high doping levels. The exciton bleach magnitude was corrected by removing the contribution of the trion band, X+, to the total area under the absorption curve (refer to Fig. S12 and calculations shown in ESI†).32 Since PT SWCNTs yield several chiralities, we expect nanotubes with larger diameter/smaller band gaps to dope faster, also observed initially in Fig. 1a. As dopant concentration increases we expect all SWCNTs to dope effectively. The calculations in the ESI† took into account several chiralities and corresponding contribution to find the best fit to correctly calculate the length of nm for each nanotube chirality present.
From the model fit in Fig. 4, additional information can be obtained. If the exciton bleach is calculated from a simple absorbance measurement, charge carrier density can be obtained for similar diameter distributions. Since the exciton bleach induced by phase-space filling occurs independent of the local SWCNT environment, the model can be used to determine carrier density in both solution-phase and solid-state SWCNT samples. As such, the extracted carrier densities can be paired with concomitantly measured conductivity values to evaluate charge carrier mobility. We demonstrate this approach in Fig. 5 by extracting dopant concentration-dependent charge carrier densities and mobilities from the exciton bleach and conductivity values reported in our recent doping study of plasma torch thin films.12 Two different dopants are compared, F4TCNQ and DDB-F72.
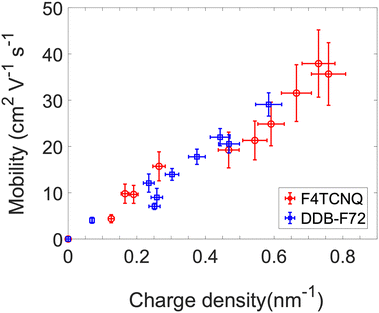 | ||
| Fig. 5 Mobility calculated from conductivity measurements based on phase-space filling doping model. PT PF-PD doped with F4TCNQ (red circles) and DDB-F72 (blue squares). | ||
Importantly, Fig. 5 demonstrates that hole mobility does not remain static, but instead steadily increases, as charge carrier density increases. This is an important finding, since charge carrier density has often been calculated from conductivity measurements based on static mobility values.17,46,47 The increase in mobility with carrier density may have several sources. Zaumseil et al.48 have attributed a similar trend in s-SWCNT field-effect transistors to energetic disorder in the SWCNT network. The semi-localized transport (SLoT) model,49 applied recently to s-SWCNT networks and a variety of semiconducting polymer films, suggests that charge carriers become more delocalized (i.e. mobility increases) as carrier density increases and the Coulomb potential wells of individual charge carriers overlap. Finally, recent calculations predict that increasing dopant concentration substantially increases the dielectric constant of the local environment in doped π-conjugated semiconductors, concomitantly decreasing the carrier-counterion binding energy.50 With a means to now quantify carrier density and mobility in these doped s-SWCNT networks, we plan to explore these hypotheses in further studies.
Conclusions
We have demonstrated an NMR-based method to directly quantify charge carrier density in redox-doped s-SWCNTs, a method that can be extrapolated to other OSCs systems and dopants with NMR active nuclei. Concentration-dependent NMR shifts for the dopant counterions suggest that the SWCNT hole density becomes more delocalized, reducing the carrier-counterion Coulomb attraction, with increasing carrier density. The calculated mobility values show a charge carrier density dependence arising from enhanced delocalization, potentially in line with recent calculations predicting a doping-induced increase of local environment dielectric constant. Mobility is an important parameter for the performance of OSCs and nanoscale semiconductors in opto-electronic devices. The proper determination of this variable is crucial to understand charge transport leading to improvements in material design or device design.Experimental section
PT SWCNT dispersion preparation
Polymer solution is first prepared with concentration of 2 mg mL−1 in deuterated toluene. Poly[(9,9-di-n-dodecyl-2,7-fluorendiyl-dimethine)-(1,4-phenylene-dinitrilomethine)] (PF-PD) was synthesized according to literature procedure.39 Heated bath sonication of the polymer solution is necessary to ensure full solvation of the polymer. Plasma-torch (PT) SWCNTs (RN-020), were purchased from NanoIntegris, Quebec, Canada. The raw soot was first rinsed with toluene and centrifuged (2500 rpm) to remove soluble fullerenes. The rinsed SWCNTs were left to dry overnight under low N2 flow. The polymer solution is added to the SWCNTs at a concentration of 2 mg mL−1 with maximum volume of ca. 15 mL in a 20 mL borosilicate scintillation vial. The mixture is then processed in the vial with a probe tip ultrasonic processor (Cole Parmer CPX-750, ½′′ tip) for 20 min at 40% amplitude. During tip sonication, the vial is submerged in a slurry of ethanol/dry ice mixture to increase the yield of dispersed SWCNTs. Immediately after tip sonication, the contents of the vial are transferred to a centrifuge tube and processed at 20 °C, 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 rpm, for 5 min (Beckman Coulter L-100 XP ultracentrifuge, SW-32 Ti rotor). The supernatant containing the dispersed SWCNTs, and excess polymer is collected via pipette. No polymer removal steps were performed to ensure SWCNT dispersion stability. The supernatant was concentrated ca. 5 times the original concentration to improve the signal-to-noise ratio (S/N) in the 19F NMR studies. PT SWCNTs contain several chiralities, the different chiralities and their distribution was determined based on PLE experiments and their fit, refer to Fig. S3–S5 and the ESI,† for a complete list and methodology.
200 rpm, for 5 min (Beckman Coulter L-100 XP ultracentrifuge, SW-32 Ti rotor). The supernatant containing the dispersed SWCNTs, and excess polymer is collected via pipette. No polymer removal steps were performed to ensure SWCNT dispersion stability. The supernatant was concentrated ca. 5 times the original concentration to improve the signal-to-noise ratio (S/N) in the 19F NMR studies. PT SWCNTs contain several chiralities, the different chiralities and their distribution was determined based on PLE experiments and their fit, refer to Fig. S3–S5 and the ESI,† for a complete list and methodology.
Doping
Dodecaborane clusters substituted with fluorinated aryl groups were synthesized according to literature procedure.35 The anhydrous deuterated toluene required additional molecular sieves treatment to ensure stability of the doping solution. A stock solution of 1 mg mL−1 was prepared for the different doping steps. DDB-F72 molecule shown with van der Waals radii included is shown in Fig. S1 (ESI†) for reference.Absorption measurements
Absorption spectra were measured for each SWCNT dispersion, both before and after achieving the desired doping level (Cary 5000 UV-Vis-NIR spectrophotometer, Agilent). Deuterated toluene was used for all measurements to prevent strong C–D stretch in the 2000–2200 nm region, and to prevent NMR line broadening by coupling to other active nuclei.19F NMR measurements
Measurements were performed on a Bruker Ascend™ 300 spectrometer operating at 300 MHz (7 Tesla). In all experiments, the spin–lattice relaxation times were considered to measure NMR spectra under quantitative conditions. Deuterated toluene was used for all samples. The internal standard used was 1,1,1,3,3,3-hexafluoro-2-propanol.Photoluminescence excitation (PLE) spectroscopy
PLE was measured using an in-house developed setup comprising a pulsed Xe-lamp for excitation (Edinburgh Instruments, custom adapted Xe900/XP920) equipped with a 300 mm focal length monochromator (Acton SpectraPro 2355). The excitation wavelength is varied in 5 nm steps from 600 nm to 1200 nm using either a 1200 g mm−1 grating with a slit-selected average resolution of 6 nm (600–1140 nm) or a 600 g mm−1 grating with a slit-selected average resolution of 12 nm (1140–1200 nm). The PL is detected under a 90° angle using a 150 mm focal length spectrograph (Acton SpectraPro 2156) with a 150 g mm−1 grating with a slit-selected average resolution of 16 nm, and with a liquid nitrogen cooled extended InGaAs photodiode array detector with a sensitivity up to 2.2 μm (Princeton Instruments OMA V:1024/LN-2.2). Samples were contained in a 60 μL quartz microcell with 3 mm path length. PLE spectra were corrected for variations in lamp excitation power, sensitivity of combined detector, gratings, and filters, and for reabsorption in the optical excitation and emission paths. To this end, samples were diluted in deuterated toluene to an absorbance of less than 0.3 (3 mm pathlength) over the full excitation and emission region to be in the linear correctable reabsorption regime.Author contributions
J. Blackburn and A. Hermosilla-Palacios: conception of the experiments, methodology, data curation, visualization, and writing original draft. A. Hermosilla-Palacios: phase-space simulation calculations. M. Martinez: NMR experiments methodology. S. Cambré and W. Wenseleers: PLE experiments and PLE fitting. E. Doud and A. Spokoyny: DDB-F72 dopants synthesis. Y. Kim: density of states calculations. T. Hertel: supervised phase-space simulation calculations. A. Ferguson: absorption fitting and analysis.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was authored, in part, by the National Renewable Energy Laboratory, operated by the Alliance for Sustainable Energy, LLC, for the US Department of Energy (DOE) under contract no. DE-AC36-08GO28308. This study was primarily supported by the Solar Photochemistry Program, Division of Chemical Sciences, Geosciences, and Biosciences, Office of Basic Energy Sciences, US DOE. This funding supported work by M. A. H. P., M. M., A. J. F., and J. L. B. on SWCNT dispersion and doping development, absorption and NMR measurements, and experimental analysis and simulation. Y. H. K. was supported by the National Research Foundation of Korea (NRF-2019M3D1A1078302), for DFT calculations. A. M. S. thanks NIGMS (MIRA, R35GM124746) for funding the synthesis of the dopant molecules. S. C. and W. W. acknowledge funding from the Research Foundation – Flanders (FWO), through its project G036618N, for work on PLE spectroscopy and simulation. The views expressed in the article do not necessarily represent the views of the DOE or the US government.References
- C.-F. Chien, Y.-J. Chen and J.-T. Peng, Manufacturing intelligence for semiconductor demand forecast based on technology diffusion and product life cycle, Int. J. Prod. Econ., 2010, 128, 496–509 CrossRef
.
-
T. Thien, T. Blank, B. Lunz and D. U. Sauer, Electrochemical Energy Storage for Renewable Sources and Grid Balancing, Elsevier, 2015, pp. 437–452 Search PubMed
.
- S. Wei, L. Liu, X. Huang, Y. Zhang, F. Liu, L. Deng, E. Bilotti and G. Chen, Flexible and Foldable Films of SWCNT Thermoelectric Composites and an S-Shape Thermoelectric Generator with a Vertical Temperature Gradient, ACS Appl. Mater. Interfaces, 2022, 14, 5973–5982 CrossRef CAS
.
- Z. Zhang, W. Yan, Y. Chen, S. Chen, G. Jia, J. Sheng, S. Zhu, Z. Xu, X. Zhang and Y. Li, Stable Doping of Single-Walled Carbon Nanotubes for Flexible Transparent Conductive Films, ACS Nano, 2022, 16, 1063–1071 CrossRef CAS PubMed
.
- X. Zhao, H. Zhang, J. Zhang, J. Liu, M. Lei and L. Jiang, Organic Semiconductor Single Crystal Arrays: Preparation and Applications, Adv. Sci., 2023, 10, 2300483 CrossRef CAS
.
- S. E. Root, S. Savagatrup, A. D. Printz, D. Rodriquez and D. J. Lipomi, Mechanical Properties of Organic Semiconductors for Stretchable, Highly Flexible, and Mechanically Robust Electronics, Chem. Rev., 2017, 117, 6467–6499 CrossRef CAS
.
- S. Hutsch, M. Panhans and F. Ortmann, Charge carrier mobilities of organic semiconductors: ab initio simulations with mode-specific treatment of molecular vibrations, npj Comput. Mater., 2022, 8, 228 CrossRef CAS
.
- V. Coropceanu, J. Cornil, D. A. Da Silva Filho, Y. Olivier, R. Silbey and J.-L. Brédas, Charge Transport in Organic Semiconductors, Chem. Rev., 2007, 107, 926–952 CrossRef CAS PubMed
.
- M. Koopmans, M. A. T. Leiviskä, J. Liu, J. Dong, L. Qiu, J. C. Hummelen, G. Portale, M. C. Heiber and L. J. A. Koster, Electrical Conductivity of Doped Organic Semiconductors Limited by Carrier–Carrier Interactions, ACS Appl. Mater. Interfaces, 2020, 12, 56222–56230 CrossRef CAS
.
- J. H. Gosling, O. Makarovsky, F. Wang, N. D. Cottam, M. T. Greenaway, A. Patanè, R. D. Wildman, C. J. Tuck, L. Turyanska and T. M. Fromhold, Universal mobility characteristics of graphene originating from charge scattering by ionised impurities, Commun. Phys., 2021, 4, 30 CrossRef CAS
.
- B. D. Paulsen and C. D. Frisbie, Dependence of Conductivity on Charge Density and Electrochemical Potential in Polymer Semiconductors Gated with Ionic Liquids, J. Phys. Chem. C, 2012, 116, 3132–3141 CrossRef CAS
.
- B. A. MacLeod, N. J. Stanton, I. E. Gould, D. Wesenberg, R. Ihly, Z. R. Owczarczyk, K. E. Hurst, C. S. Fewox, C. N. Folmar, K. Holman Hughes, B. L. Zink, J. L. Blackburn and A. J. Ferguson, Large n- and p-type thermoelectric power factors from doped semiconducting single-walled carbon nanotube thin films, Energy Environ. Sci., 2017, 10, 2168–2179 RSC
.
- S. Mouri and K. Matsuda, Exciton-hole interactions in hole-doped single-walled carbon nanotubes evaluated by absorption spectral changes, J. Appl. Phys., 2012, 111, 094309 CrossRef
.
- O. T. Zaremba, A. E. Goldt, E. M. Khabushev, A. S. Anisimov and A. G. Nasibulin, Highly efficient doping of carbon nanotube films with chloroauric acid by dip-coating, Mater. Sci. Eng. B, 2022, 278, 115648 CrossRef CAS
.
- K. Z. Milowska, M. Krzywiecki, M. C. Payne and D. Janas, Effective doping of single-walled carbon nanotube films with bromine under ultrasound, Mater. Des., 2022, 213, 110310 CrossRef CAS
.
- R. Ihly, K. S. Mistry, A. J. Ferguson, T. T. Clikeman, B. W. Larson, O. Reid, O. V. Boltalina, S. H. Strauss, G. Rumbles and J. L. Blackburn, Tuning the driving force for exciton dissociation in single-walled carbon nanotube heterojunctions, Nat. Chem., 2016, 8, 603–609 CrossRef CAS PubMed
.
- T. Dürkop, S. A. Getty, E. Cobas and M. S. Fuhrer, Extraordinary Mobility in Semiconducting Carbon Nanotubes, Nano Lett., 2004, 4, 35–39 CrossRef
.
- J. Campo, S. Cambré, B. Botka, J. Obrzut, W. Wenseleers and J. A. Fagan, Optical Property Tuning of Single-Wall Carbon Nanotubes by Endohedral Encapsulation of a Wide Variety of Dielectric Molecules, ACS Nano, 2021, 15, 2301–2317 CrossRef CAS PubMed
.
- M. Zheng and B. A. Diner, Solution Redox Chemistry of Carbon Nanotubes, J. Am. Chem. Soc., 2004, 126, 15490–15494 CrossRef CAS PubMed
.
- M. J. Shea and M. S. Arnold, 1% solar cells derived from ultrathin carbon nanotube photoabsorbing films, Appl. Phys. Lett., 2013, 102, 243101 CrossRef
.
- S. L. Guillot, K. S. Mistry, A. D. Avery, J. Richard, A.-M. Dowgiallo, P. F. Ndione, J. van de Lagemaat, M. O. Reese and J. L. Blackburn, Precision printing and optical modeling of ultrathin SWCNT/C 60 heterojunction solar cells, Nanoscale, 2015, 7, 6556–6566 RSC
.
- Y. Zhong, M. T. Trinh, R. Chen, W. Wang, P. P. Khlyabich, B. Kumar, Q. Xu, C.-Y. Nam, M. Y. Sfeir, C. Black, M. L. Steigerwald, Y.-L. Loo, S. Xiao, F. Ng, X.-Y. Zhu and C. Nuckolls, Efficient Organic Solar Cells with Helical Perylene Diimide Electron Acceptors, J. Am. Chem. Soc., 2014, 136, 15215–15221 CrossRef CAS PubMed
.
- H. Hartleb, F. Späth and T. Hertel, Evidence for Strong Electronic Correlations in the Spectra of Gate-Doped Single-Wall Carbon Nanotubes, ACS Nano, 2015, 9, 10461–10470 CrossRef CAS PubMed
.
- J. Li, P. H. Q. Pham, W. Zhou, T. D. Pham and P. J. Burke, Carbon-Nanotube–Electrolyte Interface: Quantum and Electric Double Layer Capacitance, ACS Nano, 2018, 12, 9763–9774 CrossRef CAS
.
- G. Huseynova, J. Lee, J.-H. Lee and J.-H. Lee, Charge generation efficiency of electrically doped organic semiconductors, Mater. Today Energy, 2021, 21, 100709 CrossRef CAS
.
- E. M. Levin, Effects of Ge substitution in GeTe by Ag or Sb on the Seebeck coefficient and carrier concentration derived from Te 125 NMR, Phys. Rev. B, 2016, 93, 045209 CrossRef
.
- E. M. Levin, B. A. Cook, K. Ahn, M. G. Kanatzidis and K. Schmidt-Rohr, Electronic inhomogeneity and Ag:Sb imbalance of Ag1−yPb18Sb1+zTe20 high-performance thermoelectrics elucidated by 125Te and 207Pb NMR, Phys. Rev. B, 2009, 80, 115211 CrossRef
.
- L. E. Marbella, X. Y. Gan, D. C. Kaseman and J. E. Millstone, Correlating Carrier Density and Emergent Plasmonic Features in Cu2−xSe Nanoparticles, Nano Lett., 2017, 17, 2414–2419 CrossRef CAS
.
-
W. D. Knight, Solid State Physics, Academic Press, 1st edn, 1956, vol. 2, pp. 93–136 Search PubMed
.
- J. Korringa, Nuclear magnetic relaxation and resonnance line shift in metals, Physica, 1950, 16, 601–610 CrossRef CAS
.
- F. Wang, G. Dukovic, L. E. Brus and T. F. Heinz, The Optical Resonances in Carbon Nanotubes Arise from Excitons, Science, 2005, 308, 838–841 CrossRef CAS PubMed
.
- K. H. Eckstein, F. Oberndorfer, M. M. Achsnich, F. Schöppler and T. Hertel, Quantifying Doping Levels in Carbon Nanotubes by Optical Spectroscopy, J. Phys. Chem. C, 2019, 123, 30001–30006 CrossRef CAS
.
- A. I. Wixtrom, Y. Shao, D. Jung, C. W. Machan, S. N. Kevork, E. A. Qian, J. C. Axtell, S. I. Khan, C. P. Kubiak and A. M. Spokoyny, Rapid synthesis of redox-active dodecaborane B 12 (OR) 12 clusters under ambient conditions, Inorg. Chem. Front., 2016, 3, 711–717 RSC
.
- T. L. Murrey, T. J. Aubry, O. L. Ruiz, K. A. Thurman, K. H. Eckstein, E. A. Doud, J. M. Stauber, A. M. Spokoyny, B. J. Schwartz, T. Hertel, J. L. Blackburn and A. J. Ferguson, Tuning counterion chemistry to reduce carrier localization in doped semiconducting carbon nanotube networks, Cell Rep. Phys. Sci., 2023, 4, 101407 CrossRef CAS
.
- T. J. Aubry, J. C. Axtell, V. M. Basile, K. J. Winchell, J. R. Lindemuth, T. M. Porter, J.-Y. Liu, A. N. Alexandrova, C. P. Kubiak, S. H. Tolbert, A. M. Spokoyny and B. J. Schwartz, Dodecaborane-Based Dopants Designed to Shield Anion Electrostatics Lead to Increased Carrier Mobility in a Doped Conjugated Polymer, Adv. Mater., 2019, 1805647 CrossRef PubMed
.
- B. Kumanek, K. Z. Milowska, Ł. Przypis, G. Stando, K. Matuszek, D. MacFarlane, M. C. Payne and D. Janas, Doping Engineering of Single-Walled Carbon Nanotubes by Nitrogen Compounds Using Basicity and Alignment, ACS Appl. Mater. Interfaces, 2022, 14, 25861–25877 CrossRef CAS PubMed
.
- I. E. Jacobs and A. J. Moulé, Controlling Molecular Doping in Organic Semiconductors, Adv. Mater., 2017, 29, 1703063 CrossRef
.
- I. Salzmann, G. Heimel, M. Oehzelt, S. Winkler and N. Koch, Molecular Electrical Doping of Organic Semiconductors: Fundamental Mechanisms and Emerging Dopant Design Rules, Acc. Chem. Res., 2016, 49, 370–378 CrossRef CAS
.
- T. Lei, X. Chen, G. Pitner, H.-S. P. Wong and Z. Bao, Removable and Recyclable Conjugated Polymers for Highly Selective and High-Yield Dispersion and Release of Low-Cost Carbon Nanotubes, J. Am. Chem. Soc., 2016, 138, 802–805 CrossRef CAS
.
- L. Lätsch, E. Lam and C. Copéret, Electronegativity and location of anionic ligands drive yttrium NMR for molecular, surface and solid-state structures, Chem. Sci., 2020, 11, 6724–6735 RSC
.
- Z. Hens and J. C. Martins, A Solution NMR Toolbox for Characterizing the Surface Chemistry of Colloidal Nanocrystals, Chem. Mater., 2013, 25, 1211–1221 CrossRef CAS
.
- A. C. Forse, C. Merlet, C. P. Grey and J. M. Griffin, NMR studies of adsorption and diffusion in porous carbonaceous materials, Prog. Nucl. Magn. Reson. Spectrosc., 2021, 124–125, 57–84 CrossRef CAS PubMed
.
- C. W. Haigh and R. B. Mallion, “Ring-current”’ effects on 1H-NMR chemical shifts in linear acenes, J. Chem. Phys., 1982, 76, 4063–4066 CrossRef CAS
.
- S. J. Perkins and K. Wüthrich, Ring current effects in the conformation dependent NMR chemical shifts of aliphatic protons in the basic pancreatic trypsin inhibitor, Biochim. Biophys. Acta, Protein Struct., 1979, 576, 409–423 CrossRef CAS PubMed
.
- R. D. Vernet and V. Boekelheide, Nuclear Magnetic Resonance Spectroscopy. Ring-Current Effects on Carbon-13 Chemical Shifts, Proc. Natl. Acad. Sci. U. S. A., 1974, 71, 2961–2964 CrossRef CAS
.
- J. Tan, H. Huang, D. Wang, S. Qin, X. Xiao, Z. Chen, D. Liu and L. Wang, Charge transfer complex-doped single-walled carbon nanotubes with reduced correlations between electrical conductivity and Seebeck coefficient for flexible thermoelectric generators, J. Mater. Chem. C, 2020, 8, 4827–4835 RSC
.
- L. Lyu, K. Kirihara, Y. Okigawa, M. Hasegawa, W. Ding, Y. Wang, M. Mukaida, Y. Zhou and Q. Wei, Extracting carrier mobility using a photoinduced charge transfer reaction: From conducting polymers to nanocarbon materials, Org. Electron., 2020, 78, 105615 CrossRef CAS
.
- S. P. Schießl, X. de Vries, M. Rother, A. Massé, M. Brohmann, P. A. Bobbert and J. Zaumseil, Modeling carrier density dependent charge transport in semiconducting carbon nanotube networks, Phys. Rev. Mater., 2017, 1, 046003 CrossRef
.
- S. A. Gregory, R. Hanus, A. Atassi, J. M. Rinehart, J. P. Wooding, A. K. Menon, M. D. Losego, G. J. Snyder and S. K. Yee, Quantifying charge carrier localization in chemically doped semiconducting polymers, Nat. Mater., 2021, 20, 1414–1421 CrossRef CAS PubMed
.
- M. Comin, S. Fratini, X. Blase and G. D’Avino, Doping-Induced Dielectric Catastrophe Prompts Free-Carrier Release in Organic Semiconductors, Adv. Mater., 2022, 34, 2105376 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3nh00480e |
| This journal is © The Royal Society of Chemistry 2024 |