Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A multi-cation model for the actuation of ionic membranes with ionic liquids†
Alain
Boldini

New York Institute of Technology, Department of Mechanical Engineering, Northern Boulevard P.O. Box 8000, Old Westbury, 11568, NY, USA. E-mail: aboldini@nyit.edu; Tel: +1-516-686-4958
First published on 7th May 2024
Abstract
Soft actuators based on water-swollen ionic membranes are able to operate in water, a critical feature for applications in biomedical engineering and underwater robotics. On the contrary, extended use of these actuators in air is hindered by the evaporation of water from the membrane, which negatively affects the actuation performance. To address this limitation, water solvent can be substituted by ionic liquids (ILs). The introduction of ILs in ionic membranes substantially modifies their microscopic composition, requiring dedicated models to describe their electrochemistry and mechanics. However, current physically based models of IL-swollen ionic membranes only partially capture this complex microscopic composition. This manuscript proposes a multi-cation theory, based on first physical principles, that captures the electromigration of ions produced by the dissociation of the IL in the membrane and membrane counterions. The theory, grounded in a thermodynamically consistent formulation at the continuum level, explicitly accounts for the different sizes of these mobile ions, which play a critical role on actuation. Under a series of simplifying hypotheses, we specialize this theory to beam-like actuators. We put forward a numerical solution for the resulting one-dimensional reduced-order model, which we use to perform a series of parametric analyses. We investigate the physics of actuation at steady-state by systematically varying the concentrations of ions and their sizes, the applied voltage and the thickness of the Stern layer. Our results hint at a complex interaction between ions, modulated by their relative concentration and sizes. These parameters dramatically affect the bending moments associated with hydraulic pressure and Maxwell stress, and, in turn, the actuator curvature. Our theory paves the way to more accurate descriptions of the coupled electrochemistry and mechanics of ionic membranes swollen by ILs.
1 Introduction
Ionic membranes are unique materials that allow the selective passage of either cations (cation-exchange membranes) or anions (anions-exchange membranes), blocking ionic species of the opposite charge.1,2 This fundamental property makes ionic membranes essential components in electrochemical systems for desalinization, electrodialysis and power generation.3,4Along these applications, ionic membranes have gained attention from the physical chemistry and engineering communities for their singular coupling between electrochemistry and mechanics, which allows for the design of soft electrochemical transducers, including actuators, sensors and energy harvesters.5 In their most common incarnation, these electrochemical transducers take the form of ionic polymer metal composites (IPMCs),6–9 formed by an ionic membrane sandwiched between two conductive electrodes. Biomedical engineering and soft, underwater robotics are natural application fields for IPMCs, thanks to their bio-compatibility and underwater operability.10–12 In addition to IPMCs, recent efforts have developed new contactless actuators based on bare ionic membranes.13–16
The coupling between electrochemistry and mechanics in ionic membranes is related to their peculiar microstructure, which also causes their permselectivity. Ionic membranes are porous, polymeric materials, permeated with a solution of mobile ionic species.1,2 The polymeric backbone is bonded with charged functional groups, called coions. IPMCs typically utilize cation-exchange membranes that incorporate negatively charged sulfonate groups.6,17 The permeating solution, usually water-based, contains mobile ionic species, the so-called counterions, that neutralize the charge of coions. By applying an electric field across the IPMC electrodes, counterions migrate through the membrane, along with the solvent. This migration generates differential osmotic pressure and Maxwell stress across the IPMC, resulting in macroscopic bending deformations.18–23
Unlike underwater actuation, the use of IPMCs in air is challenging. The main limitation in the adoption of IPMC actuators for in-air applications lays in the loss of solvent water to the environment due to evaporation.24,25 The loss of solvent causes a reduction in the mobility of ions in the membrane, which ultimately yields an overall decrease in the actuation performance. Special coatings have been proposed to limit solvent evaporation,26–29 at the expense of lower deformations due to the added coating stiffness.
An alternative solution is to remove completely the water within IPMCs and substitute it with non-volatile solvents, typically ionic liquids (ILs).30,31 These ionic compounds, often formed by large organic cations (IL-cations) and smaller, usually inorganic anions (IL-anions),32 are stable as liquids at the standard temperature and pressure. Since their discovery over one hundred years ago, ILs have gained attention as solvents for lithium batteries and electrochemical capacitors,33 especially in view of the development of green chemistry and technology.34
In a first strive toward the development of IPMCs with ILs as solvents (IL-IPMCs), Bennett and Leo24 demonstrated the stability of IL-IPMCs under repeated actuation in air. While water-swollen IPMCs lost any actuation capability after 104 cycles, IL-IPMCs were still functional over 105 cycles. Since this seminal work, significant research efforts have focused on the characterization of IL-IPMCs and the enhancement of their performance. Extensive measurements of microscopic properties of IL-IPMCs,35 different fabrication techniques,36,37 experimental probes of charge distribution38 and comparative studies with different membranes, counterions, ILs and IL uptake35,39–44 have been explored in the literature. More broadly, ILs have been extensively utilized for different types of actuators, based on ionic membranes,45 gel electrolytes46,47 and polymer electrolytes.48–50
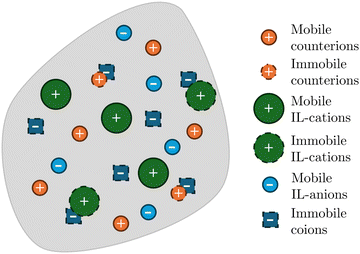
We propose to distinguish two main classes of IL-IPMCs, based on differences in their microscopic composition associated with distinct manufacturing techniques. The first class includes IL-IPMCs that still contain water as a solvent, along with the IL-cations derived from the dissociation of the IL, serving as counterions.37,42 Notably, IL-anions are not present in the membrane. These IL-IPMCs are obtained from the traditional ion-exchange technique utilized to modify the counterions within ionic membranes, by soaking them in a high-concentration water solution of a salt of the desired counterion. This class of IL-IPMCs shares strong similarities in terms of composition with water-swollen IPMCs, although water uptake is much smaller and counterions much larger in size. The second class comprises of IL-IPMCs with no water, containing the original counterions in the membrane along with both IL-cations and IL-anions.24,35 These IL-IPMCs are manufactured through soaking in a solution of IL and methanol after oven-drying the membranes to remove water. Unlike those in the first class, these actuators show substantially different compositions compared to water-swollen IPMCs. In particular, they do not contain any neutral solvent molecule, but incorporate two mobile cationic species (counterions and IL-cations) along with a mobile anionic species (IL-anions). Part of the cations may be immobilized by the coions,35 although experiments show that both counterions35 and IL-cations38 migrate through the membrane.
Despite the thorough experimental and manufacturing work on IL-IPMCs, modeling efforts remain limited. Most models of IL-IPMCs focus on microscopic descriptions of their electrochemistry and mechanics,35 or are based on phenomenological descriptions of actuation.42 Despite their ability to represent the behavior of IL-IPMCs, these models cannot provide guidelines for material scientists regarding the material parameters to optimize to improve on actuation performance. To date, the only theory of actuation for IL-IPMCs grounded in first physical principles is the one proposed by Drozdov.51 Despite its ability to qualitatively predict the macroscopic actuation behavior of IL-IPMCs, the theory can only capture a very specific case within the second class of IL-IPMCs. In fact, the model considers the migration of IL-cations and IL-anions, assuming that all counterions are immobilized by coions, which is typically not the case in IL-IPMCs.35
We argue that IL-IPMCs in the first class can be modeled through single-cation theories analogous to those for water-swollen IPMCs, provided that non-idealities associated with small water content and large size of counterions are taken into account.52–55 In this paper, we focus on developing a new physically based model to describe the actuation of IL-IPMCs belonging to the second class. We propose a continuum mechanics and thermodynamics framework56 to describe the actuation of IL-IPMCs, leveraging a thermodynamically consistent formulation of the constitutive equations. Our model accurately describes the ionic composition of the second class of IL-IPMCs, while explicitly accounting for different in sizes of ions that are expected to significantly impact both electrochemistry and mechanics.54
The novelties of the proposed framework compared to models and results available in the literature are: (1) an explicit acknowledgement of two classes of IL-IPMCs and of the need for different models to represent them; (2) the description of the migration of multiple mobile cations in the ionic membrane; (3) the inclusion of steric effects to account for the different sizes of ions, particularly important for the large cations from ILs; (4) the modeling of immobilization of counterions and IL-cations by the coions; and (5) extensive parametric analyses that highlight the role of individual model parameters on actuation of IL-IPMCs.
The paper is organized as follows. In Section 2, we introduce the continuum-level theory of IL-IPMCs, specialize it under reasonable hypotheses to a one-dimensional (1D) model of electrochemistry coupled to mechanics for beam-like actuators and propose a numerical solution for this 1D formulation. Section 3 illustrates the results of the numerical simulations, highlighting the role of the different ionic species involved and systematically analyzing the effect of their properties on ion concentrations, electric potential, hydraulic pressure and curvature. Finally, we conclude the paper in Section 4, which summarizes and comments our main findings and proposes avenues of future work to address the limitations of the current theory.
2 Theory and simulations
In this Section, we introduce the theory to describe the electrochemistry and mechanics of IL-swollen ionic membranes, which constitute the core of IL-IPMCs belonging to the second class. We consider a Lagrangian framework, in which quantities are expressed as a function of the position X in the material configuration and time t. The material configuration is such that the membrane is undeformed and electroneutral.We model IL-swollen ionic membranes as a mixture of a negatively charged solid phase and three ionic phases. The deformation is portrayed by the deformation gradient F(X,t). We describe the electrochemistry of the membranes through the electric potential ϕ(X,t) and the concentration Ci(X,t) of the i-th mobile ionic species per unit volume of undeformed mixture.
Experiments on IL-IPMCs suggest that at least part of the counterions and IL-cations in the membrane are immobilized by coions,35 such that they do not participate in the electromigration. In this vein, Ci(X,t) represents the concentration of ions of the i-th species that can actually move, not accounting for any immobilized charge or neutral ionic pair.57 Three mobile ionic species are present in the membrane (Fig. 1): the original counterions (C+(X,t)), the IL-cations (CIL+(X,t)) and the IL-anions (CIL−(X,t)). The solid phase carries a fixed charge due to the coions, with a constant concentration C−(X) per unit undeformed volume. For simplicity, we assume that both the immobilized cations and coions are uniformly distributed. Thus, in the initial configuration, also concentrations of counterions, IL-cations and IL-anions are uniformly distributed and equal to ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) +,
+, ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) IL+ and
IL+ and ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) IL−, respectively. Of the entire concentration of coions C−(X) =
IL−, respectively. Of the entire concentration of coions C−(X) = ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) −, only a fraction
−, only a fraction 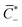 does not immobilize any cation. Thus, in general, we have
does not immobilize any cation. Thus, in general, we have ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) IL+ ≤
IL+ ≤ ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) IL−, as part of the IL-cations are immobilized. We should also require that
IL−, as part of the IL-cations are immobilized. We should also require that ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) + ≤
+ ≤ ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) −, but we decided to retain the possibility that
−, but we decided to retain the possibility that ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) + >
+ > ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) −, should the membrane undergo a further ion-exchange process to increase the concentration of counterions after the soaking in the IL-methanol solution.
−, should the membrane undergo a further ion-exchange process to increase the concentration of counterions after the soaking in the IL-methanol solution.
2.1 Continuum-level theory
We begin by introducing a continuum-level formulation of the theory of electrochemistry and mechanics of IL-swollen ionic membranes. We introduce governing equations, explicitly account for the different ionic volumes through the imposition of an incompressibility constraint and derive thermodynamically consistent constitutive equations via the definition of an appropriate Helmholtz free-energy density.| ∇X·s = 0, | (1) |
We assume that no chemical reaction can occur in the bulk of the IPMC. Thus, the mass of each of the mobile ionic species is conserved,
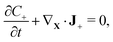 | (2a) |
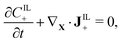 | (2b) |
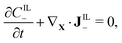 | (2c) |
Finally, we neglect any electrodynamics phenomena, such that electromigration of ions can be described through the equations of electrostatics.22 The electric potential is directly related to the electric field E(X,t) = −∇Xϕ(X,t), ∇X(·) being the gradient in the material configuration. The equations of electrostatics reduce to the Gauss equation,58
| ∇X·D = Q, | (3) |
), such that
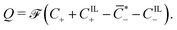 | (4) |
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) = 96
= 96![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 485 C
485 C![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mol−1 is the Faraday constant.
mol−1 is the Faraday constant.
Φsolid + ![[scr V, script letter V]](https://www.rsc.org/images/entities/char_e149.gif) +C+ + +C+ + ![[scr V, script letter V]](https://www.rsc.org/images/entities/char_e149.gif) IL+CIL+ + IL+CIL+ + ![[scr V, script letter V]](https://www.rsc.org/images/entities/char_e149.gif) IL−CIL− = det(F), IL−CIL− = det(F), | (5) |
![[scr V, script letter V]](https://www.rsc.org/images/entities/char_e149.gif) i the molar volume of the i-th ionic species. By evaluating eqn (5) in the material configuration, we can eliminate the volume fraction of the solid phase and rewrite the constraint as
i the molar volume of the i-th ionic species. By evaluating eqn (5) in the material configuration, we can eliminate the volume fraction of the solid phase and rewrite the constraint as1 + ![[scr V, script letter V]](https://www.rsc.org/images/entities/char_e149.gif) +(C+ − +(C+ − ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) +) + +) + ![[scr V, script letter V]](https://www.rsc.org/images/entities/char_e149.gif) IL+(CIL+ − IL+(CIL+ − ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) IL+) + IL+) + ![[scr V, script letter V]](https://www.rsc.org/images/entities/char_e149.gif) IL−(CIL− − IL−(CIL− − ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) IL−) = det(F). IL−) = det(F). | (6) |
Enforcing the incompressibility constraint ensures that the different sizes of the ions are explicitly accounted for. The size of ions has proven to be particularly important to accurately describe the electrochemistry of solutions, as steric effects that limit the maximum packing of ions play a critical role in the charge dynamics at the electrodes.62,63 Similarly, the size of counterions quantitatively and even qualitatively modify the electrochemistry and mechanics of water-swollen ionic membranes.54 Imposing the incompressibility constraint at the continuum scale is equivalent to enforcing steric effects for ions at the microscale, with the additional advantage of a seamless treatment of ions of different sizes.64
Similar to previous studies on IPMCs,22,55,59 we additively decompose the free-energy density Ψ into additive contributions,
| Ψ(F,C+,CIL+,CIL−,D) = Ψmec(F) + Ψmix(C+,CIL+,CIL−) + Ψpol(F,D), | (7) |
We adopt a simple Saint-Venant Kirchoff model for the strain energy,65
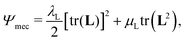 | (8) |
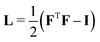 is the Green–Lagrange strain tensor, I the identity tensor, tr(·) the trace operator and λL and μL the Lamé parameters. These two parameters are related to the Young modulus E and Poisson ratio ν of the material through
is the Green–Lagrange strain tensor, I the identity tensor, tr(·) the trace operator and λL and μL the Lamé parameters. These two parameters are related to the Young modulus E and Poisson ratio ν of the material through 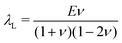 and
and 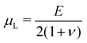 . As in this paper we ultimately focus only on small strains, this strain energy choice is equivalent to more complex hyperelastic models.66
. As in this paper we ultimately focus only on small strains, this strain energy choice is equivalent to more complex hyperelastic models.66
The free-energy associated with mixing assumes the classical form67
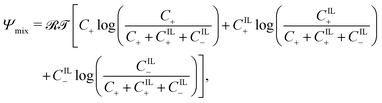 | (9) |
![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) = 8.314 J mol−1 K−1 and
= 8.314 J mol−1 K−1 and ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) are the universal gas constant and the absolute temperature, respectively. Unlike previous works on water-swollen IPMCs22,59 and IL-IPMCs,51 we do not assume the solution to be dilute, as the concentration of ions can reach large values, especially in the proximity of the electrodes, where electric double layers are formed.3,4,68
are the universal gas constant and the absolute temperature, respectively. Unlike previous works on water-swollen IPMCs22,59 and IL-IPMCs,51 we do not assume the solution to be dilute, as the concentration of ions can reach large values, especially in the proximity of the electrodes, where electric double layers are formed.3,4,68
The polarization free-energy reads22
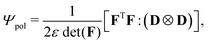 | (10) |
To impose the incompressibility constraint in eqn (6), we modify the free-energy function in eqn (7) through the Lagrange multiplier method, obtaining the functional
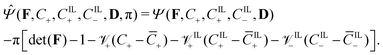 | (11) |
By applying the Coleman–Noll procedure,56 we obtain a series of constitutive equations from the differentiation of the proposed functional,
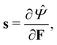 | (12a) |
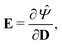 | (12b) |
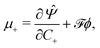 | (12c) |
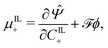 | (12d) |
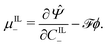 | (12e) |
Further, the Coleman–Noll procedure prescribes Ji·∇Xμi ≤ 0 for each of the ionic species i, but does not impose the form of the constitutive equations for the fluxes from the free-energy density. The simplest modeling choice is considering a Nernst–Planck form of the ionic fluxes,22,59,69
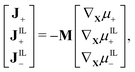 | (13) |
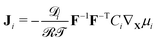 | (14) |
![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) i the diffusivity of the i-th ionic species.
i the diffusivity of the i-th ionic species.
2.2 Reduced-order model for IL-IPMC actuation
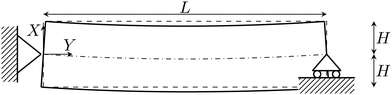
Herein, we propose a reduced-order model to describe the response of beam-like IL-IPMC actuators. To this end, we introduce a series of simplifying hypotheses, which allow us to simplify the three-dimensional (3D) theory proposed in Section 2.1 to a one-dimensional (1D) problem. Based on this 1D formulation, we define the set of nondimensional parameters that characterize the response of IL-IPMC beam-like actuators. Finally, we propose a numerical solution for the integro-differential boundary value problem (BVP) arising from the steady-state version of the 1D problem.Similar to previous works on water-swollen IPMCs,22,70,71 we put forward three simplifying hypotheses. First, we assume that the actuator experiences small strains. Such an hypothesis has been experimentally verified, even for the large tip displacements observed in IPMCs, due to the small thickness of ionic membranes.72 Second, we assume that L ≫ 2H, so that we can neglect electrochemical fluxes along the Y- and Z-axes, given that the electric field applied across the electrodes is uniform and perpendicular to the Y-axis. This hypothesis, borrowed from the parallel-plate approximation for microelectromechanical systems,73 has been previously verified through finite element simulations.70 Finally, we hypothesize that the mechanics only affects the electrochemistry through π, but does not otherwise appear in the electrochemical fluxes. Likewise, this hypothesis has been verified for water-swollen IPMCs through numerical simulations.74
Under this set of hypotheses, eqn (2)–(4) reduce to
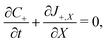 | (15a) |
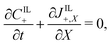 | (15b) |
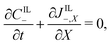 | (15c) |
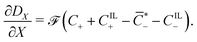 | (16) |
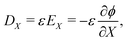 | (17a) |
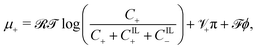 | (18a) |
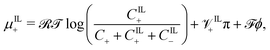 | (18b) |
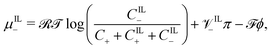 | (18c) |
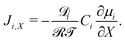 | (19) |
With the small strains hypothesis, the Green–Lagrange strain tensor L is approximated by the infinitesimal strain tensor ε.56 Similar to our previous work on water-swollen IPMCs,70 we make the additional hypothesis of plane-strain, limited to the X–Y plane. Given the simply supporting boundary conditions, we observe uniform bending with zero shear strain,70,71 such that the only components of the infinitesimal strain tensor that are non-zero are εXX and εYY. With this hypothesis, we write the in-plane components of s from eqn (12a) as
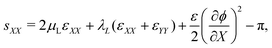 | (20a) |
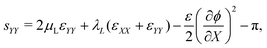 | (20b) |
| sXY = 0. | (20c) |
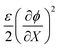 are components of the isotropic eigenstress due to hydraulic pressure and the eigenstress associated with Maxwell stress, respectively.
are components of the isotropic eigenstress due to hydraulic pressure and the eigenstress associated with Maxwell stress, respectively.
By applying mechanical equilibrium in eqn (1), we find 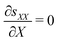 , so that the through-the-thickness stress sXX is constant along the thickness. We assume that electrodes are unloaded such that sXX(±H) = 0 at the electrodes. Thus, we must have sXX(X) = 0 throughout the entire IL-IPMC thickness. We can then invert eqn (20a) to find the through-the-thickness strain εXX,
, so that the through-the-thickness stress sXX is constant along the thickness. We assume that electrodes are unloaded such that sXX(±H) = 0 at the electrodes. Thus, we must have sXX(X) = 0 throughout the entire IL-IPMC thickness. We can then invert eqn (20a) to find the through-the-thickness strain εXX,
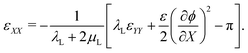 | (21) |
Based on previous studies backed by finite element simulations,70 we propose a Saint-Venant-like solution for the deformation. Specifically, we assume that the axial strain is in the form
| εYY = −kX + ε0, | (22) |
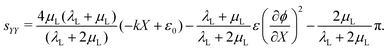 | (23) |
As the actuator is unloaded, mechanical equilibrium requires the axial force and the bending moment to be zero,
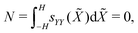 | (24a) |
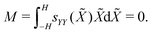 | (24b) |
Eqn (24a) offers an expression for ε0,
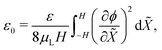 | (25) |
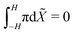 . This result can be obtained by: (1) substituting eqn (21) and (22) into eqn (6), upon considering that det(F) ≈ 1 + εXX + εYY for small, plane-strains;56 (2) integrating the resulting equation across the thickness from −H to H to evaluate ε0, leveraging mass conservation to remove the dependence on ion concentrations; and (3) equaling this expression for ε0 to that from eqn (24a). The curvature of the actuator can be computed from eqn (24b),
. This result can be obtained by: (1) substituting eqn (21) and (22) into eqn (6), upon considering that det(F) ≈ 1 + εXX + εYY for small, plane-strains;56 (2) integrating the resulting equation across the thickness from −H to H to evaluate ε0, leveraging mass conservation to remove the dependence on ion concentrations; and (3) equaling this expression for ε0 to that from eqn (24a). The curvature of the actuator can be computed from eqn (24b),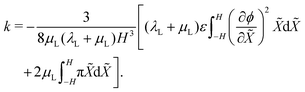 | (26) |
Eqn (25) and (26) express the integro-differential functions ε0(ϕ) and k(ϕ,π).
By substituting det(F) ≈ 1 + εXX + εYY and eqn (21) and (22) in eqn (6), we obtain an implicit integro-differential relation between ϕ, π, C+, CIL+ and CIL−,
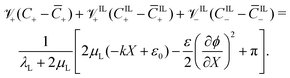 | (27) |
Eqn (15), (16) and (27), along with the constitutive equations in eqn (17)–(19) and the mechanical variables in eqn (25) and (26), constitute a system of five nonlinear integro-differential equations, with variables C+(X,t), CIL+(X,t), CIL−(X,t), ϕ(X,t) and π(X,t).
Such a system should be complemented by boundary and initial conditions, to formulate a well-defined BVP. First, we hypothesize that no reaction occurs at the electrodes and that the electrodes are perfectly blocking; thus, for each ionic species i,
| Ji,X(±H,t) = 0. | (28) |
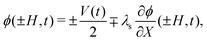 | (29) |
![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) +, CIL+(X,0) =
+, CIL+(X,0) = ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) IL+, CIL−(X,0) =
IL+, CIL−(X,0) = ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) IL− and ϕ(X,0) = 0. No boundary and initial conditions are needed for π, as this variable serves a Lagrange multiplier that is related to the other variables by the algebraic-integral constraint in eqn (27).
IL− and ϕ(X,0) = 0. No boundary and initial conditions are needed for π, as this variable serves a Lagrange multiplier that is related to the other variables by the algebraic-integral constraint in eqn (27).
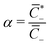 of coions that do not immobilize any cation (0 ≤ α ≤ 1); (2) the fraction
of coions that do not immobilize any cation (0 ≤ α ≤ 1); (2) the fraction 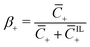 of mobile counterions over the total number of mobile cations (0 ≤ β+ ≤ 1); (3) the fraction
of mobile counterions over the total number of mobile cations (0 ≤ β+ ≤ 1); (3) the fraction 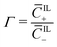 of mobile IL-cations over mobile IL-anions (0 ≤ Γ ≤ 1); (4) the ratio
of mobile IL-cations over mobile IL-anions (0 ≤ Γ ≤ 1); (4) the ratio 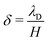 of the Debye screening length
of the Debye screening length 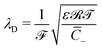 to the ionic membrane semi-thickness; (5) the ratio
to the ionic membrane semi-thickness; (5) the ratio 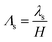 of the Stern layer thickness to the ionic membrane semi-thickness; (6) the non-dimensional Lamé parameter
of the Stern layer thickness to the ionic membrane semi-thickness; (6) the non-dimensional Lamé parameter 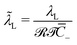 ; (7) the non-dimensional Lamé parameter
; (7) the non-dimensional Lamé parameter 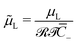 ; (8) the non-dimensional voltage applied across the electrodes
; (8) the non-dimensional voltage applied across the electrodes 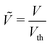 , where
, where 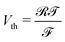 is the thermal voltage (approximatively 25 mV at room temperature); (9) the non-dimensional molar volume of counterions
is the thermal voltage (approximatively 25 mV at room temperature); (9) the non-dimensional molar volume of counterions 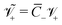 ; (10) the non-dimensional molar volume of IL-cations
; (10) the non-dimensional molar volume of IL-cations 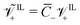 ; (11) the non-dimensional molar volume of IL-anions
; (11) the non-dimensional molar volume of IL-anions 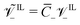 ; (12) the ratio
; (12) the ratio 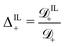 between the diffusivity of IL-cations and that of counterions; and (13) the ratio
between the diffusivity of IL-cations and that of counterions; and (13) the ratio 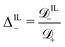 between the diffusivity of IL-anions and that of counterions. We limit our analysis to relatively small voltages, as our model does not account for decomposition of ILs at high voltages.75
between the diffusivity of IL-anions and that of counterions. We limit our analysis to relatively small voltages, as our model does not account for decomposition of ILs at high voltages.75
α, β+ and Γ can be related to the non-dimensional concentrations of counterions, IL-cations and IL-anions, 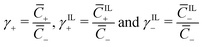 . In fact, electroneutrality at equilibrium requires
. In fact, electroneutrality at equilibrium requires ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) ++
++![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) IL+ =
IL+ = 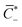 +
+![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) IL−, such that
IL−, such that
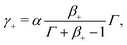 | (30a) |
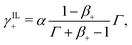 | (30b) |
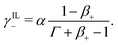 | (30c) |
If γ+ > 1, the ionic membrane contains more counterions than fixed coions. As previously discussed, we consider such a situation possible, provided that the membrane undergoes ion-exchange to substitute part of the IL-cations with counterions.
To put forward a numerical solution, we construct a mesh Xj (j = 1,…,N) on the interval [−H,H] across the membrane thickness, defining N nodes and N − 1 elements. We consider a non-uniform mesh, which is refined in the proximity of the electrodes to capture the diffuse part of the electric double layers (whose size is governed by the Debye screening length). The mid-points of each element are defined by  (j = 1,…,N − 1), while the non-uniform length of each element is
(j = 1,…,N − 1), while the non-uniform length of each element is  (j = 1,…,N − 1). At each node, we define as variables C+,j = C+(Xj), CIL+,j = CIL+(Xj), CIL−,j = CIL−(Xj), ϕj = ϕ(Xj),
(j = 1,…,N − 1). At each node, we define as variables C+,j = C+(Xj), CIL+,j = CIL+(Xj), CIL−,j = CIL−(Xj), ϕj = ϕ(Xj), 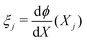 and πj = π(Xj). Accounting for the unknown value of the constant electrochemical potential
and πj = π(Xj). Accounting for the unknown value of the constant electrochemical potential ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) i for each of the three ionic species, we have to define 6N + 3 discretized equations to find the value of 6N + 3 variables.
i for each of the three ionic species, we have to define 6N + 3 discretized equations to find the value of 6N + 3 variables.
To this end, we propose a discretization of the BVP that naturally accounts for the boundary conditions.54,76 Specifically, we collocate eqn (18) for the constant electrochemical potentials of the three ionic species at the nodes, obtaining 3N equations. Other N equations are obtained from the discretization of the incompressibility constraint in eqn (27). To evaluate the integrals in eqn (25) and (26), we employ the trapezoidal rule.77
The other two equations to be discretized are ordinary differential equations in space. First, we collocate eqn (16) at the mid-points of the elements, to obtain N − 1 equations. Next, we collocate the equation that defines the variable 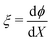 at the mid-points of the elements, to find other N − 1 equations. To approximate the first-order derivative at the mid-point of each element, we use a centered difference, such that, for a variable f,
at the mid-points of the elements, to find other N − 1 equations. To approximate the first-order derivative at the mid-point of each element, we use a centered difference, such that, for a variable f,
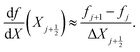 | (31) |
The other variables are approximated at the mid-point of each element as the average of their values at the nodes defining the element, such that, for a variable g,
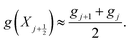 | (32) |
The remaining five discretized equations are found from two sources. First, we impose the voltage boundary conditions in eqn (29), which provide two equations: 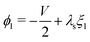 and
and 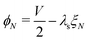 . Second, as we deal with a steady-state transport problem, we need to impose the total quantity of each ionic species i present in the membrane.78 This requirement warrants three additional constraints,
. Second, as we deal with a steady-state transport problem, we need to impose the total quantity of each ionic species i present in the membrane.78 This requirement warrants three additional constraints, 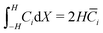 . The resulting system of 6N + 3 nonlinear discretized algebraic equations in 6N + 3 can be finally solved through a nonlinear algebraic solver. The full system of discretized equations is listed in the ESI.†
. The resulting system of 6N + 3 nonlinear discretized algebraic equations in 6N + 3 can be finally solved through a nonlinear algebraic solver. The full system of discretized equations is listed in the ESI.†
3 Results
In this section, we present the results of our simulations. As a first step, we detail the numerical implementation of the numerical method. Then, we introduce the results of the steady-state simulations, investigating the effect of non-dimensional parameters on steady-state variables.3.1 Numerical implementation
We implement the numerical algorithms introduced in Section 2.2.3 in MATLAB®, in a nondimensional format. Baseline parameters for the simulations are determined from experimental and computational results (see ESI†), focusing on a Nafion™ 117 membrane with Li+ counterions infused by 1-ethyl-3-methylimidazolium tetrafluoroborate (EMI-BF4). For all simulations, we set δ = 10−3,![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) L = 333.14 and
L = 333.14 and ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) L = 37.02. All other parameters are varied depending on the simulation. Diffusivities are not required to solve the steady-state problem.
L = 37.02. All other parameters are varied depending on the simulation. Diffusivities are not required to solve the steady-state problem.
For a Nafion™ 117 membrane with Li+ counterions, swollen with EMI-BF4, we have 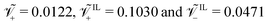 . The condition
. The condition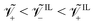 is typical for IL-IPMCs, as ILs that are commonly employed for such applications are composed by a large organic cation and a smaller (often inorganic) anion.32 In one of our parametric analyses, we will change these values to investigate the effect of different ionic sizes on steady-state curvature.
is typical for IL-IPMCs, as ILs that are commonly employed for such applications are composed by a large organic cation and a smaller (often inorganic) anion.32 In one of our parametric analyses, we will change these values to investigate the effect of different ionic sizes on steady-state curvature.
In all simulations, we utilize N = 502 mesh points, which are denser in the proximity of the electrodes. Specifically, we utilize a mesh of size λD/20 from −H to −H + 10λD and from H− 10λD to H. Further, we place 100 mesh points in the bulk, between −H + 11λD and H− 11λD. Thus, at each simulation, we seek to solve a nonlinear system of 3615 equations. A further refinement of the mesh would not considerably affect the results. In the MATLAB implementation, the mesh is also expressed in nondimensional terms.
Discretized equations are solved through the built-in MATLAB fsolve routine, which seeks to set to zero the output of a residual function. The residual function takes as input all the non-dimensional parameters, the mesh and the guess of the solution, generated by fsolve. We provide as an initial guess either the equilibrium with zero applied voltage or a solution previously computed from parametric analyses with similar input parameters. The output of the residual function is the residual vector for all the equations. Upon convergence, fsolve returns a vector with the values of the nodal variables that solve the discretized equations, which we use to evaluate dependent variables such bending moments, mid-axis strain and steady-state curvature.
3.2 Numerical results
We put forward a series of parametric analyses, to understand how different parameters (ion concentrations, applied voltage, ionic size, Stern layer thickness) affect the steady-state response of IL-IPMCs.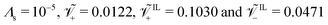 . We consider a weakly nonlinear applied voltage of Ṽ = 1 (≈25 mV); we study the effect of voltage in a separate analysis.
. We consider a weakly nonlinear applied voltage of Ṽ = 1 (≈25 mV); we study the effect of voltage in a separate analysis.
Estimates of α, β+ and Γ are not readily available from experimental results. While previous studies suggested that over a critical IL uptake all IL-cations are immobilized by coions (that is, α = 0, β+ = 1 and Γ = 0),35 direct measurements of ion distributions in the proximity of electrodes of IL-IPMCs showed that both IL-cations and IL-anions are mobile (suggesting α > 0, β+ < 1 and Γ > 0).38 In the absence of precise indications for the values of α, β+ and Γ, we propose a series of parametric analyses that cover the spectrum of possible values of these parameters.
We select three values of α, 0.1, 0.5 and 0.9, to perform our simulations. α = 0.5 indicates that half of the coions immobilize a cation, be it a counterion or an IL-cation. α = 0.1 represents a case in which almost all coions immobilize a cation, whereas α = 0.9 is a condition in which almost all cations are mobile.
Further, we consider three combinations of β+ and Γ satisfying the constraint β+ + Γ > 1. Specifically, we utilize β+ = Γ = 0.75, β+ = 0.15 & Γ = 0.9 and β+ = 0.9 & Γ = 0.15. The first pair of values corresponds to a condition in which mobile counterions are more numerous than mobile IL-cations, and a considerable fraction of IL-cations can migrate. In the condition associated with the second pair of values, mobile IL-cations are much more numerous than mobile counterions and only a few IL-cations are immobilized by coions. Finally, the third condition is one in which counterions represent the vast majority of the mobile cations, with IL-cations almost completely immobilized by coions.
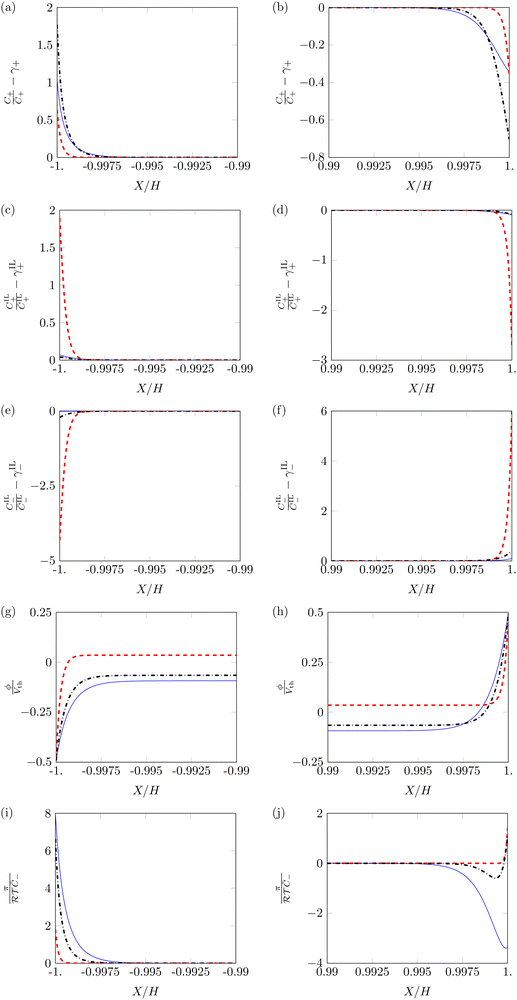
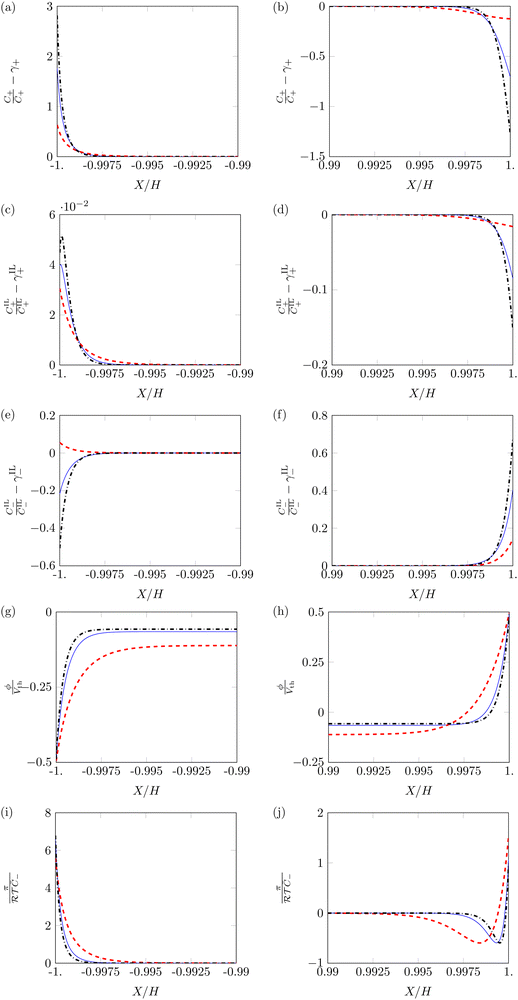
First, we study the steady-state profiles of ion concentrations, electric potential and hydraulic pressure across the membrane thickness, by setting α = 0.5 and varying β+ and Γ. Fig. 3 displays the profiles of these variables in the vicinity of the electrodes, where changes in electrochemical variables are concentrated due to the formation of diffuse layers.68
C + and CIL+ display similar profiles, with pile-up near the cathode (Fig. 3a and c) and depletion near the anode (Fig. 3b and d). However, the dependence of these two variables on β+ and Γ is very different. Changes in the concentration of counterions are more prominent for β+ = 0.9 & Γ = 0.15 than for β+ = Γ = 0.75, while reaching their minimum for β+ = 0.15 & Γ = 0.9. Changes in the concentration of IL-cations display an opposite trend, as they are large only at β+ = 0.15 & Γ = 0.9 and negligible for the other two combinations of parameters. The different tendency of the changes in concentration can be explained by which cation is more numerous in each condition. When β+ = 0.9 & Γ = 0.15 or β+ = Γ = 0.75, counterions are widely available and serve as the main charge carriers. Counterions are favored over IL-cations in the formation of diffuse layers due to their smaller size, which allows them to reach larger concentrations. Only when a small number of counterions is available (β+ = 0.15 & Γ = 0.9) we observe a significant pile-up and depletion of IL-cations, which take over the role of counterions in the formation of diffuse layers.
IL-anions show an opposite behavior to cations, as they deplete at the cathode (Fig. 3e) and pile-up at the anode (Fig. 3f). The trend of concentration changes of IL-anions with respect to β+ and Γ is the same as that of IL-cations: pile-up and depletion are relevant only for β+ = 0.15 & Γ = 0.9 and negligible in the other two conditions. Interestingly, these small changes in the concentration of IL-cations and IL-anions may suggest that IL-IPMCs could be modeled similar to water-swollen IPMCs when counterions are the dominant charge carriers.
The electric potential profiles are similar to those of water-swollen IPMCs,79 showing two boundary layers (Fig. 3g and h) and a bulk region at constant potential. Interestingly, β+ and Γ affect the symmetry of the electric potential. The profile appears almost symmetric for β+ = 0.15 & Γ = 0.9 and remarkably asymmetric in the other two conditions. This result is a consequence of the asymmetry in the migration of ions. For β+ = 0.15 & Γ = 0.9, IL-cations and IL-anions create complementary diffuse layers at the electrodes. In the other two conditions, counterions are the only significant players in the creation of diffuse layers. Such an asymmetric migration results in a pronounced asymmetry between the two diffuse layers and ultimately in the electric potential profile.
The hydraulic pressure also displays a boundary layer structure (Fig. 3i and j). Regardless of β+ and Γ, π is larger at the cathode (Fig. 3i) than in the bulk. Interestingly, the value of the pressure at the cathode is larger for β+ = Γ = 0.75 and β+ = 0.9 & Γ = 0.15 than for β+ = 0.15 & Γ = 0.9. As in the first two conditions IL-cations and IL-anions experience small concentration changes, the pile-up of counterions at the cathode generates large pressure values. On the other hand, for β+ = 0.15 & Γ = 0.9, the simultaneous pile-up of IL-cations and depletion of IL-anions at the cathode compensates for the pile-up of counterions, resulting in a lower pressure.
At the anode (Fig. 3j), we observe qualitative differences in the hydraulic pressure profile depending on the values of β+ and Γ. For β+ = Γ = 0.75, the pressure monotonically decreases from the bulk to the electrode. This trend is caused by the depletion of counterions. For β+ = 0.9 & Γ = 0.15, approaching the electrode from the bulk, we first observe a decrease in pressure, followed by an increase, reaching positive values at the electrode. We attribute this change to the pile-up of IL-anions, which increases the hydraulic pressure in proximity of the anode. This interpretation is favored by the analysis of the condition β+ = 0.15 & Γ = 0.9 that displays a robust pile-up of IL-anions, to which corresponds a monotonic increase of pressure while approaching the electrode from the bulk. In this last case, as the hydraulic pressure increases at both electrodes, its value in the bulk of the membrane is slightly negative to ensure that 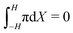 .
.
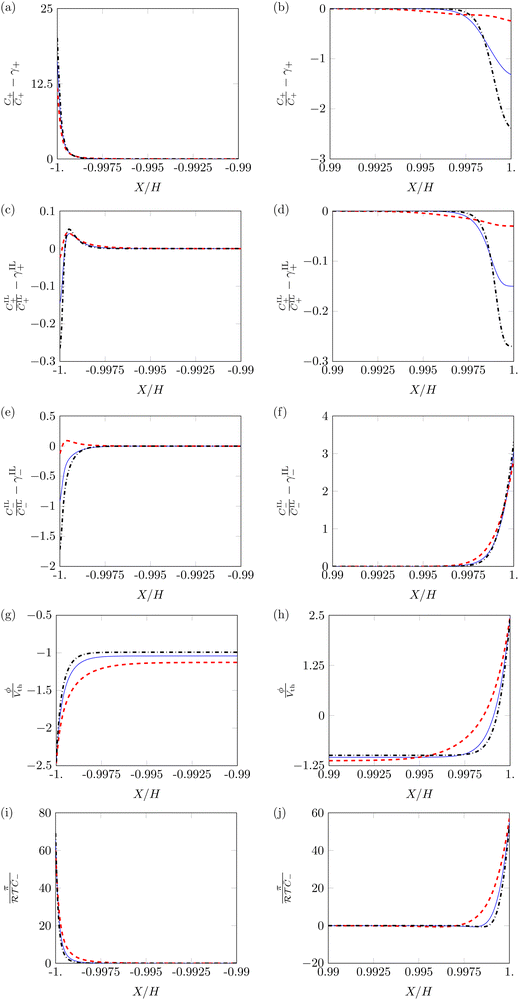
Next, we study variations of the profiles of ion concentrations, electric potential and hydraulic pressure with respect to α, by fixing β+ and Γ. In the two conditions β+ = Γ = 0.75 and β+ = 0.15 & Γ = 0.9, we find minimal qualitative differences by varying α from 0.5 to 0.1 or 0.9. On the other hand, we observe some qualitative differences when changing α in the condition β+ = 0.9 & Γ = 0.15, as shown in Fig. 4.
Profiles of counterions and IL-cations concentration at α = 0.1 and α = 0.9 are similar to those at α = 0.5 (Fig. 4a–d). The largest quantitative differences in concentration occur at α = 0.1. In this case, diffuse layers appear thicker and the maximum changes in concentration are smaller. These variations are associated with the more robust participation of IL-cations in the formation of the diffuse layer at the cathode (Fig. 4c). At the anode (Fig. 4b and d), we also find smaller changes in concentration for α = 0.1. Regardless of the value of α, the pile-up and depletion of IL-cations remain very modest.
The changes in concentration of IL-anions (Fig. 4e and f) show the most unexpected dependence on α. At the cathode (Fig. 4e), the behavior of IL-anions qualitatively changes with α: for α = 0.5 and α = 0.9, IL-anions migrate away from the electrode, while they pile-up there when α = 0.1. A potential explanation to this behavior entails the complex interdependence between electrical, entropic and hydraulic forces, which may cause a counter-intuitive inversion of fluxes, similar to the one observed with solvent in water-swollen ionic membranes.54 This surprising result has also been observed in experimental assays.38 Even with these qualitative differences, changes in concentration of IL-anions are small.
Both the electric potential (Fig. 4g and h) and pressure (Fig. 4i and j) show the same qualitative behavior, independent of the value of α. The boundary layers of both of these variable are larger for the condition α = 0.1, although they still maintain the same profile shape as α = 0.5.
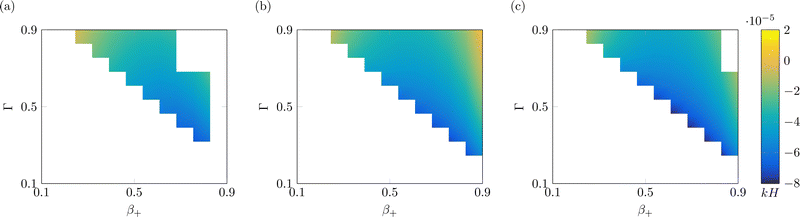
Finally, we investigate the value of the steady-state curvature of IL-IPMCs for varying αs, as a function of β+ and Γ (Fig. 5). As shown in eqn (26), the curvature is determined by two bending moments, one associated with the hydraulic pressure and the other related to Maxwell stress. The former dominates the response at low values of the applied voltage, while the latter grows in importance at high applied voltages.74 In all known conditions in water-swollen IPMCs, the bending moment associated with hydraulic pressure positively contributes to the curvature, while that related to Maxwell stress provides a negative contribution to the overall curvature. According to eqn (22), a positive (negative) curvature corresponds to deflection toward the anode (cathode).
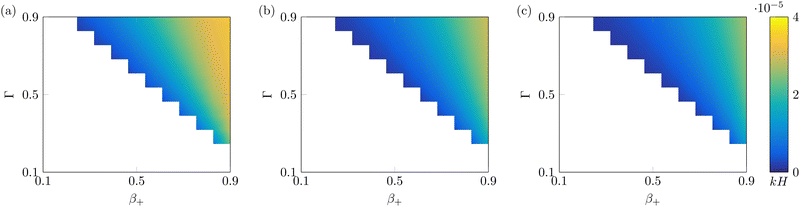 | ||
| Fig. 5 Steady-state curvature as a function of β+ and Γ, with α = 0.1 (a), α = 0.5 (b) and α = 0.9 (c). White parts of the plot indicate nonphysical solutions. All solutions are computed with Ṽ = 1. | ||
For any value of α, β+ and Γ considered, the steady-state curvature is positive (Fig. 5), that is, at steady-state, the actuator bends toward the anode. As a general trend, k increases with both β+ and Γ, although the sensitivity to β+ is larger than that to Γ. Further, the steady-state curvature decreases with an increase of α. The bending moment related to Maxwell stress is negligible for these values of applied voltage. We attribute these trends to changes in the bending moment associated with the hydraulic pressure. In fact, we observe larger pressures in the proximity of the electrodes for larger values of β+ and Γ (Fig. 3i and j) and lower values of α (Fig. 4i and j).
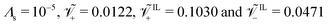 .
.
First, we look at the steady-state profiles of ion concentrations, electric potential and hydraulic pressure close to the electrodes (Fig. 6). We set β+ = 0.9 & Γ = 0.15 and consider three different values of α: 0.1, 0.5 and 0.9. Compared to the case Ṽ = 1 (Fig. 4), we observe much larger pile-ups of counterions at the cathode (Fig. 6a), independent of α. α only affects the depletion at the anode (Fig. 6b), where we observe a thicker diffuse layer and smaller maximum change in concentration for larger values of α.
IL-cations show a more complex behavior than at smaller voltages. In particular, approaching the bulk from the cathode (Fig. 6c), we observe a depletion of IL-cations followed by a pile-up in the region just outside the diffuse layer of counterions (Fig. 6a). The depletion in the very vicinity of the cathode is caused by the large hydraulic pressure generated from the pile-up of counterions, which overcomes the electrostatic forces that push the IL-cations toward the cathode. At the anode (Fig. 6d), IL-cations have an analogous behavior to counterions, also displaying the same dependence on α. Similar to smaller voltages, the changes in concentration of IL-cations are limited.
The profile of IL-anions mirrors that at lower applied voltage, with two main differences. First, the profile at the cathode (Fig. 6e) for α = 0.1 is non-monotonic, with depletion in the near proximity of the cathode followed by a pile-up toward the bulk of the membrane. This depletion, which does not appear at a lower voltage (Fig. 4e), is associated with the large pressure generated by the pile-up of counterions. Second, changes in concentration at the anode (Fig. 6f) are significantly larger than at smaller voltages (Fig. 4f), and almost independent of α.
The profile of electric potential (Fig. 6g and h) is similar to that at lower voltage (Fig. 4g and h). For all values of α, the asymmetry in the electric potential profile increases with larger applied voltage. Such a behavior is similar to water-swollen IPMCs and is caused by the fundamental asymmetry between pile-up and depletion. While pile-up is only limited by steric effects near the packing limit, depletion is restricted by the original concentration, as concentration cannot turn negative. As voltage grows, the physical constraint on depletion is reached faster than the packing limit for pile-up, causing an increasing asymmetry in the electric potential profile.74 Such an asymmetry is responsible for the growing importance of Maxwell stress on actuation.74
Finally, we analyze the hydraulic pressure distribution (Fig. 6i and j). Regardless of the value of α, we observe an increase in pressure in the proximity of both cathode (Fig. 6i) and anode (Fig. 6j). Such an increase in pressure is associated with the pile-up of counterions and IL-anions at the cathode and anode, respectively. The values of pressure at the cathode (Fig. 6i) are slightly higher than at the anode (Fig. 6j), despite the much larger changes in concentration of counterions than IL-anions. The similarity of the pressures at the two electrodes is explained by the larger volume of IL-anions compared to counterions, such that the former generate larger hydraulic pressures than the latter for the same change in concentration. In order for the pressure to satisfy the constraint 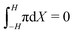 , the pressure assumes a slightly negative value in the bulk of the membrane.
, the pressure assumes a slightly negative value in the bulk of the membrane.
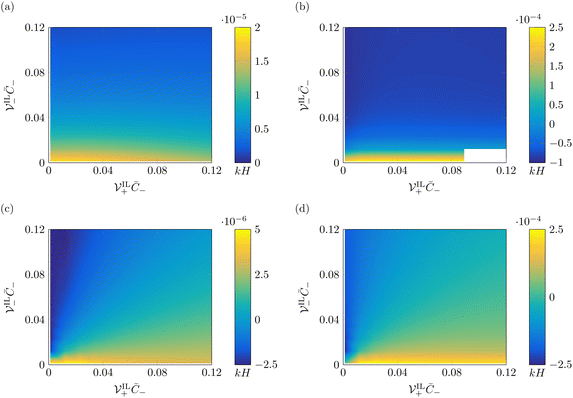
We also investigate the effect of voltage on the steady-state curvature of IL-IPMCs. At larger applied voltages, Maxwell stress starts playing an important role. The bending moment associated with Maxwell stress counteracts the one due to hydraulic pressure, causing a decrease in the steady-state curvature and potentially a change in sign, corresponding to the IL-IPMC bending toward the cathode. This phenomenon, called back-relaxation, is often observed in water-swollen and IL-IPMCs.74,80 In Fig. 7, we display the steady-state curvature at Ṽ = 5 for varying α, as a function of β+ and Γ. In almost all conditions simulated, the steady-state curvature is negative, due to the dominant effect of Maxwell stress. In only a handful of simulated conditions, with very small β+ or with large values of both β+ and Γ, we retrieve a positive steady-state curvature. The negative curvature increases in absolute value for lower values of Γ, as well as larger values of α. This dependency reflects the intensity of the electric field in the proximity of the electrodes. In fact, we observe that the slope of the electric potential profile is higher at larger α values (Fig. 6g and h), as the boundary layer is thinner.
![[scr V, script letter V]](https://www.rsc.org/images/entities/char_e149.gif) + to 10
+ to 10 ![[scr V, script letter V]](https://www.rsc.org/images/entities/char_e149.gif) +.
+.
The effects of ionic size on steady-state curvature is strongly dependent on the values of β+ and Γ. For β+ = 0.9 & Γ = 0.15, where counterions dominate the formation of the diffuse layers, the size of IL-cations has a very weak influence on the steady-state curvature, regardless of the applied voltage. This weak dependence is explained by the small changes in concentration of IL-cations, making curvature substantially independent of their size. On the other hand, we find a considerable influence of the size of IL-anions on the steady-state curvature. At low voltage (Fig. 8a), an increase in the size of IL-anions causes a decrease in the steady-state curvature. While this decrease cannot result in a change in sign of the steady-state curvature, it can significantly affect the performance of the actuator. The reduction in curvature with larger IL-anions is caused by the larger pressure generated by the pile-up of IL-anions at the anode, which counteracts the bending moment produced by the pile-up of counterions at the cathode. At larger voltages (Fig. 8b), an increase in size of IL-anions can even cause a change of sign of the steady-state curvature. Similar to the low voltage case, this dependence is explained by the decrease in the bending moment associated with hydraulic pressure, causing the bending moment related to Maxwell stress to become dominant.
The dependence on the size of IL-cations is completely different for β+ = 0.15 & Γ = 0.9 (Fig. 8c and d). In this case, IL-cations and IL-anions are the primary contributors to the formation of the diffuse layers, such that we find a strong dependency of the steady-state curvature on the sizes of both ions. Regardless of the applied voltage, for small sizes of the IL-cations, we find a robust negative steady-state curvature. Similarly, for small sizes of the IL-anions, we obtain a strong positive steady-state curvature. For large sizes of both IL-cations and IL-anions, the curvature increases with larger IL-cations and smaller IL-anions. The size of these ions affects the pressure generated from their pile-up and depletion near the electrodes. An increase in size of IL-cations boosts the pressure at the cathode and decreases it at the anode, with a positive effect on curvature, similar to counterions. Larger IL-anions have an opposite effect, as they increase the pressure at the anode and decrease it at the cathode, with a negative effect on curvature.
We offer other two interesting observations. First, at large voltages, the minimum, negative steady-state curvature for β+ = 0.9 & Γ = 0.15 (Fig. 8b) is less than half of the maximum, positive steady-state curvature. On the other hand, the minimum, negative steady-state curvature for β+ = 0.15 & Γ = 0.9 (Fig. 8d) is almost equal to the maximum, positive steady-state curvature. The difference between the two conditions depends upon the underlying force that generates negative curvatures. While in Fig. 8b negative curvatures are a consequence of Maxwell stress, in Fig. 8d they are caused by the hydraulic pressure generated by IL-anions. For large IL-cations and IL-anions (Fig. 8d), the bending moment associated with Maxwell stress decreases in magnitude, as steric effects limit the electric field.81 Due to the small contributions to pressure of counterions in the condition β+ = 0.15 & Γ = 0.9, IL-cations and IL-anions have a symmetric effect on the hydraulic pressure. Second, for β+ = 0.15 & Γ = 0.9, negative curvatures are possible even at small applied voltages (Fig. 8c), provided that large IL-anions are utilized.
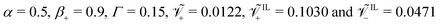 .
.
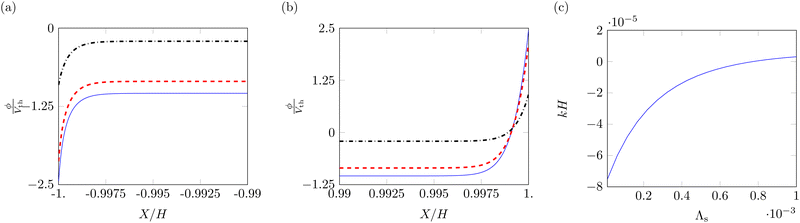
The main effect of the Stern layer thickness is to reduce the voltage and electric field in the boundary layers close to the electrodes. Fig. 9a and b shows the profiles of the electric potentials near the electrodes for three different values of Λs, 10−5, 10−4 and 10−3. At both the cathode (Fig. 9a) and the anode (Fig. 9b), the absolute value of the electric potential decreases with thicker Stern layers. Further, the asymmetry between cathode and anode is reduced, negatively impacting the magnitude of the bending moment associated with Maxwell stress.
The effect of the increase in thickness of the Stern layer on steady-state curvature is shown in Fig. 9c. Due to its effects on the electric potential profile, an increase in the Stern layer decreases the bending moment associated with Maxwell stress, which provides a negative contribution to the overall curvature. As this negative contribution decreases in absolute value, we observe an increase in the curvature, including a shift to positive values when the bending moment related to hydraulic pressure overcomes the decreasing Maxwell stress contribution. Such a trend has been previously observed in models for IL-IPMCs,51 although not directly related to the modulation of Maxwell stress.
4 Conclusions
Ionic polymer metal composites with ionic liquids (IL-IPMCs) are soft actuators that have gained traction over traditional water-swollen IPMCs for their ability to work in air over an extended number of cycles.24 This manuscript introduces a classification of IL-IPMCs, based on the way in which ionic liquids (ILs) are incorporated in the ionic membrane forming the core of IL-IPMCs. Specifically, we distinguish a first class of IL-IPMCs that contain cations from the IL (IL-cations) as counterions, no anions from the IL (IL-anions) and water as a solvent37,42 from a second class of actuators that include the original counterions in the membrane, along with both IL-cations and IL-anions and no water.24,35Available physically based models of electrochemistry and mechanics for ionic membranes only partially capture the microscopic composition of either class of IL-IPMCs. While actuators in the first class can be described through available modifications of models for water-swollen IPMCs,52–55 the second category displays a completely different electrochemical makeup, which requires the development of dedicated formulations.51 This manuscript offers a physically grounded, continuum theory to describe the electrochemistry and mechanics of this category of IL-IPMCs, along with a reduced-order model for beam-like IL-IPMC actuators. Our theory overcomes the available modeling literature by including multiple species of cations, while acknowledging the different sizes of ions in the membrane and the possibility of coions immobilizing the different types of cations. We solve the reduced-order model numerically to perform a series of parametric analyses that clarify the role of each ion in the coupled electrochemistry and mechanics of IL-IPMC actuators.
Our model of IL-IPMCs accurately reflects the microscopic composition in IL-swollen ionic membranes with mobile counterions, IL-cations and IL-anions, accounting for the possibility of immobilization of some cations by the membrane coions.35 A comparison shows that the model by Drozdov51 is analogous to a special case of our theory, provided that all counterions are immobilized by coions. This condition may not be verified in IL-swollen ionic membranes, whereby experiments show that both counterions35 and IL-cations38 are mobile.
In the model by Drozdov,51 ions are assumed to have the same size. Only boundary conditions break the symmetry between cations and anions (and that of the resulting pressure distribution), as the former are assumed to undergo a redox reaction at the electrodes, while anions experience ion-blocking conditions. While redox reactions would occur at large applied voltages, we argue that this phenomenon may not explain actuation at small applied voltages, for which redox reactions may not occur.3,4 Further, redox reactions involving IL-cations, as in the model of Drozdov,51 require electrodes that are able to produce these cations, which is typically not the case in current IL-IPMCs. In the presence of multiple cations, more accurate and species-dependent analyses are necessary to unravel which ionic species are reacting at the electrodes and at which rates. For these reasons, we opted to not include redox reactions in this first theory of IL-IPMCs with multiple cations.
Our theory generates an asymmetry between cations and anions by explicitly accounting for their different sizes. These differences are particularly pronounced in IL-IPMCs, where counterions typically consist of small metallic cations, IL-cations are bulky organic cations and IL-anions are often inorganic anions, which in general have a significantly larger volume than counterions.32 The same change in concentration generates larger pressures for ions with a larger size, thus breaking the symmetry in the pressure through-the-thickness profile, which allows for the generation of a non-zero bending moment even at small applied voltages.
Overall, we find a complex dependence of the steady-state curvature of IL-IPMCs on the relative concentrations and sizes of ions in the membrane. This dependence is produced by changes in the bending moments associated with hydraulic pressure and Maxwell stress, which are modulated by qualitative and quantitative variations in the profiles of ion concentrations and voltage. The smaller size of counterions favors their accumulation and depletion over IL-cations, such that properties of IL-cations have a weak effect on the steady-state curvature when enough counterions are available in the membrane. In this case, the size of IL-anions plays an important role, as larger IL-anions elicit smaller steady-state curvatures toward the anode, in agreement with experiments.40 At larger voltages, Maxwell stress dominates the response, leading to back-relaxation toward the cathode, observed in previous experiments with IL-IPMCs.82,83 When the relative concentration of mobile counterions is small, IL-cations and IL-anions govern the formation of diffuse layers, such that the steady-state curvature shows a significant dependence on the properties of these two ionic species. In this case, the role of Maxwell stress weakens, due to the larger sizes of ions in the diffuse layers that decrease the electric field.81 Steady-state curvature is dominated by the hydraulic pressure, which is modulated by the pile-up and depletion of IL-cations and IL-anions at the two electrodes. The relative size of these ions determines the sign of the steady-state curvature, even at low voltages. For large IL-cations and small IL-anions, we obtain a steady-state curvature toward the anode, which is observed in experiments with IL-IPMCs.24
While our theory constitutes a step forward in the accurate physical description of IL-swollen ionic membranes, it comes with a number of limitations that should be addressed in future endeavors. First, experimental and atomistic/molecular computational efforts are necessary to identify the concentrations of mobile ions of different species. While some inferences could be performed from experimental structural and electrochemical characterizations35,38 and molecular dynamics simulations,84 further work is needed to accurately measure these quantities and how they vary, as a function of manufacturing, environmental and working conditions. Further, the actual degree of dissociation of ILs, which has been studied in electrolyte solutions,57 should be investigated within ionic membranes, to shed light on the presence and quantity of neutral ionic pairs. Second, several physical phenomena remain unmodeled. Our model is limited to small voltages (<4 V), whereby we do not model the decomposition of ILs at large applied voltages.75 Multiple ions in an ionic membrane will interact non-ideally, especially large and complex ones such as IL-cations. Modeling these interactions entails the use of a modified free-energy function that considers the excess free-energy compared to an ideal mixing.52,53,55 Redox reactions at the electrodes,3,51,78 for which an accurate description is still open modeling question, even for water-swollen IPMCs, should be accounted for at large voltages. The presence of neutral ionic pairs of large size, serving as a solvent, could also considerably affect the response of IL-IPMCs.54,59 Third, the large size of IL-cations may not warrant the use of the mean-field approximation used in classical electrochemistry studies that underlie our theory.3,4 The integration of elements of colloidal models may be warranted.85 Fourth, the large number of parameters involved in the response of IL-IPMCs could cause hurdles in the adoption of physically based models in the engineering community. Procedures for the identification of parameters for water-swollen IPMCs86 shall be extended to IL-IPMCs. Finally, a systematic comparison between the two categories of IL-IPMCs identified should be performed, to characterize the fundamental differences between their responses.
The most natural follow-up study to this manuscript involves the dynamic response of IL-IPMCs, which is substantially different from that of water-swollen IPMCs.24 The continuum-level model presented in this manuscript can be utilized for this purpose, potentially with some modifications in eqn (20) to account for cross-diffusion. However, two main obstacles should be overcome toward accurate physical representations of time-varying IL-IPMC actuation. First, measurements of diffusivities of common IL-cations and IL-anions in ionic membranes are missing, with only limited molecular simulations available84,87 (see ESI†). Thus, a procedure to identify the self- and cross-diffusivities of multi-cations and anions in ionic membranes from experiments should be developed. Second, we anticipate the diffusivities of common IL-cations to be much smaller than that of IL-anions and counterions, due to the large size of the former that has a substantial impact on the tortuosity in the porous membrane. Thus, one should develop a numerical solution that can deal with the multiple time-scales of diffusion for the ions in the membrane. Upon solving these pending issues, this theory can unravel the dependence of dynamic properties of IL-IPMCs on material and ionic properties, serving as a guide to material scientists for tailored microscopic modifications that can increase the actuation performance.
Author contributions
A. Boldini: conceptualization, formal analysis, investigation, methodology, software, visualization, writing – original draft, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by New York Institute of Technology.References
- Y. Tanaka, Ion exchange membranes – Fundamentals and applications, Elsevier, 2nd edn, 2015 Search PubMed.
- T. Xu, J. Membr. Sci., 2005, 263, 1–29 CrossRef CAS.
- J. Newman and K. E. Thomas-Alyea, Electrochemical systems, John Wiley & Sons, 2012 Search PubMed.
- A. J. Bard and L. R. Faulkner, Electrochemical methods – Fundamentals and applications, John Wiley & Sons, 2001 Search PubMed.
- M. Shahinpoor, Fundamentals of Smart Materials, Royal Society of Chemistry, 2020 Search PubMed.
- Ionic Polymer Metal Composites (IPMCs): Smart Multi-Functional Materials and Artificial Muscles, ed. M. Shahinpoor, Royal Society of Chemistry, 2015 Search PubMed.
- C. Jo, D. Pugal, I.-K. Oh, K. J. Kim and K. Asaka, Prog. Polym. Sci., 2013, 38, 1037–1066 CrossRef CAS.
- J. D. Carrico, T. Tyler and K. K. Leang, Int. J. Smart Nano Mater., 2017, 8, 144–213 CrossRef.
- N. Minaian, Z. J. Olsen and K. J. Kim, Bioinspired Sensing, Actuation, and Control in Underwater Soft Robotic Systems, 2021, pp. 117–139 Search PubMed.
- Biomedical Applications of Electroactive Polymer Actuators, ed. F. Carpi and E. Smela, Wiley, 2009 Search PubMed.
- Z. Chen, Rob. Biomimetics, 2017, 4, 24 CrossRef PubMed.
- Z. J. Olsen, K. J. Kim and I.-K. Oh, Polym. Int., 2021, 70, 7–9 CrossRef CAS.
- K. J. Kim, V. Palmre, T. Stalbaum, T. Hwang, Q. Shen and S. Trabia, Mar. Technol. Soc., 2016, 50, 24–34 CrossRef.
- A. Boldini, M. Rosen, Y. Cha and M. Porfiri, Sci. Rep., 2019, 9, 1–14 CrossRef CAS PubMed.
- A. Boldini, Y. Cha and M. Porfiri, Phys. Rev. Lett., 2021, 126, 046001 CrossRef CAS PubMed.
- N. Ulbricht, A. Boldini, C. Bae, T. Wallmersperger and M. Porfiri, Adv. Mater. Interfaces, 2022, 9, 2200888 CrossRef CAS.
- K. A. Mauritz and R. B. Moore, Chem. Rev., 2004, 104, 4535–4586 CrossRef CAS PubMed.
- P. G. de Gennes, K. Okumura, M. Shahinpoor and K. J. Kim, Europhys. Lett., 2000, 50, 513 CrossRef CAS.
- S. Nemat-Nasser and J. Y. Li, J. Appl. Phys., 2000, 87, 3321–3331 CrossRef CAS.
- T. Wallmersperger, B. J. Akle, D. J. Leo and B. Kröplin, Compos. Sci. Technol., 2007, 68, 1173–1180 CrossRef.
- Z. Zhu, K. Asaka, L. Chang, K. Takagi and H. Chen, J. Appl. Phys., 2013, 114, 084902 CrossRef.
- Y. Cha and M. Porfiri, J. Mech. Phys. Solids, 2014, 71, 156–178 CrossRef CAS.
- A. Boldini and M. Porfiri, J. Mech. Phys. Solids, 2022, 164, 104875 CrossRef CAS.
- M. D. Bennett and D. J. Leo, Sens. Actuators, A, 2004, 115, 79–90 CrossRef CAS.
- C.-Y. Yu, Y.-W. Zhang and G.-D. J. Su, Sens. Actuators, A, 2015, 232, 183–189 CrossRef CAS.
- Y. Bar-Cohen, S. P. Leary, A. Yavrouian, K. Oguro, S. Tadokoro, J. S. Harrison, J. G. Smith and J. Su, Smart Structures and Materials 2000: Electroactive Polymer Actuators and Devices (EAPAD), 2000, pp. 140–146 Search PubMed.
- B. Akle and D. J. Leo, Smart Mater. Struct., 2004, 13, 1081 CrossRef.
- S. J. Kim, I. T. Lee, H.-Y. Lee and Y. H. Kim, Smart Mater. Struct., 2006, 15, 1540 CrossRef CAS.
- H. Lei, W. Li, G. Zhu and X. Tan, Smart Materials, Adaptive Structures and Intelligent Systems, 2012, pp. 35–42 Search PubMed.
- M. Freemantle, An introduction to ionic liquids, Royal Society of Chemistry, 2010 Search PubMed.
- Z. Lei, B. Chen, Y.-M. Koo and D. R. MacFarlane, Introduction: ionic liquids, 2017 Search PubMed.
- Y. Yu and Y. Chen, ACS Omega, 2021, 6, 14869–14874 CrossRef CAS PubMed.
- M. Galiński, A. Lewandowski and I. Stepniak, Electrochim. Acta, 2006, 51, 5567–5580 CrossRef.
- M. J. Earle and K. R. Seddon, Pure Appl. Chem., 2000, 72, 1391–1398 CrossRef CAS.
- M. D. Bennett, D. J. Leo, G. L. Wilkes, F. L. Beyer and T. W. Pechar, Polymer, 2006, 47, 6782–6796 CrossRef CAS.
- B. J. Akle, M. D. Bennett and D. J. Leo, Sens. Actuators, A, 2006, 126, 173–181 CrossRef CAS.
- K. Kikuchi and S. Tsuchitani, J. Appl. Phys., 2009, 106, 053519 CrossRef.
- Y. Liu, C. Lu, S. Twigg, M. Ghaffari, J. Lin, N. Winograd and Q. Zhang, Sci. Rep., 2013, 3, 973 CrossRef PubMed.
- J. Wang, C. Xu, M. Taya and Y. Kuga, Smart Mater. Struct., 2007, 16, S214 CrossRef CAS.
- J.-W. Lee and Y.-T. Yoo, Sens. Actuators, B, 2009, 137, 539–546 CrossRef CAS.
- J. Lin, Y. Liu and Q. Zhang, Polymer, 2011, 52, 540–546 CrossRef CAS PubMed.
- K. Kikuchi, T. Sakamoto, S. Tsuchitani and K. Asaka, J. Appl. Phys., 2011, 109, 073505 CrossRef.
- M. Safari, L. Naji, R. T. Baker and F. A. Taromi, Polymer, 2015, 76, 140–149 CrossRef CAS.
- K. Tozzi, R. Gonçalves, R. Barbosa, M. Saccardo, A. Zuquello, E. Sgreccia, R. Narducci, C. Scuracchio and M. di Vona, J. Appl. Electrochem., 2023, 53, 241–255 CrossRef CAS.
- Q. Zhao, J. Heyda, J. Dzubiella, K. Täuber, J. W. Dunlop and J. Yuan, Adv. Mater., 2015, 27, 2913–2917 CrossRef CAS PubMed.
- K. Mukai, K. Asaka, K. Kiyohara, T. Sugino, I. Takeuchi, T. Fukushima and T. Aida, Electrochim. Acta, 2008, 53, 5555–5562 CrossRef CAS.
- I. Takeuchi, K. Asaka, K. Kiyohara, T. Sugino, N. Terasawa, K. Mukai, T. Fukushima and T. Aida, Electrochim. Acta, 2009, 54, 1762–1768 CrossRef CAS.
- W. Lu, A. G. Fadeev, B. Qi, E. Smela, B. R. Mattes, J. Ding, G. M. Spinks, J. Mazurkiewicz, D. Zhou and G. G. Wallace, et al. , Science, 2002, 297, 983–987 CrossRef CAS PubMed.
- F. Vidal, C. Plesse, D. Teyssié and C. Chevrot, Synth. Met., 2004, 142, 287–291 CrossRef CAS.
- H. Kokubo, R. Sano, K. Murai, S. Ishii and M. Watanabe, Eur. Polym. J., 2018, 106, 266–272 CrossRef CAS.
- A. Drozdov, Acta Mech., 2016, 227, 437–465 CrossRef.
- A. R. Crothers, R. M. Darling, A. Kusoglu, C. J. Radke and A. Z. Weber, J. Electrochem. Soc., 2020, 167, 013547 CrossRef.
- A. R. Crothers, R. M. Darling, A. Kusoglu, C. J. Radke and A. Z. Weber, J. Electrochem. Soc., 2020, 167, 013548 CrossRef.
- A. Boldini and M. Porfiri, Phys. Rev. Lett., 2021, 127, 156001 CrossRef CAS PubMed.
- A. Boldini and M. Porfiri, npj Comput. Mater., 2022, 8, 144 CrossRef.
- M. E. Gurtin, E. Fried and L. Anand, The Mechanics and Thermodynamics of Continua, Cambridge University Press, 2013 Search PubMed.
- O. Nordness and J. F. Brennecke, Chem. Rev., 2020, 120, 12873–12902 CrossRef CAS PubMed.
- J. D. Jackson, Classical Electrodynamics, John Wiley & Sons, 3rd edn, 1999 Search PubMed.
- A. Leronni and L. Bardella, J. Mech. Phys. Solids, 2021, 148, 104292 CrossRef CAS.
- W. Hong, X. Zhao and Z. Suo, J. Mech. Phys. Solids, 2010, 58, 558–577 CrossRef CAS.
- G. A. Ateshian, Biomech. Model. Mechanobiol., 2007, 6, 423–445 CrossRef PubMed.
- M. S. Kilic, M. Z. Bazant and A. Ajdari, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 021502 CrossRef PubMed.
- M. S. Kilic, M. Z. Bazant and A. Ajdari, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 021503 CrossRef PubMed.
- A. Boldini and M. Porfiri, Electrochim. Acta, 2022, 426, 140781 CrossRef CAS.
- G. A. Holzapfel, Nonlinear Solid Mechanics – A Continuum Approach for Engineering, John Wiley & Sons, 2000 Search PubMed.
- R. C. Batra, Int. J. Non Linear Mech., 2001, 36, 421–432 CrossRef.
- E. Fermi, Thermodynamics, Dover, New York, 1956 Search PubMed.
- M. Z. Bazant, K. Thornton and A. Ajdari, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 70, 021506 CrossRef PubMed.
- Z. J. Olsen and K. J. Kim, Smart Mater. Struct., 2021, 30, 095024 CrossRef.
- A. Boldini and M. Porfiri, Int. J. Eng. Sci., 2020, 149, 103227 CrossRef CAS.
- A. Boldini, L. Bardella and M. Porfiri, J. Elasticity, 2020, 141, 227–272 CrossRef.
- B. J. Akle and D. J. Leo, J. Intell. Mater. Syst. Struct., 2008, 19, 905–915 CrossRef CAS.
- J. A. Pelesko and D. H. Bernstein, Modeling MEMS and NEMS, CRC Press, 2002 Search PubMed.
- M. Porfiri, A. Leronni and L. Bardella, Extreme Mech. Lett., 2017, 13, 78–83 CrossRef.
- M. C. Kroon, W. Buijs, C. J. Peters and G.-J. Witkamp, Green Chem., 2006, 8, 241–245 RSC.
- L. Quartapelle and S. Rebay, J. Comput. Phys., 1990, 86, 314–354 CrossRef.
- A. Quarteroni, R. Sacco and F. Saleri, Numerical Mathematics, Springer Science & Business Media, 2010, vol. 37 Search PubMed.
- M. Z. Bazant, K. T. Chu and B. J. Bayly, SIAM J. Appl. Math., 2005, 65, 1463–1484 CrossRef CAS.
- M. Porfiri, J. Appl. Phys., 2008, 104, 104915 CrossRef.
- K. Asaka, K. Oguro, Y. Nishimura, M. Mizuhata and H. Takenaka, Polym. J., 1995, 27, 436–440 CrossRef CAS.
- M. Porfiri, H. Sharghi and P. Zhang, J. Appl. Phys., 2018, 123, 014901 CrossRef.
- Y. Liu, S. Liu, J. Lin, D. Wang, V. Jain, R. Montazami, J. R. Heflin, J. Li, L. Madsen and Q. Zhang, Appl. Phys. Lett., 2010, 96, 223503 CrossRef.
- Y. Liu, M. Ghaffari, R. Zhao, J.-H. Lin, M. Lin and Q. Zhang, Macromolecules, 2012, 45, 5128–5133 CrossRef CAS.
- D. Sun and J. Zhou, AIChE J., 2013, 59, 2630–2639 CrossRef CAS.
- H. Ohshima, Theory of colloid and interfacial electric phenomena, Elsevier, 2006 Search PubMed.
- L. Bardella and A. Panteghini, Smart Mater. Struct., 2023, 32, 115031 CrossRef.
- C. Martins, L. Neves, I. Coelhoso, F. Vaca Chavez, J. Crespo and P. Sebastiao, Fuel Cells, 2013, 13, 1166–1176 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ma00097h |
| ‡ This modeling choice does not affect the results in this paper, as we only consider the steady-state response of IL-IPMCs. |
| This journal is © The Royal Society of Chemistry 2024 |