Performance of second generation ICP-TOFMS for (multi-)isotope ratio analysis: a case study on B, Sr and Pb and their isotope fractionation behavior during the measurements

Abstract

The performance of second generation ICP-TOFMS, equipped with a micro-channel plate (MCP) enabling multi-isotope detection, in terms of isotope ratio precision and instrumental isotopic fractionation (IIF) for (multi-)isotope ratio analysis was thoroughly assessed for B, Sr and Pb. Experimental isotope ratio precision of 0.14% for ¹¹B/¹⁰B intensity ratio, 0.15% for ⁸⁷Sr/⁸⁶Sr intensity ratio and 0.07% for ²⁰⁸Pb/²⁰⁶Pb intensity ratio were obtained at high signal levels (≥500 μg L⁻¹) which is comparable to first generation ICP-TOFMS. The long-term stability of isotope ratios, measured over several hours and expressed as repeatability, is between 0.05% and 1.8% for B, Sr and Pb. The observed IIF per mass unit is negative for B (i.e., −11% for ¹¹B/¹⁰B) which is in accordance with measurements using sector field (MC) ICP-MS. But the observed IIF per mass unit is positive for Sr (i.e., 2% for ⁸⁷Sr/⁸⁶Sr) and Pb (i.e., 4.5% for ²⁰⁸Pb/²⁰⁶Pb) which is not in accordance with measurements using sector field (MC) ICP-MS. Furthermore, different IIFs per mass unit were observed for different isotope pairs of the same isotopic system (i.e., Sr, Pb) and adjacent isotopic systems (i.e., Pb vs. Tl). This and the observations from three-isotope plots for Sr and Pb show that ion formation, ion extraction, ion transmission, ion separation and ion detection in second generation ICP-TOFMS is subject to IIF that does not follow the known mass dependent fractionation laws and is possibly caused by mass independent fractionation and/or multiple (contradictory) fractionation processes with varying contributions. The non-mass dependent IIF behavior observed for second generation ICP TOFMS has profound consequences for the IIF correction of isotope raw data, including application of multi-isotope dilution mass spectrometry (IDMS) using ICP-TOFMS. Hence, only IIF correction models that correct also for mass independent fractionation are applicable to calculate reliable isotope ratios using second generation ICP-TOFMS. In the present study, reliable δ¹¹B values, and absolute B, Sr and Pb isotope ratios could be determined using the SSB approach in single-element solutions as well as in a mixture of B, Sr and Pb, where the isotopes were measured simultaneously.

---

1. Introduction

Within the last decades, the analysis of systematic variations in the isotopic composition of B, Sr and Pb has been applied in a wide range of scientific disciplines, such as geosciences,^1,2 environmental sciences,^3–5 nuclear and forensic sciences,⁶ (food) provenance studies,^7,8 anthropology and archaeology.^9,10 The natural variation in their isotope abundances is the result of either radiogenic ingrowth or small differences in the efficiency with which their isotopes participate in physical, chemical, biological, biochemical, metabolic and climatic processes, and has very different causes.^11,12 The magnitude and direction of the variation in the abundance of B isotopes (i.e., ¹⁰B, ¹¹B) are controlled by the large relative difference in mass of the two isotopes (so called mass dependent fractionation).^11,13,14 As a light element, B is highly sensitive to mass dependent fractionation.¹³ The magnitude and direction of the variation in the abundance of Sr and Pb isotopes are governed by factors such as ratio of radioactive parent and daughter nuclides (i.e., ⁸⁷Rb to ⁸⁷Sr; ²³⁸U, ²³⁵U and ²³²Th to ²⁰⁶Pb, ²⁰⁷Pb and ²⁰⁸Pb, respectively), decay constants and time.^13,15 The potential mass dependent fractionation of the radiogenic isotopic signatures of Sr and Pb are considered to be small during geochemical and biochemical processes.¹³ Even though the relative variation in the isotopic composition of B, Sr and Pb may seem small, they are significant, robust and measurable, when using appropriate instrumentation and calibration strategies.¹⁴ Typically, the isotope ratio analyses of B, Sr and Pb are performed by either multiple collector thermal ionization mass spectrometry (MC TIMS) or multiple collector inductively coupled plasma mass spectrometry (MC ICP-MS). Under optimal conditions, MC TIMS and MC ICP-MS instruments provide isotope ratio precisions of ≤0.001% RSD (in low resolution).^16,17

Nevertheless, different types of single collector ICP-MS instruments have been applied for isotope ratio applications that could work with rather modest isotope ratio precisions. ICP-MS systems with different mass separation devices, a quadrupole filter (Q), a double-focusing sector field (SF), and a time-of-flight (TOF), are already commercially available.¹⁸ Traditionally, these single collector instruments are equipped with an electron multiplier as detector to enable (ultra-)trace analysis. This detector shows its highest sensitivity in pulse counting mode where almost every incoming ion is detected but dead time has to be taken into account.¹⁹ At high ion beam intensity, the electron multiplier is used as an analog amplifier.¹⁷ Depending on the isotopic system, with ‘traditional’ quadrupole-based ICP-MS, the isotope ratio precision is limited to ≥0.1% RSD under optimal conditions.¹⁷ In the presence of interferences, collision-cell ICP-QMS and ICP-MS/MS archive an isotope ratio precision of ≤0.1% under optimal conditions.^20–22 The isotope ratio precision achievable with sector field ICP-MS under optimal conditions (i.e., only one isotope pair is monitored) is at ≤0.05% RSD in low resolution. In medium resolution with its rather triangular peak shape the isotope ratio precision of ICP-SFMS (RSD ≥0.1%) is comparable to ‘traditional’ ICP-QMS.^16,17 With first generation ICP-TOFMS, which employed an electron multiplier as detector, the reported isotope ratio precision under optimal conditions ranged between ≤0.5% RSD and ≥0.02% RSD (see Table S1 in ESI†).^{17,18,23–25} The isotope ratio performance of the first generation ICP-TOFMS is therefore comparable to collision-cell ICP-QMS and ICP-MS/MS instruments, and under optimal conditions even comparable to ICP-SFMS instruments which is attributed to the simultaneous handling of ions formed at the same time in the plasma.¹⁷ These rather modest isotope ratio precisions as compared to MC TIMS and MC ICP-MS are the result of the combination of ICP as a rather ‘noisy’ ion source and the use of only a single detector, which allows only monitoring of a single isotope at a given time.²⁶

As the TOF mass separator accepts all ions at the same time²⁶ like an ion trap, it is capable of measuring all isotopes of the full elemental mass range quasi-simultaneously with a micro channel plate (MCP) that enables detection of multiple isotopes.²⁷ The MCP detector itself as a whole does not have a dead time.²⁸ In 1993, Myer and Hieftje have described and designed a prototype ICP-TOFMS instruments with a MCP.²⁹ Their preliminary isotope ratio analysis achieved a isotope ratio precision of <0.6% RSD.^26,30 The second generation of ICP-TOFMS (i.e., employing a MCP as detector to measure a m/z range of approx. 1–260) are now commercially available by the manufacturers TOFWERK³¹ and Nu Instruments.³² Initial studies reported isotope ratio precision between <0.6% RSD and ≥0.02% RSD.^27,33 This is comparable to the performance of the first generation of ICP-TOFMS despite the multi-elemental detection capability of the MCP. However, the unique feature of the second generation ICP-TOFMS is multi-ion-counting which enables multi-isotope ratio analysis (i.e., quasi-simultaneous detection of multiple isotope systems).²⁷

No matter which of these ICP-MS instrument is used for the isotope ratio analysis, the different efficiency of sample introduction, ion formation, ion extraction, ion transmission, ion separation and ion detection of the ICP-MS itself may result in significantly biased isotope ratios with respect to the true value.^17,34 This phenomenon is referred to as instrumental isotopic fractionation (IIF, aka mass bias, mass discrimination) and has to be corrected for.³⁴ IIF includes all discrimination effects, and it is mainly determined by mass dependent effects but mass independent fractionation has also been observed for ICP-MS. The potential occurrence of mass independent IIF has significant impact on the choice of the IIF correction model to determine reliable isotope ratios.³⁵ The understanding of the factors that cause IIF phenomena within the ICP-MS is still very limited, and appropriate correction remains a challenge.^12,34,36 A number of different strategies to calibrate an ICP-MS measurement for the effect of IIF have been proposed over the years.^35,37 For the present study, the following three approaches for IIF correction of B, Sr, and Pb isotope ratios measured by ICP-TOFMS are of interest:

(i) In case of Sr, the R_con(⁸⁷Sr/⁸⁶Sr) (hereinafter referred to as conventional ⁸⁷Sr/⁸⁶Sr isotope ratio) is corrected for IIF internally using the ⁸⁶Sr/⁸⁸Sr isotope ratio (= 0.1194 (ref. 38)) by convention assuming that there is no natural fractionation of the ⁸⁶Sr/⁸⁸Sr isotope ratio. Here, a IIF correction factor f is calculated based on empirical fractionation laws and applied under the assumption of a constant IIF correction factor f for both ⁸⁶Sr/⁸⁸Sr and ⁸⁷Sr/⁸⁶Sr isotope ratios.³⁷ This internal IIF correction model can correct for mass dependent IIF but not for any mass independent IIF.³⁵

(ii) The internal inter-elemental correction model uses another element similar in mass to the isotopic system of interest to calculate the IIF correction factor f in accordance with empirical fractionation laws, e.g., ²⁰⁵Tl/²⁰³Tl for Pb.^35,39 This IIF correction factor f is subsequently applied to the isotopic system of interest assuming a constant IIF for both elements.³⁷ The internal inter-elemental IIF correction model can correct for mass dependent IIF but not for any mass independent IIF.³⁵

(iii) The most straight forward approach is the direct comparison of the isotope ratio of the sample and a reference material with known isotopic composition. This method is also referred to as the correction factor method. The standard-sample bracketing (SSB) is a special case of the correction factor method where the IIF is monitored in possibly short time intervals by measuring the reference material (bracketing standard) before and after every sample. The SSB approach is used for calculating delta values,³⁷e.g., for B isotopes,⁴⁰ and absolute isotope ratios, e.g., B, Sr and Pb.^35,37 This external IIF correction model can correct for mass dependent and mass independent IIF.³⁵

Taking a closer look at IIF,^34,41 previous studies using the first generation of ICP-TOFMS reported that the IIF per mass unit is substantial for light elements (e.g., Li has −13%) whereas for high mass elements the IIF per mass unit is significantly lower (e.g., Pb has 0.2%).²⁴ This is similar to observations from MC ICP-MS and ICP-QMS measurements, where the IIF typically varies systematically from about −13% to −15% for Li to −0.2% for U.³⁴ Moreover, the first generation ICP-TOFMS instruments with their different geometry (i.e., orthogonal, axial) reported comparable IIF.²⁵ However, sudden shifts in the IIF per mass unit occurred that indicated non-linear response and have not been explained yet.²⁴ This odd IIF behavior required regular calibration with isotopic reference materials using⁴²e.g., the SSB approach. In previous applications of isotope dilution mass spectrometry (IDMS) using second generation ICP-TOFMS, the internal inter-elemental IIF correction model was applied.^43,44 However, the IIF behavior and the applicability of different IIF correction models have not yet been investigated in detail for isotope ratio analysis using second generation ICP-TOFMS. With this background, the present study investigated the performance of a second generation ICP-TOFMS with a MCP detector in terms of isotope ratio precision, isotope ratio trueness and IIF for (multi-)isotope ratio analysis of B, Sr and Pb. These are three isotopic system that cover almost the full mass range, for which different IIF correction strategies are commonly applied and both relative and absolute isotope ratios are reported.

2. Experimental

Throughout the present study, measurement precision under different specified conditions of measurement are considered:⁴⁵ (i) isotope ratio precision (aka internal precision), expressed as RSD, refers to the standard deviation of M runs averaged to one measurement result, (ii) repeatability is the standard deviation of N measurements taken within a short time period, and (iii) intermediate precision is the standard deviation of N measurements over several days and used here as a measure for long-term stability.

2.1. Reagents & reference materials

High-Quality water (HQ-water, Type I reagent-grade water (18.2 MΩ cm)) was obtained from a Milli-Q Integral water purification system (Merck-Millipore, Darmstadt, Germany). Analytical reagent-grade nitric acid (w(HNO₃) = 65%, Chemsolute, Th. Geyer, Renningen, Germany) was further purified by two-stage sub-boiling distillation (PicoTrace, Bovenden, Germany). Before use, polypropylene (PP) tubes were leached for at least one week with dilute nitric acid (w(HNO₃) ≈ 3%).

Isotope certified reference materials were used throughout the study: (i) NIST SRM 951a (boric acid, National Institute for Standards and Technology (NIST), Gaithersburg, USA) which is certified for ¹⁰B/¹¹B isotope ratios, (ii) NIST SRM 987 (strontium carbonate, NIST) which is certified for n(⁸⁷Sr)/n(⁸⁶Sr) isotope ratios, and NIST SRM 981 (common lead, NIST) which is certified for Pb isotope ratios n(^20xPb)/n(²⁰⁶Pb) with x = 4, 7, 8, respectively. (iv) ERM-AE120 (boric acid in water, Bundesanstalt für Materialforschung und -prüfung (BAM), Berlin, Germany), ERM-AE121 (boric acid in water, BAM) and ERM-AE122 (boric acid in water, BAM)⁴⁰ which are certified for δ_{NIST SRM951a}(¹¹B/¹⁰B) values (in the following denoted to as δ¹¹B_SRM951a), and (v) ERM-AE142 (Pb in nitric acid, BAM) which is certified for Pb isotope ratios n(^20xPb)/n(²⁰⁴Pb) with x = 6, 7,8, respectively. Further, Sr ICP-standard (Sr single element standard, Merck) which was priorly characterized for conventional ⁸⁷Sr/⁸⁶Sr isotope ratio using MC TIMS was analyzed throughout this study. In addition, Tl ICP-standard (Tl single element standard, Merck) was used as external normalization standard for Pb isotopes.

Mixtures of NIST SRM 951a, NIST SRM 987, and NIST SRM 981 were prepared volumetrically with dilute nitric acid (w(HNO₃) = 2%) to optimize the mixture ratios. These mixtures covered the following mass concentration ranges: B mass concentrations of 100 μg L⁻¹ to 5000 μg L⁻¹, Sr mass concentrations of 100 μg L⁻¹ to 500 μg L⁻¹, and Pb mass concentrations of 100 μg L⁻¹ to 2000 μg L⁻¹.

For the single-element B isotope ratio analysis, NIST SRM 951a, ERM-AE120, ERM-AE121, and ERM-122 were diluted volumetrically with dilute nitric acid (w(HNO₃) = 2%) to a B mass concentration of 5000 μg L⁻¹. For the single-element Sr isotope ratio analysis, NIST SRM 987 and Sr ICP-standard (Merck) were diluted volumetrically with dilute nitric acid (w(HNO₃) = 2%) to a Sr mass concentration of 500 μg L⁻¹. For the single-element Pb isotope ratio analysis, NIST SRM 981 and ERM-AE142 were diluted volumetrically with dilute nitric acid (w(HNO₃) = 2%) to a Pb mass concentration of 1000 μg L⁻¹.

For the multi-isotope ratio analysis, an SSB-standard mixture containing NIST SRM 951a (γ(B) = 5000 μg L⁻¹), NIST SRM 987 (γ(Sr) = 500 μg L⁻¹), and NIST SRM 981 (γ(Pb) = 1000 μg L⁻¹) was prepared volumetrically with dilute nitric acid (w(HNO₃) = 2%). Three sample mixtures were prepared volumetrically with dilute nitric acid (w(HNO₃) = 2%) containing either one of ERM-AE120, ERM-AE121, or ERM-122 (γ(B) = 5000 μg L⁻¹), Sr ICP-standard (Merck, γ(Sr) = 500 μg L⁻¹) and ERM-AE142 (γ(Pb) = 1000 μg L⁻¹).

For investigating the external normalized IIF correction, NIST SRM981 was diluted volumetrically with dilute nitric acid (w(HNO₃) = 2%) to a Pb mass concentrations of 500 μg L⁻¹ and spiked with Tl ICP-Standard (γ(Pb) = 500 μg L⁻¹).

2.2. Instrumentation

The B, Sr and Pb isotope ratio analyses of the single-element solutions and a mixture were conducted using an ICP-TOFMS (icpTOF 2R, TOFWERK, Thun, Switzerland). The ICP-TOFMS analysis was carried out with the standard sample introduction system that consists of a concentric nebulizer and a cyclonic spray chamber.

The instrument was optimized in a daily routine for sensitivity and mass calibration using a tuning solution, containing B, Sr and Pb to maintain a reliable day-to-day-performance. In addition, the instrument was optimized in a weekly routine for mass resolution using the same tuning solution. General instrumental settings for the multi-isotope ratio measurements are described in ESI Table S2.†

2.3. Measurement routines, data processing and uncertainty budget

Data collection for samples, isotope reference materials and standards was accomplished with an averaged spectrum acquisition rate of 1.98 Hz (averaged mass spectra are composed of data summed from 11 000 full mass spectra extraction frequency = 21.739 kHz), that came up to a spectral averaging time of 0.5 s. Blank correction was performed by subtracting background levels of dilute nitric acid (w(HNO₃) = 2%) measured before each sample, isotope reference material, and standards from all isotopes of interest. Data collection for the blank was accomplished over a period of 50 s. For an extended integration time,³³ signals and isotopic ratios were averaged across a time window of 10 s. This divided the total of 400 data points acquired into 20 runs (M). The samples and corresponding isotope reference material and standards were introduced into the plasma in the following sequence: standard – sample – standard, to enable correction for IIF via classical SSB.^34,46 Mass concentrations of sample and SSB standard were matched within 10%. All isotope ratio measurements were carried out with five replicates per sample (N = 5).

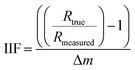
The IIF per mass unit for B, Sr, and Pb were calculated in accordance with Heumann et al.⁴¹ and Irrgeher & Prohaska:³⁴

where IIF is the IIF per mass unit in percent (%), R_true is the true/certified isotope ratio of the heavier isotope over the lighter isotope, R_measured is the measured isotope ratio of the heavier isotope over the lighter isotope and Δm is the difference in mass between the heavier isotope and the lighter isotope. Throughout this study, isotope ratios of heavier isotope over lighter isotope were considered, and the masses recommended by IUPAC/CIAAW^47,48 were used.

For B isotopes, δ¹¹B_SRM951a values were calculated relative to the average isotope ratio of the isotope standard (NIST SRM 951a) from the SSB in accordance with standard protocols.^49,50

For Sr isotopes, conventional ⁸⁷Sr/⁸⁶Sr isotope ratios were calculated as commonly agreed on:⁵¹ (i) correction for residual ⁸⁷Rb interference via peak stripping⁵² of the simultaneously measured ⁸⁵Rb and using the natural n(⁸⁷Rb)/n(⁸⁵Rb) (= 0.3856) ratio recommended by IUPAC/CIAAW,^47,48 without correction of IIF (see discussion in section 3.5). (ii) The measured ⁸⁷Sr/⁸⁶Sr isotope ratio was corrected for IIF by applying an IIF correction factor f which was obtained from the measured ⁸⁶Sr/⁸⁸Sr isotope ratio and the conventional ⁸⁶Sr/⁸⁸Sr isotope ratio defined as 0.1194 (ref. 38) by using the Russell law.⁵³ A constant IIF correction factor f for both ⁸⁶Sr/⁸⁸Sr and ⁸⁷Sr/⁸⁶Sr isotope ratios was assumed It should be noted that this step is the main difference between the conventional ⁸⁷Sr/⁸⁶Sr isotope ratio and the absolute isotope ratio n(⁸⁷Sr)/n(⁸⁶Sr), since isotope variations are neglected, and an insufficiently accurate value is used for the ⁸⁶Sr/⁸⁸Sr isotope ratio. The commonly accepted value for the conventional ⁸⁷Sr/⁸⁶Sr isotope ratio of the NIST SRM 987 is 0.71025.⁵⁴ Note, unfortunately this IIF correction model failed for ⁸⁷Sr/⁸⁷Sr isotope ratios measured by ICP-TOFMS (see discussion in Section 3.5).

Furthermore, absolute n(⁸⁷Sr)/n(⁸⁶Sr) isotope ratios were calculated following the classical SSB approach:^35,37,55 (i) correction for residual ⁸⁷Rb interference via peak stripping⁵² of the simultaneously measured ⁸⁵Rb and using the natural n(⁸⁷Rb)/n(⁸⁵Rb) (= 0.3856) ratio recommended by IUPAC/CIAAW,^47,48 without correction of IIF (see discussion in section 3.5). (ii) A correction factor k was calculated based on the observed bias between the measured ⁸⁷Sr/⁸⁶Sr isotope ratios of the NIST SRM 987 solution and its accepted values (0.71025 (ref. 54)). The measured ⁸⁷Sr/⁸⁶Sr isotope ratio of the sample was corrected for IIF via the average correction factor k of the same isotope ratio measured in the NIST SRM 987 solution introduced before and after each sample. As the same isotope pair from the SSB standard is used to correct IIF in the sample, potential mass independent IIF can be accounted for.^35,56 Note, the accepted value of conventional ⁸⁷Sr/⁸⁶Sr isotope ratios for the NIST SRM 987 was used as the anchor point to enable comparison to MC TIMS measurements.

For Pb isotopes, absolute n(²⁰⁸Pb)/n(²⁰⁴Pb), n(²⁰⁷Pb)/n(²⁰⁴Pb), n(²⁰⁶Pb)/n(²⁰⁴Pb) and n(²⁰⁸Pb)/n(²⁰⁶Pb) isotope ratios were calculated following the classical SSB approach:^35,37,55 (i) correction for residual ²⁰⁴Hg interference via peak stripping⁵² of the simultaneously measured ²⁰²Hg and using the natural n(²⁰⁴Hg)/n(²⁰²Hg) (= 0.2293) ratio recommended by IUPAC/CIAAW,^47,48 without correction of IIF (see section 3.5). (ii) A correction factor k was calculated based on the observed bias between the measured Pb isotope ratio of the NIST SRM 981 solution and its true certified value. The measured Pb isotope ratio of the sample was corrected for IIF via the average correction factor k of the same isotope ratio measured in the NIST SRM 981 solution measured introduced before and after each sample. As the same isotope pair from the SSB standard is used to correct IIF in the sample, potential mass independent IIF can be accounted for.^35,56 The certified values of Pb isotope ratio of the NIST SRM 981 were used as the respective anchor points.

In addition, the internal inter-elemental IIF correction approach for Pb isotopes using an external standard (= Tl) was investigated. The absolute n(²⁰⁸Pb)/n(²⁰⁴Pb), n(²⁰⁷Pb)/n(²⁰⁴Pb), n(²⁰⁶Pb)/n(²⁰⁴Pb) and n(²⁰⁸Pb)/n(²⁰⁶Pb) isotope ratios were calculated as follows:³⁵ (i) correction for residual ²⁰⁴Hg interference via peak stripping⁵² of the simultaneously measured ²⁰²Hg and using the natural n(²⁰⁴Hg)/n(²⁰²Hg) (= 0.2293) ratio recommended by IUPAC/CIAAW,^47,48 without correction of IIF (see section 3.5). (ii) The measured Pb isotope ratios were corrected for IIF by applying a IIF correction factor f which was obtained from the measured n(²⁰⁵Tl)/n(²⁰³Tl) ratio and the natural n(²⁰⁵Tl)/n(²⁰³Tl) ratio recommended by IUPAC/CIAAW^47,48 by using the Russell law.⁵³ A constant IIF correction factor f for all Pb and Tl isotope ratios is assumed. Note, unfortunately this IIF correction model failed for Pb isotope ratios measured by ICP-TOFMS (see discussion in Section 3.5).

For the single measurement of each sample, the total combined uncertainties for B, Sr, and Pb isotope ratios were calculated using a simplified Kragten approach.⁵⁷ The standard uncertainties (u = SE) of the sample and both bracketing standards were considered as major contributors to the uncertainty. For the mean B, Sr, and Pb isotope ratios of each sample (N = 5), the total combined uncertainties were calculated using error propagation considering the combined uncertainty of the single measurement and the standard deviation of the mean (u = SE) of the five replicates.

3. Results and discussion

3.1. Mixture of elements

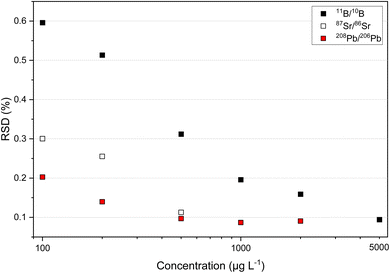
Since overloading of the MCP detector of the ICP-TOFMS occurs at high mass concentrations (total ion intensities >10⁷ s⁻¹), the composition of the mixture for simultaneous multi-isotope ratio analysis of B, Sr and Pb was optimized. Fig. 1 shows the isotope ratio precision of ¹¹B/¹⁰B, ⁸⁷Sr/⁸⁶Sr and ²⁰⁸Pb/²⁰⁶Pb for different elemental mass concentrations. The ¹¹B/¹⁰B isotope ratio reached an RSD of about 0.1% at a mass concentration of 5000 μg L⁻¹. The ⁸⁷Sr/⁸⁶Sr isotope ratio already reached an RSD of about 0.1% at a mass concentration of 500 μg L⁻¹. This is also the case for ⁸⁸Sr/⁸⁶Sr isotope ratio (see Fig. S1 in ESI†). In case of Pb isotopes, maximum precision of about 0.1% for the ²⁰⁸Pb/²⁰⁶Pb isotope ratio was reached at a mass concentration of 1000 μg L⁻¹. Furthermore, it can be observed that RSDs of about 0.1% for ²⁰⁷Pb/²⁰⁶Pb and <0.3% for ^xPb/²⁰⁴Pb were reached at a mass concentration of 1000 μg L⁻¹ (see Fig. S1 in ESI†). Consequently, for maximum precision of all B, Sr and Pb ratios in a mixture the mass concentrations were set to 5000 μg L⁻¹ for B, to 500 μg L⁻¹ for Sr and to 1000 μg L⁻¹ for Pb. At this concentration levels, the observed sensitivity was for B about 270 s⁻¹ (μg L⁻¹)⁻¹, for Sr about 4200 s⁻¹ (μg L⁻¹)⁻¹ and for Pb about 1900 s⁻¹ (μg L⁻¹)⁻¹. The mixture of B, Sr and Pb came up to a total of less than 6.5 × 10⁶ s⁻¹ for all measured isotopes which did not overload the MCP detector of the second generation ICP-TOFMS. Further, linearity of the MCP detector was seen for B, Sr and Pb over the concentration range of 100 μg L⁻¹ till 5000 μg L⁻¹ (see Fig. S2 in ESI†).

Fig. 1 Isotope ratio precision of ¹¹B/¹⁰B, ⁸⁷Sr/⁸⁶Sr and ²⁰⁸Pb/²⁰⁶Pb, expressed as RSD (%), for an acquisition time of 10 s per run (M) and M = 20, obtained for different elemental mass concentrations. The data shown are from the measurement of a mixture in which B, Sr, and Pb were detected simultaneously.

3.2. Isotope ratio precision and long-term stability

Table 1 summarizes the precision, the repeatability and the intermediate precision of B, Sr and Pb isotope ratios measured by second generation ICP-TOFMS in 30–40 discontinuous measurements over five days. This is the first time, that an isotope ratio precision, expressed as RSD, is reported for an element lighter than m/z = 14 (i.e., B) measured by second generation ICP-TOFMS. The reported precision of ¹¹B/¹⁰B isotope ratios is slightly better than reported in previous studies using first generation ICP-TOFMS for B⁵⁸ and Li²⁴ isotopes (see Table S1 in ESI†). The reported precision of ⁸⁸Sr/⁸⁶Sr and ⁸⁷Sr/⁸⁶Sr isotope ratios is slightly higher than reported in previous studies^18,24 using first generation ICP-TOFMS. Nevertheless, the reported isotope ratio precision of Sr is comparable to the previously reported precision of Cu and Ag isotopes measured by second generation ICP-TOFMS.^27,33 In case of Pb, the isotope ratio precision reported here is better than reported in most previously studies using first and second generation ICP-TOFMS^{24,27,39,42,59} except for one study using first generation ICP-TOFMS that reported comparable results¹⁸ (see Table S1 in ESI†). A previous study using second generation ICP-TOFMS investigated the relationship between integration time and isotope ratio precision and showed that the isotope ratio precision can be as good as 0.02% when extended integration times of 100 s are used.³³ This isotope ratio precision is comparable to the performance of ICP-SFMS. The same authors pointed out that the isotope ratio precision on second generation ICP-TOFMS is limited by drifts in isotope ratios which affects the RSD more at long integration times.³³ Overall, this shows that the performance in terms of isotope ratio precision is comparable between first and second generation ICP-TOFMS, despite the multi-elemental detection capability of the MCP.

Table 1 Isotope ratio precision, isotope ratio repeatability, and isotope ratio intermediate precision⁴⁵ of B, Sr and Pb measured by ICP-TOFMS in 30–40 discontinuous measurements over five days. B: NIST SRM 951a with γ(B) = 5000 μg L⁻¹, Sr: NIST SRM 987 with γ(Sr) = 500 μg L⁻¹, Pb: NIST SRM 981 with γ(Pb) = 1000 μg L⁻¹. The reported data are from measurements of both a single-element solution and a mixture

Isotope ratio	Precision – RSD	Repeatability	Intermediate precision
^11B/^10B	0.08% to 0.20% (M = 20)	0.16% (N = 5) to 0.68% (N = 10)	1.0% (N = 40)
^88Sr/^86Sr	0.08% to 0.18% (M = 20)	0.15% (N = 6) to 1.76% (N = 10)	3.4% (N = 30)
^87Sr/^86Sr	0.12% to 0.20% (M = 20)	0.24% (N = 5) to 0.90% (N = 10)	1.8% (N = 30)
^206Pb/^204Pb	0.12% to 0.34% (M = 20)	0.15% (N = 10) to 0.50% (N = 10)	1.3% (N = 30)
^208Pb/^206Pb	0.05% to 0.10% (M = 20)	0.08% (N = 10) to 0.30% (N = 5)	1.3% (N = 30)
^207Pb/^206Pb	0.05% to 0.11% (M = 20)	0.04% (N = 5) to 0.15% (N = 5)	0.8% (N = 30)

---

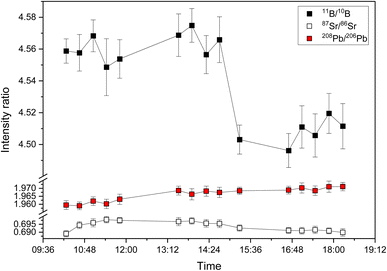
The long-term stability for 15 discontinuous measurements of ¹¹B/¹⁰B intensity ratios of NIST SRM 951a, ⁸⁷Sr/⁸⁶Sr intensity ratios of NIST SRM 987 and ²⁰⁸Pb/²⁰⁶Pb intensity ratios of NIST SRM 981 over a period of eight hours is shown in Fig. 2. The measured intensity ratio values are relatively stable for a period of several hours (e.g., ¹¹B/¹⁰B between 10 : 15 and 14 : 30) where the repeatability is < 0.2% for B, Sr and Pb. However, as previously reported for first generation ICP-TOFMS,^24,42 sudden shifts occur (e.g., ¹¹B/¹⁰B drops approx. 1.3% between 14 : 30 and 15 : 30) also for the second generation ICP-TOFMS for reasons that are not clear yet. For isotope ratio measurements, this means that regular calibration (≥2 standards h⁻¹) with an isotopic reference material is required to monitor and correct for such changes.²⁴ The repeatability of the 15 discontinuous measurements which are shown in Fig. 2 is 0.62% for ¹¹B/¹⁰B, 0.44% for ⁸⁷Sr/⁸⁶Sr, and 0.22% for ²⁰⁸Pb/²⁰⁶Pb. Consistent with previous studies^24,42 using the first generation ICP-TOFMS, the observed variation of isotope ratio values between days is higher than the within day variation (see Table 1).

Fig. 2 Long-term stability of ¹¹B/¹⁰B, ⁸⁷Sr/⁸⁶Sr and ²⁰⁸Pb/²⁰⁶Pb isotope ratios over eight hours for 15 discontinuous measurements of NIST SRM 951a, NIST SRM 987 and NIST SRM 981. Error bars correspond to 2 s (acquisition time of 10 s, M = 20). The data shown are from the measurement of a mixture in which B, Sr, and Pb were detected simultaneously.

3.3. IIF per mass unit for B, Sr and Pb

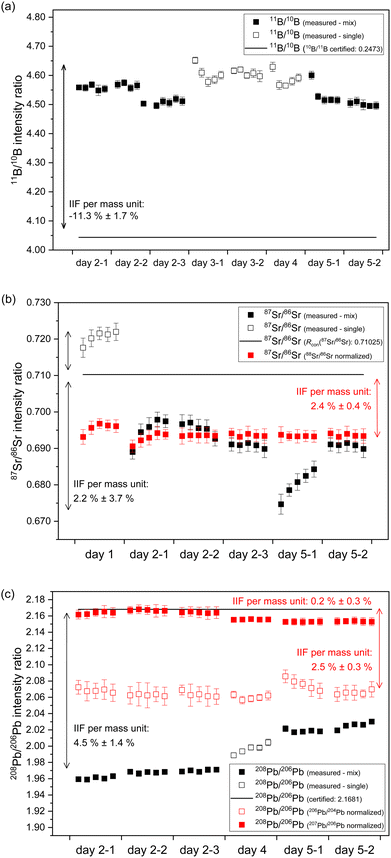
In case of B, an IIF per mass unit of −11.3% ± 1.7% (2 s, N = 40) for ¹¹B/¹⁰B intensity ratio was observed for 40 discontinuous measurements of NIST SRM 951a on four days of measurement. This corresponds to an RSD of IIF per mass unit of 8% (see Fig. 3a and Table S1†). The within day variation (expressed as RSD of IIF per mass unit) ranged between 3.2% and 5.7%. This indicates within and between day instability of the IIF per mass unit for B. The extent and algebraic sign (direction) of IIF per mass unit observed for B using second generation ICP-TOFMS is comparable to IIF per mass unit observed for Li using first generation ICP-TOFMS.²⁴

Fig. 3 (a) ¹¹B/¹⁰B intensity ratios, (b) ⁸⁷Sr/⁸⁶Sr intensity ratios and conventional ⁸⁷Sr/⁸⁶Sr isotope ratios, and (c) ²⁰⁸Pb/²⁰⁶Pb intensity ratios over a period of five days for 30–40 discontinuous measurements of NIST SRM 951a, NIST SRM 987 and NIST SRM 981. The reported data are from measurements of both a single-element solution (□) and a mixture (■) of B, Sr and Pb. For Sr and Pb, additional internal normalized values (, ) are reported. Error bars correspond to 2 s (acquisition time of 10 s, M = 20).

In case of Sr, an IIF per mass unit of 2.2% ± 3.7% (2 s, N = 30) for ⁸⁷Sr/⁸⁶Sr intensity ratio was observed for 30 discontinuous measurements of NIST SRM 987 on three days of measurement. This corresponds to an RSD of IIF per mass unit of 85% (see Fig. 3b and Table S1†). The within day variation (expressed as RSD of IIF per mass unit) ranged between 17% and 26%. This indicates within and between day instability of the IIF per mass unit for Sr which is significantly higher than observed for B. To the authors knowledge, this is the first study to report IIF per mass unit for ⁸⁷Sr/⁸⁶Sr isotope ratios using ICP-TOFMS. Previous studies using second generation ICP-TOFMS reported IIF per mass unit for similar masses (Cu, Ag^27,33) of <−3% whereas previous studies using first generation ICP-TOFMS reported IIF per mass unit for similar masses (Rb^23,24) of −1.2%. In the present study, only IIF per mass unit reported for day 1 (see Fig. 3b, day 1) are of comparable extent and algebraic sign (−1.4% ± 0.5% (2 s, N = 5)) as reported in the previous studies. For the following measurements (see Fig. 3b, day 2 till – day 5), the present study reports IIF per mass unit of reverse algebraic sign (direction) between 2.4% and 3.6%. Furthermore, similar instability for the IIF per mass unit were also observed for ⁸⁸Sr/⁸⁶Sr (−0.2% ± 3.3% (2 s, N = 5)) for 30 discontinuous measurements of NIST SMR 987 on three days of measurement. This corresponds to an RSD of IIF per mass unit of > 100% (see Fig. S3 and Table S1 in ESI†). The within day variation (expressed as RSD of IIF per mass unit) ranged between 2% and >100%. The observed IIF per mass unit, especially on day 2 (see Fig. S3 in ESI†), is comparable to a previous study on first generation ICP-TOFMS which reported IIF per mass unit for ⁸⁸Sr/⁸⁶Sr of −0.2%.²⁴ The IIF(⁸⁷Sr/⁸⁶Sr) per mass unit divided by IIF(⁸⁸Sr/⁸⁶Sr) per mass unit ranges from about 40% (day 1) to >200% (day 2 till day 5) (compare Fig. 3b and S3 in ESI†). Consequently, the two isotope pairs of Sr (i.e., ⁸⁷Sr/⁸⁶Sr and ⁸⁸Sr/⁸⁶Sr) have significantly different IIF per mass unit values, no matter whether they were measured in single-element solution or in a mixture of B, Sr and Pb. This contradicts the observations and assumptions made in MC ICP-MS measurements of constant IIF factors for the isotope pairs within an isotopic system. This issue will be further discussed in Section 3.5.

In case of Pb, an IIF per mass unit of 4.8% ± 1.4% (2 s, N = 30) for ²⁰⁸Pb/²⁰⁶Pb intensity ratio was observed for 30 discontinuous measurements of NIST SRM 981 on three days of measurement. This corresponds to an RSD of IIF per mass unit of 16% (see Fig. 3c and Table S1 in ESI†). The within day variation (expressed as RSD of IIF per mass unit) ranged between 2.3% and 3.4%. Similar to B, this indicates a lower within and between day instability of the IIF per mass unit for Pb as compared to Sr. Previous studies using second generation ICP-TOFMS reported IIF per mass unit for ²⁰⁸Pb/²⁰⁶Pb of approx. 1%²⁷ whereas previous studies using first generation ICP-TOFMS reported IIF per mass unit for ²⁰⁸Pb/²⁰⁶Pb between −0.2% and −2.2%.^18,24,42 The observed IIF per mass unit of the present study has the same algebraic sign (direction) but significantly higher value than previously reported values from studies using second generation ICP-TOFMS. Furthermore, similar instability, extent and algebraic sign (direction) was observed for the IIF per mass unit of ²⁰⁷Pb/²⁰⁶Pb (1.9% ± 1.3% (2 s, N = 30)) (see Fig. S4b and Table S1 in ESI†). Similar to Sr, a significantly different IIF per mass unit for ²⁰⁶Pb/²⁰⁴Pb (4.2% ± 1.6% (2 s, N = 30)) was observed (see Fig. S4a and Table S1 in ESI†). The IIF(²⁰⁸Pb/²⁰⁶Pb) per mass unit divided by IIF(²⁰⁷Pb/²⁰⁶Pb) per mass unit ranges from around 104% (day 1) to 112% (day 2 till day 3) (compare Fig. 3c and S4b in ESI†), whereas the IIF(²⁰⁸Pb/²⁰⁶Pb) per mass unit divided by IIF(²⁰⁶Pb/²⁰⁴Pb) per mass unit ranges from around 200% (day 1) to around 300% (day 2 till day 3) (compare Fig. 3c and S4a in ESI†). Here again, two isotope pairs of Pb (i.e., ²⁰⁸Pb/²⁰⁶Pb, ²⁰⁷Pb/²⁰⁶Pb) have significantly different IIF per mass unit values than the third isotope pair of Pb (i.e., ²⁰⁶Pb/²⁰⁴Pb), no matter whether they were measured in single-element solution or in a mixture of B, Sr and Pb. As already observed for Sr, this is at odds with the assumption of constant IIF factors for the isotope pairs within an isotope system. This issue will be further discussed in Section 3.5.

Overall, it could be observed that the IIF per mass unit of second generation ICP-TOFMS has a negative value for B (a light mass), a value around zero for Sr (a medium mass) and a positive value for Pb (a heavy mass), when measured in single-element solutions and in a mixture of all three elements. Further, different pairs of isotopes from the same element (i.e., Sr, Pb) showed significantly different IIF per mass unit, when measured in single-element solutions and in a mixture of B, Sr and Pb. To the authors knowledge, this is the first study using a second generation ICP-TOFMS that compared the IIF per mass unit of different isotope pairs of the same element. Nonetheless, previous studies using first generation ICP-TOFMS also reported different IIF per mass unit for different isotope pairs of the same element (i.e., Mg,²³ Zr,³⁰ Cd,^24,30 Nd,³⁰ Ba,²⁴ Pt,^23,24 Hg,⁶⁰ Pb^24,42) using first generation ICP-TOFMS (see Table S1 in ESI†). In contrast, in previous studies of the authors using sector field (MC) ICP-MS equipped with an ion counter or Faraday cups as detectors, highly reproducible and always negative values for IIF per mass unit were observed for all isotope pairs of an isotopic system (i.e., B of about −13% (as obtained from raw data of the ERM-AE101a certification study), Sr of about −2.1% and Pb of about −0.6% (as obtained from raw data of Retzmann et al.⁵⁵)). The nature of the odd IIF is further investigated in the following section. Potential causes for the observed (sudden) shifts and bias in the B, Sr and Pb isotope ratios when using second generation ICP-TOFMS will be discussed in detail in Section 3.6.

3.4. Potential non-mass dependent fractionation in ICP-TOFMS

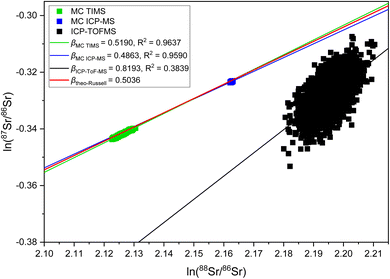
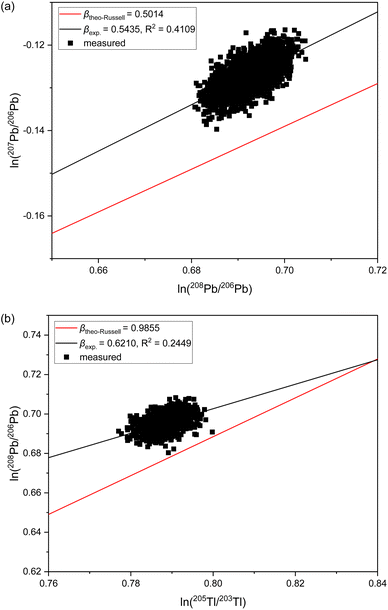
The observation of significantly different IIF per mass unit values for different isotope pairs of a same isotopic systems is an odd IIF behavior, given that the ICP-TOFMS provides quasi-simultaneously isotope detection. The three-isotope plots can be used to investigate the IIF behavior in more detail: The slope, β_exp., obtained from a three-isotopes plot is compared to the expected “theoretical” slope of common mass dependent fractionation functions, such as the Russell's law, β_theo-Russell.^53,61 When β_exp. agrees with the expected “theoretical” β_theo-Russell, it indicates mass dependent fractionation which can be corrected for using all common IIF correction model (e.g., internal IIF correction and SSB). When β_exp. differs significantly from the expected “theoretical” β_theo-Russell it indicates mass independent fractionation.^35,61,62Fig. 4 shows the three-isotope plots of the natural logarithm of ⁸⁸Sr/⁸⁶Sr vs.⁸⁷Sr/⁸⁶Sr isotope ratios from six measurements of pure NIST SRM 987 single-element solution over two hours. Fig. 5a shows the three-isotope plots of the natural logarithm of ²⁰⁸Pb/²⁰⁶Pb vs.²⁰⁷Pb/²⁰⁶Pb from six measurements of pure NIST SRM 981 single-element solution over two hours. The reported β_exp. do not agree with the expected “theoretical” β_theo-Russell, this is neither the case for the three Sr isotopes nor for the three Pb isotopes. This is also observed for measurements when Sr and Pb isotopes ratios were measured simultaneously from a mixture of B, Sr and Pb (see Fig. S7 and S8 in the ESI†). Further, there is no agreement with other mass dependent fractionation functions (i.e., equilibrium law, compare β_{theo-Equilibrium}(Sr) = 0.5065 and β_{theo-Equilibrium}(Pb) = 0.5026 with Fig. 4 and 5a). In addition, Fig. 5b shows the four-isotope plot of the natural logarithm of ²⁰⁵Tl/²⁰³Tl vs.²⁰⁸Pb/²⁰⁶Pb isotope ratios from two discontinuous measurements of NIST SRM 981 and Tl single-element standard over 30 minutes. The four-isotope plot of Tl and Pb also does not show the expected slope.

Fig. 4 Three-isotope plot for Sr from measurements over several hours of NIST SRM 987 using ICP-TOFMS (integration time 0.5 s, M = 2000), MC TIMS (integration time 24 s, M = 443) and MC ICP-MS (integration time 42 s, M = 238). Solid lines represent experimentally determined slopes (β_instrument) and predicted mass dependent fractionation line (β_theo-Russell). All data points were taken from measurements of pure NIST SRM987 single-element solution.

Fig. 5 (a) Three-isotope plot for Pb arising from six measurements over two hours of a pure NIST SRM 981 single-element solution (integration time 0.5 s, M = 2000), and (b) four-isotope plot for Tl–Pb arising from two discontinuous measurements over 30 minutes of mixture of NIST SRM 981 and Tl single-element standard (integration time 0.5 s, M = 800). Solid lines represent experimentally determined slope (β_exp.) and predicted mass dependent fractionation line (β_theo-Russell).

The three-isotope plots of Sr and Pb as well as the four-isotope plot of Tl–Pb do not show mass dependent IIF but indicate non-mass dependent fractionation (see Fig. 4 and 5). This means that the IIF factor is not the same for different isotope pairs of a same or adjacent isotopic systems and possible mass independent IIF takes place during the ion formation, ion extraction, ion transmission, ion separation and ion detection in ICP-TOFMS. Consequently, mass dependent correction models such as internal IIF correction applying the Russell law cannot be used to correct the potential mass independent IIF^35,61,62 observed for Sr and Pb isotope ratio analysis using second generation ICP-TOFMS (see Section 3.5). The applicability of IIF correction models are described in more detail in the section 3.5. Comparing the correlation quality of IIF trends for different mass spectrometer in three-isotope plots, highly correlated mainly mass dependent IIF for MC TIMS and MC ICP-MS instruments is typically observed (see Fig. 4). For second generation ICP-TOFMS, the correlation coefficients for the IIF trends for single-element solutions of Sr and Pb in Fig. 4 and 5 are very low (R² < 0.4), indicating that the single datapoints are not well correlated with each other, and mainly non-mass dependent correlations between the individual isotopes of an element were observed. Similar, it can be observed that the correlation coefficients for the IIF trends of mixtures of B, Sr and Pb in Fig. S7 and S8† (in ESI) are very low (R² < 0.6). If the experimental data of the three-isotope plot are not correlated, instrumental artefacts are possibly the reason for the observed offsets.⁶¹ Other reasons could be caused by the observed unstable IIF over time (i.e., two hours), the large scatter of the ICP-TOFMS measurement (possibly related to the short integration time), and/or multiple IIF processes occurring during ion formation, ion extraction, ion transmission, ion separation and ion detection that could be contradictory and/or of varying contributions. Further, the presence of potential non-mass dependent fractionation limits the applicability of IIF correction models are described in more detail in the Section 3.5.

3.5. Applicability of the internal IIF correction model

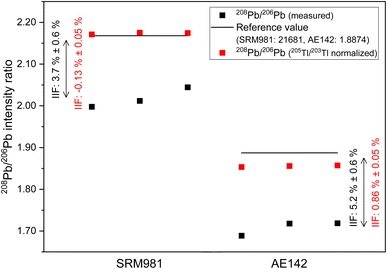
In case of Sr, the conventional ⁸⁷Sr/⁸⁶Sr isotope ratio which is corrected for IIF internally using the ⁸⁶Sr/⁸⁸Sr isotope ratio (= 0.1194 (ref. 38)) is commonly reported in MC ICP-MS and MC TIMS measurements. It is clear from Fig. 3b that the application of this internal IIF correction model fails for ⁸⁷Sr/⁸⁶Sr isotope ratio measurements using second generation ICP-TOFMS. The determined conventional ⁸⁷Sr/⁸⁶Sr isotope ratio of NIST SRM 987 is 0.69405 ± 0.00097 (U, k = 2, N = 5) in a single element solution and 0.69199 ± 0.00059 (U, k = 2, N = 25) in the mixture of B, Sr and Pb. This is significantly different from the commonly accepted value for conventional ⁸⁷Sr/⁸⁶Sr isotope ratio of the NIST SRM 987 (= 0.71025 (ref. 54)) no matter whether measured in a single-element solution or a mixture of B, Sr and Pb. This observation supports the assumption that non-mass dependent IIF occurs during ion formation, ion extraction, ion transmission, ion separation and ion detection of second generation ICP-TOFMS. Furthermore, the conventional ⁸⁷Sr/⁸⁶Sr isotope ratio obtained by ICP-TOFMS is outside the range for terrestrial ⁸⁷Sr/⁸⁶Sr values.⁶³

Fig. 3c shows the ²⁰⁸Pb/²⁰⁶Pb isotope ratios of the NIST SRM 981 normalized to the certified isotope ratios of ²⁰⁷Pb/²⁰⁶Pb and ²⁰⁶Pb/²⁰⁴Pb. As the IIF per mass unit and consequently the IIF factors of ²⁰⁸Pb/²⁰⁶Pb and ²⁰⁷Pb/²⁰⁶Pb are quite similar (see Table S1 in ESI†), internal normalization appears to be working for day 2 but not for day 4 and day 5. Similar to Sr, when the IIF per mass unit and consequently the IIF factors are significantly different, as it is the case for ²⁰⁸Pb/²⁰⁶Pb and ²⁰⁶Pb/²⁰⁴Pb (see Table S1 in ESI†), the internal IIF correction model fails no matter whether measured in a single-element solution or a mixture of B, Sr and Pb. This observation supports the assumption that non-mass dependent IIF occurs during ion formation, ion extraction, ion transmission, ion separation and ion detection of second generation ICP-TOFMS. Additionally, internal inter-elemental IIF correction using Tl isotopes which is added to the sample for this purpose has been a popular approach to determine absolute Pb isotope ratios based on the assumption of identical IIF correction factors for Pb and Tl. However, more recent studies using MC ICP-MS recognized that different elements can be isotopically fractionated and consequently the derived isotope ratios can be erroneous.⁶² It can be seen in Fig. 6 that this IIF correction approach fails for ²⁰⁸Pb/²⁰⁶Pb isotope measurements using second generation ICP-TOFMS. The determined ²⁰⁸Pb/²⁰⁶Pb isotope ratio of NIST SRM 981 is 2.1738 ± 0.0042 (2 s, N = 3) for a mixture of B, Sr, Tl and Pb. This value does not overlap within uncertainty with the certified ²⁰⁸Pb/²⁰⁶Pb value of the NIST SRM 987 (= 2.1681 ± 0.0008, U, k = 2). The determined ²⁰⁸Pb/²⁰⁶Pb isotope ratio of ERM-AE142 is 1.8556 ± 0.0038 (2 s, N = 3) for a mixture of B, Sr, Tl and Pb. This value does not overlap withing uncertainty with the certified ²⁰⁸Pb/²⁰⁶Pb value of the ERM-AE142 (= 1.8874 ± 0.0010, U, k = 2). Previous studies using first generation ICP-TOFMS and internal inter-elemental IIF correction using Tl successfully determined Pb isotope ratios,³⁹ but failed to determined reliable Hg isotope ratios.⁶⁰ Consequently, only correction models that do not rely on empirical fractionations functions and that can correct for mass dependent IIF as well as potential mass independent IIF, like the SSB approach (incl. external normalization-SSB),³⁵ are recommended to be used for isotopic analysis using second generation ICP-TOFMS. In addition, it was observed that the internal intra-elemental normalization (i.e., ⁸⁶Sr/⁸⁸Sr for ⁸⁷Sr/⁸⁶Sr, ²⁰⁷Pb/²⁰⁶Pb and ²⁰⁶Pb/²⁰⁴Pb for ²⁰⁸Pb/²⁰⁶Pb) and the internal inter-elemental normalization (i.e., Pb and Tl) significantly harmonizes and reduces the IIF per mass unit (see Fig. 3b and 6). This is seen as an indication that change in IIF throughout a ICP-TOFMS measurement is approximately the same for all the different isotopes, even if the fractionation laws do not apply: i.e., the IIF for ²⁰⁶Pb/²⁰⁴Pb changes to the same extent as that for ²⁰⁸Pb/²⁰⁶Pb; so, both IIF per mass unit increase or decrease accordingly, but do not agree with respect to the mass dependent fractionation. Assuming a parameter such as plasma power changes, it has the same effect on both isotope ratios, but without changing the ratio to each other.

Fig. 6 ²⁰⁸Pb/²⁰⁶Pb intensity ratios and absolute ²⁰⁸Pb/²⁰⁶Pb isotope ratios (internal inter-elemental IIF correction using Tl) for three measurements of NIST SRM 981 and ERM-AE142. Error bars (smaller than symbols) correspond to 2 s (acquisition time of 10 s, M = 20) and are smaller than the symbols. The data shown are from the measurement of a mixture in which B, Sr, Tl and Pb were detected simultaneously.

The internal intra-elemental normalization for isotope pairs with similar IIF factors (i.e., ²⁰⁸Pb/²⁰⁶Pb and ²⁰⁷Pb/²⁰⁶Pb) and the internal inter-elemental normalization applied for Pb works more efficiently as it reduces the IIF per mass unit to <1% than the internal intra-elemental normalization applied for isotope pairs with significantly different IIF factors of Sr and Pb (i.e., ²⁰⁸Pb/²⁰⁶Pb and ²⁰⁶Pb/²⁰⁴Pb) which only reduces the IIF per mass unit to about 2.5% (see Fig. 3b and 6). Thus, perhaps the application of the combination of internal inter-elemental IIF correction and external IIF correction (i.e., external normalization-SSB, aka combined standard-sample bracketing and internal normalization isotopic fractionation correction model) in accordance with standard protocols^34,35,56 could lead to more precise and more true isotope ratios.

3.6. Potential source of odd IIF behavior within ICP-TOFMS

In ICP-MS, IIF represents the sum of effects in the instrument that occur during sample introduction, ion formation, ion extraction, ion transmission, ion separation and ion detection which lead to a difference between the true isotope ratio and the measured isotope ratio. IIF includes all discriminating effects within the ICP-MS instrument and describes mass dependent as well as mass independent effects. The extent of IIF differs significantly between MS techniques and can be expressed by IIF per mass unit (see eqn (1)).³⁴ However, external parameters such as analyte contamination, interferences and matrix effects can also introduce bias into isotope ratio measurements using ICP-MS or even affect the IIF occurring within the instrument.

3.6.1 Analyte concentration, contamination, and interferences. No consistent trend was observed that could indicate a correlation between mass concentration and the extent of the IIF per mass unit for B, Sr and Pb isotope ratios measured using second generation ICP-TOFMS (see Section 1 in ESI†). Nonetheless, the data suggests that the sample and standard must be at the same analyte concentration (<10%) for SSB to work.

If significant amounts of analyte are present during the ICP-MS measurement (in absence of the sample), the isotope result is potentially biased.¹² This is negligible for the present study, as blank corrections were performed as part of the data reduction and blank contributions were ≤0.15% for all isotopes under investigation.

Interferences can alter, modify or disrupt the isotope measurement signal of an ICP-MS.⁵² There are two groups of interferences: (i) the spectral interferences include bias based on isobaric, polyatomic and doubly-charged ions.^12,52 As all analyses of the present study were performed with pure isotope certified reference materials either as single-element solution or as mixture of B, Sr and Pb, isobaric interferences can be neglected. Further, none of the analytes in the mixture (B, Sr, Pb) poses a problem to create doubly-charged or polyatomic interferences for one of the other analytes.⁵⁵ (ii) The non-spectral interferences refer mainly to systematic bias introduced by variable matrix (i.e., matrix effects), e.g. isobaric and polyatomic interferences, signal instability, varying instrumental isotopic fractionation effects and loss of sensitivity due to signal suppression and material deposition.⁶⁴ Further, noticeable space charge effects were observed for ICP-MS when heavy ions were added to lighter analytes.^36,65,66 The odd IIF behavior of B, Sr and Pb isotopes when measured by second generation ICP-TOFMS occurred no matter whether the isotope ratios were measured in a single-element solutions or a mixture of B, Sr and Pb (see Fig. 3). Even repeated measurements of the same mixtures of B, Sr and Pb showed different IIF on different days (compare day 2 and day 5 in Fig. 3). Same is true for the three-isotope plots of Sr and Pb where the correlation is poor no matter whether the isotope ratios were measured in a single-element solutions or a mixture of B, Sr and Pb (see Section 3.4). In addition, previous studies by the authors have shown no matrix effect of Pb on Sr isotope ratio measurements and vice versa.⁵⁵ Consequently, potential matrix effects attributable to the mixing of B, Sr and Pb are not considered here as the driving force for the odd IIF behavior observed for second generation ICP-TOFMS.

3.6.2 Instrumental noise and bias. The understanding of the causes for the IIF phenomenon (incl. mass independent IIF) within the ICP-MS is still limited but possible sources include supersonic expansion, space charge effects, ionization efficiency, diffusion repulsion, absolute isotope mass, ion density nuclear field shift and magnetic isotope effect.^34,35 IIF is usually most pronounced during sample introduction, ion formation and ion extraction (interface region) of ICP-MS instruments and the effects in this region are supposed to be the major determining factors regarding IIF (see Fig. 7).³⁴ The ions of a higher mass are more efficiently extracted by the lenses system and more efficiently transmitted than ions of a lighter mass presumably caused by supersonic expansion of ions through the sampler cone and from space-charge effects in the skimmer cone.^34–36,67 In accordance to eqn (1), this should report a negative IIF per mass unit value. The sample introduction and interface region of the ICP-TOFMS (by TOFWERK) is essentially the same as of the ICP-QMS (by Thermo Fisher).^31,33 Consequently, the IIF effect in this region of the ICP-TOFMS should be the same as observed for other ICP-MS instruments. However, for isotopic measurements of Sr and Pb using second generation ICP-TOFMS, IIF behavior favoring lighter isotopes over heavier ones was observed in this study. Accordingly, the sample introduction and interface region are not the only regions with major determining factors regarding IIF for ICP-TOFMS.

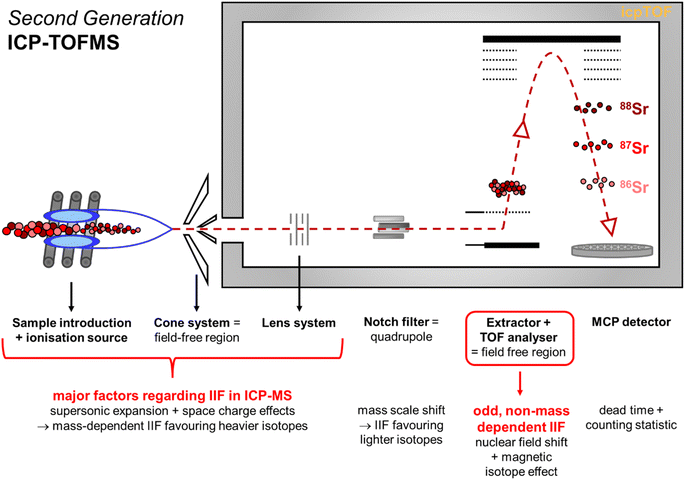Fig. 7 Schematic illustration of the second generation ICP-TOFMS highlighting potential sources for instrumental noise and instrumental bias.

The second generation ICP-TOFMS used in the present study applies a notch filter^33,68 (i.e., quadrupole) before the TOF analyzer to selectively excite and remove ions of four m/z regions (e.g., eliminate ⁴⁰Ar) from the spectra.²⁷ Additional IIF may occur in the quadrupole mass filter used due to mass scale shifts which would favor lighter isotopes over heavier ones.⁶⁹ If this IIF effect would be more pronounced than the IIF effects of the sample introduction and interface region, a positive IIF per mass unit would be reported in accordance to eqn (1). Hence, it may be assumed that the notch filter contributes to the partially reverse IIF behavior observed for the second generation ICP-TOFMS. Although in ICP-QMS also a normal IIF caused by discrimination of the lighter ions is observed^41,69 which disproves this assumption. Considering that the front section (incl. notch filter) of the ICP-TOFMS (by TOWERK) is basically a normal ICP-QMS³¹ (see Fig. 7) it is less likely that potential mass scale shifts in the notch filter are a major cause for the odd IIF behavior which only leaves the TOF analyzer.

The TOF analyzer is positioned behind the notch filter, and its working principle is significantly different to quadrupole-based and sector field-based (MC) ICP-MS instruments. The TOF analyzer consists of an extractor and a flight region (see Fig. 7).^33,70 For the ion separation, the ions are accelerated by the electric field of the extractor which should give all ions a similar kinetic energy into the TOF chamber.⁷⁰ Then the ion beam passes through two plates to which a voltage pulse is applied that creates a deflection field.²⁹ This pulsed field creates a sweeping action across the slit ahead of the flight region which sends an ion pulse (i.e., ion package) to drift through the flight region (= field free region).²⁹ At the MCP detector, the time between the ion extraction at the extractor and the collision with the detector is recorded which is a function of the ions mass and subsequent velocity.⁷⁰ Remaining variation of kinetic energy at the extractor would mean that ions of different mass in the ion pulse leave the extractor at slightly different angles.⁶⁷ This would cause somewhat different paths through the flight region and result in IIF.^29,67 It seems likely that this causes the instability in the IIF behavior within the ICP-TOFMS. Since both negative and positive IIF per mass units are reported for ICP-TOFMS, it can be assumed that the contributions of IIF caused by sample introduction and interface in relation to the contribution of IIF caused by the TOF analyzer are almost equal: For the light mass B, sample introduction and interface predominate the IIF behavior, for the medium mass Sr, the IIF effects balance each other out, and for the heavy mass Pb, the TOF analyzer predominates the odd IIF behavior. Furthermore, different IIFs per mass unit were observed for different isotope pairs of the same and adjacent isotopic system (i.e., Sr, Pb, Tl) using second generation ICP-TOFMS to measure single-element solutions and mixtures. With respect to sector field (MC) ICP-MS measurement, the authors observed previously that the IIF per mass unit ratios of several isotope pairs of the isotopic systems Sr and Pb agreed within 5% which legitimates the assumption of constant IIF factors. Previous studies that investigated several isotope pairs of the isotopic systems Mg,²³ Zr,³⁰ Cd,^24,30 Nd,³⁰ Ba,²⁴ Pt,^23,24 Hg,⁶⁰ Pb^24,42 using first generation ICP-TOFMS have also reported not constant IIF per mass units for different isotope pairs of the same element (see Table S1 in ESI†). Consequently, it is deduced here that the observed odd IIF effect of ICP-TOFMS is possibly caused by the generation of ion packages in the TOF mass separator. The same logic can be applied to the sudden shifts²⁴ already reported for the first generation ICP-TOFMS. This assumption is further supported by a study applying a thermal ionization cavity (TIC) source with a TOFMS that reported different IIF factors for different isotope pairs of the same element despite the prediction of mass dependent IIF originating from the TIC source.⁷¹

Finally, detector dead time and counting statistics may create a noise or bias to the isotope ratio measurements. According to the manufacturer of the ICP-TOFMS, the MCP detector itself as a whole does not have a dead time.²⁸ Potential contributions by counting statistics can only be minor as the odd IIF and sudden shifts²⁴ have been reported in previous studies applying first generation ICP-TOFMS which used a SEM detector instead of MCP detector (see Table S1 in ESI†). Note, intensities are reported as average of a defined number of extractions per integration time. Future studies might take a closer look into the isotope ratios per single extraction which might help refining the isotope ratio precision.

3.6.3 Causes of non-mass dependent IIF. Nuclear field shift (aka nuclear volume effect) and magnetic isotope effect (aka nuclear spin effect) are often attributed as causes for non-mass dependent IIF in ICP-MS but they are still under discussion.³⁵ In case of Sr, magnetic isotope effect can arise from interaction of the spin–spin coupling in magnetic nuclei such as ⁸⁷Sr (I = 4.5). Non-mass dependent IIF has been reported for ⁸⁷Sr in a study using MC ICP-MS.⁵⁶ In general, this could explain the observation of the present study that IIF per mass unit and consequently IIF factors of ⁸⁷Sr/⁸⁶Sr and ⁸⁶Sr/⁸⁸Sr do not agree and internal IIF correction fails. In case of Pb, non-mass dependent IIF based on nuclear field shift and magnetic isotope effect (²⁰⁷Pb: I = 0.5) is expected for ²⁰⁷Pb, but previous studies using MC ICP-MS also reported non-mass dependent IIF for ²⁰⁴Pb which cannot be expected from nuclear field shift or magnetic isotope effect (²⁰⁴Pb: I = 0.0).³⁵ In the present study, the IIF per mass unit and consequently the IIF factors of ²⁰⁸Pb/²⁰⁶Pb and ²⁰⁷Pb/²⁰⁶Pb are comparable and enabled internal IIF to some extent (see section 3.5) whereas the values for ²⁰⁶Pb/²⁰⁴Pb are significantly different (see Table S1 in ESI†). This contradicts the expectation of non-mass dependent IIF for ²⁰⁷Pb, but it supports the observation of non-mass dependent IIF for ²⁰⁴Pb although nuclear field shift and magnetic isotope effect do not indicate this. Further investigation on the causes of the odd IIF occurring during isotopic measurements using second generation ICP-TOFMS is required.

3.7. Determination of δ-values and absolute isotope ratios by ICP-TOFMS using SSB

Since potential non-mass dependent IIF was observed in this study, only isotopic results based on SSB approach are reported as successful here. If mass independent IIF is stable over time, it has no effect on the accuracy of the SSB as IIF correction model as it used the same isotope pair for IIF correction in the SSB standard and the sample,³⁵ but non-stable IIF within the ICP-MS leads to decreased accuracy and precision of the isotope data,⁶² as observed here. Furthermore, since possible mass independent IIF would also affect the applicability of mass dependent IIF correction models to correct for isobaric interferences (i.e., Rb, Hg), the interference corrections were performed without IIF in the present study.

Table 2 reports the determined δ¹¹B_SRM951a, conventional ⁸⁷Sr/⁸⁶Sr isotope ratios, and absolute n(¹¹B)/n(¹⁰B), n(⁸⁷Sr)/n(⁸⁶Sr), n(²⁰⁸Pb)/n(²⁰⁴Pb), n(²⁰⁷Pb)/n(²⁰⁴Pb), n(²⁰⁶Pb)/n(²⁰⁴Pb) and n(²⁰⁸Pb)/n(²⁰⁶Pb) isotope ratios of the investigated samples (= isotopic reference materials) applying SSB as IIF correction model. It can be observed that the determined B, Sr and Pb isotope ratios overlap within uncertainty with the reference values (see Table 2 and Fig. S9 in ESI†). This is regardless of whether the analysis was performed in a single-element solution or in the mixture of all three elements. Consequently, simultaneous multi-isotope analysis is truly possible using second generation ICP-TOFMS and the SSB approach. Nonetheless, future studies using second generation ICP-TOFMS for n(⁸⁷Sr)/n(⁸⁶Sr) and Pb isotope ratio measurements should consider the application of the external normalization-SSB approach^34,35,56 for IIF correction.

Table 2 Determined δ¹¹B_SRM951a, absolute n(¹¹B)/n(¹⁰B), conventional ⁸⁷Sr/⁸⁶Sr, absolute n(⁸⁷Sr)/n(⁸⁶Sr) and absolute n(²⁰⁸Pb)/n(²⁰⁴Pb), n(²⁰⁷Pb)/n(²⁰⁴Pb), n(²⁰⁶Pb)/n(²⁰⁴Pb) and n(²⁰⁸Pb)/n(²⁰⁶Pb) isotope ratios of isotopic reference materials. Errors correspond to expanded uncertainty (U, k = 2)

Isotope ratio	Sample	Single-element	Mixture	Reference
a Conventional ^87Sr/^86Sr isotope ratios were determined using a combination of internal IIF correction applying conventional ^86Sr/^88Sr (= 0.1194 (ref. 38)). b Determined using MC TIMS. c Absolute n(^87Sr)/n(^86Sr) isotope ratios were determined applying IIF correction by classical SSB approach using NIST SRM 987 (= 0.71025 (ref. 54)).
δ ^11BSRM951a [‰]	ERM-AE120 (N = 5)	−21.0 ± 1.7	−20.0 ± 1.6	−20.2 ± 0.6
	ERM-AE121 (N = 5)	20.5 ± 1.1	19.4 ± 1.5	19.9 ± 0.6
	ERM-AE122 (N = 5)	39.9 ± 1.6	41.1 ± 1.3	39.7 ± 0.6
n(^11B)/n(^10B) [mol mol^−1]	ERM-AE120 (N = 5)	3.959 ± 0.007	3.963 ± 0.007	3.963 ± 0.006
	ERM-AE121 (N = 5)	4.127 ± 0.004	4.132 ± 0.010	4.127 ± 0.006
	ERM-AE122 (N = 5)	4.205 ± 0.006	4.210 ± 0.005	4.205 ± 0.006
R con(^87Sr/^86Sr)^a [mol mol^−1]	Sr ICP-standard (N = 5)	0.69561 ± 0.00057	0.69145 ± 0.00097	0.70858 ± 0.00003^b
n(^87Sr)/n(^86Sr)^c [mol mol^−1]	Sr ICP-standard (N = 5)	0.70796 ± 0.00069	0.70861 ± 0.00076	0.70858 ± 0.00003^b
n(^208Pb)/n(^204Pb) [mol mol^−1]	ERM-AE142 (N = 5)	39.888 ± 0.060	39.885 ± 0.061	39.850 ± 0.044
n(^207Pb)/n(^204Pb) [mol mol^−1]		15.960 ± 0.025	15.946 ± 0.025	15.944 ± 0.017
n(^206Pb)/n(^204Pb) [mol mol^−1]		21.133 ± 0.030	21.131 ± 0.032	21.114 ± 0.017
n(^208Pb)/n(^206Pb) [mol mol^−1]		1.8874 ± 0.0010	1.8874 ± 0.0008	1.8874 ± 0.010

---

Reported relative uncertainties range from 3%–8% for δ(¹¹B/¹⁰B), about 0.10% for absolute ⁸⁷Sr/⁸⁶Sr isotope ratio and between 0.04% and 0.16% for absolute Pb isotope ratios. These are significantly worse (i.e., approx. 1 to 2 orders of magnitude) than for MC ICP-MS and MC TIMS. This is likely be explained by non-stable IIF.

4. Conclusion

The present study of B, Sr and Pb (multi-)isotope ratios using second generation ICP-TOFMS has shown that the performance in terms of isotope ratio precision is comparable between first and second generation ICP-TOFMS, despite using an MCP instead of SEM providing multi-elemental detection capability. The measured isotope ratios are stable for a period of several hours for B, Sr and Pb showing repeatability of <0.2% but consistent with other studies using first generation ICP-TOFMS, sudden shifts in IIF occur for reasons that are not clear yet but presumably originate from the TOF analyzer. The general trend, extent, and algebraic sign (direction) of IIF per mass unit observed for B, Sr and Pb using second generation ICP-TOFMS is mostly comparable to IIF per mass unit observed in previous studies using first and second generation ICP-TOFMS. However, different IIFs per mass unit were observed for different isotope pairs of the same isotopic system (i.e., Sr, Pb) and adjacent isotopic systems (i.e., Pb vs. Tl) using second generation ICP-TOFMS no matter whether measured in a single-element solution or a mixture of B, Sr and Pb. These odd IIF effects possibly origin from TOF mass analyzer, in particular the extractor, and/or notch filter. This observation and the observations from three-isotope plots for Sr and Pb showed that the IIF occurring during ion formation, ion extraction, ion transmission, ion separation and ion detection of second generation ICP-TOFMS does not follow the known mass dependent fractionation laws. Since this odd IIF behavior occurred when measuring single-element solutions as well as a mixture of B, Sr and Pb, it is not linked to interferences or matrix effects. Furthermore, the IIF behavior is possibly caused by mass independent fractionation, and/or multiple (contradictory) fractionation processes with varying contributions this should be further investigated by future studies. Consequently, the internal IIF correction model was proven to be unsuitable for Sr and Pb isotope ratio analysis using ICP-TOFMS because it relies only on mass dependent behavior of IIF. Isotope ratio analysis using ICP-TOFMS require IIF correction models that can also correct for the possible mass independent fractionation such as the SSB approach that has proven its applicability in the present study. In addition, the internal normalization has shown that it significantly harmonizes and reduces the IIF per mass unit. Therefore, future studies should investigate the external normalization-SSB model for more reliable isotope ratios using second generation ICP-TOFMS.

It was shown that reliable δ¹¹B values, and absolute B, Sr and Pb isotope ratios can be determined in single-element solutions as well as a mixture of all three elements, measured simultaneously, using second generation ICP-TOFMS and the SSB approach. The precision, uncertainty and the required analyte mass concentration is typically more than one order of magnitude worse than for measurement procedures using MC ICP-MS or MC TIMS. Nevertheless, second generation ICP-TOFMS in combination with SSB approach is a suitable tool for (multi-)isotope ratio analysis applications that could work with rather modest isotope ratio precisions like provenance studies that have significantly different endmembers (e.g., B,⁴⁹ Sr,⁷² Pb¹⁰) or geochronology.⁷³ Furthermore, the second generation ICP-TOFMS has the distinct advantage that it allows simultaneous multi-isotope analysis of short transient signals (e.g., LA-ICP-MS) which cannot be achieved by ICP-QMS, ICP-SFMS, and MC ICP-MS. It reduces effort for multi-isotope ratio analysis (does not require multiple analyses for multiple isotope systems) and provides true simultaneous multi-isotope data for the same data point.

Having an isotope ratio performance that is in the range of ICP-QMS and ICP-SFMS, second generation ICP-TOFMS should be a suitable tool for IDMS. In this context, particular attention should be paid to the unique feature of the second generation ICP-TOFMS of multi-isotope analyses, which allow multi-IDMS as already shown in a previous study.²⁷ However, care must be taken to ensure that all isotope ratios are measured within the same analytical sequence so that IIF correction factors will cancel out in the IDMS calculations.³⁷ In view of the obtained results it is highly recommended to use the SSB approach and calculate the IDMS results with already IIF corrected isotope ratios. Especially for long sequences such as in double or triple IDMS or when applying isotope dilution in hyphenated techniques the SSB correction is deemed reasonable.

Ethics approval

No human participants or animals are involved in the present study.

Conflicts of interest

The authors have no conflicts of interest to declare.

Acknowledgements

This work was funded by the Adolf Martens Fellowship Programme (2021) of BAM. The authors would like to thank Maren König (BAM) for her support in the lab.

References

1. W. P. Leeman and V. B. Sisson, Rev. Mineral. Geochem., 1996, 33, 645–707.
2. H. Marschall and G. Foster, Boron Isotopes – the Fifth Element, Springer, Cham, 2017.
3. A. Reese, T. Zimmermann, D. Pröfrock and J. Irrgeher, Sci. Total Environ., 2019, 668, 512–523.
4. M. Komárek, V. Ettler, V. Chrastný and M. Mihaljevič, Environ. Int., 2008, 34, 562–577.
5. M. R. Palmer, P. N. Pearson and S. J. Cobb, Sci., 1998, 282, 1468–1471.
6. E. J. Bartelink and L. A. Chesson, Forensic Sci. Res., 2019, 4, 29–44.
7. I. Coelho, I. Castanheira, J. M. Bordado, O. Donard and J. A. L. Silva, TrAC Trends Anal. Chem., 2017, 90, 45–61.
8. S. K. Aggarwal and C. F. You, Mass Spectrom. Rev., 2017, 36, 499–519.
9. A. G. Nord and K. Billström, Heritage Sci., 2018, 6, 25.
10. J. Vogl, M. Rosner, J. Curbera, U. Peltz and B. Peplinski, Archaeol. Anthropol. Sci., 2018, 10, 1111–1127.
11. D. Malinovsky and F. Vanhaecke, Anal. Bioanal. Chem., 2011, 400, 1619–1624.
12. J. Irrgeher and T. Prohaska, Anal. Bioanal. Chem., 2016, 408, 369–385.
13. G. Faure and T. M. Mensing, Isotopes: Principles and Applications, Wiley&Sons Inc., Hoboken, 3rd edn, 2005.
14. W. A. Brand and T. B. Coplen, Isot. Environ. Health Stud., 2012, 48, 393–409.
15. Z. Sharp, Principles of Stable Isotope Geochemistry, Pearson/Prentice Hall, Upper Saddle River, N.J., 2007.
16. N. Jakubowski, M. Horsky, P. H. Roos, F. Vanhaecke and T. Prohaska, in Sector Field Mass Spectrometry for Elemental and Isotopic Analysis, ed. T. Prohaska, J. Irrgeher, A. Zitek and N. Jakubowski, The Royal Society of Chemistry, 2015, pp. 208–318.
17. F. Vanhaecke, L. Balcaen and D. Malinovsky, J. Anal. At. Spectrom., 2009, 24, 863–886.
18. F. Vanhaecke, L. Moens, R. Dams, L. Allen and S. Georgitis, Anal. Chem., 1999, 71, 3297–3303.
19. S. M. Nelms, C. R. Quétel, T. Prohaska, J. Vogl and P. D. P. Taylor, J. Anal. At. Spectrom., 2001, 16, 333–338.
20. E. Bolea-Fernandez, L. Balcaen, M. Resano and F. Vanhaecke, J. Anal. At. Spectrom., 2016, 31, 303–310.
21. P. Lindahl, G. Olszewski and M. Eriksson, J. Anal. At. Spectrom., 2021, 36, 2164–2172.
22. D. R. Bandura, V. I. Baranov and S. D. Tanner, J. Anal. At. Spectrom., 2000, 15, 921–928.
23. X. Tian, H. Emteborg and F. C. Adams, J. Anal. At. Spectrom., 1999, 14, 1807–1814.
24. H. Emteborg, X. Tian, M. Ostermann, M. Berglund and F. C. Adams, J. Anal. At. Spectrom., 2000, 15, 239–246.
25. R. E. Sturgeon, J. W. H. Lam and A. Saint, J. Anal. At. Spectrom., 2000, 15, 607–616.
26. G. M. Hieftje, D. P. Myers, G. Li, P. P. Mahoney, T. W. Burgoyne, S. J. Ray and J. P. Guzowski, J. Anal. At. Spectrom., 1997, 12, 287–292.
27. M. Ohata and H. Hagino, Int. J. Mass Spectrom., 2018, 430, 31–36.
28. O. Borovinskaya, personal communication.
29. D. P. Myers and G. M. Hieftje, Microchem. J., 1993, 48, 259–277.
30. P. P. Mahoney, S. J. Ray and G. M. Hieftje, Appl. Spectrosc., 1997, 51, 16A–28A.
31. icpTOF – All-element, high-resolution detection for single particles, individual cells, and laser ablation imaging, https://www.tofwerk.com/wp-content/uploads/2022/08/TOFWERK-icpTOF-Brochure-Web.pdf.
32. vitesse – Time-of-Flight ICP-MS, https://www.nu-ins.com/-/media/ameteknuinstruments/files/products/brochures/vitesse_2021.pdf?la=en&revision=9003d984-cc91-4469-b999-c03acd38b8ae.
33. L. Hendriks, A. Gundlach-Graham, B. Hattendorf and D. Günther, J. Anal. At. Spectrom., 2017, 32, 548–561.
34. J. Irrgeher and T. Prohaska, in Sector Field Mass Spectrometry for Elemental and Isotopic Analysis, ed. T. Prohaska, J. Irrgeher, A. Zitek and N. Jakubowski, The Royal Society of Chemistry, 2015, pp. 107–120.
35. L. Yang, S. Tong, L. Zhou, Z. Hu, Z. Mester and J. Meija, J. Anal. At. Spectrom., 2018, 33, 1849–1861.
36. F. Albarède, E. Albalat and P. Télouk, J. Anal. At. Spectrom., 2015, 30, 1736–1742.
37. J. Irrgeher, J. Vogl, J. Santner and T. Prohaska, in Sector Field Mass Spectrometry for Elemental and Isotopic Analysis, ed. T. Prohaska, J. Irrgeher, A. Zitek and N. Jakubowski, The Royal Society of Chemistry, 2015, pp. 126–151.
38. A. O. Nier, Phys. Rev., 1938, 54, 275–278.
39. A. M. Alvarez, J. R. Estévez Alvarez, C. W. A. do Nascimento, I. P. González, O. D. Rizo, L. L. Carzola, R. A. Torres and J. G. Pascual, Environ. Monit. Assess., 2016, 189, 28.
40. J. Vogl and M. Rosner, Geostand. Geoanal. Res., 2012, 36, 161–175.
41. K. G. Heumann, S. M. Gallus, G. Rädlinger and J. Vogl, J. Anal. At. Spectrom., 1998, 13, 1001–1008.
42. X. Tian, H. Emteborg, M. Barbaste and F. C. Adams, J. Anal. At. Spectrom., 2000, 15, 829–835.
43. S. Faßbender, M. von der Au, M. Koenig, J. Pelzer, C. Piechotta, J. Vogl and B. Meermann, Anal. Bioanal. Chem., 2021, 413, 5279–5289.
44. M. von der Au, S. Faßbender, M. I. Chronakis, J. Vogl and B. Meermann, J. Anal. At. Spectrom., 2022, 37, 1203–1207.
45. J. Irrgeher and T. Prohaska, in Sector Field Mass Spectrometry for Elemental and Isotopic Analysis, ed. T. Prohaska, J. Irrgeher, A. Zitek and N. Jakubowski, The Royal Society of Chemistry, 2015, pp. 183–196.
46. M. Horsky, J. Irrgeher and T. Prohaska, Anal. Bioanal. Chem., 2016, 408, 351–367.
47. T. Prohaska, J. Irrgeher, J. Benefield, J. K. Böhlke, L. A. Chesson, T. B. Coplen, T. Ding, P. J. H. Dunn, M. Gröning, N. E. Holden, H. A. J. Meijer, H. Moossen, A. Possolo, Y. Takahashi, J. Vogl, T. Walczyk, J. Wang, M. E. Wieser, S. Yoneda, X.-K. Zhu and J. Meija, Pure Appl. Chem., 2022, 94, 573–600.
48. CIAAW, Atomic Weights of the Elements, https://www.ciaaw.org/, 2023.
49. M. Rosner, W. Pritzkow, J. Vogl and S. Voerkelius, Anal. Chem., 2011, 83, 2562–2568.
50. S. Geilert, J. Vogl, M. Rosner and T. Eichert, Rapid Commun. Mass Spectrom., 2019, 33, 1137–1147.
51. A. Kazlagić, M. Rosner, A. Cipriani, D. A. Frick, J. Glodny, E. J. Hoffmann, J. M. Hora, J. Irrgeher, F. Lugli, T. Magna, T. C. Meisel, A. Meixner, A. Possolo, A. Pramann, M. J. Pribil, T. Prohaska, A. Retzmann, O. Rienitz, D. Rutherford, G. M. Paula-Santos, M. Tatzel, S. Widhalm, M. Willbold, T. Zuliani and J. Vogl, Geostand. Geoanal. Res., 2023 DOI:10.1111/ggr.12517.
52. T. Prohaska, in Sector Field Mass Spectrometry for Elemental and Isotopic Analysis, ed. T. Prohaska, J. Irrgeher, A. Zitek and N. Jakubowski, The Royal Society of Chemistry, 2015, pp. 121–125,  10.1039/9781849735407-00121.
53. W. A. Russell, D. A. Papanastassiou and T. A. Tombrello, Geochim. Cosmochim. Acta, 1978, 42, 1075–1090.
54. J. M. McArthur, D. Rio, F. Massari, D. Castradori, T. R. Bailey, M. Thirlwall and S. Houghton, Paleogeogr. Paleoclimatol. Paleoecol., 2006, 242, 126–136.
55. A. Retzmann, T. Zimmermann, D. Profrock, T. Prohaska and J. Irrgeher, Anal. Bioanal. Chem., 2017, 409, 5463–5480.
56. J. Irrgeher, T. Prohaska, R. E. Sturgeon, Z. Mester and L. Yang, Anal. Methods, 2013, 5, 1687.
57. J. Kragten, Analyst, 1994, 119, 2161–2165.
58. A. Saha, V. G. Mishra, S. B. Deb, D. Shah and M. K. Saxena, Quantification and Isotope Ratio Measurement of Boron by ICP-TOF-MS after its Pyrohydrolytic Extraction from U3Si2-Al Fuel, Indian Society for Mass Spectrometry, India, 2014.
59. M. Barbaste, L. Halicz, A. Galy, B. Medina, H. Emteborg, F. C. Adams and R. Lobinski, Talanta, 2001, 54, 307–317.
60. R. D. Evans, H. Hintelmann and P. J. Dillon, J. Anal. At. Spectrom., 2001, 16, 1064–1069.
61. L. Yang, L. Zhou, Z. Hu and S. Gao, Anal. Chem., 2014, 86, 9301–9308.
62. L. Yang, Mass Spectrom. Rev., 2009, 28, 990–1011.
63. M. Rosner, Food Chem., 2010, 121, 918–921.
64. T. Zimmermann, A. Retzmann, M. Schober, D. Pröfrock, T. Prohaska and J. Irrgeher, Spectrochim. Acta, Part B, 2019, 151, 54–64.
65. G. R. Gillson, D. J. Douglas, J. E. Fulford, K. W. Halligan and S. D. Tanner, Anal. Chem., 1988, 60, 1472–1474.
66. R. Santos, M. J. Canto Machado, I. Ruiz, K. Sato and M. T. S. D. Vasconcelos, J. Anal. At. Spectrom., 2007, 22, 783–790.
67. H. Niu and R. S. Houk, Spectrochim. Acta, Part B, 1996, 51, 779–815.
68. C. A. Flory, S. C. Hansen and C. Myerholtz, US Pat., 5672870, Hewlett Packard Company, 1997.
69. I. S. Begley and B. L. Sharp, J. Anal. At. Spectrom., 1997, 12, 395–402.
70. TOFWERK, Advantages of Time-Of-Flight Mass Spectrometry over Quadrupole MS, https://www.tofwerk.com/advantages-time-of-flight-mass-spectrometry-over-quadrupole-ms/.
71. D. M. Wayne, W. Hang, D. K. McDaniel, R. E. Fields, E. Rios and V. Majidi, Spectrochim. Acta, Part B, 2001, 56, 1175–1194.
72. A. Retzmann, A.-M. Kriechbaum, M. Griebl, K. Wiltschke-Schrotta, M. Teschler-Nicola, J. Irrgeher and T. Prohaska, Archaeol. Austriaca, 2020, Band 104/2020, 53–87.
73. D. Chew, K. Drost, J. H. Marsh and J. A. Petrus, Chem. Geol., 2021, 559, 119917.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ja00084b

‡ These two authors contributed equally as main authors to the presented work.

---