Convection in liquid-state NMR: expect the unexpected

Abstract

Temperature gradients in liquid-state NMR samples are unavoidable, but undesirable: they lead to sample convection, and consequently to signal attenuation in experiments that use field gradients. This paper illustrates how widely the dependence of sample convection velocity on the temperature at which the sample is maintained can differ between different probes and different spectrometers, including the first such results for cryoprobe systems, and highlights the importance of understanding this dependence if the effects of sample convection are to be kept to an acceptable minimum. It is sometimes thought that efficient sample temperature control should suffice to avoid convection: alas, this is not true, and rapid sample convection can occur even with the best hardware. Previous experiments have shown that the effects of convection can sometimes be avoided by setting the sample temperature regulation to one particular temperature; here it is shown that no such temperature exists in some probes. The issue of convection is all too often swept under the carpet; these results confirm that it is a more general problem than is commonly realized.

---

Introduction

A problem that is always present in liquid state NMR, but not always easy to identify, is temperature variation across the sample. Almost any temperature gradient in the sample will lead to convective liquid motion. The most familiar form of convection, known as Rayleigh–Bénard convection,^1–3 occurs when the liquid at the bottom of the NMR tube is warmer than that at the top. The warmer portion, being less dense, tends to rise, and the colder to fall. Less familiar, but present in almost all NMR experiments, is convection driven by transverse gradients, known as Hadley convection or Hadley flow.⁴ (Marangoni convection can also be driven by transverse gradients, but its effects will be negligible for the active volume of an NMR sample, which is well below the sample surface.) Unlike Rayleigh–Bénard convection, which only occurs when the magnitude of the vertical temperature gradient exceeds a certain critical value (about 0.05 K cm⁻¹ for chloroform in a standard 5 mm NMR tube²), Hadley convection driven by transverse gradients is not a critical phenomenon and occurs for all nonzero magnitudes of gradient. The only practical situation in which the liquid in an NMR sample remains stable is where there is no transverse variation in temperature at all, and where the vertical temperature gradient is either positive (with temperature increasing monotonically up the sample) or is negative but below the critical threshold. The rate of convection in liquid NMR samples depends critically on experimental parameters such as sample size and shape, fluid characteristics (viscosity, thermal conductivity, thermal expansivity) and nominal sample temperature, but can also vary widely between different types of probe and instrument. Here comparative measurements are presented that illustrate just how different convective behavior can be in different probes and different spectrometers.

In many commercial probes available nowadays, the sample temperature is regulated by flowing temperature-controlled gas upwards past the sample. Since the base of the NMR tube is the first part to feel the gas flow, the temperature gradient is expected to be both vertical and positive (bottom colder than the top) whenever the temperature of the gas flow is below the quiescent temperature, T_Q, of the sample (the temperature of the sample in the absence of any gas flow, typically, but not always, near to room temperature), and vertical and negative when the gas temperature is above T_Q. This would be true if the probe geometry and the incoming gas flow were perfectly cylindrical, but previous studies have shown that in fact convection is found at temperatures both above and below T_Q,¹ indicating the presence of horizontal temperature gradients. Cold probes/cryoprobes present particular problems because of the extreme temperature gradients present close to the sample; in such probes T_Q is normally well below 0 °C, and it is essential to maintain gas flow past the sample at all times.

All liquid state NMR experiments suffer from convection effects to a greater or lesser extent, but pulse sequences that use field gradient pulses, whether to select coherence transfer pathways, to encode spatial position, or to enable diffusion measurement, are those most likely to exhibit anomalies due to convection. When a sample convects, drastic effects on the time evolution of nuclear magnetization during the pulse sequence can sometimes be observed, resulting e.g. in spectra containing signals with incorrect phases and amplitudes.^1,2,5 Signal loss due to convection is unwelcome in any NMR experiment, given the inherently low sensitivity of NMR spectroscopy, but is a particular problem in experiments for the measurement of diffusion. Convection leads to overestimation of the diffusion coefficient, since the coherent convective motion and the random diffusion both contribute to the signal attenuation observed.^2,3 Even small values of convection velocity (0.05 mm s⁻¹) can lead to significant errors in measured diffusion coefficient values.¹

Various strategies may be used to minimize the effects of convection on NMR experiments. As already noted, choice of solvent is critical; at room temperature, chloroform convects 20 times more readily than D₂O.¹ Sample geometry is also critical; convection in a standard 3 mm OD NMR tube is more than an order of magnitude slower than in a standard 5 mm OD tube.¹ In many experiments the effects of mild convection can be refocused using convection-compensated pulse sequences (it should be noted that in many circumstances it is preferable to suppress convection by using a smaller diameter tube rather than to use a compensated pulse sequence, since the latter normally sacrifices half of the available signal by including a second stimulated echo).^1,2,6–13 Thermal gradients in probes will also be affected by external sources of heat flow such as shim coils or decoupling, and by the use of air in conventional probes, and water in high gradient probes, to control the probe body (as opposed to sample) temperature. Temperature gradients can if necessary be measured directly, rather than inferred from measurements of convection, by using sensors in situ¹ or by imaging the chemical shift of a species with a very temperature-sensitive resonance.³

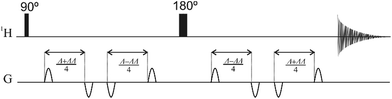
Convection-compensated pulse sequences^12,13 for diffusion measurement can be adapted to measure the rate of convection in a sample; here this approach is used to compare convection behavior across a range of instrumental configurations. The convection-compensated diffusion measurement pulse sequence of Fig. 1 with ΔΔ = 0 divides the diffusion weighting component of the sequence into two equal halves separated by a 180° pulse, thus refocusing the effects of constant-velocity flow while retaining those of diffusion. If the durations of the two halves of the sequence are deliberately unbalanced to an extent ΔΔ, measurements of the extra signal attenuation as a function of ΔΔ allow the form and width of the sample z velocity spectrum to be determined.¹ Experimental signal attenuation data as a function of ΔΔ are typically well approximated by a sinc function, corresponding to a rectangular velocity spectrum, so fitting to a sinc function is a simple and effective way to estimate the magnitude of the peak z convection velocity in an NMR sample.

Fig. 1 A simple convection-compensated spin echo pulse sequence in which each gradient pulse has a duration δ and a strength G, the total diffusion time is represented by Δ, and the delay imbalance by ΔΔ.

Experimental section

Materials and spectrometers

Measurements of convection velocity were performed using a sample of 5% v/v CHCl₃ in CDCl₃, doped with 0.2 mg ml⁻¹ chromium(III)acetylacetonate (Cr(acac)₃) to reduce the longitudinal relaxation time T₁ and hence allow faster experiments. As summarized in Table 1, experiments were performed using five different NMR spectrometers (Bruker AVANCE III 400, 500 and Ascend 500, 600 and 800, where the figures denote the frequencies for ¹H in MHz).

Table 1 Spectrometers, probes, gas flow rates, and NMR tube geometries used to acquire convection data

Spectrometer	Probes	Gas flow rates (l h^−1)	NMR tube geometries
Bruker AVANCE III 400 MHz	BBI S1	670	5 mm; 5 mm with insert; 3 mm
Bruker AVANCE III 500 MHz	BBO S2	400	5 mm; 5 mm with insert; 3 mm
Bruker Ascend AVANCE III 600 MHz	TBI S3	400	5 mm; 5 mm with insert; 3 mm
	TBO S3	400	5 mm; 3 mm
Bruker Ascend 500 MHz	CPPBBO BB	400	5 mm; 3 mm
Bruker Ascend AVANCE III 800 MHz	CPTCI	400	5 mm; 3 mm

---

The 400 MHz spectrometer was equipped with a BBI probe (double resonance broadband probe with inner coil optimized for ¹H observation), and for 500 MHz spectrometers a BBO probe (double resonance broadband probe with the inner coil tunable over the frequency range from ³¹P to ¹⁵N) and a CPPBBO BB probe (“Prodigy” nitrogen-cooled BBO) were used.

For the 600 MHz instrument two different probes were evaluated, TBO (triple resonance broad band probe with the outer coil tuned for ¹H observation or decoupling) and TBI (triple resonance broad band probe with the inner coil tuned for ¹H observation or decoupling), while the 800 MHz spectrometer was equipped with CPTCI probe (proton-optimized triple resonance NMR (TCI) inverse “cryoprobe”/“cold probe” with helium cooling). Three different NMR tube geometries were studied, standard thin-walled 5 mm and 3 mm OD NMR tubes and a standard 5 mm OD NMR tube with a 2 mm OD insert.

NMR experiments

The pulse sequence code used to acquire the convection experiments is given in the ESI.† In each experiment a set of 25 different imbalance delays (ΔΔ) (see Table S1 in ESI†) was used for each temperature, and 36 temperatures were evaluated, from 5 to 40 °C in steps of 1 °C. The duration used for the gradient recovery delay was 0.5 ms; the diffusion encoding gradient pulse duration (δ) was 2 ms, and the gradient strength used was 80% of the nominal maximum value for each spectrometer (Table S2†).

At each temperature a stabilization delay of 15 min was allowed after the nominal temperature was registered by the temperature controller unit, in order to ensure that the sample was fully equilibrated with its surroundings in the probe. Experimental data were processed in TOPSPIN 3.1 and MATLAB, using a set of AU programs and MATLAB macros (see Fig. S2†).

Results and discussion

The experimental signal amplitudes were measured using TOPSPIN, and subjected to nonlinear least squares fitting to the sinc function of eqn (1)²

F(ΔΔ) = S₀ sin(γδGA_Gv_maxΔΔ)/(γδGA_Gv_maxΔΔ) (1)

where S₀ is the maximum signal amplitude, γ is the magnetogyric ratio, G is the gradient amplitude in G cm⁻¹, A_G is the gradient pulse shape factor (2/π for half-sine pulses), v_max is the maximum convection velocity sought and ΔΔ is the delay imbalance. Fig. 2 shows plots of maximum convection velocity as a function of nominal sample temperature for each combination of spectrometer, probe and NMR tube geometry.

Fig. 2 Convection velocity versus temperature, from 5 °C to 40 °C, for spectrometers of four different frequencies (400, 500, 600 and 800 MHz), with six different probes (BBI, BBO, CPPBBO, TBI, TBO and CPTCI), and three different NMR tube geometries (5 mm – blue; 5 mm with 2 mm OD insert – green; and 3 mm – red). Each graph includes a tenfold vertical expansion. Graphs (a) to (f) illustrate the data obtained with a 5 mm NMR tube; graphs (g) to (i) a 5 mm NMR tube with 2 mm OD insert; and (j) to (p) with a 3 mm NMR tube. Full experimental data can be downloaded from DOI: 10.15127/1.301247.

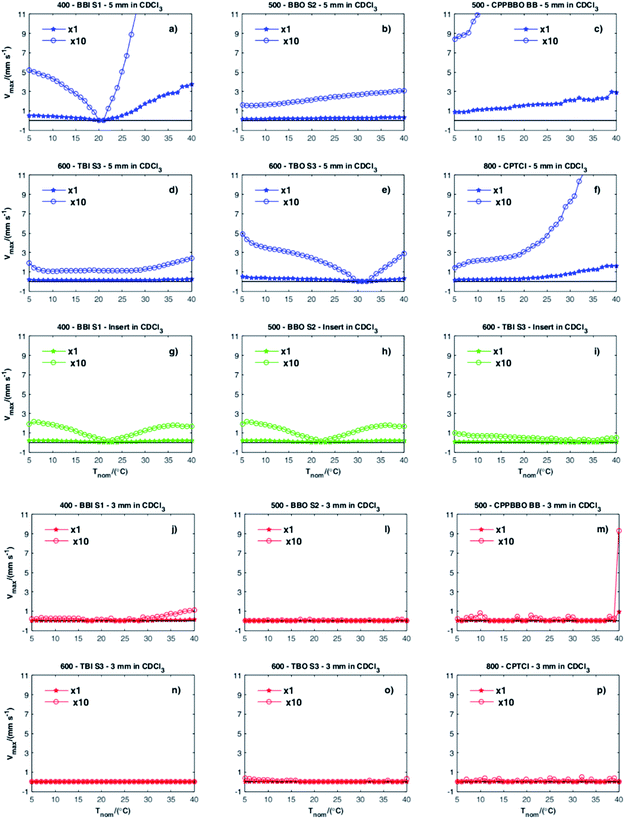
The first thing that is immediately apparent from the graphs in Fig. 2 is that all combinations of spectrometer and probe using 5 mm NMR tubes, with or without the 2 mm OD insert, show convection both above and below T_Q (Fig. 2a–i). In a previous investigation by Swan et al.¹ of a range of older instruments, all of the systems studied showed a similar pattern of variation of convection velocity with temperature, a “V” shaped curve approximately centred on the quiescent temperature T_Q, at which the convection velocity was very low. In the more modern instruments investigated here this was not always the case, with some quite different behaviours (Fig. 2b–d, f and i) observed.

The second obvious conclusion is that even in systems showing florid convection in 5 mm tubes, very little convection was observed in 3 mm samples under the experimental conditions used. This reflects both the effect of the confined sample geometry, reducing the rate of convection caused by a given temperature gradient, and the improved freedom of circulation of air around the sample, reducing the magnitudes of the sample temperature gradients. It should however be noted that convection velocities several orders of magnitude smaller than those measured here can be measured if minor changes to the experimental method are made. The most important of these is to use a reporter molecule with a low diffusion coefficient, since diffusional attenuation competes with the signal attenuation caused by convection.

The highest convection velocities recorded (approximately 4 mm s⁻¹) were for the 5 mm tube, in the room temperature BBI S1 probe at 400 MHz (Fig. 2a), at the top end of the temperature range studied; conversely, close to its T_Q of about 21 °C this combination showed some of the slowest convection measured for a 5 mm tube. As expected, the nitrogen-cooled (“Prodigy”) and helium-cooled cryoprobes (Fig. 2c and f) showed severe convection in 5 mm tubes over the full range of nominal temperatures studied. No minimum was seen in the curves of v_max versus T, since T_Q in such probes is, as noted earlier, typically below 0 °C. Even these probes, however, showed v_max less than 0.1 mm s⁻¹ in the 3 mm NMR tube. In ref. 1, all of the probe/spectrometer combinations tested showed a clear minimum in v_max at some temperature. It is not surprising that such a minimum is not seen for the cold probes of Fig. 2c and f studied here, but it is unexpected that some of the room temperature probes (Fig. 2b and d) failed to show any deep minimum in v_max over the temperature range studied.

Conclusions

The main point of this article is to illustrate the surprisingly wide range of convection behaviours likely to be encountered in modern NMR spectrometers, and in so doing to underline the rather gloomy conclusions of ref. 1. Not only is convection always with us, but the marked differences in behaviour between different instrument configurations, even those with nominal similarities, mean that there is no substitute for direct experimental investigation if convection is a potential problem. The materials presented here and in the ESI† provide the basis for making and interpreting the necessary measurements, and also add to the evidence base for evaluating the relative susceptibility to convection of different probe designs and configurations.

Acknowledgements

The authors gratefully acknowledge grants #2015/08541-6 and #2014/25903-6, São Paulo Research Foundation (FAPESP), for providing financial support for this research, and for T. M. B. scholarships (#2014/12776-6 and BEPE, #2015/19229-3); the CNPq for fellowships to R. R. and C. F. T.; and CAPES (PEV project #88881.030355/2013-01), the Chemistry Institute of UNICAMP, USP and the University of Manchester for NMR facilities. This work was also supported by the EPSRC (grant number EP/K039547). The authors thanks Michael Engelhardt and Peter Gierth of BRUKER for assistance with TOPSPIN AU programmes and for fruitful discussions about hardware.

Notes and references

1. I. Swan, M. Reid, P. W. A. Howe, M. A. Connell, M. Nilsson, M. A. Moore and G. A. Morris, J. Magn. Reson., 2015, 252, 120.
2. N. M. Loening and J. Keeler, J. Magn. Reson., 1999, 139, 334.
3. W. J. Goux, L. A. Verkruyse and S. J. Salter, J. Magn. Reson., 1990, 88, 609.
4. M. Lappa, Thermal Convection: Patterns, Evolution and Stability, John Wiley & Sons, 2009.
5. J. Lounila, K. Oikarinen, P. Ingman and J. Jokisaari, J. Magn. Reson., Ser. A, 1996, 118, 50.
6. N. Esturau, F. Sánchez-Ferrando, J. A. Gavin, C. Roumestand, M. A. Delsuc and T. Parella, J. Magn. Reson., 2001, 153, 48.
7. K. Hayamizu and W. S. Price, J. Magn. Reson., 2004, 167, 328.
8. A. Jerschow and N. Müller, J. Magn. Reson., 1998, 132, 13.
9. G. H. Sørland, J. G. Seland, J. Krane and H. W. Anthonsen, J. Magn. Reson., 2000, 142, 323.
10. K. I. Momot and P. W. Kuchel, J. Magn. Reson., 2005, 174, 229.
11. T. Iwashita, T. Konuma, E. Harada, S. Mori and K. Sugase, Magn. Reson. Chem., 2016, 54, 729.
12. M. Nilsson and G. A. Morris, J. Magn. Reson., 2005, 177, 203.
13. M. Nilsson, A. M. Gil, I. Delgadillo and G. A. Morris, Anal. Chem., 2004, 76, 5418.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra23427e

---