Renewable pine cone biomass derived carbon materials for supercapacitor application†
Abdulhakeem Belloa,
Ncholu Manyala*a,
Farshad Barzegara,
Abubakar A. Khaleedab,
Damilola Y. Momodua and
Julien K. Dangbegnona
aDepartment of Physics, Institute of Applied Materials, SARCHI Chair in Carbon Technology and Materials, University of Pretoria, Pretoria 0028, South Africa. E-mail: ncholu.manyala@up.ac.za
bDepartment of Physics, Ahmadu Bello University, Zaria, Nigeria
First published on 3rd December 2015
Abstract
The environmental degradation and hazard to human life caused by the depletion of fossils fuels and the urgent need for sustainable energy sources to meet the rising demand in energy has led to the exploration of novel materials that are environmentally friendly, low cost and less hazardous to human life for energy storage application using the green chemistry approach. Herein, we report on the transformation of the readily abundant pine cone biomass into porous carbon via KOH activation and carbonization at 800 °C as electrode materials for supercapacitors. The porous carbon material exhibited a mesoporous framework with a specific surface area of 1515 m2 g−1, a high voltage window of 2.0 V, a gravimetric capacitance of 137 F g−1, energy density of 19 W h kg−1 and excellent cyclability in neutral 1 M Na2SO4 electrolyte for a symmetric carbon/carbon electrode cell. The result shows that the material is robust and shows great promise with neutral electrolytes in high-performance energy-storage devices.
Introduction
Energy is crucial and a driving factor for the development of our society; technologically and socio-economically. The recent boom in energy demands from the energy sector due to increase in world population has led to the depletion of fossil fuels worldwide. Furthermore, the consumption of these fossil fuels is linked to environmental degradation that endangers human life, through climate changes and emission of greenhouse gases which often lead to high managements cost. Hence, there is a need for a paradigm shift from fossil fuels for the production of carbon materials for energy to a green and low-cost materials, to meet the increasing energy demand for sustainable and economic development.1,2 In this regard, it is necessary to look for materials that are abundant, renewable and sustainable sources for energy applications. Biomass is a viable renewable source of carbon materials (solid, liquid or gaseous product) for energy applications and currently supplies about ∼14% of the world's energy due to the fact that they are readily available, low cost, regenerate rapidly, and are friendly and less harmful to the environment when compared with the fossil fuels.3–7In order to meet and address the challenges of increasing demands, there has been a significant interest in the development of new, versatile, and scalable energy storage technology systems. Amongst these systems, electrochemical double layer capacitors (EDLCs also known as supercapacitors) are attractive and their energy storage mechanism is based on electrical double layer charge accumulation at the interface between the electrode and electrolyte. They hold a considerable promise for a wide range of applications, including portable electronic equipment's, regenerative breaking systems, uninterruptible power sources, load leveling and hybrid electric vehicles, and so forth due to theirs high power density, fast charging–discharging mechanism and excellent long life cycle.8,9 Generally, the design and the electrochemical performance of EDLC are mainly dependent on the development of cost-effective electrode materials with a good representation of the pore structure and morphology. Carbonaceous materials are the most widely studied supercapacitor electrode active substances. They have been shown to have reasonable electrochemical performances, long-term cyclability and good electrochemical stability which are related to electronic conductivity and high specific surface area (SSA). While the most commonly used carbon material in the commercial industry is the activated carbon.10 Other nanostructured forms of carbon such as carbon nanotubes (CNTs),11,12 carbide-derived carbons (CDCs),13,14 onion-like carbons (OLCs)15,16 and graphene17,18 are also explored as electrode materials for the next generation of EDLCs. Nevertheless, the energy density of EDLCs made from these materials is still small (<10 W h kg−1) when compared to their battery counterparts.19 Hence, all research activities and effort are aimed at improving on the properties of EDLCs either by increasing the capacity of the EDLC electrodes by modifying the carbon materials with different functionalities9,20 or by increasing the operating potential window since the energy density of an EDLC device is directly proportional to its capacity and also the square of its operating potential window. Recently, significant progress has been made in utilizing sustainable biomass for various applications. For example the production of carbon materials from organic waste for energy and absorbents applications has received much attention due to the environmental and degradation effect associated with the depletion of fossil fuels as mentioned earlier.21,22 The natural, agricultural and organic wastes such as egg shell,23 seaweeds,24 dead leaves,21 hemp basts,25 wood sawdust,26 yeast cells,27 pistachio nutshells,28 cigarette filter,29 sunflower seed shell,30 cypress31 and rice husk32 have all been explored as bio-source carbon using different synthesis methods including; hydrothermal,26 direct pyrolysis,24 chemical vapor deposition (CVD),33 gas–solid displacement reactions,34 and wet chemistry techniques, such as sol–gel processes.35 Recently human hair was carbonized at 800 °C and tested as electrode for EDLCs, the device fabricated exhibited with a specific capacitance of 340 F g−1 and 126 F g−1 both in 6 M KOH and 1 M LiPF6 ethylene carbonate/diethyl carbonate (EC/DEC) organic electrolyte, respectively, at a current density of 1 A g−1 with good stability over 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles.36 Microporous carbon with a high surface area of about 1230 m2 g−1 synthesized by single-step pyrolysis of dead plant leaves also exhibited a very high specific capacitance of 400 F g−1 and an energy density of 55 W h kg−1 at a current density of 0.5 A g−1 in aqueous 1 M H2SO4 (ref. 21) and symmetric capacitors built from seaweeds which was pyrolysed at 600 °C exhibited a potential window up to 1.6 V with excellent cycle life showing very small capacitance drop after 10
000 cycles.36 Microporous carbon with a high surface area of about 1230 m2 g−1 synthesized by single-step pyrolysis of dead plant leaves also exhibited a very high specific capacitance of 400 F g−1 and an energy density of 55 W h kg−1 at a current density of 0.5 A g−1 in aqueous 1 M H2SO4 (ref. 21) and symmetric capacitors built from seaweeds which was pyrolysed at 600 °C exhibited a potential window up to 1.6 V with excellent cycle life showing very small capacitance drop after 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles.20 Aside from the structural properties of these carbon materials, they are sustainable, low cost and pose no threat to the environment.
000 cycles.20 Aside from the structural properties of these carbon materials, they are sustainable, low cost and pose no threat to the environment.
As a potential carbon sources, pine cones are common biomass waste which are abundant and widely available. Pines are coniferous trees in the genus Pinus family of the Pinaceae which arise in a wide range of environmental conditions. It sprouts up to 50 m in height with dark green needles and 5–10 cm length cones with rounded scales. Substantial amount of cones are produced yearly throughout the world, especially in pine plantations grown for the pulp and paper industry. They are mainly composed of cellulose, lignin and resins that contain a variety of organic compounds.37,38 Porous carbon from pine cone biomass have been extensively studied as biosorbent for metal, dye waste waters, nitrate uptake and removal of lead(II) ions from aqueous solutions by adsorption.39–42 There are very few reports on the use of pine cone derived carbons for energy storage applications. For example, Karthikeyan K. et al.43 reported very high surface area activated carbons synthesized from pine cone petals. A symmetric supercapacitor fabricated from the produced carbon exhibited very high energy density of ∼61 W h kg−1 and excellent stability in 1 M LiPF6 in ethylene carbonate/dimethyl carbonate. Similar, microporous carbon were derived from pinecone hull and tested as anode material for lithium batteries, which retained a discharge capacity of 357 mA h g−1, and a coulombic efficiency of 98.9% current density of 10 mA g−1.44 In this report we demonstrate the production of porous carbon materials via hydrothermal treatment, KOH activation and carbonization of pine cones and present the electrochemical performance of symmetric capacitors with this carbon material in Na2SO4 aqueous electrolyte. A detailed analysis of the electrodes in both three- and two setups show that a voltage window of (2 V) can be obtained for a symmetric carbon/carbon capacitor operating in 1 M Na2SO4 aqueous electrolyte. The pine carbon materials were stable within this potential and showed no environmental issue like corrosion. The choice of KOH as activating reagent is based on the fact that it induces well-defined micropore size distribution at lower activation temperature and high yields in carbon materials.45 The formation mechanism of porous carbons with KOH is attributed to carbon gasification by the removal of CO2 and to the presence of oxygen material present in the matrix. During the activation process, CO2 formed from K2CO3 in the annealing process is released and becomes significant at high temperatures. The released CO2 then react with hydrochar material from the pine to open up closed pores and enlarge existing micropores. On the other hand, the potassium-containing compounds, such as K2O and K2CO3, can be reduced by carbon to form K metal, thus causing the carbon gasification and hence the formation of pores.45 The activation process takes places according to the following reaction;45
| 6KOH + C ↔ 2K + 3H2 + 2K2CO3 |
Experimental
Synthesis of activated pine carbon (APC)
The readily available pine cones (PC) collected from the University of Pretoria campus Hatfield, South Africa were used as raw materials. The cones were washed repeatedly with acetone and distilled water to remove adhering dirt and soluble impurities and dried at 60 °C. After drying, the cleaned PC was crushed to powder using a swing mill equipped with a tungsten carbide port and 8 g of the PC powder was then dispersed in 80 ml of distilled water containing 0.5 ml of sulphuric acid. The disperse was transferred into a stainless steel autoclave and was heated up to 160 °C for 12 h and then allowed to cool to room temperature. The resulting solid black product was filtered and washed with distilled water and dried overnight at 80 °C. The dried solid black product was activated by mixing with KOH with a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mass ratio in agate mortar. The mixture was then placed in a horizontal tube furnace ramped from room temperature to 800 °C at 10 °C min−1 under argon flow and kept at this temperature for 1 h for the carbonization process. The resulting dark solid material was washed with 0.1 M HCl solution, and then washed with distilled water until the neutral pH was obtained. The product was collected and dried at 80 °C in an electric oven. The resultant powder was denoted as activated pine carbon (APC). Scheme 1 shows the transformation of PC into porous carbons.
1 mass ratio in agate mortar. The mixture was then placed in a horizontal tube furnace ramped from room temperature to 800 °C at 10 °C min−1 under argon flow and kept at this temperature for 1 h for the carbonization process. The resulting dark solid material was washed with 0.1 M HCl solution, and then washed with distilled water until the neutral pH was obtained. The product was collected and dried at 80 °C in an electric oven. The resultant powder was denoted as activated pine carbon (APC). Scheme 1 shows the transformation of PC into porous carbons.
Physico-chemical characterization of the APC
Scanning electron microscopy (SEM) micrographs of the carbon were observed via Zeiss Ultra Plus 55 field emission scanning electron microscope (FE-SEM) operated at an accelerating voltage of 2.0 kV. Transmission electron microscopy (TEM) analysis was made at 200 kV on a JEOL JEM-2100F microscope with field-emission gun. Typically, TEM samples were prepared by dispersing the samples in ethanol and dropped on lacey carbon grid for analysis. The surface area measurement of the sample was performed by liquid nitrogen cryosorption at −196 °C using a surface area and pore size analyzer Micromeritics TriStar II 3020 (version 2.00). The samples were degassed at 150 °C for more than 12 h under vacuum conditions. The surface area was calculated by the Brunauer–Emmett–Teller (BET) method. X-ray photoelectron spectroscopy (XPS) was used to determine the chemistries of activated carbons in powder form. A Physical Electronics VersaProbe 5000 instrument was used employing a 100 μm monochromatic Al-Kα to irradiate the sample surface. Photoelectrons were collected by a 180° hemispherical electron energy analyzer. Samples were analyzed at a 45° angle between the sample surface and the path to the analyzer. Survey spectra were taken at pass energy of 117.5 eV, with a step size of 0.1 eV, which was used to obtain the elemental analysis of the powders. High-resolution spectra of C1s, N1s, and O1s regions were taken at pass energy of 23.5 eV, with a step size of 0.05 eV. The spectra were taken after the samples were sputtered with an Ar beam operating at 2.0 kV and 150 μA for 10 min. All binding energies were referenced to that of the binding energy of the Fermi level Ef = 0 eV. Peak fitting for the high-resolution spectra was performed using CasaXPS Version 2.3.16 RP 1.6. Prior to the peak fitting the background contributions were subtracted using a Shirley function. Raman analysis of the sample was recorded using a WiTec-alpha 300R+ confocal Raman spectrometer (WiTec GmbH) with the laser power of 1.5 mW in order to minimize heating effects. The excitation source was a 532 nm laser through a numerical aperture of 0.9 and 100× magnification. FTIR spectra were recorded on a Vertex 70v (Bruker) spectrometer in the 4000–400 cm−1 range with 4 cm−1 resolution. Sample compartment was evacuated during acquisition. Spectra were recorded and analysed with the Opus software.Electrochemical measurements
The electrochemical measurements were carried out on a multichannel VMP300 potentiostat/galvanostat (Bio-Logic, France) at room temperature. The working electrodes were prepared by mixing a paste containing 80 wt% APC material, 10 wt% poly(vinylidene fluoride) (PVDF) (in N-methylpyrrolidone) and 10 wt% carbon black coated on a nickel foam with a diameter of 16 mm. Afterwards, the working electrode was pressed and dried in vacuum at 80 °C overnight in an electric oven to ensure complete evaporation of the NMP. Each electrode has a mass loading of about 2.5 mg. The electrochemical test of the APC electrode was performed in a three electrode configuration using glassy carbon plate as counter electrode and Ag/AgCl (3 M KCl) as the reference electrode in 1 M Na2SO4 aqueous electrolyte. The symmetric devices were assembled such that two electrodes were separated by a 0.18 μm thick microfiber glass filter paper in CR2025-type coin cells. The cyclic voltammetry and galvanostatic charge–discharge tests for these devices were recorded in a potential window from 0 to 2 V at various scan rates and current densities. Electrochemical impedance spectroscopy (EIS) measurements were conducted in a frequency range of 100 kHz to 0.01 Hz with an open circuit voltage using a sinusoidal signal of 5 mV. The gravimetric capacitance for the single electrode was calculated according to:46
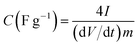 | (1) |
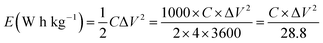 | (2) |
| P = E/Δt | (3) |
The coulombic efficiency (ε also referred to as faradaic or current efficiency) values were calculated from the charge–discharge curve using the following equations
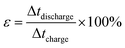 | (4) |
Results and discussion
Scanning electron microscopy (SEM) and transmission electron microscopy (TEM) were used to investigate the structure and morphology of the as-synthesized materials. Fig. 1(a) and (b) shows a low and high magnification SEM micrographs of the APC sample and it is clear from the figure that KOH activation process leads to the formation of porous cavities in the material as observed in Fig. 1(a). Higher magnification features the existence of ample amount of pores in the 3D interconnected that are linked together in the carbon frameworks with dimension from nanometers to several micrometres pores in the network. Transmission electron microscopy (TEM) micrographs, further highlights the structure of the produced carbon material. Fig. 1(c and d) show that the material consists of highly interconnected 3D hollow and porous spheres that overlap each other and some of the spheres are split open. The diameters of some of the spheres are in the range of 100–200 nm. This type of porous structure could be favourable for energy storage since it has been established that the porosity of the activated carbon materials governs its energy storage and power delivery capability.47 | ||
| Fig. 1 (a and b) SEM and (c and d) TEM micrographs of APC showing low and high magnification respectively. | ||
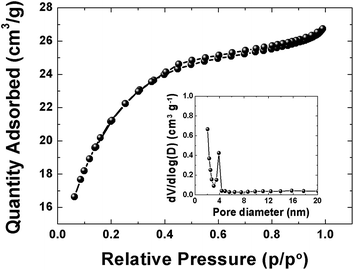
The pore texture of the APC material was analyzed by N2 adsorption/desorption measurements. Fig. 2 show that APC exhibits a type-II behavior with a H4-type hysteresis suggesting a complex material containing both micropores and mesopores. The specific surface area (SSA) and the pore volume of the material are 1515 m2 g−1 and 0.38 cm3 g−1 respectively. The pore size distributions (inset to the figure) was calculated using the Barrett–Joyner–Halenda (BJH) analysis from the desorption branch and the pore size in the material is mainly distributed within 2–100 nm range. The higher surface area and narrower pore size distribution could be beneficial in charge storage by providing high adsorbate accessibility and providing wider transport channels to micropores.48
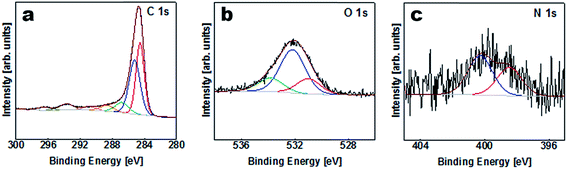
The elemental composition of the APC sample was obtained from XPS characterization of the survey spectra shown in Table S1 (ESI†) and Fig. 3. Carbon is considered to be the major element in the samples with a small amount of K, O and N on the surface. The results of the peak fitting for the sample are shown in Fig. 3(a) and Table S2.† The C1s/K2p region was fitted by six components corresponding to graphitic carbon, hydrocarbons (CHx), alcoholic (C–O–) and/or carbon nitrogen structures (C–N–), carboxyl or ester (COO), and the 2p3/2 and 2p1/2 components arising from the K2p region which might correspond to potassium oxide and/or hydroxide. The O1s region Fig. 3(b) was fitted by three components corresponding to potassium oxide and/or hydroxide, C–O– and COO. However, the N1s peak was fitted with two components corresponding to pyridine and/or amine and nitrile and/or pyrrole Fig. 3(c).
In order to further investigate the structure of this sample Raman analysis was also performed and it shown in Fig. 4(a). The Raman spectrum depicted in the figure shows the two prominent peaks located at ∼1342 and ∼1587 cm−1 corresponding to C–C graphitic lattice vibration mode with A1g symmetry and known to be characteristics of disordered graphite structure defect D-band and G-band (sp2-hybridized carbon) corresponds to an ideal graphitic lattice vibrational mode with E2G symmetry, respectively.49 The ID/IG ratios were calculated from the D and G bands intensities is 0.99 indicating a low degree of graphitic crystalline structure. A Fourier transform infrared spectroscopy (FTIR) measurement was also used to probe the surface chemistry of the sample and, confirm the XPS results and is shown in Fig. 4(b). The spectra of the raw pine before, after hydrothermal treatment and after carbonization exhibits a broad absorption band at ∼3000–3600 cm−1 with a maximum at ∼3354.9 cm−1 which is very pronounced after hydrothermal treatment and is assigned to O–H stretching vibration of the surface hydroxyl groups, while the band at ∼2958.90 cm−1 before and after hydrothermal treatment shows the presence of aliphatic group (C–H) and the peak at 1647.1 cm−1 represents C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching vibrations of ketones, aldehydes, lactones or carboxyl groups. Peaks observed between 1100.8 and 559.3 cm−1 (after hydrothermal treatment) may be assigned to the –C–C– and –CN stretching.42 The very weak band at 2650 cm−1 after carbonization represents the asymmetric vibration of –CHx hydrocarbon groups.39 Disappearance of some peak after carbonization was observed. For example the band at 3354.9 cm−1 due to (O–H) stretching is no longer visible. This is due to the fact that high temperature carbonization could lead to the breaking of the bonds of the carboxylic groups and evaporate them as volatile matter.
O stretching vibrations of ketones, aldehydes, lactones or carboxyl groups. Peaks observed between 1100.8 and 559.3 cm−1 (after hydrothermal treatment) may be assigned to the –C–C– and –CN stretching.42 The very weak band at 2650 cm−1 after carbonization represents the asymmetric vibration of –CHx hydrocarbon groups.39 Disappearance of some peak after carbonization was observed. For example the band at 3354.9 cm−1 due to (O–H) stretching is no longer visible. This is due to the fact that high temperature carbonization could lead to the breaking of the bonds of the carboxylic groups and evaporate them as volatile matter.
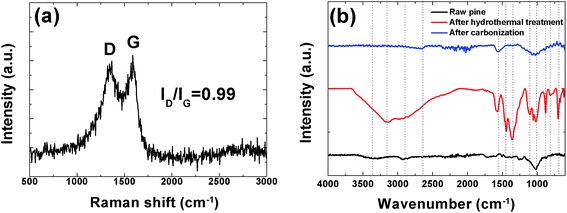 | ||
| Fig. 4 (a) Raman spectroscopy showing prominent D and G peaks and (b) FTIR spectra of raw, hydrothermal treated pine and the carbonized pine cone powder. | ||
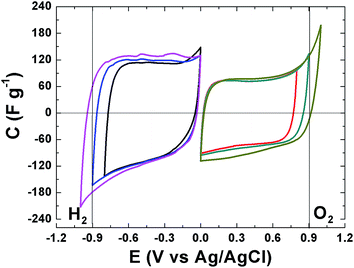
The electrochemical behavior of the APC material was evaluated and the results are presented. Fig. 5 present the cyclic voltammograms (CV) of the APC in a three electrode setup with a 1 M Na2SO4 in the negative and positive potential window, with different potential ranging from −1 V to 1 V. CV shapes are rectangular which indicating a very fast electrochemical response, confirming the good electrical conductivity for this material and demonstrate the formation of a double layer mechanism. The CVs are stable within this potential range and still within the thermodynamic stability window of water due to the increased electrolyte stable potential windows (ESPWs) when compared to both the acidic and alkaline aqueous electrolyte.50 This large potential window is not surprising as it has been shown that neutral electrolyte can reach up to 2 V due to the fact that a neutral electrolyte has lower H+ and OH− concentrations when compared to acidic and alkaline electrolytes, thus, a high over potential of for di-hydrogen evolution and oxygen evolution reactions can be expected which suggests an increase ESPW. The large potential is related with the storage of nascent hydrogen in the carbon material below the thermodynamic potential for water decomposition.20,51 Below −0.9 V and above 0.9 V cathodic and anodic current leaps are observed which are indications of di-hydrogen and oxygen evolutions as the material approach −1 V and 1 V.
The CVs of a symmetric cell which combines both negative and positive potential window are shown in Fig. 6(a) from 1 V to 2 V potential ranges. At low voltage ranges the CVs show rectangular shapes which are characteristic of a pure EDLC behavior. With increasing voltage range the CV still maintains its symmetric rectangular shape with a slight increase in capacitance value. At the maximum potential window of 2.0 V a current leap is observed which could be due to the evolution of gases or oxygenated surface functionalities generated from both the positive and/or negative electrode and the reactions with the electrolyte.19,51 The constant current charge–discharge (CD) was also measured at different voltage ranges and is presented in Fig. 6(b). The symmetrical triangular shape of the CD corroborates the formation of a double layer capacitor. The CD curves measurement show that the APC electrode material is stable at the maximum potential limit of 2 V without any distortion to the CD, hence further measurements were made at potential window of 2 V.
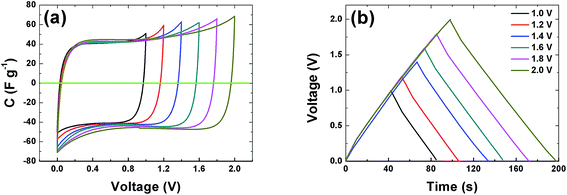 | ||
| Fig. 6 (a) Cyclic voltammogram at 20 mV s−1 and (b) galvanostatic charge–discharge at profiles of the APC at 0.5 A g−1 at different voltage ranges respectively. | ||
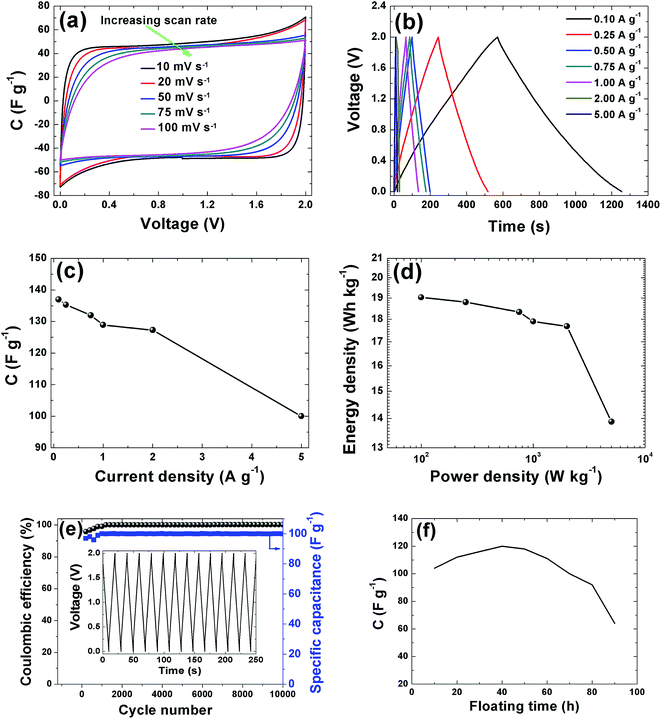
CV curves of the APC electrode at 2 V is shown in Fig. 7(a). The CVs show rectangular shapes characteristic of electrochemical double layer capacitor (EDLC) behavior. As the scan rate increases, the capacitive double layer signature of the electrode is preserved, indicating the porous and polarizable nature of the material. At 100 mV s−1, CV demonstrate a resistive CV shapes that describe the presence of increased ohmic behavior and could be attributed to the decline in capacitance observed in Fig. 7(c). This performance at high scan rates establishes the high power capability of the porous APC material. For quantitative considerations the specific capacitance calculated from the CV by using the integral area ranges from 98.5 F g−1 (10 mV s−1) to 80 F g−1 (100 mV s−1). Essentially the result obtained is attributable to the large accessible surface area achieved by good micropore volume and interconnected conducting mesopores pathways. Secondly, the presence of the functional groups present in the sample as observed from the XPS results might lead to a faradaic reaction contributing to the total capacitance of the carbon electrode. Lastly the individual properties of the electrolyte such as hydrated ion size (3.58 Å) which is similar to the PSD and ionic conductivity 50.11 S cm2 mol−1 all contributed to the capacitive properties of the activated carbon electrode.52 Galvanostatic charge/discharge measurements were applied at different current densities to evaluate the capacitance performance and the result is shown in Fig. 7(b). A symmetric triangular charge and discharge profile distinctive for ideal capacitor was observed, indicating the reversible adsorption/desorption of ions. The gravimetric capacitance was calculated from these curves according to eqn (1) and it is shown in Fig. 7(c). Fig. 7(c) shows that the specific capacitance of the sample decreases slightly with increase in current density, suggesting good rate capability. The specific capacitance at 0.1 A g−1 is about 137 F g−1 and still remains at about 100 F g−1 at a current density 5 A g−1. Fig. 7(d) shows the Ragone plot which emphasizes the energy–power characteristic of the device. The energy and power densities of 19 W h kg−1 and 100 W kg−1 were obtained respectively for this device. More specifically, compared to previously reported supercapacitors from biomass materials as shown in Table 1, our material show a reasonably higher SSA value with good distribution of micro- and mesopore volumes which greatly benefited the electrochemical performance (energy density of 19 W h kg−1) by having easy accessible SSA and reaction sites in aqueous electrolyte which is user friendly compared to most organic electrolytes. Similarly, the pine cones were also carbonized at 700 °C and 900 °C to see the effect of activation temperature on the samples and the result is present in the ESI.† However, these samples showed very low electrochemical performance, demonstrating highly resistive CV shapes at a voltage of 1 V (Fig. S1†). This low performance was related to the pore texture which exhibited a type II N2 isotherm with H2 and H3 hysteresis loop for APC-900 °C and APC-700 °C respectively (Fig. S2†). Signaling a complex pore or non-rigid aggregates structure of sigmoid or macroporous which are not beneficial for high electrochemical performance, since it has been established that the volume of active micropores present in the material (<2 nm in size) acts as ion traps for energy storage and power delivery, mesopores (2–50 nm) provides the pathways for ion transport and the macropores (>50 nm in size) playing the role of an ion buffering reservoir.53 These results further confirms and demonstrate that activation of material using KOH and carbonization 800 °C yields the optimum micropore volume in carbon materials for electrochemical energy storage.54
| Source of electrode material | Activation agent | SBET (m2 g−1) | Electrolyte | Potential (V) | Capacitance (F g−1) | Energy density (W h kg−1) | Power density (W kg−1) | Ref. |
|---|---|---|---|---|---|---|---|---|
| a Three electrode measurements.b Two electrode measurements. | ||||||||
| Waste tires | KOH | 1625 | 1 M H2SO4 | 0.75 | 135a | — | — | 55 |
| H3PO4 | 563 | 6 M KOH | 1 | 106a | ||||
| Pomelo peel | — | 2105 | 1 M NaNO3 | 1.7 | 43.5b | 17.1 | 420 | 56 |
| Human hair | KOH | 1306 | 1 M LiPF6/EC/DEC | 3 | 126b | 45.33 | — | 36 |
| Self-adhesive carbon grains (SACG) | KOH | 1704 | 6 M KOH | 1.6 | 150b | 4.297 | 173 | 57 |
| Pine cone petals | KOH | 3950 | 1 M LiPF6 | 3 | 142b | ∼61 | — | 43 |
| Pistachio nutshells | KOH | 1069 | 6 M KOH | 1.1 | 261b | 10 | 52 | 28 |
| 1 M TEABF4 | 29.3/20.1 | 39 | 286 | |||||
| Banana fibers | ZnCl2 & KOH | 1097 | 1 M Na2SO4 | 1 | 74b | — | — | 58 |
| Oil palm EFB | — | 802 | 1 M H2SO4 | 1 | 196b | 5.45 | 236 | 59 |
| Sunflower seed shell | KOH | 2584 | 3 M KOH | 0.9 | 311b | 4.8 | 240 | 30 |
| Rice husk | NaOH & KOH | 2721 | 3 M KCl | 0.6 | 210b | 60 | ||
| Cypress | 1283 | 1 M H2SO4 | 1 | 190a | — | — | 31 | |
| Sugar cane bagasse | ZnCl2 | 1788 | 1 M H2SO4 | 1 | 300b | 10 | — | 61 |
| Pine cone | KOH | 1160.3 | 1 M Na2SO4 | 2 | 137b | 19 | 100 | This work |
In addition to the excellent rate capability of this material, long cycling stability test was conducted under a constant charge at a current density of 5 A g−1 for 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles. Fig. 7(e) shows the ε and gravimetric capacitance of the symmetric cell. The capacitance retention was almost 100% retention; no notable degradation in capacitance value was observed rather there were fluctuations in the ε plot between 2000 and 4000 cycles after which the ε was stable. Cycling test based on floating was further used to investigate the long-term stability.62 Fig. 7(f) shows the stability during voltage-holding over 100 h. Floating at 2 V has a significant impact on the capacitance which slowly increases during the ageing time. As observed from the figure there was a rapid increase in the capacitance to about 120 F g−1 before starting to show decay. The increase in capacitance we attribute to the expansion and swelling of the APC porous structure during the ageing time thus creating more accessible surface for adsorption of ion from the electrolyte hence increasing the capacitance of the cell. Most importantly the specific capacitance was still ∼60 F g−1 after holding for 100 h. Such excellent cycling stability is attributed to the structural properties with a relatively high pore volume and robust network preventing crumbling or disintegration of the porous structure.
000 cycles. Fig. 7(e) shows the ε and gravimetric capacitance of the symmetric cell. The capacitance retention was almost 100% retention; no notable degradation in capacitance value was observed rather there were fluctuations in the ε plot between 2000 and 4000 cycles after which the ε was stable. Cycling test based on floating was further used to investigate the long-term stability.62 Fig. 7(f) shows the stability during voltage-holding over 100 h. Floating at 2 V has a significant impact on the capacitance which slowly increases during the ageing time. As observed from the figure there was a rapid increase in the capacitance to about 120 F g−1 before starting to show decay. The increase in capacitance we attribute to the expansion and swelling of the APC porous structure during the ageing time thus creating more accessible surface for adsorption of ion from the electrolyte hence increasing the capacitance of the cell. Most importantly the specific capacitance was still ∼60 F g−1 after holding for 100 h. Such excellent cycling stability is attributed to the structural properties with a relatively high pore volume and robust network preventing crumbling or disintegration of the porous structure.
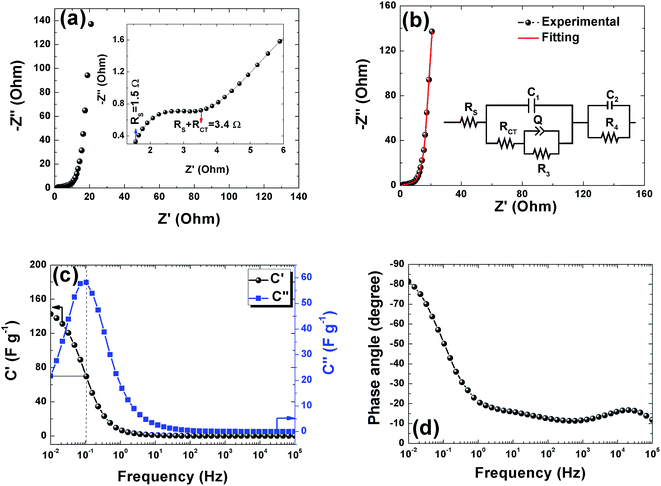
Electrochemical impedance spectroscopy was used to study the ion transport mechanism and further to demonstrate the performance of the APC-based symmetric supercapacitors. Fig. 8(a) shows the Nyquist plot with a nearly straight line in the low-frequency region and an arc in the high-frequency region indicating a distinct capacitive behavior of porous carbon electrodes. The arc in the high frequency region is related to charge transport phenomena (RCT). From the high frequency range data analysis, the ohmic resistance (RS) was estimated. RS includes the intrinsic resistance of the electrode materials, the electrolyte, and the contact resistance between the interfaces of electrodes, electrolyte, and current collector.63 The inset of Fig. 8(a) shows the magnified high frequency region showing the RS value of 1.5 Ω and the corresponding RCT was measured at the diameter of the arc as 1.9 Ω. This RCT value is related to the morphology of the APC electrode material facilitating a rapid charge transfer process. The Nyquist plot before and after cycling is shown in Fig. S3.† From the figure, an increase in the RS value was observed while a decrease in RCT was also observed. The increase in RS could be due to the formation of inactive sites caused by the partial collapse of the three dimensional structure during the cycle test.
The fitting of the Nyquist spectrum was performed by a modified Randles circuit with a set of resistors and capacitors in series and parallel using a fitting program ZFIT/EC-Lab version 10.40 and is represented in Fig. 8(b) with the equivalent circuit shown in the inset. The semicircle in the high-mid frequency region is represented by the charge transfer resistance RCT and the interface contact capacitance C1 between the active material and current collector are connected parallel to each other and are in series with RS. The RCT is connected in series with a constant phase element Q that account for the double-layer capacitance and is associated with a faradaic resistance R3. Ideally, if there is no diffusion resistance at very low frequencies, an ideal polarizable capacitive electrode would lead to a vertical line parallel to vertical axis (−Z′′) with a mass capacitance represented as C2. However, from the Nyquist plot there is a deviation from this ideal behavior. This deviation is attributed to the existence of a resistive element associated with C2. This resistance can be designated as diffusion resistance or leakage resistance R4 and is in parallel to C2. The fitting parameters are shown in Table S3 (ESI†) and values obtained are approximately within the experimental data suggesting that model used for fitting was correct with an error of 0.005. X2 represents the criterion for minimization of the fit. 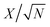 where N is the number of points.
where N is the number of points.
A complex capacitance model based on the single RC time-constant was used to characterize both real part C′ (ω) and imaginary part C′′ (ω) capacitance as function of the frequency, to investigate the frequency behavior and also estimate the relaxation time constant of porous electrodes.46 Fig. 8(c) show the real and imaginary part of the capacitance with frequency of the APC cell, the corresponding capacitance from this graph is 143 F g−1 (from topmost part of the black curve) which is comparable to the results obtained from the CD measurements. This demonstrates the fast frequency response of the porous carbon material in aqueous solution with good capacitance, retention and high power delivery. The imaginary part of the capacitance (the blue curve) corresponds to the energy dispersion. The peak at 0.1 Hz was used to estimate the relaxation time (τ), calculated from τ = 1/ωmax = 1/(2πfmax) where fmax is the characteristic frequency of the cell obtained at the phase angle of −45° corresponding to the time between the capacitive and resistive behavior of the supercapacitor electrode.46 A relaxation time of ∼9.5 s was obtained indicating that the stored energy can efficiently be delivered within this time. Fig. 8(d) shows the Bode phase plot which indicates that in the low frequency region a phase shift of ∼−81.3° close to −90° indicating characteristic of the purely capacitive double layer charge storage phenomenon.
Conclusion
High surface area porous carbon has been successfully synthesized from the abundant and readily available pine cone biomass via KOH activation and carbonization at 800 °C. Structural and morphological characterizations show that the material exhibit three dimensional porous cavities with a specific surface area of 1515 m2 g−1. Electrochemical performances of the porous carbon as active materials for supercapacitors were tested in 1 M Na2SO4 electrolyte. A high voltage window of 2.0 V was observed for a symmetric carbon/carbon electrodes cell offering good rate capability with a reasonable gravimetric capacitance of 137 F g−1, energy density of 19 W h kg−1 and excellent cyclability. These results in neutral 1 M Na2SO4 electrolyte are quite interesting, encouraging and showed the applicability of pine cones derived carbons, demonstrating the exciting potential for a low-cost porous carbon which could attract interest from the industry for potential application in energy storage, absorbent and catalysis.Disclaimer
Any opinion, finding and conclusion or recommendation expressed in this material is that of the author(s) and the NRF does not accept any liability in this regard.Acknowledgements
This work is based on the research supported by the South African Research Chairs Initiative of the Department of Science and Technology and National Research Foundation of South Africa (Grant No. 97994). F. Barzegar and D. Y. Momodu acknowledge financial support from the University of Pretoria and the NRF for their PhD bursaries, while A. Bello and A. A. Khaleed acknowledges NRF through SARChI in Carbon Technology and Materials and University of Pretoria for Postdoctoral and PhD financial support. We also thank Prof. Yury Gogotsi's group at Drexel University XPS measurements.References
- P. T. Anastas and J. C. Warner, Green chemistry: theory and practice, Oxford university press, 2000 Search PubMed.
- H. Sun, L. Cao and L. Lu, Energy Environ. Sci., 2012, 5, 6206–6213 CAS.
- R. C. Saxena, D. K. Adhikari and H. B. Goyal, Renewable Sustainable Energy Rev., 2009, 13, 167–178 CrossRef.
- A. Faaij, Mitigation and Adaptation Strategies for Global Change, 2006, 11, 335–367 CrossRef.
- K. Sanderson, Nature, 2006, 444, 673–676 CrossRef CAS PubMed.
- S. E. Koonin, Science, 2006, 311, 435 CrossRef CAS PubMed.
- R. S. Dhillon and G. von Wuehlisch, Biomass Bioenergy, 2013, 48, 75–89 CrossRef.
- B. E. Conway, Electrochemical Supercapacitors: Scientific Fundamentals and Technological Applications, Springer, 1999 Search PubMed.
- P. Simon and Y. Gogotsi, Nat. Mater., 2008, 7, 845–854 CrossRef CAS PubMed.
- Y. Zhai, Y. Dou, D. Zhao, P. F. Fulvio, R. T. Mayes and S. Dai, Adv. Mater., 2011, 23, 4828–4850 CrossRef CAS PubMed.
- S. Dörfler, I. Felhösi, T. Marek, S. Thieme, H. Althues, L. Nyikos and S. Kaskel, J. Power Sources, 2013, 227, 218–228 CrossRef.
- E. Iyyamperumal, S. Wang and L. Dai, ACS Nano, 2012, 6, 5259–5265 CrossRef CAS PubMed.
- Y. Korenblit, M. Rose, E. Kockrick, L. Borchardt, A. Kvit, S. Kaskel and G. Yushin, ACS Nano, 2010, 4, 1337–1344 CrossRef CAS PubMed.
- V. Presser, M. Heon and Y. Gogotsi, Adv. Funct. Mater., 2011, 21, 810–833 CrossRef CAS.
- P. Simon and Y. Gogotsi, Acc. Chem. Res., 2012, 46, 1094–1103 CrossRef PubMed.
- Y. Gao, Y. S. Zhou, M. Qian, X. N. He, J. Redepenning, P. Goodman, H. M. Li, L. Jiang and Y. F. Lu, Carbon, 2013, 51, 52–58 CrossRef CAS.
- B. G. Choi, M. Yang, W. H. Hong, J. W. Choi and Y. S. Huh, ACS Nano, 2012, 6, 4020–4028 CrossRef CAS PubMed.
- L. L. Zhang, R. Zhou and X. S. Zhao, J. Mater. Chem., 2010, 20, 5983–5992 RSC.
- J. W. Long, D. Bélanger, T. Brousse, W. Sugimoto, M. B. Sassin and O. Crosnier, MRS Bull., 2011, 36, 513–522 CrossRef CAS.
- M. P. Bichat, E. Raymundo-Piñero and F. Béguin, Carbon, 2010, 48, 4351–4361 CrossRef CAS.
- M. Biswal, A. Banerjee, M. Deo and S. Ogale, Energy Environ. Sci., 2013, 6, 1249–1259 CAS.
- A. Shaikjee and N. J. Coville, Carbon, 2012, 50, 3376–3398 CrossRef CAS.
- H. Tang, P. Gao, X. Liu, H. Zhu and Z. Bao, J. Mater. Chem. A, 2014, 2, 15734–15739 CAS.
- E. Raymundo-Piñero, M. Cadek and F. Béguin, Adv. Funct. Mater., 2009, 19, 1032–1039 CrossRef.
- H. Wang, Z. Xu, A. Kohandehghan, Z. Li, K. Cui, X. Tan, T. J. Stephenson, C. K. King'ondu, C. M. B. Holt, B. C. Olsen, T. Jin Kwon, D. Harfield, A. Anthony, O. Anyia and M. David, ACS Nano, 2013, 7, 5131–5141 CrossRef CAS PubMed.
- L. Wei, M. Sevilla, A. B. Fuertes, R. Mokaya and G. Yushin, Adv. Energy Mater., 2011, 1, 356–361 CrossRef CAS.
- H. Sun, W. He, C. Zong and L. Lu, ACS Appl. Mater. Interfaces, 2013, 5, 2261–2268 CAS.
- J. Xu, Q. Gao, Y. Zhang, Y. Tan, W. Tian, L. Zhu and L. Jiang, Sci. Rep., 2014, 4, 5545 CAS.
- M. Lee, G.-P. Kim, H. D. Song, S. Park and J. Yi, Nanotechnology, 2014, 25, 345601 CrossRef PubMed.
- X. Li, W. Xing, S. Zhuo, J. Zhou, F. Li, S.-Z. Qiao and G.-Q. Lu, Bioresour. Technol., 2011, 102, 1118–1123 CrossRef CAS PubMed.
- E. Ito, S. Mozia, M. Okuda, T. Nakano, M. Toyoda and M. Inagaki, New Carbon Mater., 2007, 22, 321–326 CrossRef CAS.
- S. Kumagai, M. Sato and D. Tashima, Electrochim. Acta, 2013, 114, 617–626 CrossRef CAS.
- A. R. Mohamed, M. Mohammadi and G. N. Darzi, Renewable Sustainable Energy Rev., 2010, 14, 1591–1599 CrossRef CAS.
- D. Vamvuka, Int. J. Energy Res., 2011, 35, 835–862 CrossRef CAS.
- Y. Qu, Y. Tian, B. Zou, J. Zhang, Y. Zheng, L. Wang, Y. Li, C. Rong and Z. Wang, Bioresour. Technol., 2010, 101, 8402–8405 CrossRef CAS PubMed.
- W. Qian, F. Sun, Y. Xu, L. Qiu, C. Liu, S. Wang and F. Yan, Energy Environ. Sci., 2014, 7, 379–386 CAS.
- N. Ayrilmis, U. Buyuksari, E. Avci and E. Koc, For. Ecol. Manage., 2009, 259, 65–70 CrossRef.
- J. A. Micales, J. S. Han, J. L. Davis, and R. A. Young, in Mycotoxins, Wood Decay, Plant Stress, Biocorrosion, and General Biodeterioration, Springer, 1994, pp. 317–332 Search PubMed.
- M. Momčilović, M. Purenović, A. Bojić, A. Zarubica and M. Randjelović, Desalination, 2011, 276, 53–59 CrossRef.
- A. Özhan, Ö. Sahin, M. M. Küçük and C. Saka, Cellulose, 2014, 21, 2457–2467 CrossRef.
- G. V Nunell, M. E. Fernandez, P. R. Bonelli and A. L. Cukierman, J. Colloid Interface Sci., 2015, 440, 102–108 CrossRef PubMed.
- A. E. Ofomaja and E. B. Naidoo, Chem. Eng. J., 2011, 175, 260–270 CrossRef CAS.
- K. Karthikeyan, S. Amaresh, S. N. Lee, X. Sun, V. Aravindan, Y.-G. Lee and Y. S. Lee, ChemSusChem, 2014, 7, 1435–1442 CrossRef CAS PubMed.
- Y. Zhang, F. Zhang, G.-D. Li and J.-S. Chen, Mater. Lett., 2007, 61, 5209–5212 CrossRef CAS.
- J. Wang and S. Kaskel, J. Mater. Chem., 2012, 22, 23710–23725 RSC.
- P. L. Taberna, P. Simon and J.-F. Fauvarque, J. Electrochem. Soc., 2003, 150, A292–A300 CrossRef CAS.
- C. Liu, F. Li, L.-P. Ma and H.-M. Cheng, Adv. Mater., 2010, 22, E28–E62 CrossRef CAS PubMed.
- A. G. Pandolfo and A. F. Hollenkamp, J. Power Sources, 2006, 157, 11–27 CrossRef CAS.
- A. C. A. Ferrari, Solid State Commun., 2007, 143, 47–57 CrossRef CAS.
- K. Fic, G. Lota, M. Meller and E. Frackowiak, Energy Environ. Sci., 2012, 5, 5842–5850 CAS.
- L. Demarconnay, E. Raymundo-Pinero and F. Béguin, Electrochem. Commun., 2010, 12, 1275–1278 CrossRef CAS.
- C. Zhong, Y. Deng, W. Hu, J. Qiao, L. Zhang and J. Zhang, Chem. Soc. Rev., 2015, 44, 7484–7539 RSC.
- M. Zhi, F. Yang, F. Meng, M. Li, A. Manivannan and N. Wu, ACS Sustainable Chem. Eng., 2014, 2, 1592–1598 CrossRef CAS.
- S. Murali, J. R. Potts, S. Stoller, J. Park, M. D. Stoller, L. L. Zhang, Y. Zhu and R. S. Ruoff, Carbon, 2012, 50, 3482–3485 CrossRef CAS.
- M. Boota, M. P. Paranthaman, A. K. Naskar, Y. Li, K. Akato and Y. Gogotsi, ChemSusChem, 2015, 8, 3576–3581 CrossRef CAS PubMed.
- C. Peng, J. Lang, S. Xu and X. Wang, RSC Adv., 2014, 4, 54662–54667 RSC.
- R. Farma, M. Deraman, A. Awitdrus, I. A. Talib, E. Taer, N. H. Basri, J. G. Manjunatha, M. M. Ishak, B. N. M. Dollah and S. A. Hashmi, Bioresour. Technol., 2013, 132, 254–261 CrossRef CAS PubMed.
- V. Subramanian, C. Luo, A. M. Stephan, K. S. Nahm, S. Thomas and B. Wei, J. Phys. Chem. C, 2007, 111, 7527–7531 CAS.
- N. S. M. Nor, M. Deraman, R. Omar, R. Farma, N. H. Basri, B. N. M. Dolah, N. F. Mamat, B. Yatim, M. N. M. Daud and others, Energy, 2015, 79, 183–194 CrossRef.
- Y. Guo, J. Qi, Y. Jiang, S. Yang, Z. Wang and H. Xu, Mater. Chem. Phys., 2003, 80, 704–709 CrossRef CAS.
- T. E. Rufford, D. Hulicova-Jurcakova, K. Khosla, Z. Zhu and G. Q. Lu, J. Power Sources, 2010, 195, 912–918 CrossRef CAS.
- P. Ratajczak, K. Jurewicz and F. Béguin, J. Appl. Electrochem., 2014, 44, 475–480 CrossRef CAS.
- J. Luo, H. D. Jang and J. Huang, ACS Nano, 2013, 7, 1464–1471 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ra21708c |
| This journal is © The Royal Society of Chemistry 2016 |