Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Probing Raman enhancements for a colloidal metasurface with optical gap distances in the quantum regime†
Yuan
Zeng‡
ab,
Yu
Xie‡
a,
Andrea L.
Rodarte
a,
Tyler J.
Dill
a and
Andrea R.
Tao
 *ab
*ab
aAiiso Yufeng Li Family Department of Chemical and Nano Engineering, University of California, San Diego, 9500 Gilman Drive MC 0448, La Jolla, California 92093-0448, USA. E-mail: atao@ucsd.edu
bMaterials Science and Engineering, University of California, San Diego, 9500 Gilman Drive, La Jolla, California 92093, USA
First published on 5th September 2024
Abstract
While quantum plasmonic behaviors benefit many applications in quantum optics and nanophotonics, they can have detrimental effects in optical processes such as surface-enhanced Raman spectroscopy (SERS). Here, we measure the SERS intensity for a colloidal metasurface composed of Ag nanocubes coupled to an ultra-flat Au backplane to characterize the classical, crossover, and quantum regimes of the metasurface as a function of gap distance. Gap distance is controlled via chemical modification of the nanocube and backplane surface with self-assembled monolayers composed of alkanethiols with varying chain lengths. Electrodynamic simulations employing a quantum-corrected model are used to characterize the hybrid plasmon modes and charge transfer plasmon modes of the metasurface with respect to gap distance. These results indicate the importance of charge transfer effects in dictating SERS intensities for even relatively large optical gap distances due to the presence of molecular analytes.
Introduction
Surface plasmons are capable of confining electromagnetic fields to subwavelength scales, overcoming the classical optical diffraction limit and providing optical enhancements by orders of magnitude in the near-field.1,2 However, as optical volumes shrink beyond this to the deep subwavelength scale (<1 nm), a classical description of surface plasmons becomes insufficient and quantum behaviors — such as wave-particle duality and non-local tunneling effects — start to play an important role.3 This quantum mechanics description of surface plasmons and related light-matter interactions has opened up a new research field on quantum plasmonics, combining quantum optics with modern plasmonics research.4,5 When plasmonic nanostructures approach the quantum regime, new phenomena such as the electrical excitation of plasmons6–8 and optical rectification9 are observed to occur and provide new opportunities to integrate plasmonic nanostructures for electronics,10 design sub-nanometer scale photonics for biochemical sensing and molecular spectroscopy,11 and develop novel quantum plasmonics devices includes optical scanning tunneling microscopes, quantum optical antennas,8,12 tunneling diodes,13 and optical rectifiers.14While these quantum plasmonic behaviors benefit many applications in quantum optics and nanophotonics, they can have detrimental effects in optical processes such as surface-enhanced Raman spectroscopy (SERS). The focus of over decades of research has been on maximizing the optical near-field through the fabrication of metal nanojunctions that serve as electromagnetic hot-spots. In electromagnetic SERS, incident light is used to excite localized surface plasmon resonances (LSPRs) that provide a strong optical near-field15 where the local electric field within a nanojunction is enhanced by (E/E0)2 during excitation and emission processes, resulting in a total enhancement of nearly (E/E0)4.16–18 Generally, smaller nanojunctions (<10 nm) result in larger field enhancements. However, when considering quantum behavior, tunneling current through the nanojunction results in charge neutralization on opposite sides of the nanojunction and a significant decrease in local field enhancement.11 It has been observed that SERS enhancement can decrease by orders of magnitude when quantum tunneling is prevalent19 since SERS signal is proportional to the fourth power of the local electric field, even when additional dipole moments due to the presence of analytes are accounted for.20
Metal nanoparticle dimers are widely used to characterize this trade-off between the quantum and classical plasmonic regimes because they can be fabricated with controlled nanoscale gap distances using lithorgraphic,21 electron beam,22 or self-assembly methods.23 Three optical regimes are observed when plasmonic behavior is measured as a function of nanojunction size: a classical regime, a crossover regime, and a quantum regime.24 In the classical regime (gap distance >1 nm), plasmonic coupling between nanoparticles can be described by hybridized surface plasmons that include a bonding dipolar plasmon (BDP) mode and a higher energy bonding quadrupolar plasmon (BQP) mode.22 As interparticle spacing decreases, the BQP mode becomes dominant and both modes red-shift. In the crossover regime (gap distance = 0.5–1 nm), a small amount of charge transfer across the plasmonic nanojunction11 results in a lower degree of plasmon hybridization and smaller red-shift of the BDP mode. In the quantum regime (gap distance <0.5 nm), increased electron tunneling across the nanojunction induces a charge transfer plasmon (CTP) mode which blue-shifts with decreasing interparticle distance. Through-bond tunneling (as observed by electron energy loss spectroscopy) plays a dominant role in modulating the CTP mode for nanojunctions functionalized with insulating molecules.25 However, it remains unclear how this plasmonic behavior translates to measurable SERS intensities in applications such as chemical detection and sensing. This is because electron tunneling can affect the molecules that reside within the nanojunction, depending on the number of molecules present and the arrangement of molecules relative to the nanojunction axis.26,27 Furthermore, electron tunneling (charge transfer) can modulate the chemical enhancement effect in SERS and alter the SERS intensity.28
Here, we carry out finite-difference time-domain (FDTD) simulations and SERS experiments to determine whether a simple quantum-corrected model can be used to accurately predict the measured enhancements factors associated with a real-world SERS substrate. To do so, we employ a metasurface-enhanced Raman spectroscopy (mSERS) platform that is based on a colloidal metasurface composed of Ag nanocubes (AgNCs) which we previously demonstrated for the detection of halogenated water contaminants.20 Uniquely, this platform allows us to collect mSERS signals over hundreds of nanojunctions generated between the flat facets of an AgNC and an ultra-smooth Au film, all of which are aligned with their nanojunction axes in the out-of-plane direction. The AgNC surface within the nanojunction is chemically modified with alkanethiols, which are employed both as mSERS probe molecules and as spacer molecules that dictate the optical gap height. This provides a versatile method for tuning the gap height with sub-nanometer resolution; unlike previous investigations of AgNC metasurfaces where the smallest gap size observed was 2–3 nm,29 we are able to tune gap heights between 1–3 nm, allowing us to accurately observe the onset of electron tunneling. We carried out systematic studies to characterize the optical gap modes and corresponding mSERS intensities as a function of gap height and to observe the onset of the quantum regime for the AgNC nanojunctions that comprise metasurface.
Result and discussion
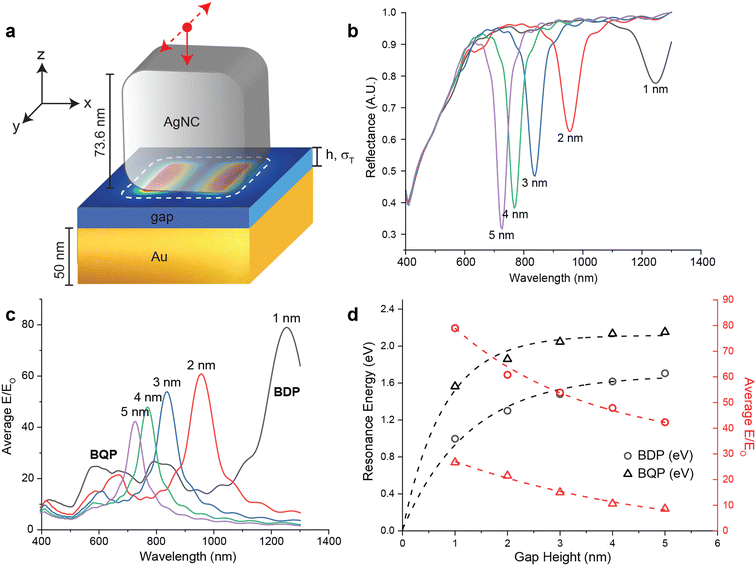
FDTD simulations were used to characterize the expected classical response (i.e. in the absence of tunneling) of the AgNC metasurfaces. Fig. 1a shows the FDTD model, where a 73.6 nm edge length (e) AgNC with a corner radius of curvature of 17 nm is placed over a 50 nm thick ( ) Au film with a gap height of h. The gap between the AgNC and the Au film is modeled as a dielectric with a refractive index of n = 1.4 and a conductivity of σT = 0. The condition of σT = 0 denotes a purely insulating gap medium, where electron tunneling probability is zero regardless of h, consistent with a classical response.11 The structure is illuminated from the top of the AgNC with a polarized plane wave source (red dot) where the electric field is polarized in y-direction (dashed arrows) and propagates in the negative z-direction (solid arrow). At the resonance frequency of the metasurface, strong plasmonic coupling between the AgNC and Au substrate generates an electromagnetic hot-spot inside the gap that results in strong far-field absorbance and a decreased optical reflectance.30Fig. 1b shows the simulated far-field reflectance spectra for metasurfaces with different gap heights between 1–5 nm, where the sharp dips between 650–1100 nm corresponds to the bonding dipolar plasmon (BDP) mode and the broad features between 400 nm and 650 nm corresponds to both the band-to-band transitions of Au and the bonding quadrupolar plasmon (BQP) mode associated with plasmonic coupling.31 As h decreases, the coupling strength across the nanojunction increases and results in a redshift of the BDP mode from 667 nm to 1089 nm, consistent with classical behavior. Fig. 1c shows the average near-field enhancement factor (EF) for metasurfaces with different gap heights, which is obtained by integrating |E/E0| over the entire nanojunction area as a function of irradiation wavelength. The peak maximum of this near-field enhancement factor increases and redshifts, correlating directly with BDP mode behavior as gap distance decreases. When h < 3 nm, enhancement behavior corresponding to the appearance of the BQP mode is consistent with strong plasmonic coupling as h further decreases.24Fig. 1d plots the h-dependence of the gap resonance energy and average EF. As h decreases, the BDP mode red-shifts from 1.86 eV to 1.14 eV and EF increases from 44-fold to 91-fold. The BQP mode also red-shifts from 2.2 eV to 1.66 eV and EF increases from 11-fold to 34-fold. As h decreases in the nanometer regime (h > 1 nm), the resonance energies of both the BDP mode and BQP mode decrease exponentially towards zero energy, consistent with what has been previously reported for quantum models of plasmonic coupling between two closely-spaced metallic rods where the gap behaves as a short circuit.11 Due to the flat surfaces that comprise the optical gap in our metasurface, this trend is not expected to continue into the sub-nanometer regime (h < 1 nm) due to the interference of multiple reflections across the gap; rather, we expect the resonance energy to experience a saturation in this red-shift as h approaches 0 nm.32,33
) Au film with a gap height of h. The gap between the AgNC and the Au film is modeled as a dielectric with a refractive index of n = 1.4 and a conductivity of σT = 0. The condition of σT = 0 denotes a purely insulating gap medium, where electron tunneling probability is zero regardless of h, consistent with a classical response.11 The structure is illuminated from the top of the AgNC with a polarized plane wave source (red dot) where the electric field is polarized in y-direction (dashed arrows) and propagates in the negative z-direction (solid arrow). At the resonance frequency of the metasurface, strong plasmonic coupling between the AgNC and Au substrate generates an electromagnetic hot-spot inside the gap that results in strong far-field absorbance and a decreased optical reflectance.30Fig. 1b shows the simulated far-field reflectance spectra for metasurfaces with different gap heights between 1–5 nm, where the sharp dips between 650–1100 nm corresponds to the bonding dipolar plasmon (BDP) mode and the broad features between 400 nm and 650 nm corresponds to both the band-to-band transitions of Au and the bonding quadrupolar plasmon (BQP) mode associated with plasmonic coupling.31 As h decreases, the coupling strength across the nanojunction increases and results in a redshift of the BDP mode from 667 nm to 1089 nm, consistent with classical behavior. Fig. 1c shows the average near-field enhancement factor (EF) for metasurfaces with different gap heights, which is obtained by integrating |E/E0| over the entire nanojunction area as a function of irradiation wavelength. The peak maximum of this near-field enhancement factor increases and redshifts, correlating directly with BDP mode behavior as gap distance decreases. When h < 3 nm, enhancement behavior corresponding to the appearance of the BQP mode is consistent with strong plasmonic coupling as h further decreases.24Fig. 1d plots the h-dependence of the gap resonance energy and average EF. As h decreases, the BDP mode red-shifts from 1.86 eV to 1.14 eV and EF increases from 44-fold to 91-fold. The BQP mode also red-shifts from 2.2 eV to 1.66 eV and EF increases from 11-fold to 34-fold. As h decreases in the nanometer regime (h > 1 nm), the resonance energies of both the BDP mode and BQP mode decrease exponentially towards zero energy, consistent with what has been previously reported for quantum models of plasmonic coupling between two closely-spaced metallic rods where the gap behaves as a short circuit.11 Due to the flat surfaces that comprise the optical gap in our metasurface, this trend is not expected to continue into the sub-nanometer regime (h < 1 nm) due to the interference of multiple reflections across the gap; rather, we expect the resonance energy to experience a saturation in this red-shift as h approaches 0 nm.32,33
When the optical gap associated with a nanojunction shrinks to sub-nanometer scales, quantum tunneling starts to play an important role in dictating near-field behavior. To model the presence of electron tunneling, time-dependent density functional theory (TDDFT)34,35 has been used to generate a quantum-mechanical model (QM) of the optical response of plasmonic materials at fully quantum ab initio resolutions. However, this fully QM model is limited to small plasmonic structures with a few thousands of conducting electrons24,36 and is not suitable for our larger plasmonic system containing millions to billions of electrons. To overcome this challenge, we applied the quantum corrected model (QCM) developed by Esteban and co-workers, which uses a fictitious conductive material to replace the purely insulating gap medium and mimic electron tunneling.11 This allows quantum optical properties to be simulated within a classical electrodynamic framework37 and has excellent agreement with fully QM calculations, indicating that QCM can be applied to larger plasmonic systems consist of multiple metallic nanostructures with arbitrary shapes and sizes.
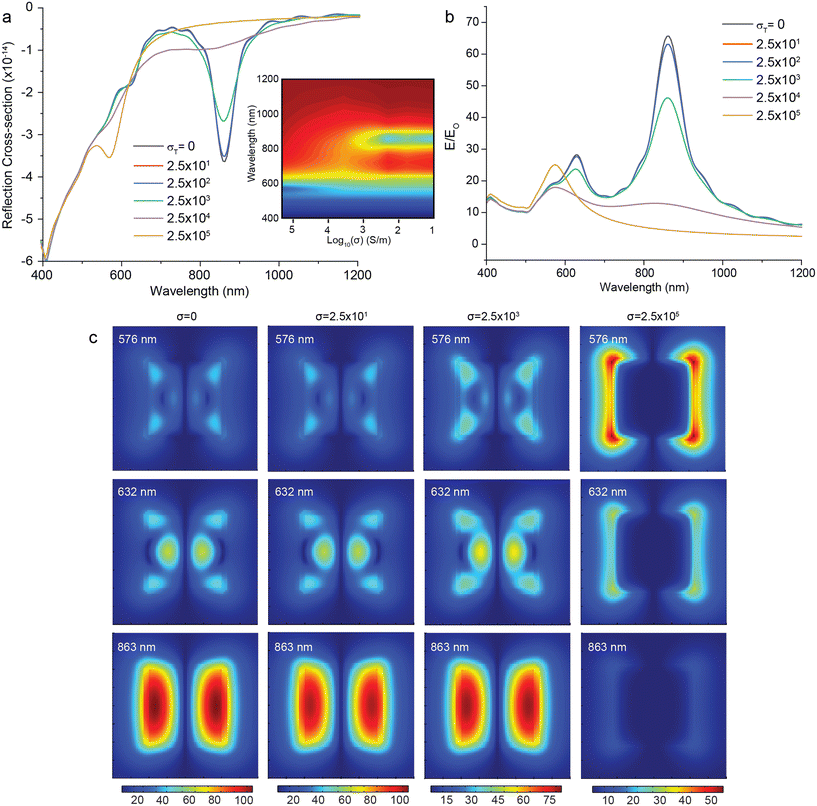
We first implemented the QCM in our FDTD simulations for a colloidal metasurface where the gap height is kept constant at h = 2 nm and the nanojunction gap is filled with a conductive medium with a non-zero σT, effectively allowing electrons to cross the gap in the model. Fig. 2a shows the simulated reflectance spectra of a metasurface as a function of increasing σT from 0 to 2.5 × 105 S m−1. The intensity dips at 632 nm (BQP) and 863 nm (BDP) gradually decrease to 0 as the increased tunneling current neutralizes the induced charges at the opposite side of the junction.31 When σT = 2.5 × 104 S m−1, an intensity dip appears at 576 nm and is assigned to a charge transfer plasmon (CTP) mode.11,22Fig. 2b shows the calculated average EF as a function of wavelength for metasurface with different gap medium conductivities. For increasing σT from 0 to 2.5 × 103 S m−1, the maximum EF associated with the BDP mode drops 30% and the EF associated with the BQP mode drops 14%. The excitation wavelength associated with these EF maxima stays constant over all values of σT. Fig. 2c shows the near-field distribution λ = 576 nm (CTP mode), λ = 632 nm (BQP mode) and λ = 863 nm (BDP mode) for increasing σT. These distribution maps indicate that the plasmonic hot-spot starts to move from the center of the optical gap to the edges of the AgNC and that the hot-spot disappears when conductivity approaches σT = 2.5 × 105 S m−1.
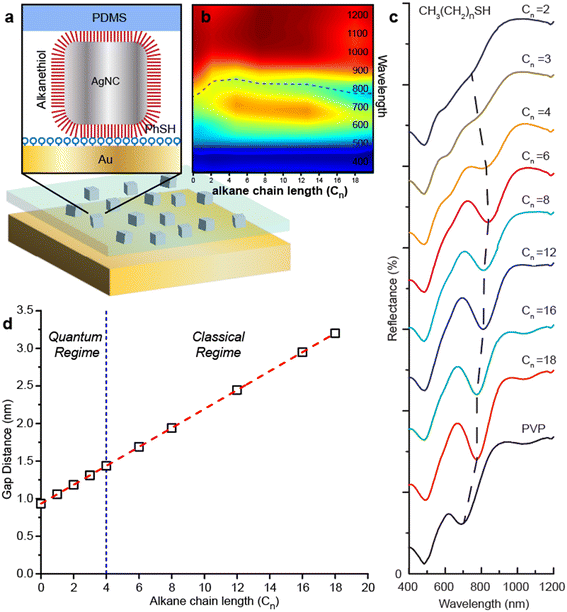
To experimentally validate these QCM simulations with mSERS measurements, we carried out experiments using a modified fabrication of the AgNC metasurface previously described by Rozin et al.30,38 A schematic of this metasurface fabrication process is shown in the ESI† S1. The top and bottom portions of the metasurface are fabricated separately. The top portion of the metasurface is comprised of AgNCs embedded into an elastomeric (PDMS) substrate. First, colloidal AgNCs with an edge length of 74 nm were synthesized using methods previously reported methods (see methods), then deposited onto a PDMS-coated support by Langmuir–Blodgett film transfer. PDMS was chosen for the metasurface because it is optically transparent and provides an easily identifiable Raman signature that does not overwhelm the mSERS intensities stemming from the analyte molecules. The AgNCs are then chemically functionalized by incubating the PDMS-AgNC substrate in 1 mM ethanol solution of an end-terminated alkanethiol (CH3(CH2)nSH) of different C-backbone lengths, Cn. The bottom portion of the metasurface is comprised of the Raman analyte (RA) layer adsorbed on a smooth 75 nm Au film (RMS roughness of 2.96 nm and average roughness of 2.27 nm). Alkanethiols are employed as the RA since they readily form an ordered molecular monolayer on Au with known and consistent heights. The PDMS-AgNC layer is then removed from its solid support and stamped into contact with the RA layer to generate the metasurface. Fig. S1b† shows a schematic of this structure, where the analyte is sandwiched inside the nanojunction gap. By changing Cn, we maintain precise control over the separation distance of the AgNC to the RA layer. The total gap height, h is dictated by both the thickness of the RA layer and Cn.
Fig. S1c† shows UV/vis reflectance spectra for an AgNC metasurface functionalized with 1-dodecanethiol (DDT, Cn = 12) and deuterated 1-hexadecanethiol (dHDT) as the RA. We calculated the gap size to be 3.27 nm (see methods) based the measured heights of DDT layers39 and taking into account interdigitation of DDT and dHDT chains.40 The BDP mode is observed as a dip in the reflectance spectrum at λ = 756 nm, consistent with other reports.29,30,41 For comparison, we include the simulated reflectance obtained from our classical model with h = 3 nm. It should be noted that this spectrum differs from the plot in Fig. 1b since it has been normalized to reproduce the AgNC surface density of the experimental metasurface shown in the inset in Fig. S1c.† There is excellent agreement between the simulated and experimental data, indicating that for h = 3.27 nm, the metasurface is well within the classical regime and no charge transfer is expected. The larger full-width half-maximum (FWHM) of the experimental data can be ascribed to the polydispersity of the AgNCs, which exhibit a size distribution of 73.6 ± 3.7 nm and corner sharpness of 17 ± 2.2 nm as observed by image analysis of scanning electron microscope (SEM) images.
We then fabricated colloidal metasurfaces functionalized with different alkanethiol lengths with Cn = 2–18. Thiophenol (PhSH) was chosen as the RA because it has a large Raman cross-section and relatively small molecule size (Fig. 3a and S2†). Fig. 3d shows the calculated h for metasurfaces fabricated with different Cn and Fig. 3b and c shows the UV/vis spectra of these metasurfaces. The gap distance is determined by sum of monolayer alkanethiol thickness and monolayer PhSH monolayer thickness (see method). Because short alkanethiols are not closely packed like long alkanethiols on the surface and there is likely an intermolecular interaction between alkanethiol and PhSH, the gap height (h) for short alkanethiols might be slightly overestimated. For decreasing Cn from 18 to 6, the dip at 780 nm redshifts to 820 nm due to decreasing h and stronger BDP mode coupling. This observation is consistent with the simulation results from our classical model in Fig. 1b. As Cn decreases from 6 to 4, the dip wavelength stays constant at 820 nm, consistent with the crossover regime where electrons begin to tunnel between the AgNCs and the Au substrate.24 In this case, the redshift induced by a decreasing h is compensated by a blueshift induced by charge transfer. As Cn decreases from 4 to 2, the BDP mode starts to blue-shift from 820 nm to 770 nm and indicates that the metasurface is in quantum regime quantum tunneling model.42–44 At Cn = 4 and h = 1.44 nm, a dip at 610 nm appears and become more prominent as Cn decreases from Cn = 6 to Cn = 3, consistent with the CTP mode in our QCM simulations and indicating this nanojunction height as a threshold h for the appearance of quantum effects. Compared to previous studies of Au nanoparticle dimers separated by an alkanedithiol monolayer where the two surfaces are chemically linked together, our threshold h is about 0.4 nm larger. The main cause of increased threshold h is 0.6 nm PhSH monolayer in the gap is more conductive due to π–π stacking. The effective tunneling barrier thickness is 0.71 nm for Cn = 3 and 0.84 nm for Cn = 4.23
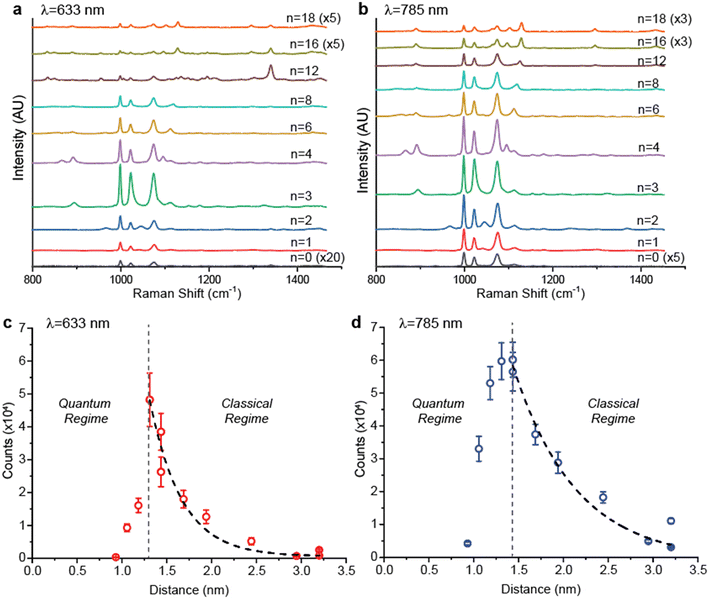
Fig. 4 shows how quantum tunneling effects quantitatively affect mSERS performance. According to the QCM results, we should expect to observe a significant decrease in mSERS intensity when the optical gap height of the nanojunction approaches the quantum regime; however, chemical enhancement generated by the tunneling current can also play a role in generating mSERS signal.36Fig. 4a and b shows mSERS spectra using λ = 633 nm and 785 nm laser excitation, respectively. Measurements were carried out laser powers <1% to ensure that mSERS intensities are collected in the linear response regime of the metasurfaces (i.e. no saturation effects). The PhSH shows a strong βCCC(a1) vibrational mode at 999 cm−1, a βCH(a1) vibrational mode at 1023 cm−1, and a βCCC(a1) vibrational mode at 1076 cm−1. For decreasing Cn from 18 to 3, we observe an increase in Raman intensity counts due to decreasing h, consistent with classical behavior. For decreasing Cn from 3 to 0 (with 0 corresponding to H2S), there is a significant decrease in Raman intensity correlating with the quantum regime, as predicted. Fig. 4c and d plot the Raman intensity (999 cm−1) for λ = 633 and λ = 785 nm, respectively, as a function of h (Table S1†). In both plots, when h corresponds with the classical regime, Raman intensity exponentially increases with decreasing h and is consistent with our classical FDTD predictions. For h < 1.31 nm, the Raman intensity experiences a sharp linear fall-off with decreasing h, consistent with our QCM prediction. Notably, in Fig. 4d we observe the appearance of the crossover regime when h = 1.31–1.44 nm, where Raman intensity remains nearly constant indicating that finite electron density is present inside the nanojunction.24 The larger crossover h observed for λ = 785 nm is consistent with previous observations of wavelength-dependent electron tunneling.42 Because 785 nm excitation is close to resonance wavelength of this metasurface, the larger crossover h is likely due to either hot carrier induced resonant charge transport or hot carrier induced molecular conductance change.45 We also note that h is relatively large compared to other reports studying nanojunctions composed of clean Ag surfaces, where quantum tunneling effects only become significant below two atomic lattice spacings22 (∼0.8 nm for Ag); the critical tunneling distance in our metasurface is approximately 0.5 nm larger at ∼1.3 nm. This increase is attributed to the presence of both aromatic PhSH molecules (which provide a conductive link through π–π stacking44,46) and alkanethiol monolayers (which provide a large electronic energy barrier and form an insulating dielectric layer47) inside the nanojunction. Our results are comparable to other nanojunctions functionalized with dithiols as “molecular shunts” that traverse across nanojunctions48 and demonstrate the presence of significant tunneling effects even in the absence of such molecular linkers.
Conclusion
Overall, we are able to experimentally validate FDTD results using a QCM that predict a decrease in electromagnetic field enhancement as nanojunction gap heights are decreased below the threshold for electron tunneling. Our results indicate that such models are able to accurately predict changes in SERS intensities for a colloidal metasurface composed of AgNCs sandwiched against an Au backplane, where the molecular analyte is located in the center of the resulting nanojunction. When gap height is decreased below 1.3 nm — even in the absence of a molecular linker that crosses the nanojunction — the charge transfer mechanism plays a dominant role in dictating SERS signal. These results demonstrate that molecular monolayers such as the alkanethiols used in these experiments serve as insufficient passivation layers to prevent charge transfer across these plasmonic nanojunctions. Because the capacitance of a parallel plate capacitor is proportional to the relative dielectric constant of material inside the gap, alternative nanojunction passivation methods, such as ultrathin coating using high-k materials49 such as HfO2, ZrO2 and TiO2, may provide alternative methods for controlling charge transfer and increasing SERS enhancement.Methods
Gold substrate fabrication
Au substrates are fabricated through sputtering (using Denton Discovery 18 sputter system). 500 um thick, 4 inches size silicon substrates were washed with ethanol, piranha solution, DI water and dried with nitrogen stream. The sputtering RF bias is used to clean the substrate for 40 seconds, and follows with Cr (400 W, 10 second) and Au film (300 W, 115 second) sputtering with the Ar gas pressure as 2.4 mTorr. Then diced into 1 cm by 1 cm pieces for later use.Ag nanocube (AgNCs) synthesis
Ag nanocubes were synthesized using a modified polyol reaction as previously described.50 Briefly, AgNO3was reduced in 1,5-pentanediol heated to ∼200 °C. CuCl2 and PVP (55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 MW) were added to control the nucleation and growth process, as well as to passivate the nanocube surfaces after growth. In order to decrease polydispersity and remove non-cubic particles, nanocubes were vacuum filtered. Millipore Durapore membranes were used in three different sizes to remove sequentially smaller nanoparticles: 650 nm, 450 nm, and 220 nm.
000 MW) were added to control the nucleation and growth process, as well as to passivate the nanocube surfaces after growth. In order to decrease polydispersity and remove non-cubic particles, nanocubes were vacuum filtered. Millipore Durapore membranes were used in three different sizes to remove sequentially smaller nanoparticles: 650 nm, 450 nm, and 220 nm.
Metasurface fabrication
Ag nanoparticles are repeatedly washed by centrifugation in ethanol and finally redispersed in chloroform. The nanoparticle solution is then carefully drop-cast onto a DI water sub-phase and allowed to equilibrate. Thin (150 μm) PDMS adhered to a silicon backing was then mechanically dipped through the film to transfer it to the substrate. Alkanethiols were used to displace the PVP and form controlled SAMs on the nanoparticle surfaces. Nanoparticle coated PDMS surfaces were submerged in a 1 mM ethanolic solution of the desired alkanethiol for 1 hour. They were then rinsed copiously with ethanol, dried in N2, and adhered immediately to an Au thin-film substrate. The Au thin-film was then either treated with a 1 mM ethanolic solution of a desired thiolated molecule prior to adhesion to the Ag nanoparticle PDMS surface, or immediately adhered to form the metasurface.Gap height determination
We used theoretical calculation to determine the gap distance. For bare Au substrates, we have used previously reported alkanethiol SAMs on Ag thickness measurements.39 For PhSH, we have assumed a linear addition of the thickness PhSH SAM on Au and the alkanethiol SAMs on Ag.51 For the gap distance of dHDT Au substrates, interdigitation was assumed to calculate gap thickness. It has been shown that opposing alkanethiol monolayers on nanoparticles will interdigitate on assembly.40 The distance calculation was followed the equation:| D = 0.458 + 0.126 × n + D (PhSH) |
UV-vis and SERS measurements
A Perkin-Elmer Lambda 1050 was used for all reflectance measurements. Data was collected with an 8° angle of incidence. Raman measurements were collected on a Renishaw inVia Raman microscope, either with a 633 nm HeNe laser or a 785 nm diode laser. All measurements were collected with <1 mW with a 0.9 NA 50× objective. 100 measurements were collected at random for each substrate.FDTD simulation
FDTD simulations were carried out with Lumerical FDTD Solutions. AgNCs (Palik dielectric data) were modeled in 3 dimensions with a flat gold film as a substrate. A spacer of various thickness was added with index of refraction (n) = 1.4 to reflect the organic SAM spacers. Incident light was normal to the substrate with s-polarized light. A 1 nm global mesh was used with a 0.5 nm local mesh at the junction added to improve accuracy. The model was solved from 300–1500 nm. The electric field enhancements were calculated in the plane of the Ag film, in the center of the gap.Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to thank Nano3 and the San Diego Nanotechnology Infrastructure (NSF Award ECCS-2025752), the UC San Diego MRSEC (NSF Award DMR-2011924), and the NanoEngineering MRC for use of their equipment and facilities. This work was supported by NSF Awards CHE-1807891 and DMR-2011924.References
- P. Mühlschlegel, H. J. Eisler, O. J. F. Martin, B. Hecht and D. W. Pohl, Applied physics: Resonant optical antennas, Science, 2005, 308, 1607–1609 Search PubMed.
- S. A. Maier, et al., Local detection of electromagnetic energy transport below the diffraction limit in metal nanoparticle plasmon waveguides, Nat. Mater., 2003, 2, 229–232 Search PubMed.
- D. Xu, et al., Quantum plasmonics: new opportunity in fundamental and applied photonics, Adv. Opt. Photonics, 2018, 10, 703 Search PubMed.
- J. M. Fitzgerald, P. Narang, R. V. Craster, S. A. Maier and V. Giannini, Quantum Plasmonics, Proc. IEEE, 2016, 104, 2307–2322 Search PubMed.
- M. S. Tame, et al., Quantum plasmonics, Nat. Phys., 2013, 9, 329–340 Search PubMed.
- J. Lambe and S. L. McCarthy, Light emission from inelastic electron tunneling, Phys. Rev. Lett., 1976, 37, 923–925 Search PubMed.
- P. Bharadwaj, A. Bouhelier and L. Novotny, Electrical excitation of surface plasmons, Phys. Rev. Lett., 2011, 106, 226802 Search PubMed.
- H. Qian, et al., Efficient light generation from enhanced inelastic electron tunnelling, Nat. Photonics, 2018, 12, 485–488 Search PubMed.
- D. R. Ward, F. HÜser, F. Pauly, J. C. Cuevas and D. Natelson, Optical rectification and field enhancement in a plasmonic nanogap, Nat. Nanotechnol., 2010, 5, 732–736 Search PubMed.
- E. Ozbay, Plasmonics: Merging photonics and electronics at nanoscale dimensions, Science, 2006, 311, 189–193 Search PubMed.
- R. Esteban, A. G. Borisov, P. Nordlander and J. Aizpurua, Bridging quantum and classical plasmonics with a quantum-corrected model, Nat. Commun., 2012, 3, 1–9 Search PubMed.
- J. Merlein, et al., Nanomechanical control of an optical antenna, Nat. Photonics, 2008, 2, 230–233 Search PubMed.
- R. C. Bowen, G. Klimeck, R. K. Lake, W. R. Frensley and T. Moise, Quantitative simulation of a resonant tunneling diode, J. Appl. Phys., 1997, 81, 3207–3213 Search PubMed.
- D. R. Ward, F. HÜser, F. Pauly, J. C. Cuevas and D. Natelson, Optical rectification and field enhancement in a plasmonic nanogap, Nat. Nanotechnol., 2010, 5, 732–736 Search PubMed.
- G. C. Schatz, M. A. Young and R. P. Duyne, Electromagnetic Mechanism of SERS, in Surface-Enhanced Raman Scattering, Springer, Berlin Heidelberg, 2006, pp. 19–45, DOI:10.1007/3-540-33567-6_2.
- M. Moskovits, Surface-enhanced Raman spectroscopy: a brief perspective, in Surface-enhanced Raman scattering: physics and applications, Springer Berlin Heidelberg, 2006, pp. 1–17 Search PubMed.
- B. Sharma, R. R. Frontiera, A. I. Henry, E. Ringe and R. P. Van Duyne, SERS: Materials, applications, and the future, Mater. Today, 2012, 15, 16–25 Search PubMed.
- P. L. Stiles, J. A. Dieringer, N. C. Shah and R. P. Van Duyne, Surface-Enhanced Raman Spectroscopy, Annu. Rev. Anal. Chem., 2008, 1, 601–626 Search PubMed.
- W. Zhu and K. B. Crozier, Quantum mechanical limit to plasmonic enhancement as observed by surface-enhanced Raman scattering, Nat. Commun., 2014, 51(5), 1–8 Search PubMed.
- Y. Zeng, et al., Metasurface-Enhanced Raman Spectroscopy (mSERS) for Oriented Molecular Sensing, ACS Appl. Mater. Interfaces, 2022, 14, 32598–32607 Search PubMed.
- H. Duan, A. I. Fernández-Domínguez, M. Bosman, S. A. Maier and J. K. W. Yang, Nanoplasmonics: Classical down to the nanometer scale, Nano Lett., 2012, 12, 1683–1689 Search PubMed.
- J. A. Scholl, A. García-Etxarri, A. L. Koh and J. A. Dionne, Observation of quantum tunneling between two plasmonic nanoparticles, Nano Lett., 2013, 13, 564–569 Search PubMed.
- H. Cha, J. H. Yoon and S. Yoon, Probing quantum plasmon coupling using gold nanoparticle dimers with tunable interparticle distances down to the subnanometer range, ACS Nano, 2014, 8, 8554–8563 Search PubMed.
- J. Zuloaga, E. Prodan and P. Nordlander, Quantum Description of the Plasmon Resonances of a Nanoparticle Dimer, Nano Lett., 2009, 9, 887–891 Search PubMed.
- S. F. Tan, et al., Quantum plasmon resonances controlled by molecular tunnel junctions, Science, 2014, 343, 1496–1499 Search PubMed.
- W. Chen, et al., Probing the limits of plasmonic enhancement using a two-dimensional atomic crystal probe, Light: Sci. Appl., 2018, 71(7), 1–11 Search PubMed.
- L. Mao, Z. Li, B. Wu and H. Xu, Effects of quantum tunneling in metal nanogap on surface-enhanced Raman scattering, Appl. Phys. Lett., 2009, 94, 243102 Search PubMed.
- S. Cong, X. Liu, Y. Jiang, W. Zhang and Z. Zhao, Surface Enhanced Raman Scattering Revealed by Interfacial Charge-Transfer Transitions, Innovation, 2020, 1(3), 100051 Search PubMed.
- J. B. Lassiter, et al., Plasmonic waveguide modes of film-coupled metallic nanocubes, Nano Lett., 2013, 13, 5866–5872 Search PubMed.
- M. J. Rozin, D. A. Rosen, T. J. Dill and A. R. Tao, Colloidal metasurfaces displaying near-ideal and tunable light absorbance in the infrared, Nat. Commun., 2015, 6, 1–7 Search PubMed.
- D. C. Marinica, A. K. Kazansky, P. Nordlander, J. Aizpurua and A. G. Borisov, Quantum plasmonics: Nonlinear effects in the field enhancement of a plasmonic nanoparticle dimer, Nano Lett., 2012, 12, 1333–1339 Search PubMed.
- R. S. J. D. Oldenburg, et al., Engineering the optical response of plasmonic nanoantennas, Opt. Express, 2008, 16(12), 9144–9154 Search PubMed.
- R. Esteban, et al., The morphology of narrow gaps modifies the plasmonic response, ACS Photonics, 2015, 2, 295–305 Search PubMed.
- M. A. L. Marques and E. K. U. Gross, TIME-DEPENDENT DENSITY FUNCTIONAL THEORY, Annu. Rev. Phys. Chem., 2004, 55, 427–455 Search PubMed.
- R. E. Stratmann, G. E. Scuseria and M. J. Frisch, An efficient implementation of time-dependent density-functional theory for the calculation of excitation energies of large molecules, J. Chem. Phys., 1998, 109, 8218–8224 Search PubMed.
- L. Mao, Z. Li, B. Wu and H. Xu, Effects of quantum tunneling in metal nanogap on surface-enhanced Raman scattering, Appl. Phys. Lett., 2009, 94, 243102 Search PubMed.
- F. J. García de Abajo and A. Howie, Retarded field calculation of electron energy loss in inhomogeneous dielectrics, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 1154181–11541817 Search PubMed.
- T. J. Dill, M. J. Rozin, E. R. Brown, S. Palani and A. R. Tao, Investigating the effect of Ag nanocube polydispersity on gap-mode SERS enhancement factors, Analyst, 2016, 141, 3916–3924 Search PubMed.
- M. M. Walczak, C. Chung, S. M. Stole, C. A. Widrig and M. D. Porter, Structure and Interfacial Properties of Spontaneously Adsorbed n-Alkanethiolate Monolayers on Evaporated Silver Surfaces, J. Am. Chem. Soc., 1991, 113, 2370 Search PubMed.
- Z. L. Wang, S. A. Harfenist, R. L. Whetten, J. Bentley and N. D. Evans, Bundling and interdigitation of adsorbed thiolate groups in self-assembled nanocrystal superlattices, J. Phys. Chem. B, 1998, 102, 3068–3072 Search PubMed.
- A. Moreau, et al., Controlled-reflectance surfaces with film-coupled colloidal nanoantennas, Nature, 2012, 492, 86–89 Search PubMed.
- K. J. Savage, et al., Revealing the quantum regime in tunnelling plasmonics, Nature, 2012, 491, 574–577 Search PubMed.
- R. Esteban, A. G. Borisov, P. Nordlander and J. Aizpurua, Bridging quantum and classical plasmonics with a quantum-corrected model, Nat. Commun., 2012, 3, 825 Search PubMed.
- F. Benz, et al., Nanooptics of molecular-shunted plasmonic nanojunctions, Nano Lett., 2015, 15, 669–674 Search PubMed.
- L. Lin, et al., Electron Transport Across Plasmonic Molecular Nanogaps Interrogated with Surface-Enhanced Raman Scattering, ACS Nano, 2018, 12, 6492–6503 Search PubMed.
- S. Pradhan, D. Ghosh, L. P. Xu and S. Chen, Interparticle charge transfer mediated by π-π stacking of aromatic moieties, J. Am. Chem. Soc., 2007, 129, 10622–10623 Search PubMed.
- E. T. Vickers, et al., Improving Charge Carrier Delocalization in Perovskite Quantum Dots by Surface Passivation with Conductive Aromatic Ligands, ACS Energy Lett., 2018, 3, 2931–2939 Search PubMed.
- M. Celebrano, et al., Mode matching in multiresonant plasmonic nanoantennas for enhanced second harmonic generation, Nat. Nanotechnol., 2015, 10, 412–417 Search PubMed.
- N. P. Maity, R. Maity, R. K. Thapa and S. Baishya, A tunneling current density model for ultra thin HfO2 high-k dielectric material based MOS devices, Superlattices Microstruct., 2016, 95, 24–32 Search PubMed.
- Y. Sun and Y. Xia, Shape-controlled synthesis of gold and silver nanoparticles, Science, 2002, 298, 2176–2179 Search PubMed.
- S. Frey, et al., Structure of thioaromatic self-assembled monolayers on gold and silver, Langmuir, 2001, 17, 2408–2415 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Schematic of metasurface fabrication and corresponding spectra; Table of Raman intensities used to plot Fig. 4c and d. See DOI: https://doi.org/10.1039/d4lf00127c |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2024 |