The mechanism of transmethylation in anisole decomposition over Brønsted acid sites: density functional theory (DFT) study†
Jiajun
Zhang
 ab,
Beatriz
Fidalgo
b,
Athanasios
Kolios
b,
Dekui
Shen
ab,
Beatriz
Fidalgo
b,
Athanasios
Kolios
b,
Dekui
Shen
 *a and
Sai
Gu
c
*a and
Sai
Gu
c
aKey Laboratory of Energy Thermal Conversion and Control of Ministry of Education, Southeast University, Nanjing, China. E-mail: 101011398@seu.edu.cn
bSchool of Water, Energy and Environment, Cranfield University, Cranfield, UK
cFaculty of Engineering and Physical Sciences, University of Surrey, Surrey, UK
First published on 15th August 2017
Abstract
In this work, the mechanism and intrinsic reaction energy barriers of transmethylation, as the initial stage of catalytic and non-catalytic anisole decomposition, were investigated by Density Functional Theory (DFT). Molecular analyses indicated that methyl free radical transfer occurred in the absence of a catalyst, and the catalytic transmethylation over Brønsted acid sites was considered based on a dual electrophilic attack mechanism with protonation and carbocation substitution. Reaction modelling for the formation of methyl-containing compounds in both non-catalytic and catalytic anisole decomposition indicated that the energy barriers were significantly decreased in the presence of a catalyst by 60 kcal mol−1 at the most in the case of o-cresol. The results also revealed that the intrinsic transmethylation orientation preferred the ortho- and para-positions on the acceptor compounds containing oxygen-rich substituents due to their large electronegativity, and the lowest energy barrier was observed in the case of transmethylation towards the para-position of the cresol molecule (54.1 kcal mol−1).
1 Introduction
Lignin is an abundant aromatic-rich bio-resource; approximately 63 million tones are extracted annually mainly from the pulp and paper industry.1,2 The fast pyrolysis of lignin has been investigated since the late 1970s, and is accepted as a feasible and viable route to convert lignin into value added fuel additives.3–5 However, the primary bio-oil produced from fast pyrolysis cannot be directly used in fuel applications. This is because of its inadequate properties, such as acidity, low calorific value, and low stability, which are a consequence of its high oxygen content in composition. The effective removal of the oxygen by catalytic upgrading is therefore crucial for making the bio-oil compatible with the existing fossil fuel infrastructure and for widening its use.6,7 Catalytic cracking of bio-oil is one of the conversion routes usually suggested for deoxygenation, and zeolites with dispersed Brønsted acid sites, such as HZSM-5, have been proven as suitable catalysts for this process.8–11The methoxy group is an oxygen containing functional group which abundantly exists in components present in the bio-oil obtained from the fast pyrolysis of lignin, such as anisole, guaiacol, syringol and their derivatives.12 Understanding the reactivity of the methoxy group is required to properly assess the complete catalytic upgrading process of these lignin-derived aromatic compounds. Anisole is often used as a model compound to investigate the reactivity of lignin-derived compounds containing the methoxy functional group, because this is the only functional group present in the molecule.13 The transmethylation reaction has been observed to be the primary reaction taking place in anisole decomposition, leading to the prominent production of phenolic compounds.14–18
Catalytic transmethylation over acid sites has been reported for phenol alkylation in the presence of methanol.19–23 A few authors have described transmethylation in the decomposition of anisole over acid sites consisting of isomerization, dealkylation, and intermolecular methyl transfer.24,25 However, the available literature mainly focused on the general study of pathways and kinetic parameters for transmethylation reactions, with little detail on catalytic mechanisms despite their importance to understand the entire catalytic process.26 Although it is widely accepted that Brønsted acid sites play a dominant role in anisole decomposition,14,19,24 the precise mechanism of transmethylation over the acid sites is still controversial. Different, and sometimes hardly consistent, reaction pathways and mechanisms have been proposed for explaining the same chemical process in previous studies.19–23 This might be attributed to the fact that the transition state is key to understanding the chemical reaction mechanism, but it is extremely unstable and hard to capture by means of experimental studies.27 Wang et al.16 have proposed hydrolysis as the first stage of the anisole conversion, with little interaction of the acid sites, followed by the alkylation of phenol with methanol. Thilakaratne et al.28 proposed a transmethylation mechanism based on the formation of a methenium ion during anisole decomposition on Brønsted acid sites. There have been other studies suggesting the formation of a methyl carbocation directly by the methyl group in the anisole molecule;14,24,25,28,29 nevertheless, these studies have seldom addressed how the carbocation is formed and to what extent it affects the transmethylation reaction. In most previous studies, further evidence to prove the proposed mechanism regarding transmethylation or to evaluate the reactions based on the mechanism was not provided.
Despite experimental results being highly valuable to understand the overall reaction and product distribution at the macroscopic level, they present limitations in unravelling the reaction mechanism at the molecular level. Density Functional Theory (DFT) modelling is based on the calculation of electron interactions and has been widely used as a systematic and convincing approach to explaining molecular properties and mechanisms for many reactions.30–34 Compared to experimental approaches, DFT calculation can provide intrinsic information on reactions regarding the detailed interaction between molecules and acid sites, independently of the very short life span of the transition states, radicals and ions existing in the reactions. The microscale modelling of catalysis by DFT can also disregard complex impacts of macroscale factors (e.g., framework effects) and allows focusing on the reaction regarding its intrinsic properties. However, DFT calculation for transmethylation and related reactions has rarely been reported in the literature.
The aim of this work is to investigate by means of DFT modelling the mechanism of transmethylation as a primary reaction of the non-catalytic and catalytic decomposition of anisole and to identify the effects of Brønsted acid sites on transmethylation. Compounds such as phenol, benzene, toluene, anisole, cresol, xylenol and tri-methyl phenol were investigated. The transfer orientation preference of the electrophilic substituents on relevant molecules was also studied. In addition, various possible reaction pathways of the transmethylation reaction were evaluated to address energy barriers during the formation of major product compounds.
2 Computational method
The first-principles density functional theory plus dispersion (DFT-D) calculations were implemented in the DMol3 module available in Materials Studio 2016 from BIOVIA.35,36 A double numerical plus polarization (DNP) basis set was used to calculate the valence orbital of all the atoms, including a polarization p-function on all hydrogen atoms. The numerical basis sets in DMol3 minimize or even eliminate basis set superposition error (BSSE), in contrast to Gaussian basis sets, in which BSSE can be a serious problem.37,38 Calculations used the generalized gradient corrected approximation (GGA)39 treated by the Perdew–Burke–Ernzerhof (PBE) exchange–correlation potential with long-range dispersion correction via Grimme's scheme.40 The self-consistent field (SCF) procedure was used with a convergence threshold of 10−6 au on the energy and electron density. Geometry optimizations were performed with a convergence threshold of 0.002 Ha Å−1 on the gradient, 0.005 Å on displacements, and 10−5 Ha on the energy. The real-space global cut-off radius was set to 5 Å. In this study, no symmetry constraints were used for any cluster models. The transition state was completely determined by the LST/QST method, and confirmed by the unique imaginary frequency as shown in Table S1 in the ESI† and intrinsic reaction coordinate (IRC) calculation. Mulliken charges were assigned to each bond to address the bond order, and Hirshfeld charges were assigned to each atom for the function selected as the Fukui field.41 Radical Fukui analysis was applied to the phenol molecule to establish its reactivity to free radical attack in non-catalytic reactions. Electrophilic Fukui analysis was applied to anisole and phenol molecules to determine their reactivity to carbocation attack in catalytic reactions. The same computational conditions were applied for both catalytic and non-catalytic modellings; in the case of catalytic reaction modelling, mainly Brønsted acid was considered. The initial configuration of the ZSM-5 catalysts was obtained from the siliceous ZSM-5 crystal, and an 8T model was used to simulate the performance of a Brønsted acid site.31,32 The energy barrier for the transmethylation reaction was determined from the difference between the transition state and reactant energies. The relative energy of the transition state and product was defined as the energy difference with the reactant, respectively. All the energies were calculated at 0 K to investigate the intrinsic reactions of transmethylation.3 Results and discussion
3.1 Mechanism of transmethylation in anisole decomposition
The weakest bond in the anisole molecule was observed for Csp3–O (as shown in Fig. S2(a),† bond ID C8–O7), indicating that both the non-catalytic and the catalytic thermal decomposition of anisole are preferably initiated at this site.29In the case of the non-catalytic decomposition of anisole, the molecule is subsequently cracked into free radicals, with a methyl radical being formed, which substitutes a hydrogen atom on a phenol molecule to produce cresols,29 and the free radical substitutions are more likely to occur at the ortho-position and para-position of the phenol molecule (based on radical Fukui analysis (Fukui (0)) of the phenol molecule, shown in Fig. S3(a)†). A previous experimental study by the group of J. Zhang et al.42 concluded the preferential formation of cresols at temperatures lower than 650 °C during the non-catalytic decomposition of anisole. It should be noticed that because there is no obvious intermediate compound existing in the non-catalytic transmethylation reactions, they are more likely to occur as one step reactions.
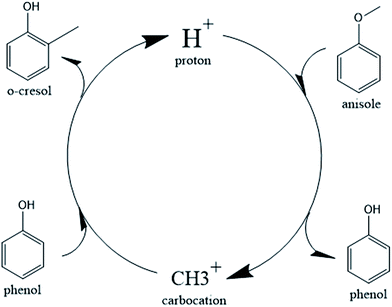
In the case of the catalytic decomposition of anisole over Brønsted acid sites, it has been largely recognized that the transmethylation reaction is induced by a proton that dissociates from the acid site and launches an electrophilic attack on the reactant.14,43–46 The transmethylation mechanism is proposed to proceed through carbocation transfers in the case of catalytic decomposition of anisole, as shown in Fig. 1.
The catalytic process of transmethylation can be divided into two steps. The first step consists of the methyl group cleavage in the anisole molecule; an initial electrophilic attack is launched by the proton dissociated from the catalyst acid site to the O atom (based on the electrophilic Fukui analysis (Fukui (−)) of the anisole molecule, as shown in Fig. S2(b)†), and a methyl carbocation is released. A second electrophilic attack is launched by the methyl carbocation group; the group is likely to substitute the hydrogen atom at the o- and p-positions on the phenol ring (based on the electrophilic Fukui analysis (Fukui (−)) of the phenol molecule, as shown in Fig. S3(b)†). The displaced free proton simultaneously interacts with the catalyst to recover the Brønsted acid site and maintain the catalytic activity throughout the reaction. Transition state compounds normally exist for a very short time due to their instability; however, the methyl carbocation attached to the active site during the transmethylation process is a relatively stable structure with zero valency. Consequently, it can be considered as an intermediate compound, rather than a transition state compound; therefore it is possible to consider the methyl carbocation cleavage and the carbocation substitution reactions as separate steps in the catalytic transmethylation. The mechanism described in Fig. 1 shows that the use of the Brønsted acid catalyst replaces the one-step reaction of direct methyl free radical transfer observed for the non-catalytic reaction by a two-step process.25 The mechanism also shows constant maintenance of acid sites in the catalyst by proton recovery throughout the reaction. Further reaction modelling was carried out considering the mechanism proposed here.
It is worth noting that in both non-catalytic and catalytic decomposition of anisole, the methyl group transfers not only to phenol but also to other compounds such as benzene, toluene, and even non-decomposed anisole present in the reaction media.42 All the transmethylation processes are initiated from methyl cleavage.
3.2 Modelling of non-catalytic and catalytic transmethylation of anisole to phenol
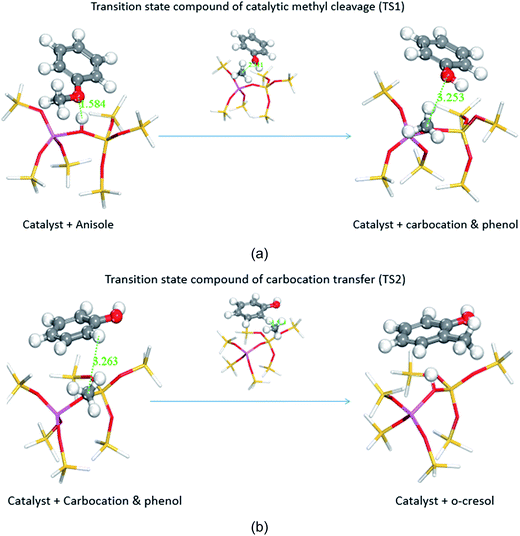
The transmethylation reactions with a phenol molecule in the non-catalytic and catalytic decomposition of anisole were modelled. Both non-catalytic and catalytic transmethylation models were built by placing equidistantly the reactant molecules (about 3 Å) to minimize any possible position-related errors. The catalytic transmethylation was modelled based on the dual electrophilic attack mechanism proposed in Fig. 1, considering the system containing a methyl carbocation on the acid site as the intermediate compound (see Fig. 2). The modelling was implemented in two stages: methyl carbocation cleavage from anisole over the catalyst active site, and transfer of the carbocation to the surrounding molecules. The transition states for both stages are denoted as TS1 and TS2, respectively. The non-catalytic transmethylation model was built according to the free radical mechanism, and the transition state of the reaction is denoted as TS. The cleavage energy of the carbocation from the anisole molecule (for TS1) and the energy barriers for the methyl carbocation transfer to the ortho-, meta-, and para-positions of phenol (for TS2) during the catalytic transmethylation of anisole to form cresol via phenol, as predicted by the model, are shown in Fig. 3. The transition state (TS) and corresponding energy barriers for the non-catalytic transmethylation of anisole to form n-cresol are shown for comparison.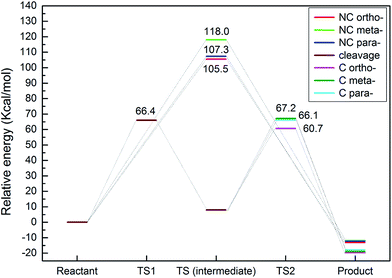 | ||
| Fig. 3 Energy barriers for transmethylation reactions of anisole to cresol (via phenol) (C denotes catalytic transmethylation; NC denotes non-catalytic transmethylation). | ||
As can be seen in Fig. 3, the transmethylation to the ortho-position of phenol presented a lower energy barrier than the meta-position and para-position transfers in both non-catalytic and catalytic decomposition. This result indicates that ortho-position transmethylation is more likely to occur to the phenol molecule, which agrees with the experimental observations found elsewhere.42 In short, experiments showed that o-cresol was formed at a lower temperature (550 °C) than p-cresol (600 °C) in non-catalytic anisole decomposition, and most multi-methyl phenolic compounds presented the ortho-position occupied by a methyl group in the catalytic anisole decomposition.42 In addition, the model pointed to the highest energy barrier for the meta-position transfer. This is in agreement with the experimental results, which exhibited no evidence of m-cresol formation.42 However, it should be noted that the results in this study show the intrinsic properties of the reaction, and the experimental yields obtained are normally subject to other effects, such as the framework topology effects of different zeolites. For example, the shape selectivity of microporous zeolites plays a key role in the catalyst promoting the production of para-cresol.25
The model also predicted that the energy barrier for the methyl cleavage in the presence of the catalyst was 66.4 kcal mol−1, which is much lower than the energy barrier values of the non-catalytic process. Moreover, compared to the non-catalytic process, the energy barrier for catalytic transmethylation to the ortho-position decreased from 105.5 kcal mol−1 to 60.7 kcal mol−1, and those for para- and meta-positions dropped from 107.3 kcal mol−1 to 66.1 kcal mol−1 and from 118.0 kcal mol−1 to 67.2 kcal mol−1, respectively. These results are also in line with the experimental data which showed that a lower temperature (approximately by 150 °C) was required to achieve a similar conversion ratio during the catalytic decomposition of anisole compared to non-catalytic decomposition.42
3.3 Modelling of non-catalytic and catalytic transmethylation of anisole to other acceptor molecules
Besides cresol, the transmethylation process also gives rise to other methyl substituted compounds.42 Therefore, transmethylation reactions with other acceptor molecules were modelled to assess the reactivity of these intermediate compounds and the selectivity of the resulting products. The formation of toluene, methyl anisole, xylene, xylenol, and trimethyl-phenol due to the addition of a methyl group to benzene, anisole, toluene, cresol and xylenol, respectively, was also modelled. The energy barriers for the different reaction pathways in non-catalytic and catalytic decomposition of anisole are shown in Table 1.| Reactant | Via | Product | Orientation | Energy Barrier (kcal mol−1) | ||
|---|---|---|---|---|---|---|
| Non-catalytic (TS) | Catalytic | |||||
| Cleavage (TS1) | Methyl cation transfer (TS2) | |||||
| Phenol | Cresol | ortho | 105.5 | 60.7 | ||
| meta | 118.0 | 67.2 | ||||
| para | 107.3 | 66.1 | ||||
| o-Cresol | Xylenol | ortho | 107.2 | 60.4 | ||
| meta | 121.1 | 61.8 | ||||
| para | 107.0 | 54.1 | ||||
| Anisole | 66.4 | |||||
| 2,4-Xylenol | 2,4,6-Phenol | ortho | 114.3 | 60.4 | ||
| 2,6-Xylenol | 2,3,6-Phenol | meta | 110.0 | 59.9 | ||
| Benzene | Toluene | — | 126.4 | 73.5 | ||
| Toluene | Xylene | ortho | 108.1 | 71.2 | ||
| meta | 112.2 | 68.3 | ||||
| para | 109.5 | 70.8 | ||||
| Anisole | Methyl-anisole | ortho | 106.9 | 63.3 | ||
| meta | 105.7 | 67.0 | ||||
| para | 108.3 | 71.7 | ||||
In the case of non-catalytic decomposition, the energy barriers of transmethylation changed significantly, depending on the acceptor molecules. This is related to the fact that the substituents on the molecule affect the electron distribution in the aromatic ring, giving rise to the site migration of substituted reactions.47 Anisole, toluene and phenolic compounds showed energy barrier values between 105.7 and 121.1 kcal mol−1 in the non-catalytic transmethylation (Table 1), and the energy barrier for the methyl transfer to benzene in the non-catalytic reaction was the highest (126.4 kcal mol−1).
It is found that the molecules containing branch chain substituents, especially oxygen-rich chains such as hydroxy and methoxy functional groups, more readily accept methyl radicals. The branch chains may have an impact on the π-bond of the benzene ring, making the ring more susceptible to methyl attack especially at the ortho- and para-positions, while the benzene ring without branch chains may have smaller electron density and therefore is more stable to radical attack.48
It was observed that transmethylation to phenol and o-cresol exhibited intrinsic preference in the ortho- and para-positions, which is in line with the results from the Fukui analyses of electrophilic attack on the phenol molecule (Fig. S3(b)†). On the other hand, toluene and anisole showed a moderate difference (within 4.1 kcal mol−1) in position preference for non-catalytic transmethylation. This is because the free pair of electrons in the oxygen of the hydroxyl group are more likely to move to the ring, and consequently affect the ring properties; while less electron migration and less impact on the ring occur with the methyl group attached either directly to the ring (in the case of toluene) or to the oxygen (in the case of anisole).49
In the case of catalytic reactions, the presence of the acid catalyst decreased notably the energy barrier values, exhibiting a big influence on promoting transmethylation. The decreases in the energy barrier values were observed to range from 36.6 kcal mol−1 (transmethylation to para-position of anisole) to 59.3 kcal mol−1 (transmethylation to the meta-position of o-cresol). The transmethylation to benzene was found to have the highest energy barrier of 73.5 kcal mol−1, even though it has been diminished by roughly 53 kcal mol−1 compared to the non-catalytic process, and this indicates the stability of the benzene ring to electrophilic attack compared to other branch chain containing compounds. In the case of the transmethylation to toluene, the model also predicted a decrease in the energy barrier value for each of the position transfers when using a catalyst (ranging between 68.3 kcal mol−1 and 71.2 kcal mol−1), but the predicted energy barriers are higher than those for most oxygen containing compounds, regardless of the position transfer. It is also noted that transmethylation to anisole at the ortho-position to produce methyl-anisole exhibited a similar energy barrier value to other phenolic intermediate compounds (63.3 kcal mol−1). This result suggests that the presence of a sole methyl group attached to the aromatic ring has a limited effect on the molecules to accept electrophilic substitution by a methyl carbocation, and this may be attributed to the lower electronegativity of the methyl group than that of oxygen containing functional groups.50 In other words, hydroxyl and methoxyl groups are the most likely ones to promote the reactivity of the aromatic ring, followed by the methyl group. The benzene molecule itself is the least reactive compound among the evaluated molecules in the catalytic transmethylation over the Brønsted acid sites. At the macroscopic level, it can be inferred that in the catalytic decomposition of anisole, the majority of toluene and xylene are probably produced from the deoxygenation of cresols and xylenols, rather than from the transmethylation to benzene over the Brønsted acid sites.
Compared to AHs, methyl phenolic compounds, i.e. phenol, cresol and xylenol, are found to be prone to accept electrophilic substitution at all positions, even though a slight preference (value difference lower than 8 kcal mol−1) for ortho- and para-positions was observed in the case of phenol and cresol. Among all the evaluated compounds, these molecules accept methyl carbocation at the lowest energy barrier values. Transmethylation of cresol to xylenol presented energy barriers ranging from 54.1 kcal mol−1 (p-position transfer) to 61.8 kcal mol−1 (m-position transfer). Transmethylation to convert xylenol into 2,3,6-methyl phenol and 2,4,6-methyl phenol exhibited similar energy barriers at around 60 kcal mol−1. These results well illustrate the experimental results during the catalytic decomposition of anisole in which the abundant production of multi-methyl phenolic compounds and the typical position preference were observed.42 The formation of these multi-methyl phenolic compounds from anisole depends on the initial formation of cresol.
4 Conclusion
This work presents the DFT modelling of transmethylation as the primary reaction taking place in both non-catalytic and catalytic anisole decomposition. Methyl radical cleavage led to the transmethylation process in non-catalytic transmethylation, which primarily occurred through methyl free radical transfer. In catalytic transmethylation, reactants interacted with the Brønsted acid sites present in the catalyst. The catalytic transmethylation was initiated by the Brønsted acid proton electrophilic attack on the oxygen atom of anisole, followed by carbocation substitution. A dual electrophilic attack mechanism was proposed for the catalytic transmethylation. Transmethylation reaction modelling, based on the proposed mechanism, proved that the Brønsted acid catalyst could significantly lower the reaction energy barrier for all reactant compounds investigated due to changes in the reaction pathways. Most of the energy barriers for the evaluated transmethylation reactions decreased more than 40 kcal mol−1 when considering the catalytic effect, with the highest decrease being observed in the case of o-cresol (around 60 kcal mol−1). Furthermore, both non-catalytic and catalytic transmethylation exhibited target molecule preference, depending on the original substituents of the acceptor, and transmethylation to most compounds showed preference for the ortho- and para-positions. Non-catalytic transmethylation to compounds with oxygen-rich substituents generally showed lower energy barriers. In the catalytic decomposition of anisole, the presence of oxygen-rich substituents also enhanced the reactivity of the ring, especially for phenolic compounds at the ortho- and para-positions. The lowest energy barrier was observed in the case of transmethylation towards the para-position of the cresol molecule (54.1 kcal mol−1).Author contributions
All authors have given approval to the final version of the manuscript.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
The authors would like to acknowledge financial support from the National Natural Science Foundation of China (project references: 51476034 and 51628601), the Natural Science Foundation of Jiangsu Province (project reference: BK20161423), and the FP7 Marie Curie iComFluid (project reference: 312261).References
- W. Boerjan, J. Ralph and M. Baucher, Annu. Rev. Plant Biol., 2003, 54, 519–546 CrossRef CAS PubMed
.
- C. S. Lancefield and N. J. Westwood, Green Chem., 2015, 17, 4980–4990 RSC
.
- A. V. Bridgwater, Biomass Bioenergy, 2012, 38, 68–94 CrossRef CAS
.
- A. V. Bridgwater and G. V. C. Peacocke, Renewable Sustainable Energy Rev., 2000, 4, 1–73 CrossRef CAS
.
- K. A. Jung, S. H. Woo, S.-R. Lim and J. M. Park, Chem. Eng. J., 2015, 259, 107–116 CrossRef CAS
.
- L. Zhang, R. Liu, R. Yin and Y. Mei, Renewable Sustainable Energy Rev., 2013, 24, 66–72 CrossRef CAS
.
- C. Liu, H. Wang, A. M. Karim, J. Sun, Y. Wang, M. Karim Ayman, J. Sun and Y. Wang, Chem. Soc. Rev., 2014, 43, 7594–7623 RSC
.
- S. Vichaphund, D. Aht-ong, V. Sricharoenchaikul and D. Atong, Renewable Energy, 2014, 65, 70–77 CrossRef CAS
.
- C. Mukarakate, J. D. McBrayer, T. J. Evans, S. Budhi, D. J. Robichaud, K. Iisa, J. ten Dam, M. J. Watson, R. M. Baldwin and M. R. Nimlos, Green Chem., 2015, 17, 4217–4227 RSC
.
- C. Mukarakate, X. Zhang, A. R. Stanton, D. J. Robichaud, P. N. Ciesielski, K. Malhotra, B. S. Donohoe, E. Gjersing, R. J. Evans, D. S. Heroux, R. Richards, K. Iisa and M. R. Nimlos, Green Chem., 2014, 16, 1444 RSC
.
- G. Yildiz, M. Pronk, M. Djokic, K. M. Van Geem, F. Ronsse, R. Van Duren and W. Prins, J. Anal. Appl. Pyrolysis, 2013, 103, 343–351 CrossRef CAS
.
- D. K. Shen, S. Gu, K. H. Luo, S. R. Wang and M. X. Fang, Bioresour. Technol., 2010, 101, 6136–6146 CrossRef CAS PubMed
.
- S. J. Hurff and M. T. Klein, Ind. Eng. Chem. Fundam., 1983, 22, 426–430 CAS
.
- Q. Meng, H. Fan, H. Liu, H. Zhou, Z. He, Z. Jiang, T. Wu and B. Han, ChemCatChem, 2015, 7, 2831–2835 CrossRef CAS
.
- T. Prasomsri, A. T. To, S. Crossley, W. E. Alvarez and D. E. Resasco, Appl. Catal., B, 2011, 106, 204–211 CAS
.
- K. Wang, X. Dong, Z. Chen, Y. He, Y. Xu and Z. Liu, Microporous Mesoporous Mater., 2014, 185, 61–65 CrossRef CAS
.
- J. Cornella, E. Gómez-Bengoa and R. Martin, J. Am. Chem. Soc., 2013, 135, 1997–2009 CrossRef CAS PubMed
.
- C. Mackie, R. Doolan and F. Nelson, J. Phys. Chem. C, 1989, 93, 664–670 CrossRef
.
- M. E. Sad, C. L. Padró and C. R. Apesteguía, Catal. Today, 2008, 133–135, 720–728 CrossRef CAS
.
- J. Xu, A. Z. Yan and Q. H. Xu, Appl. Catal., A, 1999, 10, 983–986 CAS
.
- W. Wang, P. L. De Cola, R. Glaeser, I. I. Ivanova, J. Weitkamp and M. Hunger, Catal. Commun., 2004, 94, 119–123 CAS
.
- M. Bregolato, V. Bolis, C. Busco, P. Ugliengo, S. Bordiga, F. Cavani, N. Ballarini, L. Maselli, S. Passeri and I. Rossetti, J. Catal., 2007, 245, 285–300 CrossRef CAS
.
- K. G. Bhattacharyya, A. K. Talukdar, P. Das and S. Sivasanker, J. Mol. Catal. A: Chem., 2003, 197, 255–262 CrossRef CAS
.
- M. E. Sad, C. L. Padró and C. R. Apesteguía, J. Mol. Catal. A: Chem., 2010, 327, 63–72 CrossRef CAS
.
- X. Zhu, R. G. Mallinson and D. E. Resasco, Appl. Catal., A, 2010, 379, 172–181 CrossRef CAS
.
- N. Ballarini, F. Cavani, L. Maselli, A. Montaletti, S. Passeri, D. Scagliarini, C. Flego and C. Perego, J. Catal., 2007, 251, 423–436 CrossRef CAS
.
- J. H. Baraban, P. B. Changala, G. C. Mellau, J. F. Stanton, A. J. Merer and R. W. Field, Science, 2015, 350, 1338–1342 CrossRef CAS PubMed
.
- R. Thilakaratne, J.-P. Tessonnier and R. C. Brown, Green Chem., 2016, 18, 2231–2239 RSC
.
- G. Li, L. Li, L. Shi, L. Jin, Z. Tang, H. Fan and H. Hu, Energy Fuels, 2014, 28, 980–986 CrossRef CAS
.
- Z. Geng, M. Zhang and Y. Yu, Fuel, 2012, 93, 92–98 CrossRef CAS
.
- Y. Huang, X. Dong, M. Li, Y. Yu, J. Gao, Y. Zheng, G. B. Fitzgerald, J. de Joannis, Y. Tang, I. E. Wachs, S. G. Podkolzin, Y. Huang, X. Dong, M. Li, M. Zhang and Y. Yu, Catal. Sci. Technol., 2015, 5, 1093–1105 CAS
.
- Y. Huang, X. Dong, M. Li, M. Zhang and Y. Yu, RSC Adv., 2014, 4, 14573 RSC
.
- J. Gao, Y. Zheng, G. B. Fitzgerald, J. de Joannis, Y. Tang, I. E. Wachs and S. G. Podkolzin, J. Phys. Chem. C, 2014, 118, 4670–4679 CAS
.
- Z. K. Li, Z. M. Zong, H. L. Yan, Y. G. Wang, X. Y. Wei, D.-L. Shi, Y. P. Zhao, C. L. Zhao, Z. S. Yang and X. Fan, Fuel, 2014, 120, 158–162 CrossRef CAS
.
- B. Delley, J. Chem. Phys., 1990, 92, 508–517 CrossRef CAS
.
- B. Delley, J. Chem. Phys., 2000, 113, 7756 CrossRef CAS
.
- M. Elanany, M. Koyama, M. Kubo, P. Selvam and A. Miyamoto, Microporous Mesoporous Mater., 2004, 71, 51–56 CrossRef CAS
.
- B. Kalita and R. C. Deka, Eur. Phys. J. D, 2009, 53, 51–58 CrossRef CAS
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed
.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed
.
- F. L. Hirshfeld, Theor. Chim. Acta, 1977, 44, 129–138 CrossRef CAS
.
- J. Zhang, B. Fidalgo, D. Shen, R. Xiao and S. Gu, J. Anal. Appl. Pyrolysis, 2016, 122, 323–331 CrossRef CAS
.
- J. F. Haw, B. R. Richardson, I. S. Oshiro, N. D. Lazo and J. A. Speed, J. Am. Chem. Soc., 1989, 111, 2052–2058 CrossRef CAS
.
- B. R. Richardson, N. D. Lazo, P. D. Schettler, J. L. White and J. F. Haw, J. Am. Chem. Soc., 1990, 112, 2886–2891 CrossRef CAS
.
- E. J. Munson, T. Xu and J. F. Haw, J. Chem. Soc., Chem. Commun., 1993, 75–76 RSC
.
- T. Xu, J. Zhang, E. J. Munson and J. F. Haw, J. Chem. Soc., Chem. Commun., 1994, 2733–2735 RSC
.
- F. L. Lambert, J. Chem. Educ., 1958, 35, 342–343 CrossRef
.
- T. Phuong, J. Catal., 1986, 102, 456–459 CrossRef
.
- X. Zhu, L. L. Lobban, R. G. Mallinson and D. E. Resasco, J. Catal., 2011, 281, 21–29 CrossRef CAS
.
- F. De Proft, W. Langenaeker and P. Geerlings, J. Phys. Chem., 1993, 97, 1826–1831 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7se00280g |
| This journal is © The Royal Society of Chemistry 2017 |