View PDF VersionPrevious ArticleNext Article
 
DOI: 10.1039/C7RP00135E (Paper) Chem. Educ. Res. Pract., 2017, 18, 893-902

Studying the consistency between and within the student mental models for atomic structure

Nikolaos Zarkadis a, George Papageorgiou *a and Dimitrios Stamovlasis b
aDemocritus University of Thrace, Greece. E-mail: gpapageo@eled.duth.gr
bAristotle University of Thessaloniki, Greece

Received 18th July 2017 , Accepted 2nd September 2017

First published on 2nd September 2017

Abstract

Science education research has revealed a number of student mental models for atomic structure, among which, the one based on Bohr's model seems to be the most dominant. The aim of the current study is to investigate the coherence of these models when students apply them for the explanation of a variety of situations. For this purpose, a set of six tasks describing different everyday situations was given to 225 students of the 10th and 11th grades of secondary schools from Northern Greece. Quantitative analysis of the students’ responses using Latent Class Analysis (LCA) showed that there is no consistency between models across the tasks and that the context of the task affects the distribution of students’ responses across models. Qualitative analysis showed a variety of pieces of knowledge from different models that students combine when manipulating the tasks, which possibly causes a lack of consistency within each one of the models. The findings are discussed in terms of between and within model consistency, and the conclusions contribute to the debate concerning the coherent vs. fragmented knowledge hypotheses. The empirical evidence provided by the analysis clearly demonstrates that student mental models for atomic structure were not coherent when applied in different everyday situations. Implications for theory and practice are discussed.

Introduction

Due to their importance, student mental models for atomic structure have been widely studied, in relation to a number of factors, such as age, grade, class characteristics, curriculum, individual differences, context, etc. (e.g., Harrison and Treagust, 1996, 2000; Petri and Niedderer, 1998; Tsaparlis and Papaphotis, 2002, 2009; Cokelez and Dumon, 2005; Papaphotis and Tsaparlis, 2008; Adbo and Taber, 2009; Park and Light, 2009; Cokelez, 2012; Papageorgiou et al., 2016a, 2016b). The results of these studies reveal the existence of particular mental models varying in terms of their complexity and abstractness. The most simple and concrete of them describes the atom as just a particle, whereas the most sophisticated and abstract moves within a quantum probabilistic context. Among them, the most dominant model seems to be Bohr's model, which describes electrons moving in paths around the nucleus. Although the term ‘Bohr's model’ refers to the scientific model proposed by Bohr, science education researchers usually consider it as being a category of ‘student mental model’ including any simpler form of the scientific one, even when it does not necessarily take into account the quantization idea (Papageorgiou et al., 2016a). Relevant studies have shown that students, even of higher grades of secondary education, describe the atomic structure on this basis (e.g., Petri and Niedderer, 1998; Papaphotis and Tsaparlis, 2008; Tsaparlis and Papaphotis, 2009).

However, there are some questions arising here, which concern the consistency of the use of this model by students when explaining everyday situations. Do they use the model independently of the situation that are facing, or could they switch to another model when the latter seems to be more convenient? When they use it, do they retain all of its characteristics or could some of them vary? These are in fact questions referring to the discussion concerning the coherence of the mental models (e.g., Ioannides and Vosniadou, 2002; diSessa et al., 2004). Although historically, the students mental models for the particulate nature of matter have been considered to be quite coherent, recent studies have shown that relevant student knowledge could be fragmented (Stamovlasis et al., 2013). This means that every time a student is trying to explain a situation or a phenomenon concerning the particulate nature of matter, some of the relevant ‘pieces of knowledge’ that already exist in his/her mind are activated in order to form in situ a particular mental model. Thus, depending on the situation/phenomenon, a different set of ‘pieces of knowledge’ could be activated and a different mental model could be formed in order to reach an explanation. However, some researchers (e.g.Hammer, 1996; Taber, 2008; Taber and García Franco, 2010) suggest that it is not always safe to characterize students’ knowledge as either coherent or fragmented, since this also depends on the context of the specific topic that is studied and the particular circumstances that are involved. As a result, the coherence of student mental models for ‘atomic structure’ should be tested within the context that this topic defines and under the circumstances that particular situations generate. This is where the present study focuses.

Theoretical background

Student mental models for atomic structure

Research concerning student mental models for atomic structure has revealed a number of relevant models. However, it seems that these models could be categorised into five general categories. Starting from the simpler and most concrete, the category of ‘particle model’ considers the atom as a particle, without further reference to microscopic characteristics (Griffiths and Preston, 1992; Harrison and Treagust, 1996; Cokelez and Dumon, 2005; Park and Light, 2009; Stevens et al., 2010; Cokelez, 2012; Papageorgiou et al., 2016a). This model is frequently found in younger ages, where students represent the atom as a dot, a circle or a sphere. Not far from this naive level, some students describe the atom as a living organism providing a model similar to that for the cell (e.g.Griffiths and Preston, 1992; Harrison and Treagust, 1996; Cokelez, 2012; Papageorgiou et al., 2016a). This category of ‘atom–cell model’ could also be found in older ages (e.g., grades 8–10, Harrison and Treagust, 1996). Stepping to more detailed mental models, students represent the components of the atom, the compositional relationship between them and occasionally the existence of forces between them. This is the category of the ‘nuclear model’ (Park and Light, 2009; Papageorgiou et al., 2016a) or, in other words, the ‘composition atom model’ (Cokelez and Dumon, 2005; Cokelez, 2012).

Student mental models become more interesting when the idea of paths where electrons move appears. This is probably the most discussed case of the relevant student models, the origin of which is found in the scientific model of Bohr. Although in the ‘scientific Bohr’s model’, the fundamentals of quantum theory are incorporated, science education researchers often classify into one general category all student descriptions comprising paths of electrons, either with or without references to certain levels of orbits and/or to energy quantization. This general category is reported as the ‘solar system model’ (Harrison and Treagust, 1996; Nicoll, 2001; Nakiboglu, 2003; Cokelez and Dumon, 2005; Cokelez, 2012), the ‘planetary model’ (Petri and Niedderer, 1998; Papaphotis and Tsaparlis, 2008; Adbo and Taber, 2009; Tsaparlis and Papaphotis, 2009), ‘Bohr's model’ (Fischler and Lichtfield, 1992; Nicoll, 2001; McKagan et al., 2008; Papaphotis and Tsaparlis, 2008; Park and Light, 2009; Tsaparlis and Papaphotis, 2009; Wang and Barrow, 2013; Papageorgiou et al., 2016a), the ‘planetary Bohr's model’ (Tsaparlis and Papaphotis, 2009) or the ‘Bohr/solar system model’ (Stevens et al., 2010). However, in fact, in all the above cases, researchers refer to a category that adopts ‘Bohr’s model’ as a general student mental model, where particular characteristics (e.g. quantization energy) appear only in the corresponding sub-categories.

The most sophisticated and abstract student models are those that take into account quantum theory and look into the atomic structure through a probabilistic logic. In the literature, this category includes models reported as the ‘orbital model’ (Harrison and Treagust, 1996; Kalkanis et al., 2003; Taber, 2005), ‘electron cloud model’ (Petri and Niedderer, 1998; Cokelez and Dumon, 2005; Tsaparlis and Papaphotis, 2009; Stevens et al., 2010; Cokelez, 2012), ‘quantum model’ (Taber, 2002, 2005; Park and Light, 2009), ‘Schrödinger model’ (McKagan et al., 2008) or ‘quantum mechanical model’ (Papageorgiou et al., 2016a). In the above cases of this category (let us refer to it as the ‘quantum mechanical model’), concepts such as orbital, electron cloud, uncertainty principle, energy quantization, wave function or/and probability appear quite often and define, respectively, possible sub-categories inside the model.

Among the five categories, ‘Bohr’s model’ and the ‘quantum mechanical model’ are the most discussed in terms of what student knowledge is generated for the atomic structure during the teaching and learning procedure. A number of factors, such as chemistry curriculum, grade, age, or individual differences have been revealed as significant factors having an impact on the adoption of one or the other model by students (Papageorgiou et al., 2016a, 2016b). However, Bohr's model appears to be the most dominant in student thinking and relevant ideas present a significant resistance in any change during the teaching procedure (e.g., Petri and Niedderer, 1998; Park and Light, 2009). Even when the above factors generate conditions that could facilitate the development of a more sophisticated context for the atomic structure, many students continue to use characteristics of Bohr's model in their approaches.

Consistency and coherence issues

Although the five categories of student models for the atomic structure seem to be quite distinct shaping their own particular contexts, recent studies have indicated that their characteristics are not always stable. This lack of stability is usually mentioned as inconsistency or incoherence. However, the terms ‘consistency’ and ‘coherence’ are not always clear. Thus, based on the contemporary psychometric and measurement theory (Borsboom, 2008) a distinction between latent variables and observable ones should be made at this point. A mental model is actually a latent variable, since it is a hypothetical entity responsible for students’ responses in relevant questions, which cannot be observed. However, a researcher infers the existence of such an entity from a number of observable variables (student responses), which are consistent with it. When the hypothetical entity is stable and ‘theory like’, then the mental model is coherent. This coherence possessed by a mental model is measured at the empirical level via the degree of consistency of students’ responses. If students’ responses are consistent with the mental model, then the hypothesized mental model is said to be coherent.

In probing the coherence of a mental model, two different types of inconsistency in students’ responses can be distinguished. The first one concerns the stability of the characteristics of a mental model as they are expressed by a student. For instance, when students represent the atomic structure in the context of the quantum mechanical model, often they convey a number of Bohr's model characteristics to this model. Thus, the characteristics of the quantum mechanical model seem to be instable and concepts such as shells and orbitals are used interchangeably (Nicoll, 2001; Taber, 2002, 2005; Nakiboglu, 2003; Stevens et al., 2010) or concepts such as the electron cloud and shell are confused (Harrison and Treagust, 2000). We could say that, this is a type of inconsistency within the model. That is, although the students possess the model and use it for providing interpretations, there are characteristics belonging to other models that are interchangeably used in some cases. On the other hand, there is evidence that students can switch from one model to another, when this seems to provide them with a solution. Thus, they can change their descriptions for the atomic structure moving from Bohr's model to the quantum mechanical model when either they are asked to work in another context (e.g.Tsaparlis and Papaphotis, 2009; Papageorgiou et al., 2016a) or they use a different model (mixed or made up) on their own when the needs of an explanation differ (e.g.Wang and Barrow, 2013). This is actually a second type of inconsistency, that is between the student mental models.

The above described inconsistency, independent of its type, seems to be reasonably justified by the theory known as knowledge in pieces or fragmented knowledge (e.g., Harrison et al., 1999; diSessa et al., 2004). According to this theory, a number of implicit ‘knowledge pieces’ that preexist in students’ mind, are possibly activated each time a particular situation or phenomenon is studied, in order to generate in situ an understanding or explanatory scheme. These knowledge pieces appear to be flexible structures that can be evolved, modified and enlarged over time, incorporating more general or specific components. A number of these pieces could also be coordinated with each other generating a bigger structure, which could eventually formulate a conception for a particular situation or phenomenon (diSessa, 1988; Taber and García Franco, 2010). The whole procedure, which leads to the formation of a cognitive structure, i.e. a network of interrelated knowledge elements of a variety of grain sizes and complexities, is a learning procedure.

However, this inconsistency in student mental models is not always a de facto assumption. According to some researchers (e.g.Hammer, 1996; Taber, 2008; Taber and García Franco, 2010), cognitive structures generating student models for a concept or a phenomenon could be seen as consistent or inconsistent depending on the particular topic that is studied and the general context within which it is studied. Thus, Taber (2008) argues that there are specific topics where students have developed stable mental models, whereas in other topics, student models are formed in situ showing diversity in their coherence. As a result, science researchers have to seek answers regarding the coherence/incoherence of student mental models, studying them within the context of specific topics and under particular circumstances.

Rationale of the study and research questions

In Greek secondary education, which comprises grades 7 to 12, Bohr's model is the most common basis for the study of the structure of the atom. Students work on this model up to the 11th grade, whereas only in one out of three directions of the 12th grade is the quantum mechanical model taught. Thus, when studying student mental models for situations relevant to the atomic structure in the 10th and 11th grades, one probably expects to see a dominant presence of Bohr's model in the results.

However, taking into account the coherence/incoherence issues as they were discussed above, it seems to be quite interesting to investigate how consistent the students are with the use of this model across particular everyday situations, even when they could have other alternatives, as well as how stable the characteristics of the model that they use are across these situations. For this purpose, a description of the five categories of the student mental models was briefly presented to the students, without any notice concerning their correctness in accordance to the scientific view. Students could choose any of the five models, justifying their choice and thus, providing us with the model characteristics that they used in order to explain the situation.

In this context, two research questions could be articulated:

• How can particular circumstances generated by some everyday situations affect students’ decisions in adopting a model for atomic structure in order to explain a situation? (This refers to the consistency between the student mental models.)

• Which are the characteristics (if any) of other mental models that students may incorporate into the particular model for atomic structure that they use in order to explain a situation? (This refers to the consistency within the student mental models.)

Methodology

Sample

The sample consisted of 225 students of the 10th and 11th grades (117 male and 108 female) of secondary schools from Northern Greece, who voluntarily participated in the study. Informed consent was obtained from the heads of the participating schools, the teachers of all classes and the students prior to the study. Students were also aware of the purpose of the study and of the fact that their competence in the study would not be associated with the evaluation of their performance in school. All schools were regular public ones, with mixed ability classes and students from mixed socioeconomic backgrounds. All students were attending classes that followed the National Science Curriculum for Greece (Greek Pedagogical Institute, 2003) using the same textbook. Data were collected during the last semester of the school year through an anonymous paper-and-pencil test. The completion of the test lasted one didactic hour (45 min).

Instruments

Students were provided with an instrument (Table 1) comprising two parts. In the first one, the five categories of the models for the atomic structure were presented in short as ‘views’ that have been recorded for the ‘atom’. In the second part, a set of six tasks describing different everyday situations were given. The situations were familiar to the students, since, along with their everyday experience, students had been introduced to them during the previous school years. However, these situations had not been explicitly studied in relation to the specific characteristics of Bohr's model (or any other model) and to this extent, students had to extrapolate their knowledge in order to respond to the tasks. In each one of the tasks, students were prompted to choose one of the five categories/views for the atom that could provide a satisfying response to the task (a multiple-choice question) and then, to explain how this view could respond to the task, i.e. how it could explain the situation (an open-ended question).
Table 1 An overview of the research instrument
Part 1. The five categories of the models for the atomic structure
Models Description of the models
A The atom as a living organism
B The atom as a particle (a small bit of matter, which usually looks like a sphere)
C The atom comprising a sum of electrons around a nucleus that consists of protons and neutrons
D The atom, as an entity where electrons are moving in certain paths around the nucleus (that consists of protons and neutrons)
E The atom, as an entity where there are electron clouds around the nucleus (that consists of protons and neutrons)
Part 2. Students are asked to choose one of the five categories A, B, C, D, or E in response to each task and then, to explain how this can explain the corresponding situation
Tasks Description of the situation
1 In some clocks, pointers are coated with substances consisting of atoms that make them visible in the dark as they can emit light
2 There are several living organisms (e.g. tropical fish) that are visible in the dark as they also emit light
3 When light hits a clean and smooth metal surface, we can see the surface shining
4 Current can flow through a metallic wire and thus, it is dangerous to touch it
5 A characteristic property of some materials that we call magnetic, is that they can attract some metallic objects
6 If we touch a metal rod in a point away from another that is heated over a flame, then we feel the heat

This kind of instrument design, where the choice of a response is followed by a justification or an explanation, tests also its validity and reliability. In the present case, where the instrument concerns the evaluation of students’ understanding of a specific domain (atomic structure) the focus is on the content validity (Mertens, 2005). The establishment of content validity in such cases is based on elaborated judgement and expertise.

As for the multiple-choice part of the instrument, the validity is also ensured by the fact that each one of the choices in every task is clearly linked to one of the mental models, establishing valid empirical indexes for their identification. Although the mental process for choosing the hypothesised “correct” response among alternatives has been blamed for responses biased toward specific choices (Vosniadou et al., 2004), research regarding mental tasks and reasoning has shown that multiple-choice instruments do not introduced bias in students’ responses when a proper choice of tasks is made (e.g., Thomas and Horton, 1997; Jansen and van der Maas, 2002). Regarding the reliability of the multiple-choice part, Cronbach's alpha was used in order to measure the internal consistency on the basis of an ordinal marking scheme. Although it was found to be 0.53, a value that is low, this is not unusual in social sciences studies (Hatcher and Stepansky, 1994). In studying the mental process, the measured latent variable is not unidimensional and a diversity of constructs are involved; thus, low values of Cronbach's alpha in these cases do not reflect lack of internal consistency due to low reliability (Kline, 1999).

As for the open-ended questions part of the instrument, validity and reliability issues are connected to the procedure followed for their qualitative analysis and the corresponding coding scheme. These are described below.

Analysis procedure

Since data were collected through open-ended questions and multiple-choice ones, analysis was initially implemented separately for each one of them.

Data from open-ended questions were qualitatively analyzed by two independent researchers. Each one of the researchers was extracting from each student's answer any discrete piece of knowledge that could correspond to a particular mental model for the atomic structure. For instance, the student's answer to task 6 ‘the atoms in that point (that is heated) are heated. As the atoms move through the rod, they transfer the heat to us’ includes two pieces of knowledge corresponding to model B, i.e. ‘the atom has a particular property (it can be heated)’ and ‘the atom can move through the rod (a solid material)’. Similarly, the student's answer to task 1 ‘the pointers of the clocks can emit light due to the electrons of the atoms’ includes one piece of knowledge corresponding to model C, i.e. ‘the electrons of an atom can emit light’ or, the student's answer to task 2 ‘because, when an electron jumps from an orbit of bigger radius to another of smaller radius, then it releases energy in the form of light’ includes two pieces of knowledge corresponding to model D, i.e. ‘an electron orbits in particular radii’ and ‘when an electron jumps to an inner orbit, it emits energy (light)’. Working this way, each researcher recorded all the pieces of knowledge corresponding to each one of the five mental models (A to E) for all the students’ responses to the six tasks. Any consistency/inconsistency of these pieces of knowledge with the corresponding student responses to the multiple-choice questions was not examined at this stage, but it was subject to further co-evaluation of both data from multiple-choice and open-ended questions (see also Results). The results of the whole procedure from each one of the researchers were compared to each other and any disagreement was discussed until a total agreement was reached.

Data from multiple-choice questions were quantitatively analyzed with Latent Class Analysis (LCA) using LatentGold 4.0 software (Magidson and Vermunt, 2001).

The results from both analyses were co-evaluated in order to draw particular conclusions for the consistency between and within the student mental models for atomic structure.

Latent class analysis (LCA). Methodologically, the classification procedures concerning the consistency of student's knowledge and their mental models, comprise the categorization of students to certain groups (mental models) on the basis of their patterns of responses. The most effective clustering method suitable for such studies is the LCA, which has been already used in the context of a large number of topics including the coherency of student models for the particulate nature of matter (Stamovlasis et al., 2013). LCA is a Latent Structure analysis, which assumes that both manifest and latent variables are categorical (Clogg, 1995; Dayton, 1998). LCA can obtain clusters, named Latent Classes (LCs) that are distinct in terms of different corresponding sets of responses. The classification procedure is based on a set of conditional probabilities that characterize each one of the LCs. A conditional probability is the probability of providing a certain response to an item, given that the subject belongs to a specific LC. In the present work, LCA is implemented as a confirmatory procedure aiming to support the consistency of students’ answers in line with specific mental models discussed in the preceding session. If the mental models under investigation exist as coherent entities, then a limited number of latent classes (LCs) will result and their conditional probabilities will be consistent with these mental models. If the LCA procedure leads to the formation of a single-class model, then students’ knowledge, based on their responses, is not consistent with any of the hypothesized mental models.

Beyond the fact that LCA can detect clusters of unexpected student response patterns and thus, unanticipated alternative LCs might emerge, LCA can also offer quantitative statistical measures for the success of fit, indicating how well the LC model accounts for the data. These measures are, the number of parameters (Npar), the likelihood ratio statistic (L2), the Bayesian Information Criterion (BIC), Akaike's Information Criterion, the degrees of freedom (df) and the bootstrapped p-value. Non-significant p-values greater than 0.05 are desired indicating a good fit between the theoretical model and data (Magidson and Vermunt, 2001; Vermunt and Magidson, 2002).

Results

Quantitative analysis using LCA

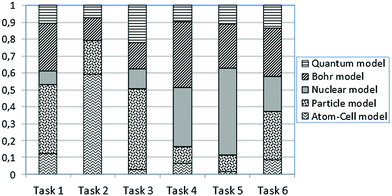
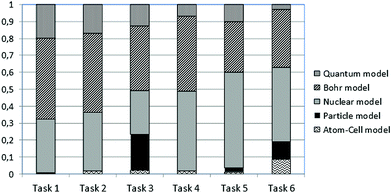
Table 2 shows the results of the classification procedure concerning the multiple-choice questions using LCA, which also included grade as a covariate. The best fitting solutions appear in Table 2. First, the one-cluster (1-LC) solution with BIC = 3461.005 was examined. However, LCA suggests that no distinct clusters exist and students’ knowledge seems to be inconsistent with the hypothesized mental models (A to E). Based on fitting indexes, the two-cluster (2-LC) solution with BIC = 3479.197 was also examined. The resulting two LC-clusters (i.e., LC1 and LC2) account for 56.84% and 43.16% of the sample, respectively. LC1 includes 45.50% students from 10th grade and 54.50% from 11th grade, whereas LC2 includes 62.25% students from 10th grade and 37.75% from 11th grade. Fig. 1 and 2 show the conditional probabilities of students’ responses in all tasks for these two emerged latent classes. Interestingly, the latent classes (LC1 and LC2) do not coincide with any of the hypothesized mental models, which are supposed to be coherent. In contrast, it is observed that these latent classes are heterogeneous in terms of students’ responses linked to different mental models in every task. For example, in Fig. 1, task 3 has the probability of 0.028 to be answered within the atom–cell model, the probability of 0.477 to be answered within the particle model, the probability of 0.118 to be answered within the nuclear model, the probability of 0.157 to be answered within Bohr's model and the probability of 0.219 to be answered within the quantum mechanical model. Thus, students’ knowledge is not coherent, since their responses do not show any consistency between the models of atomic structure under consideration.
Table 2 Results of the various LC factor solutions fitted to the 6 tasks
LL BIC (LL) N par L 2 df p-Value Class. err.
a Indicates the most parsimonious and best fitting solution: Npar, number of parameters; L2, likelihood ratio statistic; BIC, Bayesian Information Criterion; AIC, Akaike's Information Criterion; df, degrees of freedom; bootstrapped p-value; classification error.
1-Clustera −1666.87 3461.00 24 1549.889 177 0.000 0.0000
2-Clustera −1607.02 3479.19 50 1430.194 151 0.012 0.0543
3-Cluster −1561.66 3526.37 76 1339.487 125 0.002 0.0873
4-Cluster −1528.73 3598.39 102 1273.623 99 0.012 0.0979
5-Cluster −1498.08 3674.98 128 1212.325 73 0.002 0.0923
6-Cluster −1472.10 3760.92 154 1160.371 47 0.000 0.0691
7-Cluster −1452.85 3860.29 180 1121.860 21 0.000 0.0576


image file: c7rp00135e-f1.tif
Fig. 1 Conditional probabilities for latent class 1 (56.84%).

image file: c7rp00135e-f2.tif
Fig. 2 Conditional probabilities for latent class 2 (43.16%).

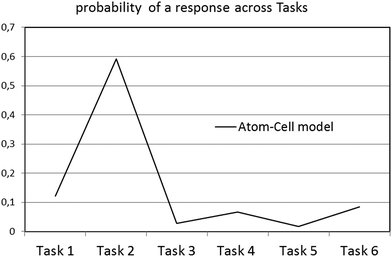
In addition, Fig. 1 and 2 show that the particularity of each situation in tasks 1 to 6 affects the distribution of probabilities to provide an answer within the context of a specific model. For instance, one can observe that in Fig. 1, the probability for task 2 to be answered within the atom–cell model is significantly higher than in any other task. Fig. 3 shows better how such a probability varies within the atom–cell model across tasks and that, for task 2 it is 0.59. Possibly, this is connected to the content of task 2, which refers to living organisms.


image file: c7rp00135e-f3.tif
Fig. 3 Probability for responding within the atom–cell model across tasks in LC1.

Qualitative analysis

Qualitative analysis of students’ answers to the open-ended questions resulted in a number of pieces of knowledge as described in the relevant examples already reported in the ‘analysis procedure’. Many of them were expected, as they were in line with the categories of the mental models chosen in the corresponding multiple-choice questions.

However, an interesting point was that a significant number of pieces of knowledge, compatible with mental models different from the ones chosen in the corresponding multiple-choice question, were found. These pieces of knowledge – let us refer to them as ‘incoherent pieces of knowledge’ – are presented in Table 3 and they are symbolized with the use of two letters, the first of which corresponds to the model chosen in the multiple-choice question and the second one corresponds to the model that is compatible with this knowledge. For instance, BC symbolizes a piece of knowledge found in an open-ended student response that has characteristics of model C, when the student had chosen model B in the corresponding multiple-choice question. In many cases, such ‘incoherent pieces of knowledge’ co-exist with the expected pieces of knowledge due to the model chosen in the multiple-choice questions.

Table 3 ‘Incoherent’ pieces of knowledge. Number of students (and percentages)
Pieces of knowledge Task 1 Task 2 Task 3 Task 4 Task 5 Task 6
BA The atom is a living particle — — — — 2(0.9) —
BC Electrons of the atoms can move 7(3.1) — — — — —
BC Atoms contain charges/electrons — 2(0.9) 3(1.3) — 5(2.2) —
BC Atoms can receive or lose charges/electrons — 5(2.2) 9(4.0) — 1(0.4) —
BC Charged atoms can move — — — 6(2.7) — —
CB The atom is a particle with particular properties (it can attract or repel, it can be burned, etc.) — — 4(1.8) — 13(5.8) 20(8.9)
CD Electrons can freely move/there are ‘free electrons’ 4(1.8) — — 14(6.2) — —
Electrons can be stimulated — 2(0.9) 8(3.6) — — —
CD There are electrons in the outer shell — — — — 2(0.9) 2(0.9)
DB The atom as a particle has particular properties (it can emit light, it can transmit heat, etc.) 14(6.2) 7(3.1) 14(6.2) — 2(0.9) 12(5.3)
DC Electrons can move (without any mention of paths/shells) 27(12.0) 24(10.6) 14(6.2) 52(23.1) 12(5.3) 33(14.7)
DC Forces exist between the electrons and the nucleus of the same or different atoms (without any mention of paths/shells) — 2(0.9) — — 18(8.0) —
DE There are electron clouds in the outer shells — — — — 2(0.9) —
EC The electron clouds contain electrons/charges 3(1.3) 4(1.8) — 1(0.4) 5(2.2) —
Electron clouds can receive or lose electrons/charges 2(0.9) 2(0.9) — — 2(0.9) —
EC Electrons of the electron clouds can move/run 6(2.7) 7(3.1) 7(3.1) 5(2.2) 3(1.3) 5(2.2)
EC Electrons of the electron clouds can emit light (due to movement, collisions etc.) 3(1.3) 3(1.3) — 2(0.9) — —
ED Electrons of the electron clouds can freely move/there are ‘free electrons’ 2(0.9) — — 1(0.4) — —
ED Electron clouds can move in shells — — — 1(0.4) — —

In Table 3, it is apparent that ‘incoherent pieces of knowledge’ can be found in students’ responses concerning particular tasks, whereas they might not be present in some other responses, advocating therefore their activation (or not) depending on the context of the everyday situation that is under study. Although their percentages are generally low in each one of these cases, they are quite significant as a sum and vary across the tasks (when present) contributing to the existence of an inconsistency within a model. Also, it is interesting that in the case where ‘Bohr’s model’ had been chosen by the students, the percentages of the ‘incoherent pieces of knowledge’ increased significantly (DB, DC and DE, Table 3). For instance, in the case of DC pieces of knowledge, although students had chosen Bohr's model, they did not use any knowledge relevant to the idea of particular ‘paths’ in their explanations, whereas in the DE case, they used this idea considering the electron as a cloud moving in such ‘paths’ around the nucleus.

Discussion and conclusions

Despite the dominance of ‘Bohr's model’ in the curriculum of Greek secondary education for the 10th and 11th grades, the results of the present study showed that students have not attained a coherent mental model that could consistently be used in their explanations when dealing with everyday situations. Students in their responses compose and use various mental models for their explanations and there is consistency neither between nor within those models. Even though this inconsistency is ameliorated in the case of 11th grade, students generally tend to use any model or any characteristic of a model that appears to be convenient for them in order to reach a ‘logical’ explanation.

Concerning the consistency between the models, LCA shows that students’ knowledge is clearly fragmented when they use atomic models for the explanation of particular situations. Taking into account the specific context of Bohr's model, in which the atomic structure is taught in Greek secondary education, it is rather surprising to see results such as those appearing in the structures of LC1 and LC2 (Fig. 1 and 2). It seems that the characteristics of Bohr's model, as they are described in the curriculum, are not incorporated into the students’ minds as possibly their designers thought. The simplification of these characteristics and/or the various ways of their interpretation by the students could possibly lead them to the ultimate formation of other mental models for the atomic structure. To this extent, the particular task under examination could also affect students’ conceptualization of the atomic structure. Thus, beyond the apparent fragmentation (inconsistency between models), one may also notice via the conditional probabilities the effect of the varying circumstances on students’ thinking (see for instance task 2 of LC1, Fig. 3). This brings to the foreground the dependence of a student answer on the task context, a ‘context dependence’ issue (e.g.Bao and Redish, 2006; Redish and Smith, 2008). As Papageorgiou et al. (2016a) reported, when students are trying to accomplish a task related to atomic structure, their answers appear to be ‘task context dependent’. Even more importantly this ‘context dependence’ is also present in the teaching/learning procedure. For instance, when Petri and Niedderer (1998) differentiated the teaching content by setting different teaching inputs during appropriately designed lessons for the atomic structure, they recorded a development of different conceptions for the atom, as a student was moving from Bohr's model (D) to the electron cloud model (E) – a case of ‘teaching context dependence’. Also, it is obvious that the conditional probabilities for ‘Bohr’s model’ and the ‘nuclear model’ in sum, are the overwhelming majority in LC2. If this fact is combined with the high percentages of the DC pieces of knowledge presented in Table 3, it is quite possible that a confusion between the characteristics of these two models occurs in students’ mind. As Adbo and Taber (2009) reported, electron movement is not always specified in student metal models and a number of them (16 year-old) believe that electrons can orbit between the shells when energy is added. Similarly, Nicoll (2001) suggests that also university students do not have a clear view of the ‘shell’ concept and their mental models often include a vague circular movement of electrons around the nucleus. These findings are probably also connected to the students’ difficulties in understanding the sub-atomic interactions and the Coulomb principles (e.g., Taber, 2003, 2013; Wang and Barrow, 2013). As students cannot understand their nature and their relation to the centripetal force concerning the electron orbit around the nucleus (Taber, 2005), they cannot probably be helped in understanding the key characteristics of Bohr's model and thus, in making a clear distinction between the two models (Bohr's and nuclear).

Regarding the consistency within the models, students seem to deviate from the initial model chosen as the most appropriate for the particular situation. In their following attempt to articulate an explanation, although students activate relevant pieces of knowledge compatible with that mental model, in cases where no ‘logical’ explanation could be obtained, they activate ‘incoherent pieces of knowledge’ belonging to other models. For instance, for six students who had initially chosen category B (Table 3, task 4), they probably realized that they could not explain ‘the current that flows through a metallic wire’ within this model and thus, they modified their model into BC accepting the idea of ‘charge’ (i.e., the existence of charged atoms moving through the wire). Similarly, although 52 students had chosen category D for their explanation in the same task (possibly due to ‘Bohr's model’ being taught in their schools), when trying to articulate an explanation, they activated pieces of knowledge within the context of category C, without using the basic characteristic of category D, i.e. the idea of elections moving in specific paths/shells.

Another interesting point is the choice of the ‘quantum mechanical model’ by some students in a number of tasks, even though they had not been taught such a model in school. Although it is not easy to imagine the rationale for their choice, a possible explanation could be that these students guessed that this was the ‘correct’ answer. This aspect is also reinforced by the fact, that students’ explanations in the corresponding open-ended question are not analogically sophisticated. For instance, students’ answers include, in task 4 ‘the current can hit us due to the existence of electron clouds’ or in task 5 ‘these electron clouds enable the atom to attract metallic objects’. Also, as Table 3 shows, very often they did not avoid mixing the characteristics of this model with those of others more familiar to them. For instance, although students accepted the ‘electron cloud’, they retained the idea of electrons as a particle (Table 3), articulating in the EC case that ‘electron clouds contain electrons’, or in the ED case, that electron clouds can move in shells in accordance with ‘Bohr's model’. Similar ideas have also been recorded by other researchers (e.g.Harrison and Treagust, 1996, 2000; Ke et al., 2005; Papaphotis and Tsaparlis, 2008; Tsaparlis and Papaphotis, 2009). Harrison and Treagust (1996), for example, reported student mental models, where electron clouds were perceived as structures in which electrons were embedded, Papaphotis and Tsaparlis (2008) found that many students’ electron cloud descriptions were influenced by the Bohr model or they were in fact a hybrid between the quantum mechanical model and the Bohr model, and Tsaparlis and Papaphotis (2009) suggest that according to a number of students the electron cloud can move in specific orbits.

In any case, some characteristics of ‘Bohr's model’ appeared to be present in students’ thoughts when confronting relevant everyday situations, but the present findings do not support its dominance as a coherent mental model, in the degree at least that the pre-existed research evidence implies (e.g., Fischler and Lichtfield, 1992; Kalkanis et al., 2003). The context of a particular situation is probably a determining factor that significantly affects both the model that a student chooses and the relevant pieces of knowledge that (s)he activates in order to reach an explanation.

Implications for science education

The implications of the present research are important for both theory and practice. It is apparent that, from a theoretical point of view, the findings advocate the fragmented nature of knowledge. The important issue however, is that the ‘fragmented knowledge’ was revealed from a study concerning a subject matter that cannot be easily experienced in everyday life. Although atom models can often be seen in social media, their understanding in scientific terms needs more analysis in classrooms and students’ knowledge on the atomic structure is basically built in schools. As Taber (2001) suggests, in such chemistry subjects, pre-existing knowledge is not based on early life experience as happens in other sciences, like in physics or in biology. Thus, this inconsistency could not be assigned to misconceptions or naïve knowledge from students’ social environment. In contrast, the majority of the students’ knowledge on this issue is basically due to the school science curriculum and teaching, which describe the atomic structure within a quite specific model. Thus, in this case, it could be anticipated that the possibility of finding stable and coherent mental models would be higher, compared to other cases, where the development of intuitive knowledge due to such everyday stimuli has been hypothesized as the cause of stable and theory-like mental models. For instance, the students’ knowledge about the earth could be affected by their intuition, since there are many every day stimuli relevant to earth matters. Thus, evidence advocating ‘theory-free’ knowledge (Nobes et al., 2005; Panagiotaki et al., 2006; Straatemeier et al., 2008) is more probable in that case, compared to this one concerning atomic structure.

The implications for educational practice are also important. Science teachers and curriculum designers can now realize that any students’ learning difficulties on the atomic structure do not originate from the resistance of their coherent mental models. The problem is rather the incapacity of the related mental processes to organize the appropriate pieces of knowledge into structures compatible with the scientific view. According to Taber (2001), this problem begins from the mismatch between the knowledge a teacher believes that students possess and the one students bring to their mind during instructions. One of the reasons causing such mismatches is the students’ inability to relate new knowledge with appropriate existing knowledge – a ‘fragmentation impediment’ according to Taber. As a result, the teachers’ efforts should focus on this point and any introduction to new concepts, phenomena or situations should be manipulated as a reorganizing process of pieces of knowledge (existed and new) and not as an issue concerning coherent mental models for atomic structure. Similarly, curriculum designers should realize that any characteristics of the models they use in a textbook unit could be connected to particular pieces of knowledge in students’ minds and thus, it is not a good idea to manipulate them as solid packages of fixed characteristics throughout a textbook. Since a knowledge of atomic structure is useful for a learner when it helps him/her in understanding other phenomena or everyday situations and taking also into account that the context of a particular situation seems to be a determining learning factor, both teachers and designers should help to this direction. Thus, any teaching content or strategy should try to help students, in realizing and clarifying the pieces of knowledge that they possess for both the particular context of the everyday situation and the atomic structure (which could contain characteristics of different mental models), in forming new pieces of knowledge for the situations under examination and in organizing all these pieces into the mental structure-target. To this extent, teachers and designers should also take into account research findings on students’ individual differences, which have revealed different sources of difficulties and thus, different ways in reorganizing existing and new pieces of knowledge (Tsitsipis et al., 2010, 2012; Papageorgiou et al., 2016a, 2016b).

Finally, a message also conveyed by the present work is the importance of the methodological tools implemented in elaborating theoretical issues in science education, the advances of which should be continuously linked with the educational practice.

Limitations of the study

The present study is limited by a number of factors. First, the sample is relatively medium-sized and even though the consequences are ameliorated by the use of bootstrapping in LCA, there are still concerns relating to the sample idiosyncrasies (Hesterberg et al., 2003). Another limitation concerns the vulnerability of the non-probability convenience sampling that was followed, where participants belonged to schools, in which there was a willingness for cooperation. In addition, the instrument for data collection was constructed for the needs of the present study in an exploratory way and thus, an evolved version in a following replication study would further support the results and the main thesis of the present work.

Conflicts of interest

There are no conflicts to declare.

References

  1. Adbo K. and Taber K. S., (2009), Learners’ mental models of the particle nature of matter: a study of 16 year old Swedish science students, Int. J. Sci. Educ., 31(6), 757–786.
  2. Bao L. and Redish E. F., (2006), Model analysis: representing and assessing the dynamics of student learning, Phys. Rev. Spec. Top. Phys. Educ. Res., 2(1), 010103.
  3. Borsboom D., (2008), Latent variable theory, Measurement, 6(1–2), 25–53.
  4. Clogg C. C., (1995), Latent class models, in Arminger G., Clogg C. C. and Sobel M. E. (ed.), Handbook of statistical modeling for the social and behavioral sciences, New York: Plenum, pp. 311–359.
  5. Cokelez A., (2012), Junior High School Students' Ideas about the Shape and Size of the Atom, Res. Sci. Educ., 42, 673–686.
  6. Cokelez A. and Dumon A., (2005), Atom and molecule: upper secondary school French students' representations in long-term memory, Chem. Educ. Res. Pract., 6(3), 119–135.
  7. Dayton C. M., (1998), Latent class scaling analysis, Thousand Oaks, CA: Sage.
  8. diSessa A. A., (1988), Knowledge in pieces, in Forman G. and Pufall P. B. (ed.), Constructivism in the computer age, Hillsdale, NJ: Lawrence Erlbaum Associates, Inc, pp. 49–70.
  9. diSessa A. A., Gillespie N. and Esterly J., (2004), Coherence versus fragmentation in the development of the concept of force, Cognit. Sci., 28, 843–900.
  10. Fischler H and Lichtfield M., (1992), Modern physics and students; conceptions, Int. J. Sci. Educ., 14(2), 181–190.
  11. Greek Pedagogical Institute, (2003), National Program of Study for Primary and Secondary Education: Science, Athens (Greece): Greek Pedagogical Institute Publications.
  12. Griffiths K. A. and Preston R. K., (1992), Grade-12 students' misconceptions relating to fundamental characteristics of atoms and molecules, J. Res. Sci. Teach., 29(6), 611–628.
  13. Hammer D., (1996), Misconceptions or p-prims: how may alternative perspectives of cognitive structure influence instructional perceptions and intentions? J. Learn. Sci., 5, 97–127.
  14. Harrison A. G. and Treagust D. F., (1996), Secondary students' mental models of atoms and molecules: implications for teaching chemistry, Sci. Educ., 80(5), 509–534.
  15. Harrison A. G. and Treagust D. F., (2000), Learning about atoms, molecules, and chemical bonds: a case study of multiple-model use in grade 11 chemistry, Sci. Educ., 84(3), 352–381.
  16. Harrison A. G., Grayson D. J. and Treagust D. F., (1999), Investigating a grade 11 student's evolving conceptions of heat and temperature, J. Res. Sci. Teach., 36(1), 55–87.
  17. Hatcher L. and Stepansky E. J., (1994), A step-by-step approach to using the SAS system for univariate and multivariate statistics, Cary, NC: SAS Institute.
  18. Hesterberg T., Monaghan S., Moore D., Clipson A. and Epstein R., (2003), Bootstrap methods and permutation tests, Washington, DC: Library of Congress.
  19. Ioannides C. and Vosniadou S. (2002), The changing meanings of force, Cognit. Sci. Q., 2, 5–62.
  20. Jansen B. R. J. and van der Maas H. L. J., (2002), The development of children's rule use on the balance scale task, J. Exp. Child Psychol., 81, 383–416.
  21. Kalkanis G., Hadzidaki P. and Stavrou D., (2003), An instructional model for a radical conceptual change towards quantum mechanics concepts, Sci. Educ., 87, 257–280.
  22. Ke J. L., Monk M. and Duschl R., (2005), Learning introductory quantum physics: sensori-motor experiences and mental models, Int. J. Sci. Educ., 27(13), 1571–1594.
  23. Kline P., (1999), Handbook of Psychological Testing, 2nd edn, London and New York: Routledge.
  24. Magidson J. and Vermunt J. K., (2001), Latent class factor and cluster models, bi-plots and related graphical displays, Soc. Methodol., 31, 223–264.
  25. McKagan S. B., Perkins K. K. and Wieman C. E., (2008), Why we should teach the Bohr model and how to teach it effectively, Phys. Rev. Spec. Top. Phys. Educ. Res., 4, 010103.
  26. Mertens D., (2005), Research and evaluation in education and psychology, London: Sage.
  27. Nakiboglu C., (2003), Instructional misconceptions of Turkish prospective chemistry teachers about orbitals and hybridization, Chem. Educ. Res. Pract., 4(2), 171–188.
  28. Nicoll G., (2001), A report of undergraduates' bonding misconceptions, Int. J. Sci. Educ., 23(7), 707–730.
  29. Nobes G., Martin A. E. and Panagiotaki G., (2005), The development of scientific knowledge of the earth, Br. J. Dev. Psychol., 23, 47–64.
  30. Panagiotaki G., Nobes G. and Banerjee R., (2006), Children's representations of the earth: a methodological comparison, Br. J. Dev. Psychol., 24, 353–372.
  31. Papageorgiou G., Markos A. and Zarkadis N., (2016a), Students' representations of the atomic structure – the effect of some individual differences in particular task contexts, Chem. Educ. Res. Pract., 17(1), 209–219.
  32. Papageorgiou G., Markos A. and Zarkadis N., (2016b), Misconceptions relating to ontological characteristics of the atom. Focusing on students' profiles, Sci. Educ. Int., 27(4), 464–488.
  33. Papaphotis G. and Tsaparlis G., (2008), Conceptual versus algorithmic learning in high school chemistry: the case of basic quantum chemical concepts. Part 2. Students' common errors, misconceptions and difficulties in understanding, Chem. Educ. Res. Pract., 9(4), 332–340.
  34. Park E. J. and Light G., (2009), Identifying Atomic Structure as a Threshold Concept: student mental models and troublesomeness, Int. J. Sci. Educ., 31(2), 233–258.
  35. Petri J. and Niedderer H., (1998), A learning pathway in high-school level quantum atomic physics, Int. J. Sci. Educ., 20(9), 1075–1088.
  36. Redish E. F. and Smith K. A., (2008), Looking beyond content: skill development for engineers, J. Engin. Educ., 97(3), 295–307.
  37. Straatemeier M., van der Maas H. L. J. and Jansen B. R. J., (2008), Children's knowledge of the earth: a new methodological and statistical approach, J. Exp. Child Psychol., 100, 276–296.
  38. Stamovlasis D., Papageorgiou G. and Tsitsipis G. (2013), The coherent versus fragmented knowledge hypotheses for the structure of matter: An investigation with a robust statistical methodology, Chem. Educ. Res. Pract., 14(4), 485–495.
  39. Stevens S. Y., Delgato C. and Krajcik J. S., (2010), Developing a hypothetical multi-dimensional learning progression for the nature of matter, J. Res. Sci. Teach., 47(6), 687–715.
  40. Taber K. S., (2001), Building the structural concepts of chemistry: some consideration from educational research, Chem. Educ. Res. Pract., 2(2), 123–158.
  41. Taber K. S., (2002), Conceptualizing quanta—illuminating the ground state of student understanding of atomic orbitals, Chem. Educ. Res. Pract., 3(2), 145–158.
  42. Taber K. S., (2003), The atom in the chemistry curriculum: fundamental concept, teaching model or epistemological obstacle? Foundat. Chem., 5(1), 43–84.
  43. Taber K. S., (2005), Learning quanta: barriers to stimulating transitions in student understanding of orbital ideas, Sci. Educ., 89(1), 94–116.
  44. Taber K. S., (2008), Conceptual resources for learning science: issues of transcience and grain-size in cognition and cognitive structure, Int. J. Sci. Educ., 30(8), 1027–1053.
  45. Taber K. S., (2013), Upper secondary students' understanding of the basic physical interactions in analogous atomic and solar systems, Res. Sci. Educ, 43(4), 1377–1406.
  46. Taber K. S. and García Franco A., (2010), Learning Processes in Chemistry: Drawing Upon Cognitive Resources to Learn About the Particulate Structure of Matter, J. Learn. Sci., 19, 99–142.
  47. Thomas H. and Horton J. J., (1997), Competency criteria and the class inclusion task: modeling judgments and justifications, Dev. Psychol., 33, 1060–1073.
  48. Tsaparlis G. and Papaphotis G., (2002), Quantum-chemical concepts: are they suitable for secondary students? Chem. Educ. Res. Pract., 3(2), 129–144.
  49. Tsaparlis G. and Papaphotis G., (2009), High-school students' conceptual difficulties and attempts at conceptual change: the case of basic quantum chemical concepts, Int. J. Sci. Educ., 31(7), 895–930.
  50. Tsitsipis G., Stamovlasis D. and Papageorgiou G., (2010), The effect of three cognitive variables on students' understanding of the particulate nature of matter and its changes of state, Int. J. Sci. Educ., 32(8), 987–1016.
  51. Tsitsipis G., Stamovlasis D. and Papageorgiou G., (2012), The effect of three cognitive variables on students' understanding of the particulate nature of matter and its changes of state, Int. J. Sci. Math. Educ., 32(8), 987–1016.
  52. Vermunt J. K. and Magidson J., (2002), Latent class cluster analysis, in Hagenaars J. A. and McCutcheon A. L. (ed.), Applied Latent Class Analysis, Cambridge University Press, pp. 89–106.
  53. Vosniadou S., Skopeliti I. and Ikospentaki K., (2004), Modes of knowing and ways of reasoning in elementary astronomy, Cognit. Dev., 19, 203–222.
  54. Wang C. Y. and Barrow L. H., (2013), Exploring conceptual frameworks of models of atomic structures and periodic variations, chemical bonding, and molecular shape and polarity: a comparison of undergraduate general chemistry students with high and low levels of content knowledge, Chem. Educ. Res. Pract., 14(1), 130–146.
This journal is © The Royal Society of Chemistry 2017