Controllable structure transitions of Mn3O4 nanomaterials and their effects on electrochemical properties†
Yating
Hu
 *a,
Yu
Zhang
b,
Du
Yuan
a,
Xu
Li
b,
Yongqing
Cai
*c and
John
Wang
*a
*a,
Yu
Zhang
b,
Du
Yuan
a,
Xu
Li
b,
Yongqing
Cai
*c and
John
Wang
*a
aDepartment of Materials Science & Engineering, National University of Singapore, 9 Engineering Drive 1, 117576, Singapore. E-mail: msewangj@nus.edu.sg
bInstitute of Materials Research and Engineering, A*STAR (Agency for Science, Technology and Research), 2 Fusionopolis Way, Innovis, Singapore 138634
cInstitute of High Performance Computing, A*Star (Agency for Science, Technology and Research), 1 Fusionopolis Way, Connexis, Singapore 138632
First published on 14th August 2017
Abstract
Mn3O4 with purposely tuned different morphologies, crystal structures and sizes is synthesized using a hydrothermal method with varying processing temperatures, together with the help of a surfactant. Systematic investigations, both by experimental and computational studies, into these Mn3O4 nanomaterials were conducted in order to find the most suitable morphology and a compatible electrolyte for energy storage applications. The Mn3O4 nanofibers with a tunnel size of 1.83 Å in the crystal structure show much higher volumetric capacitance (188 F cm−3 at a scan rate of 1 mV s−1 of cyclic voltammetry test) than two other morphologies/crystal structures, when using 1 M LiCl aq. as the electrolyte. It is demonstrated in this work that crystal morphology and particle size play important roles in determining the capacitance of an electrode material. In addition, the detailed structures, especially the atomic arrangements within the crystalline structure, are crucial in order to choose the most suitable electrolyte.
Conceptual insightsMn3O4, with a high theoretical specific capacitance of ∼1400 F g−1, is a highly promising electrode material for energy storage applications, although it is less studied compared to its MnO2 counterpart. To optimize the electrochemical performance of an electrode material, proper control of the morphology, particle size and crystal structure, and the matching electrolyte are key. In this work, three types of Mn3O4 materials with different morphologies, crystal structures and particle sizes are synthesized using a hydrothermal method, with the help of a suitable surfactant. The thermodynamic reasons behind the formation of different morphologies are discussed and the tunnel sizes in these different crystal structures are established by computational studies. The electrochemical performances of these Mn3O4 materials are then assessed in different electrolytes in order to determine the optimal conditions for supercapacitor applications. The Mn3O4 nanofibers with a tunnel size of 1.83 Å in the crystal structure show much higher volumetric capacitance than two other morphologies/crystal structures, when using 1 M LiCl aq. as the electrolyte. The systematic examination of the crystal structures, morphologies, and particle sizes of these materials and their compatibility with different electrolytes demonstrates a selection routine for the electrode material and suitable electrolyte. This could serve as a guide for future development of other supercapacitor electrode materials, in order to maximize the overall performances. |
Introduction
Manganese oxides (MnOx) have been widely studied as candidates for supercapacitor electrode materials, where great efforts have been focused on improving the specific capacitance through development of various new nanostructures with novel morphologies.1 By adjusting the synthesis conditions, different structural features and morphologies could be obtained, especially for MnO2.2–6 For example, when amorphous MnO2 is reduced under appropriate temperatures, the morphology and chemistry of hydrated MnO2 powders change significantly, towards thermodynamically favoured states.7 Among the widely studied synthesis techniques for developing MnOx nanomaterials are hydrothermal and solvothermal reactions, as they are facile and scalable chemical processes leading to different MnOx nanostructures, such as nanoparticles, nanorods, nanowires, nano-urchins, and nanotubes, by properly choosing the reaction temperature, time, and solvent and surfactant used for the reactions.1,8,9 Morphology is one of the most important factors in optimizing the electrochemical properties.7 It is thus of high interest to investigate the effect of morphology and size of the manganese oxide nanomaterials on their electrochemical performances.In developing a supercapacitor electrode, one of the key considerations that affect the specific capacitance of crystallized MnOx-based electrodes is their crystal structures. For example, MnOx can crystallize into a tunnel-type structure, thus, the capacitance is largely dependent on the features in close relation to the tunnel size and cation intercalation.7 The tunnel size in α-MnO2 and δ-MnO2 is 4.6 and 7.0 Å, respectively, which are suitable for intercalation/de-intercalation of K+ (with ion size of 3.0 Å in water). On the other hand, the tunnel sizes in λ-MnO2 and β-MnO2 are smaller than the effective size of K+ in KOH or other K+ based aqueous electrolytes, therefore, their capacitances are expectedly lower in K+ based electrolytes.1 Manganese can exist in a number of stable oxides, such as MnO, Mn3O4, Mn2O3 and MnO2. These oxides have been reported with a wide diversity of crystal forms, nanoparticle morphology, and level of porosity. Therefore, they exhibit a variety of distinct electrochemical properties.7,10
Similar to MnO2, Mn3O4 is an interesting electrode material for applications in supercapacitors, because of its low cost, environmental compatibility, and high natural abundance.11 The charge storage of Mn3O4 is mainly by Faradaic reactions occurring on the electrode surface with electrolytes, which involves the surface adsorption of electrolyte cations on Mn3O4. In addition, Mn3O4 is highly psedocapacitive, and exhibits a very high theoretical specific capacitance of ∼1400 F g−1.11 It shows similar electrochemical behavior to that of MnO2 as the redox reactions between the III and IV oxidation states of Mnx+ ions occur spontaneously during the charge–discharge process.12 Different processing techniques have been demonstrated to successfully lead to Mn3O4-based materials for use in supercapacitors, such as electrostatic spray deposition,13 hydrothermal growth14–16 and chemical batch deposition.17,18 High gravimetric capacitance (e.g., 420 F g−1 at the scan rate of 5 mV s−1 in cyclic voltammetry) has been reported for the hydrothermally synthesized Mn3O4/MWCNT (multi-walled carbon nanotubes) nanocomposites, however with very poor stability.14 In a recent work, hydrothermally synthesized Mn3O4 nanoparticles are shown with a volumetric capacitance of 55 F cm−3 (equivalent to 152 F g−1) and much improved cycling ability, due to the coexistence of reduced graphene oxide (rGO).19 In addition, the capacitance can be much improved with the nanocomposite consisting of Mn3O4 nanofibers and porous carbon aerogels obtained from anodic-electrochemical deposition (503 F g−1), but limited by the low loading mass.20 Compared to MnO2, Mn3O4 is still much less studied for electrochemical applications.11
In order to achieve a specific capacitance towards the high theoretical value of Mn3O4, it would be of interest to study the different morphologies and crystal structures and their effects on the electrochemical performances. In this work, we have investigated the different morphologies successfully developed by tuning the hydrothermal temperature and controllable crystallite sizes for Mn3O4 nano-octahedrons with the help of surfactant. The thermodynamics behind the formation of these different morphologies are discussed and the tunnel sizes of these different crystal structures are established through computational studies (1.83 to 2.04 Å). The electrochemical performances of these Mn3O4 nanomaterials are then assessed in different electrolytes in order to determine the optimal matching conditions for supercapacitor applications.
Results and discussion
Temperature of hydrothermal growth
Hydrothermal synthesis is one of the most popular solution-based synthesis methods for various nanomaterials of transition metal oxides with specifically tuneable size and morphology.21 As reported in our previous work,22 KMnO4 could be reduced by pyrrole to form manganese oxides of different oxidation states (e.g., MnO2, Mn3O4) during the gel formation reaction. A pyrrole to KMnO4 ratio of 1.0 to 2.0 mol is used to develop Mn3O4 in this work. It has been found that the hydrothermal temperature has a great impact on the morphology and crystal structure of the hydrothermally synthesized metal oxide nanomaterials.21 For example, hydrothermally synthesized WO3 transforms from hexagonal to cubic phase when the temperature is increased to over 160 °C.23 The crystallite size and crystallinity increase with the increasing hydrothermal temperature for TiO2.24 Microspheric-structured BiVO4 could be obtained at a temperature below 160 °C, and the lamina-structured BiVO4 could be developed when the temperature is controlled at 200 °C.25 Thus, through adjusting the hydrothermal temperature (85, 140 and 180 °C), three different morphologies for Mn3O4 nanoparticles are obtained, namely, nanofibers at 85 °C, nanorods at 140 °C and nano-octahedrons at 180 °C of hydrothermal treatment (Fig. 1). These samples are named as MO-F for nanofibers, MO-R for nanorods and MO-O for nano-octahedrons (the one without adding surfactant is named as MO-O0) of Mn3O4, respectively. The nanofibers are ∼10 nm in diameter and ∼100–300 nm in length (Fig. 1a). The nanorods are ∼100 nm in diameter with the lengths being around 1 μm (Fig. 1b). Unlike the stiff nanorods, the nanofibers appear flexible. The lengths of these nanofibers are not too long such that they would not entangle together, when uniform dispersion is required. The nano-octahedrons are ∼30 nm in dimensions (Fig. 1c). | ||
| Fig. 1 TEM images: (a) MO-F, (b) MO-R, and (c) MO-O0, and high resolution TEM showing lattice fringes of the samples (d) MO-F, (e) MO-R and (f) MO-O0. | ||
Individual morphologies of Mn3O4 nanoparticles have been reported, such as, Mn3O4 nanofibers synthesized by electrospinning;26,27 Mn3O4 nanorods synthesized by methods such as a hydrothermal process of different starting materials at 120 °C, grown on Ni foam or with graphene oxide (GO);11,28 and Mn3O4 nano-octahedrons synthesized by a hydrothermal process at 200 °C used as a starting material for a Li ion battery electrode.29,30 To the best of our knowledge, there is no study on the temperature effect of the hydrothermal reaction on the morphology and crystal structures of Mn3O4, as well as their electrochemical performance in comparing the Mn3O4 of different morphologies.
Fig. 2 shows X-ray diffraction (XRD) results for these three samples. It is obvious that they exhibit different crystal structures, although they all are of Mn3O4 (JCPDS #086-2337, #18-0803 and #24-0734). The high resolution TEM images of all three morphologies show good crystallinity and the corresponding crystal planes observed are (220), (211) and (200) for samples MO-F, MO-R and MO-O0, respectively (Fig. 1d–f). It is known that metal oxide crystals with high index planes (with at least one miler index larger than 1) exposed can result in improved chemical or physical performances, due to higher densities of atom steps, edges, kinks, and dangling bonds, which usually show high chemical activity.31,32 Based on the XRD traces, the nanofibers exhibit an orthorhombic crystal structure (space group Pmab) while the nanorods and nano-octahedrons exhibit tetragonal crystal structures (both are in space group I41/amd with different lattice constants).33–36 In general, the conversion from the kinetically favored tetragonal form to the thermodynamically favored orthorhombic form is believed to be driven by an enthalpy gain.37 The orthorhombic structure, which is of lower space-group symmetry is of higher energy and in a relatively metastable state, compared to the tetragonal form which has higher symmetry. This is proved by the density functional theory (DFT) calculations for the total energy of the three phases (Table 1), as the orthorhombic structured sample MO-F has the highest total energy. Therefore, the high-energy orthorhombic structured nanofibers are formed and stabilized at the lowest temperature of a hydrothermal reaction (85 °C), and the tetragonal structured nanorods and nano-octahedrons are formed at the relatively high temperatures of the hydrothermal reaction (140 and 180 °C), in the present work.
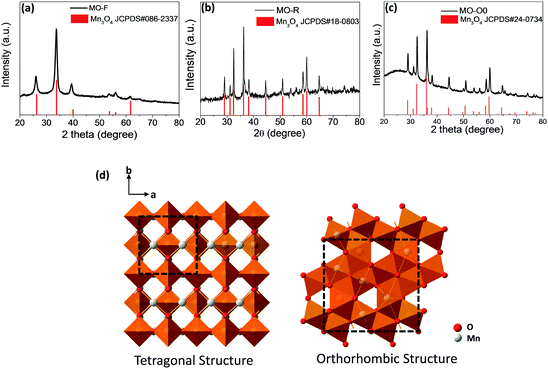 | ||
| Fig. 2 XRD patterns: (a) MO-F, (b) MO-R, and (c) MO-O0, and (d) the crystal structures of the tetragonal and orthorhombic Mn3O4 structures (space group I41/amd and Pmab). | ||
| Sample | Space group | JCPDS # | Total energy calculated (eV) |
|---|---|---|---|
| MO-F | Orthorhombic | 086-2337 | −230.47 |
| MO-R | Tetragonal | 18-0803 | −231.83 |
| MO-O0 | Tetragonal | 24-0734 | −231.78 |
Based on the crystallography data of the three samples, their structures are shown by the schematic figures (see Fig. 2d). Viewed from the c direction of the crystals, it can be seen that both the tetragonal and orthorhombic structures of Mn3O4 have 2 × 2 tunnel structures (as shown by the unit cells marked out in Fig. 2d). Our calculations (more details are shown in Fig. S1, ESI†) suggest that the tunnel size for the two tetragonal phases of Mn3O4 are 2.044 and 2.038 Å (i.e., sample MO-R and MO-O, respectively), while the one for the orthorhombic phase Mn3O4 is 1.83 Å (for sample MO-F).
As mentioned above, the ionic dimension for K+ is 3.0 Å in water, thus, K+ could not tunnel through the bulk of these Mn3O4 nanocrystals and redox reactions could take place only at the surface of the electrode material. Therefore, although KOH aq. is a widely accepted electrolyte for a number of transition metal oxides, it is not suitable for the Mn3O4 materials in this work. The ion size in water could be calculated, mainly based on the equation below:38
| Rion = dion–water − Rwater |
Tuning of particle sizes through CTAB
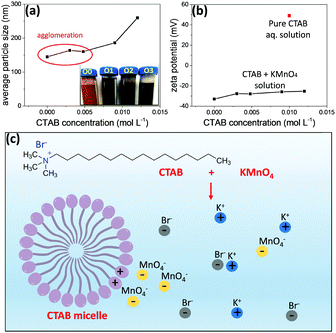
Surfactants are amphiphilic materials containing both apolar long-chain hydrocarbon “tail” and polar “head” groups.42 Cetyltrimethylammonium bromide (CTAB, CH3(CH2)15N(Br)(CH3)3) is a cationic surfactant. It can play a key role in the development of nanostructures, for example, by adsorbing to the nanoparticles to lower the surface energy.43–46 In polar solvents (e.g., water and aqueous solutions), the micellization of surfactant will take place when the concentration of the surfactant concentration is high enough, due to the dual characteristic of the amphiphile. During the micellization, the surfactant molecules arrange themselves into organized molecular assemblies known as micelles. CTAB is water soluble and forms micelles when the concentration is above its critical micelle concentration (CMC).47 The CMC for CTAB in MnO4− solution is 2.0 × 10−4 M, calculated on the basis of specific conductance vs. concentration curves.47Different amounts of CTAB were added into the precursors prior to the gel formation of Mn3O4 to develop nano-octahedrons of different sizes. The concentrations of CTAB in the three samples (MO-O1, MO-O2 and MO-O3) were controlled at 5.0 × 10−3, 9.0 × 10−3 and 1.2 × 10−2 M, respectively, while the sample MO-O0 had no CTAB added. As shown in Fig. 3, Mn3O4 nano-octahedrons of various sizes could be obtained. By adding CTAB (concentration of 5.0 × 10−3 or 9.0 × 10−3 M), the Mn3O4 nano-octahedrons increased in size from ∼30 nm to ∼50 and ∼200 nm (Fig. 3a–c). At a concentration of 1.2 × 10−2 M, the nano-octahedrons start to transform into nanocubes in addition to the size increasing from 200 nm to 300 nm (Fig. 3d). The rather uniform morphologies observed for these nano-octahedrons are shown by SEM images (Fig. S2, ESI†). It was noted that the aqueous dispersion of nano-octahedrons became darker in appearance, due to the size change (inset of Fig. 4a). Indeed, the average hydrodynamic sizes measured by the dynamic light scattering (DLS) indicates that adding CTAB had caused an increase in the particle size (Fig. 4a). The discrepancy in sizes measured between the TEM and the DLS measurements is due to the aggregation of smaller nano-octahedrons.
When the CTAB aqueous solution is added into KMnO4 aqueous solution, the CH3(CH2)15N(CH3)3+ ions from CTAB will attract MnO4− ions through electrostatic interactions. Due to the bulky CTAB micelle formed and being positively charged, MnO4− ions will be attracted to the CTAB micelle. Therefore, the local concentration of MnO4− ions is much increased (as shown in the scheme in Fig. 4c). As the inorganic species can form a stable crystalline Mn3O4 structure with high lattice energy, they show a strong tendency to precipitate from the solution and form Mn3O4 nano-octahedrons; the surfactant remains in solution and continues to accumulate MnO4− ions for the growth of Mn3O4 nano-octahedrons. With an increasing concentration of CTAB, a larger number of micelles are formed. Under electrostatic interactions, there are much more MnO4− ions around the micelles during the nuclei growth stage, thus, larger nano-octahedrons are formed.48 However, on the other hand, when the CTAB concentration is too high (e.g., 1.2 × 10−2 M for sample MO-O3), the nano-octahedrons start to transform into nanocubes (Fig. 3d and Fig. S2, ESI,† where the nano-octahedrons are marked out in yellow and nanocubes in red). These nanocubes are in a Mn2O3 crystal structure, based on the XRD phase identification results (Fig. S3, ESI†). This could be due to the fact that when the local concentration of MnO4− is too high, the reduction of MnO4− by pyrrole is not complete. Thus, some Mn2O3 is formed instead of pure Mn3O4 nanocrystals.
To further confirm this hypothesis, the zeta potential of the mixture of CTAB and KMnO4 aqueous solutions, pure KMnO4 aqueous solution (0 M CTAB) and CTAB (0.01 M) aqueous solution alone were measured (Fig. 4b). The 0.01 M CTAB aqueous solution showed a zeta potential of 50 mV, due to the micelles formed within the solution (CMC of CTAB in water is 1 × 10−3 M). In the presence of KMnO4, the zeta potentials of the mixture solutions were all negative, indicating that the negatively charged MnO4− ions are surrounding the micelle. When the concentration of CTAB is increased, the number of micelles thus increases, but the number of MnO4− ions distributed to each micelle decreases. It therefore reduces the absolute value of the zeta potential.43 To verify whether or not the CTAB was thoroughly removed from the sample after washing the hydrothermal product with DI water, FTIR analyses of the dried powders were conducted (Fig. S4a, ESI†). As shown by the FTIR spectrum, there is no stretching bands at around 3000 cm−1 (the symmetric and asymmetric stretching bands of the methylene chains in CTAB molecules are at around 2850 and 2920 cm−1, respectively).37 The bands at around 500–700 cm−1 correspond to the Mn–O stretching and bending vibrations,49 and the remaining bands at 956, 1101 and 1155 cm−1 correspond to the C–O and O–H groups from the minimal amount of the hydrothermal reaction residuals. In addition, as shown by the TGA result (Fig. S4b, ESI†), the weight drop observed at around 200 °C is less than 0.5%, indicating that there is a minimal amount of CTAB or other residuals left (the thermal decomposition temperature for CTAB is known to be around 240 °C). The slight increase in the sample weight at around 450 °C might well be due to the oxidation of Mn3O4 to MnO2.
Electrochemical characterization of Mn3O4 nanoparticles
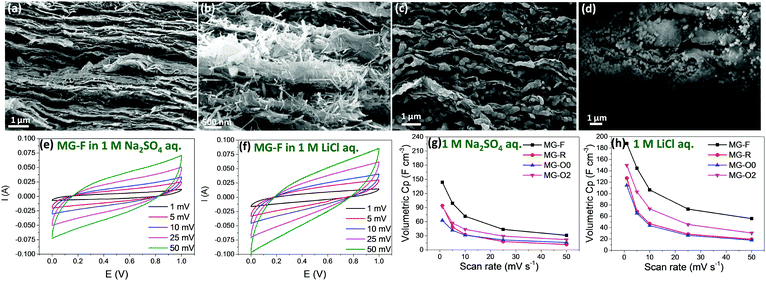
To make the best use of the pseudocapacitive MnOx materials, an electrically conductive substrate is needed when preparing the electrode. Graphene sheets, with the desired electrical, mechanical, and thermal properties have been widely used as a conductive support for electrochemical energy storage materials.50–56 By making use of graphene or rGO sheets, a flexible electrode could be obtained with high electrical conductivity and without the need for a chemical binder. Nanocomposite-type materials of graphene and metal oxides, such as Ni(OH)2/graphene,57 SnO2/graphene58 and MnO2/graphene59,60 have been demonstrated to be promising for high energy and power density energy storage devices. To examine the electrochemical properties of the above mentioned Mn3O4 nanofibers, nanorods and nano-octahedrons with different sizes, they are assembled with rGO sheets into flexible hybrid Mn3O4 nanoparticles/rGO paper (samples MG-F, MG-R, MG-O0 and MG-O2), using the method that we have previously developed.61Fig. 5a–d show the cross section SEM images of these hybrid papers. The Mn3O4 nanofibers and nanorods could be evenly dispersed among the rGO sheets (Fig. 5a and b). However, it is observed that the small-sized nano-octahedrons (∼30 nm) tend to aggregate (Fig. 5c) while the large sized nano-octahedrons (∼200 nm) could be dispersed more evenly among the rGO nanosheets (Fig. 5d).The CV and Electrical Impedance Spectroscopy (EIS) of these hybrid papers were measured using Swagelok 2-electrode cells in 1.0 M Na2SO4 and LiCl aqueous electrolytes, respectively. The loading of active materials for all samples is controlled at about 0.8 g cm−3. It is known that MnOx materials do not show redox peaks in their CV curves, as the pseudocapacitive charge storage mechanism is based on the successive multiple surface redox reactions.62 Based on the experimental results (Fig. 5e–h and Fig. S5, ESI†), we have three main observations. Firstly, the volumetric capacitance calculated from CV measurements showing that sample MG-F (hybrid Mn3O4 nanofibers/rGO paper) exhibits the highest volumetric capacitance in both electrolytes (Fig. 5g and h), assumed mainly due to the smallest dimension (i.e., 10 nm in diameter) that possesses a higher surface area than that of either nanorods or nano-octahedrons (surface area measured by N2 adsorption results shown in Fig. S6, ESI†), as well as the uniform distribution among the rGO sheets. The hybrid paper with smaller Mn3O4 nano-octahedrons (sample MG-O0) shows a lower capacitance than the one with bigger Mn3O4 nano-octahedrons (sample MG-O2), due to the aggregation of the small nano-octahedrons that would reduce the effective surface of the redox reaction for Mn3O4. The impedance results show that the electrical conductivities of all samples except for sample MG-O0 are very close to each other. MG-O0 shows a much higher diffusion resistance due to the aggregated nano-octahedrons (Fig. S5a, ESI†), as discussed above.
Secondly, when comparing individual samples measured in two different electrolytes, the volumetric capacitance obtained using 1 M LiCl aq. is much higher than that using a 1 M Na2SO4 aq. electrolyte, especially at low scan rates (volumetric capacitance for all samples under different scan rates of CV measurements and in different electrolytes are listed in Table S1, ESI†). For example, sample MG-F shows 31% increment in terms of volumetric capacitance at the scan rate of 1 mV s−1 of CV measurements, when using 1 M LiCl aq. as the electrolyte instead of 1 M Na2SO4 aq. As mentioned earlier, the size range of Li+ in water is well below the dimensional range of the tunnel sizes of all three different Mn3O4 crystal structures (1.14 to 1.44 Å for Li+vs. 1.83 to 2.04 Å for the tunnel sizes). Therefore, the Li+ in water has very high opportunities of tunnelling through into the bulk of these Mn3O4 materials. On the other hand, the size range of Na+ in water is 1.84 to 2.04 Å, which is about the same as the tunnel sizes of the Mn3O4 nanorods and nano-octahedrons, and bigger than the tunnel size of the nanofibers. Thus, the possibility of Na+ tunnelling through these Mn3O4 materials is low, especially for the nanofibers. As a result, redox reactions involving Na+ mainly take place on the surface of the Mn3O4 nanocrystal electrodes, while those involving Li+ could take place not only on the surface of the electrode but also in the bulk.
However, it is also observed that the difference in volumetric capacitance by using these two electrolytes at high scan rates is quite small. In other words, the retain rates of volumetric capacitance obtained by using LiCl are lower than those with Na2SO4 aq. electrolytes. This might well be due to the fact that, at high scan rates, the redox reactions in the bulk are limited by the slow ion diffusion.63 In addition, the cycling stabilities of all four samples are tested at 2 A cm−3 current density, in 1 M LiCl aq. for 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles (Fig. S7, ESI†). The Mn3O4 nanofibers and nanorods showed better stabilities upon cycling (∼80% retention after 10
000 cycles (Fig. S7, ESI†). The Mn3O4 nanofibers and nanorods showed better stabilities upon cycling (∼80% retention after 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles of charge–discharge), mostly due to better dispersion and less aggregation upon cycling. When compared to other Mn3O4-based supercapacitor electrodes, the Mn3O4 nanofiber also shows great improvement in terms of volumetric capacitance.64,65
000 cycles of charge–discharge), mostly due to better dispersion and less aggregation upon cycling. When compared to other Mn3O4-based supercapacitor electrodes, the Mn3O4 nanofiber also shows great improvement in terms of volumetric capacitance.64,65
In short, while crystal morphology plays an important role in determining the capacitance of an electrode material (e.g., higher surface area can contribute to more redox active sites), it is also important to study the detailed crystal structure, especially the atomic arrangements within the crystalline structure, in order to choose the most suitable electrolyte. For example, the Mn3O4 nanofiber material with a tunnel size of 1.83 Å in the crystal structure shows a much higher volumetric capacitance than the other two morphologies/crystal structures, when using 1 M LiCl aq. as the electrolyte. Therefore, it is highly recommended that for future study of other supercapacitor electrode materials, a systematic examination of the crystal structures, morphologies, and particle sizes of the material as well as the compatibility with different electrolytes should be carried out, similar to what has been done in this work, in order to maximize the electrochemical performances.
Conclusions
Mn3O4 nanoparticles of different morphologies, i.e., nanofibers, nanorods and nano-octahedrons have been developed by hydrothermal reactions at different temperatures. The effects of synthesis temperature on the morphology and crystal structure of the Mn3O4 nanoparticles are studied and clarified. The thermodynamic reasons behind the formation of the different crystal structures are discussed, where the tunnel sizes of these crystalline materials are calculated. Different-sized nano-octahedrons can be further developed by using CTAB as a surfactant during the hydrothermal process. The mechanism of how CTAB has affected the size of the resultant nano-octahedrons is examined and demonstrated. Upon examining the electrochemical properties of these Mn3O4 materials using rGO as a conductive substrate, the Mn3O4 nanofibers appear to be the most promising candidate due to their optimal sizes and good dispersion in the rGO sheets. In addition, LiCl aq. has been found to be an optimum aqueous electrolyte for the Mn3O4 nanofibers, due to the smaller size of Li+ than the tunnel size of the electrode material. The systematic examination of Mn3O4 of different crystal structures and morphologies for electrochemical applications, as well as the compatibility with different electrolytes, could serve as a guide for the future selection and development of other crystalline electrode materials for energy storage device applications.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge the support of the MOE (Singapore) for this research work (tier 2, MOE2015-T2-2-094), conducted at the National University of Singapore.References
- M. Huang, F. Li, F. Dong, Y. X. Zhang and L. L. Zhang, J. Mater. Chem. A, 2015, 3, 21380 CAS.
- M. Toupin, T. Brousse and D. Bélanger, Chem. Mater., 2002, 14, 3946 CrossRef CAS.
- X.-h. Yang, Y.-g. Wang, H.-m. Xiong and Y.-y. Xia, Electrochim. Acta, 2007, 53, 752 CrossRef CAS.
- P. Ragupathy, D. H. Park, G. Campet, H. N. Vasan, S.-J. Hwang, J.-H. Choy and N. Munichandraiah, J. Phys. Chem. C, 2009, 113, 6303 CAS.
- J. N. Broughton and M. J. Brett, Electrochem. Solid-State Lett., 2002, 5, A279 CrossRef CAS.
- M.-S. Wu, Appl. Phys. Lett., 2005, 87, 153102 CrossRef.
- W. Wei, X. Cui, W. Chen and D. G. Ivey, Chem. Soc. Rev., 2011, 40, 1697 RSC.
- M. Xu, L. Kong, W. Zhou and H. Li, J. Phys. Chem. C, 2007, 111, 19141 CAS.
- G. Cheng, S. Xie, B. Lan, X. Zheng, F. Ye, M. Sun, X. Lu and L. Yu, J. Mater. Chem. A, 2016, 4, 16462 CAS.
- G. Wang, L. Zhang and J. Zhang, Chem. Soc. Rev., 2012, 41, 797 RSC.
- J. W. Lee, A. S. Hall, J.-D. Kim and T. E. Mallouk, Chem. Mater., 2012, 24, 1158 CrossRef CAS.
- Q. Jiangying, G. Feng, Z. Quan, W. Zhiyu, H. Han, L. Beibei, W. Wubo, W. Xuzhen and Q. Jieshan, Nanoscale, 2013, 5, 2999 RSC.
- K.-W. Nam and K.-B. Kim, J. Electrochem. Soc., 2006, 153, A81 CrossRef CAS.
- A. Guimin, Y. Ping, X. Meijun, L. Zhimin, M. Zhenjiang, D. Kunlun and M. Lanqun, Nanotechnology, 2008, 19, 275709 CrossRef PubMed.
- C.-C. Hu, Y.-T. Wu and K.-H. Chang, Chem. Mater., 2008, 20, 2890 CrossRef CAS.
- H. Jiang, T. Zhao, C. Yan, J. Ma and C. Li, Nanoscale, 2010, 2, 2195 RSC.
- D. P. Dubal, D. S. Dhawale, R. R. Salunkhe, S. M. Pawar, V. J. Fulari and C. D. Lokhande, J. Alloys Compd., 2009, 484, 218 CrossRef CAS.
- D. P. Dubal, D. S. Dhawale, R. R. Salunkhe, V. J. Fulari and C. D. Lokhande, J. Alloys Compd., 2010, 497, 166 CrossRef CAS.
- T. Xiong, W. S. V. Lee, X. Huang and J. Xue, J. Mater. Chem. A, 2017, 5, 12762 CAS.
- Y. H. Lin, T. Y. Wei, H. C. Chien and S. Y. Lu, Adv. Energy Mater., 2011, 1, 901 CrossRef CAS.
- X. Xia, Y. Zhang, D. Chao, C. Guan, Y. Zhang, L. Li, X. Ge, I. M. Bacho, J. Tu and H. J. Fan, Nanoscale, 2014, 6, 5008 RSC.
- Y. Hu and J. Wang, J. Power Sources, 2015, 286, 394 CrossRef CAS.
- R. Huang, Y. Shen, L. Zhao and M. Yan, Adv. Powder Technol., 2012, 23, 211 CrossRef CAS.
- J. Yu, G. Wang, B. Cheng and M. Zhou, Appl. Catal., B, 2007, 69, 171 CrossRef CAS.
- D. Ke, T. Peng, L. Ma, P. Cai and K. Dai, Inorg. Chem., 2009, 48, 4685 CrossRef CAS PubMed.
- K.-N. Jung, J.-I. Lee, S. Yoon, S.-H. Yeon, W. Chang, K.-H. Shin and J.-W. Lee, J. Mater. Chem., 2012, 22, 21845 RSC.
- C. Shao, H. Guan, Y. Liu, X. Li and X. Yang, J. Solid State Chem., 2004, 177, 2628 CrossRef CAS.
- D. Li, F. Meng, X. Yan, L. Yang, H. Heng and Y. Zhu, Nanoscale Res. Lett., 2013, 8, 535 CrossRef PubMed.
- F. Wang, X. Wang, Z. Chang, Y. Zhu, L. Fu, X. Liu and Y. Wu, Nanoscale Horiz., 2016, 1, 272 RSC.
- J.-S. Kim, K. Kim, W. Cho, W. H. Shin, R. Kanno and J. W. Choi, Nano Lett., 2012, 12, 6358 CrossRef CAS PubMed.
- X.-G. Han, H.-Z. He, Q. Kuang, X. Zhou, X.-H. Zhang, T. Xu, Z.-X. Xie and L.-S. Zheng, J. Phys. Chem. C, 2009, 113, 584 CAS.
- W. Zhong Lin, J. Phys.: Condens. Matter, 2004, 16, R829 CrossRef.
- S. Gupta, Y. Zhong, M. Mahapatra and P. Singh, Int. J. Hydrogen Energy, 2015, 40, 13479 CrossRef CAS.
- H. Zhang, L. Jing, J. Zeng, Y. Hou, Z. Li and M. Gao, Nanoscale, 2014, 6, 5918 RSC.
- C. Zhang, L. Han, W. Liu, H. Yang, X. Zhang, X. Liu and Y. Yang, CrystEngComm, 2013, 15, 5150 RSC.
- X. Sun, P. Liu, Y. Gu, T. E. Rufford and X. S. Zhao, RSC Adv., 2016, 6, 44717 RSC.
- K. Robeyns, P. Herdewijn and L. Van Meervelt, Acta Crystallogr., Sect. F: Struct. Biol. Cryst. Commun., 2010, 66, 1028 CrossRef CAS PubMed.
- Y. Marcus, Chem. Rev., 1988, 88, 1475 CrossRef CAS.
- K. Zhang, X. Han, Z. Hu, X. Zhang, Z. Tao and J. Chen, Chem. Soc. Rev., 2014, 44, 699 RSC.
- L. P. Wang, L. Yu, X. Wang, M. Srinivasan and Z. J. Xu, J. Mater. Chem. A, 2015, 3, 9353 CAS.
- M. D. Slater, D. Kim, E. Lee and C. S. Johnson, Adv. Funct. Mater., 2013, 23, 947 CrossRef CAS.
- A. Dominguez, A. Fernandez, N. Gonzalez, E. Iglesias and L. Montenegro, J. Chem. Educ., 1997, 74, 1227 CrossRef CAS.
- I. Gorelikov and N. Matsuura, Nano Lett., 2008, 8, 369 CrossRef CAS PubMed.
- H. Yan, X.-h. Zhang, J.-m. Wu, L.-q. Wei, X.-g. Liu and B.-s. Xu, Powder Technol., 2008, 188, 128 CrossRef CAS.
- Y.-X. Wang, J. Sun, X. Fan and X. Yu, Ceram. Int., 2011, 37, 3431 CrossRef CAS.
- Y.-K. Peng, C.-W. Lai, C.-L. Liu, H.-C. Chen, Y.-H. Hsiao, W.-L. Liu, K.-C. Tang, Y. Chi, J.-K. Hsiao, K.-E. Lim, H.-E. Liao, J.-J. Shyue and P.-T. Chou, ACS Nano, 2011, 5, 4177 CrossRef CAS PubMed.
- M. A. Malik and Z. Khan, Colloids Surf., B, 2009, 72, 253 CrossRef CAS PubMed.
- Y. Liu, Y. Zhang and J. Wang, CrystEngComm, 2013, 15, 791 RSC.
- D. P. Dubal, D. S. Dhawale, R. R. Salunkhe and C. D. Lokhande, J. Electrochem. Soc., 2010, 157, A812 CrossRef CAS.
- P. Xiong, J. Zhu, L. Zhang and X. Wang, Nanoscale Horiz., 2016, 1, 340 RSC.
- Y. Hu, C. Guan, Q. Ke, Z. F. Yow, C. Cheng and J. Wang, Chem. Mater., 2016, 28, 7296 CrossRef CAS.
- F. Xiao, S. Yang, Z. Zhang, H. Liu, J. Xiao, L. Wan, J. Luo, S. Wang and Y. Liu, Sci. Rep., 2015, 5, 9359 CrossRef CAS PubMed.
- C.-C. Tu, L.-Y. Lin, B.-C. Xiao and Y.-S. Chen, J. Power Sources, 2016, 320, 78 CrossRef CAS.
- H. Gao, F. Xiao, C. B. Ching and H. Duan, ACS Appl. Mater. Interfaces, 2012, 4, 7020 CAS.
- Q. Wu, Y. Xu, Z. Yao, A. Liu and G. Shi, ACS Nano, 2010, 4, 1963 CrossRef CAS PubMed.
- C. Yang, J. Shen, C. Wang, H. Fei, H. Bao and G. Wang, J. Mater. Chem. A, 2014, 2, 1458 CAS.
- J. W. Lee, T. Ahn, D. Soundararajan, J. M. Ko and J.-D. Kim, Chem. Commun., 2011, 47, 6305 RSC.
- S. Wang, S. P. Jiang and X. Wang, Electrochim. Acta, 2011, 56, 3338 CrossRef CAS.
- J. Zhu and J. He, ACS Appl. Mater. Interfaces, 2012, 4, 1770 CAS.
- Y. M. He, W. J. Chen, X. D. Li, Z. X. Zhang, J. C. Fu and C. H. Zhao, ACS Nano, 2013, 7, 174 CrossRef CAS PubMed.
- Y. Hu, C. Guan, G. Feng, Q. Ke, X. Huang and J. Wang, Adv. Funct. Mater., 2015, 25, 7291 CrossRef CAS.
- P. Simon and Y. Gogotsi, Nat. Mater., 2008, 7, 845 CrossRef CAS PubMed.
- A. Ghosh, V. T. Le, J. J. Bae and Y. H. Lee, Sci. Rep., 2013, 3, 2939 CrossRef PubMed.
- T. Xiong, W. S. V. Lee, X. Huang and J. M. Xue, J. Mater. Chem. A, 2017, 5, 12762 CAS.
- J.-X. Feng, S.-H. Ye, X.-F. Lu, Y.-X. Tong and G.-R. Li, ACS Appl. Mater. Interfaces, 2015, 7, 11444 CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental details and supporting results. See DOI: 10.1039/c7nh00078b |
| This journal is © The Royal Society of Chemistry 2017 |