Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Imaging the dynamics of ion–molecule reactions
Eduardo
Carrascosa
 ,
Jennifer
Meyer
,
Jennifer
Meyer
 and
Roland
Wester
and
Roland
Wester
 *
*
Institut für Ionenphysik und Angewandte Physik, Universität Innsbruck, Technikerstraße 25, 6020 Innsbruck, Austria. E-mail: roland.wester@uibk.ac.at; Tel: +43 512 507 52620
First published on 14th November 2017
Abstract
A range of ion–molecule reactions have been studied in the last years using the crossed-beam ion imaging technique, from charge transfer and proton transfer to nucleophilic substitution and elimination. This review presents the detailed insights that have been gained with respect to the dynamics of both cation–molecule and anion–molecule reactions studied with this method. In particular, we show the recent progress that has been achieved to understand the atomistic energetics and dynamics of ion–molecule reactions, such as the effects of vibrational quantum states, the formation of carbon–carbon bonds, and the competition between nucleophilic substitution and elimination.
Introduction
Ion–molecule reactions constitute an interdisciplinary research area that bridges chemistry and physics. This area has already attracted interest for many decades and still continues to rejuvenate itself. Ions are found in gaseous, liquid, and solid forms of matter, their spectral and collisional properties are therefore of interest for very different applications. In the gas phase, reactions of isolated ions with other neutral atoms or molecules are described by collisional cross sections that are much larger than usual neutral–neutral scattering cross sections.1 The long-range interaction between the charge of the ion and the electrical polarizability, dipole or quadrupole moment of the neutral is responsible for this and renders ion–molecule reactions very important for the time evolution of ionized gases. The Earth's ionosphere, atmospheres of other planets or planetary satellites, and the gas clouds in the interstellar medium of our and other galaxies are important examples from our natural environment.2–4 Plasma discharges used for semiconductor etching or tokamak plasmas and plasma-wall interactions in fusion research represent technical applications where ion–molecule reactions are important.5 The temperatures at which ion–molecule reactions occur under these vastly different conditions range from few Kelvin in interstellar space to many thousands of Kelvin in atmospheric or technical plasmas.It has already been known for the most part of the last century that gas phase reactions of ions with neutral atoms or molecules are important in weakly ionized media, such as the ionosphere. Many types of ion–molecule reactions have been identified and studied, but for many ion–molecule reactions that occur in our environment or in the interstellar medium detailed information on their reaction kinetics, product branching ratios, and reaction dynamics are still lacking. The simplest type of reaction, charge transfer, is often the starting point for chemical reaction networks, initiated when photon impact, cosmic ray ionization, or electron impact ionization creates a positively charged ion. Driven by the difference in ionization potential, this simple reaction can show intriguing features, because the ionization energy difference may be released to either product kinetic energy or to internal excitation depending on the details of the interaction potential. As discussed below for reactions of argon cations, this can also affect the total reaction cross section. Proton transfer and insertion reactions are other types of reactions that are frequently found for positively charged ions. For instance, interstellar chemistry is generally accepted to be initiated by reactions of the trihydrogen cation (H3+) with abundant interstellar atoms or molecules such as C, O, N2 or CO.6,7 These reactions open up different astrochemical networks that ultimately lead to aldehydes, carboxylic acids, amino acids etc.8
Anion–molecule reactions9 are also important in many environments, in particular when the densities are high enough that free electrons can attach to neutrals to form negative ions, such as in the lower ionosphere of the Earth. Negative ions have also been found in the atmosphere of the moon Titan and in several interstellar molecular clouds, which has sparked a lot of interest in the formation and destruction of these anions. Negative ion reactions often feature a sizable potential barrier at short range, which can be attributed to electron–electron repulsion by electrostatic forces and the Pauli exclusion principle. Together with the long-range attractive interaction this leads to potential energy landscapes with two characteristic minima along the reaction coordinate. A range of reaction types are found for negative ions, such as associative detachment, nucleophilic substitution, and base-induced elimination. The dynamics of such reactions are discussed below.
The primary interest in an ion–molecule reaction is usually the total reaction cross section or rate coefficient. Several experimental techniques have been developed to measure ion–molecule reaction rate coefficients as a function of temperature or collision energy and investigate how they compare to the classical Langevin or capture cross section.10,11 Widely used techniques to measure ion–molecule reaction kinetics are selected ion flow tubes,12 guided ion beams,13 supersonic flows (CRESU),14 or radiofrequency ion trapping.15 Recently, the combination of ion and neutral atom cooling and trapping has opened up an active field studying ultracold ion-atom collisions.16
To understand in detail why and how a reaction occurs, one has to move beyond the total reaction cross section and investigate the reaction dynamics. This is the topic of the present review. The term dynamics in general refers to the characteristics that describe how a set of reactants evolve into product atoms or molecules.11 In the time-dependent description of quantum mechanics, the dynamics can be described by a multidimensional molecular wavepacket that is initialized at the reactants and evolves into products. In the equivalent time-independent description, the dynamics are described by the fully differential reactive scattering cross section, which depends on the internal quantum states of all reactants and products, on the relative velocity, and on the initial and final orbital angular momentum. Experimentally, neither the full time-dependent nor time-independent dynamics can be observed with state-of-the art techniques. In practice, many reaction dynamics experiments probe the time-independent differential scattering cross section as a function of initial and final velocity and scattering angle. Additional control of the internal quantum states of the reactants is exerted as far as can be achieved. In this review, the dynamics of ion–molecule reactions are discussed as obtained from crossed-beam studies with the velocity map imaging technique.17 In principle, also direct femtosecond pump–probe experiments on chemical reactions can be performed, but there the reactants have to be already in close proximity when a pump pulse initiates the dynamics.18–20
Reaction dynamics are driven by the interaction potential, usually the relevant Born–Oppenheimer potential hypersurface or several coupled hypersurfaces. For ion–molecule reactions, the interaction is strongly attractive at large reactant separations and leads to deep energy minima that may or may not show one or several barriers at short internuclear separation. Such barriers, even if they are energetically below the energy of the reactants can have a profound influence on the dynamics. Furthermore, the dwell time of the reaction complex in the energy minima and the statistical or non-statistical coupling among the rovibrational degrees of freedom change the reaction dynamics and the branching into different open product channels. All these aspects can depend on the translational energy and the thermal or non-thermal excitation of internal quantum states of the reactants.
To experimentally unravel reaction dynamics, crossed-beam reactive scattering experiments have been performed in the past on a number of ion–molecule reactions using the rotatable detector technique.21 Furthermore, the guided-ion-beam technique was employed to extract total and differential scattering cross sections.22 These studies focused mostly on three- or four-atom reactions, where the count rates of the experiments and the preparation of reactant ion beams did not pose severe limitations. The development of the velocity map imaging (VMI) technique17,23 has changed this and offered a substantially improved method to measure product differential scattering cross sections. A VMI spectrometer acts as a detector with a 4π solid angle of acceptance, which improves the detection efficiency for reaction products by orders of magnitude compared to a rotatable detector. It also decouples sensitivity and angular resolution.24,25 Examples for crossed-beam scattering experiments for neutral molecules that have exploited the VMI technique are studies of the H + D2 reaction26 or reactions of F, Cl and O with CH4.27–29
The first application of velocity map imaging to study ion–molecule reactive scattering came in 2002 by Weisshaar and co-workers, who studied reactions of cobalt cations with different hydrocarbon molecules. In their experiment the cations were created by pulsed laser ionization directly in the interaction region.30 In the experiment that we have set up a few years later a spatially separated ion source was employed,31 which had also been the concept used in previous experiments employing rotatable detectors. This yields a lot of flexibility to create and control different ionic species, in particular also negative ions. In addition our setup includes a radiofrequency ion trap15,32 to pre-cool the ions prior to crossing the neutral reactant beam. This facilitates the reduction of the collision energy spread down to about 200 meV (FWHM) and allows for the preparation of internally cold molecular ions.32 Our velocity map imaging spectrometer, which incorporates correlated position and arrival time measurements to determine three-dimensional product velocity distributions, has been described in detail in previous publications.33–37 We therefore do not present the experimental method in this review. In the ion–molecule imaging experimental setup by Farrar and co-workers a versatile ion beam is combined with a supersonic beam source that is also equipped to produce neutral radicals. Scattering images are acquired with a two-dimensional spectrometer. The images are then unfolded with an experimental machine function.38
In the following, this article provides an account of the reaction dynamics experiments on ion–molecule reactions that have been carried out during the last years using the velocity map ion imaging technique. The interpretation of the experimental results always benefits substantially from comparison with high-level dynamics calculations and several references to such calculations will be given. The next section discusses different types of cation–molecule reactions, followed by a description of negative ion–molecule reactions. At the end we give an outlook with our personal view on the future of the field.
Cation-neutral reactions
Cations can be formed by interactions with energetic particles. Thus, their chemistry is important in high energy environments such as the upper planetary atmosphere, regions of the interstellar medium or technical plasmas. The charge transfer between a cation and a neutral molecule is a prominent reaction channel once it is energetically accessible. It is a conceptually simple reaction just transferring an electron, but it is often a first step that triggers a cascade of further elementary reactions.39,40 In the case of near resonance between both reactants, the transfer of an electron will happen with minimal momentum transfer. The newly formed ion will move with the same velocity as the neutral precursor. However, resonance phenomena can dominate the dynamics and energetics and lead to a break down of the Born–Oppenheimer approximation. In reactants with a hydrogen bond, the hydrogen atom transfer reaction competes with the charge transfer. Hydrogen transfer reactions take up key positions in molecular networks within the interstellar medium,41,42 the atmosphere of planets43 and also biomolecular environments.44,45 The hydrogen can be transferred as proton H+, H atom radical or even as a hydride H− anion. Reactive collisions might also lead to the formation of new bonds with heavier elements, such as carbon or nitrogen. The reactions investigated in the next paragraphs range from resonance effects in atom–diatom charge transfer to bond forming reactions. In many reactions, charge transfer is only the first elementary reaction which is followed by secondary processes such as dissociation. A special case of competing pathways is the formation of isomeric species which will be discussed for the formation of HOC+/HCO+.Resonances in Ar+ diatom charge transfer reactions
Charge transfer reactions commonly proceed at long range with minimal momentum transfer between both reactants. However, the change in charge state is likely to induce a structural change of the molecule's shape going from the neutral to the ionic species, which affects its vibrational motion.46,47 Near-resonant channels along the reaction coordinate, which lead to product ions in specific rovibrational states, can result in a break down of the Born–Oppenheimer approximation48 which makes the accurate theoretical description of the experimental results challenging.In the reaction of the argon cation Ar+ with molecules resonant charge transfer channels involving specific vibrational states have been observed.40,49–51 In the reaction with molecular nitrogen N2 (reaction (1)),
| Ar+(2PJ) + N2(1Σ+g) → Ar(1S0) + N2+(2Σ+g,v′) | (1) |
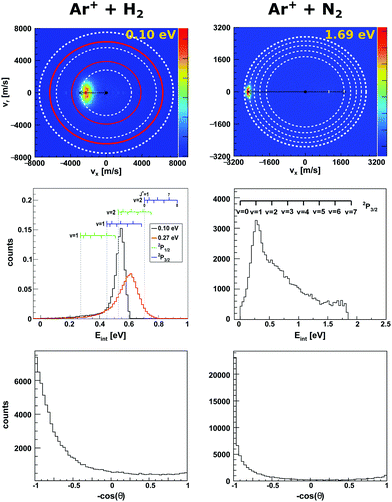 | ||
| Fig. 1 Experimental reactive scattering results for the charge transfer reactions Ar+ + H2 (left column) and Ar+ + N2 (right column). The upper panels show the H2+ and N2+ product velocity distributions. The right color bars represent a linear ion intensity scale. For Ar+ + H2, the rings drawn into the velocity distributions give the kinematic limit for Ar+(2P1/2) (white rings) and Ar+(2P3/2) (red rings) with the outermost rings for the H2+ vibrational ground state and the inner rings for one or two quanta of vibrational excitation. For Ar+ + N2 the rings give the vibrational levels for the reaction with Ar+(2P3/2). The middle panels depict the corresponding product internal energy distributions. For the reaction with H2, a forward cone of 30° was evaluated. The insets visualizes the vibrational and rotational levels of H2+. The upward ticks represent reactions with ortho-H2 and downward ticks of para-H2. In case of N2+ only vibrational levels are given. The lower panels present the integrated product scattering angle distributions. The data are reproduced from ref. 55 and 54. | ||
In the reaction of Ar+ with molecular hydrogen H2 and its isotope D2,
| Ar+(2PJ) + H2/D2(X,v,J) → Ar(1S0) + H2+/D2+(X,v′,J′) | (2) |
| → ArH+(X,v′,J′) + H(2S1/2) | (3) |
In the reaction with N2 the two spin orbit states of Ar+ show no difference in reactivity, with the excited state being even slightly less reactive.60 In the reaction with H2 the spin orbit excited Ar+ 2P1/2 state is significantly more reactive than the 2P3/2 ground state.59 The H2+ is predominantly formed in the second vibrationally excited state (v′ = 2). This is caused by a quasi resonance in the energetics of entrance and exit channel for Ar+(2P1/2) → Ar + H2+ (v′ = 2). A seam between the potential energy surfaces due to an avoided crossing61–63 opens an efficient reaction pathway. This resonance can no longer be observed in the reaction with D2. Additionally, the reactivity for both spin orbit states of Ar+ in the reaction with D2 is comparable.
To gain a full understanding of the involved dynamics, recent experiments recorded full angle and energy differential cross sections by crossed beam velocity map imaging for the reaction Ar+ + H2. In reaction with spin orbit excited argon ions, forward scattering into H2+ in v′ = 2 is the dominant scattering feature in the image55 (see Fig. 1, left column). The dashed rings indicate the vibrational state of the H2+ product ion. The outermost ring corresponds to the vibrational ground state of H2+. In the reaction with ground state argon only the first excited vibrational level is energetically accessible given the experimental conditions. The spin–orbit excited level of Ar+ lies 178 meV above the ground state and this allows also the second vibrational level to be populated. Contrary to prior experiments recording angle differential cross sections,64 only a minor backward fraction was observed. Analysis of the internal energy distribution revealed significant rotational excitation of the product H2+ ions. A maximum of four quanta of rotational excitation can be found at a collision energy of Ecoll = 0.1 eV (see middle row Fig. 1) and up to 8ħ at a collision energy of Ecoll = 0.28 eV.55 The reactant H2 beam was generated by supersonic expansion and molecules can be considered to be mostly in the rovibrational ground state at the experimental conditions. Given the single collision conditions in the experiment, more than one rotational quantum has to be transferred into rotational excitation in a single reactive collision. A two step model was proposed to explain the rotational excitation. In a first step, the electron jumps form the H2 to Ar+ at long range. This changes the potential from Ar+–H2 to Ar–H2+, on which rotational inelastic scattering may take place as a second step. In the inelastic collisions angular momentum is transferred into rotational excitation of H2+. The energy transfer in these inelastic collisions can be very effective as recently shown for He + H2+.65 The same degree of rotational excitation can be found for the backward scattered H2+ ions. At these small impact parameter collisions less total angular momentum is available. Thus, the transfer of angular momentum to rotational excitation must be even more efficient than in the atomistic mechanism leading to forward scattering.
Charge transfer and hydrogen transfer in heavy–light heavy reactions
In exothermic charge transfer reactions a significant amount of energy might become available to the reactants. Under single collision conditions in gas phase experiments this energy cannot be dissipated to surrounding solvent molecules but has to be redistributed among the reaction products. Farrar and co-workers investigated the dynamics of charge transfer reactions using crossed beam velocity map imaging experiments at several electron volt collisions energy. The high collision energy combined with the exothermicity of the reaction enables the transfer of a considerable amount of energy into internal degrees of freedom of molecular products. This opens the possibility of dissociative charge transfer, where the primary molecular product fragments due to the high degree of internal excitation.66 This process often happens on such fast time scales that the dissociation reaction is considered to be a direct dynamical process. Similar to the initial charge transfer product ion, almost no momentum transfer occurs to the fragment ion, and the differential scattering cross section will be similar to that of the parent molecular ion. The charge transfer happens in a stripping-like mechanism leading to forward scattering with little momentum transfer. This situation is encountered in the reaction of N+ + CH467 or for N+/O+ + CH3OD.68 In the reaction of N+ with methane| N+ + CH4 → N + CH4+ → N + CH3+ + H | (4) |
| → N + CH2+ + H2 | (5) |
In many of the systems investigated by Farrar and co-workers, charge transfer is dominant over proton transfer. Through a variation of the charge state (OH+/− + C2H2)69,70 or the proton donor (H2O+/H3O+ + NH3),71,72 they were able to investigate the proton transfer dynamics. A direct stripping mechanism was found to be the only reaction pathway. Their experiments reveal forward scattering close to the kinematic cut-off with little momentum transfer to the ionic product. The mechanism is dominant in any of the investigated systems. Reaction exothermicties are almost completely transferred into internal degrees of freedom of the reaction product. Whereas even at high collision energies the reactant velocity is conserved within the velocity of the proton transfer product due to the lack of momentum transfer during the reactive collision. This is a signature of a fast stripping mechanism which occurs at large impact parameters. The direct comparison of OH+ and OH− in reaction with C2H2 reveals similar dynamics for the proton transfer reaction, which occurs for both charge states.
In the reaction of the carbon cation C+ with ammonia NH3
| C+ + NH3 → NH3+ + C | (6) |
| → HCNH+/CNH2+ + H | (7) |
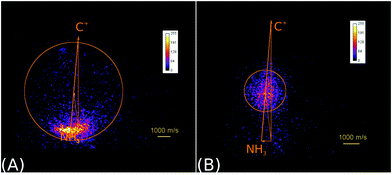 | ||
| Fig. 2 Raw product ion velocity distributions for the reaction of C+ + NH3 from crossed beam velocity map imaging experiments at 2.1 eV relative collision energy. Left panel: The charge transfer product NH3+ (reaction (6)) is the dominant reaction channel. Right panel: A complex mediated mechanism leads to the formation of a new C–N bond in the product ions HCNH+/CNH2+ (reaction (7)). The isomers cannot be assigned. The newton diagrams inset into the scattering images give the relative orientation of the velocity vectors. The circle around the center of mass indicates the maximum product ion velocity considering energy and momentum conservation. Reprinted with permission from ref. 38. | ||
Isomer specificity in proton transfer reactions: HCO+/HOC+ formation
Gas phase proton transfer reactions are thought to be one of the most relevant type of bimolecular interactions influencing the composition of the interstellar medium.4,77,78 Arguably the most relevant products of interstellar proton transfer processes are the formyl (HCO+) and isoformyl (HOC+) isomer cations,79 which can be formed via a variety of reactions, such as:| H3+ + CO → HCO+ + H2 + 1.76 eV → HOC+ + H2 + 0.03 eV | (8) |
| HOCO+ + CO → HCO+ + CO2 + 0.55 eV → HOC+ + CO2 − 1.18 eV | (9) |
There has been a long and still open debate regarding the interstellar HOC+/HCO+ branching ratio.80–82 More specifically, it seems that the ratio does strongly depend on the specific chemical environment of each investigated interstellar region. Reaction (8) forms both the stable HCO+ or the metastable HOC+via two exothermic and barrierless channels, with the former being considerably more exothermic. Each pathway proceeds via an intermediate ion–dipole complex that follows dissociation to the final products.83 In contrast to H3+ + CO, reaction (9) leads to formation of only HCO+ under thermal conditions, with formation of HOC+ being endothermic by 1.18 eV. The enthalpy difference between both proton transfer channels in reactions (8) and (9) amounts to 1.73 eV, resembling the difference in proton affinity of the carbon- and oxygen ends of CO.84 Proton migration between both isomers has been shown to be efficiently catalyzed by neutral molecules such as CO2 and H2, which possess a higher proton affinity than the O-side of CO.85 Moreover, HCO+ ↔ HOC+ autoisomerization can occur between highly internally energized product ions, after overcoming a potential barrier of 3.57 eV above the energy of the formyl cation product.86 The stationary points and main pathways for reaction (8) are schematically depicted in Fig. 3(A).
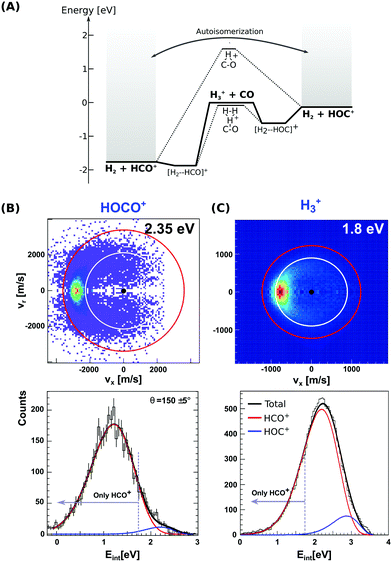 | ||
| Fig. 3 (A) Calculated minimum energy paths for the reactions H3+ + CO (from ref. 83). The energetics for H2-catalyzed isomerization and autoisomerization between internally hot HCO+/HOC+ cations are indicated. (B and C) Center-of-mass velocity distributions of product HCO+/HOC+ ions from reactions H3+ + CO and HOCO+ + CO. The red and white rings mark the kinematic limits for formation of HCO+ and HOC+, respectively. Lower panels: Corresponding product internal energy distributions fitted to a sum of Gaussians resembling the contribution of HCO+ and HOC+ products. Events falling left from the grey bar at 1.73 eV can only correspond to HCO+ ions. The data are reproduced from ref. 87 and 88. | ||
Given the large difference in reaction enthalpies for the formation of either isomer in both reactions, it should be possible to distinguish between product isomers in a velocity map ion image thanks to energy conservation. This has been the focus of two recent studies on reactions (8) and (9), where we have crossed a beam of H3+ or HOCO+ ions at an internal temperature equal to room temperature with a supersonically expanded CO molecular beam at varying collision energies.87,88
Fig. 3(B) and (C) depict the center-of-mass product velocity images and associated internal energy distributions for the above-mentioned reactions. The depicted red and white circles denote the kinematic limits for the formation of formyl and isoformyl cations, respectively. These limits represent the maximum center-of-mass speed allowed for the product ions given the collision energy and the respective reaction enthalpy. Thus, in the ideal case of minimal collision energy spread, a product event scattered with velocities larger than the radius of the white circle can solely be ascribed to the HCO+ isomer. Forward scattering in the direction of the initial CO, as well as a high degree of product internal excitation, are obtained for both reactions at all relative collision energies. Most importantly, a monomodal velocity distribution is observed, preventing a direct estimation of isomer ratios. While the major fraction of product events fall inside both kinematical limits in H3+ + CO due to high product internal excitation, HOCO+ + CO presents a different situation, with almost all reactive events are scattered with velocities larger than the given kinematic limit for HOC+ formation (see Fig. 3B).
In order to extract the product isomer ratio, the corresponding internal energy distributions are fitted using a sum of two Gaussian distribution functions, as shown in the lower left panel of Fig. 3. An upper limit of 24% HOC+ is obtained at a scattering energy of 1.8 eV, whereas the value decreases to less than 10% for the two smaller collision energies of 0.2 and 0.6 eV. For HOCO+ + CO, a maximum contribution of (1.5 ± 0.2)% for HOC+ is obtained, making this system an HCO+-specific product forming reaction even at relative collision energies above the threshold for HOC+ formation.
From a statistical perspective, the higher density of rovibrational states for the HCO+ geometry than for the HOC+ geometry is supposed to favor the transfer of the proton to the carbon end of CO. In addition, possible reorientation effects in CO towards a H–C interaction may play a role. The possibility of H2/CO2-catalyzed isomerization from HOC+ to HCO+ is predicted to be a slow process if compared to fast proton exchange and is thus not expected to affect the isomer branching ratio. This is supported by the lack of low velocity products ions that would most likely result from such a rearrangement.
Competing formation channels in O+ + CH3Y reactions
The oxygen cation O+ is an important constituent of the atmospheric chemical network. Methyl halide molecules of anthropogenic origin can be found in the atmosphere.89,90 Pei et al. studied the reaction| O+(4S) + CH3Y → CH3Y+ + O | (10) |
| → Y+ + CH3 + O | (11) |
| → CH3+ + YO | (12) |
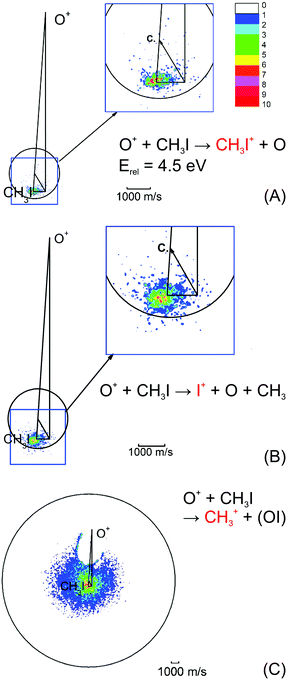 | ||
| Fig. 4 Velocity map images for all three possible product channels in the reaction CH3I + O+: (A) CH3I+, (B) I+ and (C) CH3+. The formation of CH3+ is the dominant product channel in the reaction with CH3I (65%). The charge transfer product CH3I+ is the least abundant (15%). The circle indicates the maximum ion velocity considering energy and momentum conservation. Reprinted with permission from ref. 96. | ||
The most abundant reaction product is the methyl cation CH3+. The distribution is centered isotropically around the center of mass at far lower velocities compared to the product ions from the other two reaction pathways, which are centered at the neutral beam velocity (see Fig. 4). Analysis of the kinetic energy distribution reveals two contributions to the differential cross section. The first, a peak at almost zero kinetic energy, shows strong forward scattering, while the second contribution is a high energy tail that extends to almost 3 eV kinetic energy. This tail contains almost 75% of the ion flux and shows no angular dependence. These findings indicate two independent atomistic reaction pathways. The forward scattering pathway results from a cleavage of the carbon–halogen bond on the initial spin surface.92 Along the second pathway, in a first step a CH3OY+ complex is formed which lives longer than at least one rotational period leading to the observed isotropic scattering.97 The CH3+ formation from the CH3OY+ complex is spin forbidden on the initial ground state doublet surface of the intermediate complex. After complex formation, the reaction coordinate has to cross to the quartet surface to proceed to the CH3+ formation. This process is mediated by spin–orbit coupling and thus explains the different behavior seen for the three investigated methyl halides. The branching ratio, as well as the contribution of the complex mediated pathway to the CH3+ formation, is strongly dependent on the halide ion. The contribution of the CH3+ channel is highest for methyl iodine.
Metal ion–hydrocarbon reactions
The reactivity of hydrocarbons in reactions with transition metal ions has already been investigated for several decades.98–100 The group of James Weisshaar extended their experiments with crossed beams101–105 to investigate the reaction of the cobalt cation with small saturated hydrocarbon molecules using velocity map imaging:30,106| Co+(3F4) + nC3H8 → CoC3H8+ | (13) |
| → CoC2H4+ + CH4 | (14) |
| → CoC3H6+ + H2 | (15) |
Weisshaar and co-workers tested the general concept derived for the reaction with propane (reactions (13)–(15)) by replacing a hydrogen atom by a methyl group and investigated the reaction of Co+ with iso-butane:30
| Co+(3F4) + iso C4H10 → CoC4H10+ | (16) |
| → CoC3H6+ + CH4 | (17) |
| → CoC4H8+ + H2 | (18) |
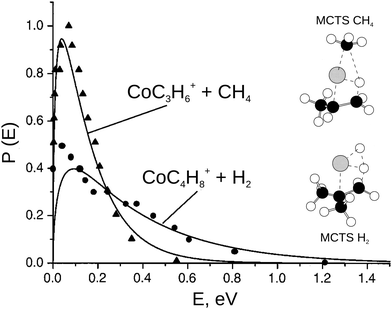 | ||
| Fig. 5 The product translational energy distribution P(E) for the CH4 elimination and the H2 elimination channel in the reaction Co+ + iso-C4H10 (solid lines) in comparison with prior work from the Bowers group (triangles = CH4 products and circles = H2 products, data from ref. 113). Only about 10% of the available energy is partitioned into product translation in CH4 channel compared to 35% for the H2 channel. The H2 shows a non-statistical high energy tail. The insets show the geometry of the multi center transition states for both reaction pathways. Reprinted with permission from ref. 30. | ||
Cation-radical reactions
The reactivity of radicals is of great importance in many environments, e.g. the atmosphere and the interstellar medium. Radicals are highly reactive and are often formed as intermediate species. The reaction of H3+ with the methyl radical CH3| H3+ + CH3 → CH3+ + H2 + H | (19) |
| → CH4+ + H2 | (20) |
The formation of new C–C bonds is of central importance in synthetic chemistry. The use of carbon based radicals is one possible pathway. Pei et al. investigated the reaction of C+ in reaction with the allyl radical C3H5:91
| C+ + C3H5 → C3H5+ + C | (21) |
| → C4H5+ | (22) |
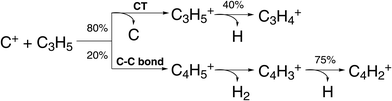 | ||
| Fig. 6 Scheme of reaction pathways for the reaction C+ + C3H5 forming the product species observed by Pei et al.91 The percentage numbers indicate the obtained branching fractions for following the different steps along the reaction pathway. | ||
Anion-neutral reactions
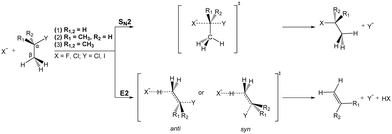
Most natural elements and many molecules are known to efficiently form stable anions. Their stability is directly correlated with the electron affinity of the respective neutral counterpart. As anions often bind their outer electrons rather weakly, they play an important role for the ion-neutral chemistry in environments where they are formed. In low density regimes such as planetary atmospheres or the interstellar medium, formation of anions commonly proceeds via radiative association. Several anions have been identified in various astronomical environments,117,118 and the understanding of their formation mechanisms is an ongoing field of research.119,120 In solution, anion-induced reactions are common in the formation or cleavage of bonds. Among the large number of organic reactions where ionic intermediates play a deciding role, bimolecular nucleophilic substitution (SN2) and base-induced elimination (E2) reactions are perhaps the two most common processes in synthetic pathways leading to carbon bond formation or functional group displacements.121 In both reactions, bond formation and bond cleavage occur in a concerted way and under stereospecific conditions, which makes these pathways crucial steps for the production of stereochemically pure compounds. Studying the mechanism of such model organic reactions in solvent-free conditions is fundamental to understanding and controlling organic and biomolecular processes. In addition, investigations on micro-solvated reactions provide a precise way of determining the effect of solvent interactions on the reaction on a molecular level.Elementary nucleophilic substitution reactions
SN2 reactions have been extensively studied, both experimentally and theoretically, for more than a century.122–130 The simplest case of an SN2 reaction corresponds to the attack of a monatomic nucleophile on an alkyl halide,| X− + CH3Y → [X–CH3–Y]− → Y− + CH3X. | (23) |
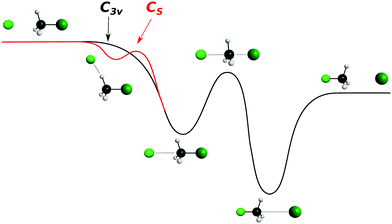 | ||
| Fig. 7 Schematic representation of a typical minimal energy path for the collinear (C3v) and X–H bonded (Cs) nucleophilic substitution reaction. The optimized chemical structures shown for the most important stationary points have been taken from ref. 143. | ||
Despite often being submerged with respect to reactants, it has been shown that this barrier can have a significant effect on the overall reaction kinetics.134 In particular, it has been demonstrated that X− + CH3Y type systems do not behave statistically with respect to energy redistribution at the transition state, but are rather driven by efficient coupling of specific rovibrational modes to the reaction coordinate.124,135–138 The reaction probability depends on the interplay between complex lifetime and redistribution of energy between inter- and intramolecular degrees of freedom.
The collinear geometry (C3v) in SN2 reactions is favored by an efficient overlap of the highest occupied molecular orbital (HOMO) of the nucleophile's lone pair with the backside lobe of the lowest unoccupied σ* molecular orbital (LUMO) of C–Y in the neutral reactant.139 The sideways interaction is hindered by steric crowding and inefficient molecular orbital overlap.140 While this approach symmetry has been assumed as being the only valid picture of an SN2 reaction for decades, initial theoretical investigations already suggested the presence of alternative approach geometries.141,142
Gas phase reactive scattering experiments performed in our laboratory using the crossed beam velocity map imaging technique have provided direct evidence for a large variety of reaction mechanisms in a set of X− + CH3Y reactions:
| Cl− + CH3I → I− + CH3I + 0.55 eV | (24) |
| CN− + CH3I → I− + CH3CN + 1.98 eV | (25) |
| → I− + CH3NC + 1.05 eVF− + CH3Cl → Cl− + CH3F + 1.35 eV | (26) |
| F− + CH3I → I− + CH3F + 1.84 eV | (27) |
| OH− + CH3I → I− + CH3OH + 2.8 eV | (28) |
• A direct rebound mechanism corresponding to the textbook collinear rebound reaction, with the leaving ion being scattered in backward direction with respect to its original motion.
• A stripping process where X− approaches the neutral molecule from the side and strips off the CH3 moiety, leading to a forward scattered Y− ion.
• The formation of a transition state complex with a lifetime longer than its rotational period, which leads to a slow Y− that is isotropically scattered over all angles. The formation of this stable complex has been found to occur via both collinear and X–H bonded pre-reaction complexes.152
Additional mechanisms such as the roundabout, frontside attack or double inversion pathways have been also reported for some reactions141,144,151 and are a further indication of the mechanistic richness in SN2 processes. Fig. 8 shows typical simulated trajectories for the most relevant reaction mechanisms.
 | ||
| Fig. 8 Exemplary trajectories along the reaction coordinate of a typical SN2 reaction showing some of the major atomistic mechanisms found in the theoretical simulations:144,153 (A) direct backward; (B) forward stripping; (C) indirect; (D) roundabout. The full animations of the trajectories can be found at http://hase-group.ttu.edu/animations.html. | ||
Fig. 9 presents the experimental product velocity distributions for reactions (24)–(28) at low (0.4 eV) and high (1.9 eV) relative collision energy.
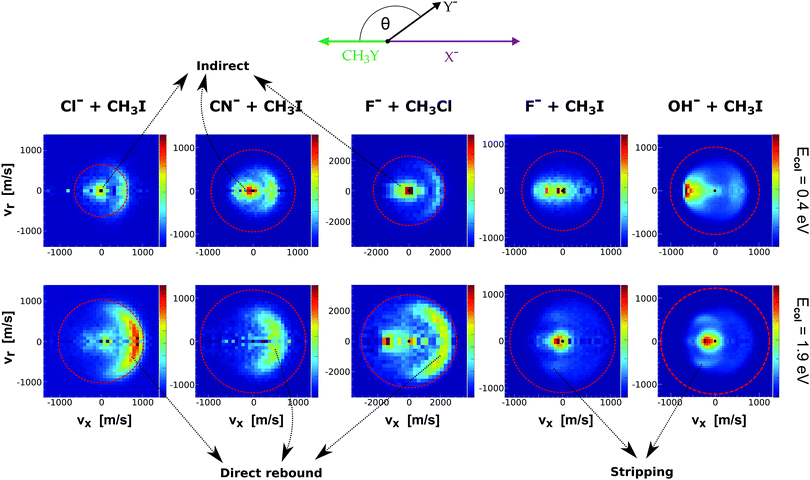 | ||
| Fig. 9 Center-of-mass velocity distributions of product Y− ions for five different SN2 reactions: Cl− + CH3I,144 CN− + CH3I,146 F− + CH3Cl,143 F− + CH3I,34 OH− + CH3I.145 The data are reproduced from the respective references. The right color bars represent a linear ion intensity scale. Typical scattering patterns ascribed to the direct rebound, stripping, and indirect mechanisms are indicated. | ||
Electronic structure and direct dynamics simulations can be used to interpret the mechanistic patterns from Fig. 9. The reactions Cl− + CH3I, CN− + CH3I and F− + CH3Cl show dominant isotropic scattering at low relative collision energy and a contribution of direct backward scattering. Isotropic scattering has been ascribed to an indirect mechanism associated with efficient translational to rotational energy transfer via coupling of the reactant orbital angular momentum and the CH3Y rotational angular momentum.135 The direct rebound mechanism is the major pathway at high collision energies and has been found to be particularly efficient at small impact parameters.150 While these direct reactions are probable only at small X–C–Y angles around the direct backside attack, collisions tend to occur at larger angles due to the insufficient time for reactant pre-orientation,154 which explains the decrease of the reaction rate coefficient with relative collision energy observed for several X− + CH3Y systems.142,155,156 In general, the computational analysis renders product ion scattering angle and energy distributions that agree very well with the experimental findings.143,144,153
In contrast to the previous results, the product velocity distributions from F− + CH3I and OH− + CH3I are markedly different, with isotropic and forward scattering at low collision energies and the indirect and stripping mechanisms dominating the reaction dynamics at high relative collision energies.34,145 This substantial change in the dynamics has been traced back to several factors. Most significantly, it has been demonstrated that both F− and OH− strongly favor a non-collinear, X–H bonded pre-reaction complex formation (see Fig. 7), a feature consistent with the high proton affinity of these anions.152,157,158 In contrast to the above described dynamics, the reaction between F− and CH3Cl shows a strong preference for direct rebound dynamics, albeit F− being the attacking anion.143 While the calculated ab initio potential energy surface of F− + CH3Cl also shows the presence of a F–H bonded pre-reaction complex, clear differences in the energy of the dihalide interaction were found. As shown in Fig. 10, a deep energy minimum is obtained for the geometry associated to an F–I interaction in F− + CH3I, while the interaction is weaker by about a factor of ten for the F–Cl interaction in F− + CH3Cl.159
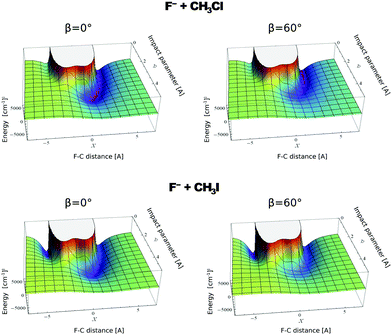 | ||
| Fig. 10 Computed potential energy for F− approaching CH3Cl (up) and CH3I (low) as a function of impact parameter (b) and F–C distance. The two values of β represent the two possible dihedral angles between the C, Y, H and X atoms. The potentials are reproduced with permission from ref. 159. | ||
Proton transfer and dihalide formation
Reactions of negative ions with methyl halides not only lead to nucleophilic displacements, but also promote the formation of alternative reaction products. This is the case of the proton transfer and halogen abstraction channels. These reactions have shown to compete with SN2 under excess energy conditions in reactions involving F− and OH−, in particular F− + CH3I and OH− + CH3I.160–162 For the former reaction, the formation of CH2I− (proton transfer) and IF− (dihalide formation) are endothermic by 0.6 ± 0.1 eV and 0.7 ± 0.3 eV, respectively. The latter reaction is exothermic and it was found that for temperatures as low as 200 K the proton transfer and the SN2 reaction have nearly equal reaction probability.163The proton transfer and halogen abstraction channels have only recently started to receive theoretical attention.157,163–165 For example, it has been shown for F− + CH3I that the proton transfer channel features the same X–H bonded pre-reaction complex (Cs minimum in Fig. 7) found for the nucleophilic substitution channel. In a recent experimental work, we have investigated the branching ratio and reaction dynamics of these pathways in F− + CH3I as a function of relative collision energy.166 Formation of a protonated dihalide anion [FHI]− was identified for the first time during this study. While the SN2 channel is the dominant product at all studied relative collision energies, all other channels contribute to a considerable extent at energies above 1 eV. In particular, the proton abstraction induced CH2I− fragment reaches a maximum branching ratio of 0.2. At energies above 2.6 eV IF− becomes the second major channel, related to the possible occurrence of C–I bond dissociation at these energies. [FHI]− appears only above 1 eV relative collision energy, consistent with a calculated reaction enthalpy of 0.9 ± 0.2 eV, and remains a minor channel throughout the studied energy range.
Fig. 11 depicts the center-of-mass velocity distributions of all ions produced in F− + CH3I at 2.3 eV (up), as well as the corresponding internal energy distributions (bottom). Both dihalide formations and the proton abstraction reaction present a substantial degree of energy partitioning to product internal degrees of freedom. The fraction of total internal excitation in the proton abstraction channel ranges from 0.55 to 0.35 and decreases with increasing collision energy. The values are in good agreement with a recent theoretical prediction at 1.55 eV164 and are found to be comparable to the degree of excitation observed in OH− + CH3I.157 Compared to the CH2I− channel, formation of both dihalide species is found to occur under significantly stronger energy partitioning to internal degrees of freedom. In summary, this work shows that alternative product formation channels compete with SN2 under excess energy conditions in reactions where non-traditional reactant approach geometries are favored.
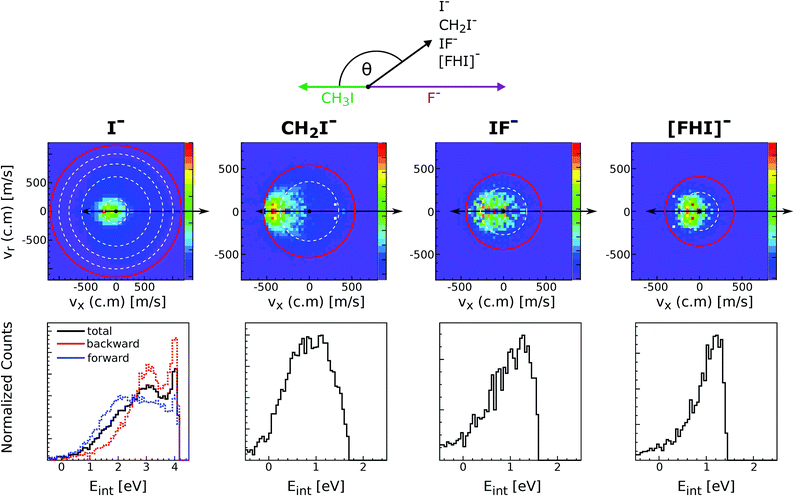 | ||
| Fig. 11 Experimental scattering results for the different reaction channels in F− + CH3I at a relative collision energy of 2.3 eV. The upper panels show the velocity distributions of product I−, CH2I−, IF− and [FHI]− ions. The lower panels depict the internal energy distributions associated to each of the product formations. The data are reproduced from ref. 166. | ||
Effects of micro-solvation on the dynamics of nucleophilic substitution reactions
Reaction dynamics in the liquid phase are driven by the interplay between the intrinsic reaction dynamics due to the reactants and the interactions induced by solvent molecules.167 Therefore, the role of individual solvent molecules is of great interest. Studies on bimolecular reactions in solution on the picosecond timescale have revealed a lot of information.20 Further, it was found that characteristics of the gas phase dynamics persist in solution.131 Solvent molecules affect the energetics along the reaction coordinate by either stabilizing selected intermediates and transition states or destabilizing them. Hence, kinetics, dynamics, and product branching ratios of a reaction are influenced by the solvent interaction.To bridge the gap between gas and liquid phase, experiments using “micro-solvation” are employed. In these experiments, a selected number of solvent molecules is added to one or more reactants. Mass spectrometry allows control of the degree of solvation by accurately determining the mass of the solvated reactant,168 thereby counting the number of attached solvent molecules. In nucleophilic substitution a polar solvent is commonly used, which motivated investigations with water–nucleophile complexes. One of the studied nucleophiles is the hydroxyl anion OH−. Rate constants and product branching ratios have been determined at different temperatures (200 to 500 K) for OH− (H2O)0–4 and OD− (D2O)0–2 reacting with CH3Cl or CH3Br.169–173 The solvent leads to a suppression of the reaction rate coefficient.174 As main product channel the formation of the free or only partially solvated ionic product was found, even though the fully solvated ionic product is thermodynamically favored. This non-statistical behavior means that the reaction pathway is strongly influenced by the dynamics. Also numerous theoretical studies investigated the effects of micro-solvation of the nucleophile.175–182 Several studies showed that the presence of water molecules attached to the nucleophile reduces its reactivity in SN2 reactions174,177 as seen by experiments. Further insight was gained by investigating the effect of micro-solvation on individual intermediates.183–185
Insights into the effects micro-solvation has on the dynamics has been gained from crossed beam velocity map imaging experiments. The nucleophilic substitution reaction of OH−(H2O)n + CH3I with n = 0–2 has been investigated.186 The differential scattering cross sections for the formation of the non-solvated I− significantly change with the degree of solvation (see Fig. 12). Whereas the free OH− in reaction with CH3I shows predominant forward scattering (see Fig. 9), forward scattering can no longer be seen upon micro-solvation. At lower collision energies, once one water molecule is attached to the OH−, the scattering distribution becomes isotropic around the center of mass at low product ion velocity. This is common for a complex mediated atomistic reaction pathway. At the higher collision energy, the direct rebound opens and competes with the indirect mechanism. In the course of the direct rebound a co-linear arrangement of the O-atom of the attacking OH− with the C–I bond has to be established. It was found that the interaction of the water molecule with a hydrogen atom of the methyl group steers the OH− into place. The evolution of the trajectories for both mechanisms are given in Fig. 13. For OH− (H2O)2, indirect dynamics are observed at both collision energies. The formation of these low velocity products is assumed to be associated with the formation of a long lived complex which lifetime exceeds at least one rotational period.186 Direct chemical dynamics simulations support these findings and provide a wealth of additional information on the different reaction mechanisms underlying the observed differential scattering.187,188
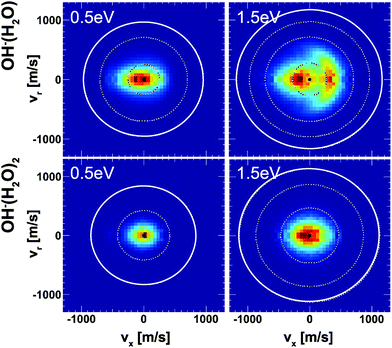 | ||
| Fig. 12 Velocity map images of I− product ions from the reaction of OH− (H2O)1,2 with CH3I at two collision energies. The outermost ring indicates the kinematic cut-off and the inner rings isospheres of 1 eV translational energy. The data are reproduced from ref. 186. | ||
 | ||
| Fig. 13 Exemplary molecular structures along the trajectories of (A) the direct rebound and (B) the indirect mechanism forming the non-solvated SN2 product ion I− in the reaction OH−(H2O) + CH3I.187 The full animations of the trajectories can be found at http://hase-group.ttu.edu/animations.html. | ||
In the crossed beam experiments, the unsolvated product ion is found to be the dominant product ion. Specifically, the ratio between I− and the singly solvated I−(H2O) has been determined for reactions of OH−(H2O) + CH3I189 showing no dependence on collision energy for the low-energy complex mediated mechanism. The abundance of the thermodynamically favored solvated product was found to be less than 5%. This branching ratio has been confirmed by trajectory simulations.187,190,191 The water molecule leaves before crossing over the barrier forming the product ion (see Fig. 13). In case of the indirect mechanism the water molecule leaves at the same moment the bond rearrangement takes place. At higher collision energies that lead to direct rebound, the water molecule leaves upon impact and the reaction proceeds along the OH−–CH3I reaction coordinate. In both cases, the reaction coordinate bypasses the solvated transition state and the dissociation of the micro-solvated complex is either concerted with the bond breaking and formation or even prior to it.
The proton transfer reaction forming the CH2I− is accessible at room temperature and constitutes a competing product channel to nucleophilic substitution. For the bare OH− the proton transfer accounts for almost a third of the product ions already at 0.5 eV.32 The proton transfer also appears in the micro-solvated case. Here, a remarkable agreement between theory and experiments could be achieved.188
A trade-off between energetic and steric effects in the reaction of micro-solvated flouride ions F− with methyl iodide has been found in theoretical studies. Investigations of singly solvated F−(H2O)174,181,192 have been extended up to three attached water molecules, F−(H2O)0–3.173 It was found that the reaction coordinate does not cross the barrier of the fully solvated transition state complex. Subsequent loss of one or two water molecules occurs and the barrier is crossed at the F−(H2O) level. This leads again to favoring the thermodynamically less stable product which is the free I− like for micro-solvated OH−.
Base induced elimination
A very interesting example for the competition of two different reactions is the competition between nucleophilic substitution (SN2) and base-induced elimination (E2), both important reactions in organic chemistry. X− + CH3Y type reactions can only produce the fragment Y−via SN2, irrespective of the specific mechanism involved. However, if the hydrogen atoms in CH3Y are replaced by one or more methyl groups, the base-induced elimination (E2) reaction starts to play an important role. The extreme case of CH3 addition to CH3Y is represented by a tert-butyl halide, (CH3)3CY, where the anion can attack one out of nine equivalent hydrogen atoms. In addition, the bulky CH3 groups will strongly hinder a potential nucleophilic attack to the central carbon. Both SN2 and E2 share several similarities: they are concerted processes and produce exactly the same product ion. Due to the fact that strong nucleophiles are usually also strong bases these two processes are in intrinsic competition with each other. Fig. 14 illustrates the textbook transition state structures and products for both SN2 and E2. As depicted in this figure, an α-C denotes the carbon atom attached to a functional group, e.g. the halogen, while a β-carbon is the C-atom adjacent to this central carbon.The mechanism of E2 reactions is commonly assumed to follow an initial attack of the base to an H-atom. Subsequently, the cleavage of the Cβ–H bond leading to XH and the exit of the Y− leaving group occur in a concerted way, whereby the X–H and Cα–Y bonds are contained in the same plane. This geometry is called coplanar or periplanar configuration. Finally, a double bond is formed between both carbon atoms, which changes the hybridization of the molecular orbitals from sp3 to sp2. Base-induced elimination usually occurs via a so called anti-periplanar geometry, where the X–H and the C–Y bonds lie in the same plane but point in opposite directions. Alternative formation of a syn-oriented transition state (same plane and same direction of X–H and C–Y bonds) is also possible and has been found to be thermodynamically stable for several systems.193
Due to the fundamental and synthetical relevance of the SN2/E2 competition, several theoretical and experimental studies have been devoted to understand which physicochemical factors determine the relative efficiency of these pathways. Given the complexity of the systems, density functional theory has been the usual method of choice to study the electronic structure of the stationary points along E2 and SN2 pathways.193–197 Based on these calculations, some works have established reaction rates for each process using statistical theories.198 Other studies based on the activation strain model of chemical reactivity199 have predicted the dominance of E2 over SN2 in gas phase reactions of increasing complexity due to a more stabilizing transition state interaction.196,200
Many experimental gas-phase studies have been carried out towards providing a direct measure of the branching ratios and a qualitative picture of the effects governing this competition. The challenge of disentangling substitution and elimination products by conventional mass spectrometry is connected to the fact that both reactions generate the same ionic species. Indirect mass spectrometric branching ratios have been deduced by measuring the deuterium kinetic isotope effect (KIE) of reactions with subsequently substituted alkyl halides.129,201 Experiments have also been attempted to obtain direct branching ratios between both reactions. Brauman and coworkers have measured the reaction rate of SN2 and E2 in systems where the SN2 ion–molecule complex undergoes an internal proton transfer.202 Gronert and coworkers have employed dianions as nucleophiles, therefore producing distinct ionic elimination and substitution products.126,203,204
Recently, our group has exploited the capabilities of crossed beam velocity map imaging to disentangle the reaction mechanisms of E2 and SN2 reactions by monitoring the scattering angle and velocity distribution of product Y− and correlating them with the respective channels.205 Several nucleophile-leaving group combinations at stepwise methylated alkyl halides have been investigated,
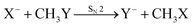 | (29) |
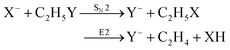 | (30) |
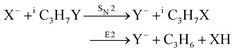 | (31) |
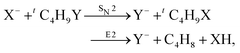 | (32) |
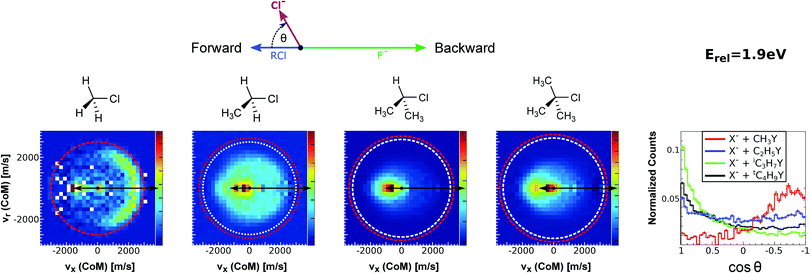 | ||
| Fig. 15 Center-of-mass velocity distribution and scattering angle of product Cl− ions produced in the reactions (from left to right) F− + CH3Cl, F− + C2H5Cl, F− + iC3H7Cl and F− + tC4H9Cl. The kinematical limits for the SN2 and E2 channels are indicated by a red and white circle, respectively. The right panel depicts the resulting Cl− product scattering angle distributions for the four investigated reactions. The arrows above the images show the relative velocities of the reaction counterparts, as well as the product scattering angle θ. The data are reproduced from ref. 205. | ||
In order to confirm this assignment, the experimental results are supported by electronic structure calculations206 and classical trajectory simulations on F− + C2H5I at a collision energy of 1.9 eV. While the computed reactive trajectories show several different reaction mechanism, the direct anti-periplanar E2 is predicted to be the dominant pathway. Fig. 16 shows exemplary snapshots along the reaction coordinate for the three main mechanisms, direct anti-E2, direct syn-E2 and direct backward SN2, all of them occurring over a timescale of several hundred femtoseconds. Further inspection of the reaction probability as a function of impact parameter sheds light into the distinct probability of the direct anti-E2 pathway at high impact parameters, in accordance with a stripping-like mechanism leading to forward scattering of the product I−. This work has provided first evidence of E2-specific mechanistic features. Extraction of quantitative branching ratios between SN2 and E2 reactions based on the different dynamics is one of the next goals in order to precisely evaluate how steric substitution and relative collision energy affect the competition between these processes. Theoretical efforts towards performing trajectory calculations on similar systems such as F− + C2H5Cl are also underway207 and will very likely help to further discriminate the distinct dynamics of SN2 and E2 reactions.
 | ||
| Fig. 16 Snapshots along the most representative reaction trajectories for direct anti-E2 (A), direct syn-E2 (B) and direct backward SN2 (C) reactions.205 The animations of the trajectories can be found at (http://hase-group.ttu.edu/animations.html). | ||
Summary & future directions
Velocity map ion imaging has provided crossed-beam scattering experiments with a great detection technique. Its application to ion–molecule reactive scattering has allowed for numerous studies of cation– and anion–molecule reactions during the last decade. Differential scattering cross sections could be measured for a range of different reactions, from elementary charge transfer and proton transfer to the competition of nucleophilic substitution with base-induced elimination. In many cases state-of-the-art dynamics calculations compare very well with the experiments and have provided valuable insight into the dynamics. Quantum mechanical scattering calculations are, however, still lacking for most ion–molecule reactions.Many important questions are still unsolved that require further and more advanced scattering experiments. Quantum state-cooling by cryogenic pre-trapping and quantum state-preparation by infrared laser-excitation are two techniques that will allow for improved state-to-state differential scattering and more stringent tests of scattering calculations. In particular, tests of quasiclassical versus quantum scattering calculations can be expected from this. Furthermore, quantum-state selection may offer new means to control competing reaction mechanisms, such as SN2 versus E2 reactions.
The dynamics of more complex reactions, i.e. reactions involving an increasing number of atoms, can be expected to receive more attention. Possible cases are the formation of long carbon chain molecules, in particular the detected interstellar negative ions, or the observation of ring closure leading to aromatic hydrocarbons. The field of micro-solvation reaction dynamics using crossed-beam imaging has only been started and many aspects of the dynamics are still to be uncovered, such as the role of the cluster temperature or how shell closure around the ion affects the dynamics.
Complexity can also enter via the coupling of different electronic hypersurfaces. Charge-transfer and ion-radical reactions are cases that allow to investigate such couplings and possible breakdowns of the Born–Oppenheimer approximation. Coupled potential energy surfaces of different electron spin configuration also influence the dynamics of transition metal ion–molecule reactions. Understanding such reactions is particularly relevant to gain insight into the functioning and the improving of bond activation in catalysis.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are very grateful to all their co-workers without whom the described experiments would not have been possible. We also thank our collaboration partners in chemical dynamics theory, in particular Bill Hase and Gábor Czakó. This work was supported by the Austrian Science Fund (FWF), project P25956-N20. E. C. acknowledges support from a DOC-Fellowship by the Austrian Academy of Sciences (ÖAW).References
- C.-Y. Ng, Adv. Chem. Phys., 1992, 82, 401 CrossRef CAS.
- D. Smith and P. Spanel, Mass Spectrom. Rev., 1995, 14, 255 CrossRef CAS.
- A. A. Viggiano, Phys. Chem. Chem. Phys., 2006, 8, 2557 RSC.
- M. Larsson, W. Geppert and G. Nyman, Rep. Prog. Phys., 2012, 75, 066901 CrossRef CAS PubMed.
- J. Benedikt, Int. J. Mod. Phys. D, 2010, 43, 043001 Search PubMed.
- E. Herbst, Philos. Trans. R. Soc., A, 2000, 358, 2523–2534 CrossRef CAS.
- N. de Ruette, K. A. Miller, A. P. O'Connor, X. Urbain, C. F. Buzard, S. Vissapragada and D. W. Savin, ApJ, 2016, 816, 31 CrossRef.
- P. Ehrenfreund and M. A. Sephton, Faraday Discuss., 2006, 133, 277–288 RSC.
- J. Mikosch, M. Weidemüller and R. Wester, Int. Rev. Phys. Chem., 2010, 29, 589–617 CrossRef CAS.
- M. Langevin, Ann. Chim. Phys., 1905, 5, 245 Search PubMed.
- R. D. Levine, Molecular Reaction Dynamics, Cambridge University Press, 2005 Search PubMed.
- D. K. Böhme, Int. J. Mass Spectrom., 2000, 200, 97 CrossRef.
- P. B. Armentrout, Annu. Rev. Phys. Chem., 2001, 52, 423 CrossRef CAS PubMed.
- I. R. Sims and I. W. M. Smith, Annu. Rev. Phys. Chem., 1995, 46, 109 CrossRef CAS PubMed.
- R. Wester, J. Phys. B: At., Mol. Opt. Phys., 2009, 42, 154001 CrossRef.
- S. Willitsch, Int. Rev. Phys. Chem., 2012, 31, 175–199 CrossRef CAS.
- A. T. J. B. Eppink and D. H. Parker, Rev. Sci. Instrum., 1997, 68, 3477–3484 CrossRef CAS.
- N. F. Scherer, C. Sipes, R. B. Bernstein and A. H. Zewail, J. Chem. Phys., 1990, 92, 5239 CrossRef CAS.
- R. Wester, A. E. Bragg, A. V. Davis and D. M. Neumark, J. Chem. Phys., 2003, 119, 10032–10039 CrossRef.
- A. J. Orr-Ewing, Annu. Rev. Phys. Chem., 2015, 66, 119–141 CrossRef CAS PubMed.
- J. M. Farrar, Annu. Rev. Phys. Chem., 1995, 46, 525 CrossRef CAS PubMed.
- S. Scherbart and D. Gerlich, J. Chem. Phys., 1989, 90, 1610 CrossRef.
- A. Eppink and D. Parker, J. Chem. Phys., 1998, 109, 4758–4767 CrossRef CAS.
- A. J. R. Heck and D. W. Chandler, Annu. Rev. Phys. Chem., 1995, 46, 335 CrossRef CAS PubMed.
- K. Liu, Annu. Rev. Phys. Chem., 2001, 52, 139 CrossRef CAS PubMed.
- T. N. Kitsopoulos, M. A. Buntine, D. P. Baldwin, R. N. Zare and D. W. Chandler, Science, 1993, 260, 1605 CAS.
- J. J. Lin, J. Zhou, W. Shiu and K. Liu, Science, 2003, 300, 966 CrossRef CAS PubMed.
- B. Zhang, W. Shiu, J. J. Lin and K. Liu, J. Chem. Phys., 2005, 122, 131102 CrossRef PubMed.
- B. Zhang and K. Liu, J. Chem. Phys., 2005, 122, 101102 CrossRef PubMed.
- E. L. Reichert, G. Thurau and J. C. Weishaar, J. Chem. Phys., 2002, 117, 653 CrossRef CAS.
- J. Mikosch, U. Frühling, S. Trippel, D. Schwalm, M. Weidemüller and R. Wester, Phys. Chem. Chem. Phys., 2006, 8, 2990–2999 RSC.
- R. Otto, J. Xie, J. Brox, S. Trippel, M. Stei, T. Best, M. R. Siebert, W. L. Hase and R. Wester, Faraday Discuss., 2012, 157, 41 RSC.
- S. Trippel, M. Stei, R. Otto, P. Hlavenka, J. Mikosch, C. Eichhorn, U. Lourderarj, J. X. Zhang, W. L. Hase, M. Weidemüller and R. Wester, J. Phys.: Conf. Ser., 2009, 194, 012046 CrossRef.
- J. Mikosch, J. Zhang, S. Trippel, C. Eichhorn, R. Otto, X. Sun, W. de Jong, M. Weidemüller, W. Hase and R. Wester, J. Am. Chem. Soc., 2013, 135, 4250 CrossRef CAS PubMed.
- M. Stei, J. von Vangerow, R. Otto, A. H. Kelkar, E. Carrascosa, T. Best and R. Wester, J. Chem. Phys., 2013, 138, 214201 CrossRef PubMed.
- R. Wester, Phys. Chem. Chem. Phys., 2014, 16, 396 RSC.
- J. Meyer and R. Wester, Annu. Rev. Phys. Chem., 2017, 68, 333 CrossRef CAS PubMed.
- L. Pei and J. M. Farrar, J. Chem. Phys., 2012, 136, 204305 CrossRef PubMed.
- T. Van Voorhis, T. Kowalczyk, B. Kaduk, L.-P. Wang, C.-L. Cheng and Q. Wu, Annu. Rev. Phys. Chem., 2010, 61, 149–170 CrossRef CAS PubMed.
- S. Falcinelli, P. Candori, F. Pirani and F. Vecchiocattivi, Phys. Chem. Chem. Phys., 2017, 19, 6933–6944 RSC.
- A. G. G. M. Tielens, Rev. Mod. Phys., 2013, 85, 1021–1081 CrossRef CAS.
- W. D. Geppert and M. Larsson, Chem. Rev., 2013, 113, 8872–8905 CrossRef CAS PubMed.
- J. H. Waite, D. T. Young, T. E. Cravens, A. J. Coates, F. J. Crary, B. Magee and J. Westlake, Science, 2007, 316, 870–875 CrossRef CAS PubMed.
- K. Schowen, H.-H. Limbach, G. Denisov and R. Schowen, Biochim. Biophys. Acta, 2000, 1458, 43–62 CrossRef CAS.
- J. M. Mayer, Acc. Chem. Res., 2011, 44, 36–46 CrossRef CAS PubMed.
- P. Tosi, F. Eccher, D. Bassi, F. Pirano, D. Cappelletti and V. Aquilanti, Phys. Rev. Lett., 1991, 67, 1254–1257 CrossRef CAS PubMed.
- A. W. Kleyn, V. N. Khromov and J. Los, J. Chem. Phys., 1980, 72, 5282–5283 CrossRef CAS.
- Y. Huang, C. T. Rettner, D. J. Auerbach and A. M. Wodtke, Science, 2000, 290, 111–114 CrossRef CAS PubMed.
- A. L. Rockwood, S. L. Howard, W.-H. Du, P. Tosi, W. Lindinger and J. H. Futrell, Chem. Phys. Lett., 1985, 114, 486 CrossRef CAS.
- K. Birkinshaw, A. Shukla, S. L. Howard and J. H. Futrell, Chem. Phys., 1987, 113, 149 CrossRef CAS.
- S. L. Howard, Chem. Phys. Lett., 1990, 178, 65 CrossRef.
- R. Candori, S. Cavalli, F. Pirani, A. Volpi, D. Cappelletti, P. Tosi and D. Bassi, J. Chem. Phys., 2001, 115, 8888 CrossRef CAS.
- R. Candori, F. Pirani, D. Cappelletti, P. Tosi and D. Bassi, Int. J. Mass Spectrom., 2003, 223, 499 CrossRef.
- S. Trippel, M. Stei, J. A. Cox and R. Wester, Phys. Rev. Lett., 2013, 110, 163201 CrossRef CAS PubMed.
- T. Michaelsen, B. Bastian, E. Carrascosa, J. Meyer, D. H. Parker and R. Wester, J. Chem. Phys., 2017, 147, 013940 CrossRef PubMed.
- C. â. Liao, R. Xu, S. Nourbakhsh, G. D. Flesch, M. Baer and C. Y. Ng, J. Chem. Phys., 1990, 93, 4832–4844 CrossRef CAS.
- G. Gioumousis and D. P. D. P. Stevenson, J. Chem. Phys., 1958, 29, 294–299 CrossRef CAS.
- D. P. Stevenson and D. O. Schissler, J. Chem. Phys., 1958, 29, 282–294 CrossRef CAS.
- K. Tanaka, J. Durup, T. Kato and I. Koyano, J. Chem. Phys., 1981, 74, 5561–5571 CrossRef CAS.
- T. Kato, K. Tanaka and I. Koyano, J. Chem. Phys., 1982, 77, 834–838 CrossRef CAS.
- E. A. Gislason and G. Parlant, J. Chem. Phys., 1991, 94, 6598–6606 CrossRef CAS.
- M. Hawley and M. A. Smith, J. Chem. Phys., 1992, 96, 1121 CrossRef CAS.
- C. Uiterwaal, J. van der Weg, J. van Eck, P. van Emmichoven and A. Niehaus, Chem. Phys., 1996, 209, 195–203 CrossRef CAS.
- P. M. Hierl, V. Pacek and Z. Herman, J. Chem. Phys., 1977, 67, 2678–2686 CrossRef CAS.
- M. Hernandez-Vera, F. A. Gianturco, R. Wester, H. da Silva Jr, O. Dulieu and S. Schiller, J. Chem. Phys., 2017, 146, 124310 CrossRef PubMed.
- L. Pei and J. M. Farrar, J. Chem. Phys., 2013, 138, 124304 CrossRef PubMed.
- L. Pei and J. M. Farrar, J. Chem. Phys., 2012, 137, 154312 CrossRef PubMed.
- L. Pei and J. M. Farrar, J. Chem. Phys., 2015, 143, 084304 CrossRef PubMed.
- L. Liu, C. Martin and J. M. Farrar, J. Chem. Phys., 2006, 125, 133117 CrossRef PubMed.
- L. Liu, Y. Li and J. M. Farrar, J. Chem. Phys., 2006, 124, 124317 CrossRef PubMed.
- Y. Li and J. M. Farrar, J. Phys. Chem. A, 2004, 108, 9876–9886 CrossRef CAS.
- Y. Li and J. M. Farrar, J. Chem. Phys., 2004, 120, 199–205 CrossRef CAS PubMed.
- O. J. Martinez, N. B. Betts, S. M. Villano, N. Eyet, T. P. Snow and V. M. Bierbaum, ApJ, 2008, 686, 1486 CrossRef CAS.
- D. Edvardsson, P. Baltzer, L. Karlsson, B. Wannberg, D. M. P. Holland, A. D. Shaw and E. E. Rennie, J. Phys. B: At., Mol. Opt. Phys., 1999, 32, 2583 CrossRef CAS.
- D. J. Levandier and Y.-H. Chiu, J. Chem. Phys., 2010, 133, 154304 CrossRef PubMed.
- R. A. Curtis and J. M. Farrar, J. Chem. Phys., 1986, 84, 127–134 CrossRef CAS.
- E. Roueff and E. Herbst, J. Phys.: Conf. Ser., 2009, 192, 012008 CrossRef.
- E. F. van Dishoeck, Faraday Discuss., 2014, 168, 9–47 RSC.
- D. Buhl and L. E. Snyder, Nature, 1970, 228, 267 CrossRef CAS PubMed.
- R. C. Woods, C. S. Gudeman, R. F. Goldsmith, G. R. Huguenin, W. M. Irvine, A. Hjalmarson, L.-A. Nyman and H. Olofsson, Astrophys. J., 1983, 270, 583–588 CrossRef CAS.
- L. M. Ziurys and A. J. Apponi, Ap. J. Lett., 1995, 455, L73 CAS.
- A. J. Apponi and L. M. Ziurys, Astrophys. J., 1997, 481, 800–808 CrossRef CAS.
- T. Li, H. Hirano, T. Amano and R. J. Le Roy, J. Phys. Chem., 2008, 129, 244306 CrossRef PubMed.
- S. J. Klippenstein, Y. Georgievskii and B. J. McCall, J. Phys. Chem. A, 2010, 114, 278–290 CrossRef CAS PubMed.
- M. A. Smith, S. Schlemmer, J. von Richthofen and D. Gerlich, ApJ, 2002, 578, 87–90 CrossRef.
- M. Mladenovic and S. Schmatz, J. Chem. Phys., 1998, 109, 4456–4470 CrossRef CAS.
- E. Carrascosa, M. Stei, M. A. Kainz and R. Wester, Mol. Phys., 2015, 113, 3955 CrossRef CAS.
- E. Carrascosa, M. A. Kainz, M. Stei and R. Wester, J. Phys. Chem. Lett., 2016, 7, 2742–2747 CrossRef CAS PubMed.
- K. R. Redeker, N.-Y. Wang, J. C. Low, A. McMillan, S. C. Tyler and R. J. Cicerone, Science, 2000, 290, 966–969 CrossRef CAS PubMed.
- R. C. Rhew, J. Geophys. Res., 2011, 116, G03026 CrossRef.
- L. Pei and J. M. Farrar, J. Phys. Chem. A, 2016, 120, 6122–6128 CrossRef CAS PubMed.
- C. M. Nichols, Z. Yang, B. B. Worker, D. R. Hager, N. M. M. Nibbering and V. M. Bierbaum, Phys. Chem. Chem. Phys., 2013, 15, 561–567 RSC.
- Z. Herman, J. H. Futrell and B. Friedrich, Int. J. Mass Spectrom. Ion Processes, 1984, 58, 181 CrossRef CAS.
- A. K. Shukla, K. Qian, S. L. Howard, S. G. Anderson, K. W. Sohlberg and J. H. Futrell, Int. J. Mass Spectrom. Ion Processes, 1989, 92, 147–169 CrossRef CAS.
- A. K. Shukla, K. Qian, S. Anderson and J. H. Futrell, J. Am. Soc. Mass Spectrom., 1990, 1, 6 CrossRef CAS PubMed.
- L. Pei and J. M. Farrar, Int. J. Mass Spectrom., 2015, 377, 93–100 CrossRef CAS.
- M. K. Bullitt, C. H. Fisher and J. L. Kinsey, J. Chem. Phys., 1974, 60, 478–491 CrossRef CAS.
- H. Schwarz, Angew. Chem., 1991, 103, 837–838 CrossRef CAS.
- J. Roithova and D. Schroeder, Chem. Rev., 2010, 110, 1170–1211 CrossRef CAS PubMed.
- P. B. Armentrout, Science, 1991, 251, 175–179 CAS.
- S. S. Yi, M. R. A. Blomberg, P. E. M. Siegbahn and J. C. Weisshaar, J. Phys. Chem. A, 1998, 102, 395–411 CrossRef CAS.
- M. Blomberg, S. S. Yi, R. J. Noll and J. C. Weisshaar, J. Phys. Chem. A, 1999, 103, 7254–7267 CrossRef CAS.
- S. S. Yi, E. L. Reichert and J. C. Weisshaar, Int. J. Mass Spectrom., 1999, 185-187, 837–846 CrossRef.
- R. J. Noll, S. S. Yi and J. C. Weisshaar, J. Phys. Chem. A, 1998, 102, 386–394 CrossRef CAS.
- E. L. Reichert, S. S. Yi and J. C. Weisshaar, Int. J. Mass Spectrom., 2000, 195/196, 55–69 CrossRef CAS.
- E. L. Reichert, G. Thurau and J. C. Weishaar, J. Phys. Chem. A, 2002, 106, 5563 CrossRef CAS.
- S. S. Yi, E. L. Reichert, M. C. Holthausen, W. Koch and J. C. Weisshaar, Chem. – Eur. J., 2000, 6, 2232–2245 CrossRef CAS.
- J. Sugar and C. Corliss, J. Phys. Chem. Ref. Data, 1985, 14(Suppl. 2), 644 Search PubMed.
- P. A. M. Van Koppen, P. R. Kemper and M. T. Bowers, J. Am. Chem. Soc., 1992, 114, 10941–10950 CrossRef CAS.
- P. M. van Koppen, M. T. Bowers, E. R. Fisher and P. B. Armentrout, J. Am. Chem. Soc., 1994, 116, 3780–3791 CrossRef CAS.
- P. A. M. Van Koppen, J. Brodbelt-Lustig, M. T. Bowers, D. V. Dearden, J. L. Beauchamp, E. R. Fisher and P. B. Armentrout, J. Am. Chem. Soc., 1991, 113, 2359–2369 CrossRef CAS.
- M. A. Hanratty, J. L. Beauchamp, A. J. Illies and M. T. Bowers, J. Am. Chem. Soc., 1985, 107, 1788–1789 CrossRef CAS.
- M. A. Hanratty, J. L. Beauchamp, A. J. Illies, P. Van Koppen and M. T. Bowers, J. Am. Chem. Soc., 1988, 110, 1–14 CrossRef CAS.
- P. Pechukas, J. C. Light and C. Rankin, J. Chem. Phys., 1966, 44, 794 CrossRef CAS.
- L. Pei, E. Carrascosa, N. Yang, S. Falcinelli and J. M. Farrar, J. Phys. Chem. Lett., 2015, 6, 1684–1689 CrossRef CAS PubMed.
- A. Cunje, C. F. Rodriquez, M. H. Lien and A. C. Hopkinson, J. Org. Chem., 1996, 61, 5212 CrossRef CAS.
- M. C. McCarthy, C. A. Gottlieb, H. Gupta and P. Thaddeus, Ap. J. Lett., 2006, 652, 141 CrossRef.
- P. Thaddeus, C. A. Gottlieb, H. Gupta, S. Brünken, M. C. McCarthy, M. Agundez, M. Guelin and J. Cernicharo, ApJ, 2008, 677, 1132 CrossRef CAS.
- S. Schlemmer, W. Geppert, A. Wolf, J. Glosik, D. Parker, L. Wiesenfeld, H. Kreckel, D. W. Savin and O. Asvany, Gas Phase Chemistry, Wiley-VCH Verlag GmbH & Co., KGaA, 2014, pp. 109–228 Search PubMed.
- R. C. Fortenberry, J. Phys. Chem. A, 2015, 119, 9941–9953 CrossRef CAS PubMed.
- M. B. Smith and J. March, March's Advanced Organic Chemistry: Reactions, Mechanisms and Structure, John Wiley & Sons, 2007 Search PubMed.
- P. Walden, Ber. Dtsch. Chem. Ges., 1896, 29, 133–138 CrossRef.
- E. D. Hughes and C. K. Ingold, J. Chem. Soc., 1935, 244–255 RSC.
- A. A. Viggiano, R. A. Morris, J. S. Paschkewitz and J. F. Paulson, J. Am. Chem. Soc., 1992, 114, 10477–10482 CrossRef CAS.
- W. L. Hase, Science, 1994, 266, 998–1002 CAS.
- A. E. Flores and S. Gronert, J. Am. Chem. Soc., 1999, 121, 2627–2628 CrossRef CAS.
- J. K. Laerdahl and E. Uggerud, Int. J. Mass Spectrom., 2002, 214, 277–314 CrossRef CAS.
- G. Vayner, K. N. Houk, W. L. Jorgensen and J. I. Brauman, J. Am. Chem. Soc., 2004, 126, 9054–9058 CrossRef CAS PubMed.
- J. Garver, N. Eyet, S. Villano, Y. Zhibo and V. Bierbaum, Int. J. Mass Spectrom., 2011, 301, 151–158 CrossRef CAS.
- J. Xie and W. L. Hase, Science, 2016, 352, 32–33 CrossRef CAS PubMed.
- J. M. Garver, Y. R. Fang, N. Eyet, S. M. Villano, V. M. Bierbaum and K. C. Westaway, J. Am. Chem. Soc., 2010, 132, 3808–3814 CrossRef CAS PubMed.
- A. J. Orr-Ewing, J. Chem. Phys., 2014, 140, 090901 CrossRef PubMed.
- M. L. Chabinyc, S. L. Craig, C. K. Regan and J. I. Brauman, Science, 1998, 279, 1882–1886 CrossRef CAS PubMed.
- W. Olmstead and J. Brauman, J. Am. Chem. Soc., 1977, 99, 4219 CrossRef CAS.
- W. L. Hase and Y. J. Cho, J. Chem. Phys., 1993, 98, 8626–8639 CrossRef CAS.
- L. Sun, K. Song and W. L. Hase, Science, 2002, 296, 875–878 CrossRef CAS PubMed.
- S. T. Graul and M. T. Bowers, J. Am. Chem. Soc., 1994, 116, 3875–3883 CrossRef CAS.
- Y. Wang, H. Song, I. Szabo, G. Czako, H. Guo and M. Yang, J. Phys. Chem. Lett., 2016, 7, 3322–3327 CrossRef CAS PubMed.
- A. P. Bento and F. M. Bickelhaupt, J. Org. Chem., 2008, 73, 7290–7299 CrossRef CAS PubMed.
- I. Fernandez and F. M. Bickelhaupt, Chem. Soc. Rev., 2014, 43, 4953–4967 RSC.
- M. N. Glukhovtsev, A. Pross and L. Radom, J. Am. Chem. Soc., 1996, 118, 6273–6284 CrossRef CAS.
- L. A. Angel and K. M. Ervin, J. Phys. Chem. A, 2001, 105, 4042–4051 CrossRef CAS.
- M. Stei, E. Carrascosa, M. A. Kainz, A. Kelkar, J. Meyer, I. Szabo, G. Czako and R. Wester, Nat. Chem., 2016, 8, 151 CAS.
- J. Mikosch, S. Trippel, C. Eichhorn, R. Otto, U. Lourderaj, J. X. Zhang, W. L. Hase, M. Weidemüller and R. Wester, Science, 2008, 319, 183 CrossRef CAS PubMed.
- R. Otto, J. Brox, S. Trippel, M. Stei, T. Best and R. Wester, Nat. Chem., 2012, 4, 534–538 CrossRef CAS PubMed.
- E. Carrascosa, M. Bawart, M. Stei, F. Linden, F. Carelli, J. Meyer, W. D. Geppert, F. A. Gianturco and R. Wester, J. Chem. Phys., 2015, 143, 184309 CrossRef CAS PubMed.
- U. Lourderaj, R. Sun, S. C. Kohale, G. L. Barnes, W. A. de Jong, T. L. Windus and W. L. Hase, Comput. Phys. Commun., 2014, 185, 1074–1080 CrossRef CAS.
- I. Szabó, A. G. Császár and G. Czakó, Chem. Sci., 2013, 4, 4362 RSC.
- I. Szabó, H. Telekes and G. Czakó, J. Chem. Phys., 2015, 142, 244301 CrossRef PubMed.
- J. Xie, R. Otto, J. Mikosch, J. Zhang, R. Wester and W. L. Hase, Acc. Chem. Res., 2014, 47, 2960 CrossRef CAS PubMed.
- I. Szabó and G. Czakó, Nat. Commun., 2015, 6, 5972 CrossRef PubMed.
- J. Zhang, J. Mikosch, S. Trippel, R. Otto, M. Weidemüller, R. Wester and W. L. Hase, J. Phys. Chem. Lett., 2010, 1, 2747–2752 CrossRef CAS.
- J. Zhang, U. Lourderaj, R. Sun, J. Mikosch, R. Wester and W. L. Hase, J. Chem. Phys., 2013, 138, 114309 CrossRef PubMed.
- T. Su, H. Wang and W. L. Hase, J. Phys. Chem. A, 1998, 102, 9819–9828 CrossRef CAS.
- J.-L. Le Garrec, B. R. Rowe, J. L. Queffelec, J. B. A. Mitchell and D. C. Clary, J. Chem. Phys., 1997, 107, 1021–1024 CrossRef CAS.
- L. A. Angel and K. M. Ervin, J. Am. Chem. Soc., 2003, 125, 1014–1027 CrossRef CAS PubMed.
- J. Xie, R. Sun, M. Siebert, R. Otto, R. Wester and W. L. Hase, J. Phys. Chem. A, 2013, 117, 7162 CrossRef CAS PubMed.
- R. Sun, J. Xie, J. Zhang and W. L. Hase, Int. J. Mass Spectrom., 2015, 377, 222–227 CrossRef CAS.
- I. Szabó, B. Olasz and G. Czakó, J. Phys. Chem. Lett., 2017, 8, 2917–2923 CrossRef PubMed.
- R. A. Morris and A. A. Viggiano, J. Phys. Chem., 1994, 98, 3740–3746 CrossRef CAS.
- D. M. Cyr, M. G. Scarton, K. B. Wiberg, M. A. Johnson, S. Nonose, J. Hirokawa, H. Tanaka, T. Kondow and R. A. Morris, J. Am. Chem. Soc., 1995, 117, 1828–1832 CrossRef CAS.
- L. A. Angel and K. M. Ervin, J. Phys. Chem. A, 2004, 108, 9827–9833 CrossRef CAS.
- J. Xie, S. C. Kohale, W. L. Hase, S. G. Ard, J. J. Melko, N. S. Shuman and A. A. Viggiano, J. Phys. Chem. A, 2013, 117, 14019 CrossRef CAS PubMed.
- J. Zhang, J. Xie and W. L. Hase, J. Phys. Chem. A, 2015, 119, 12517–12525 CrossRef CAS PubMed.
- B. Olasz, I. Szabó and G. Czakó, Chem. Sci., 2017, 8, 3164–3170 RSC.
- E. Carrascosa, T. Michaelsen, M. Stei, B. Bastian, J. Meyer, J. Mikosch and R. Wester, J. Phys. Chem. A, 2016, 120, 4711 CrossRef CAS PubMed.
- J. Chandrasekhar, S. F. Smith and W. L. Jorgensen, J. Am. Chem. Soc., 1984, 106, 3049 CrossRef CAS.
- D. L. Thomsen, J. N. Reece, C. M. Nichols, S. Hammerum and V. M. Bierbaum, J. Am. Chem. Soc., 2013, 135, 15508–15514 CrossRef CAS PubMed.
- D. K. Bohme and G. I. Mackay, J. Am. Chem. Soc., 1981, 103, 978–979 CrossRef CAS.
- P. M. Hierl, A. F. Ahrens, M. Henchman, A. A. Viggiano, J. F. Paulson and D. C. Clary, J. Am. Chem. Soc., 1986, 108, 3140–3142 CrossRef CAS.
- P. M. Hierl, A. F. Ahrens, M. J. Henchman, A. A. Viggiano, J. F. Paulson and D. C. Clary, Faraday Discuss., 1988, 85, 37–51 RSC.
- A. A. Viggiano, S. T. Arnold, R. A. Morris, A. F. Ahrens and P. M. Hierl, J. Phys. Chem., 1996, 100, 14397–14402 CrossRef CAS.
- X. Liu, J. Xie, J. Zhang, L. Yang and W. L. Hase, J. Phys. Chem. Lett., 2017, 8, 1885–1892 CrossRef CAS PubMed.
- L. Yang, X. Liu, J. Zhang and J. Xie, Phys. Chem. Chem. Phys., 2017, 19, 9992–9999 RSC.
- J. V. Seeley, R. A. Morris, A. A. Viggiano, H. B. Wang and W. L. Hase, J. Am. Chem. Soc., 1997, 119, 577–584 CrossRef CAS.
- J. V. Seeley, R. A. Morris and A. A. Viggiano, J. Phys. Chem. A, 1997, 101, 4598–4601 CrossRef CAS.
- S. Raugei, G. Cardini and V. Schettino, J. Chem. Phys., 2001, 114, 4089–4098 CrossRef CAS.
- H. Tachikawa, M. Igarashi and T. Ishibashi, Chem. Phys. Lett., 2002, 363, 355–361 CrossRef CAS.
- H. Tachikawa, J. Chem. Phys., 2006, 125, 133119 CrossRef PubMed.
- I. Adamovic and M. S. Gordon, J. Phys. Chem. A, 2005, 109, 1629–1636 CrossRef CAS PubMed.
- J. Zhang, L. Yang and L. Sheng, J. Phys. Chem. A, 2016, 120, 3613–3622 CrossRef CAS PubMed.
- C. K. Regan, S. L. Craig and J. I. Brauman, Science, 2002, 295, 2245 CrossRef CAS PubMed.
- R. A. J. O'Hair, G. E. Davico, J. Hacaloglu, T. T. Dang, C. H. DePuy and V. M. Bierbaum, J. Am. Chem. Soc., 1994, 116, 3609–3610 CrossRef.
- W.-P. Hu and D. G. Truhlar, J. Am. Chem. Soc., 1994, 116, 7797 CrossRef CAS.
- K. Doi, E. Togano, S. S. Xantheas, R. Nakanishi, T. Nagata, T. Ebata and Y. Inokuchi, Angew. Chem., Int. Ed., 2013, 52, 4380 CrossRef CAS PubMed.
- R. Otto, J. Brox, M. Stei, S. Trippel, T. Best and R. Wester, Nat. Chem., 2012, 4, 534–538 CrossRef CAS PubMed.
- J. Xie, R. Otto, R. Wester and W. L. Hase, J. Chem. Phys., 2015, 142, 244308 CrossRef PubMed.
- J. Xie, M. J. Scott, W. L. Hase, P. M. Hierl and A. A. Viggiano, Z. Phys. Chem., 2015, 229, 1747–1763 CrossRef CAS.
- R. Otto, J. Brox, S. Trippel, M. Stei, T. Best and R. Wester, J. Phys. Chem. A, 2013, 117, 8139 CrossRef CAS PubMed.
- J. Xie, M. McCellan, R. Sun, S. C. Kohale, N. Govind and W. L. Hase, J. Phys. Chem. A, 2015, 119, 817–825 CrossRef CAS PubMed.
- J. Xie, X. Ma, J. Zhang, P. M. Hierl, A. A. Viggiano and W. L. Hase, Int. J. Mass Spectrom., 2017, 418, 122–129 CrossRef CAS.
- J. Zhang, L. Yang, J. Xie and W. L. Hase, J. Phys. Chem. Lett., 2016, 7, 660 CrossRef CAS PubMed.
- F. M. Bickelhaupt, E. J. Baerends, N. M. M. Nibbering and T. Ziegler, J. Am. Chem. Soc., 1993, 115, 9160–9173 CrossRef CAS.
- S. Gronert, J. Am. Chem. Soc., 1993, 115, 652–659 CrossRef CAS.
- P. Bento, M. Sola and F. M. Bickelhaupt, J. Chem. Theory Comput., 2008, 4, 929–940 CrossRef PubMed.
- X. Wu, X. Sun, X. Wei, Y. Ren, N. Wong and W. Li, J. Chem. Theory Comput., 2009, 5, 1597–1606 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, J. Chem. Theory Comput., 2010, 6, 1104–1108 CrossRef CAS.
- W.-P. Hu and D. G. Truhlar, J. Am. Chem. Soc., 1996, 118, 860–869 CrossRef CAS.
- F. M. Bickelhaupt, J. Comput. Chem., 1999, 20, 114–128 CrossRef CAS.
- L. P. Wolters, Y. Ren and F. M. Bickelhaupt, ChemistryOpen, 2014, 3, 29–36 CrossRef CAS PubMed.
- S. M. Villano, S. Kato and V. M. Bierbaum, J. Am. Chem. Soc., 2006, 128, 736–737 CrossRef CAS PubMed.
- B. D. Wladkowski and J. I. Brauman, J. Am. Chem. Soc., 1992, 114, 10643–10644 CrossRef CAS.
- C. H. DePuy, S. Gronert, A. Mullin and V. M. Bierbaum, J. Am. Chem. Soc., 1990, 112, 8650–8655 CrossRef CAS.
- S. Gronert, A. E. Fagin and L. Wong, J. Am. Chem. Soc., 2007, 129, 5330–5331 CrossRef CAS PubMed.
- E. Carrascosa, J. Meyer, J. Zhang, M. Stei, T. Michaelsen, W. L. Hase, L. Yang and R. Wester, Nat. Commun., 2017, 8, 25 CrossRef PubMed.
- L. Yang, J. Zhang, J. Xie and C. Zhao, J. Phys. Chem. A, 2017, 121, 1078–1085 CrossRef CAS PubMed.
- V. Tajti and G. Czako, J. Phys. Chem. A, 2017, 121, 2847 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2017 |