Crossed beam polyatomic reaction dynamics: recent advances and new insights
Abstract
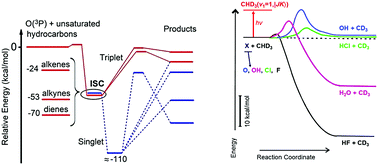
Over the past ten years or so, great advances in our understanding of the dynamics of elementary (bimolecular) polyatomic reactions in the gas-phase have occurred. This has been made possible by critical improvements (a) in crossed molecular beam (CMB) instruments with rotating mass spectrometric detection and time-of-flight analysis, especially following the implementation of soft ionization (by tunable low energy electrons or vacuum-ultraviolet synchrotron radiation) for product detection with increased sensitivity and universal detection power, and (b) in REMPI-slice velocity map ion imaging (VMI) detection techniques in pulsed CMB experiments for obtaining product pair-correlated information through high-resolution measurements directly in the center of mass system. The improved universal CMB method is permitting us to identify all primary reaction products, characterize their formation dynamics, and determine the branching ratios (BRs) for multichannel non-adiabatic reactions, such as those of ground state oxygen atoms, O(3P), with unsaturated hydrocarbons (alkynes, alkenes, dienes). The improved slice VMI CMB technique is permitting us to explore at an unprecedented level of detail, through pair-correlated measurements, the reaction dynamics of a prototype polyatomic molecule such as CH4 (and isotopologues) in its ground state with a variety of important X radicals such as F, Cl, O, and OH. In this review, we highlight this recent progress in the field of CMB reaction dynamics, with an emphasis on the experimental side, but with the related theoretical work, at the level of state-of-the-art calculations of both the underlying potential energy surfaces and the reaction dynamics, noted throughout. In particular, the focus is (a) on the effect of molecular complexity and structure on product distributions, branching ratios and role of intersystem crossing for the multichannel, addition–elimination reactions of unsaturated hydrocarbons with O atoms, and (b) on the very detailed dynamics of the abstraction reactions of ground-state methane (and isotopologues) with atoms (F, Cl, O) and diatoms (OH), with inclusion of also rotational mode specificity in the vibrationally excited methane reactions.
- This article is part of the themed collection: Chemical reaction dynamics


 Please wait while we load your content...
Please wait while we load your content...