Vibrational energy relaxation dynamics of diatomic molecules inside superfluid helium nanodroplets. The case of the I2 molecule†
Arnau
Vilà‡
 ab,
Miguel
Paniagua
ab,
Miguel
Paniagua
 b and
Miguel
González
b and
Miguel
González
 *a
*a
aDepartament de Ciència de Materials i Química Física and IQTC, Universitat de Barcelona, c/ Martí i Franquès, 1, 08028 Barcelona, Spain. E-mail: miguel.gonzalez@ub.edu; Fax: +34934021231
bDepartamento de Química Física Aplicada, Universidad Autónoma de Madrid, c/ Francisco Tomás y Valiente, 7, 28049 Cantoblanco, Spain
First published on 27th November 2017
Abstract
The vibrational energy relaxation (VER) of a homonuclear diatomic molecule (X2) in a 4He superfluid nanodroplet (HeND; T = 0.37 K) was studied adapting appropriately a hybrid theoretical quantum approach recently proposed by us. In the first application the interesting case of the I2(X) molecule was examined and, as far as we know, this corresponds to the first theoretical investigation on the VER of molecules embedded in HeND. Vibrational relaxation of I2 takes place according to a cascade mechanism [sequential transitions between two consecutive vibrational levels (ν → ν − 1; ν − 1 → ν − 2; …; 2 → 1; 1 → 0), where an arbitrary relaxation, e.g., ν − 1 → ν − 2, can only occur once the previous relaxation has taken place, and so on]. The global relaxation from the initial excited state ν down to the ground state (ν = 0) happens on the nanosecond scale. Data on the VER of molecules in HeND are very scarce and a vibrational lifetime not far from the I2 one for ν = 1 has been estimated experimentally for Na3(24E′) on HeND (a qualitatively similar 0 → 1 vibrational energy gap occurs in both species), but metastability has not been reported in the second case. The cascade mechanism was understood once the values of the coupling matrix elements were examined, and the time evolution of the populations of two consecutive vibrational levels was adequately described using a non-linear two-state Hamiltonian model for I2 in the HeND. According to the calculations, superfluid liquid helium is very efficient in releasing the excess of energy arising from the I2 vibrational de-excitation, as it should be. However, the number of He atoms evaporated is small compared to what is expected. We hope that this first theoretical work on the molecular VER dynamics in HeND will encourage researchers to investigate this important process about which we still know very little.
1. Introduction
Vibration is one of the three basic types of molecular motion and vibrational energy relaxation (VER) is perhaps the most important molecular relaxation mechanism, together with electronic relaxation, and it is also relevant in the context of the chemical reactivity.1 VER can occur by means of energy exchange with other atoms or molecules, or by exchanging energy with other degrees of freedom of the same excited species, which is known as intramolecular vibrational relaxation (IVR).The VER mechanism strongly depends on the phase in which the molecules reside. In the gas phase this process is mediated by binary collisions between the gas molecules and, therefore, this is not a very effective process. In contrast, the mechanism is much more efficient in condensed phases due to the much larger number of molecules surrounding the species that is relaxing.2,3 Moreover, the investigation of VER in the condensed phase provides a sensitive probe of the structure and dynamics of the liquid phase intermolecular dynamics and of the solute–solvent interactions.4
In the last few decades, the advent of novel ultrafast time-resolved spectroscopic techniques has enabled us to gain a lot of knowledge on the VER mechanism in the condensed phase.5,6 Generally, pump–probe techniques are used, in which a first ultrashort pulse excites the molecules and a delayed second pulse probes the vibrational populations.2,3,7 Different ways to pump (excite) and probe exist, depending on the process that is addressed.8 In general, the excitation involves stimulated Raman scattering or infrared (IR) absorption, while the probe depends on the particular experiment. In experiments focused on the phase coherence, VER is studied using sub-picosecond IR pump–probe spectroscopy as well as coherent anti-Stokes Raman spectroscopy (CARS) and photon echo.9
From a theoretical perspective, several approaches have been proposed to investigate VER in condensed phases. In a classical mechanics description of this process in the liquid phase, the friction exerted by the liquid on the vibrational motion of the solvated molecule damps its amplitude while heating the bath. This can be described by means of a Langevin equation for a damped oscillator subject to a fluctuation force (in the long time limit the phenomenological dissipation force is related to fluctuations).10 An efficient relaxation takes place when the frequencies of the excited oscillator and the solvent fluctuations match. This classical approach works well for low frequencies or high temperatures.
The most simple quantum approach for VER uses first order time dependent perturbation theory (i.e., the Fermi's Golden Rule) to calculate the rate constant for the transition between two vibrational levels. This is determined by the Fourier transform of the time correlation function of the interaction potential energy. Due to the large number of solvent molecules, in general it is not feasible to compute the quantum time correlation function, and so different treatments are used to evaluate this function. One possibility is to find the classical analog for the rate constant equation assuming the detailed balance principle and the equivalence between the classical and the real part of the quantum correlation functions.2 Then, the classical correlation function is derived from the molecular dynamics (MD) simulations. Another strategy is to model the liquid with a bath of independent harmonic oscillators, and carry out the calculation of the quantum correlation function.11
Finally, another theoretical approach consists in performing real-time simulations of the VER dynamics. Owing to the large number of solvent particles present, up to now this strategy has been only computationally feasible for a classical non-equilibrium MD coupled to quantum oscillators.5,6,10 These calculations are very demanding due to the different time scales that are present and due to the large number of particles.
In the present work, which is situated in the context of the processes occurring in superfluid 4He nanodroplets (HeND; T = 0.37 K),12–15 we report a real-time simulation of the VER, considering a full quantum description of a system formed by a homonuclear diatomic molecule (X2) embedded in a superfluid 4He nanodroplet. To do this we have used a hybrid approach recently proposed by us,16 but with important modifications in the numerical time propagation of the wave functions, since the VER in HeND is a very slow process (nanosecond time scale, as will be seen in the Results section). As a first application, we have studied the VER of the iodine molecule in the ground electronic state (I2(X)). The cornerstone for the feasibility of such quantum simulations is the use of the time dependent density functional theory (TDDFT) for the description of the superfluid liquid helium, that has allowed us to study recently the dynamics of different physico-chemical processes involving HeND (photodissociation of diatomics,16–18 capture of atoms,19 reactions,20 and nanodroplet relaxation21).
Superfluid helium nanodroplets have very special properties that have stimulated a wide range of applications in the field of chemical physics/physical chemistry in which they play a key role,12–15 such as high-resolution spectroscopy of atoms and molecules, stabilization of metastable species, and the synthesis of metal nanoparticles22,23 and nanowires.24,25 The superfluidity and the inert chemical character of helium atoms are probably the most important characteristics of this solvent.
Regarding the I2 molecule, it has become a benchmark for the investigation of the vibrational and rotational motions and its high-resolution spectroscopy has been widely reported in several contexts.26–34 The energy gap between two consecutive vibrational levels of I2 is quite small, νe = 214.502 cm−1 (308.621 K),35 which provides a high density of states. Therefore, this leads to relatively fast vibrational relaxation rates, in comparison to other molecules, making this system very attractive. Thus, e.g., VER of I2(X) has been investigated in the gas phase (He–I2(X) mainly36–38) and condensed media (including mesitylene39 and liquid Xe40–51).
Rovibrational spectroscopy has been extensively studied in HeND.12–14 The solvent induces small vibrational line shifts (less than 2 cm−1 for most of the molecules studied) and band broadening. The interaction of the solute with the liquid helium is not strong enough to induce vibrational splitting and, therefore, for the molecules in HeND the vibrational symmetry is not modified with respect to the gas phase. Regarding the VER of molecules in helium nanodroplets, only a few investigations have been carried out. Thus, e.g., IR spectroscopy and bolometric detection have been used to investigate the VER of some molecules and binary complexes.52–55
The vibrational relaxation of HF in HeND is very slow (t ≥ 0.5 ms)54 due to the large energy gap that exists between two consecutive vibrational levels (νe = 4138.32 cm−1 (5954.12 K)),35 which does not couple efficiently with the nanodroplet excitations and, consequently, presents an important metastability. For this case, the nanodroplet size dependent line shifts and broadening indicate that the coupling with the HeND surface excitations (ripplons) is the main relaxation mechanism.54 For binary complexes such as Ne, Ar, Kr–HF(ν), the relaxation from ν = 1 to ν = 0 takes place in a time scale similar to that of the previous experiment (0.5 ms), and the relaxation rate is also size dependent.55
Besides, the vibrational relaxation and dephasing of some alkali dimers (Rb2, Na2, and K2) placed in a dimple on the surface of a HeND,56–58 and the photoinduced non-adiabatic dynamics in quartet states of Na3 and K3 also formed on the HeND surface have been also studied,59 providing information on the vibrational relaxation of Na3 in the 24E′ excited state. Moreover, the de-alignment of the I2(X) rotation in HeND has been reported very recently.60
The contents of the paper are organized as follows. The hybrid theoretical approach employed for the simulation of the real-time VER dynamics of a X2 diatomic molecule in HeND is described in Section 2. The main results obtained in the application of this method to the I2(X) molecule for several initial excitations are reported in Section 3; and a two-state quantum model to interpret the previous results is developed in Section 4. The summary and conclusions are presented in Section 5.
2. Theoretical methods
Here, we have described theoretically the dynamical evolution of the vibrational relaxation of a homonuclear diatomics X2 in a superfluid helium nanodroplet, considering as a first example of application the relaxation of I2 in its electronic ground state (I2(X)), prompted by a sudden vibrational excitation of the molecule (e.g., using Raman techniques). Owing to the very low temperature of these nanodroplets (T = 0.37 K), only the vibrational ground state (ν = 0) of the molecule is populated once the doped nanodroplet reaches the thermal equilibrium. Thus, the zero time condition to launch the dynamics is represented by the helium density corresponding to the I2(X, ν = 0)@4HeN ground state doped nanodroplet, but with a sudden change of the vibrational wave function of I2 from ν = 0 to a particular excited vibrational level ν (0 → ν vibrational transition). The vibrational excitation and the global vibrational relaxation processes correspond to| I2(X,ν = 0)@4HeN + hν → [I2(X,ν)@4HeN]* + hν′ | (1a) |
| [I2(X,ν)@4HeN]* → [I2(X,ν = 0)@4HeN′]* + (N–N′)4He, | (1b) |
Since the interaction between the iodine and the helium is relatively large, compared to the helium–helium interaction, this impurity is placed in the center of the nanodroplet in the ground state. This fact, together with the symmetry of the system, allows us to keep frozen the I2 center of mass (CM) during the vibrational relaxation dynamics.16 Besides, the huge mass of the I2 CM compared to the helium one (253.809 vs. 4.003 amu, respectively) justifies a classical description of this degree of freedom, i.e., not to consider its zero point motion. At the low temperature of the HeND most of the rotational population of I2 will be in the rotational quantum level corresponding to the j = 0 rotational quantum number, and even though the rotational motion of I2 is very slow (rotational period for I2(X) in the j = 1 rotational state τrot ≈ h/(2Be) = 446 ps and it is likely that the molecule will be prepared in excited vibrational states involving higher rotational states) it is faster than the vibrational relaxation and should be included in the theoretical modeling. Nevertheless, in this first theoretical attempt to investigate the VER in HeND and due to the large difficulties involved in the quantum dynamics study, the molecule has been described taking into account only the vibrational degree of freedom.
In the theoretical study of complex systems hybrid approaches are often used (“divide and conquer” strategy). In this way, a small but very important part of the system is described at a substantially higher theoretical level than the rest of the system. Here, to carry out the real-time quantum simulations of VER we have combined a commonly used method to study rather large systems of the bosonic superfluid liquid 4He (TDDFT)16–21,61–64 and the usual method to study atoms or molecules in the gas phase (time dependent wave function).16–20
The TDDFT calculations have been performed using the so-called Orsay–Trento (OT) phenomenological density functional,65 and we have neglected the non-local contributions to the helium correlation energy and the back-flow term for computational reasons, as usual16–21,61–64 This strategy allows us to deal with nanodroplets with a relatively large number of helium atoms (making possible the comparison with experimental results), while keeping the computational cost affordable. In addition, the vibrational degree of freedom of the X2 molecule has been described by standard quantum mechanics, considering suitable time dependent wave functions. It should be noted that a modification has been added to the OT density functional that avoids unphysical helium densities when the interaction between the dopant molecule and helium is strong.66
According to this method, the equations of motion for the different degrees of freedom are found by minimizing the quantum action 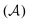 :
:
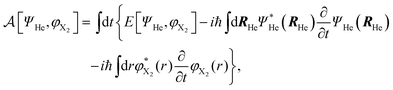 | (2) |
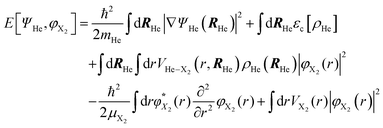 | (3) |
The εc[ρHe] term corresponds to the potential energy and correlation energy densities of the superfluid liquid helium. The term VHe–X2(r,RHe) stands for the interaction potential energy between the helium and the diatomic molecule. Here, this term has been taken from ref. 67 and the VI2(r) potential energy curve describing the interaction between the two atoms of the molecule has been described by a Morse function (eqn (4)), using the experimental parameters from ref. 35 (re = 2.6663 Å, De = 18052.42 K and a = 1.857608 Å−1), where
| VI2(r) = De(1 − e−a(r−re))2 | (4) |
Although an accurate RKR (Rydberg–Klein–Rees) potential energy curve68 could have been used to describe the I2 molecule instead of the Morse one, it should be noted that for the low and relatively low vibrational levels examined here the Morse function is also accurate and, in addition, there are analytical expressions available for the corresponding vibrational wave functions.
The minimization of the action has been performed considering its variation with respect to each one of the wave functions; and this leads to the next two coupled time dependent Schrödinger-like nonlinear equations governing the evolution of helium and the molecule, respectively:
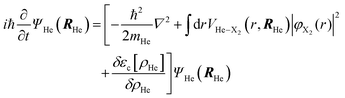 | (5a) |
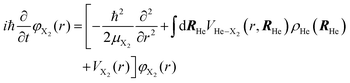 | (5b) |
These are the same equations employed by us in the investigation of the photodissociation of Cl2(B ← X) in superfluid helium nanodroplets.16 However, this physical phenomenon is very different from the vibrational energy relaxation process considered here, since for the VER the motion of the relative coordinate wave function always takes place in the region of the electronic well (i.e., around the equilibrium distance, re, of the potential energy curve of the diatomics). For that reason in the present study we have proposed a much more efficient strategy to account for the dynamic evolution of the system, consisting in expressing the vibrational wave function in terms of the vibrational eigenfunctions basis set {φi(r)} of the vibrational Hamiltonian operator of the isolated molecule; i.e., without including the interaction of X2 with the helium environment. Hence, we have expressed φX2(r) as
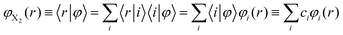 | (6) |
Thus, this approach switches the description of the relative coordinate degree of freedom from the position (relative coordinate “r”), which would be in fact numerically discretized in a grid of points, into the vibrational eigenvectors {|i〉} representation. This procedure allows us to transform the spatial eqn (5b) into the algebraic eqn (7b), which can be solved in a much more efficient way, in terms of both numerical accuracy and computational time. In this way the equations of motion that have been used in this work for the description of the VER dynamics in helium nanodroplets are the following:
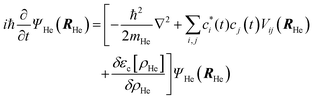 | (7a) |
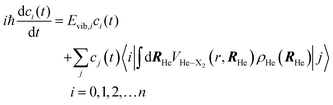 | (7b) |
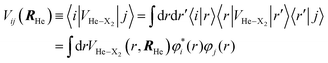 | (8) |
In order to converge the time propagation of eqn (7a) and (7b), for a given initial excited level ν, typically, it has been enough to include in the calculations all vibrational levels from ν = 0 up to ν = ν + 3.
This strategy highly reduces the computational cost of the numerical description of the vibrational wave function, since a very dense grid is needed for an oscillating wave function, which turns out to involve a large basis set (grid points). In contrast to this, just a few vibrational wave functions (basis set) are required to accurately describe the oscillating wave function, according to the transformation described here.
The determination of the initial time ground state I2(X,ν = 0)@4HeN configuration has been obtained by looking for the stationary solution of eqn (7a) but keeping fixed the vibrational wave function of the molecule to the ν = 0 one (c0 = 1,ci = 0,i ≠ 0). That is to say, this approximation neglects the effect of the helium environment on the vibration of the iodine molecule. In spite of this, this is essentially correct due to the large differences that exist between the involved energies (I2 chemical bond versus the van der Waals (vdW) I2–He interaction). This is also manifested in the dynamical calculations, since the asymptotic vibrational wave function, i.e., that corresponding to the global relaxation time, has been determined to be just φ0(r).
The equation describing the time evolution of the helium effective wave function (eqn (7a)) has been solved numerically discretizing the space in a grid of points in which the spatial derivatives of the kinetic energy terms have been calculated using the fast Fourier transform (FFT) as implemented in the FFTW package.69 The numerical time integration has been carried out employing a fourth order predictor–corrector method,70 initiated by a fourth-order Runge–Kutta method,71 and the time step has been fixed at 1.0 × 10−3 ps.
The selected Cartesian grid used has a spacing of 0.40 Å for the x and y axis and of 0.30 Å for the z axis (where the molecule is placed) and each one of them has a total length of 38.0 Å. A quartic negative imaginary potential (NIP)72 has been defined in the edges of the grid, in order to absorb the possible fragments of the helium wave function off the droplet that come from the evaporation of helium, avoiding in this way artificial reflections. This imaginary potential has the following form:
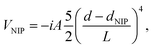 | (9) |
Concerning the numerical time integration of eqn (7b), we employed a very different strategy, which benefits from the basis set expansion of the molecular vibrational wave function; and for the evaluation of the required integrals the basis set functions were described using a grid of 1000 points between r = 2.3 Å to 3.5 Å. Thus, we have proceeded in the following sequential manner:
(1) At a given time t, the matrix representation of the full effective vibrational Hamiltonian of the diatomics (eqn (5b)), Hv, that is expressed in terms of {|i〉}, is diagonalized, obtaining Hα.
(2) In the new vibrational basis set {|α〉} obtained before, the time evolution (t → t + δt) of the coefficients {cα} of the I2 vibrational vector state is particularly simple, as we are considering stationary states: cα(t + δt) = cα(t)exp(−Eαδt/ħ).
(3) The ci(t + δt) coefficients are obtained from the cα(t + δt) ones coming back to the original/reference basis set {|i〉}.
(4) The procedures indicated in (1)-(2)-(3) are repeated for the new time t + δt to determine the time evolution t + δt → t + δ2t, and so on.
The diagonalization procedure is performed by means of the Jacobi method, since the Hamiltonian matrix is real and symmetric. This procedure turns out to be faster and much more numerically stable than the usual method employed to solve eqn (7b),16–18,20 since the error only comes from the diagonalization and round-off numerical computer errors occurring during the operations. Keeping in mind that the vibrational relaxation processes take a long time and that they are probably slower in HeND (superfluid + chemically very inert), this approach has become determinant in order to make possible this investigation (in fact, several unsuccessful attempts were made by our group previously, trying to solve this problem using common procedures).
A large number of test calculations have been performed in order to determine the optimal numerical parameters (grids, density of points in the grids, time step and NIPs properties), to be employed in the time dependent quantum dynamics calculation in order to obtain converged results, as is usual when carrying out this type of study.
3. Results
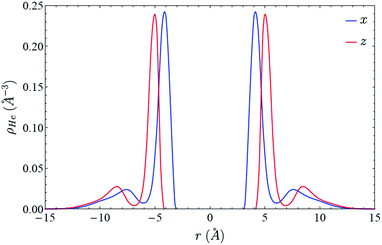
The vibrational energy relaxation of a I2(X) molecule embedded in a superfluid helium nanodroplet of 100 4He atoms has been studied, considering a sudden excitation of I2(X) from the vibrational ground state (ν = 0) to a given vibrational excited state ν (ν = 1, 2, 3, 4, 5, 6 and 8). The selection of this small size nanodroplet is based on computational reasons, since the VER process implies a very long time scale; and due to this a very large number of iterations is needed to complete the simulated time. However, we expect this process in a liquid to be mainly dominated by the interaction of the embedded species with the nearest atoms or molecules of the solvent5 (first solvation shell), which makes our choice reasonable. The I2(X,ν = 0)@4He100 ground state doped nanodroplet is shown in Fig. 1.The temporal evolutions of the vibrational level populations for the relaxations after the initial excitations to ν = 1, 3 and 8 are presented in Fig. 2. For the global de-excitation process, [I2(X,ν)@4He100]* → [I2(X,ν = 0)@4He100−m]* + m4He, a nanosecond time scale can be inferred, the concrete values increasing with the initial excitation (≈3.0, 7.5 and 14.0 ns for ν = 1, 3 and 8, respectively). The changes experimented by the HeND and the evaporation of helium atoms as a consequence of the VER will be examined at the end of this section.
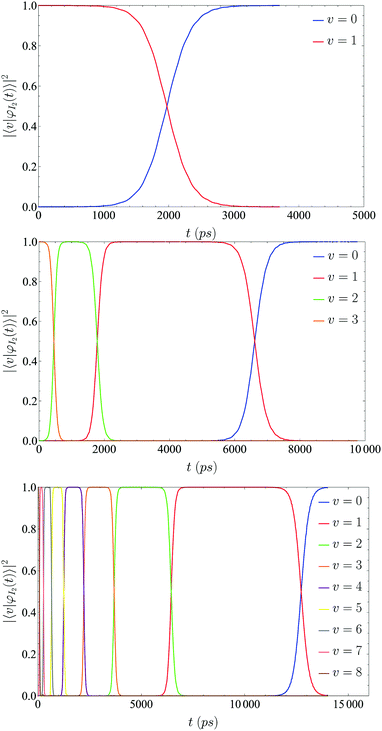 | ||
| Fig. 2 Vibrational populations for three different initial excitations (ν = 1, 3 and 8, from the top to the bottom of the figure, respectively), as a function of time. The decay of the ν = 8 initial level population cannot be seen clearly in the bottom figure because it is very fast (see Fig. S1 and S2 in the ESI†). | ||
It is worth noting that the final vibrational wave function has only a significant contribution of |ν = 0〉. Hence, the very inert environment created by the helium does not significantly affect the vibrational structure of the I2(X) embedded molecule. This is due to the largely different energy scales involved: the I–I(X) interaction corresponds to a chemical bond (De = 18052.42 K),35 while the I2–(4He)100 interaction potential energy is of the vdW type and has a value around 700 K.67 In more detail, it can be stated that the presence of liquid helium adds a potential energy in the I–I well region, which is most relevant for the present purposes (r = 2.3 Å to 3.5 Å), and which varies by about 250 K; while for the same interval of distances the variation of the I–I(X) potential energy curve is of the order of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K. Therefore, the resulting global potential energy for I–I is quite similar to the molecular potential energy of the isolated molecule (VI2).
000 K. Therefore, the resulting global potential energy for I–I is quite similar to the molecular potential energy of the isolated molecule (VI2).
These data support the approximation made in the calculation of the ground state of the doped nanodroplet, I2(X,ν = 0)@4HeN, described in Section 2. In contrast to this, in a recent study on the formation of the Ne2 vdW dimer in a nanodroplet [Ne2@(4He)N′] from the Ne + Ne@(4He)N reactants, a significant influence of the nanodroplet on the structure of the dimer has been found.20 This result, of course, could be expected because both the Ne–Ne and Ne–He interactions are of the van der Waals type.
For the low to moderate excitations studied here, VER takes place in a subsequent number of well-defined steps, each one of them involving the transition between two consecutive vibrational levels (cascade mechanism).73 Therefore, the energy excess of I2 is not released continuously but in well-defined steps, each one of them correlating with the transition between two consecutive vibrational levels, ν → ν − 1, which requires some time to occur; and each transition involves the evaporation of a helium atom.
This shows the existence of metastability for each vibrational level involved in the VER. In order to be more quantitative, we have defined the lifetime of each metastable ν-level as the elapsed time during which its probability (population) is equal to or greater than 0.50. For each vibrational level this corresponds to the elapsed time between the corresponding two consecutive curve crossings that can be seen in Fig. 2. Two main features are shown by the vibrational lifetimes (Table 1). They decrease when increasing the vibrational level as expected and, for a given vibrational level, the lifetime increases with the initial vibrational excitation. However, the amount in which it increases is gradually reduced as the initial excitation increases, reaching a limit or asymptotic value.
| ν | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| 1 | 1972 | |||||||
| 2 | 3187 | 808 | ||||||
| 3 | 4830 | 1331 | 455 | |||||
| 4 | 5531 | 2110 | 762 | 296 | ||||
| 5 | 5647 | 2224 | 1253 | 506 | 204 | |||
| 6 | 6029 | 2493 | 1248 | 897 | 357 | 143 | ||
| 8 | 6277 | 2764 | 1460 | 969 | 590 | 394 | 192 | 79 |
It deserves to be highlighted that we have observed these behaviors in the present (converged) results and also in the large number of test calculations addressed to determine the optimal parameters for this dynamics study. The vibrational lifetime of a given level is directly related with the time it takes the liquid to oscillate in phase with the vibration of the molecule, as will be seen in the next section. The calculations suggest that it is easier for the liquid to oscillate in phase with the molecule when the liquid is initially not oscillating, or oscillating with a small number of frequencies, than when it is oscillating in many frequencies (a progressively higher number of frequencies is involved for increasingly higher initial excitations).
The vibrational lifetimes are within the 0.079–6.28 ns time interval (Table 1). These values correspond to the lifetimes of the ν = 8 and ν = 1 levels, respectively, when the initial excitation ν = 0 → ν = 8 is considered. Besides, the transition time (or relaxation time) of an arbitrary ν-level is defined as the time it takes for the probability of the ν − 1 level to rise from 1% to 99%. The transition times values are in the range 0.105–1.74 ns and these times are for ν = 8 and ν = 1, respectively, for the situation indicated above (Table 2). Moreover, the transition time of a given vibrational level is essentially independent of the initial excitation.
| ν | 1 → 0 | 2 → 1 | 3 → 2 | 4 → 3 | 5 → 4 | 6 → 5 | 7 → 6 | 8 → 7 |
|---|---|---|---|---|---|---|---|---|
| 1 | 1703 | |||||||
| 2 | 1704 | 765 | ||||||
| 3 | 1697 | 765 | 460 | |||||
| 4 | 1702 | 765 | 460 | 319 | ||||
| 5 | 1704 | 765 | 460 | 319 | 236 | |||
| 6 | 1711 | 765 | 461 | 319 | 236 | 175 | ||
| 8 | 1741 | 779 | 466 | 322 | 237 | 176 | 134 | 105 |
The weakness of the I2–solvent interaction breaks down the stationary character of the gas phase (isolated molecule) vibrational levels but it does it very slightly, leaving them metastable. This physical process has an intrinsic quantum nature, since no discrete stationary states exist for the classical oscillator, and its physical origin will be clarified in the following section.
Data on the vibrational relaxation of molecules in HeND for comparison are very scarce. Vibrational lifetimes of 4.42 and 1.80 ns have been estimated experimentally for the (ν = 1, j = 1/2) and (ν = 2, j = 5/2) pseudo-rovibrational levels of the Na3 trimer, in the excited 24E′ electronic state, on the surface of a HeND.59 These levels relax according to the (1, 1/2) → (0, 0) and (2, 5/2) → (0, 0) processes, respectively [the energies of (ν = 1, j = 1/2) and (ν = 2, j = 5/2) with respect to (ν = 0, j = 0) are equal to 52.66 cm−1 (75.77 K) and 100.20 cm−1 (144.17 K), respectively]. In addition, the vibrational relaxation of HF from ν = 1 to ν = 0 inside a HeND is a very slow process (t ≥ 0.5 ms),54 due to the large vibrational energy gap of the molecule (νe = 4138.32 cm−1 (5954.12 K));35 while for the binary complexes Ne, Ar, Kr–HF this relaxation occurs in a similar time scale (0.5 ms for Ar–HF).55
The lifetime of the vibrational level ν = 1 obtained here for I2 after the initial excitation from ν = 0 to ν = 1 (1.97 ns) is not far from the Na3(24E′) value and much smaller than the HF one. This can be interpreted, at least in part, on the basis of the qualitatively similar 0 → 1 vibrational energy gap of I2(X) and Na3(24E′). The lifetime of ν = 1 (0 → 1) determined here is also similar to the theoretical values reported on I2(X) employing a very different solvent. Thus, in liquid Xe at T = 303 K and a density of 3.0 g cm−3, vibrational relaxation times of 1.67 and 2.58 ns have been reported in equilibrium and non-equilibrium MD simulations, respectively.41 Hence, from comparison with the results obtained for other systems it seems that the present results are reasonable. Additionally, it should be noted that, different from what happens for I2(X) in HeND, metastability has not been reported for ν = 1 neither for Na3(24E′) on HeND nor for I2(X) in liquid Xe.
Regarding the structure of the helium nanodroplet, it does not change significantly during the VER process, and the interaction energy between the molecule and the nanodroplet remains almost constant when the vibrational state changes, i.e., it does not depend on the vibrational level, but fluctuates a few Kelvin when the transition is taking place. The number of 4He atoms of the nanodroplet (NHe) and the mean energy per helium atom (eHe ≡ EHe/NHe, where EHe strictly corresponds to the helium energy in the nanodroplet, i.e., without including the I2–helium interaction energy) follow very closely the cascade pattern described above for the vibrational relaxation (Fig. 3 and 4, respectively). This is in agreement with the high efficiency of superfluid liquid helium in releasing the excess energy, which in this case arises from the vibrational de-excitation. This fact is probably more evident in Fig. 4, where it can be seen that, for a given vibrational transition, the excitation generated to the liquid is rapidly released by the evaporation of a single helium atom (0.95 atoms really, since the DFT method is used to describe helium) long before the next transition takes place.
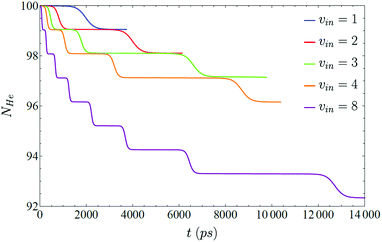 | ||
| Fig. 3 Number of 4He atoms of the nanodroplet for five different initial excitations (ν = 1, 2, 3, 4 and 8), as a function of time. | ||
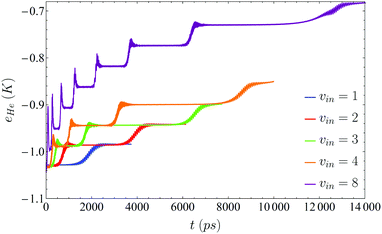 | ||
| Fig. 4 Energy per 4He atom of the nanodroplet for five different initial excitations (ν = 1, 2, 3, 4 and 8), as a function of time. | ||
As a result of each transition, the vibrational energy of I2 diminishes according to the associated vibrational energy gap, whose value is in the 287.52–305.98 K energy range (energy gaps of the 8 → 7 and 1 → 0 transitions, respectively). This energy is removed from the nanodroplet very efficiently by evaporation of a single 4He atom, that leaves the droplet carrying with it an important amount of energy. For all the initial ν levels investigated, once the ν = 0 level has been reached in the relaxation process, the eHe value of the nanodroplet is only very slightly above (∼10−2 K) the corresponding ground state value. In addition, the increase in the value of eHe as the vibrational relaxation progresses arises from the change in the number of atoms of the nanodroplet (ΔeHe ∼ 4 × 10−2 K/4He atom and ΔEHe ∼ 4.4 K for each 4He atom evaporation).
Even though we have seen in the calculations that the superfluid liquid helium very efficiently releases the excess energy after each vibrational de-excitation step of the molecule (as expected for a superfluid), the single helium atom evaporated in each step contrasts with the number of evaporated atoms estimated from the ratio between the energy to be removed from the HeND and the binding energy of a helium atom in the nanodroplet (ratio ≈ 296.7 K (average value)/7.2 K = 41.2), i.e., assuming that the evaporated atoms have a negligible translational kinetic energy. A related discrepancy has been reported by us in a recent theoretical study (using the same approach as here, i.e., a DFT treatment for superfluid helium and a standard quantum treatment of the diatomic relative motion) on a very different problem:20 the Ne + Ne@4HeN → Ne2(ν = 0)@4HeN′ + (N–N′)4He van der Waals reaction, where the number of evaporated atoms obtained is too low, with the exception of what happens for the lower initial velocity of the attacking (outer) Ne atom studied in that work (120 m s−1). This difficulty probably arises from the continuous nature of the DFT approach employed to describe the superfluid liquid helium which, in some situations, can lead to some fraction of the liquid leaving the nanodroplet with too much kinetic energy. When transforming the density to atoms this would lead to a smaller number of evaporated atoms.
Nowadays, the study of physico-chemical processes in superfluid liquid helium involving atoms or molecules is only possible using a hybrid approach, where the helium is described employing a phenomenological density functional (cf. Section 2). The Orsay–Trento density functional65 is the best one available and has been employed here and in all or almost all the dynamics studies reported so far on superfluid helium and atomic/molecular species.
The results obtained here on the vibrational relaxation of the I2 molecule in HeND seem reasonable and the numerical technique employed to solve the time dependent Schrödinger-like equations for long time simulations is very efficient. In addition, we must bear in mind that this work corresponds to the starting point for the theoretical study of this type of processes, which are very interesting and about which we still know very little.
To conclude this section, it is worth noting that an exploration on the effect of the nanodroplet size on VER has been made by performing a few auxiliary calculations with doped nanodroplets formed by 500 4He atoms. The results achieved in this case show the same behaviors as those observed for I2(X,ν = 0)@4He100, but with slightly faster de-excitations. This is an expected result, as in the bigger nanodroplets the molecule is at least a little more solvated and, therefore, there is a somewhat stronger I2-helium interaction.
4. Discussion
The main goal of this section is to provide a simple and physically meaningful model of the vibrational relaxation process investigated in this paper. To do this we have taken into account both the results presented in the former section and some reasonable physical assumptions. The VER has been described by means of a two-state system to account for the molecular oscillator (I2), and the effect of the bath (liquid helium) has been included in an effective way, through a suitable Hamiltonian operator governing its dynamics.From the time evolution of the populations (Fig. 2) it is clear that a maximum of two vibrational levels are involved at the same time (|ν〉 and |ν − 1〉), and this happens when an arbitrary vibrational transition (ν → ν − 1, ν − 1 → ν − 2,…, or ν = 1 → ν = 0) is taking place. Hence, it seems reasonable to describe the VER process studied here adopting as a model a two-level system.
This fact results from the magnitude (absolute value) of the 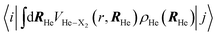 coupling matrix elements. They are of the order of the Kelvin for |i − j| = 1, of ∼10−1 K for |i − j| = 2, of ∼10−2 for |i − j| = 3, and negligible for higher |i − j| values. That is to say, significant couplings only occur for two consecutive vibrational levels, which supports the modelling of the oscillator as a two-level system. Moreover, it should be noted that the coupling matrix elements are larger (absolute value) for the higher vibrational levels, which correlates with the somewhat stronger interaction of these levels with the environment. The coupling matrix elements are always fluctuating and the amplitude of the fluctuations is remarkably increased when the vibrational transition takes place.
coupling matrix elements. They are of the order of the Kelvin for |i − j| = 1, of ∼10−1 K for |i − j| = 2, of ∼10−2 for |i − j| = 3, and negligible for higher |i − j| values. That is to say, significant couplings only occur for two consecutive vibrational levels, which supports the modelling of the oscillator as a two-level system. Moreover, it should be noted that the coupling matrix elements are larger (absolute value) for the higher vibrational levels, which correlates with the somewhat stronger interaction of these levels with the environment. The coupling matrix elements are always fluctuating and the amplitude of the fluctuations is remarkably increased when the vibrational transition takes place.
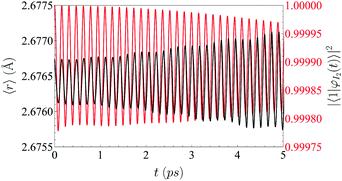
Two main contributions to the VER process can be distinguished depending on their physical origin: the static and dynamic couplings. The main contribution comes from the former, which is related to the solvation of the molecule by the liquid (the environment). This breaks down the stationary character of the ν-states of the isolated molecule and leads to very small oscillations of the probability of each |ν〉. This is manifested in the oscillation of the probability density of the vibrational wave function of the molecule (Fig. 5). In a two-level system this behavior is analogous to what happens for a spin under the influence of a static magnetic field in a particular direction (precession at the Larmor's frequency).
On the other hand, the dynamical change of the vibrational wave function of the I2 molecule slightly perturbs the liquid that is placed close to the molecule; i.e., there is also a breakdown of its stationary character. The small fraction of helium that fluctuates generates the dynamic part of the coupling. All in all, when iodine is in a given vibrational state, fluctuations of both its wave function and the liquid close to it take place. Besides, as these fluctuations are coupled they will tend to oscillate in phase. Effective energy exchange is not produced until the fluctuations are in phase (this situation is analogous to that of a spin under a dynamic magnetic field, when the transition only takes place when the frequency of the laser is the resonant one for the system). This corresponds to a situation when only a single vibrational level has an important contribution to the I2 vibrational wave function. Therefore, the faster the fluctuations become in phase the lower the lifetime of the vibrational level. At this point, we have assumed that in the end it is the liquid helium which adapts to the vibration of I2, because of the large difference in masses implied.
In the following, we will focus on the dissipative process, i.e., on the VER process. This has been modeled by means of a two-state system with a Hamiltonian operator that contains the key contribution of the environment. The two vibrational levels are separated by ΔE > 0 (zero energy at the lowest energy level) and the coupling between them arises from the two contributions described above. Thus, we can split and model the full Hamiltonian operator H into static, H0, and dynamic, Hnl (non linear), contributions. To force the dynamical coupling to have the frequency of the I2 oscillation, we have taken it as proportional to the expected value of the oscillator coordinate (ξ ≡ r − re), i.e., proportional to 〈ξ〉. This would somehow represent the average oscillation experienced by the liquid, and also oscillates with the same frequency of the probability (population) |ci(t)|2 of the wave function (Fig. 5). With these considerations, the most general Hamiltonian operator in matrix form for the two-state system model reads:
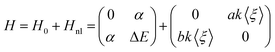 | (10) |
Now, we are in the position of calculating the time evolution of the expectation value of H0 and characterize the complex number a in order to have a dissipative system.
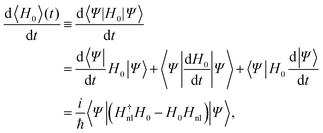 | (11) |
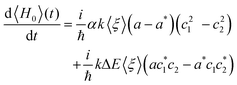 | (12) |
Furthermore, the expression of 〈ξ〉 for a two-state system is equal to
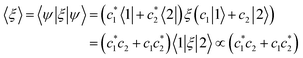 | (13) |
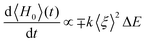 | (14) |
Now, from the Schrödinger equation with the Hamiltonian model, eqn (10), and using the polar form of the coefficients, 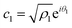 and
and 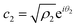 , the time evolution of the probability of the state |1〉 (the state of lower energy) is given by:
, the time evolution of the probability of the state |1〉 (the state of lower energy) is given by:
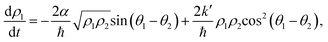 | (15) |
At this point, we can see that the oscillating terms sin(θ1 − θ2) and cos2(θ1 − θ2) have a larger frequency than the time-scale for the state transition and, therefore, we can approximate them by their temporal average. Thus, the first term is null while the cosine squared averages 1/2 and it follows that the dynamic evolution of the population of state |1〉 is described by:
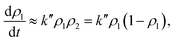 | (16) |
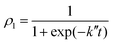 | (17) |
To check the validity of this model we just need to generalize this function with a temporal shift, as transitions do not occur for t = 0 (i.e., t − t0 has been used in eqn (17)). This is related to the time needed for the liquid helium to oscillate in phase with the iodine. In Fig. 6 is shown the vibrational transition 1 → 0 and its fit to eqn (17). A very good agreement is found, which supports the physical picture of the VER process proposed in this section (although the very small oscillations which are present in the time evolution of the populations are not reproduced by the simple model considered).
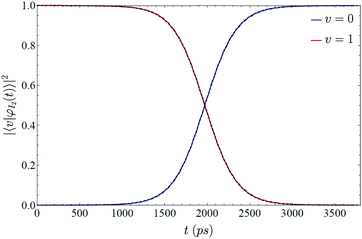 | ||
| Fig. 6 Comparison between the time evolution of the populations of ν = 1 and 0 obtained from the relaxation dynamics (red and blue lines, respectively) and the curves (dashed lines) obtained from the fitting of the populations of ν = 1 to eqn (17). | ||
To conclude, we can now interpret the little shorter lifetimes for the N = 500 nanodroplets taking into account the fact that higher solvation leads to higher static couplings, and hence greater amplitude of the oscillations and so a lesser time is needed for the liquid to oscillate in phase.
5. Summary and conclusions
We have investigated theoretically the vibrational energy relaxation process of a homonuclear diatomic molecule embedded in a 4He superfluid nanodroplet (T = 0.37 K), adapting in a suitable way a hybrid theoretical approach recently proposed by us for the study of the photodissociation dynamics of a X2 molecule in HeND. The time evolution of helium and X2 has been described using the TDDFT and time dependent wave function quantum dynamics methods, respectively. The study of this slow relaxation process, which takes place in the nanosecond time scale, has been possible thanks to the different strategy followed here to solve the time dependent Schrödinger-like equations for helium and X2: the X2 vibrational wave function in HeND has been expressed in terms of the vibrational stationary states of the X2 free molecule, and appropriate diagonalizations of the X2 (vibrational) Hamiltonian operator in HeND have been made along the propagation.In the initial application of this approach we have considered the I2(X) molecule, due to its importance in the vibrational relaxation framework and, to the best of our knowledge, this is the first theoretical contribution on the VER of molecules embedded in 4He superfluid nanodroplets. In the simulations we have considered that the vibrational excitation of I2 from ν = 0 to a given ν state (ν = 1, 2, 3, 4, 5, 6 and 8) takes place suddenly (t = 0). Vibrational de-excitations of the I2 molecule in HeND occur in a cascade fashion involving transitions between two consecutive vibrational levels (ν → ν − 1; ν − 1 → ν − 2; …; 2 → 1; 1 → 0), in such a way that the relaxation ν − 1 → ν − 2 only occurs after the previous relaxation has been completed, and so on. The complete de-excitation from ν up to the ground state (ν = 0) takes place at the nanosecond scale (≈2 and 14 ns for the initial ν = 1 and 8 levels, respectively). Besides, for the ν, ν − 1, ν − 2,… vibrational levels the lifetime decreases as the vibrational quantum number increases, and for a given vibrational level the lifetime increases with the initial (t = 0) vibrational excitation.
The information available on the VER of molecules in HeND is very limited and vibrational lifetimes not far from those determined here for I2 have been estimated experimentally for the Na3(24E′) trimer. This can be interpreted to some extent taking into account the qualitatively comparable 0 → 1 vibrational energy separation of both molecules. The lifetime of ν = 1 (0 → 1) determined here is also similar to the theoretical values reported on I2 employing a very different solvent (liquid Xe at T = 303 K and density of 3.0 g cm−3). The comparisons suggest that the present results are reasonable. In addition and different from what happens for I2(X) in HeND, metastability has not been reported neither for Na3(24E′) (ν = 1) on HeND nor for I2(X) (ν = 1) in liquid Xe.
Furthermore, the cascade mechanism has been understood on the basis of the values of the coupling matrix elements 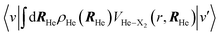 for |ν − ν′| = 1, |ν − ν′| = 2, and |ν − ν′| = 3, and the time evolution of the populations of two consecutive vibrational levels has been satisfactorily described using a non-linear two-state Hamiltonian model for the X2 molecule in HeND.
for |ν − ν′| = 1, |ν − ν′| = 2, and |ν − ν′| = 3, and the time evolution of the populations of two consecutive vibrational levels has been satisfactorily described using a non-linear two-state Hamiltonian model for the X2 molecule in HeND.
Regarding the behavior of the nanodroplet, we have seen theoretically that superfluid liquid helium very efficiently releases the excess of energy following each vibrational de-excitation step of the I2 molecule, as expected; but the number of helium atoms evaporated is small in comparison to the expected values.
In the future it would be also interesting to investigate the rotational energy relaxation of molecules in superfluid helium nanodroplets. This study could be carried out extending the hybrid theoretical approach employed here and, among the different questions to answer, it would be of interest to analyze the influence of molecular rotation on the metastability (lifetime) of the vibrational levels and the cascade mechanism. Finally, we hope that this initial theoretical contribution on the dynamics of molecular VER in superfluid helium nanodroplets will encourage both theoreticians and experimentalists to investigate this important process about which our knowledge is very limited.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work has been supported by the Spanish Ministry of Science and Innovation (project ref. CTQ2011-27857-C02-01) and by the University of Barcelona (Theoretical Chemistry Institute (IQTC) and the Faculty of Chemistry). We also want to acknowledge support from the Autonomous Government of Catalonia (projects refs. 2014SGR 25 and XRQTC). Thanks are also given to Dr Rita Prosmiti (Instituto de Física Fundamental, CSIC (Madrid)) for making available the I2–He intermolecular potential energy code and to two anonymous referees for their valuable comments.References
-
R. D. Levine, Molecular reaction dynamics, Cambridge University Press, Cambridge, 2005 Search PubMed
.
- D. W. Oxtoby, Vibrational population relaxation in liquids, Adv. Chem. Phys., 1981, 47, 487–519 CrossRef CAS
.
- D. W. Oxtoby, Vibrational relaxation in liquids: quantum states in a classical bath, J. Phys. Chem., 1983, 87, 3028–3033 CrossRef CAS
.
- Q. Shi and E. Geva, Semiclassical theory of vibrational energy relaxation in the condensed phase, J. Phys. Chem. A, 2003, 207, 9059–9069 CrossRef
.
-
A. Nitzan, Chemical dynamics in condensed phases, Oxford University Press, Oxford, 2006 Search PubMed
.
-
B. Bagchi, Molecular relaxation in liquids, Oxford University Press, Oxford, 2012 Search PubMed
.
- J. C. Owrutsky, D. Raftery and R. M. Hochstrasser, Vibrational relaxation dynamics in solutions, Annu. Rev. Phys. Chem., 1994, 45, 519–555 CrossRef CAS PubMed
.
-
Ultrashort laser pulses. Generation and applications, ed. W. Kaiser, Springer, Berlin, 1993 Search PubMed
.
-
S. Mukamel, Principles of nonlinear optical spectroscopy, Oxford University Press, New York, 1999 Search PubMed
.
- A. Tokmakoff, Time-dependent quantum mechanics and spectroscopy, http://https://tdqms.uchicago.edu/page/tdqms-notes accessed January 2017.
- J. S. Bader and B. J. Berne, Quantum and classical relaxation rates from classical simulations, J. Chem. Phys., 1994, 100, 8359–8366 CrossRef CAS
.
- J. P. Toennies and A. F. Vilesov, Superfluid helium droplets: a uniquely cold nanomatrix for molecules and molecular complexes, Angew. Chem., Int. Ed., 2004, 43, 2622–2648 CrossRef CAS PubMed
.
- M. Y. Choi, G. E. Douberly, T. M. Falconer, W. K. Lewis, C. M. Lindslay, J. M. Merritt, P. L. Stiles and R. E. Miller, Infrared spectroscopy of helium nanodroplets: novel methods for physics and chemistry, Int. Rev. Phys. Chem., 2006, 25, 15–75 CrossRef CAS
.
-
A. Slenczka and J. P. Toennies, in Low Temperature and Cold Molecules, ed. I. W. M. Smith, Imperial College Press, London, 2008, pp. 345–392 and references cited therein Search PubMed
.
- S. Yang and A. M. Ellis, Helium droplets: a chemistry perspective, Chem. Soc. Rev., 2013, 42, 472–484 RSC
.
- A. Vilà, M. González and R. Mayol, Photodissociation dynamics of homonuclear diatomic molecules in helium nanodroplets. The case of Cl2@(4He)N, J. Chem. Theory Comput., 2015, 11, 899–906 CrossRef PubMed
.
- A. Vilà, M. González and R. Mayol, Quantum interferences in the photodissociation of Cl2(B) in superfluid helium nanodroplets (4He)N, Phys. Chem. Chem. Phys., 2015, 17, 32241–32250 RSC
.
- A. Vilà and M. González, Mass effects in the photodissociation of homonuclear diatomic molecules in helium nanodroplets: inelastic collision and viscous flow energy exchange regimes, Phys. Chem. Chem. Phys., 2016, 18, 27630–27638 RSC
.
- A. Vilà, M. González and R. Mayol, Quantum dynamics of the pick up process of atoms by superfluid helium nanodroplets: the Ne + (4He)1000 system, Phys. Chem. Chem. Phys., 2016, 18, 2006–2014 RSC
.
- A. Vilà and M. González, Reaction dynamics inside superfluid helium nanodroplets: the formation of the Ne2 molecule from Ne + Ne@(4He)N, Phys. Chem. Chem. Phys., 2016, 18, 31869–31880 RSC
.
- A. Vilà, M. González and R. Mayol, Relaxation dynamics of helium nanodroplets after photodissociation of a dopant homonuclear diatomic molecule. The case of Cl2@(4He)N, Phys. Chem. Chem. Phys., 2016, 18, 2409–2416 RSC
.
- J. Tiggesbäumker and F. Stienkemeier, Formation and properties of metal clusters isolated in helium droplets, Phys. Chem. Chem. Phys., 2007, 9, 4748–4770 RSC
.
- S. Yang, A. M. Ellis, D. Spence, C. Feng, A. Boatwright, E. Latimer and C. Binns, Growing metal nanoparticles in superfluid helium, Nanoscale, 2013, 5, 11545–11553 RSC
.
- L. F. Gomez, E. Loginov and A. F. Vilesov, Traces of vortices in superfluid helium droplets, Phys. Rev. Lett., 2012, 108, 155302 CrossRef PubMed
.
- E. Latimer, D. Spence, C. Feng, A. Boatwright, A. M. Ellis and S. Yang, Preparation of ultrathin nanowires using superfluid helium droplets, Nano Lett., 2014, 14, 2902–2906 CrossRef CAS PubMed
.
- R. Zadoyan, J. Almy and V. A. Apkarian, Lattice dynamics from the ‘eyes’ of the chromophore. Real-time studies of I2 isolated in rare gas matrices, Faraday Discuss., 1997, 108, 255–269 RSC
.
- J. Almy, K. Kizer, R. Zadoyan and V. A. Apkarian, Resonant Raman, hot, and cold luminiscence of iodine in rare gas matrices, J. Phys. Chem. A, 2000, 104, 3508–3520 CrossRef CAS
.
- M. Karavitis, R. Zadoyan and V. A. Apkarian, Time resolved coherent anti-Stokes Raman scattering of I2 isolated in matrix argon: vibrational dynamics on the electronic ground state, J. Chem. Phys., 2001, 114, 4131–4140 CrossRef CAS
.
- Z. Bihary, M. Karavitis and V. A. Apkarian, Onset of decoherence: six-wave mixing measurements of vibrational decoherence on the excited electronic state of I2 in solid argon, J. Chem. Phys., 2004, 120, 8144–8156 CrossRef CAS PubMed
.
- M. Karavitis, T. Kumada, I. U. Goldschleger and V. A. Apkarian, Vibrational dissipation and dephasing of I2(ν = 1–19) in solid Kr, Phys. Chem. Chem. Phys., 2005, 7, 791–796 RSC
.
- T. Kiviniemi, J. Aumanen, P. Myllyperkiö, V. A. Apkarian and M. Petterson, Time-resolved coherent anti-Stokes Raman-scattering measurements of I2 in solid Kr: vibrational dephasing on the ground electronic state at 2.6–32 K, J. Chem. Phys., 2005, 123, 064509 CrossRef PubMed
.
- M. Gruebele and A. H. Zewail, Femtosecond wave packet spectroscopy: coherences, the potential, and structural determination, J. Chem. Phys., 1993, 98, 883–902 CrossRef CAS
.
- Q. Liu, C. Wan and A. H. Zewail, Solvation ultrafast dynamics of reactions 13. Theoretical and experimental studies of wave packet reaction coherence and its density dependence, J. Phys. Chem. A, 1996, 100, 18666–18682 CrossRef CAS
.
- J.-K. Wang, Q. Liu and A. H. Zewail, Solvation ultrafast dynamics of reactions 9. Femtosecond studies of dissociation and recombination of iodine in argon clusters, J. Chem. Phys., 1995, 99, 11309–11320 CrossRef CAS
.
-
K. P. Huber and G. Herzberg, Molecular spectra and molecular structure IV. Constants of diatomic molecules, Van Nostrand Reinhold Co., New York, 1979 Search PubMed
.
-
D. W. Schwenke and D. G. Truhlar, The effect of Wigner singularities on low-temperature vibrational relaxation rates, J. Chem. Phys., 1985, 83, 3454–3461 Search PubMed
.
- Z. Ma, S. D. Jons, C. F. Giese and W. R. Gentry, Crossed beam studies of state-to-state vibrational energy transfer from the ν = 5 excited state of I2(X1Σg+) prepared by stimulated emission pumping, J. Chem. Phys., 1991, 94, 8608–8610 CrossRef CAS
.
- M. L. Nowlin and M. C. Heaven, Energy transfer rate constants for highly excited rovibrational levels of I2(X), J. Chem. Phys., 1993, 99, 5654–5660 CrossRef CAS
.
- H. J. Liu, S. H. Pullen, L. A. Walker II and R. J. Sension, The vibrational relaxation of I2(X1Σg+) in mesitylene, J. Chem. Phys., 1998, 108, 4992–5001 CrossRef CAS
.
- S. Li and W. H. Thomson, Simulations of the vibrational relaxation of I2 in Xe, J. Phys. Chem. A, 2003, 107, 8696–8704 CrossRef CAS
.
- S. Li and W. H. Thomson, Molecular dynamics simulations of the vibrational relaxation of I2 in Xe on an ab initio-based potential function, Chem. Phys. Lett., 2004, 383, 326–331 CrossRef CAS
.
- S. A. Egorov and J. L. Skinner, A theory of vibrational relaxation in liquids, J. Chem. Phys., 1996, 105, 7047–7058 CrossRef CAS
.
- D. W. Miller and S. A. Adelman, Time correlation function approach to liquid phase vibrational energy relaxation: dihalogen solutes in rare gas solvents, J. Chem. Phys., 2002, 117, 2672–2687 CrossRef CAS
.
- S. A. Adelman, R. Muralidhar and R. H. Stote, Time correlation function approach to vibrational energy relaxation in liquids: revised results for monatomic solvents and a comparison with the isolated binary collision model, J. Chem. Phys., 1991, 95, 2738–2751 CrossRef CAS
.
- J. K. Brown, C. B. Harris and J. C. Tully, Studies of chemical reactivity in the condensed phase IV. Density dependent molecular dynamics simulations of vibrational relaxation in simple liquids, J. Chem. Phys., 1988, 89, 6687–6696 CrossRef CAS
.
- D. J. Nesbitt and J. T. Hynes, Vibrational energy transfer from highly excited anharmonic oscillators. Dependence on quantum state and interaction potential, J. Chem. Phys., 1982, 76, 6002–6014 CrossRef CAS
.
- R. H. Stote and S. A. Adelman, Theory of vibrational energy relaxation in liquids: diatomic solutes in monatomic solvents, J. Chem. Phys., 1988, 88, 4415–4420 CrossRef CAS
.
- R. E. Larsen and R. M. Stratt, Instantaneous pair theory for high-frequency vibrational energy relaxation in fluids, J. Chem. Phys., 1999, 110, 1036–1052 CrossRef CAS
.
- A. Bastida, C. Cruz, J. Zúñiga, A. Requena and B. Miguel, Surface hopping simulation of the vibrational relaxation of I2 in liquid xenon using the collective probabilities algorithm, J. Chem. Phys., 2004, 121, 10611–10622 CrossRef CAS PubMed
.
- M. E. Paige, D. J. Russell and C. B. Harris, Studies of chemical reactivity in the condensed phase II. Vibrational relaxation of iodine in liquid xenon following geminate recombination, J. Chem. Phys., 1986, 85, 3699–3700 CrossRef CAS
.
- M. E. Paige and C. B. Harris, Ultrafast studies of chemical reactions in liquids: validity of gas phase vibrational relaxation models and density dependence of bound electronic state lifetimes, Chem. Phys., 1990, 149, 37–62 CrossRef CAS
.
- K. Nauta and R. E. Miller, Solvent mediated vibrational relaxation: superfluid helium droplet spectroscopy of HCN dimer, J. Chem. Phys., 1999, 111, 3426–3433 CrossRef CAS
.
- S. Grebenev, M. Havenith, F. Madeja, J. P. Toennies and A. F. Vilesov, Microwave-infrared double resonance spectroscopy of an OCS molecule inside a 4He droplet, J. Chem. Phys., 2000, 113, 9060–9066 CrossRef CAS
.
- K. Nauta and R. E. Miller, Metastable vibrationally excited HF (ν = 1) in helium nanodroplets, J. Chem. Phys., 2000, 113, 9466–9469 CrossRef CAS
.
- K. Nauta and R. E. Miller, Vibrational relaxation of Ne, Ar, Kr-HF (ν = 1) binary complexes in helium nanodroplets, J. Chem. Phys., 2001, 115, 4508–4514 CrossRef CAS
.
- B. Grüner, M. Schlesinger, P. Heister, W. T. Strunz, F. Stienkemeier and M. Mudrich, Vibrational relaxation and dephasing of Rb2 attached to helium nanodroplets, Phys. Chem. Chem. Phys., 2011, 13, 6816–6826 RSC
.
- P. Claas, G. Droppelmann, C. P. Schulz, M. Mudrich and F. Stienkemeier, Wave packet dynamics in triplet sates of Na2 attached to helium nanodroplets, J. Phys. Chem. A, 2007, 111, 7537–7541 CrossRef CAS PubMed
.
- M. Schlesinger, M. Mudrich, F. Stienkemeier and W. T. Strunz, Dissipative vibrational wave packet dynamics of alkali dimers attached to helium nanodroplets, Chem. Phys. Lett., 2010, 490, 245–248 CrossRef CAS
.
- J. H. Reho, J. Higgins, M. Nooijen, K. K. Lehmann, G. Scoles and M. Gutowski, Photoinduced nonadiabatic dynamics in quartet Na3 and K3 formed using helium nanodroplet isolation, J. Chem. Phys., 2001, 115, 10265–10274 CrossRef CAS
.
- B. Shepperson, A. A. Søndergaard, L. Christiansen, J. Kaczmarczyk, R. E. Zillich, M. Lemeshko and H. Stapelfeldt, Laser-induced rotation of iodine molecules in helium nanodroplets: revivals and breaking free, Phys. Rev. Lett., 2017, 118, 203203 CrossRef PubMed
.
- D. Mateo, A. Hernando, M. Barranco, E. Loginov, M. Drabbels and M. Pi, Translational dynamics of photoexcited atoms in 4He nanodroplets: the case of silver, Phys. Chem. Chem. Phys., 2013, 15, 18388–18400 RSC
.
- N. B. Brauer, S. Smolarek, E. Loginov, D. Mateo, A. Hernando, M. Pi, M. Barranco, W. J. Bruma and M. Drabbels, Critical Landau velocity in helium nanodroplets, Phys. Rev. Lett., 2013, 111, 153002 CrossRef PubMed
.
- A. Leal, D. Mateo, A. Hernando, M. Pi and M. Barranco, Capture of heliophobic atoms by 4He nanodroplets: the case of cesium, Phys. Chem. Chem. Phys., 2014, 16, 23206–23213 RSC
.
- D. Mateo, F. Gonzalez and J. Eloranta, Rotational superfluidity in small helium droplets, J. Phys. Chem. A, 2015, 119, 2262–2270 CrossRef CAS PubMed
.
- F. Dalfovo, A. Lastri, L. Pricaupenko, S. Stringari and J. Treiner, Structural and dynamical properties of superfluid helium: a density-functional approach, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 1193–1209 CrossRef CAS
.
- F. Ancilotto, M. Barranco, F. Caupin, R. Mayol and M. Pi, Freezing of 4He and its liquid-solid interface from density functional theory, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 214522 CrossRef
.
- L. Delgado-Tellez, A. Valdés, R. Prosmiti, P. Villarreal and G. Delgado-Barrio, HeI2 interaction potential based on an interpolation scheme, Int. J. Quantum Chem., 2012, 112, 2971–2975 CrossRef CAS
.
- R. J. Leroy, RKR1: a computer program implementing the first-order RKR method for determining diatomic molecule potential energy functions, J. Quant. Spectrosc. Radiat. Transfer, 2017, 186, 158–166 CrossRef CAS
.
- M. Frigo and S. G. Johnson, The design and implementation of FFTW3, IEE Proceedings, 2005, 93, 216–231 CrossRef
.
-
A. Ralston, in Mathematical Methods for Digital Computers, ed. A. Ralston and H. S. Wilf, John Wiley & Sons, New York, 1960, vol. 1, pp. 95–109 Search PubMed
.
- R. J. Thompson, Improving round-off in Runge-Kutta computations with Gill's method, Commun. ACM, 1970, 13, 739–740 CrossRef
.
- A. Vibók and G. G. Balint-Kurti, Parametrization of complex absorbing potentials for time-dependent quantum dynamics, J. Phys. Chem., 1992, 96, 8712–8719 CrossRef
.
- For the initial excitation to ν = 8 a small contributions of a third level can be observed during the relaxation of the highest vibrational levels, i.e., for ν = 8 → ν = 7 and ν = 7 → ν = 6.
Footnotes |
| † Electronic supplementary information (ESI) available: Fig. S1. Vibrational populations for the initial excitation v = 8 as a function of time; Fig. S2. Vibrational populations for the initial excitation v = 8 as a function of time, considering only the v = 4–8 levels. See DOI: 10.1039/c7cp05694j |
| ‡ Present address: Department of Physics and Astronomy, University College London, Gower Street, London WC1E 6BT, UK. |
| This journal is © the Owner Societies 2018 |